On the effectiveness of the new estimators obtained from the Bayes estimator

1.   Introduction

Estimation of the mean parameters in random variables is a significant problem that has garnered considerable attention from researchers in various fields, including statistics, economics, and social sciences. Accurately estimating these parameters is crucial for effective decision-making and inference in many applications, particularly when dealing with multivariate normal distributions (MNDs). The complexity of these distributions requires advanced estimation techniques that can yield reliable results, even in challenging scenarios. The motivations for this work stem from the limitations of traditional estimation methods, particularly the maximum likelihood estimator (MLE). While the MLE is widely used due to its desirable properties under certain conditions, it can fall short in high-dimensional settings or when the sample size is small. This has led to a growing interest in developing shrinkage estimators, which can improve upon the MLE by reducing variance and enhancing the overall estimation accuracy. Researchers have sought to create shrinkage estimators that not only outperform the MLE but also exhibit lower risks, making them more robust in practice.

Numerous studies have contributed to the understanding of shrinkage estimators. Early foundational work by Stein ^[11], followed by contributions from James and Stein ^[6] and Yang and Berger ^[12], laid the groundwork for exploring the minimax properties of these estimators. Their research established that shrinkage can lead to improved performance in terms of mean squared error compared with traditional estimation methods.

A comprehensive bibliographic review reveals further advancements in the field. For instance, Khan and Saleh ^[3] investigated the estimation problem of the mean in univariate normal distributions with unknown variance, incorporating uncertain non-sample prior information. This work highlights the potential benefits of utilizing prior knowledge in parameter estimation. Similarly, Singh ^[8] addressed the challenges of estimating variances and means in k-variate normal distributions when samples are subject to truncation or censoring on both sides for s variables (s<k). Both studies primarily employed the quadratic loss function to compute risk functions, emphasizing the need for more nuanced approaches.

In more recent developments, Hamdaoui et al. ^[5] demonstrated the minimaxity of specific shrinkage estimators for the mean of an MNDs, focusing particularly on the risk ratios of the James-Stein estimator (JSE) and its positive-part version compared with the MLE under the balanced loss function (BLF). Their findings underscore the importance of using alternative loss functions to capture the performance of estimators more accurately.

Benkhaled and Hamdaoui ^[1] further advanced this discussion by examining estimators that approximate the mean of the multivariate normal distribution, particularly when the variance is unknown. They proposed two categories of shrinkage estimators, with the first category focusing on the minimax properties of these estimators and identifying the optimal estimator, known as the JSE. Their second category included an estimator that exceeded the performance of the JSE, assessed through risk functions calculated using the BLF.

Gomez-Deniz ^[10] investigated the application of the BLF in actuarial statistics, particularly within the framework of credibility theory. His work highlights the advantages of the BLF in Bayesian estimation, demonstrating its ability to balance accuracy and robustness. While his research primarily focused on actuarial applications, the underlying principles of the BLF are widely applicable in statistical estimation. Our study extends the application of the BLF to Bayesian estimation of the mean in the MNDs. Unlike Gomez-Deniz's actuarial focus, we explore how the BLF can enhance the estimation accuracy in multivariate settings, particularly when prior information is available. The novelty of this manuscript lies in its emphasis on the balanced loss function and the integration of prior information within a Bayesian framework, which can significantly enhance the estimation accuracy and robustness. By leveraging the strengths of both Bayesian and shrinkage approaches, we aim to provide a comprehensive solution to the estimation of mean parameters in MNDs. This shift not only broadens the applicability of the BLF but also enables more refined risk assessments by moving beyond the commonly used quadratic loss function.

The structure of the paper is as follows: Section 2 presents the preliminary results and theoretical foundations that will be utilized throughout the study. In Section 3, we detail our primary findings and the performance of the proposed estimators. Section 4 focuses on a simulation study conducted to validate our results and assesses the practical implications of our findings. Section 4 presents an application of the estimators on a real-world problem. Finally, we conclude the paper with a discussion of our results and suggestions for future research directions.

2.   Preliminaries

This manuscript addresses the estimation of an unknown parameter $\mu$ within the framework of the model $Z\vert\mu \sim \mathcal{N}{q}\left(\mu, \sigma^{2}I{q}\right)$. The prior distribution for $\mu$ is assumed to be $\mu \sim \mathcal{N}{q}\left(\eta, \rho^{2}I{q}\right)$, where the value of $\sigma^{2}$ is unknown and is estimated using the statistic $S^{2}\sim \sigma^{2}\chi_{n}^{2}$. The hyperparameters $\eta$ and $\rho^{2}$ may be known or unknown.

To evaluate the performance of the introduced estimators, we employ the BLF, which can be defined as follows: The following holds for all estimators $\Lambda$ of the parameter $\mu$

where $\Lambda_{0}$ represents the target estimator of $\mu$, $\omega$ corresponds to the weight assigned to the nearness value of $\Lambda$ to $\Lambda_{0}$, and $1-\omega$ represents the weighting factor attributed to the accuracy of the estimation component.

We will denote the risk function of the estimator $\Lambda$ under loss (2.1) as

and the Bayesian risk as

The MLE of $\mu$ is commonly known to be $Z: = \Lambda_{0}$. The risk function of the MLE with respect to the loss function (2.1) is equal to $\mathcal{R}_{\omega}(Z, \mu) = (1-\omega)q\sigma^{2}$. Furthermore, the MLE is both minimax and inadmissible when $q\geq3$. Hence, any estimator that improves upon it is also minimax.

Under the model defined above, we recall some known results of the Bayes estimator. From Lindley and Smith ^[7], we assume that the posterior is considered to be Gaussian

Thus, the Bayes estimator of $\mu$ is

In order to compute the expectation functions of a variable following a non central chi-square distribution, we recall the following definition:

Definition 2.1. Let us assume $U \sim \chi_{q}^{2}\left(\lambda \right)$, representing a non central chi-square distribution with $q$ degrees of freedom and a non centrality parameter $\lambda$. The probability density function of $U$ is expressed as follows:

The expression on the right-hand side of this equation corresponds to the formula

In light of this definition, we can infer that if $U \sim \chi_{q}^{2}\left(\lambda \right)$, where $\chi_{q+2k}^{2}$ denotes the density of the central $\chi^{2}$ distribution with $q+2k$ degrees of freedom. Therefore for any integrable function $\phi: \mathbb{R}_{+} \longrightarrow \mathbb{R}$, we have the following relationship:

In this context, where $P\left(\frac{\lambda }{2};dk\right)$ represents the Poisson distribution with the parameter value being equal to $\frac{\lambda }{2}$, and $\chi_{q+2k}^{2}$ denotes the central chi-square distribution with degrees of freedom equal to $q+2k$, we can introduce the subsequent lemma.

Lemma 2.1. Let $U\sim\chi_{q}^{2}(\lambda)$ be a non central chi-square with $q$ degrees of freedom and let $\lambda$ be the non centrality parameter. Then for $0\leq r < \frac{q}{2}$,

where $K$ has a Poisson distribution with the mean $\frac{\lambda}{2}$.

We would like to recall the subsequent lemmas, provided by ^[2,9] and Hamdaoui et al. ^[4], which will be frequently utilized in the subsequent analysis.

Lemma 2.2. Assume that $Y$ is a real random variable following a standard normal distribution $\mathbb{N}\left(0, 1\right)$, and let $g: \mathbb{R} \longrightarrow \mathbb{R}$ be an indefinite integral of a Lebesgue measurable function $g^{\prime}$, which can be considered to be the derivative of $g$. Furthermore, suppose that $\mathbb{E}\left\vert g^{\prime}\left(Y\right) \right\vert < +\infty$. Then the following statement holds true:

Lemma 2.3. For any real function $h$ such that the expectation $\mathbb{E}\left(h\left(\chi_{q}^{2}\left(\lambda \right)\right) \chi_{q}^{2}\left(\lambda \right)\right)$ exists, we can establish the following relationship:

The following lemma shows a lower bound and an upper bound of the expectation of the functions $f_{1}(u) = \frac{1}{u+\alpha}$ (respectively $f_{2}(u) = \frac{1}{(u+\alpha)^{2}}$), where $\alpha$ is a strictly positive real number, relative to the random variable $\chi_{n+2}^{2}$ (respectively, to the $\chi_{n+4}^{2}$ random variable).

Lemma 2.4. Let $V\sim\chi_{n+2}^{2}$ be a central chi-square with $n+2$ degrees of freedom and let $W\sim\chi_{n+4}^{2}$ be a central chi-square with $n+4$ degrees of freedom. For any real $\alpha > 0$, we have

and

3.   The main results

In this section, we introduce novel estimators for the mean parameter $\mu$ based on both the MLE and the Bayes estimator presented in (2.4). We then investigate their minimaxity properties and the asymptotic behavior of their risk ratios relative to the MLE when both the dimensionality of the parameter space $q$ and the sample size $n$ approach infinity. Our main results are presented in two distinct parts. First, we consider the same model as described above, assuming that the hyperparameters $\eta$ and $\rho^{2}$ are known. Second, we examine the same model, but with the hyperparameter $\eta$ being known and the hyperparameter $\rho^{2}$ being unknown.

3.1.   Estimator Type 1

Now, let $Z\vert\mu \sim \mathcal{N}_{q}\left(\mu, \sigma^{2}I_{q}\right)$ and $\mu \sim \mathcal{N}_{q}\left(\eta, \rho^{2}I_{q}\right)$, where the value of $\sigma^{2}$ is unknown and is estimated by the statistic $S^{2}\sim \sigma^{2}\chi_{n}^{2}.$ The hyperparameters $\eta, \rho^{2}$ are known.

Hamdaoui et al. ^[4] showed that the statistic $\frac{S^{2}}{S^{2}+n\ \rho^{2}}\ $ is an asymptotically unbiased estimator of the ratio $\frac{\sigma^{2}}{\rho^{2}+\sigma^{2}}$. If we substitute the ratio $\frac{\sigma^{2}}{\sigma^{2}+\rho^{2}}\ $ in Formula (2.4) with the estimator $\frac{S^{2}}{S^{2}+n\rho^{2}}$, we can introduced a new estimator derived from the Bayes estimator, which can be expressed as

3.1.1.   Minimaxity

Proposition 3.1. Under the BLF $\mathfrak{L}_{\omega}$, the Bayesian risk of the estimator $\Lambda_{DB, \gamma}(Z, S^{2})$ demonstrated in (3.1) is

Proof. By utilizing the risk function linked to the BLF defined in (2.1), we derive the following expression:

By exploiting the independence between two random variables $S^{2}$ and $Z$, we arrive at the following result:

and

Thus,

and

because $\mathbb{E}\left(\frac{Z-\mu}{\sigma} \right) = 0.$

Therefore

Using Lemma 2.3 we get,

and

Therefore,

Thus, the Bayesian risk of the estimator $\Lambda_{DB, \gamma}(Z, S^{2})$ under the BLF $\mathfrak{L}_{\omega}$ is

Theorem 3.2. Assume the estimator $\Lambda_{DB, \gamma}(Z, S^{2})$ as defined in (3.1). If

then under the BLF $\mathfrak{L}_{\omega}$ given in (2.1), the estimator $\Lambda_{DB, \gamma}(Z, S^{2})$ dominates the MLE and thus it is minimax.

Proof. From Proposition 3.1, a sufficient condition for the estimator $\Lambda_{DB, \gamma}(Z, S^{2})$ to dominate the MLE is

which is equivalent to

Using Lemma 2.4, we have the following inequality:

Therefore, we can deduce that if

the inequality (3.3) is satisifed, and thus the estimator $\Lambda_{DB, \gamma}(Z, S^{2})$ has a risk smaller than that of the MLE. This last point indicates that $\Lambda_{DB, \gamma}(Z, S^{2})$ is a minimax estimator.

3.1.2.   Limit of the risk ratio for estimator Type 1

In this section, we investigate the asymptotic behavior of the risk ratio of our estimator $\Lambda_{DB, \gamma}(Z, S^{2})$ in response to the MLE when $0 \leq \gamma \leq \frac{2(1-\omega)n}{n+2}$.

If we take the real constant $\alpha$ ($0 < \alpha \leq 2),$ our aims is to show that for any $\gamma$, such as $\gamma = \frac{\alpha(1-\omega)n}{n+2},$ the risk ratio $\frac{\mathcal{R}_{\omega, b}\left(\Lambda_{DB, \gamma}(Z, S^{2}); \eta, \rho^{2}, \sigma^{2}\right)}{\mathcal{R}_{\omega}\left(Z, \mu \right)}$ tends to a value inferior to one, when $n$ tends to infinity.

Theorem 3.3. Assume the estimator $\Lambda_{DB, \gamma}(Z, S^{2})$ defined in 3.1. If $\gamma = \frac{\alpha(1-\omega)n}{n+2}$ where $0 < \alpha \leq 2,$ then

Proof. From Proposition 3.1, we have

Using Lemma 2.4, we get

and

By passing to the limit, we get

and

Thus,

because $0\leq (2-\alpha)\alpha \leq 1$ and $0 < 1-\omega \leq 1.$

3.1.3.   Algorithm of estimator Type 1

The algorithm of estimator Type 1 can be summarized as follows:

3.2.   Estimator Type 2

Next, we consider the model $Z\vert\mu \sim \mathcal{N}_{q}\left(\mu, \sigma^{2}I_{q}\right)$ and $\mu \sim \mathcal{N}_{q}\left(\eta, \rho^{2}I_{q}\right)$, where the parameter $\sigma^{2}$ is unknown and is also estimated by the statistic $S^{2}\sim \sigma^{2}\chi_{n}^{2}$, and the hyper parameter $\eta$ is known and the hyper parameter $\rho^{2}$ is unknown.

Hamdaoui et al. ^[4] showed that the statistic $\frac{q-2}{n+2}\frac{S^{2}}{\Vert Z-\eta \Vert^{2}}$ is an asymptotically unbiased estimator of the ratio $\frac{\sigma^{2}}{\rho^{2}+\sigma^{2}}$. Therefore, if we substitute the ratio $\frac{\sigma^{2}}{\sigma^{2}+\rho^{2}}\ $ in Formula (2.4) with the estimator $\frac{q-2}{n+2}\frac{S^{2}}{\Vert Z-\eta \Vert^{2}}$, we can consider the new estimator derived from the Bayes estimator, expressed as

where the positive real parameter $\beta$ can depend on $n$ and $q.$

3.2.1.   Minimaxity

Proposition 3.4. The Bayesian risk of the estimator $\Lambda_{DB, \beta}(Z, S^{2})$ given in Eq (3.4), which has been derived from the BLF illustrated in (2.1), can be expressed as

Proof. By utilizing the risk function linked to the BLF $\mathfrak{L}_{\omega}$ defined in (2.1), we derive the following expression:

In the one hand, since the random variables $Z$ and $S^{2}$ are independent, we can have:

As $S^{2}\sim \sigma^{2} \chi_{n}^{2}$, the marginal distribution of $Z$ is $:Z\sim N_{q}\left(\eta, \left(\rho^{2}+\sigma^{2}\right) I_{q}\right)$.By employing Definition 2.1, we get

and

Thus

On the other hand, we have

Let $W = \left(W_{1}, W_{2}, ..., W_{q}\right)^{t} = \frac{Z-\mu }{\sigma}$. It is clear that $W\vert\mu \sim \mathcal{N}_{q}\left(0, I_{q}\right)$, and thus

From Stein's Lemma 2.2, we have

This is in line with Formulas (3.6)–(3.8) and the fact that

and

Theorem 3.5. Relative to the BLF $\mathfrak{L}_{\omega}$ given in (2.1), a sufficient condition for the estimator $\Lambda_{DB, \beta}(Z, S^{2})$ defined in (3.4) to be minimax is

Proof. On the basis of Proposition 3.4, we can readily determine that a sufficient condition for the estimator $\Lambda_{DB, \beta}(Z, S^{2})$ to be minimax is,

which is equivalent to

If we used the convexity of the risk function $\mathcal{R}_{\omega, b}\left(\Lambda_{DB, \beta}(Z, S^{2}); \eta, \rho^{2}, \sigma^{2}\right)$ with respect to $\beta$, it becomes apparent that the optimal value of $\beta$ that minimizes the function is $\widehat{\beta} = \frac{(1-\omega)\left(q-2\right) }{n+2}.$ By substituting the value of $\beta$ with $\widehat{\beta}$ in Eq (3.4), we then derive the best estimator in the class of estimators $\Lambda_{\beta}$, which is defined as

Furthermore, its risk function related to the BLF is given by

We can then deduce that the estimator $\Lambda_{DB, \widehat{\beta}}(Z, S^{2})$ dominates the MLE; thus, it is minimax.

3.2.2.   Limit of the risk ratio for estimator Type 2

In this section, we examine the asymptotic behavior of the risk ratio of the estimator $\Lambda_{DB, \widehat{\beta}}(Z, S^{2})$ relative to the MLE as the parameter $q$ approaches infinity while the parameter $n$ remains fixed, and when both parameters $q$ and $n$ simultaneously tend to infinity. Consequently, we infer that the estimator $\Lambda_{DB, \widehat{\beta}}(Z, S^{2})$ exhibits a stable minimax property even in the scenario where the dimension of the parameter space $q$ tends to infinity while the sample size $n$ remains fixed, as well as when both the dimension of the parameter space $q$ and the sample size $n$ simultaneously tend to infinity.

Theorem 3.6.

Proof. From Formula (3.10), we have

We can then easily deduce that

3.2.3.   Algorithm of estimator Type 2

The algorithm of estimator Type 2 can be summarized as follows:

4.   Simulation

The aim of this simulation was to prove the effectiveness of this study by comparing the estimators $\Lambda_{DB, \widehat{\gamma}}(Z, S^{2})$, $\left(\widehat{\gamma} = \frac{(1-\omega)n}{n+2}\right)$, and $\Lambda _{DB, \widehat{\beta}}(Z, S^{2})$ with the MLE $Z$.

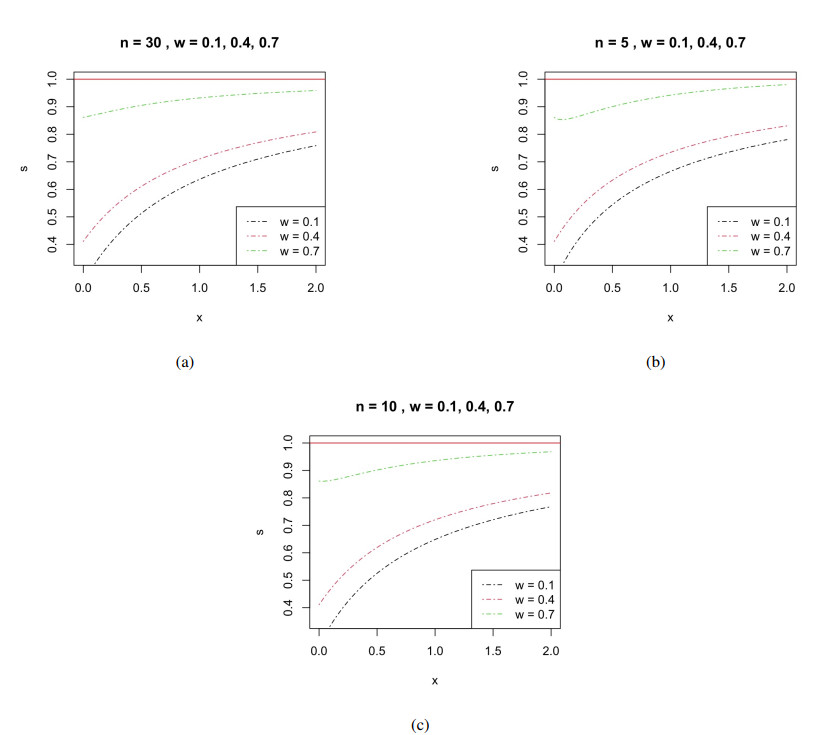
First, we apply the risk ratio of the estimator $\Lambda_{DB, \widehat{\gamma}}(Z, S^{2})$ to the MLE $Z$, $\frac{\mathcal{R}_{\omega} \left(\Lambda_{DB, \widehat{\gamma}}(Z, S^{2}); \eta, \rho^{2}, \sigma^{2}\right)}{\mathcal{R}_{\omega}(Z, \mu)}$ as a function of $\frac{\rho^{2}}{\sigma^{2}}$ for various values of $n$ and $\omega$.

We see that in Figure 1, the risk ratio is less than 1, i.e., the shrinkage estimator $\Lambda_{DB, \widehat{\gamma}}(Z, S^{2})$ dominates the natural estimator $Z$. We also see that if $\omega$ increases, the improvement decreases, and become negligible whenever $\omega$ is near to one. Rasing the value of $n$ gives a small improvement.

The same applies for the estimator $\Lambda _{DB, \widehat{\beta}}(Z, S^{2})$, except that here, the risk ratio depends on $n$, $\omega$, and the dimension of the parameter space $q$. As shown in Figures 2–4 the shrinkage estimator $\Lambda _{DB, \widehat{\beta}}(Z, S^{2})$ is better than the natural estimator $Z$. We also see the same for the estimator $\Lambda _{DB, \widehat{\gamma}}(Z, S^{2})$. Furthermore, we note that the influence of the parameter $q$ on the improvement is the same as that of the parameter $n$.

Secondly, we plot the risk difference $\Upsilon_{\mathcal{R}_{\omega}} = \mathcal{R}_{\omega, b}\left(\Lambda_{DB, \widehat{\gamma}}(Z, S^{2}); \eta, \rho^{2}, \sigma^{2}\right) - \mathcal{R}_{\omega}\left(Z, \mu \right)$ and $\Upsilon^{'}_{\mathcal{R}_{\omega}} = \mathcal{R}_{\omega, b}\left(\Lambda_{DB, \widehat{\beta}}(Z, S^{2}); \eta, \rho^{2}, \sigma^{2}\right) - \mathcal{R}_{\omega}\left(Z, \mu \right)$ of the estimators $\Lambda_{DB, \widehat{\gamma}}(Z, S^{2})$ and $\Lambda_{DB, \widehat{\beta}}(Z, S^{2})$ to the MLE $Z$ as a function of $x = \sigma^{2}$ and $y = \rho^{2}$ for $n = 7,$ $q = 15,$ and various values of $\omega$ ($\omega = 0.1, 0.3, 0.6, 0.9$). In Figures 5 and 6, we see that the risk differences $\Upsilon_{\mathcal{R}_{\omega}}$ and $\Upsilon^{'}_{\mathcal{R}_{\omega}}$ are entirely negative. This indicates that the estimators $\Lambda_{DB, \widehat{\gamma}}(Z, S^{2})$ and $\Lambda_{DB, \widehat{\beta}}(Z, S^{2})$ dominate the maximum likelihood estimator $Z.$

5.   Application

As in the simulation section, we demonstrate the effectiveness of the new estimators by comparing the estimators \(\Lambda_{DB, \widehat{\gamma}}(Z, S^{2}) \) (where \(\widehat{\gamma} = \frac{(1-\omega)n}{n+2} \)) and \(\Lambda_{DB, \widehat{\beta}}(Z, S^{2}) \) with the MLE \(Z \) on a real dataset. The dataset that we will use is the Batting dataset from the Lahman package in the R program, which contains baseball statistics. Our focus is on evaluating the effectiveness of the new estimators in estimating batting averages. We create a scenario where we sample only a limited number of observations from a group of players.

We then compare how accurately the MLE and the proposed estimators predict the actual values. For this comparison, we analyze the risk ratio of each estimator to the MLE using the BLF in (2.1) as the loss function. Table 1 shows that for various values of size, dimension, and $\omega$, both new estimators achieve a ratio that is less than one. This means that the estimations derived from estimator Type 1 and estimator Type 2 are more efficient than the MLE and reduce the variance through shrinkage.

6.   Conclusions, limitations, and future research

In this research article, we conducted a thorough investigation into the estimation of the mean of a multivariate normal distribution from a Bayesian perspective using the BLF. Our primary objective was to assess the performance of the proposed estimator in comparison with the conventional MLE through a comprehensive simulation study. To begin with, we focused on establishing the minimaxity property of the modified Bayes estimator and analyzing the behavior of the risk ratios between this estimator and the MLE. Specifically, we examined the scenario where both the sample size $n$ and the dimension of the parameter space $p$ tend to infinity. By investigating the asymptotic behavior of these risk ratios, we gained valuable insights into the relative efficiency of the modified Bayes estimator and the MLE in settings with large samples. This analysis provided a deeper understanding of the estimator's performance and its robustness under different scaling conditions. Furthermore, we explored the domination of a class of estimators that encompassed the empirical modified Bayes estimator over the MLE. Through rigorous mathematical proofs and empirical evidence, we demonstrated the superiority of this class of estimators over the MLE. This dominance result further supported the efficacy and advantages of the proposed Bayesian approach within the context of estimating the mean of a multivariate normal distribution.

Overall, our research shed light on the Bayesian estimation of the mean under the BLF framework and showcased the performance of the proposed modified Bayes estimator. The extensive simulation study, the application, and theoretical analysis provided valuable insights into the estimator's behavior and its superiority over the traditional MLE. These findings contribute to the existing literature on Bayesian estimation and offer practical implications for data analysis in scenarios where accurate estimation of the mean is of paramount importance. The inconvenience of our constructed estimators can be deduced from Figures 1–4: We see that if the values of the variance $\sigma^{2}$ of the variable $Z\vert\mu \sim \mathcal{N}_{q}\left(\mu, \sigma^{2}I_{q}\right)$, exceed $1/4$ of the variance $\rho^{2}$ of the prior distribution $\mu \sim \mathcal{N}_{q}\left(\eta, \rho^{2}I_{q}\right)$, the improvement of the our proposed estimators to the MLE becomes negligible, and this shows the poor performance of the suggested estimators. This limitation requires further investigation, which we will address in future work.

Author contributions

A. Alahmadi and A. Benkhaled conceived the idea; A. Alahmadi developed the theory and performed the computations; A. Benkhaled and W. Almutiry verified the analytical methods and supervised the findings of this paper. All authors discussed the results and contributed to the final manuscript.

Acknowledgments

The author would like to thank the Deanship of Scientific Research at Shaqra University for supporting this work.

Conflict of interest

The authors declare that there is no conflict of interest regarding the publication of this paper.