Mixed-attitude three-way decision model for aerial targets: Threat assessment based on IF-VIKOR-GRA method

1.   Introduction

Aerial target threat assessment (TA) is a vital aspect of the modern information battlefield. As the information environment becomes increasingly uncertain and ambiguous, addressing this problem becomes increasingly difficult. Typically, the problem is resolved through three key steps: model construction, threat evaluation and target ranking ^[1,2,3,4,5]. However, with the evolution of information technology, knowledge handling in aerial combat situations could become even more challenging due to the emergence of uncertainties.

Researchers have extensively explored mathematical tools for describing the TA problem in uncertain environments. Among these tools, intuitionistic fuzzy sets (IFSs) have gained considerable attention for their unique features and advantages ^[6,7,8]. Intuitionistic fuzzy numbers (IFNs) may be employed to represent target attributes and combined using various operators to produce a final target TA value for ranking purposes ^[9,10,11]. In this study, we developed an approach to modeling aerial target TA problems in an intuitionistic fuzzy (IF) environment, which is highly adaptable to real-world scenarios.

Regarding threat evaluation and target ranking, most previous studies have followed a binary decision-making model centered on the choices "to attack" or "not to attack". However, this binary approach is not suitable for common situations in modern warfare, where immediate decisions are often impossible due to insufficient or unreliable target information. Originally proposed by Yao, the three-way decision (3WD) theory expands upon the traditional binary-decision model by introducing a third option: hesitation. This extended model has been widely applied to decision-making problems and investigated at length by previous scholars ^{[12,13,14,15,16,17,18,19]}. In the context of aerial target TA, it is common practice to utilize a three-way decision model (3WDM) in conjunction with decision-theoretic rough sets (DTRSs) ^{[20,21,22,23,24,25,26]}. The TA process yields target conditional probabilities, which are then compared to classification thresholds based on loss estimation. In establishing the proposed approach, we incorporated 3WDM with DTRSs to address IF-based TA problems.

The next critical challenge is the computation of conditional probabilities, a task heavily reliant on target information. Typically, this is accomplished through multi-attribute decision-making (MADM) methods like VIKOR ^[27] and TOPSIS ^[28]. VIKOR generates a compromise ranking list by balancing group utility and personal regret, then revealing the alternative closest to the ideal solution ^[29]. TOPSIS, conversely, directly computes and sequences the Euclidean distances between targets and ideal solutions, then designates the best alternative as the one that has the shortest distance from the ideal solution and longest distance from the negative-ideal solution without considering their relative importance ^[30]. Recognizing the limitations of IF-TOPSIS for effectively evaluating targets on the perpendicular of ideal and negative-ideal solutions, Gao et al. ^[31,32] introduced the IF-VIKOR method. Additionally, researchers have explored the application of the grey relational analysis (GRA) method, which incorporates the closeness of alternatives to ideal solutions in the selection and ranking of weaponry ^[33]. A hybrid GRA-TOPSIS approach was later proven effective in managing aerial target classification in complex and uncertain battlefield scenarios ^[20]. This approach evaluates targets comprehensively based on attribute values and trends and can manifest fluctuating trends in target attributes. Building on these observations and advancements, we developed the IF-VIKOR-GRA approach to calculate conditional probabilities for final classifications.

The final issue to be resolved pertains to estimating the loss function and establishing classification thresholds. The majority of previous researchers have computed loss functions using crisp numbers and calculated thresholds based on minimum-risk decision rules ^[34,35,36], with possible losses solely dependent on target attribute values. However, this approach may not be suitable for the uncertain combat environment, necessitating the incorporation of additional factors into the decision model. To address this issue, we utilized IFNs to represent the loss function. Additionally, human cognitive features can be leveraged to develop decision rules that are adaptable to the risk preferences of decision-makers (DMs). Previous research efforts have used these features to enhance the generality and accuracy of decision-making processes such as the establishment of classification thresholds. Regarding risk preferences, individuals can be roughly categorized as either optimists or pessimists ^[37]. Optimists tend to predict favorable future outcomes while pessimists envision unfavorable circumstances befalling them. Various interpretations of these phenomena can be found throughout the literature. Fan et al. ^[38], for example, constructed optimistic and pessimistic multi-granulation IF 3WDMs for target recognition; the former applied a more rigorous decision rule for the negative region while the latter used one for the positive region. Zhang et al. ^[39] also proposed a pair of positive and negative IF 3WDMs, constructing them concerning membership and non-membership degrees of loss values. Unlike ^[38], Zhang et al. ^[39] considered the dual thresholds simultaneously, with optimistic DMs more inclined to decisive actions (i.e., attack or not attack) while pessimistic DMs tend towards deferment. However, both works overlooked the fact that DMs often have mixed attitudes, falling between absolute optimism and total pessimism. This feature can be further quantified using numerical equations. In this study, we expanded and integrated Zhang's models to create a mixed-attitude IF 3WDM that allows for adjustable proportions of optimism and pessimism among DMs.

This paper presents an effective IF-VIKOR-GRA algorithm that utilizes a 3WDM. We introduce a method that separately manages membership and non-membership degrees, combining the resulting optimistic and pessimistic 3WDMs (when α₂(x) > α₁(x) and β₂(x) > β₁(x)) into a mixed-attitude 3WDM with an adjustment coefficient. This integration condenses two pairs of thresholds representing different attitudes into a single set. We conducted numerical simulations and comparisons against other state-of-the-art methods to validate the mixed-attitude 3WDM based on the IF-VIKOR-GRA method. It is important to note that attribute values and loss values are directly designated in this paper. Corresponding determination approaches were intentionally left as open problems to prevent deviation from the primary theme of our work and avoid straying into unrelated topics.

The remainder of this paper is organized as follows: Section 2 briefly introduces some fundamental concepts, theories and methods related to IFNs, VIKOR, GRA and 3WDs. Section 3 presents the proposed mixed-attitude 3WD TA method with IF-VIKOR-GRA. Section 4 discusses our numerical examples and comparative analysis. Section 5 provides a summary and concluding remarks.

2.   Preliminaries

Basic concepts, theories and formulas relevant to IFNs, VIKOR, GRA and 3WDs are briefly reviewed in this section.

2.1.   IFNs

Definition 1 ^[40]. An IFS A in a fixed set U can be defined as follows:

where the functions $\mu_{A}(x)$, $\nu_{A}(x)$ denote the degree of membership and non-membership of element x $\in$ U to A, respectively. Here, $\mu_{A}(x)$: U $\rightarrow$ [0, 1], $\nu_{A}(x)$: U $\rightarrow$ [0, 1], for $\forall$ x $\in$U, obviously 0 ≤$\mu_{A}(x)$ + $\nu_{A}(x)$ ≤ 1. The non-determinacy degree of element x to set $A$ can be defined as the value of function $\pi_{A}(x)$:

Similarly, $\pi_{A}(x)$: U $\rightarrow$ [0, 1]. A shortened form of an IFN is also allowed:

For two IFNs $A\left(x_{1}\right)$ and $A\left(x_{2}\right)$, the following basic operations hold:

2.2.   VIKOR and GRA method

To operate VIKOR ^[41] and GRA ^[42] methods, first let $\boldsymbol{T}$ be a set of alternatives, $\boldsymbol{T} = \left\{T_{i}\right\}(i = 1, 2, \cdots, m)$, denote $\boldsymbol{A}$ as a set of attributes, $\boldsymbol{A} = \left\{A_{j}\right\}(j = 1, 2, \cdots, n)$ and set $z_{{ij}}$ as the information data for the jth attribute over the ith alternative. Let $w_{j}$ be the weight of the jth attribute. Next, define the positive and negative ideal solution series of attributes as follows:

where $\boldsymbol{A}^{+}$ denotes the set of benefit attributes and $\boldsymbol{A}^{-}$ is the set of cost attributes.

2.2.1.   VIKOR method

1) Calculate group utility $S_{i}$ and individual regret $R_{i}$ by the relations

2) Calculate the compromise solution $Q_{i}$ by the relation

where $v$ is the compromise coefficient, $v \in[0, 1]$. The coefficient is introduced as the weight of the maximum group utility. Consequently, $1-v$ is the weight of the minimum individual regret.

2.2.2.   GRA method

1) Determine the reference sequence as $\boldsymbol{z}_{i} = \left(z_{i1}, z_{i2}, \cdots, z_{i n}\right)$, and denote the positive and negative comparison sequences as $\boldsymbol{Z}^{+} = \left(Z_{1}^{+}, Z_{2}^{+}, \cdots, Z_{n}^{+}\right)$ and $\boldsymbol{Z}^{-} = \left(Z_{1}^{-}, Z_{2}^{-}, \cdots, Z_{n}^{-}\right)$, respectively.

2) Non-dimensionize the data to be calculated.

3) Calculate the difference sequences $\Delta_{i+}(j)$ and $\Delta_{i-}(j)$, then determine the maximum differences and minimum differences. Respectively compute the positive and negative coefficients $\xi_{i+}(j)$ and $\xi_{i-}(j)$, and finally the grey relational degrees $\gamma_{i+}$ and $\gamma_{i-}$. Calculate $\gamma_{i+}$ as follows:

Similarly, compute $\gamma_{i-}$ as

2.3.   3WD based on decision-theoretic rough set model

Definition 2 ^[43,44]. Taking both the Bayesian decision procedure and 3WD into consideration, Yao ^[44] proposed a DTRS model that derives thresholds that separate three regions of probabilities. Given an information table S = (U, AT, VA, f), where all the sets are nonempty and finite, AT is an attribute set and VA is a value set. f: U $\rightarrow$ VA and a nonempty finite set X $\subseteq$ U. For every x $\in$ U, the rough membership function $\mu_{A T}(x)$ can be defined as:

where $|·|$ denotes the cardinality of a finite set and ${Pr}(X \mid[x])$ is the conditional probability of an object in $X$ given that it is in $[x]$.

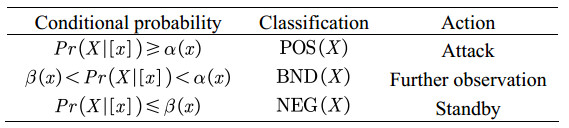
Consider a set of two states $\Omega$ = {X, ¬X}. For simplicity, sign X also denotes a target belonging to X, and vice versa. Each state has three actions denoted by A = {P, B, N}, which represents the action of classifying x into POS (X), BND (X) and NEG (X), respectively. A 3 $\times$ 2 matrix of loss function L = $\left\{\lambda_{\iota \kappa}\right\}_{3 \times 2}$ ($\iota$ = P, B, N, and $\kappa$ = P, N) is also introduced to clarify the classification cost during this decision process (Table 1). Let $\iota$ represent the three actions and $\kappa$ indicate whether a target belongs to X. Thus, $\lambda_{\iota \kappa}$ represents the cost for action $\iota$ in the state $\kappa$.

Given the cost matrix above, the predicted losses R($\iota$|[x]) in response to the different decisions made for targets in [x] can be calculated as follows:

According to the Bayesian decision procedure, decision rules that minimize the risks are suggested as follows:

Given the prerequisites ${Pr}(X \mid[x])$ + ${Pr}(\neg X \mid[x])$ = 1, consider λ_PP ≤ λ_BP < λ_NP and λ_NN ≤ λ_BN < λ_PN. Accordingly, the above rules can be rewritten as:

The parameters $\alpha$, $\beta$ and $\gamma$ are:

3.   Mixed-attitude 3WD TA method with IF-VIKOR-GRA

The proposed method was developed to address the dynamic nature of battlefield situations, allowing for the full utilization of time-variant target information. This approach was designed to deliver objective and comprehensive assessment results that can be tailored to individual preferences. The assessment process, which includes an improved VIKOR-GRA method and a mixed-attitude 3WDM-IF, is visually depicted in Figure 1 and explained in detail in Algorithm 1.

3.1.   Dynamic information integration

Real-world battlefield scenarios are characterized by turbulence and urgency. To grasp an adversary's status rapidly and comprehensively, it is crucial to select an appropriate aggregation operator for the information collected at various time intervals. Recognizing that the significance of target information intensifies as the present moment approaches, a set of time points (or moments) can be denoted as $\boldsymbol{t} = \left\{t_{1}, t_{2}, \ldots, t_{p}\right\}$ with the corresponding weight vector $\boldsymbol{\eta} = \left(\eta_{1}, \eta_{2}, \ldots, \eta_{p}\right)$. This sequence can be calculated using the inverse form of the Poisson distribution, resulting in a monotonically increasing sequence ^[45]:

where $\eta_{k} \geq 0$, $\sum\limits_{k = 1}^{p} \eta_{k} = 1$ and $\varphi \in(0, 2)$.

Let T be a set of incoming targets, $\boldsymbol{T} = \left\{T_{i}\right\}(i = 1, 2, \cdots, m)$, while A is a set of target attributes, $\boldsymbol{A} = \left\{A_{j}\right\}(j = 1, 2, \cdots, n)$. Denote $z_{ij}$ as the information data for the ith target over the jth attribute. In IFNs $z_{ij} = \left\langle\mu_{ij}, \nu_{i j}\right\rangle(i = 1, 2, \cdots, m; j = 1, 2, \cdots, n)$, where $\mu_{ij}$ denotes the membership degree of the target T_i to the attribute A_j and $\nu_{ij}$ represents the non-membership degree of the target T_i to the attribute A_j. This yields the following integrated IF target information matrix Z:

3.2.   Steps for target attribute weight matrix construction

Here, IF entropy is introduced to calculate target attribute weights in the IF environment. By minimizing the total entropy, the weight can be distributed to acquire maximized reliability.

1) Determine the IF entropy $E_{j}$ for target attribute $j$:

2) Construct a nonlinear programming model for target attribute weights $\boldsymbol{w} = \left\{w_{j}\right\}_{1 \times m}$:

3) Calculate the target attribute weights using the Lagrange function with the Lagrange factor $\lambda$:

3.3.   Conditional probability calculation based on the IF-VIKOR-GRA method

The traditional IF technique for order preference, as applied in the TOPSIS method, involves sorting targets by comparing the Euclidean distance between the targets and positive and negative solutions, which is a straightforward approach. However, the VIKOR method goes further by aiming to simultaneously maximize group benefits while minimizing individual regrets. In the context of dynamic TA, it also becomes imperative to evaluate the evolving threat levels of targets. To address this issue, we propose an IF-VIKOR-GRA method designed to compute the conditional probabilities of targets.

The positive and negative ideal solution series are defined as follows:

where $z_{j}^{+}$ and $Z_{j}^{-}$ can be calculated by

and $\mathit{\boldsymbol{A}}^{+}$ denotes the set of benefit attributes while ${\mathit{\boldsymbol{A}}^ - }$ is the set of cost attributes.

Next, calculate the distance between two IFNs $\alpha = \left(\mu_{\alpha}, \nu_{\alpha}\right)$ and $\beta = \left(\mu_{\beta}, \nu_{\beta}\right)$ according to the following distance measure method ^[46]:

Let $\mu_{\alpha}^{\prime} = \mu_{\alpha}\left(1+\frac{2}{3} \pi_{\alpha}\left(1+\pi_{\alpha}\right)\right)$, $\nu_{\alpha}^{\prime} = \nu_{\alpha}\left(1+\frac{2}{3} \pi_{\alpha}\left(1+\pi_{\alpha}\right)\right)$, $\mu_{\beta}^{\prime} = \mu_{\beta}\left(1+\frac{2}{3} \pi_{\beta}\left(1+\pi_{\beta}\right)\right)$, $\nu_{\beta}^{\prime} =$ $\nu_{\beta}\left(1+\frac{2}{3} \pi_{\beta}\left(1+\pi_{\beta}\right)\right)$.

Denote the distance between positive-ideal, negative-ideal solutions and target $i$ as $d\left(z_{i}, Z^{+}\right)$ and $d\left(z_{i}, Z^{-}\right)$, then compute the following:

Next, calculate the ranking value of the IF-VIKOR method ^[32] and IF-GRA ^[20].

The group utility S_i, individual regret R_i and compromise solution Q_i for the ith target are calculated as follows:

The coefficient $v$ is dependent on the DM's risk preference between overall benefits and personal opinions. If it is set to 0.5, the DM has no specific preference; higher or lower values suggest a certain preference. A smaller Q_i value signifies a larger threat posed by the target $i$. Hence, the conditional probability generated from the VIKOR method can be computed as follows:

Apart from making comparisons regarding the targets' relative closeness to ideal solutions, the target-ideal similarity of the sequence curve geometry should also be examined.

First, calculate the positive and negative grey relational degrees $\varsigma\left(z_{i}, Z^{+}\right)$, $\varsigma \left(z_{i}, Z^{-}\right)$ using Eqs (3.19) and (3.20):

where $\varsigma$ is the discrimination coefficient ranging from 0 to 1, normally taken as 0.5. Next, normalize these values according to Eqs (3.21) and (3.22):

A larger $\varsigma_{i}^{+}$ indicates that the target $i$ is more dangerous. Thus, the conditional probability can be calculated as:

To fully leverage the strengths of both VIKOR and GRA methods, their weighted average value can be calculated as follows:

where $\eta$ is the preference value, which ranges from 0 to 1 depending on the DM's preference towards either method.

Additionally, considering the fluctuating challenge levels posed by various types of incoming weapons and their varying combat capabilities, we introduce a new coefficient, $\rho(\rho \in[0, 1])$, to further fine-tune the assessment results. Its value increases as the importance of the weapon type to which a target belongs increases. The comprehensive conditional probability can thus be expressed as follows:

Finally, define IFN $T(x) = \left\langle\mu_{T}(x), \nu_{T}(x)\right\rangle$, whereas $\mu_{T}(x) = {Pr}(X \mid[x])$, $\nu_{T}(x) = p-{Pr}(X \mid[x])$, $0 \le \mu_{T}(x)+\nu_{T}(x) = \rho \le 1$.

3.4.   Target classification 3WDM with IFNs

This section introduces the novel mixed-attitude 3WDM-IF model, where the cost parameter values are also designated as IFNs ^[39].

First, construct the IF cost parameter matrix L = $\left\{A\left(\lambda_{\iota\kappa}\right) = \left\langle\mu_{A}\left(\lambda_{\iota\kappa}\right), \nu_{A}\left(\lambda_{\iota\kappa}\right)\right\rangle\right\}_{3 \times 2}$ ($\iota$ = P, B, N, and $\kappa$ = P, N) as shown in Table 2.

Under the prerequisites

the classification cost $R(\iota \mid[x])$ ($\iota$ = P, B, N) can be calculated as follows:

In reference to Definition 1, the above equation can be rewritten as follows:

For simplicity, denote $R(\iota \mid[x])$ as $\left\langle\mu_{\iota}, \nu_{\iota}\right\rangle$. Next, with respective consideration to $\mu_{\iota}$ and $\nu_{\iota}$, the optimistic and pessimistic 3WDM-IF can be constructed based on Eqs (2.22) and (2.23).

First, define two sets of thresholds: $\left(h_{11}(x), h_{12}(x), h_{13}(x)\right)$ and $\left(h_{21}(x), h_{22}(x), h_{23}(x)\right)$ for decision rules made based on the membership and non-membership degrees. Calculate the variants using Eqs (3.29)–(3.34).

The given prerequisites in this case are:

We can infer that $h_{i 3}(x) < h_{i 2}(x) < h_{i 1}(x)$ where $h_{i 2} \in(0, 1)$, $h_{i 1} \in(0, 1]$ $(i = 1, 2)$, so the following definitions hold:

DMs are faced with open sets of choices when $\alpha_{1}(x) \neq \alpha_{2}(x)$ and $\beta_{1}(x) \neq \beta_{2}(x)$, as illustrated in Figure 2.

In the scenario described above, it is reasonable to assume that optimistic individuals would lean towards making bold decisions (i.e., categorizing targets into either positive or negative regions). Pessimistic individuals, conversely, would tend to favor more choices, potentially labeling more targets as "to be further confirmed". Ideally, this divergence in decision-making approaches would result in noticeable differences in the decisions, as visually depicted in Figures 3 and 4.

For individuals who do not fall expressly into optimist or pessimist categories, and rather exhibit a certain degree of preference that falls between these opposing attitudes, the scenario must be approached differently. The novel mixed-attitude 3WDM-IF was designed to facilitate rational, precise and expeditious decision-making in such cases. This approach harmoniously blends the aforementioned optimistic and pessimistic strategies to ensure overall accuracy. In Eq 3.37), linear combinations are made between the two pairs of thresholds applied in the previously discussed strategies. The values of the newly generated thresholds are adjustable through the modification of the adjustment coefficient $\varepsilon$.

With some adjustments to Eq (2.23), the mixed-attitude 3WDM-IF can be expressed as:

as is shown in both Figure 5 and Table 3.

Targets categorized within the positive region necessitate an immediate organization of an attack. Those situated in the boundary region, on the other hand, require further observation in case of sudden changes in the situation. As for the remaining targets, it is advisable to stay on standby as no further action is necessary.

4.   Illustrative example analysis

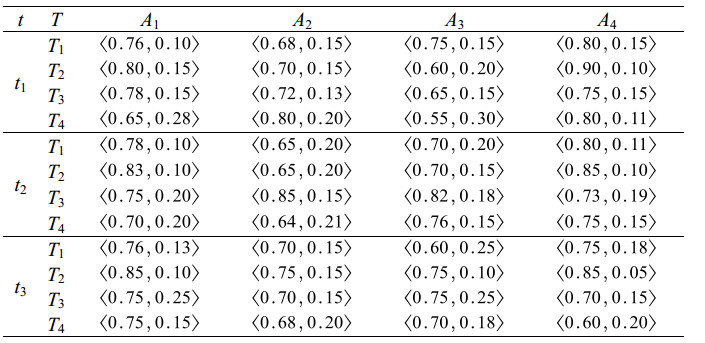
Consider an ongoing air-defense combat scenario involving four incoming targets $T = \left\{T_{i}\right\}$ ($i$ = 1, 2, 3, 4) under surveillance. These targets are defined by attributes denoted as $A = \left\{A_{i}\right\}$ ($i$ = 1, 2, 3, 4) representing their combat capability, speed, distance and angle, respectively. Combat capability and speed fall under the benefit attribute category, where higher values indicate a higher level of threat. Distance and angle are categorized as cost attributes, where lower values signify a higher level of threat. The IF evaluation information for all the targets ^[20] at three consecutive moments, $\boldsymbol{t} = \left\{t_{i}\right\}$ ($i$ = 1, 2, 3) is presented in Table 4. Assume here that $t_{3}$ is the current time.

According to Eq 3.1), let $\varphi$ = 1.5, then $\boldsymbol{\eta}$ = (0.2, 0.2667, 0.5333). The integrated IF target information matrix Z can be obtained based on Eqs (3.1)–(3.3):

The present comprehensive attribute weight vector based on Eqs 3.4)–3.7) is:

According to Eqs 3.8)–(3.11), the positive and negative ideal solution series are:

Select 0.75 as the value of the compromise coefficient $v$ for the VIKOR method. According to Eqs (3.12)–(3.18), the corresponding conditional probability can be calculated as: (1, 0, 0.5628, 0.2365). Similarly, the conditional probability generated from the GRA method can be obtained as (0.6120, 0.4759, 0.5624, 0.5177).

Take $\eta = 0.5$, ρ = (0.95, 0.75, 0.8, 0.85), so based on Eqs 3.24) and (3.25), the final comprehensive conditional probability ${Pr}(X \mid[x])$ is $(0.7657, 0.1785, 0.4501, 0.3206)$ and the target ranking is: T₁ > T₃ > T₄ > T₂. Table 5 presents an IF cost parameter matrix L that can be utilized to further obtain the optimistic and pessimistic thresholds for 3WD.

After obtaining the thresholds described above, set $\varepsilon$ as 0.5 and calculate the final thresholds for 3WDM. Table 6 lists the final conditional probabilities, thresholds and classification decisions of all the targets and corresponding actions, which are further illustrated in Figure 6. Based on the mixed-attitude 3WDM-IF, $I_{1} \in \operatorname{POS}(X)$, $T_{2}, T_{3}, T_{4} \in \operatorname{BND}(X)$; $T_{1}$ requires an immediate attack while $T_{2}$, $T_{3}$ and $T_{4}$ need further confirmation.

To validate the efficacy of the mixed-attitude 3WDM, we conducted numerical simulations to explore its performance in comparison to different TA methods and with various coefficients.

We first compared the proposed VIKOR-GRA with the TOPSIS-GRA method ^[20] and the VIKOR method using ρ = (0.95, 0.75, 0.8, 0.85) and $\varepsilon$ = 0.5. Figure 7 clearly shows where the threat rankings produced by all three methods were identical, affirming the effectiveness of the proposed method. In terms of classification results, the three methods converged on the classification of T₃ and T₄ in the boundary zone but exhibited notable discrepancies for T₁ and T₂: VIKOR-GRA and VIKOR classified T₁ in the positive zone, while TOPSIS-GRA classified it into the boundary zone; VIKOR placed T₂ in the negative zone while the other two methods assigned it to the boundary zone. This observation suggests that the proposed method surpasses mere absolute distance comparisons between targets and ideal solutions. It factors in a trade-off between individual regrets and group benefits, as well as the correlations between curves. In essence, the method combines the strengths of VIKOR and GRA while accounting for target types, resulting in more comprehensive and reasonable evaluation outcomes.

Next, we examined the impact of $\varepsilon = 0.5$ with ρ ranging from 0.5 to 1 on the target membership degree and classification. The results are shown in Figure 8. Coefficient ρ serves as a measure of the risk level for each target according to its type, directly influencing the target's hesitancy degree given that $\pi_{T}(x) = 1-\left(\mu_{T}(x)+\nu_{T}(a)\right) = 1-\rho$. The target's hesitancy degree decreases as ρ increases, with the target's membership degree and non-membership degree increasing proportionally. This aligns with the expectation that riskier targets yield higher assessment results. The thresholds also rise concurrently, as illustrated in Figure 8. The values of α and β both increase with ρ, but α increases relatively faster, leading to an expansion in the negative and boundary zones and contraction in the positive zone. Although seemingly contradictory, this phenomenon is consistent with the concept that riskier targets necessitate more cautious decision-making. It is also worth noting that as ρ varies, the final target ranking and classification decisions remain unaffected for targets of the same type. However, for targets with different combat capabilities, ρ assists in prioritizing them.

Next, we fixed ρ at 0.75 and proceeded to examine the influence of the adjustment coefficient for the optimistic 3WDM and pessimistic 3WDM on mixed-attitude 3WDM thresholds. As Eq (3.37) demonstrates, the adjustment coefficient ε directly reflects and quantifies the DM's attitude towards both ends of the decision spectrum. Ranging from 0 to 1, ε indicates that the DM leans toward a pessimistic decision when below 0.5 and implies the opposite when it exceeds 0.5. Figure 9 provides a visual representation of how ε influences the thresholds in the mixed-attitude 3WDM. The region between α and β gradually widens as ε increases, also indicating the expansion of the boundary zone. Though the changes in α and β are not substantial, they do reflect the precision of the method. This observation aligns with the notion that more pessimistic DMs make more cautious decisions. Therefore, the combination of 3WDMs with opposing attitudes and the adjustment coefficient ε makes the proposed 3WDM adaptable to the subjective tendencies of DMs, leading to more accurate results.

The simulation results further verify the feasibility of the mixed-attitude 3WDM. This new model can facilitate 3WDs for aerial targets in dynamic IF environments. It may also have broader applications, including addressing target TA and classification problems in more complex battlefield scenarios.

5.   Conclusions

This paper proposes a novel 3WD TA model that leverages DTRS and fuzzy set theories for application in uncertain battlefield environments. Both target attributes and loss functions are represented using IFNs. The conditional probability for 3WD is derived through an innovative IF-VIKOR-GRA method, which considers a trade-off between group utility and individual regret, as well as data trend similarities. We obtained two sets of decision thresholds reflecting optimistic and pessimistic attitudes based on the 3WDM with IFNs. We then constructed the mixed-attitude 3WDM-IF by combining optimistic and pessimistic 3WDM-IFs, taking into account risk preferences to enable more flexible decision rules. We conducted numerical simulations to verify the reliability of the TA method comprising IF-VIKOR-GRA and mixed-attitude 3WDM-IF. The IF-VIKOR-GRA method was found to be capable of producing comprehensive and rational evaluation results, while the generality of the mixed-attitude 3WDM-IF allows for more precise classification rules based on the preferences of DMs.

Future research may focus on conducting comprehensive evaluations of the strengths and weaknesses of various mathematical tools employed for describing battlefield uncertainties, as well as refining the hybrid TA algorithm concerning the time scale. This exploration could contribute to improving battlefield knowledge management, target descriptions and response timeliness.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was partly supported by the Natural Science Foundation of Shandong Province (Grant No. ZR2020MF090).

Conflict of interest

The authors declare there is no conflict of interest.