1. Introduction

Composite Fiber Reinforced Polymers (CFRP) are becoming increasingly used in a variety of applications (aerospace, transportation, medical devices…), because of their high resistance/weight ratio. For example, like the Boeing 787, the A350 XWB uses carbon fiber in the wings, wing box, flight-control surfaces, empennage and fuselage. Machining is always needed after the demolding of composite parts. Trimming is the first machining operation and is carried out to remove the matrix overflow from the sides of the composite part. These machining operations are performed in order to obtain the final geometries of the parts in order to ensure their role in the final structure, but also to make the assembly of different parts possible. However, the machining operations are always accompanied by defects and delamination ^{[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]}. These defects are affected several parameters, which can be, the machining process ^[1,2], the cutting parameters ^[3,8], the tool geometry ^[5,6], fiber orientations ^[7], tool wear ^[8], cutting parameters range ^[4], but also by the fiber content percentage ^[13] and the manufacturing process ^[14].

The average arithmetic roughness (Ra) remains the qualifying parameter for the surface in composite structures. This criterion widely used in industry and which serves to predict the mechanical behavior of metallic structures, poses a number of problems when trying to extend it to composite materials. In the experimental works of ^[6], the authors were interested on the mechanical tensile tests. These tests are carried out on unidirectional specimens (UD) oriented at 45° with respect to the load axis. The results show that the tensile stress increases with the increase of the average surface roughness (Ra). However, the work of ^[15] show that stress rupture of UD specimens, oriented at 0° and subjected to compression, decrease with the increase of the average surface roughness (Ra).

The authors in ^[16] showed that the mechanical strength of multidirectional long fiber composite materials decreases while increasing the surface roughness but also the machining temperature. In ^[17,18], the authors studied a multidirectional CFRP and found that the bending mechanical resistance of abrasive water jet machining (AWJM) samples decrease with the increase of the average surface roughness (Ra). This observation is confirmed while considering compressive and inter laminar shear tests on AWJM samples ^[2]. Other works of ^{[19,20,21,22]} have also shown the effect of the machining process on the mechanical behavior of long fiber composite materials. For example Ramulu and al. ^[21] showed that abrasive water jet trimming of graphite/epoxy laminates tented to produce exit ply delaminations. However they also found that these delaminations did not significantly reduce the strength of the laminate. Nevertheless, the delaminations that were induced in edge finishing did result in significant reductions in strength.

The operation of rectification is always used after the machining operations. This operation produces composites parts characterized with a similar surface roughness and improves highly the surface quality. This improvement of the surface quality is supposed to bring a great amelioration on the mechanical behavior of composite structures. This statement is not confirmed any-where. The rectification concerns all machined specimens whatever are their surface qualities and the machining process used. However this aspect is never taken into account when considering the rectified specimens, indeed the composite parts are supposed to have the same mechanical behavior induced by similar surface roughness.

To help answer this question, two carbon/epoxy composite unidirectional materials, the T700/M21-GC and the IMS/977-2, are considered. These long fiber composite materials are manufactured on an autoclave. The stacking sequence chosen is representative of structural parts used in aeronautics. The same multidirectional stacking sequence is chosen for both long fiber composite materials. Two set of specimens were machined by two different cutting processes: diamond cutter (ADS) and edge trimming. To generate specimens with different levels of surface quality, different machining conditions were chosen during machining by edge trimming. After the machining operation, some specimens are rectified using grinding. The surfaces roughness of the specimens is characterized by a roughness tester and Scanning Electron Microscope (SEM) observations. To study the influence of surface defects on the mechanical behavior, all specimens were tested under quasi-static compressive and inter laminar shear tests.

---

2. Materials and Method

---

2.1. Material Preparation

Carbon-fiber reinforced plastic (CFRP) composite of 5.2 mm thickness (20 layers) was used for conducting the trimming studies. The CFRP composite was made using unidirectional prepregs supplied by Hexcel referenced under T700/M21-GC and IMS/977-2. The staking sequence of the laminate is [90/90/-45/0/45/90/-45/90/45/90]_S so as to get a multidirectional laminate. Curing was then carried out at 180 °C for 120 min during which the pressure was maintained at 7 bars in an autoclave. The technical details are summarized in table 1.

---

2.2. Samples preparation

First, the specimens were prepared using two cutting processes, conventional cutting tool machining and diamond cutter (ADS).

Edge trimming experiments are performed using a “DUBUS” 3-axis milling machine with a maximum spindle speed of 75000 rpm. These experiments were conducted using a full experimental design (3 × 3) with different cutting conditions (Table 1). In addition six specimens were prepared, for compressive tests only, with cutting conditions recommended by the tool manufacturer. These conditions are, cutting speed of 150 m/min and feed speed of 1000 mm/min.

To get consistent values and in order to remove the influence of tool wear, each experimental condition was performed with a new tool. To carry out the full experimental design, nine burr tools SGS-CCR-20M of tungsten carbide with 6 mm diameter were used. The radial depth of cut is fixed to 2 mm.

Rectified specimens from both materials are firstly machined by conventional cutting tools, using the same cutting conditions as specified in table 1 and then 0.5 mm is removed from each side of the samples so as to get continuous surface. The rectification is made by grinding with the presence of lubricant (water) to remove the thermal effect on the rectified specimens (Figure 1).

ADS samples were machined using a saw referenced DIAMFORCE JANTE CONTINUE-D100-AL19-GR 427.

Rectified specimens from both materials are firstly machined by ADS cutter, and then 0.5 mm is removed from each side of the sample so as to get continuous surface. Also, five specimens were prepared for each quasi static mechanical test.

---

2.3. Surface defects characterization

The machined surfaces are analyzed using a surface roughness tester “Mitutoyo SJ 500” is used to measure the surface roughness, the total measuring length is set to 5 mm to avoid overflowing. The results obtained with both materials are correlated with the scanning electron microscope (SEM) images obtained from a scanning electron microscope “JEOL-JSM 5310/N° MP 17210037”.

---

2.4. Mechanical experiments

Mechanical quasi-static tests were performed on an Instron testing machine. The compressive and inter-laminar shear experiments were conducted according to the standards AFNOR NF T 51-120-3 and AFNOR NF T 57-104 respectively. The experiment design for compressive tests performed with hydraulic grips to avoid slippage.

---

3. Results and Discussion

---

3.1. Effect of rectification on the machined surfaces

The influence of cutting parameters on the machined surfaces is well documented ^{[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]}. In this study the specimens are machined at high speed ^[4,5,6,7,8]. The effect of cutting parameters on the surface defects is reminded in follows.

The SEM image of the machined surface obtained after trimming at a feed of 500 mm/min and a cutting speed of 700 m/min (Figure 2-a) show a small regions of the fibers pull out. From this image, a neat machined surface can be observed. Similar results have been observed when the cutting speed is inferior or equal to 700 m/min, and for all feed rates (125 mm/min, 250 mm/min and 500 mm/min).

With the increase of cutting distance the surface roughness increases, this is related directly to the increase of the tool wear (Figure 2-b) where more damaged zones were observed. It is also observed that fiber pull out areas increase with the increase of the cutting speed from 700 m/min to 1400 m/min (Figure 2-c). In addition, the areas of matrix degradation appeared. These damages are higher when the feed rate decreased (Figure 2-d). The damaged zones are located on the 45°, 0° and 90° plies, which correspond to −45°, 0° and 90° when considering the cutting direction (down milling). These observations are in agreement with the observations made on orthogonal cutting ^[23] and trimming at low cutting speeds ^[1]. This poor quality of surface can be explained by the fact that, with the tool wear the cutting edge radius increases, higher than the carbon fiber diameter (≈ 7 μm). Therefore, the fibers are not cut but pushed and pulled, this mechanism can be more similar to wrenching ^[4].

The SEM observations (Figure 3) show two specimens machined from both long fiber composite materials by ADS machining and two other specimens after rectification. The defects generated after machining with the ADS cutting process have mostly the form of streaks (Figure 3-b, 3-d). These streaks represent wrenched areas and follow the tool trajectory. They are caused by the random distribution of diamond grains with different sizes and shapes on the cutting face of the abrasive diamond cutter (ADS). The trajectory of the defects is strongly linked to the cutting tool trajectory, while the fiber directions have no effect on these damages. For this reason, the ADS defects are observed on the entire machined surface and the distinction of the different fiber orientations is impossible. The nature of these damages depends mainly of the feed speed (in this case, it is controlled manually by the operator) and the size of diamond grains. It is clearly seen that rectification improves the machined surface quality (Figure 3-a, 3-c). It is noted that the machining streaks seen in figures 3-b and 3-d have totally disappeared. After rectification continuous surfaces without apparent defects in the case of material T700/M21-GC (Figure 3-a) are observed. However, the rectification of the composite material IMS/977-2 generates some damage on the plies oriented at +45° (see Figure 3-c). According to the SEM observations, these damages are confined, and are not observed in the entire rectifiedsurface.

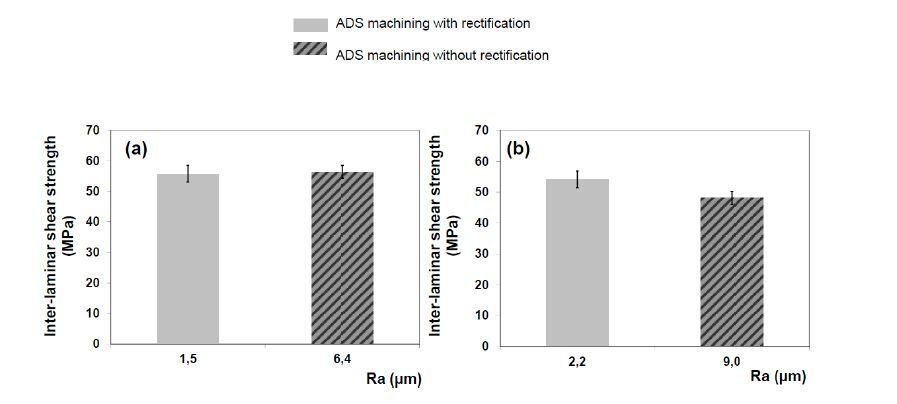
The rectification of the machined surfaces, obtained by trimming of both long fiber composite materials by a conventional cutting tool, is similar to those observed earlier (cf. Figure 3). These rectified surfaces are also characterized by a similar surface roughness Ra. In the case of the composite material T700/M21-GC the surface roughness (Ra) is 1.5 µm and its value is 2.2 µm in the case of the composite material IMS/977-2.

---

3.2. Mechanical behavior in compressive tests

---

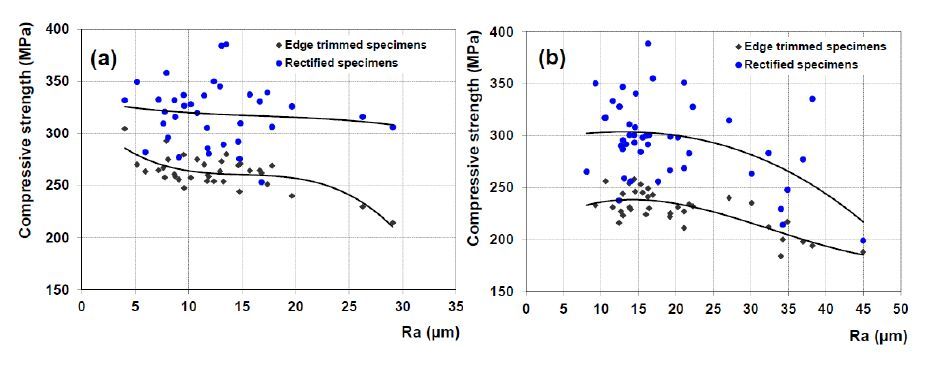
Figure 4 shows the variation of compressive strength as a function of the surface roughness of machined specimens with a conventional cutting tool with and without rectification.

It is noticed that the increase of the surface roughness leads to a decrease of the compressive mechanical behavior. This decrease is about 29% when the surface roughness varies from 7 µm to 34 µm concerning the composite material T700/M21-GC.

It is also observed that independently of the surface roughness, the rectification provides a significant improvement in the compressive strength (Figure 4-a). However, a larger dispersion is obtained for the rectified specimens. Concerning the composite material T700/M21-GC, the value of the minimum compressive strength is 253 MPa, and the maximum compressive strength is 386 MPa. When it comes to the composite material IMS/977-2, the minimum stress is 200 MPa and the maximum is 388 MPa. The gain in mechanical strength after rectification varies from 7% to 43% for the composite material T700/M21-GC. This gain is comprised between 6% and 72% for the composite material IMS/977-2. The largest gains on compressive strength are recorded for the IMS/977-2. This can be explained by the fact that the damage generated during machining IMS/977-2 are greater than those generated during the machining of the composite material T700/M21-GC. It is than obvious that rectification can improve the compressive strengths of long fiber composite materials, however the results obtained with this method are more dispersed and in some cases very close to the specimens without rectification.

Considering the composite material IMS/977-2 (Figure 4-b), the improvement after the rectification of samples of average surface roughness of 45 µm is 7% however the result obtained after rectification is lower to those obtained even without rectification for Ra < 33 µm. This can be explained by the fact that rectification removes the damage present on the surface of the machined specimen, however it fails to remove the deep micro-delamination damages .It is than wiser to generate specimens of small surface roughness before rectification. More importantly, the surface roughness criterion is not adapted for composite materials.

---

Figure 5 shows the compressive stress of ADS specimens with and without rectification. In the case of the composite material T700/M21-GC rectification improves the average compressive strength by 10% (Figure 5-a). Concerning the composite material IMS/977-2, the rectification has no impact on the mechanical behavior in compression (Figure 5-b). It is than obvious that the improvement on compressive strength is influenced by the composite material it-self. The rectification does not bring an improvement on compressive strength for all long fiber composite materials.

When considering the composite material IMS/977-2, and comparing the results obtained by edge trimming (cf. Figure 4-b) and ADS machining (Figure 5-b), it becomes clear that the improvement on compressive strength depends mainly on the machining process.

---

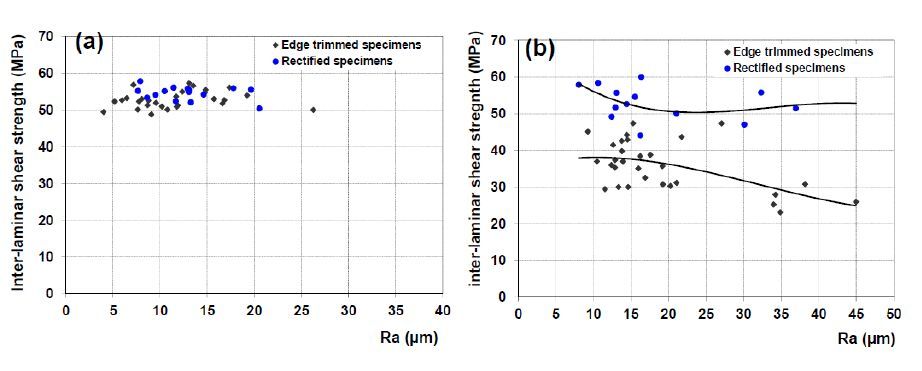
3.3. Mechanical behavior in inter laminar shear tests

---

Figure 6 shows the effect of rectification on the inter-laminar shear strengths of both composite materials. It is observed that the rectification has no effect on the inter-laminar shear strength of the material T700/M21-GC (Figure 6-a). However, a significant improvement in the inter-laminar shear strength of the material IMS/977-GC is observed (Figure 6-b). It is than clear that the improvement on inter-laminar shear strength is influenced by the composite material it-self.

When considering the composite material T700/M21-GC, and comparing the results obtained by edge trimming in the case of compressive tests (cf. Figure 4-a) and the case of inter-laminar shear tests (Figure 6-a), it is observed that rectification brings an improvement on compressive strength but do not bring any significant improvement in the case of the inter-laminar shear strength. It can be assumed that the improvement on mechanical strength of composite materials depends also on the nature of the solicitation.

---

Figure 7 shows the inter-laminar shear strength of the ADS specimens with and without rectification for both materials. It is observed that rectification, also in this case, has no influence on the inter-laminar shear strength when considering the material T700/M21-GC. An amelioration of 6% is observed in the case of the composite material IMS/977-2. Here also a significant effect of the composite material it-self is observed. The rectification does not bring an improvement on inter-laminar shear strength for all composite materials.

The surface roughness of T700/M21-GC was always found to be lower than the surface roughness of IMS/977-2 (cf. Figures 4-7). This may be related to the presence of thermoplastic nodules in the case of the composite material T700/M21-GC (Figure 8) in addition to the thermoplastic present in the matrix for both composite materials. These nodules improve the surface quality of the composite material T700/M21-GC by filling the cracks present on the machined surface. The presence of high machining temperatures ^[16] added to the compressive forces directed towards the surfaces of the specimens during the trimming process, causes the thermoplastics to fill the craters observed but also to stick and to merge with the matrix inside the composite material T700/M21-GC. This phenomenon can explain the difference on the surface roughness recorded for the two materials. The surface roughness is always less in T700/M21-GC than in IMS/977-2, the mechanical behavior is better (less affected by the surface roughness and the machining temperatures) in the case of composite material T700/M21-GC. Thus, thermoplastic nodules improve the machined surface quality and increase the mechanical strength of composite materials. Since these nodules are added to improve the mechanical behaviour of composite materials in term of delamination, they may explain the high resistance of this material in inter laminar shear tests, which promote rupture by delamination whatever the surface roughness (Figure 6). Even after the rectification the results obtained in inter-laminar shear tests steel very close to those obtained before rectification.

---

4. Conclusion

The main results obtained after the machining and testing of two long fiber composite materials having the same stacking sequence under compressive and inter-laminar shear tests are:

1 The quality of machined surfaces and the size of the defects generated during machining are strongly influenced by the cutting parameters and the component parts of the composite material.

2 The rectification improves the quality of machined surfaces, however this operation generates dispersed results in term of mechanical resistance.

3 To generate high mechanical resistance, it is recommended to generate specimens of small surface roughness before rectification.

4 The rectification induced an amelioration of the compressive strength of edge trimmed specimens for both materials. It had also improved the inter-laminar shear strength of the material IMS/977-2 for both machining processes. However the rectification did not permit an amelioration of compressive strength of the IMS/977-2 specimens generated by ADS cutting and the inter-laminar shear strength of the composite material T700/M21-GC for both machining processes.

5 The quasi-static tests show that the improvement on mechanical strength depends mainly on the machining process, the composite material components and the nature of solicitation.

---

Acknowledgements

The authors wish to acknowledge the financial support of the French Ministry of research.

---

Conflict of Interest

The authors declare no conflicts of interest regarding this paper.

---