Pseudo-ordering and $\delta^{1}$-level mappings: A study in fuzzy interval convex analysis

1.   Introduction

Inequalities are essential and instrumental in dealing with several complex mathematical quantities that appeared in diverse domains of physical sciences. They have been investigated from multiple aspects, including expanding the applicable domain and eliminating the limitations of already proved results and utilizing various approaches from functional analysis, generalized calculus, and convex analysis. Originally, they were pivotal to acquiring bounds for different mappings, integrals, the uniqueness and stability of solutions, error analysis of quadrature algorithms, information theory, etc. Based on these factors, this theory has grown exponentially through convex analysis. Additionally, the impact of concavity is exemplary in inequalities due to plenty of factors, particularly the fact that several inequalities can be derived from the premise of convexity. This suggests that one of the main motives for studying classical inequalities is to characterize convexity and its generalizations. One of the notable classes of convexity depending upon quadratic support is known to us as strong convexity, which generalizes the classical concepts and is highly applied to conclude the novel refinements of already proven results. This class has inspired the development of several new mapping classes in the literature. For comprehensive details on generalizations of strongly convex, consult ^{[1,2,3,4,5,6]}. In 2007, Abramovich et al. ^[7] demonstrated another concept of a super-quadratic mapping incorporated with translations of itself and a support line. It is defined as:

A mapping ${\Psi}:[0, \infty)\rightarrow \mathbb{R}$ is considered to be a super-quadratic for ${{\mu}}\geq0$ if there exist a constant $C({{\mu}})\in\mathbb{R}$, such that

It can also be interpreted as:

Definition 1.1 (^[7]). A mapping ${\Psi}:[0, \infty)\rightarrow \mathbb{R}$ is called super-quadratic if, and only if,

holds $\forall\, {\mu}, y\geq0$ and $0\leq {{\varphi}}\leq 1$.

Here, we provide some instrumental results to discuss super-quadratic mappings.

Lemma 1.1 (^[7]). If ${\Psi}:[0, \infty)\rightarrow \mathbb{R}$ is a super-quadratic mapping, then

(1) ${\Psi}(0)\leq 0$,

(2) $C({{\mu}}) = {\Psi}'({{\mu}})$, when ${\Psi}({{\mu}})$ is differentiable with ${\Psi}(0) = {\Psi}'(0) = 0$, for all ${{\mu}}\geq0$,

(3) for all ${{\mu}}\geq0$, if ${\Psi}({{\mu}})\geq 0$, then ${\Psi}$ is convex and ${\Psi}(0) = {\Psi}'(0) = 0$.

Kian and his coauthors ^[8,9] came up with the idea of operator super-quadratic mappings and Jensen's kinds of inequalities that are related to them. Oguntuase and Persson ^[10] discussed Hardy-like inequalities utilizing the notion of super-quadratic mappings. Study these additional papers for more comprehensive research on super-quadraticity, ^{[11,12,13,14,15]}.

Varosanec ^[16] proposed the unified class of convexity through control mapping and provided new insight to conduct research in the following field. Throughout the investigation, let ${\hslash_{\circ}}:(0, 1)\rightarrow \mathbb{R}$ be a mapping such that $\hslash_{\circ}\geq0$.

Definition 1.2 (^[16]). A mapping ${\Psi}:[{s_{3}}, {s_{4}}]\rightarrow \mathbb{R}$ is considered to be a ${\hslash_{\circ}}$-convex, if

Inspired by the idea presented in ^[16], Alomari and Chesneau ^[17] developed a general class of super-quadratic mappings and investigated some of their essential properties, defined as:

Definition 1.3 (^[17]). Any mapping ${\Psi}:[{s_{3}}, {s_{4}}]\rightarrow \mathbb{R}$ is regraded as ${\hslash_{\circ}}$-super-quadratic, If

Lemma 1.2 (^[17]). Suppose ${\Psi}:[{s_{3}}, {s_{4}}]\rightarrow \mathbb{R}$ is a ${\hslash_{\circ}}$-super-quadratic mapping, then

(1) ${\Psi}(0)\leq 0$,

(2) for all ${{\mu}}\geq0$, if ${\Psi}({{\mu}})\geq 0$, then ${\Psi}$ is ${\hslash_{\circ}}$-convex such that ${\Psi}(0) = {\Psi}'(0) = 0$.

The Jensen's inequality for this class of mappings is given as

Theorem 1.1 (^[17]). Suppose ${\Psi}:[{s_{3}}, {s_{4}}]\rightarrow \mathbb{R}$ is a ${\hslash_{\circ}}$-super-quadratic mapping, then

Also, they proved the Jensen-Mercer inequality for $\hslash_{\circ}$-super-quadratic mappings.

Theorem 1.2 (^[17]). Let ${\Psi}:[{s_{3}}, {s_{4}}]\rightarrow \mathbb{R}$ be a ${\hslash_{\circ}}$-super-quadratic mapping, then

Set-valued analysis and its subdomains are cornerstones in mathematical sciences to generalize the previously obtained results. In this regard, Moore ^[18] applied the set-valued mappings to establish bounded solutions of differential equations. Recently, researchers have focused on decision-making, multi-objective optimization, numerical analysis, mathematical modeling, and advanced nonlinear analysis through interval-valued mapping. Probabilistic and interval-valued techniques are utilized to extract the results from data having randomness. However, these approaches are not applicable to quantities that possess vagueness. To deal with such problems, Zadeh ^[19] proposed the idea of a fuzzy set based on generalized indicator mapping and also presented the idea of a fuzzy convex set. This theory emerged as a potential theory in the last few decades. The contribution of these concepts in optimization, decision-making, inequalities, differential equations, mathematical modeling, approximation methodologies, dynamic systems, and computer science is unprecedented. Note that this theory is not statistical in nature but sets new trends in possibility theory. Dubois and Prade ^[20] researched preliminary terminologies related to area and tangent problems and offered new insights to carry new developments. Nanda and Kar ^[21] explored diverse groups of fuzzy convex mappings and reported their essential characterization.

As we move ahead, let us go over certain previously laid-out concepts and implications of fuzzy interval analysis. Assume that $K_c$ symbolizes the space of all closed and bounded intervals in $\mathbb{R}$, while $K_c^+$ represents the space of positive intervals. The interval $_{1}\chi$ is defined as:

Given $\chi, \phi \in K_c$ and $\delta^{1}\in\mathbb{R}$, Minkowski's operations are given as:

Then the Minkowski addition ${\chi}+{\phi}$ and ${\chi}\times{\phi}$ for ${\chi}, {\phi}\in K_c$ are defined by

and

Definition 1.4 (^[22]). For any compact intervals $A = [s_{3*}, s_{3}^{*}]$, $B = [s_{4*}, \, s_{4}^{*}]$ and $C = [c_{*}, \, c^{*}]$, the generalized Hukuhara difference (gH-difference) is explored as:

Also, the gH-difference can be illustrated as:

Also for $A\in K_{c}$, the length of interval is computed by $l(A) = s_{3}^{*}-s_{3*}$. Then, for all $A, B\in K_{c}$, we have

Definition 1.5 (^[23]). The "$\leq_\rho$" relation over $K_c$ is provided as:

if and only if,

for all $[{\phi}_*, {\phi}^*], [{\chi}_*, {\chi}^*]\in K_c$ is a pseudo-order or left-right (LR) ordering relation.

Theorem 1.3 (^[23,24]). Every fuzzy set and ${{\delta^{1}}}\in(0, 1]$, the representations of ${{\delta^{1}}}$-level set of ${{^{1}\pi} }$ are examined in the following order: ${^{1}\pi} _{{\delta^{1}}} = \{\mu\in\mathbb{R}:{{^{1}\pi} }(\mu)\geq{{\delta^{1}}}\}$ and $supp({{^{1}\pi} }) = cl\{\mu\in \mathbb{R}: {{^{1}\pi} }(\mu) > 0\}$. The fuzzy sets in $\mathbb{R}$ are represented by $\Theta_{\delta^{1}}$ and ${{^{1}\pi} }\in \Theta_{\delta^{1}}$. A ${{^{1}\pi} }$ is considered to be a fuzzy number (interval) if it is normal, fuzzy convex, semi-continuous, and has compact support. The space of all real fuzzy numbers are specified by $\Upsilon_{\delta^{1}}$.

Let ${^{1}\pi} \in \Upsilon_{\delta^{1}}$ be a fuzzy interval if, and only if, ${{\delta^{1}}}$-levels $[{^{1}\pi}]^{{\delta^{1}}}$is a compact convex set of $\mathbb{R}$. Now, we deliver the representation of fuzzy number:

where

Thus, a fuzzy-interval can be investigated and characterized by a parameterized triplet. For more details, see ^[26].

These two endpoint mappings ${^{1}\pi} _{*}({{\delta^{1}}})$ and ${^{1}\pi} ^{*}({{\delta^{1}}})$ play a vital role in exploring the fuzzy numbers.

Proposition 1.1 (^[25]). If ${V}, {\chi}\in \Upsilon_{\delta^{1}}$, then the relation "$\preceq$" explored on $\Upsilon_{\delta^{1}}$ by

${V} \preceq {\chi}$ if, and only if, $[{V}]^{{\delta^{1}}} \leq_\rho [{\chi}]^{{\delta^{1}}}$, for all ${{\delta^{1}}}\in[0, 1]$, this relation is known as a partial order relation.

For ${V}, {\chi} \in \Upsilon_{\delta^{1}}$ and $c\in \mathbb{R}$, the scalar product $c\cdot{\chi}$, sum with constant, the sum ${V}{\oplus}{\chi}$, and product ${V}\odot{\chi}$ are defined by:

The level wise difference of the fuzzy number is stated as follows:

Definition 1.6 (^[27]). Let ${V}$, ${\chi}$ be the two fuzzy numbers. Then the level-wise difference is defined as

To overcome the limitations of Hukuhara difference, the following difference is defined as follows.

Definition 1.7 (^[22]). Let ${V}$, ${\chi}$ be the two fuzzy numbers. Then the generalized Hukuhara difference (gH-difference) of ${V}{\ominus_{g}}{\chi}$ is a fuzzy number ${\xi}$ such that

Also the gH-difference based on $\delta^{1}$ can be illustrated as:

Also for $V\in \Upsilon_{\delta^{1}}$, the length of the fuzzy interval is given by $l(V(\delta^{1})) = V^{*}(\delta^{1})-V_{*}(\delta^{1})$. Then, for all $V, \chi\in \Upsilon_{\delta^{1}}$, we have

Note that a function $\Psi:[{s_{3}}, {s_{4}}]\subseteq\mathbb{R}\rightarrow \Upsilon_{\delta^{1}}$ is said to be $l$-increasing, if length function $len\left([\Psi(\mu)]^{\delta^{1}}\right) = {\Psi}^*(\mu, {{\delta^{1}}})-{\Psi}_*(\mu, {{\delta^{1}}})$ is increasing with respect $\mu$ for all $\delta^{1}\in[0, 1]$. Mathematically, for any $\mu_{1}, \mu_{2}\in[{s_{3}}, {s_{4}}]$ and $\mu_{1}\leq\mu_{2}$. Then $len\left([\Psi(\mu_{2})]^{\delta^{1}}\right)\geq len\left([\Psi(\mu_{1})]^{\delta^{1}}\right), \, \, \forall \delta^{1}\in[0, \, 1]$. For more details, see ^[28].

Proposition 1.2 (^[28]). Let $\Psi: T = ({s_{3}}, {s_{4}})\subseteq\mathbb{R}\rightarrow \Upsilon_{\delta^{1}}$ be a Fuzzy number valued ($\verb"F".\verb"N".\verb"V"$) mapping. If $\Psi(\mu+h)\ominus_{g} \Psi(\mu)$ exists for some $h$ such that ${\mu}+h\in T$, then one of the following conditions hold:

Remark 1.1. From Proposition 2.4, the $\Psi(\mu+h)\ominus_{g} \Psi(\mu)$ can be written by the definition of the fuzzy interval as:

Definition 1.8 (^[25]). If ${\Psi}:[{s_{3}}, {s_{4}}]\subset\mathbb{R}\rightarrow \Upsilon_{\delta^{1}}$ is an $\verb"F".\verb"N".\verb"V"$ mapping. For each ${{\delta^{1}}}\in[0, 1]$, whose ${{\delta^{1}}}$-cuts highlight the bundle of $\verb"I".\verb"V".\verb"F"$, such that ${\Psi}_{{\delta^{1}}}:[{s_{3}}, {s_{4}}]\subset\mathbb{R}\rightarrow K_c$ is described as ${\Psi}_{{\delta^{1}}}(\mu) = [{\Psi}_*(\mu, {{\delta^{1}}}), {\Psi}^*(\mu, {{\delta^{1}}})]$, $\mu\in[{s_{3}}, {s_{4}}]$. Every ${{\delta^{1}}}\in[0, 1]$, the left and right real valued mappings ${\Psi}_*(\mu, {{\delta^{1}}}), {\Psi}^*(\mu, {{\delta^{1}}}):[{s_{3}}, {s_{4}}]\rightarrow \mathbb{R}$ are sometimes referred to as ${\Psi}$ end points.

Definition 1.9 (^[29]). Let ${\Psi}: [{s_{3}}, {s_{4}}]\subset\mathbb{R}\rightarrow \Upsilon_{\delta^{1}}$ be an $\verb"F".\verb"N".\verb"V"$ mapping. Then, fuzzy integral of ${\Psi}$ over $[{s_{3}}, {s_{4}}]$ is projected as $(FR)\int_{s_{3}}^{s_{4}} {\Psi}(\mu)\mathrm{d}\mu$,

for all ${{\delta^{1}}}\in[0, 1]$, where $\mathcal{R}_{([{s_{3}}, {s_{4}}], {{\delta^{1}}})}$ describes the space of integrable mappings.

Theorem 1.4 (^[26]). If ${\Psi}:[{s_{3}}, {s_{4}}]\subset\mathbb{R}\rightarrow \Upsilon_{\delta^{1}}$ is an $\verb"F".\verb"N".\verb"V"$ mapping. For each ${{\delta^{1}}}\in[0, 1]$, whose ${{\delta^{1}}}$-cuts highlight the bundle of $\verb"I".\verb"V".\verb"F"$, such that ${\Psi}_{{\delta^{1}}}:[{s_{3}}, {s_{4}}]\subset\mathbb{R}\rightarrow K_c$ is described as ${\Psi}_{{\delta^{1}}}(\mu) = [{\Psi}_*(\mu, {{\delta^{1}}}), {\Psi}^*(\mu, {{\delta^{1}}})]$, $\mu\in[{s_{3}}, {s_{4}}]$. Then, ${\Psi}$ is fuzzy Riemann integrable ($FR$-integrable) over $[{s_{3}}, {s_{4}}]$, $\Leftrightarrow$ ${\Psi}_*(\mu, {{{\delta^{1}}}}), {\Psi}^*(\mu, {{{\delta^{1}}}})\in \mathcal{R}_{([{s_{3}}, {s_{4}}], {{\delta^{1}}})}$, then

for all ${{\delta^{1}}}\in[0, 1]$, where $FR$ represents interval Riemann integration of ${\Psi}_{{{\delta^{1}}}}(\mu)$. For all ${{\delta^{1}}}\in [0, 1]$, $F\mathcal{R}_{([{s_{3}}, {s_{4}}], {{\delta^{1}}})}$ specifies the class of all $FR$-integrable $\verb"F".\verb"N".\verb"V"$ mappings over $[{s_{3}}, {s_{4}}]$.

Definition 1.10 (^[21]). A mapping ${\Psi}:[{s_{3}}, {s_{4}}]\rightarrow \Upsilon_{\delta^{1}}$ is termed as an $\verb"F".\verb"N".\verb"V"$ LR-convex mapping on $[{s_{3}}, {s_{4}}]$ if

for all $\mu, {\mathcal{Y}}\in[{s_{3}}, {s_{4}}], {\varrho_{\circ}}\in[0, 1]$, where ${\Psi}(\mu)\succcurlyeq\tilde{0}$ for all $\mu\in[{s_{3}}, {s_{4}}]$.

Definition 1.11 (^[26]). Let ${\tau} > 0$ and $Ł({s_{3}}, {s_{4}}, \Upsilon_{\delta^{1}})$ be the space of all Lebesgue measurable $\verb"F".\verb"N".\verb"V"$ mapping on $[{s_{3}}, \, {s_{4}}]$. Then, the fuzzy left and right RL-fractional integral operator of ${\Psi}\in Ł({s_{3}}, {s_{4}}, \Upsilon_{\delta^1})$ are defined as:

and

Furthermore, the left and right RL-fractional operator based on left and right endpoint mappings can be defined, that is,

where

and

By similar argument, we can define the right operator.

The authors ^[30] employed interval-valued unified approximate convexity to examine new refinements of inequalities. Nwaeze et al.^[31] proposed the class of interval-valued $\vartheta$-polynomial convex mappings and reported several interesting inequalities. Abdeljawad et al. ^[32] utilized the $p$ mean to develop the idea of interval-valued $p$ convexity and presented some corresponding general inequalities of Hermite-Hadamard type. Shi and his colleagues ^[33] studied the totally ordered unified convexity in the perspective of integral inequalities. Through interval-valued log-convexity and $cr$-harmonic convexity, Liu et al. ^[34,35] found the trapezium and Jensen's-like inequalities.

Budak et al. ^[36] implemented the interval-valued RL-fractional operators and convexity to derive the trapezoidal inequalities. Vivas-Cortez ^[37] introduced the totally ordered $\tau$-convex mappings and analyzed several Jensen's, Schur's, and fractional Hadamard's and kinds of inequalities. Cheng et al. ^[38] looked at new kinds of Hadamard-like inequalities using fuzzy-valued mapping and fractional quantum calculus. Bin-Mohsin et al. ^[39] bridged the harmonic coordinated convexity and fractional operators relying on Raina's special mapping to establish new 2-dimensional inequalities. For comprehensive details, consult ^{[40,41,42,43,44]}.

Recently, Fahad ^[45] proposed some novel bounds of classical inequalities pertaining to center-radius ordered geometric-arithmetic convexity and some interesting applications to information theory. Authors ^[46] explored the unified class of stochastic convex processes relying on quasi-weighted mean and cr ordering relation to conclude new forms of inequalities. For the first time, Khan and Butt established the new counterparts of classical inequalities depending upon partially and totally ordered super-quadraticity, respectively, in ^[47,48].

Costa et al. ^[49] implemented the fuzzy-valued mappings to acquire some boundaries in a one-point quadrature scheme. Zhang and his coauthors ^[50] focused on set-valued Jensen-like inequalities along with some interesting applications. Khan et al. ^[51] examined fractional analogues of fuzzy interval-valued integral inequalities. In ^[52], authors discussed fuzzy valued Hadamard-like inequalities associated with log convexity. Abbaszadeh and Eshaghi employed the fuzzy valued $r$ convex mappings to establish the trapezium type inequalities. Bin-Mohsin ^[53] introduced the idea of fuzzy bi-convex mappings and derived the various inequalities. For comprehensive details, see ^{[54,55,56,57,58]}.

The above literature is evidence that theories of inequalities are interlinked with convexity. Several classes of convexity have been introduced to reduce the limitations of classical convexity or to acquire better estimations of existing results. Researchers have applied several techniques to produce better estimations of mathematical quantities. The principle motivation is to explore super-quadratic mappings in fuzzy environments through a unified approach. First, we will propose a new class of fuzzy number-valued super-quadratic mappings based on left and right ordering relations. Further, we will give a detailed description of newly developed concepts along with their potential cases. Most importantly, we will derive classical inequalities like the trapezoidal inequality, the weighted form for symmetric mappings, and Jensen's and its related inequalities. Later on, some fractional inequalities will be presented and graphed. To increase the reliability and accuracy, some visuals and related numerical data will be provided. Finally, we will present applications based on our primary findings. This is the first study regarding super-quadraticity via fuzzy calculus.

2.   Primary findings

This part contains the results related to newly proposed notion of fuzzy super-quadratic mappings.

2.1.   Fuzzy-number-valued ${\hslash_{\circ}}$-super-quadratic functions

First, we investigate the fuzzy-valued $\hslash_{\circ}$-super-quadratic mapping.

Definition 2.1. Suppose $\hslash_{\circ}\geq0$. Let ${\Psi}:[{{s_{3}}}, {{s_{4}}}]\subseteq [0, \infty)\rightarrow \Upsilon_{\delta^{1}}$ be an $\verb"F".\verb"N".\verb"V"$ mapping such that ${\Psi}_{\delta^{1}}({\gamma}) = [{\Psi}_{*}(\delta^{1}, {\gamma}), \, {\Psi}^{*}(\delta^{1}, {\gamma})]$, and $len\left([\Psi(\gamma)]^{\delta^{1}}\right) = {\Psi}^*(\gamma, {{\delta^{1}}})-{\Psi}_*(\gamma, {{\delta^{1}}})$ is increasing with respect $\gamma$ for all $\delta^{1}\in[0, 1]$. Then ${\Psi}$ is considered to be an $\verb"F".\verb"N".\verb"V"$ $\hslash_{\circ}$-super-quadratic mapping if

holds $\forall {{\gamma}}, {y}\in[{{s_{3}}}, {{s_{4}}}]$ such that $\gamma < y$ and $|y-\gamma| < \gamma$ where ${{{{\varphi}}}}\in[0, 1]$.

Now, we enlist some potential deductions of Definitions 2.1.

● Inserting ${\hslash_{\circ}}({{{\varphi}}}) = {{{\varphi}}}$, we recapture the class of $\verb"F".\verb"N".\verb"V"$ super-quadratic mappings.

● Inserting ${\hslash_{\circ}}({{{\varphi}}}) = {{{\varphi}}}^s$, we recapture the class of $\verb"F".\verb"N".\verb"V"$-$s$-super-quadratic mappings:

● Inserting ${\hslash_{\circ}}({{{\varphi}}}) = {{{\varphi}}}^{-s}$, we recapture the class of $\verb"F".\verb"N".\verb"V"$-$s$ Godunova super-quadratic mappings:

● Inserting ${\hslash_{\circ}}({{{\varphi}}}) = {{{\varphi}}}(1-{{{\varphi}}})$, we recapture the class of $\verb"F".\verb"N".\verb"V"$-$tgs$ super-quadratic mappings:

● Inserting ${\hslash_{\circ}}({{{\varphi}}}) = 1$, we recapture the class of $\verb"F".\verb"N".\verb"V"$-$P$ super-quadratic mappings:

● Inserting ${\hslash_{\circ}}({{{\varphi}}}) = \exp({{{\varphi}}})-1$, we recapture the class of $\verb"F".\verb"N".\verb"V"$-exponential super-quadratic mappings:

● Selecting $\Psi_{*}({\gamma}, \delta^{1}) = \Psi_{*}({\gamma}, \delta^{1})$ and $\delta^{1} = 1$, we acquire the notion of $\hslash_{\circ}$-super-quadratic mapping defined in ^[17].

The spaces of ${\hslash_{\circ}}$-super-quadratic mappings and ($\verb"F".\verb"N".\verb"V"$)–${\hslash_{\circ}}$ $l$-increasing super-quadratic mappings defined over $[{{s_{3}}}, {{s_{4}}}]$ are represented by $SSQF([{{s_{3}}}, {{s_{4}}}], \hslash_{\circ})$ and $SSQFNF([{{s_{3}}}, {{s_{4}}}], {\hslash_{\circ}})$ respectively.

Proposition 2.1. Let ${\Psi}, g:[{{s_{3}}}, {{s_{4}}}]\rightarrow \Upsilon_{\delta^{1}}$ be two $\verb"F".\verb"N".\verb"V"$ mappings. If ${\Psi}, g \in SSQFNF([{{s_{3}}}, {{s_{4}}}], {\hslash_{\circ}})$, then

● ${\Psi}+g \in SSQFNF([{{s_{3}}}, {{s_{4}}}], {\hslash_{\circ}})$.

● $c{\Psi}\in SSQFNF([{{s_{3}}}, {{s_{4}}}], {\hslash_{\circ}})$, $c\geq0$.

Proof. The proof is obvious. □

Proposition 2.2. If ${\Psi}\in SSQFNF([{{s_{3}}}, {{s_{4}}}], {\hslash_{\circ}}^1)$ and ${\hslash_{\circ}}^{1}({{\varphi}})\leq \hslash_{\circ}^{2}({{\varphi}})$, then ${\Psi}\in SSQFNF([{{s_{3}}}, {{s_{4}}}], {\hslash_{\circ}}^{2})$.

Now we prove the criteria to investigate the class of $\verb"F".\verb"N".\verb"V"$–$\hslash_{\circ}$ super-quadratic mappings.

Proposition 2.3. If ${\Psi}\in SSQFNF([{{s_{3}}}, {{s_{4}}}], {\hslash_{\circ}}^1)$ and ${\hslash_{\circ}}^{1}({{\varphi}})\leq \hslash_{\circ}^{2}({{\varphi}})$, then ${\Psi}\in SSQFNF([{{s_{3}}}, {{s_{4}}}], {\hslash_{\circ}}^{2})$.

Now we prove the criteria to investigate class of $\verb"F".\verb"N".\verb"V"$–$\hslash_{\circ}$ super-quadratic mappings.

Proposition 2.4. Let ${\Psi}:[{{s_{3}}}, {{s_{4}}}]\subseteq [0, \infty)\rightarrow \Upsilon_{\delta^{1}}$ be an $\verb"F".\verb"N".\verb"V"$ mapping. For any $\gamma, y\in [s_{3}, \, s_{4}]$ such that ${\gamma} < y$ and satisfying the condition that $|y-\gamma| < \gamma$. Then, ${\Psi}\in SSQFNF([{{s_{3}}}, {{s_{4}}}], {\hslash_{\circ}})$ if, and only if, ${\Psi}_{*}({\gamma}, \delta^{1}), {\Psi}^{*}({\gamma}, \delta^{1})\in SSQF([{{s_{3}}}, {{s_{4}}}], \hslash_{\circ})$ and $len\left([\Psi(\gamma)]^{\delta^{1}}\right) = {\Psi}^*(\gamma, {{\delta^{1}}})-{\Psi}_*(\gamma, {{\delta^{1}}})$ is increasing with respect $\gamma$ for all $\delta^{1}\in[0, 1]$.

Proof. Let ${\Psi}_{*}, {\Psi}^{*}\in SSQF([{{s_{3}}}, {{s_{4}}}], \hslash_{\circ})$ and $\forall {{\gamma}}, {y}\in[{{s_{3}}}, {{s_{4}}}]$ such that $\gamma < y$ and satisfying the condition $|y-\gamma| < \gamma$. Then:

and

Combining (2.1) and (2.2) by definition of pseudo ordering relation, we have

Then by Case (ⅰ) of Remark (1.1), we have

This completes the proof of first part. For the converse part, consider ${\Psi}\in SSQFNF([{{s_{3}}}, {{s_{4}}}], {\hslash_{\circ}})$, then

The above inequality can be written as

From Definition 2.1, it is clear that $len\left([\Psi(\gamma)]^{\delta^{1}}\right)$ is increasing. Using Case (ⅰ) of Remark 1.1, we have

From (2.3), we can write as

and

It is evident from (2.4) and (2.5) that both ${\Psi}_{*}, {\Psi}^{*}\in SSQF([{{s_{3}}}, {{s_{4}}}], \hslash_{\circ})$. Hence, the result is proved. □

It is noteworthy to mention that Proposition 2.4 provides the necessary and sufficient condition for $\verb"F".\verb"N".\verb"V"$–$\hslash_{\circ}$ super-quadratic mapping. It is noteworthy to mention that Proposition 2.4 provides the necessary and sufficient condition for the $\verb"F".\verb"N".\verb"V"$–$\hslash_{\circ}$ super-quadratic mapping.

Example 2.1. Let us consider $\verb"F".\verb"N".\verb"V"$. ${\Psi}:[{s_{3}}, \, {s_{4}}] = [0, 2]\rightarrow \mathbb{\mathbb{R}}_{\circ}$, which is defined as follows

Then, for ${\delta^{1}}\in[0, 1]$, we have

Notice that both endpoint mappings ${\Psi}({{\mu}}, {\delta^{1}}) = 3{\delta^{1}}{{\mu}}^3$ and ${\Psi}({{\mu}}, {\delta^{1}}) = (6-3 {\delta^{1}}){{\mu}}^3$ are $\hslash_{\circ}$-super-quadratic mappings, respectively. So, $\Psi\in SSQFNF([{{s_{3}}}, {{s_{4}}}], {\hslash_{\circ}})$. Also $len\left([{\Psi}({{\mu}})]^{\delta^{1}}\right) = (6-6 {\delta^{1}}){{\mu}}^3$ is increasing with respect to $\mu$ for all $\delta^{1}\in[0, 1]$.

Now, we prove an alternative definition of this class of convexity for $\vartheta$ different points of $[{{s_{3}}}, {{s_{4}}}]$ known as Jensen's inequality. This inequality is useful for the development of further integral inequalities.

Theorem 2.1. Let ${\hslash_{\circ}}:(0, 1]:\rightarrow [0, \infty)$ be a nonnegative super-multiplicative mapping. If ${\Psi}\in SSQFNF([{{s_{3}}}, {{s_{4}}}], {\hslash_{\circ}})$, then

for ${{\mu}}_{\nu}\in[{{s_{3}}}, {{s_{4}}}], {{{{\varphi}}}}_{{\nu}}\in[0, 1]$ such that ${{\mathcal{C}}_{{\vartheta}}} = \sum_{{\nu} = 1}^{{\vartheta}}{{{\varphi}}}_{{\nu}}$.

Proof. If ${\Psi}\in SSQFNF([{{s_{3}}}, {{s_{4}}}], {\hslash_{\circ}})$, then it can be written as:

By pseudo order relation, one can resolve the above inequality as:

and

We employ induction technique to prove both inequalities $(2.7)$ and $(2.8)$. Fixing ${\vartheta} = 2$ and $\frac{{{{\varphi}}}_{1}}{{\mathcal{C}}_{2}} = \alpha$ and $\frac{{{{\varphi}}}_{2}}{{\mathcal{C}}_{2}} = 1-\alpha$ in (2.7), we acquire the definition of $\hslash_{\circ}$-super-quadratic mapping. To proceed further, we assume that (2.7) holds true for $\vartheta = {\nu}-1$, then

Next, we prove the validity of (2.6).

Using (2.9) in (2.10) and the super-multiplicative property of ${\hslash_{\circ}}$, we recapture

Thus, we have

By similar proceedings, we have

Comparing inequalities (2.11) and (2.12) through Pseudo ordering relation, we have

Finally, it can be transformed as

Hence, the result is accomplished. □

We deliver some corollaries of Theorem 2.1.

● Setting $\sum_{{{\nu}} = 1}^{\vartheta}{{{\varphi}}}_{{{\nu}}} = {\mathcal{C}}_{{\vartheta}} = 1$ in Theorem 2.1, we attain the generalized Jensen's inequality:

● To attain Jensen's inequality for the fuzzy interval-valued super-quadratic mapping, we set ${\hslash_{\circ}}({{{\varphi}}}) = {{{\varphi}}}$ in Theorem 2.1.

● To attain Jensen's inequality for the fuzzy interval-valued $s$-super-quadratic mapping, we set ${\hslash_{\circ}}({{{\varphi}}}) = {{{\varphi}}}^s$ in Theorem 2.1.

● To attain Jensen's inequality for the fuzzy interval-valued $s$ Godunova-Levin super-quadratic mapping, we set ${\hslash_{\circ}}({{{\varphi}}}) = {{{\varphi}}}^{-s}$ in Theorem 2.1.

● To attain Jensen's inequality for the fuzzy interval-valued $P$-super-quadratic mapping, we set ${\hslash_{\circ}}({{{\varphi}}}) = 1$ in Theorem 2.1.

● To attain Jensen's inequality for the fuzzy interval-valued exponential super-quadratic mapping, we set ${\hslash_{\circ}}({{{\varphi}}}) = \exp({{{\varphi}}})-1$ in Theorem 2.1.

● By taking $\Psi_{*}({\mu}, \delta^{1}) = \Psi_{*}({\mu}, \delta^{1})$ and $\delta^{1}$ in Theorem 2.1, we get Theorem 1.1.

Next, the result is the Schur inequality for the fuzzy interval-valued super-quadratic mappings.

Theorem 2.2. If ${\Psi}\in SSQFNF([{{s_{3}}}, {{s_{4}}}], {\hslash_{\circ}})$ and ${{\mu}}, {y}, {{\mu}}_{3}\in [{{s_{3}}}, {{s_{4}}}]$ with ${{\mu}} < {y} < {{\mu}}_{3}$ such that ${y}-{{\mu}}, {{\mu}}_{3}-{y}$ and ${{\mu}}_{3}-{{\mu}}\in [0, 1]$, then

Proof. Assume that ${{\mu}}, {y}, {{\mu}}_{3} \in I$ with ${{\mu}} < {y} < {{\mu}}_{3}$ such that ${y}-{{\mu}}, {{\mu}}_{3}-{y}$ and ${{\mu}}_{3}-{{\mu}}\in [0, 1]$. Since ${\Psi}\in SSQFNF([{{s_{3}}}, {{s_{4}}}], {\hslash_{\circ}})$, and ${\hslash_{\circ}}$ is a super-multiplicative mapping, then

Multiplying both sides of the aforementioned inequality by ${\hslash_{\circ}}({{\mu}}_{3}-{{\mu}})$ and utilizing the supermultiplicative property, we recapture

Likewise, we can prove that

From (2.13) and (2.14), we get the desired containment. □

Remark 2.1. For different substitution of $\hslash_{\circ}({\varphi}) = {\varphi}, {\varphi}^s, {\varphi}^{-s}, {\varphi}(1-{\varphi})$, we get a blend of new counterparts for different classes of super-quadraticity. By taking $\Psi_{*}({\mu}, \delta^{1}) = \Psi_{*}({\mu}, \delta^{1})$ and $\delta^{1} = 1$ in Theorem 2.2, we get the reverse Jensen's inequality, and that is proved in ^[17].

Through Theorem 2.2, we construct reverse Jensen's inequality leveraging the fuzzy number valued super-quadraticity.

Theorem 2.3. For ${{{\varphi}}}_{{\nu}}\geq 0$ and $(v, V)\subseteq I$. Let ${\hslash_{\circ}}:(0, 1]\rightarrow [0, \infty)$ be nonnegative super-multiplicative mapping and ${\Psi}\in SSQFNF([{{s_{3}}}, {{s_{4}}}], {\hslash_{\circ}})$. Then,

Proof. Substitute ${{\mu}}_{{\nu}} = v, {y} = {{\mu}}_{{\nu}}$ and ${{\mu}}_{3} = V$ in Theorem 2.2 and multiply both sides by ${\hslash_{\circ}}\left(\frac{{{{\varphi}}}_{{\nu}}}{{\mathcal{C}}_{{\vartheta}}}\right)$. Finally, we apply the sum up to ${\vartheta}$ to acquire the desired estimate. □

Now, we prove the Jensen-Mercer inequality pertaining to the fuzzy interval-valued super-quaraticity.

Theorem 2.4. Let ${\Psi}\in SSQFNF([{{s_{3}}}, {{s_{4}}}], {\hslash_{\circ}})$ and ${{\mu}}_{{\nu}}\in ({{s_{3}}}, {{s_{4}}})$ and ${{{\varphi}}}_{{\nu}}\geq0$, then

Proof. Let ${\Psi}_{*}, \Psi^{*}\in SSQF([{{s_{3}}}, {{s_{4}}}], {\hslash_{\circ}})$, then from Theorem 1.2, we get the following inequalities.

and

Bridging (2.15) and (2.16) through Pseudo ordering, we acquire the fuzzy-valued Jensen-Mercer inequality. □

Remark 2.2. For different substitution of $\hslash_{\circ}({\varphi}) = {\varphi}, {\varphi}^s, {\varphi}^{-s}, {\varphi}(1-{\varphi})$, we get fuzzy number-valued Jensen-Mercer inequalities for different classes of super-quadraticity. By taking $\Psi_{*}({\mu}, \delta^{1}) = \Psi_{*}({\mu}, \delta^{1})$ and $\delta^{1} = 1$ in Theorem 2.2, we get Jensen-Mercer inequality, and that is proved in ^[17].

Theorem 2.5. If ${\Psi}\in SSQFNF([{s_{3}}, {s_{4}}], {\hslash_{\circ}})$, then

Proof. Since ${\Psi}:[{{s_{3}}}, {{s_{4}}}]\rightarrow \mathbb{R}^+_I$ is a fuzzy interval-valued ${\hslash_{\circ}}$-super-quadratic mapping, we first consider ${{{\varphi}}} = \frac{1}{2}$, then we get

The above inequality can be transformed as

Integrating with respect to ${{\varphi}}$ on $[0, 1]$, we get

By similar arguments, we have

This implies that,

Since ${\Psi}\in SSQFNF([{s_{3}}, {s_{4}}], {\hslash_{\circ}})$, then

and

Adding (2.19) and (2.20), we have

This can be transformed as

Integrating (2.21) with respect to ${{\varphi}}$ on $[0, 1]$,

Through a similar strategy, we acquire

Combining inequalities (2.25) and (2.26), we recapture the desired result. So, the result is accomplished. □

Now, we present some deductions of Theorem 2.5.

● Taking ${\hslash_{\circ}}({{\varphi}}) = {{\varphi}}$, we recapture

● Taking ${\hslash_{\circ}}({{\varphi}}) = {{\varphi}}^s$, we recapture

● Taking ${\hslash_{\circ}}({{\varphi}}) = {{\varphi}}^{-s}$, we recapture

● Taking ${\hslash_{\circ}}({{\varphi}}) = 1$, we recapture

Remark 2.3. We can a get a blend of new Hermite-Hadamard's type inequalities for different values of $\hslash_{\circ}$ and by taking $\Psi_{*}({\mu}, \delta^{1}) = \Psi_{*}({\mu}, \delta^{1})$ and $\delta^{1} = 1$ in Theorem 2.5, we get the classical Hermite-Hadamard inequality for super-quadratic mappings, which is derived in ^[15].

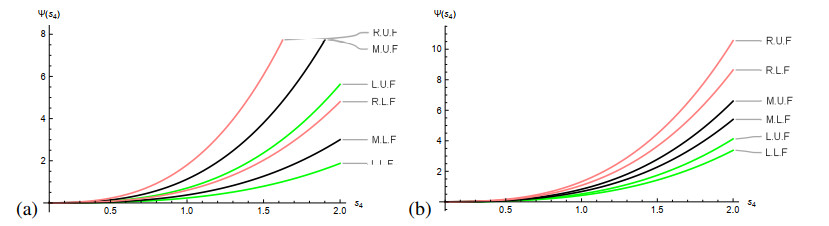
Example 2.2. Let ${\Psi}:[{s_{3}}, \, {s_{4}}] = [0, 2]\rightarrow \Upsilon_{\delta^{1}}$ be a fuzzy valued super-quadratic mapping, which is defined as

and its level cuts are ${\Psi}_{{\delta^{1}}} = \left[3{\delta^{1}} {{\mu}}^3, \, (6-3 {\delta^{1}}){{\mu}}^3 \right]$. It fulfils the condition of Theorem 2.5, then

To visualize the above formulations, we fix $\delta^{1}$ and vary ${s_{4}}$.

Note that L.L.F, L.U.F, M.L.F, M.U.F, R.L.F, and R.U.F are specifying the endpoint mappings of left, middle, and right terms of Theorem 2.5.

Theorem 2.6. If ${\Psi}\in SSQFNF([{s_{3}}, {s_{4}}], {\hslash_{\circ}})$ and $g:[s_{3}, {s_{4}}]\rightarrow \mathbb{R}$ is a symmetric mapping, then

Proof. Since ${\Psi}:[{{s_{3}}}, {{s_{4}}}]\rightarrow \mathbb{R}^+_I$ is a fuzzy interval-valued ${\hslash_{\circ}}$-super-quadratic mapping, then by multiplying (2.17) by ${g}(\varphi{s_{4}}+(1-{{\varphi}})a)$ and integrating with respect to ${{\varphi}}$ on $[0, 1]$, we get

Since $g$ is a symmetric mapping about $\frac{{s_{3}}+{s_{4}}}{2}$, then $g({{{\varphi}}}{s_{4}}+(1-{{\varphi}}){s_{3}}) = g((1-{{{\varphi}}}){s_{4}}+{{{\varphi}}}{s_{3}})$. Using this fact in the above inequality, we get

This implies that

Similarly, we have

Combining the last two inequalities in the Pseudo ordering relation, we have

Finally, we can write

Multiplying (2.21) by ${g}({{{\varphi}}}{s_{4}}+(1-{{{\varphi}}}){s_{3}}, \delta^{1})$ and integrating with respect to ${{{\varphi}}}$ on $[0, 1]$, we get

We can write

Also,

Combining (2.25) and (2.26), we achieve the required inequality. Hence, the result is completed. □

Remark 2.4. By selecting $\hslash_{\circ}({\varphi}) = {\varphi}, {\varphi}^s, {\varphi}^{-s}, {\varphi}(1-{\varphi})$ in Theorem 2.6, we get $\verb"F".\verb"N".\verb"V"$ Hermite-Hadamard-Fejer's inequalities for different classes of super-quadraticity. If we take $g({{\mu}}) = 1$ in Theorem 2.6, we obtain the Hermite-Hadamard's inequality. Also by taking $\Psi_{*}({\mu}, \delta^{1}) = \Psi_{*}({\mu}, \delta^{1})$ and $\delta^{1} = 1$ in Theorem 2.6, we obtain the Hermite-Hadamard-Fejer inequality.

Example 2.3. Let ${\Psi}:[{s_{3}}, \, {s_{4}}] = [0, 2]\rightarrow \Upsilon_{\delta^{1}}$ be fuzzy valued super-quadratic mapping, which is defined as

and its level cuts are ${\Psi}_{{\delta^{1}}} = \left[3{\delta^{1}} {{\mu}}^3, \, (6-3 {\delta^{1}}){{\mu}}^3 \right]$. Also $g:[0, 2]\rightarrow \mathbb{R}$ is a symmetric integrable mapping and is defined as $g({\mu}) = \left\{ \begin{array}{ll} {\mu}, \quad {\mu}\in[0, 1] \\ 2-{\mu}, \quad {\mu}\in (1, 2]. \end{array} \right.$. Both mappings fulfill the condition of Theorem 2.6, then

To visualize the above formulations, we fix $\delta^{1}$ and vary $\tau$.

Note that L.L.F, L.U.F, M.L.F, M.U.F, R.L.F, and R.U.F are specifying the endpoint mappings of left, middle, and right terms of Theorem 2.6.

3.   Fractional Hadamard and Fejer inequalities

This section contains fractional trapezoidal-like inequalities incorporated with $\verb"F".\verb"N".\verb"V"$-$\hslash_{\circ}$ super-quadratic mappings.

Lemma 3.1. If ${\Psi}\in SSQFNF([{s_{3}}, {s_{4}}], {\hslash_{\circ}})$, then

Proof. Let ${\Psi}:[{s_{3}}, {s_{4}}]\rightarrow \mathbb{R}^{+}_I$ be $\verb"F".\verb"N".\verb"V"$ $\hslash_{\circ}$-super-quadraticity, and we have

We can break the above inequality as

and

Furthermore, we can write:

Moreover, we have

Comparing (3.1) and (3.2), we achieve the final result. □

Lemma 3.2. If ${\Psi}\in SSQFNF([{s_{3}}, {s_{4}}], {\hslash_{\circ}})$, then

Proof. Assume that ${\Psi}:[{s_{3}}, {s_{4}}]\rightarrow \mathbb{R}^{+}_I$ is a $\verb"F".\verb"N".\verb"V"$-${\hslash_{\circ}}$ super-quadratic mapping on $[{s_{3}}, {s_{4}}]$, then

Substitute ${{\mu}} = ((1-{{{\varphi}}}){s_{4}}+{{{\varphi}}}{s_{3}})$, then

Replacing ${{\mu}}$ by ${s_{3}}+{s_{4}}-{{\mu}}$ in (3.3), we get

Adding (3.3) and (3.4), we have

Similarly,

Comparison of (3.5) and (3.6) through Pseudo ordering relation, we get our final outcome. □

Theorem 3.1. If ${\Psi}\in SSQFNF([{s_{3}}, {s_{4}}], {\hslash_{\circ}})$, then

Proof. Since ${\Psi}$ is an $\verb"F".\verb"N".\verb"V"$ super-quadratic mapping, then

Through Lemma 3.1, we can interpret

From (3.9), we have

Also,

Combining (3.10) and (3.11) via pseudo order relation, we acquire the first inequality of (3.7). From Lemma 3.2, we can write

Similarly, we have

Comparing (3.12) and (3.13) through Pseudo ordering relation, we achieve our desired result. □

Remark 3.1. For $\tau = 1$, the Theorem 3.1 transformed into Theorem 2.5. By selecting $\hslash_{\circ}({\varphi}) = {\varphi}, {\varphi}^s, {\varphi}^{-s}, {\varphi}(1-{\varphi})$ in Theorem 3.1, we get various fractional $\verb"F".\verb"N".\verb"V"$ Hermite-Hadamard's inequalities for different classes of super-quadraticity. Also by taking $\Psi_{*}({\mu}, \delta^{1}) = \Psi_{*}({\mu}, \delta^{1})$ and $\delta^{1} = 1$ in Theorem 3.1, we obtain the fractional Hermite-Hadamard's inequality for ${\hslash_{\circ}}$–super-quadratic mappings, which is given in ^[59].

Example 3.1. Let ${\Psi}:[{s_{3}}, \, {s_{4}}] = [0, 2]\rightarrow \Upsilon_{\delta^{1}}$ be a fuzzy valued super-quadratic mapping which is defined as

and its level cuts are ${\Psi}_{{\delta^{1}}} = \left[3{\delta^{1}} {{\mu}}^3, \, (6-3 {\delta^{1}}){{\mu}}^3 \right]$. It fulfills the condition of Theorem 3.1, then

To visualize the above formulations, we fix $\delta^{1}$ and vary $\tau$.

Note that L.L.F, L.U.F, M.L.F, M.U.F, R.L.F, and R.U.F are specifying the endpoint mappings of left, middle, and right terms of Theorem 3.1.

Now, we prove the weighted Hermite-Hadamard's inequality for symmetric mappings.

Theorem 3.2. If ${\Psi}\in SSQFNF([{s_{3}}, {s_{4}}], {\hslash_{\circ}})$ and ${g}:[{s_{3}}, {s_{4}}]\rightarrow \mathbb{R}$ is a nonnegative integrable symmetric mapping about $\frac{{s_{3}}+{s_{4}}}{2}$, then

Proof. Since ${\Psi}:[{{s_{3}}}, {{s_{4}}}]\rightarrow \mathbb{R}^+_I$ is a fuzzy interval-valued ${\hslash_{\circ}}$-super-quadratic mapping, then by multiplying (2.17) by ${{{\varphi}}}^{\tau-1}{g}(\varphi{s_{4}}+(1-{{\varphi}})a)$ and applying integration with respect to ${{\varphi}}$ on $[0, 1]$, we get

Since $g$ is symmetric mapping about $\frac{{s_{3}}+{s_{4}}}{2}$, then $g({{{\varphi}}}{s_{4}}+(1-{{\varphi}}){s_{3}}) = g((1-{{{\varphi}}}){s_{4}}+{{{\varphi}}}{s_{3}})$. Using this fact in the above inequality, we get

After some simple computations, we have the following inequality

By following a similar procedure, we get

Implementing the pseudo ordering relation on (3.14) and (3.15) results in the following relation

Now, we establish our second inequality. Multiplying (2.21) by ${{{\varphi}}}^{\tau-1}{g}({{{\varphi}}}{s_{4}}+(1-{{{\varphi}}}){s_{3}})$ and integrating with respect to ${{{\varphi}}}$ on $[0, 1]$, we get

After performing some computations, we get

Similarly, we have

Inequalities (3.17) and (3.18) produce the following relation

Finally, bridging inequalities (3.16) and (3.19), we achieve the Hermite-Hadmard-Fejer inequality. □

Now we discuss some special scenarios of Theorem 3.2.

● By setting $\hslash_{\circ}({\varphi}) = {\varphi}$ in Theorem 3.2, we have

● By setting $\hslash_{\circ}({\varphi}) = {\varphi}^s$ in Theorem 3.2, we have

● By setting $\hslash_{\circ}({\varphi}) = 1$ in Theorem 3.2, we have

Remark 3.2. For $\tau = 1$, the Theorem 3.2 transformed into Theorem 2.6. By selecting $\hslash_{\circ}({\varphi}) = {\varphi}^{-s}, {\varphi}(1-{\varphi}), \exp({{{\varphi}}})-1$ in Theorem 3.1, we get various fractional $\verb"F".\verb"N".\verb"V"$ Hermite-Hadamard-Fejer's inequalities for different classes of super-quadraticity. Also by taking $\Psi_{*}({\mu}, \delta^{1}) = \Psi_{*}({\mu}, \delta^{1})$ and $\delta^{1} = 1$ in Theorem 3.2, we obtain the fractional Hermite-Hadamard-Fejer's inequality for ${\hslash_{\circ}}$–super-quadratic mappings.

Example 3.2. Let ${\Psi}:[{s_{3}}, \, {s_{4}}] = [0, 2]\rightarrow \Upsilon_{\delta^{1}}$ be a fuzzy valued super-quadratic mapping, which is defined as

and its level cuts are ${\Psi}_{{\delta^{1}}} = \left[3{\delta^{1}} {{\mu}}^3, \, (6-3 {\delta^{1}}){{\mu}}^3 \right]$. Also $g:[0, 2]\rightarrow \mathbb{R}$ is a symmetric integrable mapping and is defined as $g({\mu}) = ({\mu}-1)^2$. Both mappings fulfill the condition of Theorem 3.2, then

To visualize the above formulations, we fix $\delta^{1}$ and vary $\tau$.

Note that L.L.F, L.U.F, M.L.F, M.U.F, R.L.F, and R.U.F are specifying the endpoint mappings of left, middle, and right terms of Theorem 3.2.

4.   Applications

Now, we give some applications of our proposed results. First, we recall the binary means of positive real numbers.

$(1)$ The arithmetic mean:

$(2)$ The generalized $\log$-mean:

Proposition 4.1. For ${s_{3}}, {s_{4}}\geq0$, then

Proof. This result is acquired by applying ${\Psi}({\mu}) = [3\delta^{1} {{\mu}}^3, (6-3\delta^{1}){{\mu}}^3]$ on Theorem 2.5. □

Note that Proposition 4.1 provides the bounds for generalized logarithmic mean. Next, we give the refinements of the triangular inequality.

Proposition 4.2. Let $\{{{\mu}}_{{\nu}}\}\in [{s}_{3}, {s}_{4}]$ be an increasing positive sequence. Then from Theorem 2.2, we have

and

Proof. Since ${\Psi}({{\mu}}) = |{{\mu}}|$ and ${\Psi}({\mu}) = \|{\mu}\|$ are $\hslash_{\circ}$ super-quadratic mappings, by applying these mappings on Theorem 2.2 by taking $\hslash_{\circ}({{\mu}}) = \frac{1}{{{\mu}}}$, $w_{{\nu}} = 1$, $\Psi_{*}({{\mu}}, \delta^{1}) = \Psi^{*}({{\mu}}, \delta^{1})$, and $\delta^{1} = 1$, we acquire our desired inequalities. □

Proposition 4.3. Let $\{{{\mu}}_{{\nu}}\}\in [{s}_{3}, {s}_{4}]$ be an increasing positive sequence. Then, from Theorem 2.2, we have

Particularly, we have

Proof. Since ${\Psi}({{\mu}}) = |{{\mu}}|^r$ where $r\geq1$ is $\hslash_{\circ}$ super-quadratic mapping, by applying ${\Psi}({{\mu}})$ on Theorem 2.2, and taking $\hslash_{\circ}({{\mu}}) = {{{\mu}}}$, $w_{{\nu}} = 1$, $\Psi_{*}({{\mu}}, \delta^{1}) = \Psi^{*}({{\mu}}, \delta^{1})$, and $\delta^{1} = 1$, we acquire our desired inequalities. □

Proposition 4.4. Let $\{{{\mu}}_{{\nu}}\}\in [{s}_{3}, {s}_{4}]$ be an increasing positive sequence. Then, from Theorem 2.4, we have

and

Proof. Since ${\Psi}({{\mu}}) = |{{\mu}}|^r$ and ${\Psi}({\mu}) = \|{\mu}\|^r$ for $r\geq1$ are $\hslash_{\circ}$ super-quadratic mappings, by applying these mappings on Theorem 2.4, and taking $\hslash_{\circ}({\varphi}) = {\varphi}$, $w_{{\nu}} = 1$, $\Psi_{*}({{\mu}}, \delta^{1}) = \Psi^{*}({{\mu}}, \delta^{1})$, and $\delta^{1} = 1$, we acquire our desired inequalities. □

5.   Conclusions

The theory of inequalities is the main source used to investigate the various mapping classes. We've talked about the idea of a fuzzy number-valued super-quadratic mapping that works with the LR partially ordered ranking relation, $\delta^{1}$-levels mappings, and a nonnegative mapping $\hslash_{\circ}$. This class is novel and new in literature; it reduces to several mapping classes of super-quadraticity, like fuzzy-valued super-quadratic mappings, fuzzy-valued $s$ super-quadratics, fuzzy-valued Godunova $s$ super-quadratic mappings, and many more. Also, results obtained from this class of mappings refined classical inequalities. We have developed several Jensen's and Hadamard's-like inequalities pertaining to this class of mappings. This study is significant due to various aspects because the first-time idea of super-quadratic mapping in a fuzzy environment is investigated. The proposed definition is novel due to its unified nature and strengthening the properties of the class of fuzzy numbered valued mappings. Also, this is the first study exploring the fuzzy numbered valued Hermite-Hadamard-Fejer type inequalities for strong convexity. The obtained results provides the better approximation as compared to existing results. In the future, we will try to address these inequalities by leveraging the concepts of generalized fractional operators, quantum, and symmetric quantum calculus to analyze the bounds for error inequalities like the Ostrowski inequality, Simpson's inequality, Bullen's and Boole's inequality, etc. By utilizing this class of mappings, Hausdorff-Pompeiu distance, and generalized differentiability of mappings based on Hukuhara differences as well as adopting a similar technique, one can introduce more general function classes and their applicable aspects in different domains. We will also talk about fuzzy-valued inequalities for totally ordered fuzzy-valued super-quadratic mappings and how they can be used in optimization. We hope the strategy, techniques, and ideas developed in our study will create new sights for research.

Author contributions

Muhammad Zakria Javed: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Writing-original draft, Writing-review and editing, Visualization; Muhammad Uzair Awan: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Writing-review and editing, Visualization, Supervision; Loredana Ciurdariu: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Writing-review and editing, Visualization; Omar Mutab Alsalami: Conceptualization, Software, Validation, Formal analysis, Investigation, Writing-review and editing, Visualization. All authors have read and agreed for the publication of this manuscript.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Funding

This research was funded by TAIF University, TAIF, Saudi Arabia, Project No. (TU-DSPP-2024-258).

Acknowledgments

The authors are thankful to the editor and anonymous reviewers for their valuable comments and suggestions. The authors extend their appreciation to TAIF University, Saudi Arabia, for supporting this work through project number (TU-DSPP-2024-258).

Conflict of interest

The authors declare no conflicts of interest.