Biological emergent properties in non-spiking neural networks

1.   Introduction

Population ageing has become a global social issue. Aged people are more susceptible to Parkinson's disease and accidents, which result in various types of physical disabilities. Clinical studies have shown that reasonable rehabilitation training can help patients restore some limb functions. It also helps patients regain some of their living and working abilities. At present, robotics has been widely used in various industries. Robots have also successively started to be used in social services, medical care, rehabilitation, and other fields.

Surface electromyography (sEMG) has been considered a reliable source of biosignals for human-computer interaction control ^[1]. sEMG is not easily affected by the external environment, such as light and ambient sound changes. During human movement, sEMG is generated by the muscle groups associated with the movement. sEMG can reflect the specific movement intention of the body to some extent ^[2], and it can better establish a human-machine collaborative control system for rehabilitation robots. Compared to inertial sensors, sEMG-based control systems have more potential to enable human-machine collaboration.

In remote control, robots can be used as replacements for safe and diverse tasks. However, the performance of current robotic systems is far below the expected level compared to human control and interaction capabilities during task execution ^[3]. Therefore, human motion or control capabilities are transferred to the robot through a neural interface to enhance the robot's functionality and interaction capabilities ^[4]. SEMG decoding of the continuous joint angle provides a more natural and effective solution for the realization of human-computer interaction ^[5]. For example, sEMG signals can be used to control a robotic arm ^[6] remotely. A human activity-aware shared control solution for medical human-robot interaction is a hot research topic. Human-machine interactions based on sEMG can generate remote object operations that are more suitable for human perception. For example, shared human-robot control incorporates the advantages of both humans and robots and is an effective way to facilitate efficient surgical procedures ^[7]. sEMG-based perspective prediction for human activity-aware shared control solutions for medical human-computer interaction.

Rehabilitation robots in the medical field are a successful example of human-robot interaction. Since rehabilitation robots can provide practical rehabilitation training, they can meet the shortage of rehabilitation resources while satisfying patients' rehabilitation training ^[8]. In addition, rehabilitation robots can improve the actual movement of human-robot interactions and provide behavioral predictions. Although the trigger control of traditional rehabilitation robots can meet training needs, the safety and comfort of control cannot be guaranteed to a certain extent ^[9]. Continuous control of the rehabilitation robot based on sEMG is a more feasible control strategy. The key is to obtain the shoulder and elbow angular motion by sEMG.

Early on, only a small number of discrete motions could predict joint angles, which could have been more intuitive for implementing control schemes close to the natural hand. Continuous control of the upper limb rehabilitation robot using sEMG signals can simulate the continuous movement of human upper limbs and guide the rehabilitation training of patients. Therefore, continuous joint angle estimation by sEMG has become a hot topic of current research. The raw sEMG signal contains a large amount of information indicating the intention of upper limb movement. However, the random and nonsmooth nature of the raw signal cannot be directly applied to action recognition, so feature extraction of the sEMG signal is required ^[10]. The quality of feature extraction determines the output. Therefore, good feature engineering helps predict the upper limb's continuous angle ^[11]. Researchers usually choose time-domain, frequency-domain, and time-frequency domain features for sEMG feature extraction ^[12]. Time-domain features are commonly used, such as the mean absolute value (MAV), root mean square (RMS), and zero crossings (ZC). MAV is the average of the absolute values of the amplitude of the sEMG signal, RMS reflects the energy level of the sEMG during muscle activity, and ZC is the number of times the sEMG value crosses the transverse coordinate ^[13].

Researchers have used various regression models to establish a mapping relationship between sEMG and joint angles. Wang et al. ^[14] proposed using wavelet packet energy entropy in a particular subspace as a feature of the sEMG signal and using the Elman neural network optimized by a genetic algorithm to predict the shoulder and elbow joint angles. Jing et al. ^[15] used a BP artificial neural network to establish a mapping model between sEMG signals and elbow joint angles to predict elbow joint angles. Tang et al. ^[16] used the particle swarm optimization (PSO) algorithm to optimize the LSTM, and they used the optimized network to create a mapping between the sEMG signal and the joint angles.

To improve the prediction of continuous motion angles of upper limb joints and the robustness of the model, we propose a neural network of SE-TCN. We improve the TCN network model to increase the accuracy of joint angle prediction. The experimental results indicate that the method proposed in this paper has high accuracy and robustness. The main contributions of this paper are as follows:

1) We recorded sEMG of seven human upper limb movements as a dataset for the model.

2) In this paper, the depth of TCN is extended to extract sEMG feature information while preserving the original data.

3) The temporal features of the muscle blocks dominating upper limb movements are not obvious, resulting in low joint angle accuracy. In this paper, the SE-Net incorporated in the model can increase the weight of important feature information and improve the accuracy of joint angle prediction.

4) To demonstrate the prediction performance of the SE-TCN model proposed in this paper in human-computer interaction. This paper plots the predicted joint angle curves and the corresponding actual joint angle curves to visualize the model performance. Each model's learning and generalization abilities were also analyzed using RMSE, R², and correlation coefficients.

The rest of this paper is organized as follows. Section 2 describes the acquisition, presentation, and preprocessing process of sEMG signals in the dataset and introduces the basic principles of the SE-TCN. The experimental results obtained via the proposed and two reference models and their comparative analysis are presented in Section 3. The conclusions and future work are discussed in Section 4.

2.   Materials and methods

2.1.   Data acquisition

A total of ten healthy subjects (five males and five females) were invited to participate in this data acquisition experiment to collect continuous motion angles and sEMG signals of the upper limb joints. The statistics on the subject's height, weight, and body mass index (BMI) are given in Table 1.

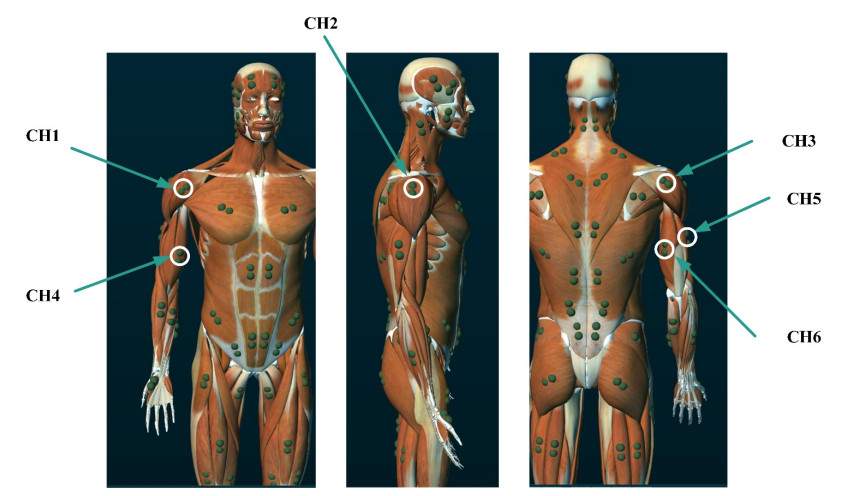
A 16-channel wireless electromyography (EMG) device from NORAXON, USA, was used to acquire sEMG signals and joint angles, with a sampling frequency of 1500 Hz. Wireless EMG sensors were placed on the anterior deltoid, middle deltoid, posterior deltoid, biceps, lateral triceps, and medial triceps. The position location of the electrodes is shown in Figure 1. The sensor designations and sites are listed in Table 2.

The angle acquisition device used NORAXON's angle sensors. As shown in Figure 2, the angle sensors were placed on the shoulder and elbow joints of the subjects.

Detailed information on the EMG and angle sensors used is given in Table 3.

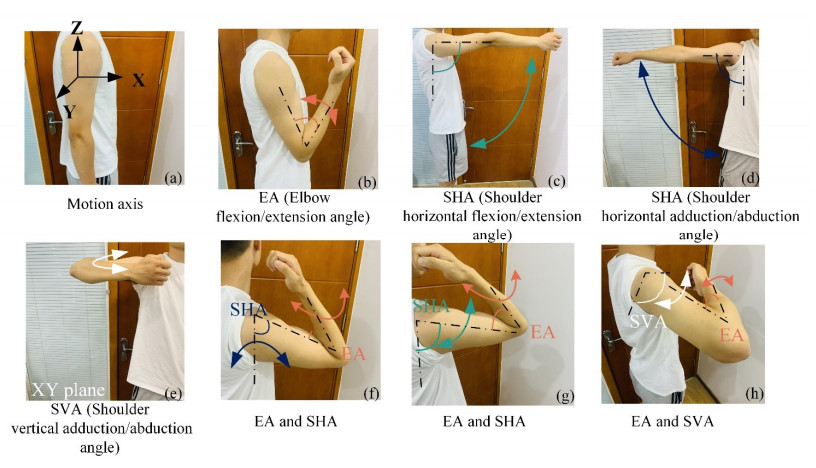
For good contact between the sensor and the arm muscles, the skin surface of the recording area was wiped clean with alcohol before placing the sensor. When the subject's skin was dehydrated, the area was tapped with medical tape to remove the skin cells. This helped to improve the quality of the obtained sEMG signal. In this paper, seven movements were designed, as shown in Figure 3, to simulate the angle of the elbow and shoulder joints of the actual movement. These movements were (ⅰ) elbow joint flexion/extension, (ⅱ) shoulder joint flexion/extension, (ⅲ) shoulder joint horizontal adduction/abduction, (ⅳ) shoulder joint vertical adduction/abduction, (ⅴ) shoulder joint horizontal adduction/abduction and elbow flexion/extension, (ⅵ) shoulder joint flexion/extension and elbow flexion/extension, and (ⅶ) shoulder joint vertical adduction/abduction and elbow flexion/extension.

To simulate actual upper limb movements, subjects performed the following actions: elbow joint flexion/extension (in the XZ plane, Figure 3(b)), shoulder joint flexion/extension (in the XZ plane, Figure 3(c)), shoulder joint horizontal adduction/abduction (in the YZ plane, Figure 3(d)), shoulder joint vertical adduction/abduction (in the XY plane, Figure 3(e)), and three shoulder adduction/abduction and elbow flexion/extension simultaneous movements (in YZ plane—Figure 3(f), XZ plane—Figure 3(g) and XY plane—Figure 3(g)). For example, Figure 3(b) shows that the shoulder joint remained unchanged when measuring the elbow joint angle. Meanwhile, when measuring the shoulder joint, the elbow joint remained unchanged, as shown in Figure 3(c)–(e). When measuring the elbow joint and shoulder joint angle at the same time, the crankshaft was shifted before the shoulder joint (Figure 3(f)–(h)). Simultaneous measurement of EA, SVA, and SHA angles was also performed.

Before the sEMG signal and angle signal acquisition, these basic movements had to be familiarized. sEMG signals and upper limb joint angles were acquired simultaneously to maintain correspondence. Subjects were asked to perform these movements at the same speed within three minutes, repeating each movement five times. At the beginning of the action, the acquisition device records the sEMG signal and the angle sensor signal with a sampling frequency of 1500 Hz. It saves the data after completing all the actions. For example, it took 3 min for subject 1 to complete all the activities and store 270,000 data samples. We constructed the dataset by saving data from each subject and then used 70% of the collected experimental data as the training set, 20% as the validation set, and 10% as the test set. The study complied with the Declaration of Helsinki regulations, and the Ethics Committee approved the protocol. All subjects gave written informed consent and permitted their photographing and data to be included in publications for scientific and educational purposes.

2.2.   Data preprocessing

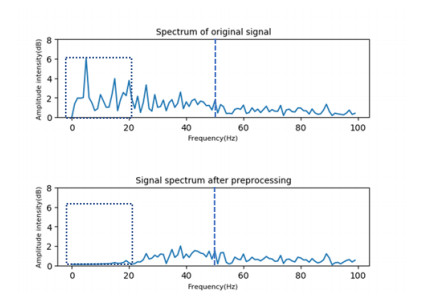
Acquiring sEMG signals may be disturbed by environmental noise, so the received sEMG signals had to be denoised. Since the effective information of the sEMG signals is mainly distributed between 20 and 200 Hz, this paper used the third-order Butterworth bandpass filter to retain frequencies between 20 and 200 Hz. The attenuation rate of the filter was 18 dB per octave. At the same time, this paper uses a notch filter to remove 50 Hz power frequency interference. To prove the filter's effectiveness, the signal spectrograms before and after sEMG filtering were obtained and plotted in Figure 4. As can be seen from the dotted line in Figure 4, the filter is able to effectively remove low frequency signals from 0 to 20 and 50 Hz of industrial frequency interference signals.

2.3.   Feature extraction

In this paper, the method of selecting a sliding time window for data segmentation was chosen, and the signal features were calculated and analyzed by obtaining several sEMG subdata segments. A sliding window of 100 ms was selected, and the signal was characterized by feature extraction with a sliding step of one sample. Currently, time domain, frequency domain, and time-frequency domain features have been widely used to analyze and process sEMG signals ^[17,18]. Three time-domain features of variance (VAR), mean absolute value (MAV), root mean square (RMS), and median frequency (MF) were used in this study. These features of the sEMG signal can be described as follows:

VAR:

MAV:

RMS:

MF:

2.4.   SE-TCN

In recent years, temporal convolutional network (TCN) networks have achieved remarkable results in dealing with temporal feature regression and multiclass classification. TCN networks have the following characteristics ^[19].

Parallelism: Since convolutional neural networks use the same convolutional kernel for each layer, a long sequence of inputs can be processed in parallel with TCNs, unlike RNNs ^[20] and LSTMs ^[21], which are processed sequentially.

Flexible receptive field: The introduction of hole convolution can expand the field of perception without increasing pooling, so the TCN network has a flexible field of perception.

Variable input length: 0-padding is added to the temporal convolutional network to enable the network to input data of different lengths.

More stable gradients: They do not explode or disappear due to sharing parameters in different time periods.

Less memory: The same layer of convolutional kernels in a temporal convolutional network is shared to take up less memory ^[22].

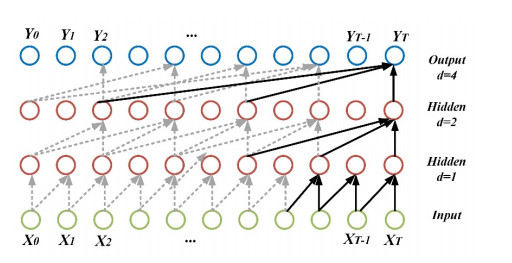
TCN consists of causal convolution, inflation convolution, and residual links. The difference between causal convolution and traditional convolutional neural networks is that it cannot see future data and is a one-way structure, not a two-way one. The value at the moment of causal convolution depends only on the value at the moment of the previous layer and the value before it, so it is known that causal convolution strictly adheres to the time constraint.

The structure diagram of causal convolution is shown in Figure 5. The input sequence of the causal convolution layer is $X = \left({x}_{1}, {x}_{2}, \cdots , {x}_{T}\right)$, and the filter is $F = \left({f}_{1}, {f}_{2}, , \cdots {f}_{k}\right)$. The causal convolution at ${x}_{t}$ can be defined as Eq (5):

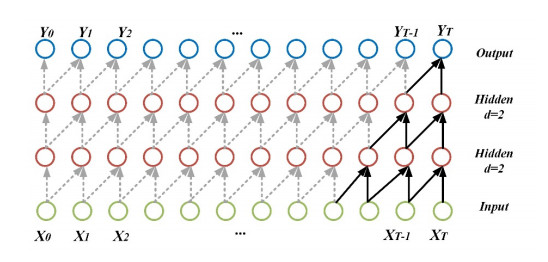
Causal convolution also suffers from the deficiency that the size of the convolution kernel limits the modeling length of time. For longer correlations to be captured, many layers must be stacked linearly. Researchers have proposed inflated convolution to solve this problem, as shown in Figure 6 ^[23].

Inflationary convolution allows for interval input sampling during convolution, and the sampling rate is controlled by $d$ in Figure 6. When $d = 1$, extended convolution is the regular causal convolution operation. Generally, the value of $d$ is 1, 2, 4, etc. The value of $d$ increases as the number of layers of the network structure increases. In the network training process, deepening the number of layers of the network structure, increasing the filter size, and increasing the expansion factor $d$ can effectively increase the perceptual field of the convolutional network. In a network with a large receptive field, the neurons can involve a more extensive range of sequence data in the convolution operation of that layer, which helps to extract more global information. Conversely, a network with a smaller receptive field can obtain more detailed information in the sequence. Assuming that the expansion coefficient at ${x}_{t}$ is $d$, the expansion convolution can be defined as follows:

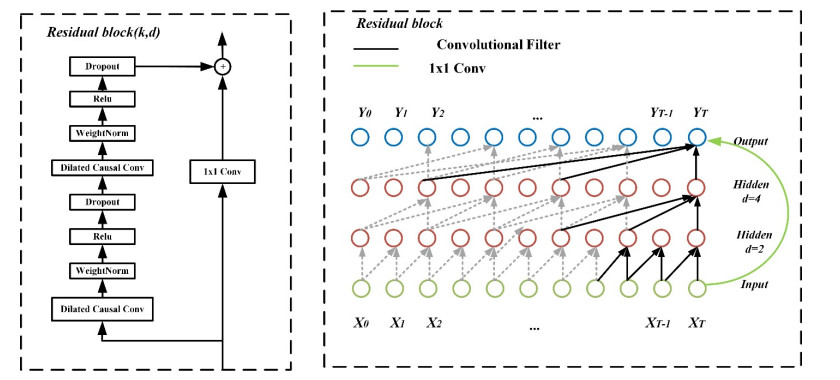
As the network layers deepen, the input data need to be operated several times with the constantly updated weight parameters, and the network structure will become more complex. To alleviate network degradation and other problems, the improved TCN structure incorporates residual connections, whose structural diagram is shown in Figure 7 ^[19].

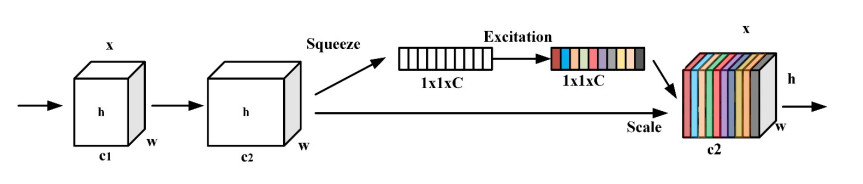
The input to the TCN network is the extracted sEMG features, but there is a problem of importance loss for different feature channels during convolutional pooling. Squeeze and excitation networks (SE-Net) emerged to solve the problem of feature importance loss that occurs in the traditional convolution process ^[24]. SE-Net defaults that each feature channel is equally important, while the importance of different channels varies in the actual problem.

SE-Net contains two parts, squeeze and excitation, and its structure is shown in Figure 8. Here $w$ and $h$ are the feature map width and height, respectively; $c$ is the number of channels; and the input feature map size is h ×w × c. Supposing the input is a feature channel of h × w × c, first perform a global average pooling on it, after the compression operation, the feature map is compressed into a 1 × 1 × c feature map, and then two fully connected layers are used to perform a nonlinear transformation of the squeeze result. Finally, there is the Scale section, where the results obtained using excitation are multiplied by the input features of the corresponding channel ^[25].

Since the problem of feature channel importance loss is solved using SE-Net, the latter is placed before the TCN network. The sEMG signal features input to the TCN are first adjusted by SE-Net to adjust the weights, and then the upper limb joint angles are predicted by the TCN. The network adjusts the weights of SE-Net according to the loss function so that the individual sEMG signal features of the input model can adjust the weights they occupy. This allows the dominant muscle to occupy a higher weight when predicting the shoulder or elbow joint angle, depending on the dominant muscle.

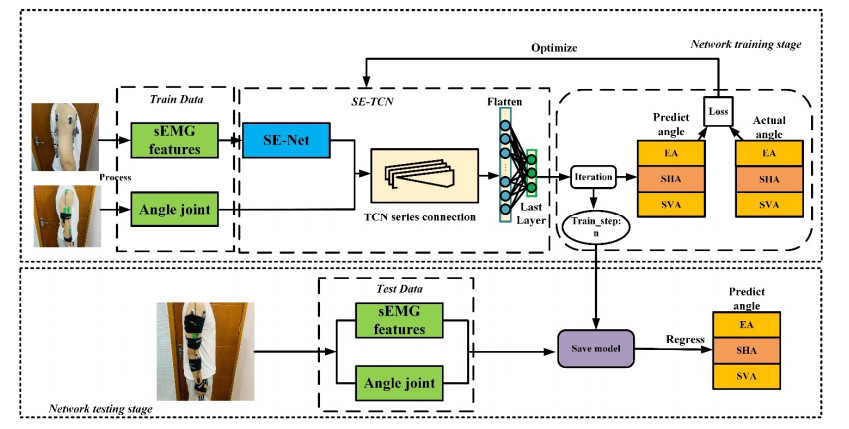
In addition, the depth of the TCN is extended, and the convolution module and residual module continue to be added to the original TCN network. Connecting the original input information with the convolved features. The number of outputs of the last fully connected layer is the same as the number of predicted joint angles. To maintain the integrity of the initial input information, the convolutional expansion factor $d$ = 1 in the residual module, and the structure of the tandem TCN is shown in Figure 9. The features extracted by each muscle are input into the SE-TCN module, and the algorithm flowchart is shown in Figure 10.

In Figure 10, the SE-TCN model is trained using the training set in the network training stage. The network parameters are updated by the mean square error of the predicted angle of the model with respect to the actual angle. The best trained model is kept in the n iterations of the training network (Save model in Figure 10). In the Network testing stage, the saved model is used to predict the joint angle from the test set data.

In the selection of the parameters of the network model, we tried many times and finally selected the best set of parameters. The resulting SE-TCN model had a SE-Net filter size of 32, with 21 neurons in the second fully connected layer. The first TCN input layer had a filter size of 16, a convolutional kernel size of k = 3 and an expansion factor d = 2. The hidden layer had a filter size of 16, a convolutional kernel size k = 2, and d = 4. The second TCN input layer had a filter size of 32, a convolutional kernel size k = 3, an expansion factor d = 8, a filter size of the hidden layer of 64, a perceptual field k = 3, d = 16, a filter size of the output layer of 64, and a convolution kernel k = 1. Therefore, we used the mean square error $\left(mse\right)$ to be the loss function, as shown in Eq (7):

The optimizer uses Adam, an algorithm that can replace the traditional stochastic gradient descent process for first-order optimization, which can iteratively update the network weights based on training data. It has the advantages of simple implementation, high computational efficiency, and small memory requirements. The learning rate of Adam was set to 0.01 in this paper.

2.5.   Other models

2.5.1.   Backpropagation (BP) network

The BP network consists of an input, hidden, and output layer. Researchers have already implemented BP networks to predict upper limb joint angles ^[26]. This study used the input BP network with a 20-dimensional sEMG signal feature and angle signal, and the output was a three-dimensional angle signal. The number of neurons in the input layer of the BP network was 20, the number of neurons in the middle layer was 15, and the number of neurons in the output layer was 3.

2.5.2.   Long Short-Term Memory (LSTM) network

LSTM is a recurrent neural network (RNN) architecture consisting of a forgetting, input, and output gate. Researchers have proposed LSTM-based methods for estimating continuous joint angle motion ^[16]. The input LSTM was a 20-dimensional sEMG signal feature and angle signal, and the output was a three-dimensional angle signal. There were three layers of LSTM in the model, and the number of neurons in each layer of LSTM was 50. The learning rate was 0.001, the loss function was MSE, and the optimizer was the Adam algorithm.

2.6.   Evaluation indicators

This study used the root mean square error (RMSE) and the mean coefficient of determination $({R}^{2}$) to evaluate the angular prediction performance. The correlation coefficient is the metric used for the analysis to describe the estimation performance accurately. Ten subjects were tested separately using the correlation coefficient (CC).

A smaller value of RMSE means better model prediction results. The RMSE is calculated as follows.

where $N$ is the length of the joint angle, ${y}_{n}^{{{'}}}$ is the estimated joint angle, and ${y}_{n}$ is the actual joint angle. ${R}^{2}$ is calculated as follows:

where ${y}_{n}$ is the actual joint angle, $\stackrel{-}{{y}_{n}}$ is the average of ${y}_{n}$, and ${y}_{n}^{{{'}}}$ is the estimated joint angle. R² is between 0 and 1. The closer the result of R² is to 1, the better the regression fit is. When the fit is greater than 0.8, the model is considered to have a better fit.

The correlation coefficient measures the strength of the relationship between two sets of series and can be used to assess how well the predicted joint angles match the actual joint angles.

where $r$ denotes the correlation coefficient, $cov(y{{'}}, y)$ denotes the covariance of $y{{'}}$ and $y$, and $var$ denotes the variance. The closer the correlation coefficient is to 1, the stronger and more positively correlated the correlation is.

3.   Results

The results of all analyses were based on data from ten healthy subjects summarized in Table 1. Seven movements were designed to simulate the movements of the elbow and shoulder joints, each repeated five times. Seventy percent of the collected experimental data were used as the training set, 20% as the validation set, and 10% as the test set. In this paper, we used the angle estimation results to validate the accuracy and feasibility of the model versus other available models.

3.1.   Performance with and without SE-Net

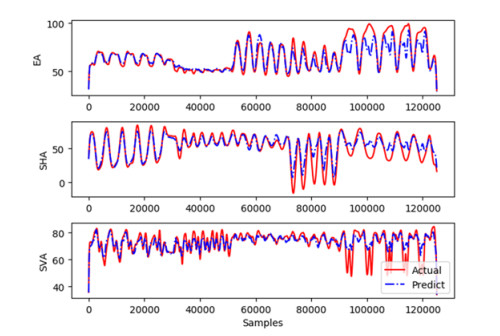
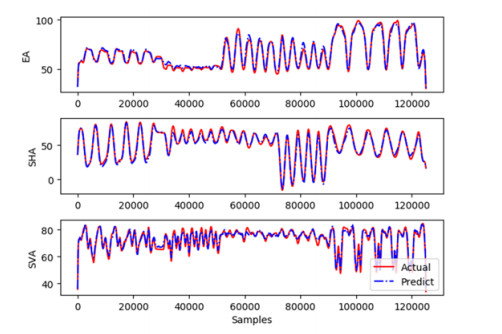
Before comparing the models, experiments were conducted to check whether SE-Net improves the TCN network. The prediction results of the training set before adding SE-Net are shown in Figure 11. The poor joint angle fit is the feature loss due to the different feature importance of the channels in the convolution pooling process. For example, the deltoid muscle dominates the shoulder joint extension, and the joint angle is poorly fitted when predicting the shoulder joint angle due to the nondominance of the deltoid feature among the input multidimensional features. With the inclusion of SE-Net, the prediction results of the training set were obtained, as shown in Figure 12. It can be seen from the figure that the angle prediction result is better than that of the network without SE-Net. The input sEMG signal features first went through the SE-TCN to predict the angle, and the network adjusted the weight of SE-Net according to the loss function so that the features of the dominant motor muscle occupied a higher weight.

In addition, the parameters of the network model remained consistent during the testing. All left-axis units are angles (°) for an accurate comparison of the results. It can be seen that the angles predicted by TCN became more accurate after adding SE-Net.

3.2.   Comparison of angle estimation results of different models

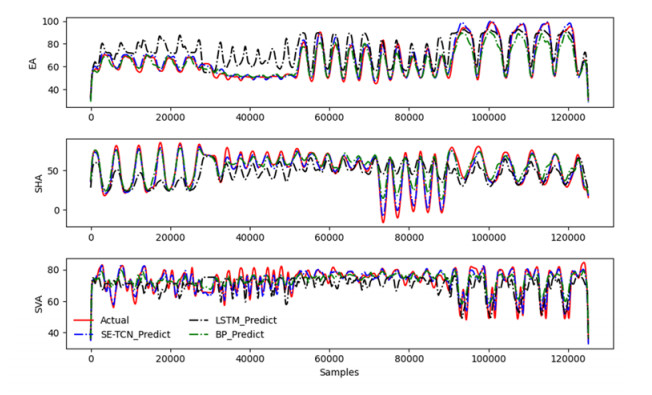
In this section, the performance of the proposed SE-TCN model for joint angle estimation was investigated and compared with the BP network and LSTM models. For model comparison, the proposed model and the other two models were based on the TensorFlow and Keras ^[27] frameworks, and the sEMG data after preprocessing and feature extraction were used as a comparison between each input validation model. To estimate the shoulder and elbow joint angles of the subjects, the processed sEMG signals were fed into the BP, LSTM and SE-TCN networks for training. The proposed SE-TCN model had significantly better fitting ability than the BP network and the LSTM model.

As shown in Figure 13, BP and LSTM had poorer angle prediction results than SE-TCN. The prediction errors of the BP and LSTM models were more apparent when the joint motion amplitude was large. Meanwhile, the proposed SE-TCN model could predict the joint motion most precisely, and the prediction curves nearly overlapped with the actual curves.

After training, the test set was fed into the BP network (Figure 14(a)), the LSTM model (Figure 14(b)), and the SE-TCN model (Figure 14(c)) for prediction. The BP network was less accurate and smoother in predicting SVA angles, and the LSTM network improved slightly but was still lacking in fine angle prediction. The proposed SE-TCN network had more precise and smoother angles than the BP and LSTM networks in three consecutive motions. Because no effective feature weighting was performed before input to the network, the muscle features dominating the motion of a joint did not occupy more weight in predicting the joint angle.

3.3.   Comparative analysis of the three models' performances

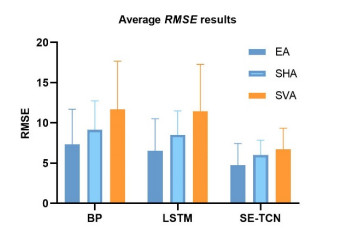
The RMSE results on the joint angle prediction via the BP network, LSTM, and SE-TCN models for ten subjects are listed in Table 4. When the sEMG signals after preprocessing and feature extraction were input into the network structure, the continuous estimated values of the BP network (EA: 8.479, SHA: 10.854, SVA: 11.530) and LSTM networks (EA: 7.168, SHA: 9.974, SVA: 10.705) were significantly higher than the continuous estimated values of the SE-TCN network (EA: 5.353, SHA: 6.121, SVA: 5.818). The mean RMSE of SE-TCN compared to BP and LSTM decreased by (EA: 25.3% SHA: 38.6%, SVA: 45.6%) and (EA: 36.8%, SHA: 43.6%, SVA: 49.5%). The lower the RMSE result is, the better the fitting performance of the model. Therefore, the prediction results of the SE-TCN were significantly better than those of BP and LSTM.

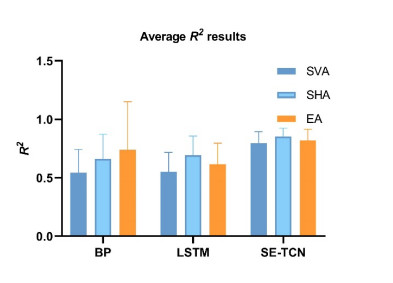
The continuous estimated R² evaluation results of the BP, LSTM, and SE-TCN networks are summarized in Table 5. When the sEMG signals after preprocessing and feature extraction were incorporated into the network structure, the continuous estimated R² values of the BP network (EA: 0.721, SHA: 0.708, SVA: 0.640) and the LSTM network (EA: 0.588, SHA: 0.640, SVA: 0.627) were significantly lower than the continuous estimated R² values of the SE-TCN network (EA: 0.819, SHA: 0.843, SVA: 0.827). The mean R² of SE-TCN compared to BP and LSTM increased by (EA: 13.60%, SHA: 19.01%, SVA: 29.22%) and (EA: 39.20% SHA: 31.72%, SVA: 31.89%). The higher the result of R² is, the better the fitting performance of the surface model. The results show that the prediction results of the SE-TCN were significantly better than those of BP and LSTM.

The RMSE and R² values of the ten subjects are plotted in Figures 15 and 16, respectively. The SE-TCN has the lowest RMSE and the highest R² values. The prediction results of the three networks show that the SE-TCN network has the best performance.

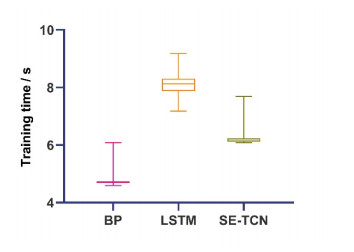
Reducing the training time can improve the system's response speed, thereby improving the real-time performance of the system. Therefore, a more comprehensive comparative analysis of the models was conducted. The same data set and the same computer were used in this study to train the LSTM and SE-TCN networks and record the running time of the two models according to the comparative experiment. The time of each training session was recorded, as shown in Figure 17. It can be seen that the model training speed of SE-TCN is much faster than LSTM.

3.4.   Comparison of model salience

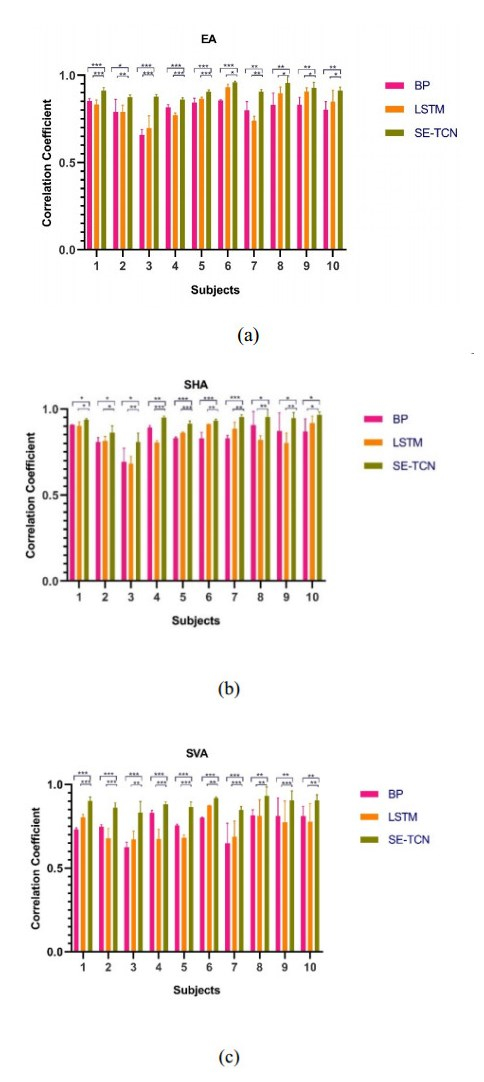
These ten subjects were tested to demonstrate the reproducibility and accuracy of the method systematically. For each model, ten runs were made, and correlation coefficients were recorded for three angles. The mean values of the correlation coefficients for the subjects are listed in Table 6. The results of the SE-TCN network (EA: 89.4%, SHA: 90.8%, SVA: 87.2%) were better than those of the LSTM network (EA: 80.9%, SHA: 83.7%, SVA: 80.9%) and BP networks (EA: 79.9%, SHA: 82.7%, SVA: 73.3%). To further verify whether the proposed SE-TCN model outperformed the BP and LSTM models, a t-test was performed. The test results and correlation coefficients of the ten subjects are presented in Figure 18, confirming that the SE-TCN model significantly outperformed the BP and LSTM models. The stars (^*) represent significance.

4.   Discussions

This study attempted to improve the prediction of upper limb joint angles using sEMG signals by comprehensively combining SE-Net and series TCN network components. The prediction results for multiple joint angles of the upper limbs show that the proposed SE-TCN features adjustable feature channel weights and a gradient-free burst of the TCN. It offers high accuracy and high performance in the task of predicting angles.

After several evaluations, the proposed SE-TCN and available BP and LSTM networks could predict upper limb joint angles based on sEMG signals. Through comprehensive experiments, it was found that all three networks could fit the actual joint angles during training. Statistical results show that the mean RMSE of SE-TCN compared to BP and LSTM decreased by (EA: 25.3% SHA: 38.6%, SVA: 45.6%) and (EA: 36.8%, SHA: 43.6%, SVA: 49.5%). Compared to BP and LSTM, the mean R² of SE-TCN increased by (EA: 13.60%, SHA: 19.01%, SVA: 29.22%) and (EA: 39.20% SHA: 31.72%, SVA: 31.89%). SE-TCN has better performance than other networks. By comparison of significance, the SE-TCN model outperformed the BP ($\rho < 0.001$) and LSTM ($\rho < 0.01$) models among the ten subjects. Although the BP network had the disadvantage of underpredicting temporal sequences, it was better than LSTM in some aspects, as in subject 4.

The BP network was unable to explore the correlation of the sequence data in processing the time series, resulting in a poor fit of the BP network. Besides, although LSTM did outperform the BP network, due to the linear mode of processing it took longer training time under normal circumstances. Because TCN networks can perform convolution in parallel, the training time was much shorter. In addition, TCN solved the disadvantage of gradient explosion of LSTM. The SE-Net used in this paper alleviates the problem of missing feature importance in the traditional convolution process. The SE-TCN model had the best overall estimation performance in terms of joint angle prediction.

However, this study had some limitations. The sensor we used is the NORAXON companion angle sensor. When the subject moved, it arched along with the elevated muscles. In human-machine interaction applications such as robot-assisted minimally invasive surgery, finer sensors are required to capture angular data.

In a follow-up study, finer sensors will be used, and the network structure will be improved to extract better the information hidden in the time series. A larger population of participants with a broader age, weight, and BMI range will be recruited, and more significant sEMG features will be extracted further to improve the prediction of upper limb joint angles.

5.   Conclusions

The maturity of human-computer interaction technology has made possible the use of sEMG to control exoskeleton robots and intelligent prostheses. However, the angle control of the upper limb rehabilitation robot still has the disadvantage of inflexibility. Although BP and LSTM can predict the joint angles, they have the disadvantages of poor smoothness, high memory consumption, and low accuracy. In addition, LSTM typically requires a long training time.

In this paper, we proposed the SE-TCN algorithm. Deepen and extend the network depth of the TCN to solve the problem of the long training time of LSTM. In addition, the temporal features of the muscle blocks dominating the upper limb movements are not apparent, resulting in low joint angle accuracy. SE-Net was added to adjust the feature weights of the network. Finally, we design experiments to compare the proposed SE-TCN network with the BP and LSTM networks. The results show that the SE-TCN proposed in this paper shows high accuracy and performance in predicting angles.

The approach presented in this paper improved several aspects, including accuracy and training time. In the future, we will use this network further to expand the application of bioelectricity signals and human-computer interaction.

Acknowledgments

The authors would like to thank all the colleagues that have supported this work. This work is jointly supported by Natural Science Foundation of Hebei Province (No. F2021201002, No. F2021201005); Science and Technology Project of Hebei Education Department (No. ZD2020146); Key Research and Development Program of Baoding Science and Technology Bureau (No.1911Q001); The Program for Top 80 Innovative Talents in Colleges and Universities of Hebei Province (No. SLRC2017022).

Conflict of interest

We declare that we have no financial and personal relationships with other people or organizations that can inappropriately influence our work, there is no professional or other personal interest of any nature or kind in any product, service and/or company that could be construed as influencing the position presented in, or the review of, the manuscript entitled 'SE-TCN network for continuous estimation of upper limb joint angles'.