The Parathyroid Hormone Family of Ligands and Receptors

1.   Introduction

The traveling salesman problem (TSP) is one of the most intensively studied combinatorial optimization problems in the field of graph theory and operations research. It is believed that the TSP was first studied by Hamilton and Kirkman ^[1]. Since then, many and various algorithms and approximation algorithms have been proposed.

Given a set of nodes (cities) and the pairwise cost (or travel distance), the TSP is to find the best possible cycle of visiting all the cities and returning to the starting point that minimize the total travel cost. The general solution algorithm that guarantees the shortest path has exponential complexity, and no known efficient algorithm exists to date, since TSP is also an NP-hard problem.

The TSP naturally finds many applications in the field of transportation and logistics, such as arranging school bus routes to pick up the children ^[2], scheduling stacker cranes in warehouses ^[3], and delivering ordered meals to the customers ^[4]. Slightly modified, TSP can be applied to some problems which are unlike the path finding problems at first sight. For example, in the DNA sequencing problem ^[5], the node represents DNA fragments, and distance cost is defined as the similarity measure between DNA fragments.

Various methods have been proposed to solve TSP, such as violence enumeration, dynamic programming (DP) ^[6], and Hopfield neural network (HNN) ^[7]. Violence enumeration, as the simplest method, has the time complexity $ O(n!) $. DP decomposes the problem into couples of sub-problems which has much smaller time complexity as $ O(n^22^n) $ ^[6]. As an intelligent method, Hopfield neural network algorithm(HNN) ^[7] handles the permutation matrix which is mapped to the legal solution of TSP, and minimizes the energy function intelligently. The drawback of this method is that it may suffer from slow convergence and low accuracy when used to solve the TSP ^[8].

Using swarm intelligence ^[9,10] to address TSP has become a new trend in the past decades. Many metaheuristics has been reported excelling in solving TSP, such as genetic algorithm (GA) ^[11,12], particle swarm optimization (PSO) ^[13,14], and ant colony optimization (ACO) ^[15]. Ant colony optimization (ACO) is proposed by Marco Dorigo in 1992, which is inspired by the ant colony behavior of searching food.

ACO is one of the most frequently studied algorithm for solving TSP. Fevrier Valdez et al. ^[16] implemented the algorithms elitist ant system (EAS) and rank based ant system (ASrank); Gao Shupeng et al. ^[17] proposed a pheromone initialization strategy; Zhang Yuru et al. ^[18] developed an improved 2-opt and hybrid algorithm based on ACO; Dewantoro et al. ^[19] used tabu search algorithm as the local search in ACO.

In recent years, as researchers made slow progress in developing better methods for TSP, some researchers shifted their interests to some promoted problems, such as vehicle routing problem (VRP) and multiple traveling salesman problem (MTSP). MTSP means that multiple salesmen only visit a certain number of cities once and only once, and then return to their original cities with the smallest total cost. MTSP is closely related to some optimization problems such as task assignment ^[20].

Optimization problems with multiple solutions widely exist in the real world, and TSP is no exception. In the TSP, the salesman prefers couples of optimal solutions at hands in case that some solutions become unavailable for some reasons. Ting Huang et al. ^[21] proposed a benchmark to study the performance of algorithms for the multi-solution TSP (MSTSP), though few algorithms had been proposed at that time. NMA ^[22] integrates niche strategies with the memetic algorithm to address the MSTSP. NGA ^[21] groups related individuals and performs the GA operations including crossover and mutation in each group. NACS ^[23] is based on the ACO, in which ants are guided to search for different areas through multiple pheromone matrices.

Since ACO is the most successful metaheuristics reported to solve TSP, we also use the ACO in this paper as the base optimization method to address the MSTSP. We use 2-opt strategy to improve the local search ability. The 2-opt strategy provides an effective search operation, while requires less computation than 3-opt or more. We propose a new distance metric named "circular Jaccard distance" instead of other frequently used distance metrics, which brings a considerable improvement in the optimization performance. The circular Jaccard distance is defined as the minimal distances between two paths in various transformation modes such as flip and circular shift. We test the proposed method on the benchmark problems of 25 MSTSP instances, with two evaluation criteria designed for MSTSP. Experimental results indicate that the proposed method substantially improves the performance of multi-solution optimization.

The rest of the article is organized as follows. Section 2 introduces TSP, ACO, and how to solve TSP using ACO. In Section 3, we propose a novel niching strategy, and introduce the 2-opt algorithm and circular Jaccard distance to it, thus proposing the CJD-MSO algorithm. Section 4 describes MSTSP benchmarks, and evaluates the CJD-MSO with experiments. Section 5 concludes the paper finally.

2.   Related work

In this section, we first introduce TSP and the ACO algorithm. Then we introduce how to solve the TSP using ACO algorithm. Finally, we introduce the basic multi-solution optimization algorithm for MSTSP.

2.1.   Traveling salesman problem

Let $ G = (V, E) $ be a graph with set of vertexes $ V $ and set of edges $ E = \{(x, y)|x, y\in V\} $. Each edge $ e\in E $ is assigned a cost $ c_{e} $. If the graph is directed, then the cost of $ (x, y) $ is equal to the cost of $ (y, x) $ for all $ (x, y)\, {\in}\, E $. The equality does not hold for undirected graph.

Without loss of generality, we suppose graph $ G $ is a complete graph. Let the set of vertices be $ V = \{v_{1}, v_{2}, ..., v_{n}\} $. The cost matrix is given by $ C = (c_{ij})_{n\times n} $, where the cost of the edge from $ v_{i} $ to $ v_{j} $ is denoted $ c_{ij} $.

In the context of the traveling salesman problem, the vertexes correspond to cities and the edges correspond to the path between those cities. Let $ {H} $ be the set of all Hamiltonian cycles which visit each vertex exactly once except for the starting point, in $ G $. The traveling salesman problem (TSP) is to find a Hamiltonian cycle $ h\, {\in}\, {H} $ such that the total costs in the cycle is minimized.

The TSP may be formulated as an integer linear programming (ILP) problem ^[24]. Let

For $ i = 0, 1, \cdots, n $, define $ u_i $ as an artificial variable. Then TSP can be rewritten as the following ILP problem:

The first set of equalities requires each city to be arrived from exact one other city. The second set of equalities requires each city to be a departure to exact one other city. The last constraints with the artificial variable $ u_i $ ensure that it is a Hamiltonian cycle. The ILP can be relaxed and solved as a linear programming (LP) using the simplex method. Other exact solution methods include the cutting plane method ^[25] and branch-and-cut ^[26].

2.2.   Ant colony optimization for traveling salesman problem

The exact solution methods suffer from high computational complexity. Therefore, some metaheuristics such as ACO and GA were suggested for addressing the TSP. Ant colony optimization algorithm (ACO) is a swarm intelligence optimization algorithm, which is inspired by the foraging behavior of ants ^[15].

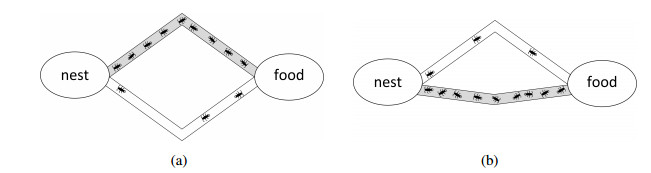
When the ants search for food, they wander around the nest randomly. If some ant finds food, it carries the food back to the nest and lays down pheromones along the road. Other ants nearby can perceive the pheromone and follow the path, and thus increasing the pheromone density. At the same time, the pheromone always evaporates. The more time it takes for an ant to travel along the path, the more time the pheromone evaporates. Hence the pheromone density becomes higher on the shorter path than the longer one. Other ants tend to take the short path and lay down new pheromones. Pheromones attracts more and more ants move on the shorter paths, and finally find the shortest path.

Figure 1 illustrates two scenarios about how the ants choose path through pheromones. Figure 1(a) contains two paths with the same length, it can be observed that most ants chose the upper path. The main reason is that once the upper path is first taken by some ant, it deposits pheromone on the path, which attracts other ants to choose the upper path. As the number of ants that choose the upper path increase, resulting in a higher pheromone density on the path than the lower one, more other ants tend to choose the upper path.

Figure 1(b) shows that most ants prefer the shorter path. Since the accumulation rate of pheromone on the short path is relatively high, the higher density of pheromone on the short path encourages more ants to choose the short path between the nest and the food.

ACO is a popular metaheuristic for addressing the TSP ^[27]. Next, we show how to use ACO to solve the TSP. At the beginning, $ m $ ants are randomly placed in $ n $ cities. The pheromone initial value on all paths between city and city are equal. The ant $ k $ ($ k = 1, 2, \cdots, m $) calculates the transition probability according to Eq (2.2), before choosing the next city.

where $ P_k(i, j) $ is the transition possibility that ant $ k $ moving from city $ i $ to city $ j $; $ \alpha $ is used to control the concentration of pheromone; $ \beta $ is used to control the role of heuristic information; $ \tau(i, j) $ is pheromones on edges ($ i $, $ j $); $ \eta(i, j) $ is the heuristic factor for moving from city $ i $ to city $ j $; $ J_{k}(i) $ is a collection of candidate cities which ant $ k $ is allowed to visit next.

The $ R^k $ is used to record the vertexes which the ant $ k $ has visited. When $ m $ ants have completed the tour and go back to the departure vertex, the total cost of the $ n $ edges traveled by each ant is calculated. Then, the minimum cost is saved, and the pheromone on each edge is updated. During the iteration, the amount of pheromone remaining on the path after evaporating is calculated as follows:

where $ \rho $, between 0 and 1, is pheromone volatilization coefficient. $ \Delta\tau_k(i, j) $ is the pheromones released by the $ k $ ant during this tour, which is defined as:

where $ C_k $ represents the path length of the ant $ k $.

Algorithm1 presents the pseudocode.

2.3.   Multi-Solution optimization

Most swarm intelligence optimization algorithms are developed to solve the single-solution optimization problems. It is necessary to introduce some strategies to make these algorithms suitable for solving multi-solution optimization problems.

Niching method is one of the most widely used strategies. Niching method is a category of techniques to prevent population convergence to a single optimum by maintaining multiple niches. It should be mentioned that some improved ACO versions and various other metaheuristics may have good mechanism for exploration. Although good exploration ability promotes diversity of the solution, it is preferable to use the niching method for maintaining multiple niches.

The classic niching methods were developed in the early 70s such as crowding method ^[28]. After that, various niching methods were developed including fitness sharing ^[29], clearing ^[30], RTS ^[31], speciation ^[32] and clustering ^[33,34].

Fitness sharing ^[29] is inspired by the sharing phenomenon in nature. The resource in a niching is limited, so individuals have to share their resources with other individuals occupying the same niching. When there are too many individuals in a niche, the fitness of the individual will be reduced, thus leading to reduce the number of individuals. Or, conversely, a small number of individuals in a niche may increase the population size. Fitness is adjusted by the population size in a niche, thus facilitating finding multiple optimal solutions.

Crowding ^[28] is a technique to maintain diversity during the course of iteration through careful population replacement. First, a number of individuals are selected from the parent generation. The number of individuals are determined by a crowding factor (CF). Then, the new individuals most similar to parent individuals are selected to replace parent individuals. Since the population is initialized with evenly distribution, the evenly distribution can be maintained during the course of iteration. Algorithm 2 depicts the procedure of crowding.

Clearing ^[30] is a strategy easy to implement. In each iteration, the current optimal individual in the population is selected as the center. Then, all the individuals within the specified clearance radius are removed from the population. The procedure repeats until the original population has no individual, thus obtaining a set of optimal solutions finally.

The principle of speciation is to divide the population into several niches, and the populations in each niche evolve parallelly. Algorithm 3 presents the pseudocode of speciation.

The goal of clustering ^[33] is to group individuals into clusters such that individuals in each cluster have greater similarity than inter-clusters. $ K $-means algorithm is a typical clustering algorithm used in niching method, where $ K $ represents the number of clusters ^[34]. Algorithm 4 is the pseudocode of $ K $-means algorithm for niching.

2.4.   Similarity metrics

The similarity metric plays an essential role in multi-solution optimization. As shown in Algorithm 5, whether the new individual is discarded or not is up to the similarity between the new path and the old one. Next, we introduce couples of similarity metrics which may be used in the multi-solution optimization.

2.4.1.   Pearson correlation coefficient

Pearson correlation coefficient (PCC) ^[35], or the bivariate correlation, is a widely used measure of the similarity between vectors. If there are two variables: $ X $ and $ Y $, PCC can be formulated as follows:

where $ E $ is the mathematical expectation; $ \mu_X $ is the expectation of the $ n $-dimensional vector $ X $; $ \mu_Y $ is the expectation of $ Y $.

The greater the absolute value of the correlation coefficient is, the stronger correlation they have. The correlation with PCC 0 is the weakest correlation.

2.4.2.   Distance correlation coefficient

Distance correlation coefficient (DCC) ^[36], or distance covariance, is a measure of dependence between two arbitrary vectors, not necessarily equal in dimension. The DCC is zero if and only if the vectors are independent. The formula for DCC is as follows:

where $ E $ is the mathematical expectation, $ D $ is the variance. The similarity between $ X $ and $ Y $ is closer if the DCC is greater.

Distance correlation (DC) defined in ^[36] is the complement set of DCC. It can be formulated as follows:

Therefore, the similarity between $ X $ and $ Y $ is closer if their DC is smaller.

2.4.3.   Common edge similarity

Two vectors with more common edges should have stronger similarity. Suppose $ P_1 $ and $ P_2 $ represent two vectors, the common edge similarity(CES) is defined as follows:

The CES similarity is between 0 and 1. Only when the similarity equals to 1, does it mean that the two vectors are identical.

2.4.4.   Jaccard distance

The Jaccard index ^[37], or the Jaccard similarity coefficient, is widely used for comparing the similarity or difference between limited sample sets. Given two sets $ A $ and $ B $, the Jaccard coefficient is defined as the ratio of the intersection to the union of $ A $ and $ B $, namely,

The Jaccard index has value between 0 and 1. Specifically, when both $ A $ and $ B $ are empty sets, their Jaccard index is defined as 1.

Jaccard distance ^[38] is also a metric used to measure the difference between two sets. It is the complement index of Jaccard similarity coefficient. The formula of the Jaccard distance is as follows:

where the symmetric difference $ A \Delta B = |A \cup B| - |A \cap B| $.

When the Jaccard distance is used to measure the similarity, the result of the completely identical calculation equals to 0, and the result of the completely different calculation equals to 1.

3.   Circular Jaccard distance based multi-solution ant colony optimization

In this section, we first propose a novel niching strategy for multi-solution optimization. Next, we propose a circular Jaccard distance as the similarity metric which plays an important role in our algorithm. Then, we introduce the 2-opt strategy which is used as the local search method. Finally, we summarize the whole multi-solution optimization algorithm.

3.1.   Distancing

We develop a novel niching method based on the "radius" strategy which is used in the clearing strategy. After initializing a population of path randomly, we select a set of paths from the population with a given ratio, which is regarded as the parent population. In each iteration, a batch of new individual is generated following the rule of the base metaheuristics. For each new individual, if it has a high similarity to the previous one, then the new individual will be discarded. Otherwise, the new individual is saved in the population pool as the offspring candidate. We calculate the fitness of the parent population together with the offspring population, and sort them in ascending order. Then, a number of good individuals are chosen from the queue head to form a new parent population. The strategy requires that the individual in the next generation keeps a certain distance from the current generation. As shown in Figure 2, let 1, 2 and 3 (or 3' or 3") be the possible positions of an individual in the 1st, 2nd and 3rd generation. 2 is a step from 1. And then 3 (or 3' or 3") is a step from 2 $ \cdots\cdots $. With high probability, the distance from 3 (or 3' or 3") to 1 is greater than the distance between 2 to 1. Hence it maintains diversity during the course of search.

The procedure repeats until the stopping criteria are met and the optimal set of individuals is obtained finally. The proposed niching method is different from any other niching method proposed previously, such as crowding, fitness sharing, and clearing. And it is easy to implement compared with clearing. We name it as "distancing".

Algorithm 5 gives the pseudocode of the distancing method we proposed. In Algorithm 5, ACO is the base metaheuristics.

3.2.   Circular Jaccard distance

The similarity metrics mentioned previously, such as Jaccard distance, are used to promote diversity of the population during the course of iteration, which is also the key measure of quality of the multiple solutions. The valid path in the TSP is always a Hamiltonian cycle. If we use the similarity metrics for vectors in MSTSP, then the property of cycle is not explored and utilized fully.

We take an example to reveal the limitation of Jaccard distance. Suppose there are three paths: "0-6-5-3-7-8-2-4-1" (path 1), "0-1-4-2-8-7-3-5-6" (path 2) and "2-8-7-3-5-6-0-1-4" (path 3). The Jaccard distance between path 1 and path 2 equals to 1. The Jaccard distance between path 2 and path 3 also equals to 1. The Jaccard distance between path 1 and path 3 also equals to 0.889. However, the path 1, 2 and 3 are all the same for the TSP. Therefore, we propose a novel metric named Circular Jaccard Distance (CJD) in this paper to overcome the limitation.

The CJD respects the invariance of the path, which means the paths transformed by cycling or flipping are regarded the same as the original path. When calculating the CJD, first, one of the two paths is transformed by cycling and flipping. Then the Jaccard distance between each pairs are calculated. Finally, the CJD is obtained by minimizing these JDs.

For example, suppose the original path is "0-1-4-2-8-7-3-5-6". The new generated path is the path "6-5-3-8-2-4-1-0-7". By transforming the second path, one can obtain "6-5-3-8-2-4-1-0-7", "5-3-8-2-4-1-0-7-6", "3-8-2-4-1-0-7-6-5", "8-2-4-1-0-7-6-5-3", "2-4-1-0-7-6-5-3-8", "4-1-0-7-6-5-3-8-2", "1-0-7-6-5-3-8-2-4", "0-7-6-5-3-8-2-4-1", "7-6-5-3-8-2-4-1-0", "6-7-0-1-4-2-8-3-5", "5-6-7-0-1-4-2-8-3", "3-5-6-7-0-1-4-2-8", "8-3-5-6-7-0-1-4-2", "2-8-3-5-6-7-0-1-4", "4-2-8-3-5-6-7-0-1", "1-4-2-8-3-5-6-7-0", "0-1-4-2-8-3-5-6-7" and "7-0-1-4-2-8-3-5-6". As shown in Figure 3, Figure 3(a) is the original path. Figure 3(b) is the path obtained by clockwise or counter-clockwise rotation. Figure 3(c) is the path obtained by flipping. The CJDs between the converted paths and the original path are 1, 0.78, 1, 0.67, 1, 0.78, 1, 1, 0.89, 1, 1, 1, 1, 0.89, 1, 1, 0.5 and 0.67 respectively.

3.3.   2-opt strategy

In optimization, $ n $-opt is a simple local search method for solving combinatorial optimization problems ^[39]. The $ n $-opt treatment involves deleting $ n $ edges in a tour, reconstructing the path in some other possible ways.

Take the 2-opt as example, as shown in Figure 4, Figure 4(a) is the original path. In every 2-opt strategy, two edges of the solution are deleted and two new edges are added to obtain a new path. If the new path is better, the original path is replaced. Specifically, since $ d(V_1, V_3) + d(V_2, V_4) > d(V_1, V_2) + d(V_3, V_4) $, the edges $ {(V_1, V_3)} $ and $ {(V_2, V_4)} $ are removed, and the edges $ {(V_1, V_2)} $ and $ {(V_3, V_4)} $ are added instead, thus forming a new path, see Figure4(a). Here $ d $ represents the distance or similarity. Again, in Figure 4(c), since $ d(V_1, V_7) + d(V_4, V_5) > d (V_1, V_5) + d (V_4, V_7) $, the edges $ {(V_1, V_7)} $ and $ {(V_4, V_5)} $ are removed, and the edges $ {(V_1, V_5)} $ and $ {(V_4, V_7)} $ are added instead, see Figure 4(b).

The 3-opt strategy is able to create more choices of new paths. However, the computational complexity becomes $ O(n^3) $ which is not affordable for most applications. Therefore, we use 2-opt as the main local search method in this paper.

3.4.   Circular Jaccard distance based multi-solution optimization algorithm based on ant colony optimization

In this paper, we propose a circular Jaccard distance based multi-solution optimization (CJD-MSO) algorithm to improve the performance for solving the traveling salesman problem.

First, we initialize pheromone matrix, randomly place the ants to the initial cities, calculate the next city according to the transition probabilities, and thus obtain the first generation parent population. In the iterative process, the 2-opt algorithm is used to improve the quality of the solution and the distancing strategy is used to maintain diversity. The circular Jaccard distance between each new individual with the last individual path is calculated. If the similarity value is higher than a preset value, which means that two paths are significantly different, then it is retained. Otherwise, the new individual is discarded. The parent population and offspring population are mixed together, and a set of good individuals with higher fitness is chosen to be the next generation of parent population. Algo.6 shows the entire process of CJD-MSO.

4.   Experiments

In this section, first we describe the benchmark TSPs on which we shall test our proposed algorithm. Next, we introduce the evaluation criteria we shall use. Then, we exhibit our experimental results including the performance of CJD-MSO and some comparison details.

4.1.   Benchmark TSPs

Ting Huang ^[21] proposed a benchmark set for MSTSPs in 2018, which contains 25 MSTSP instances, as shown in Table 1. In the benchmark set, MSTSPs are classified into three categories: simple MSTSPs (from MSTSP1 to MSTSP6), geometry MSTSPs (from MSTSP7 to MSTSP12), and composite MSTSPs (from MSTSP13 to MSTSP25). The number of cities in the MSTSPs ranges from 9 to 66. And the number of optimal scales ranges from 2 to 196. We test our algorithm on the benchmark set.

4.2.   Evaluation criteria

We use two evaluation criteria to test our work: $ F_\beta $ and the diversity indicator (DI) ^[21].

$ F_\beta $ is an indicator calculated from the precision value $ P $ and the recall value $ R $. The formula is as follows:

where $ P $ represents the proportion of optimal solutions, and $ R $ represents the proportion of the found optimal solutions to known optimal solutions. When $ \beta $ is set to 1, $ P $ and $ R $ have the same importance. We set $ \beta $ as 0.3 to attach more importance to the precision.

The formula of $ P $ and $ R $ are as follows:

The true positive, $ TP $, represents the number of optimal solutions obtained by the algorithm; The false positive, $ FP $, represents the number of non-optimal solutions obtained by the algorithm; The false negative, $ FN $, represents the optimal solutions that the algorithm did not find.

The $ P $, $ R $, and $ F_\beta $ are real values between 0 and 1. If the solutions obtained by the algorithm are all optimal solutions, then $ P $ equals to 1. If the algorithm finds all known optimal solutions, then $ R $ equals to 1. $ F_\beta $ is 1, if the values of $ P $ and $ R $ both are 1. Larger $ F_\beta $ means better performance.

The $ DI $ helps to assess the diversity performance of the multiple solutions. $ DI $ is defined by the average maximum similarity between the obtained solutions and the ground-truth solutions. The formula of $ DI $ is as follows:

where $ P $ represents the known optimal solution set; $ S $ represents the solution set obtained by the algorithm; $ P_i $ represents the $ i $-th solution in the set $ P $; $ S_j $represents the $ j $-th solution in the set $ S $; and $ S(P_i, S_j) $ represents the similarity. Larger $ DI $ means that more solutions have been found, given the known optimal solutions.

4.3.   Experimental results

In this section, we conduct a series of numerical experiments to evaluate the proposed algorithm. Firstly, we test the performance of ACO in finding single optimal solution for the MSTSP. Secondly, we compare the algorithmic performance with various similarity metrics including PCC, DC, CES and JD. Thirdly, we compare the algorithmic performance with circular Jaccard distance to that with JD. Finally, we compare CJD-MSO with NACS ^[23], NGA ^[21], NMA ^[22], and give the values of $ F_\beta $ and $ DI $.

The parameter settings are as follows: $ \alpha = 1.0, \beta = 2.0, \rho = 0.5 $. The threshold value of the CJD is set to 0.4. All algorithms are implemented in Python language and run on the Mac OS Catalina system.

We use the MSTSP instances to test the ACO algorithm. Although the MSTSP instances are designed for testing multi-solution optimization algorithms, it is also eligible for testing the single solution optimization algorithms.

Figure 5 presents the convergence curves of ACO. For simple and geometry MSTSPs, the ACO converges to the optimal solution rapidly. The ACO without niching method can find only one optimum in a single run. For some composite MSTSPs such as Figure 5(c), the ACO cannot find any optimum within 3000 iterations, which indicates that composite MSTSPs are really hard problems.

Next, we improve the original ACO by adding "distancing" strategy. This time, we find couples of different solutions for MSTSPs including the simple MSTSPs, the geometry MSTSPs, and the composite MSTSPs, as shown in Figure 6.

We compare the performance of $ F_\beta $ and $ DI $ on MSTSP among various similarity metrics including PCC, DC, CES and JD.

As shown in Figure 7 and Table 2, the four similarity metrics work well in the simple MSTSPs. For geometry MSTSPs and composite MSTSPs, JD considerably outperforms the other three methods.

For MSTSPs with more optimal solutions or more cities, such as MSTSP18 and MSTSP22, since the $ F_\beta $s almost drop to 0 for all similarity metrics. We compare their $ DI $s in Figure 8.

From Figure 8, one can observe that JD considerably outperforms PCC and DC, and is slightly better than CES. So, we believe that JD is a good similarity metric for solving the MSTSPs. Next, we compare the performance of CJD with that of JD. Table 3 gives $ F_\beta $ value of the algorithms with CJD and CD.

From Figure 9 and Table 3, we can observe that CJD significantly outperforms JD, indicating that CJD facilitates maintaining the diversity of the population.

Finally, we perform experiment to compare CJD-MSO with NGA ^[21], NMA ^[22] and NACS ^[23]. Table 4 compares the $ F_\beta $ value of these algorithms. The best $ F_\beta $ for each MSTSP instance is marked in bold. BRPS represents the total of bold items.

We use the pseudo-color plot (Figure 10) to exhibit the comparison results. Only eight "+" exists, which indicates that CJD-MSO perform very well compared with other multi-solution optimization algorithms.

We calculate the $ DI $ of CJD-MSO, and compare with other algorithms in Table 5 and Figure 11. For simple MSTSPs and geometry MSTSPs, the DIs of CJD-MSO are stably good. Seven MSTSPs have a DI value of 1, and the left MSTSPs are approximately 1. From MSTSP19 to MSTSP25, CJD-MSO significantly outperforms other algorithms too.

The results of the proposed method is based on the repeated experiments. Figure 12 gives the box plots of $ F_\beta $, DI, and number of found solutions on 25 MSTSPs.

5.   Conclusions

In this article, we proposed a new multi-solution optimization algorithm named "CJD-MSO" to address the MSTSPs. In the algorithm, we proposed a novel niching technique named "distancing" method, together with a novel similarity metric named "circular Jaccard distance", to maintain population diversity during the course of searching multiple optimal solutions. The "distancing" strategy, different from all niching method emerge so far, were easy to implement. And " circular Jaccard distance" played an essential role in improving the performance of multi-solution optimization.

We also employed basic ACO as the base metaheuristic and employed the 2-opt strategy as the local search method in CJD-MSO. We laid greater emphasis on the strategy of niching and metric definition than compare many and various classic metaheuristics or their improved versions. Experimental results in 25 MSTSP instances showed that CJD-MSO significantly outperforms other multi-solution optimization algorithms, in terms of $ F_\beta $ and DI.

We believe that the " circular Jaccard distance" metric and the "distancing" strategy can be applied to other base metaheuristics for addressing some other combinatorial optimization problems.

Acknowledgements

This work was supported by Ministry of Education in China (MOE) under project grants of Humanities and Social Sciences (No.21YJAZH040).

Conflict of interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.