1.
Introduction
FinTech refers to the transformation of the financial industry through technological innovation, leading to significant impacts on financial markets, services, and products by creating new business models, technology applications, and service processes (Hendershott et al., 2021). As an organic combination of finance and technology, FinTech is not only gradually being applied in traditional financial institutions but also enables non-financial institutions with technological advantages to continually penetrate financial businesses through its application ecosystem. As leading countries in the FinTech sector, China and the United States have, for many years, actively promoted the rapid development of FinTech based on their own market systems, even in highly challenging market environments characterized by high inflation, high interest rates, and ongoing geopolitical conflicts (Ding et al., 2022; Lagna and Ravishankar, 2022). In January 2022, the People's Bank of China issued the FinTech Development Plan (2022–2025), which outlined the vision for FinTech development during the 14th five-year plan period, clearly stating that the next phase should "promote FinTech to enter a new stage of high-quality development, more fully leverage the enabling role of FinTech, and enhance the ability and efficiency of financial services to support the real economy". In the meantime, the most mature FinTech market, the United States, consistently sees FinTech investment amounts exceeding half of the global total, and the Consumer Financial Protection Bureau (CFPB) continues to advance its layout of the FinTech industry. It is clear that FinTech will remain favored by capital markets for a long time.
Due to different regulatory focuses, China and the United States have formed two distinct FinTech development models: the China model, which is market-initiated, and the U.S. model, which is technology-driven. In China, before the targeted strengthening of special regulations and guidance began in 2015, FinTech regulation was relatively lenient, allowing innovations beyond prohibited stipulations. China's market demand and the need to improve the existing financial service system provided ample space for FinTech development (Tao et al., 2022). Meanwhile, the U.S.'s talent advantage and superior capital environment shaped a FinTech landscape driven primarily by technological innovation. The U.S. imposes relatively strict functional regulations on FinTech, prioritizing stability and emphasizing that FinTech forms must capture the core principles of finance (Erel and Liebersohn, 2022). The development of FinTech and the financial industry can be seen as a relationship between supply and demand. The advancement of FinTech offers new technological tools and services to the financial market, boosting the supply capacity of financial services. Concurrently, the evolving demands of the financial market also drive FinTech innovation and application; within this interactive relationship, is it supply-led or demand-led? In other words, does FinTech drive financial development, or does financial development spur the growth of FinTech? What kinds of dynamic transformation processes exist within this relationship? FinTech has not only generated new business models, applications, processes, or products but has also had a profound impact on financial markets and institutions as well as the provision of financial services. Utilizing technology in the delivery of financial services is crucial to FinTech (Thakor, 2020). This is the primary question of this research.
The rise of FinTech and its relationship with traditional financial institutions have always been the focus of academic attention. These interactions are mainly reflected in three aspects. First, FinTech companies compete with traditional financial institutions in similar market segments and business areas (Yao et al., 2018; Kommel et al., 2019; Saklain, 2024). Second, cooperation between the two is increasingly close (Berg et al., 2022). Third, traditional financial institutions are increasingly investing in FinTech companies (Lee and Shin, 2018). These multiple connections create an interactive relationship between supply and demand in FinTech and financial development. Other related studies also suggest that FinTech activities may exacerbate risk contagion and asset volatility in the financial system (Benoit et al., 2017).
The contributions of this paper are as follows. First, by applying the TVP-SV-VAR model, this study provides new insights into how FinTech influences financial development through the bidirectional interaction between supply and demand. Second, this study provides cross-national empirical evidence by comparing the FinTech development models of China and the United States, thereby enhancing the understanding of the economic and policy differences that underlie the mutual influence between FinTech and financial development. With time series data, it fills gaps in prior research by offering a broader spatial and temporal perspective. Furthermore, these findings provide guidance for policymakers, financial institutions, and technology companies in managing the risks and opportunities associated with the rapid growth of FinTech. The paper offers practical recommendations, particularly for developing flexible regulatory frameworks and regional strategies in response to policy changes and external shocks.
The structure of the following text is arranged as follows. The second part theoretically explores the relationship between FinTech and financial industry development. The third part is the research design, introducing the data and models used in this paper. The fourth part presents and discusses empirical results, including interval impulse response and point-in-time impulse response analysis. The fifth part provides the conclusions and implications of this paper.
2.
Literature reviews and theoretical analysis
Research grounded in the supply-driven perspective underscores the pivotal role of technological innovation in catalyzing transformation within the financial industry. Specifically, FinTech firms are reshaping financial services by integrating advanced technologies such as big data, artificial intelligence, biometrics, and blockchain (Bollaert et al., 2021; Moro-Visconti et al., 2023). The synergy of these technologies enables FinTech companies to deliver services that surpass the capabilities of traditional banks and financial institutions, thus better addressing the evolving demands of contemporary consumers (Lagna and Ravishankar, 2022). This perspective further asserts that FinTech development introduces novel tools, platforms, and service models into financial markets, significantly improving the efficiency, accessibility, and diversity of financial services. Anagnostopoulos (2018) posited that RegTech, by incorporating advanced compliance technologies, enhances the effectiveness of financial regulation, facilitating prompt responses and mitigating potential financial risks. This, in turn, ensures greater stability and security across the financial services landscape. Similarly, artificial intelligence–driven deep-learning algorithms allow FinTech companies to analyze consumer behavior and preferences, offering personalized financial product recommendations; biometric technology augments the security and convenience of identity verification processes; and blockchain ensures transparency and immutability in financial transactions (Christensen, 2013; Drasch et al., 2018). On a macroeconomic scale, FinTech contributes to cost reduction, accelerates financial service delivery, improves service quality, expands access to the unbanked population globally, and fosters a more diverse and stable credit environment (Buchak et al., 2018; Chaklader et al., 2023; Gomber et al., 2017). Muganyi et al. (2022) confirmed that FinTech enhances the financial sector by improving accessibility to loans, deepening deposit services, and increasing savings within Chinese financial institutions, although FinTech companies also compete with traditional financial entities. Thus, FinTech serves as a significant supply-side driver, shaping the development of the financial industry.
Conversely, from the demand-driven perspective, the resource allocation mechanisms within financial markets are critical for enhancing economic efficiency and innovation capacity, both of which are foundational to fostering innovation (Hirsch-Kreinsen, 2011). In the FinTech domain, the relationship between traditional financial institutions and FinTech firms has grown increasingly intricate. The expansion of traditional financial institutions often leads to greater investment in FinTech entities (Lee and Shin, 2018), yet this simultaneously escalates the risk of spillover and contagion between FinTech and traditional financial sectors, amplifying the risks faced by financial institutions and potentially precipitating systemic risks (Li et al., 2020; Wen et al., 2023). Nevertheless, traditional financial institutions continue to develop FinTech platforms or establish partnerships with FinTech companies, illustrating how the advancement of the financial industry fosters FinTech growth. Boot et al. (2021) supported the notion that financial institutions are incentivized to embrace FinTech due to its potential for improving resource allocation efficiency, mitigating issues such as moral hazard and adverse selection, reducing matching frictions, and lowering competitive barriers for FinTech entrants. Di Maggio and Yao (2021) further demonstrated that FinTech lenders capture market share by targeting initially higher-risk borrowers, followed by those with stronger credit profiles. As borrowers engage with FinTech lenders, their financial standing and creditworthiness tend to improve (Alyakoob et al., 2021). This suggests that the increasing complexity and scale of traditional financial businesses, whether through enhanced resource allocation or expanded market reach, necessitates FinTech support to drive further growth, ultimately accelerating FinTech development.
There has been some research on whether the development of FinTech promotes financial development or if financial development spurs the growth of FinTech. These studies are mainly based on the current mutual promotion and competition between the two, but significant differences can be found in literature from different data sources. These differences are largely reflected between countries such as China and the United States, Australia, and Germany. This paper not only innovatively verifies the relationship between FinTech and financial development from a supply and demand perspective but also conducts an empirical comparative study using data from China and the United States, based on potential differences in FinTech development models due to different market systems in these countries.
3.
Empirical design
3.1. Indicators and data sources
This paper studies the interactive relationship between FinTech development and financial industry development. However, using daily data results in too high frequency and small index changes, which fail to reflect the intervals of volatility changes; using quarterly or annual data, however, leads to the issue of too few samples. Since the majority of the literature on financial industry development uses monthly data, this paper also selects monthly data, covering the period from January 2012 to February 2024, with a total of 134 months of data. Specifically, the China FinTech index used in this study originates from the Shenzhen Stock Exchange's FinTech sector index (399699), which was first released in June 2017. Based on the composition and weight of its constituent stocks, we selected FinTech companies listed before 2012 as new index constituents to construct a longer-span FinTech sector index, extending it to 2012.
The U.S. FinTech index is the NASDAQ Financial Technology index. The financial industry development indices used in this paper are the SSE Financial Index for China and the NASDAQ Financial 100 Index for the United States. To control for the overall trends of the stock market, we included China's SSE Composite Index and the U.S.'s NASDAQ Composite Index (COMP) in the TVP-SV-VAR model. The TVP-SV-VAR model can analyze two different types of impulse response functions. The interval impulse response function reflects dynamic changes over different periods, while the point-in-time impulse response function indicates changes at specific time points, which often have typical characteristics or special meanings and can influence the empirical results.
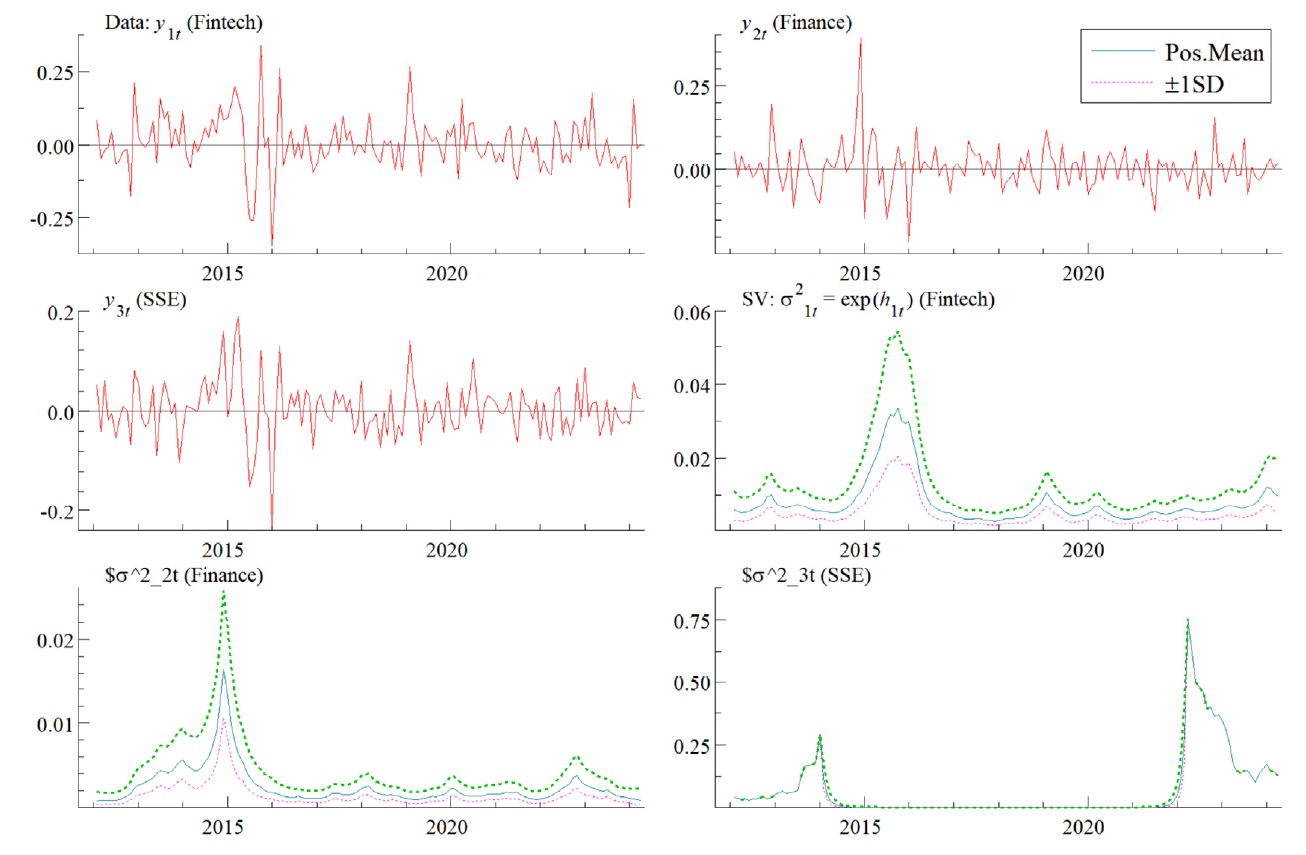
This paper selects time intervals with lags of 1, 2, and 3 periods, representing short-term, medium-term, and long-term impacts, respectively. Figures 1 and 2 show the time series data and volatility changes between FinTech and the financial industry. The top-left, top-right, and middle-left panels show the time series changes in FinTech, financial industry development, and the SSE index, respectively. Overall, as the lag period increases, the impact gradually weakens, which is consistent with the basic expectations of the financial market. Around 2015, the volatility of the three variables in China's data showed significant peaks, possibly related to the stock market crash at that time, which needs to be noted. The peaks in China's financial market appeared before the fluctuations in the FinTech index, but for U.S. data, changes in FinTech volatility preceded those in the financial market around 2021. This indicates that the synchronization of these peaks might suggest that external shocks could have a common impact on FinTech and the financial industry. However, the order of volatility changes varies between China and the U.S., indicating the necessity to further clarify the supply and demand relationship between FinTech development and financial development or to discuss it within the context of different market systems.
3.2. Empirical model
The development of FinTech in any economy will change with domestic development trends and fluctuations in the international economic situation. Shocks of the same magnitude have different impacts on endogenous variables at different times. Therefore, it is crucial to accurately understand the time-varying characteristics of FinTech development and financial industry development. This paper uses a time-varying parameter vector autoregression model with stochastic volatility (TVP-SV-VAR) to conduct the study, as its time-varying characteristics can meet this requirement. The time-varying parameter vector autoregression (TVP-VAR) model was initially proposed by Cogley and Sargent (2001) and later expanded by (Primiceri, 2005) and Nakajima (2011) to develop the comprehensive TVP-SV-VAR model. The main difference between the TVP-SV-VAR and TVP-VAR models is that the latter only considers the time variation of the VAR coefficients, while the former allows the VAR coefficients and conditional variances to vary over time. The index data used in this study may exhibit volatility clustering or conditional heteroscedasticity, making the TVP-SV-VAR model more suitable for capturing these characteristics. Before analyzing the relationships between variables, this paper first normalizes the variables and then calculates the impulse response functions between them.
The VP-SV-VAR model can be derived from the structural vector autoregression (SVAR) model, and a typical SVAR model can be represented as follows:
Further transforming equation (1) into the following form of the VAR model:
where Bi=A−1iFi, where i=1,2⋯,s. Further simplification leads to the following equation (2):
where β is the column vector of dimension (k2s×1), formed by stacking the elements of Bi. Xt=Ik⊗(yt−1,⋯,yt−s), where ⊗ denotes the Kronecker product. Based on equation (3), by allowing the parameters βt,At,∑tϵt to vary over time, the TVP-SV-VAR model is obtained as the following equation (4):
The relevant parameters follow a first-order random walk process, which can capture the nonlinear characteristics of structural changes.
4.
Empirical results and discussion
4.1. Estimation results of MCMC simulation method
To estimate using the TVP-SV-VAR model, this paper first adds time-varying coefficient matrices and covariance matrices to the TVP-VAR model and then uses the MCMC algorithm for Bayesian parameter estimation to complete parameter identification. By considering stochastic volatility in the TVP-VAR model, we obtained the TVP-SV-VAR model. Using AIC and SC criteria, the optimal lag order of the TVP-SV-VAR model was determined to be 1. We conducted 11,000 MCMC iterations, discarding the initial 1,000 pre-simulation samples. The estimation results are shown in Figures 1 and 2 and Tables 1 and 2. Figure 3 displays the sample autocorrelation coefficients, sample paths, and posterior distribution results for Chinese data, while Figure 4 shows the same for the U.S. data. It can be observed that the sample autocorrelation coefficients exhibit a continuously declining trend, and the sample paths indicate that the sampled data are stationary. From Table 1, it can be seen that the convergence statistic (Geweke value) does not reject the null hypothesis of the posterior distribution at the 95% confidence interval. The inefficiency factors for China and the U.S. are less than 44.32 and 78.64, respectively, indicating reasonable levels. Therefore, the samples obtained through MCMC sampling are uncorrelated and valid, indicating that the MCMC algorithm is effective for estimation.
4.2. Time-varying impulse response analysis
The TVP-SV-VAR model can analyze two different types of impulse response functions. The interval impulse response function reflects dynamic changes over different periods, while the point-in-time impulse response function indicates changes at specific time points, which often have typical characteristics or special meanings and can influence the empirical results. This paper selects time intervals with lags of 1, 2, and 3 periods representing short-term, medium-term, and long-term impacts, respectively. A lag of 1 year captures immediate responses, making it an appropriate representation of short-term effects. Similarly, a lag of 2 years can reflect medium-term adjustments, as it allows for transitional responses; a 3-year lag is suitable for analyzing long-term impacts, capturing structural changes in the financial system. Therefore, the chosen time intervals align with the dynamic characteristics of the FinTech industry. Based on the volatility characteristics of FinTech development and different external shocks in the financial industry development cycle, this paper sequentially analyzes the dynamic paths between FinTech development and financial development in China and the United States. Figures 5, 6, and 7 describe the time-varying effects between FinTech development and financial development in China at different lag periods, with SSE representing the Shanghai Stock Exchange Index. It can be observed that the impact of FinTech on financial development has been increasing, while the effect gradually diminishes as the lag period increases, which is consistent with our previous theoretical analysis. However, the impact effects differ between the United States and China.
The response of FinTech development to shocks in financial development varies across different periods, as shown in the middle section of the first row in Figure 5. Prior to mid-2021, the response of FinTech development to such shocks was negative, with significant fluctuations in impulse values. This suggests that, during this period, FinTech exerted crowding-out and siphoning effects on the traditional financial sector. Particularly during the 2018 Sino-U.S. trade friction and the 2020 COVID-19 pandemic, the financial industry experienced considerable disruption, and increased investment in FinTech further impeded capital inflows into the financial sector. However, beginning in the second half of 2021, as China relaxed its stringent pandemic control measures, FinTech started to integrate more organically with the traditional financial industry, enhancing its development. Consequently, the impact of FinTech on financial development transitioned to being positive. Figure 5 also illustrates that the effect of financial development on FinTech development in China is negative in the short term but elicits a positive response with a two-period lag. This pattern can be attributed to the highly concentrated nature of China's financial market, where large banks and financial institutions dominate market share, exerting substantial competitive pressure on FinTech firms. This intense competition hinders the rapid growth of FinTech companies in the short term (Parlour et al., 2022). Despite advancements in technological innovation, FinTech firms remain at a competitive disadvantage relative to traditional financial institutions, and their growth is constrained by these institutions. Consequently, technological breakthroughs are difficult to achieve during the early stages of financing.
Therefore, overall, the development of FinTech and the financial market in China is a bidirectional interactive process. Specifically, before the first half of 2021, the process was primarily demand-driven, meaning the development and demand of the financial market in the medium-to-long term would drive the innovation and application of FinTech. After the second half of 2021, the development of FinTech, by providing new technological tools and services, enhanced the supply capacity of financial services, thereby promoting the development of the financial market. As the market gradually matures, the originally unidirectional interactive relationship begins to change. During this process, the dominance of supply and demand gradually achieves coexistence. This bidirectional interaction not only promotes dynamic market balance but also steadily improves the interactive effects over time.
Figures 8, 9, and 10 describe the time-varying effects between FinTech development and financial development in the U.S. at different lag periods. Aside from the diminishing effects with longer lag periods, the impact in China and the United States exhibits a fundamentally opposite pattern. This paper uses the NASDAQ index to represent U.S. FinTech development, with COMP representing the overall market trend. Observing the middle of the first row in Figure 8, the impact of FinTech development shocks on financial development is shown. In the short term, the financial industry's response is negative, but from the second half of 2022, as U.S. FinTech infrastructure services, such as embedded payment methods, gradually improve, the financial industry's response strengthens, indicating that FinTech development has a positive impact on the financial development. Observing the middle of the first column in Figure 8, the short-term impact of the financial development on FinTech development is positive, followed by a decline in the medium term, which is the opposite of the lagged positive impact seen in China. FinTech development in China is mainly concentrated in areas such as payments and consumer finance, with relatively low penetration in high-value-added fields like asset management and insurance.
The U.S. FinTech market has diversified demand, covering payments, lending, wealth management, insurance, and other areas, with relatively flexible regulation. This also indicates that a policy environment that encourages innovation is more conducive to the development of FinTech. Overall, the supply-demand relationship between FinTech development and financial development in the U.S. was mainly supply-driven before the first half of 2022, but the impact was more timely compared to China. After the second half of 2022, FinTech development enhanced the supply capacity of financial development, similar to the situation in China. The interactive effects have also been steadily improving.
4.3. Time-point impulse response analysis
Figure 11 shows the impulse responses between FinTech development and financial development at four specific points in time, covering the early, mid, and late stages of FinTech development: November 2012, the rise of Bitcoin; March 2020, the COVID-19 pandemic promoting the adoption of digital payments; January 2022, when the People's Bank of China issued the FinTech Development Plan (2022–2025); October 2023, when the Central Financial Work Conference was held. At any given point in time, the single impulse response function curve undergoes a rapid rise from 0 followed by a flattening process. After three lags, it levels off and begins to show a trend of converging toward 0. The curve shows features consistent with interval impulse response analysis; within a four-year timescale, the mutual influence between FinTech development and financial development changes over time, with the shock effects being particularly significant in the early stages. Additionally, specific time points with different characteristics display varying impulse effects. These differences can be primarily attributed to two aspects: market-driven quantitative changes and external policy-induced shocks.
1. Market-specific time point impulse response analysis. First, we analyze the rise of Bitcoin at two different points in time in China and the United States. In November 2012, the price of Bitcoin in the Chinese market exceeded $10 for the first time. In January 2017, the price of Bitcoin in the U.S. cryptocurrency market exceeded $1,000 for the first time, sparking widespread investment enthusiasm. This marked a new phase of FinTech, launching a new era of cryptocurrencies and indicating the potential of decentralized financial technology. The proliferation of digital payments has brought new opportunities for innovation and development in global FinTech. With the global outbreak of the COVID-19 pandemic, the demand for online and contactless payment methods surged. This event accelerated the adoption of digital payments and drove the rapid development of payment technologies and FinTech companies (Fu and Mishra, 2022). In this context, companies like PayPal and Square experienced significant increases in users and transaction volumes, demonstrating the importance of digital payments in responding to public health emergencies. During the COVID-19 pandemic, contactless payment has not only increased the convenience and safety of transactions but also brought new opportunities for development in the financial technology industry.
Observing the middle of the first row in Figures 11 and 12, it can be seen that in both China and the U.S., FinTech development has a significant negative impact on financial development in the short term under market-specific point-in-time impulses, but this effect gradually stabilizes to a slight positive impact after a period of adjustment. Observing the middle of the first column in Figures 11 and 12, the impact of financial development on FinTech development in China is significantly negative in the short term, but as time progresses and the market adapts, this impact gradually fades and turns slightly positive. In the U.S., the impact of financial development on FinTech development is significantly positive in the short term but turns slightly negative in the lag period. This indicates that in China, FinTech needs time to adapt to changes in financial industry development; after adjustment, it can benefit from the development of the financial industry and achieve positive growth. In the U.S., the significant short-term positive impact of financial development on FinTech development is mainly due to the support from capital, market demand, and policy environment. However, as time goes on, market saturation, intensified competition, and countermeasures by traditional financial institutions cause this positive impact to gradually weaken and turn slightly negative. Overall, market-driven FinTech development positively influences financial development in the long term, but it requires a period of adjustment and adaptation. Market education and confidence building may be important factors in this process (Gopal and Schnabl, 2022). The impact of financial development on FinTech involves a combination of supply-driven and demand-driven dynamics.
2. Policy-specific time point impulse response analysis. In China, in January 2022, the People's Bank of China issued the FinTech Development Plan (2022–2025). This plan set the direction for FinTech development in China over the next few years, highlighting the crucial role of FinTech in enhancing the quality and efficiency of financial services. This plan reflects the Chinese government's emphasis on and support for FinTech development, aiming to foster deep integration of FinTech with the real economy, promote the digital transformation of financial services, and enhance the stability and competitiveness of the financial system. In October 2023, the Central Financial Work Conference was held, emphasizing the unwavering commitment to the path of financial development with Chinese characteristics. Financial technology is one of the "five major financial topics" mentioned at the meeting; from then on, FinTech development became a national development strategy. In the United States, in April 2023, the Federal Reserve launched a digital dollar pilot project to explore the feasibility of central bank digital currency (CBDC). This project marked an important step for the U.S. in the field of digital currency, aiming to enhance the efficiency and security of the financial system. The digital dollar pilot not only exemplifies FinTech innovation but also demonstrates the central bank's exploration and experimentation in the field of digital currency. This move serves as an important example of the global development of central bank digital currencies. In March 2024, the U.S. Treasury Department issued a new regulatory framework for cryptocurrency transactions. Since then, FinTech entered a stage of standardized development, promoting the healthy and sustainable growth of the entire industry.
Observing the middle of the first row in Figures 11 and 12, it can be seen that in both China and the U.S., FinTech development and financial development are significantly positive under policy-specific point-in-time impulses, but this impact gradually stabilizes to a slight negative shock after a period of adjustment. Observing the middle of the first column in Figures 11 and 12, the impact of financial industry development on FinTech in China is significantly negative in the short term, gradually turning slightly positive in the lag period; in the U.S., the impact of the financial industry on FinTech is significantly positive in the short term, but turns slightly negative in the lag period. Observing the middle of the first column in Figures 11 and 12, the impact of financial development on FinTech development in China is significantly negative in the short term, gradually turning slightly positive in the lag period; in the U.S., the impact of the financial development on FinTech development is significantly positive in the short term, but turns slightly negative in the lag period. This suggests that the effects of policy-specific point-in-time shocks are similar to those of market-specific shocks (Lovreta and López Pascual, 2020).
4.4. Comparison of the situation between China and the United States
There are similarities and differences between China and the United States. China's financial development is under relatively strict regulation, with the government emphasizing risk control and financial stability. In contrast, the United States has relatively relaxed regulations, emphasizing innovation and market freedom. This results in different characteristics of FinTech development in these two countries with distinct regulatory frameworks (Roh et al., 2024). In China, the domestic market is characterized by a concentration of patent holders. Data on public patent applications from financial institutions show that the top ten institutions contribute nearly 80% of the patents. Leading technology financial institutions have a clear technical advantage and serve as advanced role models. They drive the evolution of the financial ecosystem with their scale, fostering technological and model innovation. Meanwhile, small and medium financial institutions focus on specialization, differentiation, and localization in FinTech development. Multiple FinTech development measures have enabled China to rapidly advance the accessibility and inclusiveness of FinTech services, but the initially stringent regulations may increase operational risks and compliance costs for financial institutions.
The mature and stable market in the United States has attracted most FinTech investments, primarily in payment technology, insurance technology, regulatory technology, cybersecurity, and other sectors. The U.S. supports the early growth of tech companies with developed venture capital, creating a friendly public financing environment through multi-tiered capital markets. Active direct financing, such as the high-yield bond market, continuously broadens financing channels. In the long term, issues like data privacy, cybersecurity, and the impact on traditional financial industries require financial institutions to strengthen management with FinTech.
These heterogeneous market characteristics determine that the impulse effect of financial development on FinTech development in China is negative in the short term and slightly positive in the long term, whereas, in the U.S., it is positive in the short term and slightly positive in the long term. There are instances where different causes, but similar effects, appear in the impulse response results of FinTech on financial industry development. After the COVID-19 pandemic ended, various countries issued multiple economic stimulus policies, and FinTech served as a catalyst for the financial industry to quickly absorb liquidity. In 2021, the Chinese government increased regulation on large tech companies, including Ant Group. Although these measures caused some short-term impacts on FinTech companies, a regulated market environment benefits the healthy development of FinTech in the long run. In the United States, major FinTech companies such as PayPal and Square saw significant increases in users and transaction volumes during the pandemic, driving the financial market's reliance on and demand for FinTech, thus promoting the development of financial services.
5.
Conclusions and implication
This study utilized the TVP-SV-VAR model to conduct an in-depth analysis of the dynamic relationship between FinTech development and financial development, discovering that their interaction dynamically shifts with changes in time, market environment, and policy direction. In China, before the first half of 2021, the impact of financial development on FinTech development was primarily demand-driven; afterward, as FinTech matured and the policy environment improved, the impact of FinTech development on the financial development shifted to supply-driven. The United States also experienced a similar transition, indicating that the interaction between FinTech development and financial development is a complex bidirectional process. Additionally, this paper found that specific events like the rise of Bitcoin and the outbreak of COVID-19 can have significant impulse effects on financial development. These effects may initially manifest as negative shocks in the short term but will turn positive in the long term.
The rapid FinTech development has profoundly impacted global financial markets, enhanced the efficiency of financial services, and drove market transformation. Policy recommendations should be targeted and forward-looking, tailored to different countries and regions. Chinese regulatory authorities should improve its regulatory framework for FinTech, establish specialized regulatory bodies, and formulate flexible policies to address the FinTech challenges. At the same time, traditional financial institutions should be encouraged to collaborate with FinTech companies to enhance service efficiency and coverage. China's FinTech development plan should also consider the investment and financing markets and regulatory systems of developed countries.
Future research may deeply explore the complexity and dynamic characteristics of the interaction between FinTech and financial markets, particularly the features and development paths in different market environments and policy contexts. To this end, macroeconomic policies, international economic conditions, and other exogenous variables can be introduced to analyze their impact on the interaction between FinTech development and financial development. At the same time, focus should be placed on the application of emerging technologies such as blockchain and artificial intelligence in financial services, assessing their potential impact on financial development. Cross-national comparative research is also an important direction. By comparing FinTech development in different countries and regions, insights and references can be provided for the global development of FinTech, offering more scientific and systematic decision-making bases for policymakers.
Author contributions
Tu, Z: Conceptualization, Formal analysis, Data curation, Software, Investigation, Methodology, Writing – original draft, Writing – review & editing. Yang, R: Data curation, Software, Resources, Visualization, Writing – original draft, Writing – review & editing. Yang, C: Funding acquisition, Project administration, Supervision, Validation, Writing – original draft, Writing – review & editing.
Acknowledgments
This work was supported by the National Office for Philosophy and Social Science of China, grant number 22AGL027; the Shanghai Planning Office of Philosophy and Social Science, grantnumber 2023ZGL003, 2020BJB010. The authors also express their gratitude to the anonymous reviewers for their constructive suggestions.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: