1.
Introduction
Mutualistic interactions are ubiquitous in nature and have been suggested to be the backbone of ecological communities [1,2,3,4]. Since mutualisms are found in all organismal kingdoms and in all ecosystems, they have become the focus of many empirical studies. Even so, mutualisms remain somewhat understudied relative to negative interactions such as competition, predation, and parasitism–especially with regard to theoretical studies [5]. We are also still far from making good predictions about the fate of mutualistic communities under threats such as habitat fragmentation and climate change [2].
Interspecific interactions affect populations both directly (e.g., density-mediated effects) and indirectly (e.g., trait-mediated indirect effects). For example, most predator-prey studies are concerned with the rate of prey consumption by a predator and those effects on prey density (a density-mediated effect), as opposed to influence of the predator on the phenotype of the surviving prey (a trait-mediated indirect effect) (see [6,7,8]). In fact, the authors in [6] have argued that ecological communities are replete with trait-mediated indirect effects arising from phenotypic plasticity and these effects are important to community dynamics. These trait-mediated indirect effects are also expected to contribute strongly to many phenomena that traditionally have been solely attributed to density-mediated effects [6,7].
Trait-mediated behavioral responses to other species can affect the dynamics of a population significantly (see [6] and [9]). One such effect is trait-mediated dispersal, in which an organism changes its dispersal patterns due to the presence of another species, which can, in turn, modify population dynamics and species interactions (see [10], for example). This idea has been studied in the predator-prey context (though scarcely), where increased predation risk was shown to increase emigration rates of prey. In [11], the authors found evidence of predator-induced emigration in a spider (predator) and planthopper (prey) system, and even concluded that at high predator density, the predator had a greater impact on prey density through induced emigration than consumption (also see [12,13,14]). However, few studies have been devoted to trait-mediated dispersal in other interaction scenarios, e.g., mutualism or competition [15]. One example of trait-mediated dispersal in a mutualism involves ant tending of aphids. Aphids produce honeydew, a sugar-rich byproduct of feeding on phloem sap of plants. Aphids exchange honeydew for protection by ants from predators and parasitoids [16]. Interestingly, ant-derived substances have been shown to reduce the production of alates (winged morphs), delay dispersal, and restrict the mobility of wingless aphids [17,18,19]. In other protection mutualisms, plant-produced volatiles can arrest the dispersal of parasitoids and predators, leading to higher mortality of the plant’s herbivores [20]. Given the presumed benefits of the mutualistic interaction, trait-mediated indirect effects that alter dispersal are likely much more common than the published literature would suggest.
Fragmentation of habitats has been greatly exacerbated by human activities over the past centuries (e.g., [21,22,23]). This fragmentation creates landscape-level spatial heterogeneity which in turn influences the population dynamics of the resident species. Often, it leads to declines in abundance of the species due to increased susceptibility to edge effects between the remnant habitat patches and the lower quality human-modified "matrix" surrounding these focal patches [24,25,26]. Matrix composition and hostility can have profound effects on persistence of a single species (e.g., [27,28,29,30,31]), as well as coexistence of a system of interacting species (e.g., a host-parasitoid system in [32] and a competitive system in [26] and [33]). In fact, matrix quality degradation has been shown to cause a reversal in competitive dominance in a theoretical model of two competitive species (see [26] and [33]).
In this paper, we explore the consequences of fragmentation and trait-mediated dispersal on the coexistence of a system of two mutualists by employing a model built upon the reaction diffusion framework. Specifically, we consider a theoretical system of two mutualists that both exhibit trait-mediated dispersal in that each species reduces its emigration from their focal patch in the presence of the other species. Both organisms inhabit a patch surrounded by a hostile matrix, in which their movement follows a random walk (diffusion) inside the patch but follows a biased random walk at the patch boundary. In particular, the probability of remaining inside the patch upon reaching the boundary is an increasing function of the other organism's population density at the boundary. Effects of habitat fragmentation are integrated into the model via parameters for patch size and effective matrix hostility. We further assume that their density-mediated effects are negligible, i.e., the presence of the other organism inside the patch has no effect on their own density. As it is difficult to differentiate between impacts from density-mediated effects and trait-mediated indirect effects (see [6], for example), we aim to isolate the effects of trait-mediated dispersal on the system and attempt to draw more general conclusions regarding that mechanism. Thus, our model is not intended to be a detailed description of any particular system but is intended to be a caricature designed to explore the effects of habitat fragmentation on a mutualistic system that exhibits trait-mediated dispersal. The modeling approach employed here is based on a system of reaction diffusion equations.
In Section 1.1, we detail the modeling framework, followed by preliminary results in Section 2. Statement of our main results is found in Section 3, followed by proofs of main results in Section 4. Finally, we discuss their implications in Section 5.
1.1. Modeling framework
We present and study a system built upon the reaction diffusion framework which will model interactions of two mutualistic species that obey logistic growth laws and exhibit trait-mediated dispersal. Reaction diffusion models have been used extensively in the literature, see [34,35,36,37,38,39,40] and references therein for a detailed history of the framework. Here, we assume a situation where two organisms are dwelling in a single focal patch Ω0={ℓx | x∈Ω} with patch size ℓ>0, Ω=(0,1) or Ω⊂Rn having unit measure (e.g., if n=2 then the area of Ω is one) and smooth boundary with n=2,3, that is surrounded by a hostile matrix, denoted by ΩM=Rn∖¯Ω0, where it is assumed that organisms are experiencing exponential decay at fixed rate (say, S0>0). We also denote the boundary of Ω0 by ∂Ω0. Here, the variable t represents time and x represents spatial location within the patch. The two organisms are following an unbiased random walk inside both patch and matrix, while following a biased random walk on the patch/matrix interface, i.e., a discontinuity between the density in the patch and matrix is allowed at the interface, while maintaining continuity in the flux (see e.g., [41,42,43]). In particular, organisms recognize the patch/matrix interface and modify their random walk movement probability (i.e., probability of an organism moving at a given time step in the random walk process), random walk step length (i.e., distance that an organism moves during a given time step), and probability of remaining in the patch (say α). In this patch-level setting, dispersal from the patch is equated to organisms reaching the patch/matrix interface, leaving the patch with probability 1−α that may depend upon conspecific or even interspecific density, and entering the matrix, where they still have the opportunity to re-enter the patch at the interface. Following the derivation given in [30], the following reaction diffusion system:
will exactly model the study system in the case of a one-dimensional patch in the sense that steady states of (1.1) and their stabiltiy properties will be exactly the same as those of the study system (see Appendix C of [30] and references therein) and provide a reasonable approximation of the study system in the case of a simply connected, convex patch in two- or three-dimensions. Here, Di>0 represents patch diffusion rate, ri>0 the patch intrinsic growth rate, u0(x),v0(x) initial population density distributions in the patch, and αi the probability of an individual remaining in the patch upon reaching the boundary (i=1 for u and i=2 for v). The term ∂∂η denotes the outward normal derivative operator. Note that the parameter S∗i≥0 is a measure of hostility of the matrix towards the organism, has units of length by time, and can assume different forms depending upon the patch/matrix interface assumptions (see [30]). If αi≡0 then the boundary is absorbing, i.e., all individuals that reach the boundary will emigrate, whereas if αi≡1 then the boundary is reflecting, i.e., the emigration rate is zero. Also, a given relationship between density and emigration can be included in the model by selecting appropriate αi's (see, for example, [28,29,30,44,45]).
We now introduce a standard scaling,
After applying this scaling and dropping the tilde, (1.1) becomes
with corresponding steady state equation:
where λ=r1ℓ2D1, r0=r2r1, D0=D2D1, r=r0D0, g(v)=S∗1√r1D11−α1(v)α1(v), and h(u)=S∗2√r1D1D01−α2(u)α2(u) are all unitless. Also, recall that Ω has length, area, or volume of one. Thus, for fixed r1,r2,D1,D2, the composite parameter λ is proportional to patch size squared, g(0) represents the effective matrix hostility towards u, and h(0) the effective matrix hostility towards v. Here, we assume that α1,α2 are smooth increasing functions of v,u, respectively, such that g,h∈C1([0,∞),(0,∞)) are decreasing functions of v,u, respectively. Also, r can be written as r=r2D2r1D1 and interpreted as a means to compare the two species by their growth to diffusion ratio, defined as the ratio of patch intrinsic growth rate to patch diffusion rate. Thus, there are three cases: (1) if r=1, then both growth to diffusion ratios are the same, (2) if r>1 then v's growth to diffusion ratio is greater than u's, and (3) if r<1 then u's ratio is greater than v's.
2.
Preliminaries
We first note that the general theory for reaction diffusion systems such as (1.3) is well established (e.g., see [39] and [46]). Since our assumption on g,h ensures that (1.3) is a quasimonotone nondecreasing system, an application of Theorem 3.1 of Chapter 9 in [46] with subsolution (0,0) and supersolution (M1,M2) (M1,M2≥1) of (1.3) guarantees existence and uniqueness of a solution to (1.3). Moreover, solutions with nonnegative initial data exist and remain nonnegative for all time. Predictions of persistence, coexistence, and extinction in reaction diffusion systems can be explored via determination of the stability of the trivial steady state (0,0) and semitrivial steady states (u∗,0) and (0,v∗). Generally, stability of trivial and semitrivial steady states is determined by the sign of principal eigenvalues of their linearizations around the trivial or semitrivial steady states (for example, see [39]). In this paper, we will assume the conventional view of "invasibility implies persistence" (see [39], for example). In this setting, prediction that an organism can invade the patch with small positive initial density implies that the organism can colonize the patch and persist. In the remainder of this section, we discuss some eigenvalue problems for which our coexistence results are built upon, beginning with the eigenvalue problem:
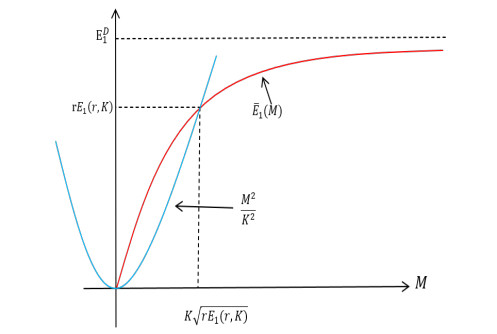
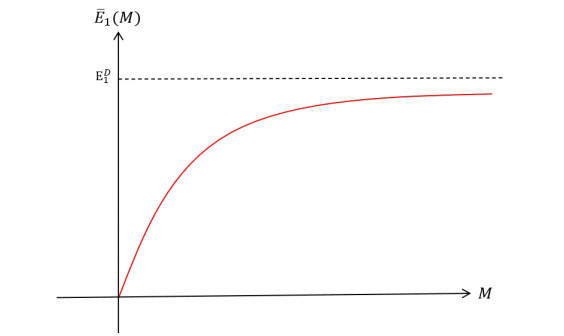
for a given M∈[0,∞). In [47], the authors proved that for each M∈[0,∞), (2.1) has a positive principal eigenvalue ˉE1(M), ˉE1(0)=0, and the eigencurve ˉE1:[0,∞)→[0,∞] is Lipschitz continuous, strictly increasing and concave (see Figure 1). Furthermore, ˉE1(M)→ED1 as M→∞ where ED1 is the principal eigenvalue to the Dirichlet eigenvalue problem:
Next, we recall the eigenvalue problem discussed in [48]:
where K is a positive parameter. For fixed r and K, let E1(r,K) denote the principal eigenvalue of (2.3). See [48] for the existence of this principal eigenvalue. Namely, rE1(r,K) is the y-coordinate of the intersection of the curves ˉE1(M) and M2K2 (see Figure 2).
For a fixed r, it is easy to see that E1(r,K) is an increasing function of K, E1(r,K)→ED1 as K→∞, and E1(r,K)→0 as K→0. Also, since the intersection of ˉE1(M) and M2K2 is independent of r, we must have
By (2.4), it is easy to see that for a fixed K, E1(r,K) is decreasing in r, E1(r,K)→0 as r→∞, and E1(r,K)→∞ as r→0. Furthermore, it is easy to see that the following lemma holds:
Lemma 2.1. For any K1,K2 positive constants there exists r∗=r∗(K1,K2)>0 such that E1(1,K1)=E1(r∗,K2). Moreover, r∗>1 when K1<K2, r∗<1 when K1>K2, and r∗=1 when K1=K2.
Now, we consider (1.4) in the cases when one population is present and the other is absent, namely:
and
In other words, (2.5) is the governing steady state equation for the species u in the absence of v and (2.6) is the governing steady state equation for the species v in the absence of u. The solution structure of (2.5) and (2.6) can be completely determined by consideration of the eigenvalue problems:
and
We note that, together, (2.7) and (2.8) comprise the linearization of (1.4) around (0,0). Let σ1=σ1(Ω,λ,g(0)) and σ2=σ2(Ω,λ,r,h(0)) be the principal eigenvalues of (2.7) and (2.8), respectively, with corresponding normalized eigenfunctions ϕ1 and ϕ2 chosen such that ϕ1,ϕ2>0;¯Ω.
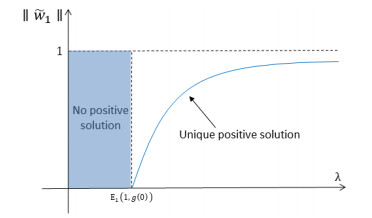
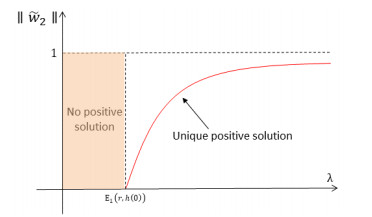
In [48], the authors established the following lemma which guarantees the existence of ˜w1 and ˜w2.
Lemma 2.2. We have the following:
(1) If σ1≥0 then w1≡0 is the only nonnegative solution of (2.5) and is globally asymptotically stable.
(2) If σ1<0 then the trivial solution of (2.5) is unstable. Furthermore, there exists a unique positive asymptotically stable solution ˜w1 of (2.5).
(3) If σ2≥0 then w2≡0 is the only nonnegative solution of (2.6) and is globally asymptotically stable.
(4) If σ2<0 then the trivial solution of (2.6) is unstable. Furthermore, there exists a unique positive asymptotically stable solution ˜w2 of (2.6).
Moreover, ˜wi≤1;ˉΩ for i=1,2.
Namely, they established the exact bifurcation diagrams (λ,||˜w1||) and (λ,||˜w2||) illustrated in Figures 3 and 4.
Finally, we consider two eigenvalue problems involving ˜w1 and ˜w2:
and
Notice that (2.9) and (2.10) are part of the linearizations of (1.4) about (˜w1,0) and (0,˜w2), respectively. Let σ3=σ3(Ω,λ,r,h(˜w1)), σ4=σ4(Ω,λ,g(˜w2)) be the principal eigenvalues and ϕ3, ϕ4>0;¯Ω be the corresponding normalized eigenfunctions of (2.9) and (2.10), respectively.
With these principal eigenvalues defined, we can now differentiate the cases of the composite parameter r in terms of predictions from the model. Since this comparison deals with intrinsic properties of the species, we assume here that the effective matrix hostility is the same for both u and v, i.e., g(0)=h(0). In the case that r=1 (growth to diffusion ratios are the same for u and v), we have that E1(1,g(0))=E1(r,h(0)) implying that both species will have the same minimum patch size requirement in order to invade and persist in the patch. Using this a comparison tool, the species are essentially the same. In the case that r>1 (growth to diffusion ratio of v is larger than that of u), we have that E1(1,g(0))>E1(r,h(0)) implying that, v is better able to invade and persist, in the absence of any mutualistic assistance, in smaller patches than u. The opposite is true in the case that r<1 (growth to diffusion ratio of u is larger than that of v), since we have that E1(1,g(0))<E1(r,h(0)) implying that u is better able to invade and persist than v, in the absence of any mutualistic assistance, in smaller patches than v. As an example, if both species have the same patch diffusion rate, but u has a larger intrinsic growth rate (i.e., r1>r2) then u is better able to invade and persist than v due to the higher growth rate being able to offset losses due to encountering mortality at the boundary of the patch. On the other hand, if both species have the same intrinsic growth rate, but u has a larger patch diffusion rate then v is better able to invade and persist due to the higher diffusion rate causing more of the u population to encounter the boundary of the patch and be exposed to mortality from the hostile matrix.
Finally, we give a characterization of the stability of the trivial and semitrivial steady states of (1.3) in Table 1. These stability results, which are taken in the Lyapunov sense, can be proved using similar ideas as those presented in [46] and are included to help provide greater context to our coexistence results. Rigorous proofs of these properties are forthcoming in [49].
3.
Main results
In this section, we present sufficient conditions for coexistence to occur and conditions for which coexistence cannot be attained.
Theorem 3.1. Let r>0 be given and define λ∗=max{E1(1,g(1)),E1(r,h(1))} and λ∗∗=max{E1(1,g(0)),E1(r,h(0))}. Then the following hold:
(a) If λ<λ∗ then (1.4) has no positive solution, i.e., coexistence is not possible.
(b) If λ>λ∗∗ then (1.4) has at least one positive solution. All positive solutions, (u∗,v∗), of (1.4) satisfy (u∗,v∗)>(˜w1,˜w2); ¯Ω. Furthermore, any solution of (1.3), (u,v), with small positive initial density will satisfy (u(t,x),v(t,x))>(˜w1(x),˜w2(x)); t>t1,x∈¯Ω, for some t1>0 that depends on the initial density.
Remark
It is possible for λ∗ to be greater than either E1(1,g(0)) or E1(r,h(0)), giving rise to a situation in which one organism could invade and survive in the patch regardless of the presence of the other species, but the patch size is still too small to foster coexistence. For simplicity of presentation, we only display the case that λ∗ is less than both E1(1,g(0)) and E1(r,h(0)).
We now provide sufficient conditions, split into three cases depending on the comparison of E1(1,g(0)) and E1(r,h(0)), that will guarantee coexistence in the patch. Following these results, we provide a table depicting the portions of the parameter space corresponding to each of the three cases, and a brief description of their biological interpretation.
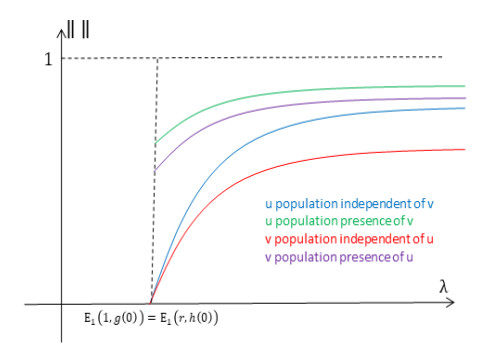
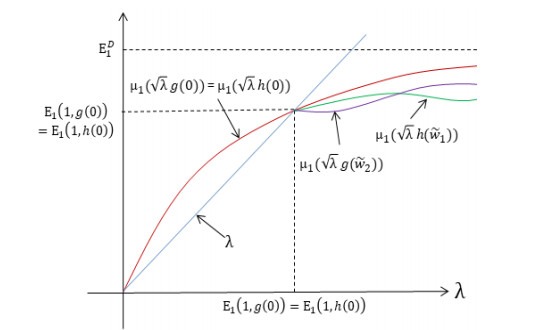
First, we consider the case when E1(1,g(0))=E1(r,h(0)) with a pictorial description given in Figure 5 and a bifurcation diagram showing one possibility for the complete solution structure of (1.4) in the case of a one-dimensional patch in Figure 6. Details regarding creation of bifurcation diagrams representing the solution structure of (1.4) can be found in [49], which is forthcoming.
Theorem 3.2. Let g(0),h(0) and r be fixed such that E1(1,g(0))=E1(r,h(0)). Then
(a) σ1,σ2≥0 for λ≤E(1,g(0))
(b) σ1,σ2,σ3,σ4<0 for λ>E1(1,g(0))
(c) λ∗<E1(1,g(0))=E1(r,h(0)).
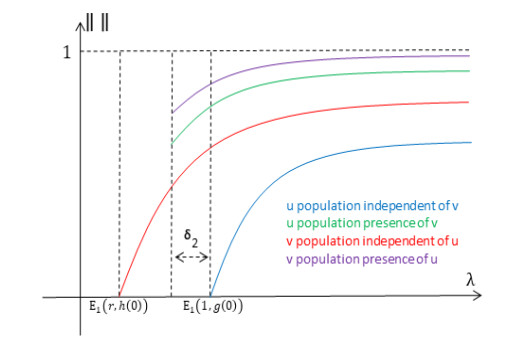
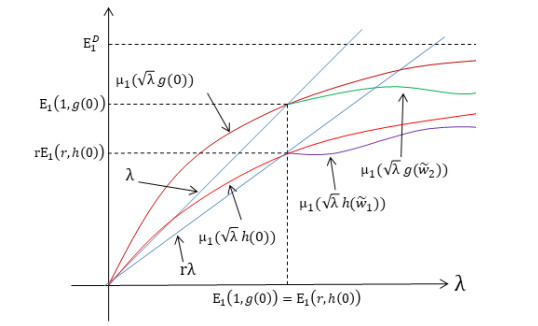
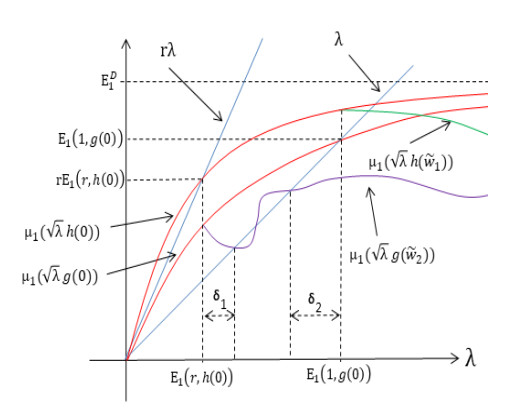
Next, we consider the case when E1(1,g(0))>E1(r,h(0)) with a pictorial description given in Figure 7 and a bifurcation diagram showing one possibility for the complete solution structure of (1.4) in the case of a one-dimensional patch in Figure 8 (see [49]).
Theorem 3.3. Let g(0), h(0) and r be fixed such that E1(1,g(0))>E1(r,h(0)) then there exist δ1=δ1(g(0),h(0),r) and δ2=δ2(g(0),h(0),r), both positive, such that
(a) σ1≥0 for λ≤E1(1,g(0)) and σ1<0 for λ>E1(1,g(0))
(b) σ2≥0 for λ≤E1(r,h(0)) and σ2<0 for λ>E1(r,h(0))
(c) σ3<0 for λ>E1(1,g(0))
(d) σ4>0 for λ∈(E1(r,h(0)),E1(r,h(0))+δ1) and σ4<0 for λ>E1(1,g(0))−δ2
Moreover, for λ∈(E1(1,g(0))−δ2,E1(1,g(0))) (1.4) has a positive solution and there exists an ϵ1>0 such that any solution of (1.3) with (u(0,x),v(0,x))≥(≈) (ϵϕ4(x),˜w2(x)); Ω and ϵ<ϵ1 will converge to a positive coexistence steady state of (1.3) as t→∞ (see region (E) in Figure 7).
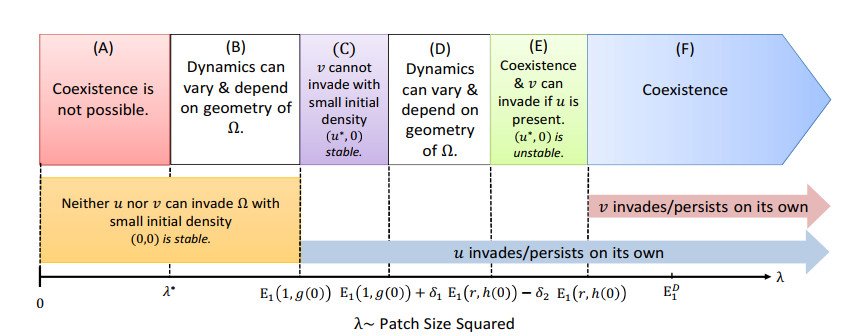
We now consider the case when E1(1,g(0))<E1(r,h(0)) with a pictorial description given in Figure 9 and a bifurcation diagram, showing one possibility for the complete solution structure of (1.4) in the case of a one-dimensional patch in Figure 10 (see [49]).
Theorem 3.4. Let g(0), h(0) and r be fixed such that E1(1,g(0))<E1(r,h(0)) then there exist δ1=δ1(g(0),h(0),r) and δ2=δ2(g(0),h(0),r), both positive, such that
(a) σ1≥0 for λ≤E1(1,g(0)) and σ1<0 for λ>E1(1,g(0))
(b) σ2≥0 for λ≤E1(r,h(0)) and σ2<0 for λ>E1(r,h(0))
(c) σ4<0 for λ>E1(r,h(0))
(d) σ3>0 for λ∈(E1(1,g(0)),E1(1,g(0))+δ1) and σ3<0 for λ>E1(r,h(0))−δ2
Moreover, for λ∈(E1(r,h(0))−δ2,E1(r,h(0))) (1.4) has a positive solution and there exists an ϵ1>0 such that any solution of (1.3) with (u(0,x),v(0,x))≥(≈) (˜w1(x),ϵϕ3(x)); Ω and ϵ<ϵ1 will converge to a coexistence steady state of (1.3) as t→∞ (see region (E) in Figure 9).
Remark
In the forthcoming paper [49], we give a more detailed description of model predictions of persistence as λ varies in the case of a one-dimensional patch, as well as some numerically generated examples of actual steady state density profiles in the case of coexistence (e.g., in (E) and (F) from Figure 7). Preliminary results indicate that in ranges where trait-mediated coexistence occurs (e.g., (E) in Figure 7), the actual steady state density profiles are symmetric about the patch center (x=12), with the organism that is able to colonize the patch having a much larger steady state maximum than the organism which requires the first to colonize the patch.
Finally, we present a table to help depict the portions of the parameter space corresponding to each of the three cases. It is easy to see that each of the three cases discussed previously are possible regardless of the difference in patch intrinsic growth rate and diffusion rate between the species. The main determining factor here appears to be the effective matrix hostility as represented in g(0) for u and h(0) for v.
3.1. Biological interpretation
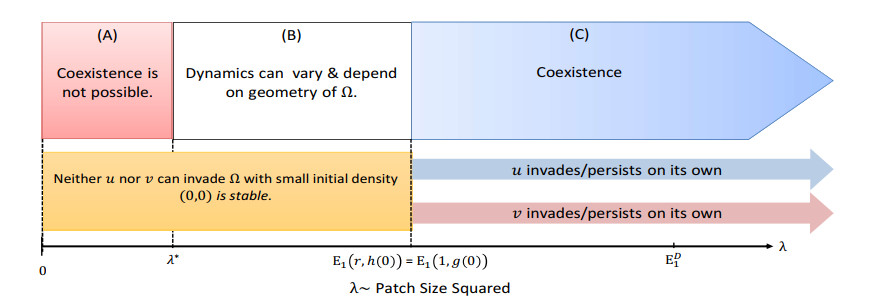
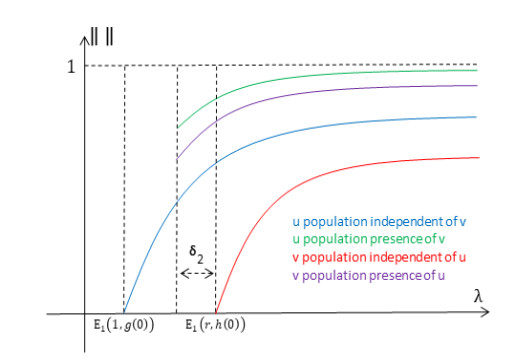
In each of the three cases of comparison for E1(1,g(0)) and E1(r,h(0)), the model predicts coexistence for patch sizes large enough such that λ>λ∗∗ (see (C) in Figure 5, for example). This is due to the fact that sufficiently large patches have a core region large enough to ensure persistence, even in the presence of mortality from interacting with the hostile matrix at the patch boundary. Note that exactly the opposite effect is seen for patches so small that their λ-value falls below λ∗ (see (A) in Figure 5, for example), in that the model predicts extinction regardless of the initial population density.
In the case that E1(1,g(0))=E1(r,h(0)), there is a stark change in model outcomes as λ drops below E1(1,g(0)) (see (B) and (C) in Figure 5), with the model predicting that neither species is able to invade the patch with small positive initial density. Since λ∗<E1(1,g(0)), a situation can arise where coexistence is still possible for patch sizes with corresponding λ-values in (λ∗,E1(1,g(0))). In that case, coexistence is due directly to the effect of trait-mediated dispersal since presence of the other organism causes a decrease in emigration out of the patch, i.e., we have a situation with dispersal-mediated coexistence.
Since the remaining two cases are symmetric, we will only give a biological interpretation for the case when E1(1,g(0))>E1(r,h(0)). As previously noted, a mutualistic system can fall into this case regardless of which species is better able to invade and persist in the patch. In fact, all that is required is that v's effective matrix hostility is sufficiently small compared with u's effective matrix hostility. For patch sizes corresponding to λ∈(E1(1,g(0))−δ2,E1(1,g(0))) (see (E) in Figure 7), the model predicts that, on its own, u is unable to successfully invade the patch, whereas v is able to invade the patch with small initial positive density independent of u. Most interestingly, the model predicts that u is able to invade with small initial population density and coexist in the patch as long as v is already established in the patch and near its steady state (independent of u), i.e., dispersal-mediated coexistence. The mechanism directly responsible for this outcome is trait-mediated dispersal. In other words, the presence of v in the patch decreases u's emigration rate low enough that u is able to persist in the patch. We also note that in this case, the role of coexistence facilitator can be reversed by increasing the facilitator's effective matrix hostility or decreasing the other species hostility. This reversal is in the same spirit as the one observed in a competitive system studied in [26] and [33], where changing the matrix hostility caused a competitive dominance reversal.
For patch sizes with λ∈(λ∗,E1(r,h(0)) or λ∈(E1(r,h(0))+δ1,E1(1,g(0))−δ2) (see (B) or (D) in Figure 7), our methods are not able to give general results regarding model predictions. In other words, the dynamics can vary greatly depending on the patch geometry and parameter values. Patch sizes giving a λ in (E1(r,h(0)),E1(r,h(0))+δ1) (see (C) in Figure 7) yield a model prediction that even with v being established in the patch is not enough to allow u to invade the patch and persist. However, our results do not exclude the possibility of dispersal-mediated coexistence for λ in (E1(r,h(0)),E1(r,h(0))+δ1) and certain ranges of r, g(0), and h(0). In the case of trait-mediated coexistence, the model would predict a type of Allee effect for λ in this range, as the semitrivial steady state (0,v∗) and a positive coexistence steady state would both be stable, giving rise to a dispersal-mediated Allee effect. This case has actually been observed by the authors in a model similar to (1.3), but for a one-dimensional patch (see [49]). Finally, for patch sizes corresponding to λ∈(λ∗,E1(r,h(0))) (see (B) in Figure 7), the model outcome is the same as in the case when E1(1,g(0))=E1(r,h(0)).
4.
Proofs of main results
We first introduce definitions of a subsolution and a supersolution of (1.4) and then state a lemma from [46] that will be employed to prove our existence results for positive solutions of (1.4).
By a subsolution of (1.4), we mean a pair of functions (ψ1,ψ2)∈C2(Ω)∩C1(¯Ω) that satisfies:
By a supersolution of (1.4), we mean a pair of functions (z1,z2)∈C2(Ω)∩C1(¯Ω) that satisfies:
Then the following result holds (see [46]).
Lemma 4.1. Let (ψ1,ψ2) and (z1,z2) be a subsolution and a supersolution of (1.4) respectively such that (ψ1,ψ2)≤(z1,z2). Then (1.4) has a solution (u,v)∈C2(Ω)∩C1(¯Ω) such that (ψ1,ψ2)≤(u,v)≤(z1,z2).
Now, we consider the eigenvalue problem:
where β is a nonnegative continuous function on ∂Ω. Let μ1=μ1(β) denote the principal eigencurve of (4.1). Note that μ1 increases in β (see [39]). For a fixed K>0, when β=√λK, by Lemmas 2 & 3 in [48], the principal eigencurve μ1(√λK)=ˉE1(√λK) is strictly increasing and concave in λ. Moreover, μ1(0)=0 and μ1(√λK)→ED1 as λ→∞ where ED1 is the principal eigenvalue of (2.2). Thus, comparing (2.7), (2.8), (2.9) and (2.10) with (4.1) we obtain
respectively.
Now, we will provide proofs of Theorem 3.1–3.3. Note that the proof of Theorem 3.4 is not provided since it is very similar to the proof of Theorem 3.3.
Proof of Theorem 3.1
(a) We first introduce the eigenvalue problems:
and
Let ˜σ1=˜σ1(Ω,λ,g(1)), ˜σ2=˜σ2(Ω,λ,r,h(1)) be the principal eigenvalues and ψ1, ψ2>0;¯Ω the corresponding normalized eigenfunction of (4.3) and (4.4), respectively. Comparing (4.3) and (4.4) with (4.1), we obtain
Note that at λ=E1(1,g(1)), μ1(√E1(1,g(1))g(1))=E1(1,g(1)) and at λ=E1(r,h(1)),
μ1(√E1(r,h(1))h(1))=rE1(r,h(1)). Since μ1(√λK) is concave, we must have that μ1(√λg(1))>λ for λ<E1(1,g(1)) and μ1(√λh(1))>λr for λ<E1(r,h(1)). Then (4.5) and (4.6) imply that ˜σ1>0 for λ<E1(1,g(1)) and ˜σ2>0 for λ<E1(r,h(1)) respectively. Assume to the contrary that (u,v) is a positive solution of (1.4) for λ<λ∗.
Case Ⅰ: E1(r,h(1))≤E1(1,g(1))
By Green's Second Identity, we obtain
while
giving rise to a contradiction.
Case Ⅱ: E1(r,h(1))>E1(1,g(1))
while
again providing a contradiction.
(b) Following an argument such as one in [29], we have that if λ>λ∗∗ then σ1,σ2<0. By Lemma 2.2, the unique positive solution ˜w1 of (2.5) exists, and the unique positive solution ˜w2 of (2.6) exists. Now since g and h are decreasing functions, ˜w1 and ˜w2 satisfy:
and
Thus, (˜w1,˜w2) is a strict subsolution of (1.4). Since g and h are positive functions it is easy to see that (1,1) is a supersolution of (1.4). Hence, by Lemma 4.1 there exists a positive solution (u∗,v∗) of (1.4) such that (˜w1,˜w2)≤(u∗,v∗)≤(1,1);¯Ω. Since (˜w1,˜w2) is a strict subsolution of (1.4), all positive solutions of (1.4), (u∗,v∗), must satisfy (u∗,v∗)>(˜w1,˜w2); ¯Ω. Finally, the furthermore statement holds since, by an analogous version of Theorem 5.1 in Chapter 10 of [46], any solution of (1.3), (u,v), with small positive initial density will converge to a minimal positive steady state of (1.3) in ⟨(˜w1,˜w2),(1,1)⟩ as t→∞. This completes the proof.
Next, we prove Theorem 3.2.
Proof of Theorem 3.2
Parts (a) and (c) are clear. To prove (b), we consider three cases, namely, r=1, r<1, and r>1. Note that we only provide proofs of the cases r=1 and r<1, as the case when r>1 is almost identical to the r<1 case.
Case Ⅰ: r=1 (which implies that g(0)=h(0))
When β=√λg(0)=√λh(0), we have μ1(√λg(0))=μ1(√λh(0)). Also, we have that
μ1(√E1(1,g(0))g(0))=E1(1,g(0)) at λ=E1(1,g(0)) and μ1(√E1(1,h(0))h(0))=E1(1,h(0)) at λ=E1(1,h(0)). Now, since μ1(√λK) is concave in λ and by (4.2), we obtain σ1=μ1(√λg(0))−λ≥0, σ2=μ1(√λh(0))−λ≥0 for λ≤E1(1,g(0)) and σ1<0, σ2<0 for λ>E1(1,g(0)). Since g and h are decreasing, we have μ1(√λg(˜w2))<μ1(√λg(0)) and μ1(√λh(˜w1))<μ1(√λh(0)). This implies σ3=μ1(√λg(˜w2))−λ<0 and σ4=μ1(√λh(˜w1))−λ<0 for λ>E1(1,g(0)). Figure (12) illustrates the main argument of this case.
Case Ⅱ: r<1 (which implies that g(0)>h(0))
When β=√λg(0)>√λh(0), we have μ1(√λg(0))>μ1(√λh(0)). We also have that
μ1(√E1(1,g(0))g(0))=E1(1,g(0)) at λ=E1(1,g(0)) and μ1(√E1(r,h(0))h(0))=rE1(r,h(0)) at λ=E1(r,h(0)). Now, since μ1(√λK) is concave in λ and by (4.2), we obtain that σ1≥0, σ2≥0 for λ≤E1(1,g(0)) and σ1<0, σ2<0 for λ>E1(1,g(0)). Since g and h are decreasing, we have that μ1(√λg(˜w2))<μ1(√λg(0)) and μ1(√λh(˜w1))<μ1(√λh(0)). This implies σ3=μ1(√λg(˜w2))−λ<0 and σ4=μ1(√λh(˜w1))−λr<0 for λ>E1(1,g(0)). Figure (13) provides an illustration of the main argument of this case.
This completes the proof.
We now prove Theorem 3.3.
Proof of Theorem 3.3
Proof of (a) and (b) are clear. Next, we prove part (c). By part (a), σ1<0 for λ>E1(1,g(0)). Now, by Lemma 2.2, ˜w1 exists for λ>E1(1,g(0)). Here, we note that at λ=E1(r,h(0)),
Then, since μ1(√λh(0)) is concave in λ,
Since h is decreasing, the inequality
holds for λ>E1(1,g(0)). Now (4.7) and (4.8) imply that μ1(√λh(˜w1))<rλ for λ>E1(1,g(0)). Thus, σ3=μ1(√λh(˜w1))−rλ<0 for λ>E1(1,g(0)). This completes the proof of (c).
In order to prove (d), we must consider three cases: g(0)<h(0), g(0)=h(0), and g(0)>h(0). However, we will only provide a proof for the first case, as the remaining cases are almost identical to the first.
Case Ⅰ: (g(0)<h(0))
First, we note that
Since μ1(√λg(0)) is concave in λ, the inequality:
holds for λ<E1(1,g(0)). This implies that
Note that μ1(√λg(˜w2))<μ1(√λg(0)) for λ>E1(r,h(0)) and μ1(√λg(˜w2))→μ1(√E1(r,h(0))g(0)) as λ→E1(r,h(0))+. This with (4.10) and by continuity imply that there exists δ1(r,g(0),h(0)) such that λ<μ1(√λg(˜w2)) for λ∈(E1(r,h(0)),E1(r,h(0))+δ1). This implies σ4=μ1(√λg(˜w2))−λ>0 for λ∈(E1(r,h(0)),E1(r,h(0))+δ1).
Since E1(1,g(0))=μ1(√E1(1,g(0))g(0)) and μ1(√E1(1,g(0))g(˜w2))<μ1(√E1(1,g(0))g(0)), by continuity, there exists δ2(g(0),h(0),r)>0 such that μ1(√λg(˜w2))<λ for λ>E1(1,g(0))−δ2. This implies σ4=μ1(√λg(˜w2))−λ<0 for λ>E1(1,g(0))−δ2. Also see Figure (14). In this case, E1(1,g(0))<E1(1,h(0)) since g(0)<h(0). Using (2.4) we obtain E1(1,g(0))<rE1(r,h(0)). Now this with E1(1,g(0))>E1(r,h(0)) implies r>1.
Next, we provide a proof of coexistence. Since λ>E1(r,h(0)) we have that σ2<0. Thus, by Lemma 2.2, the unique solution ˜w2 of (2.6) exists. Also, part (d) implies that σ4<0 for λ>E1(1,g(0))−δ2. Let y1=ϵϕ4 and y2=˜w2. Now choose ϵ>0 and ϵ≈0 such that σ4≤−λϵϕ4 and ϵϕ4≤1. Now by (2.10), y1 satisfies:
Further, since h is decreasing, y2 satisfies:
Thus (ϵϕ4,˜w2) is a subsolution of (1.4). Since g and h are positive functions it is easy to see that (1,1) is a supersolution of (1.4). Hence, by Lemma 4.1 there exists a positive solution (u,v) of (1.4) such that (ϵϕ4,˜w2)≤(u,v)≤(1,1);¯Ω. Finally, by an analogous version of Theorem 5.1 in Chapter 10 of [46], any solution of (1.3), (u,v), with (u(0,x),v(0,x))≥(≈) (ϵϕ4(x),˜w2(x)); Ω and ϵ<ϵ1 will converge to a minimal positive steady state of (1.3) in ⟨(ϵϕ4(x),˜w2),(1,1)⟩ as t→∞. This completes the proof.
5.
Conclusions
Our mathematical analysis of the model (1.1) demonstrates that trait-mediated dispersal can have important impacts on coexistence of mutualists. Specifically, one species can invade and persist because it has either a high growth rate, low diffusion rate, or a lower effective matrix hostility. Either way, the population for that species can build up in the patch which can favor the coexistence of the other species by reducing that species likelihood of leaving the patch. We also found that the role of coexistence facilitator can be reversed by increasing the facilitator's effective matrix hostility or decreasing the other species hostility. As most mutualistic relationships are identified on the basis of density-mediated effects, it is easily possible that such a trait-mediated effect may be overlooked. Our study complements the existing research that trait-mediated dispersal can affect the interactions and coexistence between predators and their prey and competing species. The presence of predators or their cues can elicit the production of wings [50] or an increase in emigration rate (e.g., [11,12,13,14]). Numerous studies have explored the role of dispersal in affecting the coexistence of predators and prey in fragmented landscapes (e.g., [51,52,53,54]). Similarly, although much less studied, the occurrence of interspecific competitors can also promote increased dispersal [55,56]. One commonly reported mechanism promoting the coexistence of competitors is a tradeoff between dispersal and interspecific competition whereby poorly competitive but highly dispersive species can coexist with highly competitive but poorly dispersive species (e.g., [57,58,59]). For animal species engaged in mutualisms, studies in addition to our own have shown that dispersal can affect species coexistence [60]. To date, few empirical studies of trait-mediated dispersal have been conducted with mutualists (but see e.g., [17,18,19,20,61]). However, we submit that dispersal mediated indirect effects are likely as common and important in mutualisms as they are in predator-prey and competing-species interactions.
From a conservation point of view, our results greatly support the need to more carefully consider trait-mediated effects in the conservation effort. For example, an endangered species in a trait-mediated dispersal relationship with an unknown second species may setup a situation where the unidentified mutualist is responsible for allowing the endangered species to thrive in a patch. If this supporting species is somehow expelled from the patch, our results indicate that habit fragmentation via reduction of patch size or increase of matrix hostility may push the endangered species into a situation where its population suddenly crashes.
Our results are quite general in the sense that we did not make any assumptions on the patch geometry (other than assuming that the patch boundary is smooth), patch dimension, or the density dependent emigration relationship, other than assuming it's mutualistic. Furthermore, in an effort to isolate the effects of trait-mediated dispersal on the mutualistic system, we assumed that the two species did not exhibit any direct density-mediated effects. This indicates that predictions of our model are likely to be found in mutualistic systems that exhibit trait-mediated dispersal. However, in reality, it is probably very unlikely that a mutualistic system would exhibit trait-mediated dispersal without density-mediated effects. We are currently exploring the system in the case where density-mediated effects are also included in the model.
Acknowledgments
This material is based upon work supported by the National Science Foundation under Grant No. DMS-1853359, DMS-1853372, & DMS-1853352.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: