Powerlifting score prediction using a machine learning method

1.   Introduction

In recent years, along with the development of economy and society, sport is more and more interested in people. Sports help people to increase resistance, reduce work stress and enhance solidarity among people, etc. ^[1,2,3]. According to the World Health Organization, each year about 2 million people die from lack of exercise. Lack of exercise will reduce the body's immunity and make adolescents develop abnormally ^[4,5].

Powerlifting is a popular sport. In competition, the impact on powerlifters' performance is mainly due to age, weight, fitness and psychology ^{[6,7,8,13,14,17]}. Therefore, the training methods of coaches for powerlifters are extremely important, and studying the factors that influence athletes' performance is an inseparable task in training process ^[9,10,11]. Solberg et al. ^[12] based on the data powerlifting data in the international competitions; they calculated the score of powerlifters at their peak performance, thereby giving the development trend of athletes, helping experts to evaluate more correctly about the athletes' abilities before playing. Latella et al. ^[13] analyzed the long-term strength adaptation of powerlifters through 15 years of data. They evaluated the daily strength growth rate of 1897 powerlifters. The results show that men and women have similar strength adaptability, and the rate of strength gain differs by strength quartile for females. These findings provide new evidence for strength adaption and provide a reliable basis for powerlifting coaches. Latella et al. ^[14] pointed out that there is little understanding of the factors that affect the strength of powerlifters, and studied the strength of powerlifters through age and weight. The results provide important information for the factors affecting athletes' strength performance and provide basis for coaches in long-term training plans. Anton et al. ^[15] analyzed the strength performance of world-class powerlifters with age. They concluded that powerlifters of different ages performed differently, and that women's abilities declined faster. Jame et al. ^[16] studied a method to improving the performance of weaker and inexperienced powerlifters. After testing this method, the performance was significantly improved. Pearson et al. ^[17] investigated the influence of competition frequency on the strength of powerlifters within 12 months. The results show that powerlifters who participate in multiple competitions each year are more likely to achieve higher overall results. Coker et al. ^[18] reported that the success or failure of each lift attempt has a correlation with Wilks points. The limitation in this study is that they did not relate their findings to competitive outcomes.

Age, weight and psychology are critical to the performance of powerlifters. In a competition, the score of the previous competition content will directly affect the next content. Therefore, studying and predicting the performance of powerlifters is extremely important for calculating the individual scores. It can be used as a basis for choosing the right weight in the next competition. Traditional prediction methods usually have the disadvantages of low accuracy and unable to immediately predict the performance of athletes in the competition ^[19]. In recent years, artificial intelligence has developed dramatically and is applied in many fields such as performance fitness and error metrics ^[20,21]. So, the application of artificial intelligence in predicting the score of athletes has profound implications. Extreme learning machine (ELM) algorithm ^[22,23] is a novel method of artificial intelligence. This algorithm has very fast training speed and high analysis accuracy, and has attracted the attention of many researchers. Huang et al. ^[24] proposed the kernel ELM to further improve the generalization ability of ELM and it perform better in classification and regression problems. Tang et al. ^[25] brought the unsupervised learning algorithm into the ELM theory and proposed a multilayer ELM algorithm. The algorithm does not require fine-tuning, and has better learning efficiency than typical deep learning algorithms. Compared with the current popular multi-layer learning method, this algorithm can achieve better and faster convergence. Deng et al. ^[26] proposed a regularized ELM algorithm, which added the structural risk minimization principle and the weighted least squares algorithm. The experiments show that the generalization performance of ELM has been significantly improved. Zheng et al. ^[27] used the maximum mixture correntropy criterion as an optimization algorithm to improve the kernel ELM, which overcomes the shortcoming of the minimum mean square error of the Gaussian assumption. Cao et al. ^[28] improved the ELM algorithm based on the maximum entropy criterion in order to alleviate the poor effect when processing with large outliers, and verified the effectiveness of their proposed method on more benchmark data sets. Ertugrul et al. ^[29] proposed a reservoir computing-ELM (RC-ELM) algorithm based on the reservoir computing theory. RC-ELM does not need to fine-tune any parameters. In most experimental results, RC-ELM performance is better than ELM.

Based on the age, weight and field score of powerlifters, we study the best performance of powerlifters and develop a model for predicting the best score. The model is based on the RC-ELM algorithm, but the parameters of RC-ELM are initialized randomly, which leads to unstable model performance. Therefore, in order to further improve the prediction accuracy of the model, this study uses a novel whale optimization algorithm to optimize the parameters. Finally, we use the MATLAB software for modeling and testing to verify the performance of the proposed method.

2.   Methods

2.1.   Reservoir computing extreme learning machine

The function of a hidden layer neural network is shown in Eq (1)

where, ${\beta _j} \in {\bf{R}}$ is the output weight, ${\bf{w}} = {[{{\rm{w}}_{j1}}, {{\rm{w}}_{j2}}, ..., {{\rm{w}}_{jn}}]^T} \in {{\bf{R}}^n}$ is the input weight, ${b_j} \in {\bf{R}}$ is the bias, ${{\bf{x}}_i} = {\left[ {{x_{i1}}, {x_{i2}}, \cdots , {x_{in}}} \right]^T} \in {{\bf{R}}^n}$ is input data, ${{\bf{t}}_i} = {\left[ {{t_{i1}}, {t_{i2}}, \cdots , {t_{in}}} \right]^T} \in {{\bf{R}}^m}$ is expected output; $g(.)$ is the activation function, and L is number of hidden layer nodes.

The $f({\bf{x}})$ is equal to Eq (2).

where,

N is number of samples.

According to the proof of ELM, we can calculate the ${\bf{ {\bf{ \pmb{\mathsf{ β}} }} }}$.

where, ${{\bf{H}}^ + }$ is the Moore-Penrose generalized inverse of ${\bf{H}}$.

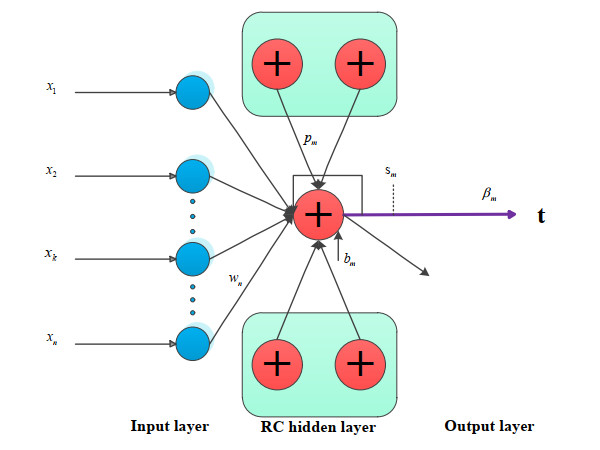
In the reservoir computing extreme learning machine (RC-ELM) network, the ith neuron in the reservoir can be obtained as Eq (6) in Figure 1.

where S is the summation of inputs of a neuron, p is the weights of the neurons in the reservoir, and m is the number of neurons in the reservoir. The summation of inputs of a neuron in the reservoir can be obtained as Eq (7).

Each of the summations of inputs of a neuron can be calculated by obtained as Eqs (8) and (9).

Finally, the ${\bf{ {\bf{ \pmb{\mathsf{ β}} }} }}$ can calculated by Eq (10).

2.2.   Whale optimization algorithm

Whale optimization algorithm (WOA) ^[30,31] is a new swarm intelligence optimization algorithm based on whale's unique hunting strategy. The WOA optimization process is divided into three phases: foraging, bubble-net preying and searching for food.

(a) Foraging

The whales find food by working with the swarm. When the food is detected, all individuals in the swarm will gradually approach the food. Assuming that the location of the food is the best target, the steps to approach this target is shown in Eq (11).

where i is the current number of iterations, ${X_i}$ is the current position, ${X_{i + 1}}$ is the position after iteration i, $X_i^*$ is the current optimal position of the all whales, and A and C are coefficients, these coefficients are calculated according to the Eqs (12) and (13).

where ${t_1}$ and ${t_2}$ are random numbers in the range of [0, 1]. As the number of iterations increases, the value of a decreases linearly from 2 to 0.

(b) Bubble-net preying

At this phase, the predation behavior of whales includes two processes: shrink wrapping and spiral uprising. The probability of choosing between these two processes is 0.5. Through these two processes, we can achieve local optimization. This phase is represented mathematically according to Eq (14).

where l is a random number in the range (−1, 1), p is a random number in the range (0, 1), and b is a constant of the spiral.

(c) Searching for food

At this phase, each whale is assigned a random location for global search (when A > 1). The calculation of the random location is shown in Eq (15).

where ${X_{{\rm{rand}}}}$ is the random location.

2.3.   Propose an optimal method for RC-ELM by WOA

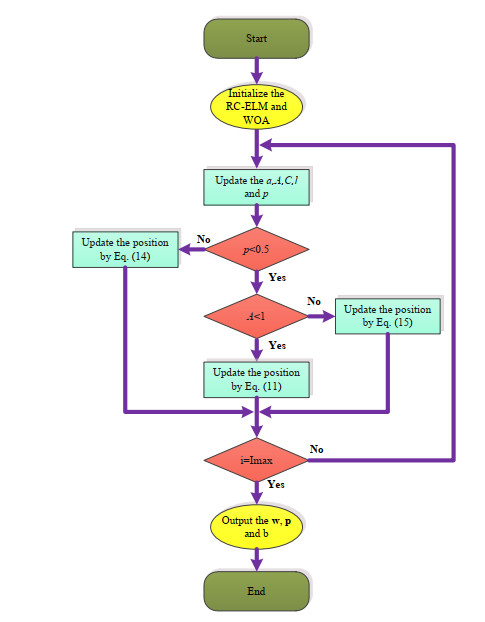
As mentioned above, the weights and bias of the RC-ELM are randomly generated, which will greatly affect the model performance. Therefore, to improve the efficiency and increase the stability of the model, we propose a method to optimize the weights and bias of RC-ELM by using WOA (this method is called WOA- RC-ELM). The WOA-RC-ELM algorithm flowchart is showed in Figure 2.

Algorithm 1: WOA-RC-ELM algorithm

Initialize the WOA-RC-ELM algorithm

for i = 1: Imax

  for j = 1: N (where N is the number of whale groups)

    Update a, A, C, l and p

    if p < 0.5

      if A < 1

        Update the position by Eq (11)

      else

        Update the position by Eq (15)

      end if

    else

      Update the position by Eq (14)

    end if

  end for

end for

Output optimized w, p and b.

3.   Results and discussions

3.1.   Data collection and analysis

We collected the scores of world-class powerlifters from 1972 to 2017 ^[32,33], such as the World Masters Powerlifting Championships, and the World Open Powerlifting Championships. There are a total of 5500 male powerlifters' features, and the age ranges from 20–35. These features include age, body weight, weight class, best squat, best bench, and best deadlift. We randomly selected 4500 samples as the training set and 1000 samples as the test set. The data is normalized to (0, 1). Choose the best bench as the output value, and the remaining features as the input value.

For the powerlifters, about 12 age is the initial stage of training development. Entering the age of 14 is a sensitive period, and proper training methods must be available at this stage. Around the age of 16, the powerlifters have developed basic skills. Over 20 years old is the peak period of performance ^[34].

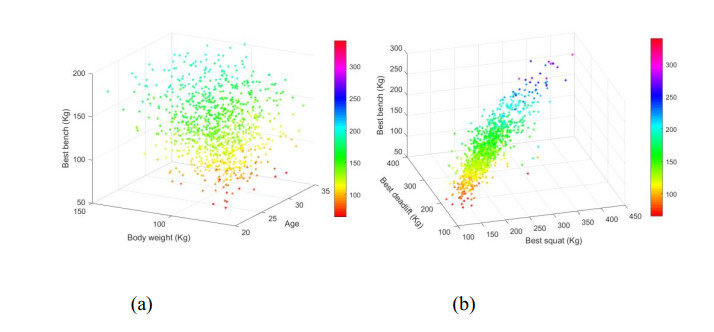
Based on the features of powerlifters, we draw the relationship between them. Figure 3 shows this relationship. Figure 3(a) is the effect of age and weight on the best bench. We can see that as the weight value increases, the best bench value also increases. Powerlifters basically have the greatest strength and rich experience between the ages of 20 and 35. At this stage athletes can reach peak state and break their own records. For the mathematical modeling angle, the points in the Figure 3(a) are relatively discrete and nonlinear. Figure 3(b) is the relationship between best squat, best bench, and best deadlift. It can be seen that these features have a strong linear relationship. This implies that if the performance of the powerlifters is good at squat and deadlift, then the bench performance will also be good. Conversely, if the squat and deadlift performance is not good, then the bench is also performing poorly. Therefore, we can rely on these features to predict the performance of powerlifters during the competition, and it is necessary to build a mathematical model to calculate these scores.

3.2.   Score prediction model

Based on the WOA-RC-ELM algorithm, we design a score prediction model for male powerlifters. The coefficient of determination (R²) and root-mean-square error of prediction (RMSEP) ^[35,36]0 were used to evaluate the model. The calculation of these two indicators is as follows:

where ${y_i}$ is the actual value, $\bar y$ is the mean value, and ${\hat y_i}$ is the predictive value, ${n_{test}}$ is the number of samples. The closer the value of R² is to 1 and the smaller the value of RMSEP, the better the prediction effect of the model.

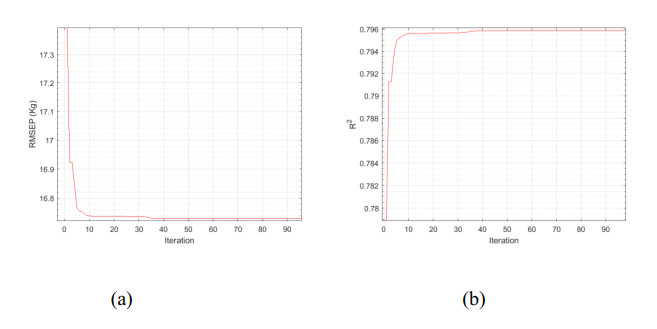
Figure 4 shows the performance of the WOA-RC-ELM algorithm. Where, the number of iterations is 100 and the parameter m of RC-ELM is 20. We can see that the WOA-RC-ELM algorithm converges quickly. When the number of iterations is 35, the global optimal state is reached. RMSEP decreased from 17.41 to 16.73, and R² increased from 0.7786 to 0.7958, the result proves the effectiveness of the proposed method. WOA can effectively optimize the multi-dimensional parameter matrix and improve the accuracy and stability of the RC-ELM algorithm. The results can be used to assist experts in predicting the score of powerlifters and lay the foundation for coaches' training methods.

3.3.   Comparison of different methods

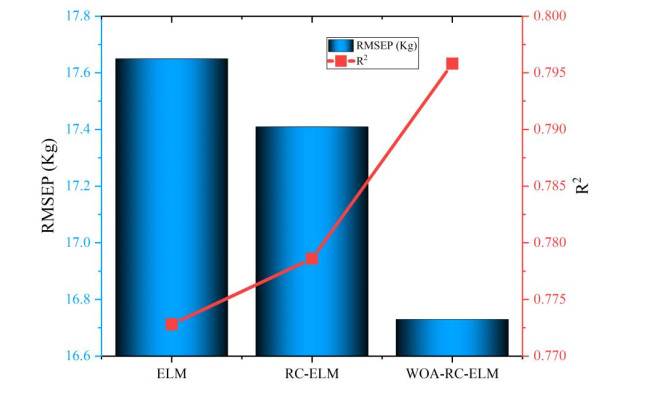
This study compares WOA-RC-ELM, RC-ELM and ELM, and Figure 5 shows the comparison results. We can see that the best performance is the WOA-RC-ELM method, with an RMSEP of 16.73 and R² of 0.7958. The performance of RC-ELM is better than ELM method. The RMSEP and R² of RC-ELM method are 17.41 and 0.7786, respectively. The RMSEP of the ELM method is 17.65 and R² is 0.7728. The comparison results once again demonstrate the effectiveness of the proposed method. WOA can improve the performance of RC-ELM algorithm and proves that WOA is an effective optimization algorithm. The proposed model is a reliable method for predicting powerlifting performance, which can provide a reference for the best score of powerlifters before the competition.

4.   Conclusions

Male powerlifters of different ages and weights have different performances. This research established a score prediction model based on the characteristics of male powerlifters and a machine learning method. The model uses the age, body weight, weight class, best squat, best bench, and best deadlift features of powerlifters, and the WOA algorithm is used to improve the predictive ability of the model. Specifically, a 23 years old powerlifter with weight is 99 kg, our model predicts the best bench score is 141 kg, which is 1.5 kg different from the actual value. The results show that our proposed method can effectively predict the score of male powerlifters, which provides a reliable prediction method for powerlifting before competitions.

Acknowledgments

This work is supported by Ministry of Education Fund Project of Vietnam (No. B-2021-STS-01).

Conflict of interest

All authors declare no conflicts of interest in this paper.