Research on performance evaluation of higher vocational education informatization based on data envelopment analysis

1.   Introduction

The solution of the mixed Volterra-Fredholm integral equations has been a subject of considerable interest. Studies on population dynamics, parabolic boundary value problems, the mathematical modeling of the spatio-temporal development of an epidemic and various physical and biological models lead to the mixed Volterra-Fredholm integral equations. A discussion of the formulation of such models is given in ^[1].

The linear mixed Volterra-Fredholm integral equation is given by

where f(x) is a known continuous function on the interval [a, b], the kernel k(r, t), is known and continuous on the region D = {r, t: a≤t≤b & a≤r≤x≤b}, and λ, ∈$\mathscr{R} \backslash\{0\}$, while u(x) is the unknown continuous function in [a, b] that must be determined. The solution of this type of equation using Fibonacci collocation method has been discussed by Mirzaee and Hoseini in ^[2], while the numerical solution via modification of the hat function was presented in ^[3]. The existence and uniqueness results of equation (1) can be found in ^[4]. The reproducing kernel method and a study over the role of iterative methods for solving linear and mixed integral equations with variable coefficients were recently investigated in ^[5,6]. Several other fixed point type and numerical methods were discussed in the literature, see for more ^[7,8,9,10] and the references therein.

A linear system of second kind mixed Volterra-Fredholm integral equations (LSMVFIE2^nd) can be written as:

where

The functions f_i(x), i = 1, 2, …, n are continuous on the interval [a, b] and all kernels k_ij(r, t), for i, j = 1, 2, …, n are continuous on D = {r, t: a≤t≤b & a≤r≤x≤b}, while u_i(x), i = 1, 2, …, n are the unknown continuous functions to be determined.

During the last 20 years, significant progress has been made in the numerical analysis for the linear and nonlinear versions of (2), since finding the exact solution in most cases is challenging or even not possible. To recall some of such works, Rabbani and Jamali used variational iterative method to find the solution of nonlinear system of Volterra-Fredholm ^[11], while Chasemi et al. presented an analytical method to solve this problem using the so called h-curves ^[12], Wazwaz also approximated the exact solution by Adomian decomposition method and discussed the procedure in the book ^[13].

Some other well known techniques including collocation methods which are based on the discretization of the spatial domain are discussed in ^[14,15,16]. Kakde et al. used fixed point (FP) approach to solve differential and integral equations in ^[17]. In addition, a fixed oint type scheme was used for solving non-linear quadratic Volterra integral equation in ^[18], while in ^[19], the appropriate condition and performance of fixed-point method for Volterra-Hammerstein equation are studied. Finally, in the book ^[20], Jerri used a fixed-point approach to solve linear Volterra integral equations.

In this paper, we have made an attempt to propose a numerical scheme to approximate the solution of (2) based on the contractive mapping and a fixed-point method. We study the appropriate conditions and performance of this method for (1). This method has two advantages that encourage us to use it. Firstly, there is not any system of linear equations with its relevant difficulties. Furthermore, it is simple to be applied when programming.

The main goal of this work is in studying the existence and uniqueness of a continuous solution of the presented system in the Banach space based on the FP theory. In fact, the approximation of the solution is also discussed using an iterative method of fixed point. Finally several experiments are presented to show the efficiency and accuracy of the proposed methods.

Before going to the next section, several definitions and theorems are reminded as follows ^[13,15].

Definition 1. For a metric space (M, d), let M°⊆M with a map f:M°→M, a point p∈M° is said to be a fixed point of f if f(p) = p.

Definition 2. Let (M, d) be a complete metric space, a mapping f:M→M is said to be contraction if $\exists \alpha \in \mathcal{R}$ for 0 ≤ α < 1 such that

Theorem 1.1. (Fixed-point Theorem; FPT) If the mapping f:M→M is contraction on a complete metric space (M, d), then f has a unique fixed point x∈M.

2.   Contractive mapping for LSMVFIE2^nd

The FPM provides a scheme which is used to solve LSMVFIE2^nd by starting with an initial approximation that will be used in a recurrence relation to find the other approximate solutions. First, consider the system (2) and define the operator T as follows:

where F, U and K are defined in Section 1, while $T = {\left[{{T_1}, {T_2}, \ldots, {T_n}} \right]^t}$. The solution of the system (2) is fixed-point of T. Choose ${u_i}^0\left(x \right) \in C\left[{a, b} \right]$ as an initial function and the following fixed-point iteration will be introduced ^[4]:

Applying (4) will determine multiple approximations ${u_i}^r\left(x \right)$, for i = 1, 2, …, n, r≥1 and the sequence $\left\{ {{u_i}^n} \right\}$ converges to U(x) as n→∞. It is just the contractive property which is responsible for clustering the sequence $\left\{ {{u_i}^n} \right\}$ towards a limit point. Then the major concepts that required to the FPT are contraction mapping and a complete metric space.

The theorem below shows that T becomes a contractive mapping under some assumptions.

Theorem 2.1. For a complete metric space (C[a, b], ${\left\| \cdot \right\|_\infty }$), and the continuous functions F∈C[a, b] and K∈C([a, b]×[a, b]), if the following conditions satisfied

Then, the mapping T that defined in (3) becomes a contractive mapping.

Proof: Since the kernels are continuous on abounded region, then $\left| {{K_{ij}}\left({r, t} \right)} \right| \le {M_{ij}}, \forall i, j = 1, 2, \ldots, n$ for some positive real numbers M_ij. For such functions we work with the complete metric space (C[a, b], ${\left\| \cdot \right\|_\infty }$).

Now, to find a sufficient condition for the mapping TU in (3) to be a contractive mapping, consider the ith equation of the equation system (2) as follows:

Now for some $\mathit{\boldsymbol{v}} = \left\{ {{v_1}, {v_2}, \ldots, {v_n}} \right\}$ and for each i = 1, 2, …, n; we have

Thus, it is possible to find

Now, we have

and

Let

Hence, if

or similarly as long as we have

Then, the mapping T of the LSMVFIE is a contractive mapping. The proof is complete now.

3.   Existence of a unique solution for LSMVFIE2^nd

To show that there exists only one solution for LSMVFIE2^nd, we have to prove that T has a unique FP and the generated sequence $\left\{ {{u_i}^n} \right\}_{n = 0}^\infty$ in (4) converges to this FP. The following theorem justifies the convergence of ${u_i}^r\left(x \right)$.

Theorem 3.1. Let (C[a, b], ${\left\| \cdot \right\|_\infty }$) be a complete metric space and T_i be n contraction mapping on the LSMVFIE2^nd as defined in equation (3) then for each i = 1, 2, …, n, we obtain:

ⅰ. T_i has a unique fixed-point ${u_i}^* \in C\left[{a, b} \right]$ such that ${u_i}^* = {T_i}\left({{\mathit{\boldsymbol{u}}^*}} \right)$

ⅱ. For any ${u_i}^0 \in C\left[{a, b} \right]$, the sequence $\left\{ {{u_i}^r\left(x \right)} \right\} \subset C\left[{a, b} \right]$ defined by ${u_i}^r\left(x \right) = {T_i}\left({{\mathit{\boldsymbol{u}}^{r - 1}}} \right)$, for r = 0, 1, …, converges to ${u_i}^*$.

Proof: ⅰ. Taking limits of both sides of ${u_i}^r\left(x \right) = {T_i}\left({{\mathit{\boldsymbol{u}}^{r - 1}}} \right)$, we have:

where T_i is the contraction mapping for each i, and T_i is continuous. So, we obtain:

Thus, ${u_i}^{\rm{*}} = {T_i}\left({{\mathit{\boldsymbol{u}}^*}} \right)$, for ${\mathit{\boldsymbol{u}}^*} = {u_1}^*, {u_2}^*, \ldots, {u_n}^*$. Hence T_i has a fixed-point i = 1, 2, …, n. Now by reductio ad absurdum, suppose that (if possible) v_i^* is also a fixed-point of T_i, this means that ${v_i}^{\rm{*}} = {T_i}\left({{\mathit{\boldsymbol{v}}^*}} \right)$ for ${\mathit{\boldsymbol{v}}^*} = {v_1}^*, {v_2}^*, \ldots, {v_n}^*$, then

This means α_i≤1, this is a contradiction. Thus ${u_i}^{\rm{*}} = {v_i}^{\rm{*}}$.

ⅱ. From part (ⅰ), we have:

Let $\mathop {max}\limits_{j = 1,2, \ldots ,n} {\left\| {{u_j}^{r - 1} - {u_j}^*} \right\|_\infty } = {\left\| {{u_{l1}}^{r - 1} - {u_{l1}}^*} \right\|_\infty }$ and then we have

Thus, we get the following inequality to complete this part:

where ${\alpha ^r} = max\left\{ {{\alpha _i}, {\alpha _{l1}}, {\alpha _{l2}}, \ldots, {\alpha _{l\left({r - 1} \right)}}} \right\}$. Thus $\mathop {\lim }_{r \to \infty } {\left\| {{u_i}^r\left( x \right) - {u_i}^*\left( x \right)} \right\|_\infty } \le \mathop {\lim }_{r \to \infty } {\alpha ^r}{\left\| {{u_{lr}}^0 - {u_{lr}}^*} \right\|_\infty }$. Since 0≤α < 1, α^r→0 as r→∞. This means that ${u_i}^r \to {u_i}^*$, for i = 1, 2, …, n. The proof is ended now.

4.   An algorithm based on the FPM

As discussed in section 1 and since the exact solution of the LSMVFIE2^nd could be found in all cases, here an approximate-analytic solution is presented to find the solution specially for cases at which there is no special peak or oscillation in the solution of the problem.

Perform the steps below to get the approximation for LSMVFIE2^nd by using FPM:

Step 1: Choose a, b as the integration bound, n as the number of unknown functions, and m as the number of points in the interval [a, b].

Step 2: Let ${u_i}^0\left(x \right) = {f_i}\left(x \right)$ be an initial solution.

Step 3: Calculate ${u_i}^r\left(x \right)$ in (3) for all i = 1, 2, …, n.

Step 4: Repeat Step 3 until desired level of accuracy is reached.

Step 5: Find ${u_i}^r\left({{x_j}} \right), {\rm{}}{x_j} \in \left[{a, b} \right]$, where ${x_j} = {\rm{}}{x_0} + jh$, for j = 1, 2, …, m where $h = \frac{{b - a}}{m}$.

Step 6: Compute $\left| {{u_i}\left({{x_j}} \right) - {\rm{}}{u_i}^r\left({{x_j}} \right)} \right|$, for any i and j.

5.   Computational experiments

To show the implementation of the method and the accuracy of the approach two tests will be solved in this section.

Example 1. Consider the following LSMVFIE2^nd

where

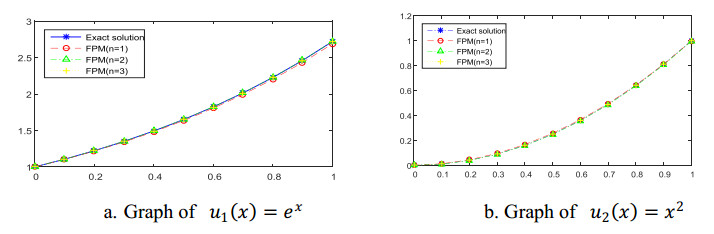
and the exact solution is given by ${u_1}\left(x \right) = {e^x}, \; {\rm{and}}\; {u_2}\left(x \right) = {x^2}$. Recalling that the solution does not have sharp behaviors including oscillations or peaks and thus the system is a good candidate for taking into account the approximate-analytic methods, such as the one discussed in section 4.

First, we let

Now by using (4) the values of ${u_1}^i\left(x \right)$ and ${u_2}^i\left(x \right)$ will be determined for all i = 1, …, 10. The absolute errors for the approximate solutions ${u_1}^{10}\left(x \right)\; {\rm{and}}\; {u_2}^{10}\left(x \right)$ are listed in Tables 1 and 2 respectively.

Table 1.  The results for ${u_1}^{10}\left(x \right)$ and the absolute errors of Example 1.

${x_j}$	Exact solution ${u_1}\left({{x_j}} \right)$	Approximate Values of $u_1^{10}({x_j})$	Absolute error $\left| {{u_1}\left({{x_j}} \right) - {\rm{}}u_1^{10}\left({{x_j}} \right)} \right|$
0.1	1.10517091807	1.10517091808	9.034 e-12
0.2	1.22140275816	1.22140275817	1.7206 e-11
0.3	1.34985880757	1.34985880760	2.4518 e-11
0.4	1.49182469764	1.49182469767	3.0969 e-11
0.5	1.64872127070	1.64872127073	3.6558 e-11
0.6	1.82211880039	1.82211880043	4.1287 e-11
0.7	2.01375270747	2.01375270751	4.5155 e-11
0.8	2.22554092849	2.22554092854	4.8161 e-11
0.9	2.45960311115	2.45960311120	5.0306 e-11
1.0	2.71828182845	2.71828182851	5.1592 e-11

---

 | Show Table

DownLoad: CSV

Table 2.  The results $u_2^{10}\left(x \right)$ and the absolute errors of Example 1.

${x_{\rm{j}}}$	Exact solution ${u_2}\left({{x_{\rm{j}}}} \right)$	Approximate Values of $u_2^{10}({x_j})$	Absolute error $\left| {{u_2}\left({{x_{\rm{j}}}} \right) - {\rm{}}u_2^{10}\left({{x_{\rm{j}}}} \right)} \right|$
0	0	0	0
0.1	0.01	0.00999999999	9.808 e-12
0.2	0.04	0.03999999998	1.927 e-11
0.3	0.09	0.08999999997	2.840 e-11
0.4	0.16	0.15999999996	3.718 e-11
0.5	0.25	0.24999999995	4.563 e-11
0.6	0.36	0.35999999995	5.373 e-11
0.7	0.49	0.48999999994	6.149 e-11
0.8	0.64	0.63999999993	6.891 e-11
0.9	0.81	0.80999999992	7.599 e-11
1	1	0.99999999992	8.273 e-11

---

 | Show Table

DownLoad: CSV

Comparison between the exact and approximate solutions have been made and illustrated depending on least square error (L.S.E.) and the time required for running the program (R.T.) together in Table 3. While, Figure 1 shows the convergence of the method for ${u_1}^i\left(x \right)\; {\rm{and}}\; {u_2}^i\left(x \right)$ with i = 1, 2, 3.

Table 3.  The exact solution is compared with the numerical method for different iterates.

n	3-iterations	6-iterations	9-iterations	12-terations
L.S.E u1	1.17e-03	8.35 e-11	3.73 e-17	5.45 e-24
L.S.E u2	2.73 e-04	5.07 e-10	7.43 e-18	1.18 e-23
R.T.	2.4s	5.6s	9.1s	14.5s

---

 | Show Table

DownLoad: CSV

Figure 1.  The exact and numerical solution with n = 1, 2, 3 for Example 1.

DownLoad: Full-Size Img PowerPoint

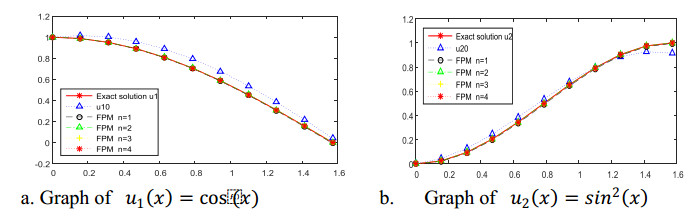
Example 2. Consider the following system of integral equations:

where the exact solution is given by ${u_1}\left(x \right) = \cos \left(x \right)$, and ${u_2}\left(x \right) = {\sin ^2}\left(x \right)$.

Applying the algorithm of FPM with n = 10, gives the results in Tables 4 and 5. While, Figure 2 shows the convergence of the method for $u_1^i\left(x \right)\; {\rm{and}}\; u_2^i\left(x \right)$ for i = 1, 2, 3.

Table 4.  The results $u_1^{10}\left(x \right)$ of Example 2, compared with exact solution ${u_1}\left(x \right)$.

${x_j}$	Exact solution ${u_1}\left({{x_j}} \right)$	Approximate Values of $u_1^{10}({x_j})$	Absolute error $\left| {{u_1}\left({{x_j}} \right) - {\rm{}}u_1^{10}\left({{x_j}} \right)} \right|$
0.1(π)	0.95105651630	0.95105651644	1.52318 e-10
0.2(π)	0.80901699437	0.80901699463	2.55728 e-10
0.3(π)	0.58778525229	0.58778525260	3.10231 e-10
0.4(π)	0.30901699437	0.30901699469	3.15826 e-10
0.5(π)	0	2.72513 e-10	2.72513 e-10

---

 | Show Table

DownLoad: CSV

Table 5.  The results $u_2^{10}(x)$ of Example 2, compared with exact solution ${u_2}\left(x \right)$.

${x_j}$	Exact solution ${u_2}\left({{x_j}} \right)$	Approximate Values of $u_2^{10}({x_j})$	Absolute error $\left| {{u_2}\left({{x_j}} \right) - {\rm{}}u_2^{10}\left({{x_j}} \right)} \right|$
0.1(π)	0.09549150281	0.09549150289	8.2427 e-11
0.2(π)	0.34549150281	0.34549150294	1.3157 e-10
0.3(π)	0.65450849719	0.65450849734	1.4742 e-10
0.4(π)	0.90450849719	0.90450849732	1.3003 e-10
0.5(π)	1	1.00000000008	7.9341 e-11

---

 | Show Table

DownLoad: CSV

Figure 2.  The exact solution and the numerical solution with n = 1, 2, 3, 4 for Example 2.

DownLoad: Full-Size Img PowerPoint

6.   Conclusion

In summary, the existence of a unique solution was verified and proved for linear system of mixed Volterra-Fredholm integral equations of the second kind and the result was obtained by using some principles of Banach's contraction in complete metric space. Also, an iterative technique based on fixed point method was discussed for solving the system, and an algorithm is constructed. Here our programs are written by Matlab software 2015Ra, and two experiments were presented for illustration. Good approximations were obtained, while better results have been found by increasing the number of iterations (n). Moreover, comparison between the exact and approximate solutions was made to demonstrate the application method. It is worth mentioning that the technique can be used as a very accurate algorithm for solving linear system of mixed Volterra-Fredholm integral equations of the second kind. These claims are supported by the results of the given numerical examples in Tables 1–5 and Figures 1–2.

Conflict of interest

The authors declare no conflict of interest in this paper.