Estimate of traffic emissions through multiscale second order models with heterogeneous data

Caterina Balzotti; Maya Briani; Caterina Balzotti; Maya Briani

doi:10.3934/nhm.2022030

Networks and Heterogeneous Media

2022, Volume 17, Issue 6: 863-892. doi: 10.3934/nhm.2022030

Previous Article Next Article

Estimate of traffic emissions through multiscale second order models with heterogeneous data

Caterina Balzotti ^{1
,},
Maya Briani ^{2
,
,}

1.
SISSA Scuola Internazionale Superiore di Studi Avanzati, Mathlab, Trieste, Italy
2.
Istituto per le Applicazioni del Calcolo - Consiglio Nazionale delle Ricerche, Rome, Italy

Received: 01 March 2022 Revised: 01 July 2022 Published: 25 August 2022
Primary: 35L65; Secondary: 35F25, 90B20, 62P12

In this paper we propose a multiscale traffic model, based on the family of Generic Second Order Models, which integrates multiple trajectory data into the velocity function. This combination of a second order macroscopic model with microscopic information allows us to reproduce significant variations in speed and acceleration that strongly influence traffic emissions. We obtain accurate approximations even with a few trajectory data. The proposed approach is therefore a computationally efficient and highly accurate tool for calculating macroscopic traffic quantities and estimating emissions.

Keywords:

Citation: Caterina Balzotti, Maya Briani. Estimate of traffic emissions through multiscale second order models with heterogeneous data[J]. Networks and Heterogeneous Media, 2022, 17(6): 863-892. doi: 10.3934/nhm.2022030

Related Papers:

[1]	Zhoujin Cui, Xiaorong Zhang, Tao Lu . Resonance analysis and time-delay feedback controllability for a fractional horizontal nonlinear roller system. AIMS Mathematics, 2024, 9(9): 24832-24853. doi: 10.3934/math.20241209
[2]	P. Pirmohabbati, A. H. Refahi Sheikhani, H. Saberi Najafi, A. Abdolahzadeh Ziabari . Numerical solution of full fractional Duffing equations with Cubic-Quintic-Heptic nonlinearities. AIMS Mathematics, 2020, 5(2): 1621-1641. doi: 10.3934/math.2020110
[3]	Nasser. A. Saeed, Amal Ashour, Lei Hou, Jan Awrejcewicz, Faisal Z. Duraihem . Time-delayed control of a nonlinear self-excited structure driven by simultaneous primary and 1:1 internal resonance: analytical and numerical investigation. AIMS Mathematics, 2024, 9(10): 27627-27663. doi: 10.3934/math.20241342
[4]	Rashid Ali, Rabia Imtiaz, Moin-ud-Din Junjua, Fuad A. Awwad, Emad A. A. Ismail, Ahmed S. Hendy . Multiplicity of kink and hump structures in Van der Waals gas system. AIMS Mathematics, 2025, 10(5): 12493-12518. doi: 10.3934/math.2025564
[5]	Sunil Kumar, Jai Bhagwan, Lorentz Jäntschi . Numerical simulation of multiple roots of van der Waals and CSTR problems with a derivative-free technique. AIMS Mathematics, 2023, 8(6): 14288-14299. doi: 10.3934/math.2023731
[6]	Gamal M. Ismail, Maha M. El-Moshneb, Mohra Zayed . A modified global error minimization method for solving nonlinear Duffing-harmonic oscillators. AIMS Mathematics, 2023, 8(1): 484-500. doi: 10.3934/math.2023023
[7]	Hany Bauomy, A. T. EL-Sayed, A. M. Salem, F. T. El-Bahrawy . The improved giant magnetostrictive actuator oscillations via positive position feedback damper. AIMS Mathematics, 2023, 8(7): 16864-16886. doi: 10.3934/math.2023862
[8]	Changdev P. Jadhav, Tanisha B. Dale, Vaijanath L. Chinchane, Asha B. Nale, Sabri T. M. Thabet, Imed Kedim, Miguel Vivas-Cortez . On solutions of fractional differential equations for the mechanical oscillations by using the Laplace transform. AIMS Mathematics, 2024, 9(11): 32629-32645. doi: 10.3934/math.20241562
[9]	Guanghua Wei, Xiaorong Zhang, Zhoujin Cui . Primary resonance analysis of a novel fractional-order coronary artery model. AIMS Mathematics, 2025, 10(6): 14996-15011. doi: 10.3934/math.2025672
[10]	Guijun Xing, Huatao Chen, Zahra S. Aghayan, Jingfei Jiang, Juan L. G. Guirao . Tracking control for a class of fractional order uncertain systems with time-delay based on composite nonlinear feedback control. AIMS Mathematics, 2024, 9(5): 13058-13076. doi: 10.3934/math.2024637

Abstract

1. Introduction

Fractional calculus is an ancient mathematical topic from the 17th century. Although Fractional calculus is a mathematical subject with a history of more than 300 years, its application in physics and engineering did not attract wide attention until recent decades. In the past twenty years, significant progress has been made in fractional calculus and fractional order dynamical systems ^[1,2,3,4]. Previous studies have shown that fractional calculus is a mathematical tool, which is applicable to anomalous social and physical systems with non-local, frequency- and history-dependent properties, as well as intermediate states such as soft materials that are neither ideal solids nor ideal fluid ^[5,6,7]. Moreover, applications of fractional calculus have been reported in many areas such as signal processing, image processing, automatic control and robotics ^[8,9,10,11]. Research has even applied fractional derivatives to specific fields of research: psychological and life sciences ^[12,13]. In a word, virtually no area of classical analysis has been left untouched by fractional calculus. These examples and many other similar samples perfectly clarify the importance of consideration and analysis of dynamical systems with fractional-order models.

For the reason that nonlinear vibration systems exist in a large number of engineering technology and scientific practice, the research of nonlinear vibration systems has attracted the attention of many engineering and technical personnel and researchers. As a combination of two typical nonlinear systems, the nonlinear part of the Duffing-van der Pol system contains not only the nonlinear damping term for maintaining self-excited vibration of the van der Pol system, but also the cubic nonlinear restoring force term of the Duffing system, which has particularly rich dynamic characteristics. The Duffing-van der Pol oscillator is also a typical system to simulate some physical phenomena, and its simple nonlinear structure has led to an in-depth study of its dynamic behavior, which can be used as a research model in many fields, such as engineering, electronics, biology and neurology ^{[14,15,16,17]}. Furthermore, the fractional Duffing-van der Pol oscillator is considered to be one of the most commonly used equations in various system designs, including dynamics, biology, seismology, etc. ^[18,19]. Therefore, it is of practical significance to further study the dynamic behavior of such systems.

Many scientists have done a lot of research on the nonlinear dynamic behavior of the Duffing-van der Pol equation, including integer and fractional order cases ^{[20,21,22,23,24,25]}. Specially, in ^[22], a three-dimensional autonomous Van der Pol-Duffing type oscillator is proposed. Using the Routh-Hurwitz stability criterion and the linear stability analysis of equilibrium points, it was found that there is a Hopf bifurcation in the three-dimensional autonomous Van der Pol-Duffing oscillator. In ^[23], the damping characteristics of two Duffing-van der Pol oscillators with damping terms described by fractional derivative and time delay are studied by the residue harmonic balance method. A Duffing-van der Pol oscillator having fractional derivatives and time delays is investigated by the residue harmonic method in ^[24]. The dynamical properties of fractional order Duffing-van der Pol oscillators are studied in ^[25], and the amplitude-frequency response equation of the primary resonance is obtained by the harmonic balance method.

According to current research results, many studies focus on only Duffing-van der Pol equations with lower power terms under different excitations, while relatively few studies focus on the system with high power nonlinear terms. The Duffing-van der Pol systems with high power nonlinear terms are more worthy of study, because in the process of simplifying the actual model to the Duffing equation or van der Pol equation, in order to reduce the error between the system and the actual process, the nonlinear terms need to be approximately expressed as higher powers by power series to study the richer dynamic characteristics of the system. In addition, for the reason that the nonlinear dynamic behavior of the Duffing-van der Pol oscillator is very rich in bifurcation, chaos, primary resonance, superharmonic or subharmonic resonance, stochastic resonance and other vibration characteristics, the dynamic characteristics of the fractional Duffing-van der Pol oscillator are worthy of further exploration and research. It should be noted here that the primary resonance of a fractional Duffing-van der Pol oscillator can be studied by perturbation methods such as harmonic balance method or averaging method. Although a multiple scale method has been commonly used in the study of integer-order models, they are rarely involved in the study of fractional-order related problems. Therefore, it is also very necessary to use the multiple scale method to study the resonance characteristics of fractional Duffing-van der Pol oscillators, for example, to understand how the system parameters affect the periodic solutions resulted from resonance of the fractional Duffing-van der Pol oscillator.

The paper is organized as follows: In Section 2, the approximately analytical solution is obtained by the multiple scale method. The amplitude frequency equation is obtained and the stability conditions for the steady-state solution are given, while numerical simulations of the time history and phase diagrams are also provided. In Section 3, the bifurcations of primary resonance are investigated and the influence of parameters on fractional-order models is investigated. In Section 4, the comparisons of the approximate analytical solution and numerical solution are fulfilled. Finally, concluding remarks and implications in Section 5 close the paper.

2. Mathematical analysis

2.1. Primary resonance

The fractional Duffing-van der Pol oscillator with quintic nonlinear-restoring force is given by a second-order non-autonomous differential equation as follows

$\begin{equation} \ddot{x}-\mu(1-x^2)D_t^{q} x+\alpha x+\lambda x^3+\beta x^5 = f\cos \omega t, \end{equation}$

(2.1)

where $x$ is the position coordinate and is a function of time $t$ , $D_t^{q}x$ is the $q$ -order derivative of $x$ with respect to time, $\mu$ is a positive fractional damping coefficient, $\omega_0$ is the natural frequency, $\alpha$ , $\lambda$ and $\beta$ are coefficients of nonlinear restoring forces, the external excitation have amplitude and frequency parameters which are $f$ and $\omega$ , respectively. There are many definitions available for the fractional-order derivative, and in this study, $D_t^{q}x$ with $0 < q\leq1$ is the Caputo's fractional derivative of $x(t)$ described by

$\begin{equation} D_t^q x(t) = \frac{1}{\Gamma(1-q)}\int_{0}^t\dot{x}(\tau)(t-\tau)^{-q}d\tau,\notag \end{equation}$

in which $\Gamma(z)$ is Gamma function satisfying $\Gamma(z+1) = z\Gamma(z)$ . Under certain conditions, primary resonance with limited amplitude occurs in the fractional Duffing-van der Pol oscillator (2.1) when $\omega = \omega_0\overset{{\text{def}}}{ = }\sqrt{\alpha}$ or $\omega\approx\omega_0$ . That is, the primary resonance means the excitation frequency is close to the natural one.

In order to find an approximate resonant solution of Eq (2.1), the multiple scale method will be used, for which a small parameter $\varepsilon$ is required. Let $T_n = \varepsilon^n t, (n = 0, 1)$ be two independent time variables, an approximate solution of Eq (2.1) with small amplitudes in three time scales can be represented by

$\begin{equation} x = x_0(T_0,T_1)+\varepsilon x_1(T_0,T_1)+\cdots. \end{equation}$

(2.2)

With such a small parameter $\varepsilon$ , in order to balance the effect of the nonlinearity, damping and excitation, the following scaling is used

$\begin{equation} \mu \rightarrow \varepsilon\mu,\quad\lambda\rightarrow \varepsilon\lambda,\quad \beta\rightarrow \varepsilon\beta,\quad f\rightarrow \varepsilon f. \end{equation}$

(2.3)

Then, Eq (2.1) becomes

$\begin{equation} \ddot{x}-\varepsilon\mu(1-x^2)D_t^{q} x+\omega_0^2 x+\varepsilon\lambda x^3+\varepsilon\beta x^5 = \varepsilon f\cos \omega t. \end{equation}$

(2.4)

The derivatives with respect to $t$ can be expressed in terms of the new scaled times $T_n$ using chain rule as follows:

$\begin{equation} \frac{{\rm d}}{{\rm d}t} = D_0+\varepsilon D_1+\cdots, \end{equation}$

(2.5a)

$\begin{equation} \frac{{\rm d}^2}{{\rm d}t^2} = D_0^2+2\varepsilon D_0D_1+\varepsilon^2 D_1^2+\cdots, \end{equation}$

(2.5b)

$\begin{equation} D_t^q = D_0^q+q\varepsilon D_0^{q-1}D_1+\cdots, \end{equation}$

(2.5c)

in which $D_0^q = \frac{\partial^q}{\partial T_0^q}$ , $D_n = \frac{\partial}{\partial T_n}$ , $D_n^2 = \frac{\partial^2}{\partial T_n^2}$ and $n = 0, 1$ .

For the primary resonance with $\omega = \omega_0: = \sqrt{\alpha}$ or $\omega\approx\omega_0$ , a detuning parameter $\sigma$ describing the nearness of $\omega$ to $\omega_0$ is introduced by

$\begin{equation} \omega = \omega_0+\varepsilon \sigma, \end{equation}$

(2.6)

then $\omega t = \omega_0T_0+\sigma T_1$ . Substituting (2.2), (2.5b) and (2.5c) into (2.4) leads to the following equation

$\begin{equation} \begin{aligned} &(D_0^2+2\varepsilon D_0D_1+\varepsilon^2 D_1^2)(x_0+\varepsilon x_1)-\varepsilon\mu [1-(x_0+\varepsilon x_1)^2]\cdot(D_0^q+q\varepsilon D_0^{q-1}D_1)(x_0+\varepsilon x_1) \\&+\omega_0^2 (x_0+\varepsilon x_1)+\varepsilon\lambda (x_0+\varepsilon x_1)^3+\varepsilon\beta (x_0+\varepsilon x_1)^5 \\& = \varepsilon f\cos (\omega_0T_0+\sigma T_1).\notag\end{aligned} \end{equation}$

Equating the coefficients of the same power of $\varepsilon$ , a set of linear differential equations are obtained

$\begin{equation} O(\varepsilon^0):D_0^2x_0+\omega_0^2x_0 = 0, \end{equation}$

(2.7)

$\begin{equation} O(\varepsilon^1):D_0^2x_1+\omega_0^2x_1 = -2D_0D_1x_0+\mu(1-x_0^2)D_{0}^q x_0-\lambda x_0^3-\beta x_0^5+f\cos (\omega_0T_0+\sigma T_1), \end{equation}$

(2.8)

from which $x_0$ and $x_1$ can solved one-by-one, respectively. In this way, the resonant solution $x$ is dominated by $x_0$ and collected by $\varepsilon x_1$ .

In order to obtain the primary resonance solutions, it is necessary to eliminate the secular term when solving the Eqs (2.7) and (2.8) one by one, so as to find the amplitude-frequency response equation, from which the influence of various parameters on the resonance solution can be studied.

The general solution of Eq (2.7) is of the form,

$\begin{equation} x_0 = A(T_1){\rm e}^{{\rm i}\omega_0T_0}+\overline{A}(T_1){\rm e}^{-{\rm i}\omega_0T_0}, \end{equation}$

(2.9)

where $A(T_1)$ and $\overline{A}(T_1)$ are unknown functions, $\overline{A}(T_1)$ denotes the complex conjugate of $A(T_1)$ .

To solve Eq (2.8), for sufficient large $t\gg1$ , the $q$ th-order $(0\leq q\leq1)$ derivative of ${\rm e}^{{\rm i}\Omega t}$ is approximated with

$\begin{equation} D_{t}^q {\rm e}^{{\rm i}\Omega t}\approx _{-\infty}D_{t}^q {\rm e}^{{\rm i}\Omega t} = ({\rm i}\Omega)^q{\rm e}^{{\rm i}\Omega t}, \end{equation}$

(2.10)

according to the "Short Memory Principle" ^[13,26], where

$\begin{equation*} _{-\infty}D_t^qx(t) = \frac{1}{\Gamma(1-q)}\int_{-\infty}^t\dot{x}(\tau)(t-\tau)^{-q}{\rm d}\tau.\notag \end{equation*}$

Substituting Eqs (2.9) and (2.10) into Eq (2.8) and using

$\begin{equation*} \cos (\omega_0T_0+\sigma T_1) = \frac{{\rm e}^{{\rm i}(\omega_0T_0+\sigma T_1)}+{\rm e}^{-{\rm i}(\omega_0T_0+\sigma T_1)}}{2}, \end{equation*}$

the right-hand of Eq (2.8) becomes

$\begin{equation*} [-2{\rm i}\omega_0D_1A+\mu(1-2A\bar{A})A ({\rm i}\omega_0)^q-3\lambda A^2\bar{A}-10\beta A^3\bar{A}^2 +\frac{f}{2}{\rm e}^{{\rm i}\sigma T_1}]{\rm e}^{{\rm i}\omega_0T_0}+NST+cc, \end{equation*}$

where $NST$ stands for the terms that do not produce secular terms, $cc$ denotes the complex conjugate of the preceding terms.

In order that $x_1$ is periodic, the secular terms with ${\rm e}^{{\rm i}\omega_0T_0}$ must be zero, namely

$\begin{equation} -2{\rm i}\omega_0D_1A+\mu(1-2A\bar{A})A ({\rm i}\omega_0)^q-3\lambda A^2\bar{A}-10\beta A^3\bar{A}^2 +\frac{f}{2}{\rm e}^{{\rm i}\sigma T_1} = 0. \end{equation}$

(2.11)

To analyze the solution of Eq (2.11), it is convenient to express $A(T_1)$ in the polar form as

$\begin{equation} A(T_1) = \frac{a(T_1)}{2}{\rm e}^{{\rm i}\theta(T_1)}. \end{equation}$

(2.12)

In addition, the Euler formula gives

$\begin{equation} {\rm i}^q = ({\rm e}^{{\rm i}\pi/2})^q = {\rm e}^{{\rm i}q\pi/2} = \cos\frac{q\pi}{2}+{\rm i}\sin\frac{q\pi}{2}.\notag \end{equation}$

Let $\label{eq14}\varphi\overset{{\text{def}}}{ = }\sigma T_1-\theta$ . By separating the real and imaginary parts of Eq (2.11), the differential equations governing amplitude $a(T_1)$ and $\varphi(T_1)$ of $A(T_1)$ are as follows respectively

$\begin{equation} D_1a = \mu(1-\frac{a^2}{2})\frac{a}{2}\omega_0^{q-1}\sin\frac{q\pi}{2}+\frac{f}{2\omega_0}\sin\varphi, \end{equation}$

(2.13a)

$\begin{equation} aD_1\varphi = \sigma a+\mu (1-\frac{a^2}{2})\frac{a}{2}\omega_0^{q-1}\cos\frac{q\pi}{2}-\frac{3\lambda}{8\omega_0} a^3-\frac{5\beta}{16\omega_0} a^5+\frac{f}{2\omega_0}\cos\varphi. \end{equation}$

(2.13b)

We are interested in the steady solutions satisfying $D_1a = 0$ , $D_1\varphi = 0$ in (2.13a) and (2.13b), namely

$\begin{equation} \frac{\mu(2-a^2)}{4}a\omega_0^{q-1}\sin\frac{q\pi}{2} = -\frac{f}{2\omega_0}\sin\varphi, \end{equation}$

(2.14a)

$\begin{equation} \sigma a+\frac{\mu(2-a^2)}{4}a\omega_0^{q-1}\cos\frac{q\pi}{2}-\frac{3\lambda}{8\omega_0} a^3-\frac{5\beta}{16\omega_0} a^5 = -\frac{f}{2\omega_0}\cos\varphi. \end{equation}$

(2.14b)

Because $\sin^2\varphi+\cos^2\varphi = 1$ , by eliminating $\varphi$ from Eqs (2.14a) and (2.14b), the amplitude-frequency response equation can be obtained as follows

$\begin{equation} \begin{aligned} &[(4\mu(2-a^2)\omega_0^{q}\sin\frac{q\pi}{2})^2+(16\sigma\omega_0+4\mu(2-a^2)\omega_0^{q}\cos\frac{q\pi}{2}-6\lambda a^2-5\beta a^4)^2] a^2 = (8f)^2. \end{aligned} \end{equation}$

(2.15)

The real solution $a$ of Eq (2.15) determines the dominant part $x_0$ of the primary resonance response amplitude. Similar results have been discussed in ^[21] for the case when $q = 1$ , but the calculation error in the derivation process of this paper leads to inaccurate amplitude-frequency response equation.

2.1.1. Feedback control

The fractional Duffing-van der Pol oscillator with negative acceleration feedback considered is as follows

$\begin{equation} \ddot{x}-\mu(1-x^2)D_t^{q} x+\omega_0^2 x+\lambda x^3+\beta x^5 = f\cos \omega t-u\ddot{x}, \end{equation}$

(2.16)

in which $-u$ is the feedback gain reflecting the magnitude of a feedback force. Similar to the previous discussion, the method of multiple time scales is used to obtain a uniformly valid, asymptotic expansion of the solution for Eq (2.16). Let $T_n = \varepsilon^n t, (n = 0, 1)$ be two independent time variables, an approximate solution of Eq (2.16) with small amplitudes in three time scales can be represented by

$\begin{equation} x = x_0(T_0,T_1)+\varepsilon x_1(T_0,T_1)+\cdots. \end{equation}$

(2.17)

With such a small parameter $\varepsilon$ , in order to balance the effect of the nonlinearity, damping and excitation, the following scaling is used

$\begin{equation} \mu \rightarrow \varepsilon\mu,\quad\lambda\rightarrow \varepsilon\lambda,\quad \beta\rightarrow \varepsilon\beta,\quad f\rightarrow \varepsilon f, \quad u\rightarrow \varepsilon u. \end{equation}$

(2.18)

Then, Eq (2.16) becomes

$\begin{equation} \ddot{x}-\varepsilon\mu(1-x^2)D_t^{q} x+\omega_0^2 x+\varepsilon\lambda x^3+\varepsilon\beta x^5 = \varepsilon f\cos \omega t-\varepsilon u\ddot{x}. \end{equation}$

(2.19)

Substituting (2.17), (2.5b) and (2.5c) into (2.19) leads to the following equation

Similar to the previous discussion, the following differential equations about amplitude and phase can be obtained,

$\begin{equation} D_1a = \mu(1-\frac{a^2}{2})\frac{a}{2}\omega_0^{q-1}\sin\frac{q\pi}{2}+\frac{f}{2\omega_0}\sin\varphi, \end{equation}$

(2.20a)

(2.20b)

The steady solutions satisfying $D_1a = 0$ , $D_1\varphi = 0$ in (2.20a) and (2.20b), namely

$\begin{equation} \frac{\mu(2-a^2)}{4}a\omega_0^{q-1}\sin\frac{q\pi}{2} = -\frac{f}{2\omega_0}\sin\varphi, \end{equation}$

(2.21a)

$\begin{equation} \sigma a+\frac{\mu(2-a^2)}{4}a\omega_0^{q-1}\cos\frac{q\pi}{2}-\frac{3\lambda}{8\omega_0} a^3-\frac{5\beta}{16\omega_0} a^5+u\omega_0\frac{a}{2} = -\frac{f}{2\omega_0}\cos\varphi. \end{equation}$

(2.21b)

By eliminating $\varphi$ from Eqs (2.21a) and (2.21b), the amplitude-frequency response equation can be obtained as follows

$\begin{equation} [(4\mu(2-a^2)\omega_0^{q}\sin\frac{q\pi}{2})^2+(16\sigma\omega_0+4\mu(2-a^2)\omega_0^{q}\cos\frac{q\pi}{2}-6\lambda a^2-5\beta a^4+8u\omega_0^{2})^2] a^2 = (8f)^2. \end{equation}$

(2.22)

It should be noted that a fractional dynamical system does not have an exact periodic solution, see ^[27,28], and it may have one if the fractional derivative is defined over $(-\infty, t]$ ^[28]. When the asymptotic behaviors of the fractional system are addressed, a fractional derivative over $[0, t]$ with large $t$ equals approximately the corresponding one over $(-\infty, t]$ , according to the "Short Memory Principle" of fractional derivatives ^[26]. Thus, a periodic solution of a fractional system should be understood as an asymptotic solution with transients before a finite time neglected. All the periodic solutions mentioned in this paper are understood in this sense.

2.2. Stability of the steady resonant solutions

To determine the stability of the steady resonant solutions, suppose that $(a, \varphi) = (a^*, \varphi^*)$ is a steady solution of Eqs (2.20a) and (2.20b), let

$\begin{equation} \begin{aligned} {\rm\Delta} a = a-a^*,\;\;{\rm\Delta}\varphi = \varphi-\varphi^*\end{aligned} \end{equation}$

(2.23)

are perturbations which are assumed to be small compared to $a^*$ and $\varphi^*$ . Substituting Eq (2.23) into Eqs (2.20a) and (2.20b), using Eqs (2.21a) and (2.21b), then the linearized differential equations governing ${\rm\Delta}a$ and ${\rm\Delta}\varphi$ are

$\begin{equation} D_1{\rm\Delta} a = \frac{2-3(a^*)^2}{4}\mu\omega_0^{q-1}\sin\frac{q\pi}{2}{\rm\Delta} a+\frac{f}{2\omega_0}\cos\varphi^*\,{\rm\Delta}\varphi, \end{equation}$

(2.24a)

$\begin{equation} D_1{\rm\Delta}\varphi = [\frac{\sigma}{a^*}+\frac{2-3(a^*)^2}{4a^*}\mu\omega_0^{q-1}\cos\frac{q\pi}{2}-\frac{9\lambda a^*}{8\omega_0}-\frac{25\beta (a^*)^3}{8\omega_0}+\frac{u\omega_0}{2a^*}]{\rm\Delta} a -\frac{f}{2\omega_0 a^*}\sin \varphi^*\,{\rm\Delta}\varphi. \end{equation}$

(2.24b)

Let $M$ $=$ $\sigma$ $+$ $\frac{2-(a^*)^2}{4}\mu\omega_0^{q-1}\cos\frac{q\pi}{2}$ $-$ $\frac{3\lambda}{8\omega_0} (a^*)^2$ $-$ $\frac{5\beta}{16\omega_0} (a^*)^4$ $+$ $\frac{u\omega_0}{2}$ , $N$ $=$ $\sigma$ $+$ $\frac{2-3(a^*)^2}{4}\mu\omega_0^{q-1}\cos\frac{q\pi}{2}$ $-$ $\frac{9\lambda}{8\omega_0}$ $(a^*)^2-$ $\frac{25\beta}{8\omega_0}$ $(a^*)^4$ $+$ $\frac{u\omega_0}{2}$ . According to Eqs (2.21a) and (2.21b), the characteristic equation can be written as

$\begin{equation*} \left |\begin{array}{cccc} \frac{2-3(a^*)^2}{4}\mu\omega_0^{q-1}\sin\frac{q\pi}{2}-\lambda & \quad -a^*M \\ \frac{1}{a^*}N & \quad \frac{2-(a^*)^2}{4}\mu\omega_0^{q-1}\sin\frac{q\pi}{2}-\lambda \\ \end{array}\right| = 0. \end{equation*}$

By expanding the determinant, we can get

$\begin{equation} \lambda^2+[(a^*)^2-1]\mu \omega_0^{q-1}\sin\frac{q\pi}{2}\lambda+\Lambda = 0, \end{equation}$

(2.25)

in which $\Lambda = \frac{[2-3(a^*)^2][2-(a^*)^2]}{16}(\mu\omega_0^{q-1}\sin\frac{q\pi}{2})^2+MN$ .

Thus, the steady solution $(a, \varphi) = (a^*, \varphi^*)$ is asymptotically stable if and only if the real parts of all roots of the characteristic Eq (2.25) are negative.

2.3. Numerical simulation

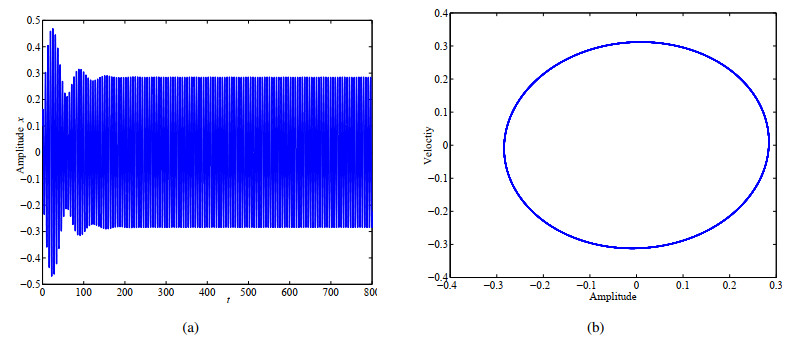
In this section, time history diagrams are used to briefly illustrate the impact of feedback control on the model. shows the time history of the system without controller. The various parameters of the system in are $\omega_0 = 1$ , $q = 0.9$ , $\mu = 0.01$ , $\lambda = 0.04$ , $\beta = 0.01$ and $f = 0.06$ . It can be observed that the amplitude fluctuates significantly in the first 150s and the steady-state amplitude of the system is about 0.28. The phase diagram shows a limit cycle, indicating that there is no chaos in the system. Different initial conditions were tested and it was found that the steady-state amplitude of the system is not sensitive to the initial conditions.

Figure 1. The time history and phase diagram of (2.1) without controller.

DownLoad: Full-Size Img PowerPoint

shows the time history of the system with feedback controller. The various parameters of the system in are $\omega_0 = 1$ , $q = 0.9$ , $\mu = 0.01$ , $\lambda = 0.04$ , $\beta = 0.01$ , $f = 0.06$ and $u = 0.1$ . From Figure 2, it can be seen that the steady-state amplitude of the system has decreased to approximately 0.115, this indicates the effectiveness of the controller. The steady-state value appears after 150s without control, while it appears before 50 seconds with control, which also reflects the effect of adding control.

Figure 2. The time history and phase diagram of (2.16) with feedback controller.

DownLoad: Full-Size Img PowerPoint

3. Analysis of the resonant solutions

Rewritten Eqs (2.15) and (2.22) in terms of the original system parameters as follows

$\begin{equation} [(4\mu(2-a^2)\omega_0^{q}\sin\frac{q\pi}{2})^2+(16(\omega-\omega_0)\omega_0+4\mu(2-a^2)\omega_0^{q}\cos\frac{q\pi}{2}-6\lambda a^2-5\beta a^4)^2] a^2 = (8f)^2, \end{equation}$

(3.1)

and

$\begin{equation} [(4\mu(2-a^2)\omega_0^{q}\sin\frac{q\pi}{2})^2+(16(\omega-\omega_0)\omega_0+4\mu(2-a^2)\omega_0^{q}\cos\frac{q\pi}{2}-6\lambda a^2-5\beta a^4+8u\omega_0^{2})^2] a^2 = (8f)^2. \end{equation}$

(3.2)

The effect of different parameters on the amplitude of the resonant solutions is investigated numerically. Here, the difference between the model with quintic nonlinear term and the model without quintic power is given by the amplitude-frequency response curve, as shown in Figure 3.

Figure 3. Response curves with

$q = 0.9$ ,

$\mu = 0.01$ ,

$\omega_0 = 1$ ,

$f = 0.06$ .

DownLoad: Full-Size Img PowerPoint

It can be seen from the figure that the bending degree, resonance region and jump phenomena of the model have obvious changes after considering the quintic nonlinear terms, indicating that it is very important to consider the role of higher order terms for studying the nonlinear characteristics of the model.

3.1. Parameter influence on the amplitudes of the resonant solutions

This section discusses the influence of parameters on the hardening/softening characteristics and resonance peak value based on Eq (3.1). As shown in –, typical hardening/softening characteristics can be observed also in the curves of the resonant amplitudes with respect to the changes of $\lambda$ , $\beta$ , $q$ , $\mu$ and $f$ , respectively.

Figure 4. Response curves with

$q = 0.9$ ,

$\mu = 0.01$ ,

$\omega_0 = 1$ ,

$f = 0.06$ .

DownLoad: Full-Size Img PowerPoint

Figure 5. Effect of the fractional-order

$q$ on the amplitude-frequency curves when

$\omega_0 = 1$ ,

$\mu = 0.01$ ,

$\lambda = 0.04$ ,

$\beta = 0.01$ ,

$f = 0.06$ .

DownLoad: Full-Size Img PowerPoint

Figure 6. Effect of the damping coefficient

$\mu$ on the amplitude-frequency curves when

$\omega_0$

$= 1$ ,

$q = 0.9$ ,

$\lambda = 0.04$ ,

$\beta = 0.01$ ,

$f = 0.06$ .

DownLoad: Full-Size Img PowerPoint

Figure 7. Effect of the excitation amplitude

$f$ on the amplitude-frequency curves when

$\omega_0 = 1$ ,

$q = 0.9$ ,

$\mu = 0.01$ ,

$\lambda = 0.04$ ,

$\beta = 0.01$ .

DownLoad: Full-Size Img PowerPoint

The influence of the nonlinear terms on the amplitude-frequency response curve can be identified with the changes of $\lambda$ , $\beta$ . Typical softening characteristic can be observed in with $\lambda = -0.04$ and $\beta = -0.01$ , and the frequency response curve bends to low frequency. When $\lambda = 0.04$ and $\beta = 0.01$ , hardening characteristic can be observed and the frequency response curve bends to high frequency.

The effect of the fractional-order $q$ on the amplitude-frequency curves is shown in . If the fractional order $q$ is closer to 0, the fractional differential term degenerates to linear stiffness, while if $q$ is closer to 1, it degenerates to linear damping. It is further known that the smaller the order $q$ is, the larger the maximum amplitude is. The integer-order model is the lowest. Compared with the integer order case when $q = 1$ , the bending degree, resonance peak and resonance region of the amplitude-frequency curve of the fractional-order model change accordingly with the decrease of the fractional-order $q$ .

shows the effect of the damping coefficient $\mu$ on the amplitude-frequency curves. With the increase of $\mu$ , the nonlinear jump of the system weakens and the resonance amplitude of the system decreases. In other words, as $\mu$ increases, the unstable portions decrease.

The effect of the excitation amplitude $f$ on the amplitude-frequency curves can be seen in . With the increase of the excitation amplitude $f$ , the frequency response curve will generate a multivalued region, the nonlinear jump of the system is more obvious and the resonance range and resonance amplitude of the system increase.

Figures 5–7 present parameter effects on resonant amplitudes with respect to excitation frequency. With fixed parameter values, all the figures exhibit typical characteristics of hardening spring. Let us take a different view on the resonant solutions. Now, the excitation frequency is fixed, and then with the change of a parameter, the amplitude of the primary resonant solution changes in different ways. In –, the images reflect characteristics similar to hardening spring, where the peak of amplitude is bent to the right as $f$ varies, as $\lambda$ varies or as $\beta$ varies, respectively.

Figure 8. Resonant amplitude with respect to

$f$ for

$\omega_0 = 1$ ,

$q = 0.9$ ,

$\mu = 0.01$ ,

$\lambda = 0.04$ ,

$\beta = 0.01$ .

DownLoad: Full-Size Img PowerPoint

Figure 9. Resonant amplitude for increasing non-linear parameter

$\lambda$ and

$\beta$ when

$\omega_0 = 1$ ,

$q = 0.9$ ,

$\mu = 0.01$ .

DownLoad: Full-Size Img PowerPoint

Figure 10. Resonant amplitude with respect to

$\lambda$ and

$\beta$ for

$\omega_0 = 1$ ,

$q = 0.9$ ,

$\mu = 0.01$ ,

$f = 0.04$ .

DownLoad: Full-Size Img PowerPoint

3.2. Parameter influence on the resonant solutions under feedback control

Through Eq (3.2), this section discusses the influence of parameters on the resonant solutions under feedback control. Figure 11 considers the influence of the gain value of the feedback control on the vibration state of the system. The red line in Figure 11 shows the primary resonance amplitude frequency response curve of the system without feedback control. It can be seen from Figure 11 that compared with the amplitude frequency curve of the primary resonance of the system without feedback control, after adding the feedback control, the resonance curve of the system moves to the left, and the resonance domain of the system changes. When the amplitude of the value of the gain of the control is increased, the deviation of the amplitude frequency response curve becomes larger.

Figure 11. Influence of the gain value of the feedback control on the vibration state for

$\omega_0 = 1$ ,

$q = 0.9$ ,

$\mu = 0.01$ ,

$\lambda = 0.04$ ,

$\beta = 0.01$ ,

$f = 0.06$ .

DownLoad: Full-Size Img PowerPoint

shows the influence of the frequency parameters on the vibration state of the system. The closer the external excitation frequency $\omega$ is to the primary resonance frequency $\omega_0$ , the smaller the offset of amplitude frequency curve is, and the smaller the change of resonance domain is. On the contrary, the more the phase difference, the larger the offset of the amplitude frequency curve. The peak amplitude of the primary resonance in Figure 12 does not change, but changes the position where it appears.

Figure 12. Resonant amplitude with respect to

$u$ for

$\omega_0 = 1$ ,

$q = 0.9$ ,

$\mu = 0.01$ ,

$\lambda = 0.04$ ,

$\beta = 0.01$ ,

$f = 0.04$ .

DownLoad: Full-Size Img PowerPoint

4. Comparison between approximate analytical solution and numerical solution

According to Eq (3.1), the primary resonance amplitude-frequency response curve of the system can be drawn. For comparison, this paper adopts the power series method introduced in references [3,29], and its calculation formula is

$\begin{equation} D_{t_n}^q[y(t_n)]\approx h^{-q}\sum\limits_{j = 0}^{n}C_j^qy(t_{n-j}), \end{equation}$

(4.1)

where $t_n = nh$ is the sample points, $h$ is the sample step and $C_j^q$ is the fractional binomial coefficient with the iterative relationship as

$\begin{equation} C_0^q = 1,\;\; C_j^q = (1-\frac{1+q}{j})C_{j-1}^q. \end{equation}$

(4.2)

According to Eqs (4.1) and (4.2), the numerical scheme for Eq (2.4) can be expressed as

$\begin{equation} x(t_n) = y(t_{n-1})h-\sum\limits_{j = 1}^{n}C_j^1x(t_{n-j}), \end{equation}$

(4.3a)

$\begin{equation} y(t_n) = \{f\cos (\omega t_n)-\alpha x(t_n)-\lambda x^3(t_n)-\beta x^5(t_n)+\mu [1-x^2(t_n)] z(t_{n-1})\}h-\sum\limits_{j = 1}^{n}C_j^1y(t_{n-j}), \end{equation}$

(4.3b)

$\begin{equation} z(t_n) = y(t_{n})h^{1-q}-\sum\limits_{j = 1}^{n}C_j^{1-q}z(t_{n-j}). \end{equation}$

(4.3c)

The numerical amplitude-frequency curve marked with circle in , where the stepsize of time is $h = 0.005$ , and the total computation time is 100s with the first 25s neglected. It shows that the resonant amplitude calculated from Eq (3.1) is in good agreement with the numerical results, especially when the $\omega\approx\omega_0$ .

Figure 13. Comparison between approximate analytical solution and numerical solution when

$\omega_0 = 1$ ,

$q = 0.85$ ,

$\mu = 0.03$ ,

$\lambda = 0.03$ ,

$\beta = 0.005$ ,

$f = 0.02$ .

DownLoad: Full-Size Img PowerPoint

5. Conclusions

We study the primary resonance and feedback control of the fractional Duffing-van der Pol oscillator with quintic nonlinear-restoring force. The approximate analytical solution and the amplitude-frequency equation are obtained by the multiple scale method. The stability condition for steady-state solution is obtained based on the Lyapunov theory. The influence of parameters on system characteristics was studied using the amplitude frequency response equation and phase plane technology, and bifurcation analysis was conducted to verify the stability of the system. It can also be concluded that fractional orders and damping coefficients are very important in the fractional Duffing-van der Pol oscillator. For example, larger fractional orders and larger damping coefficients can reduce the effective amplitude of resonance and change the resonance frequency.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The author expresses gratitude to the anonymous reviewers for their helpful comments and suggestions, as well as to the financial support from High Level Talent Research Launch Fund of Jiangsu Second Normal University (No. 928201/058).

Conflict of interest

The author declares that the research was conducted in the absence of any conflict of interest.

References

[1]	K. Ahn, A. Trani, H. Rakha and M. Van Aerde, Microscopic fuel consumption and emission models, in Proceedings of the 78th Annual Meeting of the Transportation Research Board, Washington, DC, USA, 1999.
[2]	Numerical simulation of air pollution due to traffic flow in urban networks. J. Comput. Appl. Math. (2017) 326: 44-61.
[3]	Optimal control of urban air pollution related to traffic flow in road networks. Math. Control Relat. F. (2018) 8: 177-193.
[4]	C. Balzotti, M. Briani, B. De Filippo and B. Piccoli, A computational modular approach to evaluate $\mathrm {NO_x}$ emissions and ozone production due to vehicular traffic, Discrete Cont. Dyn.-B.
[5]	C. Balzotti, M. Briani and B. Piccoli, Emissions minimization on road networks via generic second order models, arXiv preprint arXiv: 2004.11202.
[6]	M. Barth, F. An, T. Younglove, G. Scora, C. Levine, M. Ross and T. Wenzel, Development of a Comprehensive Modal Emissions Model: Final Report, Technical report, National Research Council, Transportation Research Board, National Cooperative Highway Research Program, NCHRP Project 25-11, 2000.
[7]	Mixing microscopic and macroscopic representations of traffic flow: Hybrid model based on Lighthill–Whitham–Richards theory. Transp. Res. Rec. (2003) 1852: 193-200.
[8]	Networked traffic state estimation involving mixed fixed-mobile sensor data using Hamilton-Jacobi equations. Transportation Research Part B: Methodological (2017) 104: 686-709.
[9]	A conservative scheme for non-classical solutions to a strongly coupled PDE-ODE problem. Interfaces Free Bound. (2017) 19: 553-570.
[10]	A mixed ODE-PDE model for vehicular traffic. Math. Methods Appl. Sci. (2015) 38: 1292-1302.
[11]	A traffic model aware of real time data. Math. Models Methods Appl. Sci. (2016) 26: 445-467.
[12]	An interface-free multi-scale multi-order model for traffic flow. Discrete Contin. Dyn. Syst. Ser. B (2019) 24: 6189-6207.
[13]	The cell transmission model: A dynamic representation of traffic consistent with the hydrodynamic theory. Transport. Res. B-Meth. (1994) 28: 269-287.
[14]	S. Fan, Y. Sun, B. Piccoli, B. Seibold and D. B. Work, A collapsed generalized Aw-Rascle-Zhang model and its model accuracy, arXiv preprint arXiv: 1702.03624.
[15]	Coupling of microscopic and phase transition models at boundary. Netw. Heterog. Media (2013) 8: 649-661.
[16]	M. Garavello and B. Piccoli, Boundary coupling of microscopic and first order macroscopic traffic models, NoDEA Nonlinear Differential Equations Appl., 24 (2017), Paper No. 43, 18 pp.
[17]	N. García-Chan, L. J. Alvarez-Vázquez, A. Martínez and M. E. Vázquez-Méndez, Optimal control of atmospheric pollution because of urban traffic flow by means of stackelberg strategies, arXiv preprint arXiv: 2004.07889.
[18]	Coupling of non-local driving behaviour with fundamental diagrams. Kinet. Relat. Models (2012) 5: 843-855.
[19]	A mesoscopic integrated urban traffic flow-emission model. Transportation Research Part C: Emerging Technologies (2017) 75: 45-83.
[20]	Coupling of microscopic and macroscopic traffic models at boundaries. Math. Models Methods Appl. Sci. (2010) 20: 2349-2370.
[21]	J.-P. Lebacque, The Godunov scheme and what it means for first order flow models, in Proceedings of the 13th International Symposium on Transportation and Traffic Theory, Lyon, France, July, vol. 2426, 1996.
[22]	J.-P. Lebacque, A two phase extension of the LWR model based on the boundedness of traffic acceleration, in Transportation and Traffic Theory in the 21st Century, Emerald Group Publishing Limited, 2002.
[23]	J.-P. Lebacque, S. Mammar and H. Haj Salem, Generic second order traffic flow modelling, in Transportation and Traffic Theory 2007, 2007, 755-776.
[24]	Hybrid approaches to the solutions of the "Lighthill–Whitham–Richards" model. Transp. Res. Part B Meth. (2007) 41: 701-709.
[25]	On kinematic waves II. A theory of traffic flow on long crowded roads. Proc. Roy. Soc. London Ser. A (1955) 229: 317-345.
[26]	Modelling instantaneous traffic emission and the influence of traffic speed limits. Sci. Total Environ. (2006) 371: 270-285.
[27]	On estimation of a probability density function and mode. Annals of Mathematical Statistics (1962) 33: 1065-1076.
[28]	Shock waves on the highway. Oper. Res. (1956) 4: 42-51.
[29]	Remarks on some nonparametric estimates of a density function. Annals of Mathematical Statistics (1956) 27: 832-837.
[30]	Real-time estimation of pollution emissions and dispersion from highway traffic. Comput.-Aided Civ. Inf. (2014) 29: 546-558.
[31]	J. H. Seinfeld and S. N. Pandis, Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, John Wiley & Sons, 2016.
[32]	Validation of road vehicle and traffic emission models – a review and meta-analysis. Atmos. Environ. (2010) 44: 2943-2953.
[33]	B. Sportisse, Fundamentals in Air Pollution: From Processes to Modelling, Springer-Verlag, 2010.
[34]	US department of transportation and federal highway administration, Next Generation Simulation (NGSIM), http://ops.fhwa.dot.gov/trafficanalysistools/ngsim.htm.
[35]	(1991) Chemistry of Atmospheres. Oxford: Clarendon Press.
[36]	Integrated macroscopic traffic flow, emission, and fuel consumption model for control purposes. Transp. Res. Part C Emerg. Technol. (2013) 31: 158-171.
[37]	S. K. Zegeye, Model-Based Traffic Control for Sustainable Mobility, PhD thesis, TU Delft, 2011.
[38]	A unified follow-the-leader model for vehicle, bicycle and pedestrian traffic. Transportation Res. Part B (2017) 105: 315-327.

This article has been cited by:

1.	Guohui Li, Ruiting Xie, Hong Yang, Study on fractional-order coupling of high-order Duffing oscillator and its application, 2024, 186, 09600779, 115255, 10.1016/j.chaos.2024.115255
2.	M.N. Abd El-Salam, Rageh K. Hussein, Reducing the Primary Resonance Vibrations of a Cantilever Beam Using a Proportional Fractional-Order Derivative Controller, 2025, 13, 2227-7390, 1886, 10.3390/math13111886
3.	Marina V. Shitikova, Elena I. Osipova, Combinational and Primary Simultaneous Resonance at Nonlinear Vibrations of a Fractionally Damped Plate, 2025, 20, 2224-3429, 79, 10.37394/232011.2025.20.10

Reader Comments

Your name:*

Email:*
© 2022 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)