Phospholipid—the dynamic structure between living and non-living world; a much obligatory supramolecule for present and future

1.   Introduction

As for now, the blue planet earth is unique in the universe as it harbors life. The existence of life in any other celestial object is the biggest unresolved question till-date. Whatever it may be the answer, no life exists without a boundary (i.e., the cell wall) which demarcates the surrounding environment. Ever since the first microbe appeared 4 billion years ago, bacterial population alone accounts for 5 × 10³⁰, i.e., five million trillion. Universal rule in chemistry “Like dissolves like” is also applicable to living organisms. It refers to “polar” and “nonpolar” solvents and solutes. Organic compounds will dissolve in the organic solvent and inorganic compound in inorganic solvents. All organisms are roughly made-up of 80 percent of water, which is a universal solvent. The extracellular environment and the cytoplasm are both aqueous in nature, whereas, the membrane separating environment and cytoplasm is made-up of lipid [1],[2]. The evolutionary challenge is that this unique membrane constituted of phospholipids also acts as a regulatory membrane [3],[4]. This boundary membrane also denoted as phospholipid bilayer, plasmalemma, or plasma membrane, and cell membrane.

Phospholipid asymmetry is clearly seen in plasma membrane and membranes of cell organelles like Golgi complex, and endoplasmic reticulum. Fatty acids are one of the ubiquitous entities in eukaryotic and prokaryotic cells. They are the precursors of major building blocks such as phospholipids, sphingolipids, sterols, as secondary metabolites and signaling molecules. Due to changes in the grade of saturation of phospholipids, alterations on membrane fluidity may occur and help in the adaptation to physical changes like temperature. The degradation of fatty acids yields a high amount of ATP as well as it represents a suitable storage for energy and carbon [5]. Every single living cell has plasma membrane, which comprises of two classes of molecules, lipids and proteins. Phospholipids are the major part of lipid molecules present in the membrane and they comprise of saturated and unsaturated fatty acids. Any adjustment in the segment of cell membrane individual fatty acids may result in changes on membrane functions and properties [6].

2.   Significance of phospholipids

Membranes not only help to maintain the integrity of the cell but also play a major role in survival and other physiological activities of the cell. Phospholipids have an important participation in all living cell membranes, which act as the building block of cell membranes in all organisms [7]. Lipids act as one of the most important components of the biological system [8]. They protect organisms from harsh environments by giving them specific structure and by contributing in cellular functions, through participation both in cellular and intercellular signals [9]. They participate in the transduction of biological signals across the membrane and act as signaling compounds to control vital biological processes [10].

Phospholipids can take part in crucial processes, which give structural integrity to membranes, assists in the functions of the cell to carry out metabolism-related processes. In higher organisms, all of their body organs and cells energetically retain a supply of phospholipids across the plasma membrane [11]. Phospholipids play a major role in growth and metabolism. They manage many membrane-associated activities like enzyme-catalysis, transport of solutes and receptor-mediated signaling [12]. They act as the precursor for the production of other lipid molecules [13] or saccharide macromolecules containing lipids (lipo-polysaccharides). Phospholipids help in protein alteration for membrane association and activation of molecular chaperones [14]. In recent years, phospholipids have been recognized as the intracellular messengers, which ensure that they have roles other than being structural components of membranes. Phospholipids become intriguing as they can offer the different options such as drug carriers, bio-emulsifiers, and surface-active wetting agents [15]. This review is an effort to extract out important characteristics of phospholipids, their role in microbes, plants and animals along with lipid profiling. This communication will bridge the gap in phospholipid studies.

3.   Phospholipid structure and molecular components

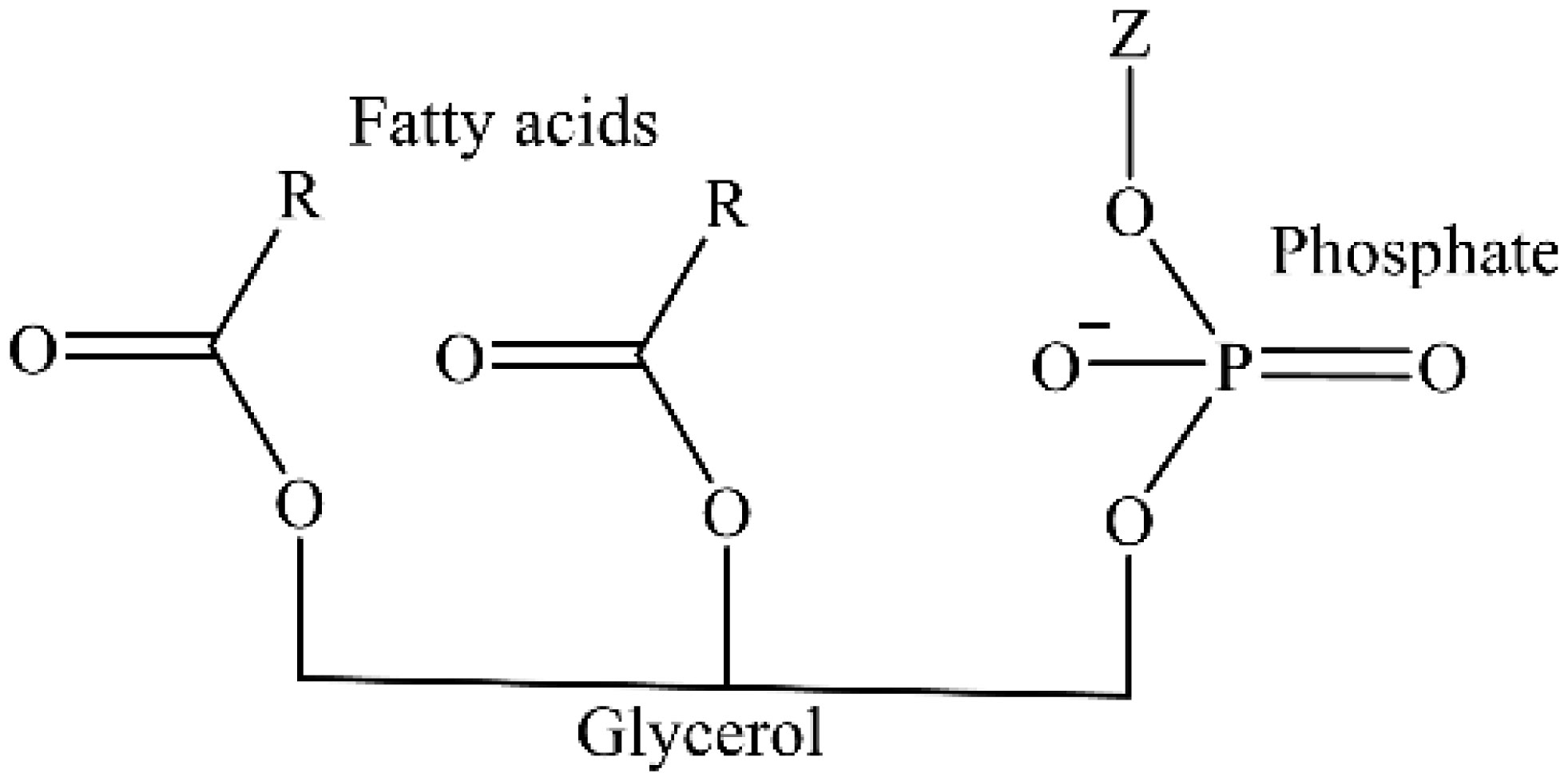
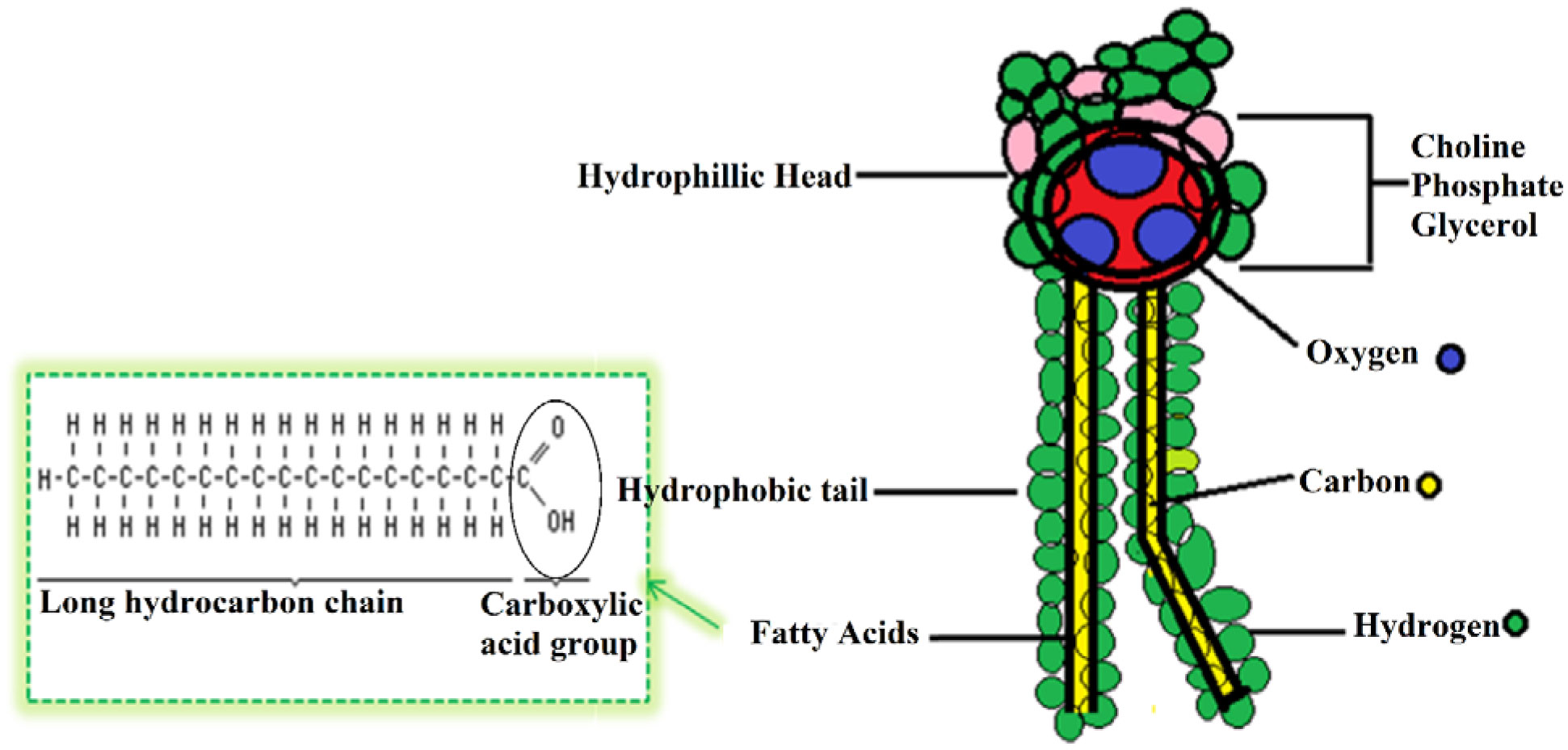
Study of the structure of phospholipid is important because of their relevance in health sciences, development of drug delivery, polymer science, nourishment and beautifying agent and biomedical engineering etc. [16]. Phospholipids keep up the integrity of the cell or organelles by forming a semipermeable barrier that separates them from their outside surroundings [17]. The cell membrane with phospholipids is generally made-up of saturated fatty acids. These fatty acids are having dissimilar structures and less fluidity that enables them to integrate with the essential fatty acids. Phospholipid contains one saturated and one unsaturated fatty acids connected to glycerol head (Figure 1). The alcohol group present in glycerol is attached to the molecule of phosphate, which is also attached to a small molecule also containing an alcohol group, as for example the one known as choline. Phosphate group combined with glycerol make the head of phospholipid hydrophilic, while the fatty acid moieties confer hydrophobicity to the molecule [18].

Figure 1.  General structure and constituents of phospholipids (In this example: phosphatidyl choline).

DownLoad: Full-Size Img PowerPoint

Fatty acids are hydrocarbon chains of varying lengths and degrees of unsaturation (defined as the presence of double bonds), with a carboxyl group at one end and a methyl group at the other. Most naturally occurring fatty acids have an even number of carbon atoms, typically 12 to 28 [19]. Fatty acids are important sources of energy because, when metabolized, they yield large quantities of ATP [20]. Long-chain FA cannot cross the blood-brain barrier (BBB), while the short- and medium-chain FA do, which makes the latter groups a potential source of energy for the brain along with glucose and ketone bodies [21]. Fatty acids are one of the major components of glycerolipid and thus are major structural constituents of living cells [22]. Besides being major structural constituents of the cell, fatty acids and fatty acid metabolites also play roles as modulators of many signal transduction pathways [23]. Phospholipids are recognized to have amphiphilic nature as they have a polar head bunch and non-polar saturated and/or unsaturated fat tails agammaegated as a bilayer [24]. These particular properties permit phospholipids to assume an important part in the formation of phospholipids bilayer.

The head of a phospholipid is hydrophilic, while the tail is hydrophobic. In the membrane bilayer, the hydrophobic parts of the molecules are sandwiched in the middle, while the hydrophilic parts form the surface of the bilayer. Phospholipid's hydrophilic heads are present on both outer sides of the bilayer, thus attracting water present inside the cell and outside the cell. On the other hand, the hydrophobic parts of phospholipid molecules sandwich themselves inside the bilayer [25],[26]. These self-organized bilayers give shape to cells, cell organelles and maintain physiochemical properties, generating a domain inside a cell that is essential for protein interaction and functioning [27]. The differentiation in head group, aliphatic chain and alcohol groups leads to the existence of a wide variety of phospholipids. The different types of phospholipids such as soybean phosphatidyl-choline, synthetic phosphatidylcholine, and hydrogenated phosphatidylcholine are usually used in various types of formulations [28].

3.1.   Nomenclature and classification

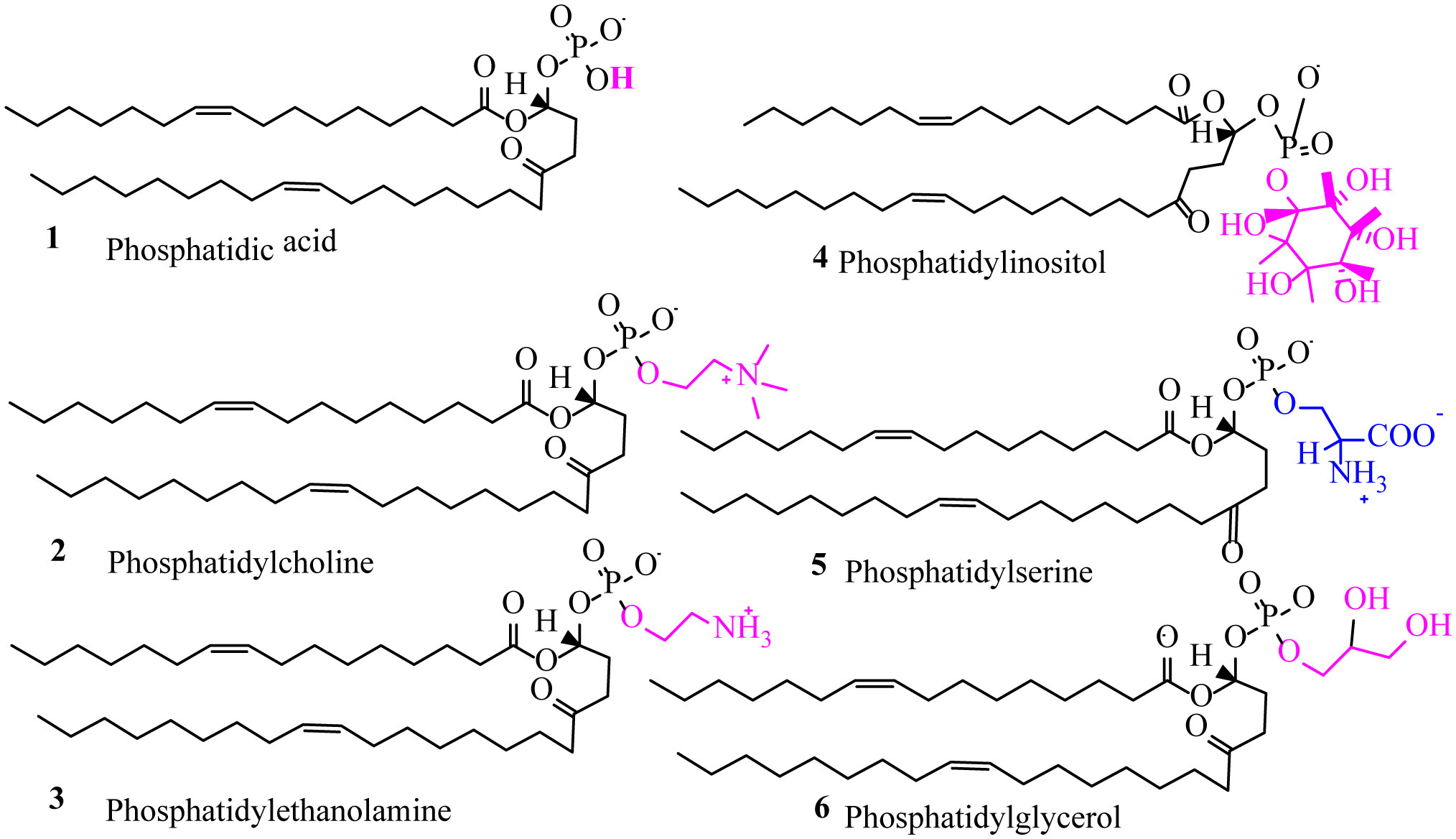
Phospholipid classification depends on the polar group, namely for instance serine glycerophospholipid, glycerol glycerophospholipid, ethanolamine glycerophospholipid and choline glycerophospholipid [29],[30]. Lipid head groups are substituents that join to the glycerol (Figure 2), sphingosine, or cholesterol spines of polar layer lipids. Phospholipids and glycolipids have head groups connected to the backbone through phosphodiester bond [31],[32]. The stereospecific classification of glycerol phospholipids locates the phosphate at the stereospecific numbering (Sn)-3 positions (Figure 3). Glycerol acts as the backbone for hydrophobic tail and hydrophilic head. Based on their backbone, these phospholipids are grouped into four major types as glycerophospholipid (GPL), sphingolipids (SL), phospholipids and ether phospholipids (EPL) [33],[34]. The structure of glycerophospholipid comprises of two chains (saturated and/or unsaturated) as well as a phosphorylated alcohol molecule and a glycerol backbone [35].

Figure 2.  Schematic representation of lipid head group (Z) that act as a substituent to connect with glycerophospholipid.

DownLoad: Full-Size Img PowerPoint

The hydroxyl cluster at the third carbon atom of the glycerol backbone is esterified to phosphoric functional group, which can be further esterified to the hydroxyl group of various alcohol moieties like ethanolamine, inositol, choline and serine. Phospholipids like phosphatidyl ethanolamine (PE), phosphatidylinositol (PI), phosphatidylcholine (PC), and phosphatidylserine (PS) are dominant in the cell membrane [36],[37]. Sphingolipids consist of a long-chain amino alcohol, commonly trans-1,3-dihydroxy-2-amino-4-octadecene [38]–[40]. Depending on the diversity of head groups, sphingolipids are classified into three types—sphingomyelin, cerebro sulfatide, and cerebroside [41],[42]. Phospholipids comprise polar head groups bound to ceramide or diacylglycerol. PLs are used as surface-active wetting agents and also as the coating agents on the surface of crystals to improve the hydrophilicity of hydrophobic drugs [28],[43]. Ether phospholipid contains an alkyl group linked to oxygen atoms of glycerol. These alkyl groups present in phospholipids occur naturally in O-alkyl group [44]. Ether phospholipids contain an alkyl group linked to an oxygen atom of glycerol and are mostly present in plasma and nervous tissue [45].

Figure 3.  Functional groups and the name of phospholipids along with corresponding structures representing asymmetrical distribution of phospholipid generally found in the cytoplasmic layer.1. Phosphatidic acid; 2. Phosphatidylcholine; 3. Phosphatidylethanolamine; 4. Phosphatidylinositol; 5. Phosphatidylserine; 6. Phosphatidylglycerol.

DownLoad: Full-Size Img PowerPoint

4.   Membrane dynamics of phospholipids

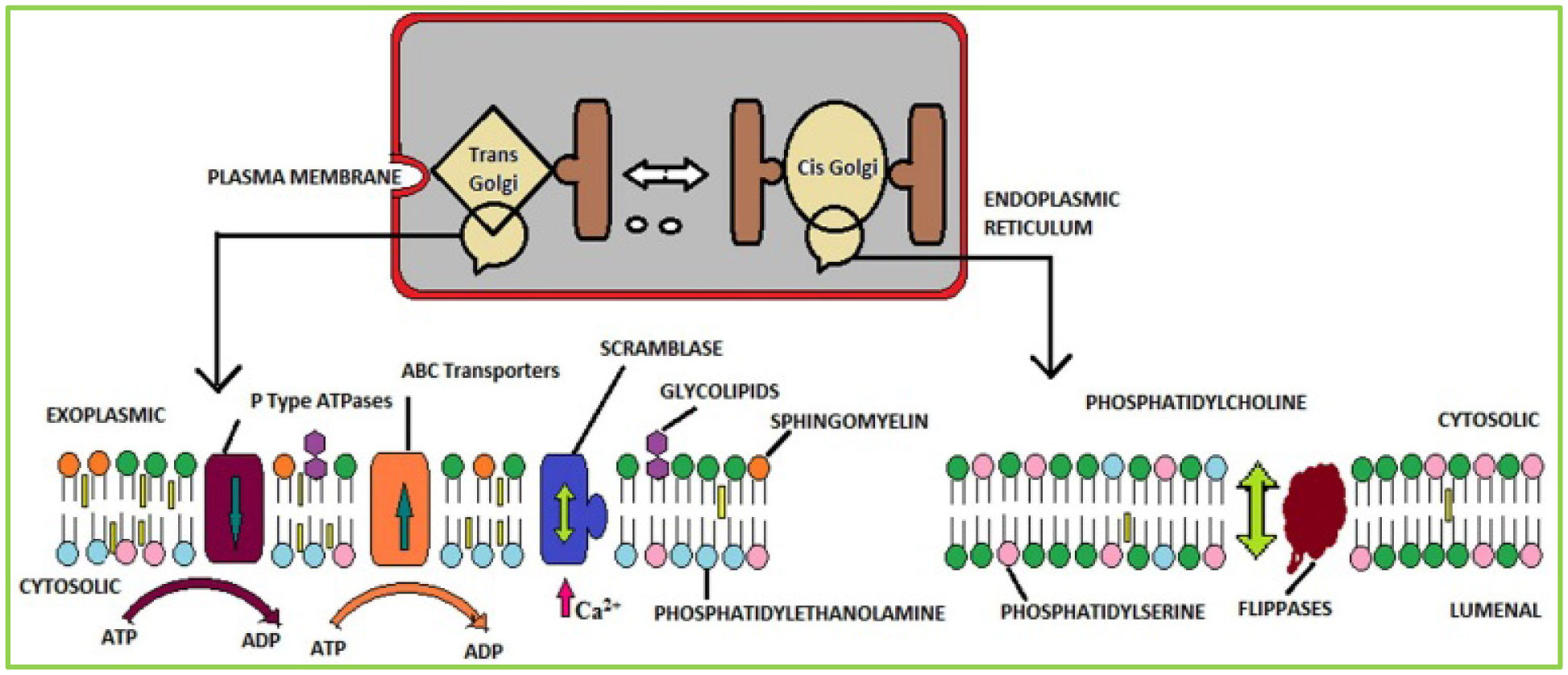
Asymmetrical circulation of phospholipids is generally found in the cytoplasmic layer (Figure 4). In typical cells, phospholipids are unevenly distributed in internal and external leaflets of the plasma membrane [46]–[48]. PC and sphingomyelin (SM) are present in the external leaflets, PS, and PE in the internal leaflets of the plasma membrane [49],[50]. A number of studies have revealed that the PL asymmetry plays a significant role in the cellular and biological processes. Generally, PL asymmetry plays a role in subcellular distribution of proteins (e.g., apoptosis/fusion of organelle), preserve biophysical properties of particular membrane, maintain membrane trafficking/maturing/vehicle, support cell shape and alteration of PL asymmetry can also play prominent role in initiating biological processes, for example, blood coagulation, cytokinesis, cell fusion, identifying and discarding of apoptotic cells [51]–[53]. The PL asymmetry can have other essential cellular functions that are still to be found and analyzed. Membrane lipids in eukaryotic cells also show irregular distribution between subcellular organelles and between two membrane leaflets of specific organelles [54]–[57].

Flippases are transmembrane lipid transporter proteins found in the membrane which belong to ATP-binding cassette transporters (ABC transporters) family. Figure 4 explains about how flippases hydrolyze ATP to form asymmetric phospholipid distribution among the bilayer [58]–[63]. In endoplasmic reticulum, membrane proteins make it easier the instantaneous flip-flop of lipids and permit them to equilibrate between the two membrane leaflets not depending on ATP hydrolysis [64]. This method can agammaegate given lipids in one leaflet, consequently causing an asymmetric lipid distribution over the layer. The characteristically dissimilar phospholipid arrangement of the two leaflets of a membrane bilayer is generated and maintained by bi-directional transport (flip-flop) of lipids between the leaflets [65]. Therefore, ATP-dependent flippases can preserve asymmetric lipid dispersion by moving particular lipid pumps (P-type ATPases/E₁-E₂ ATPases) towards or far from the cytosolic leaflet (ABC transporters). Cell apoptosis initiation activated by cytosolic calcium can break down the lipid asymmetry by the transient movement of an ATP-independent scramblase [1],[2],[66].

Figure 4.  Hydrolyzing process of ATP to form asymmetric phospholipid distribution among the bilayers by flippases and scramblase.

DownLoad: Full-Size Img PowerPoint

5.   Phospholipids in microorganisms

Phospholipids in microorganisms work as a wetting agent and thus affect the membrane fluidity in several ways [16],[68],[69]. The Corynebacterium is a genus of Gram-positive, rod-shaped bacteria, which contains phospholipids like glycerophospholipid, diphosphatidylglycerol, and phosphatidylinositol [70]. Its cell layer contains small quantities of phosphatidylethanolamine and its methylated subsidiaries (<10%) (Table 1). Corynebacterium species contain Acyl phosphatidylglycerol (APG), a rare phospholipid. APG releases three different fatty acids subsequently to the methanolysis or saponification [71]. Furthermore, a few species such as Corynebacterium equi, C. bovis, C. diphtheria, and C. xerosis, contain mannophosphoinositides. The quantitation of Corynebacterium lipid species showed that the presence of diphosphatidyl glycerol (DPG) was 1%, whereas phosphatidylglycerol was 91% [71],[72]. Corynebacterium phospholipids were recognized by the occurrence of extended chain isomer of medium chain length [73].

Table 1.  Types of lipids and their contents present in Gram⁺ and Gram⁻ bacterial cells.

S.No.	Bacteria	Lipid	Amount	References
1	Corneybacterium (Gram-positive)	Phosphatidylethanolamine	<10%	[71]
		Diacylphosphoglycerol	1%
		Phosphoglycerides	91%
2	E. coli (Gram-negative)	Phosphatidylethanolamine	80%	[74]
		Phosphatidylglycerol	15%
		Cardiolipin	5%
3	Pseudomonas aeruginosa (Gram-negative)	Phosphatidylethanolamine	71.6 ± 1.4%	[75]
		Phosphatidyl glycerol	11.8 ± 0.4%
		Diphosphatidyl glycerol	0.8 ± 0.4%
		Phosphatidic acid	2.4 ± 0.6%
		Lysophosphatidyl ethanolamine	1.6 ± 0.3%
		Phosphatidylcholine	7.9 ± 0.3%
		Lysophosphatidylcholine	3.9 ± 0.7%
4	Borrelia burgdofer (Gram-positive/negative)	Phosphatidylglycerol	Nil	[77]
		Phosphatidylcholine
5	Alcanivorax borkumensis (Gram-negative)	Ester links fatty acids	Nil	[79]

---

 | Show Table

DownLoad: CSV

Escherichia coli is a Gram-negative bacteria. The membrane lipids of E. coli consist of glycerophospholipids, principally phosphatidylethanolamine (80%), phosphatidylglycerol and cardiolipin. The culture in exponential phase has 15% phosphatidylglycerol and 5% cardiolipin. In the stationary phase, the cardiolipin content increases at the expense of phosphatidylglycerol [74]. Pseudomonas is a genus of Gram-negative bacteria. Phospholipids present in these bacteria are Phosphatidylethanolamine (PE), phosphatidylglycerol (PG), diphosphatidyl glycerol (DPG), phosphatidic acid (PA), lysophosphatidyl ethanolamine (LPE), phosphatidylcholine (PC), and lysophosphatidylcholine (LPC). The molar proportion of acidic and neutral phospholipid is 0.18 [75].

Borrelia burgdofer differs from numerous microbes in phospholipids content. It contains just two primary phospholipids, phosphatidylglycerol and phosphatidylcholine [76]. By default, it is Gram-negative since the saffron was used as a dye in the test, however in general rule spirochetes are not classified as either Gram-positive or Gram-negative [77]. Lysophosphatidyl ethanolamine occurs in considerable amount among a number of the marine bacteria. Some of them contain significant quantities of poly-β-hydroxybutyrate. Alcanivorax borkumensis: A marine bacterium (Gram-negative) contains phosphatidylethanolamine, phosphatidylglycerol and diphosphatidylglycerol, predominantly [78]. A. borkumensis is a hydrocarbon-degrading marine bacterium, which contains phospholipid ester-linked fatty acids [79].

6.   Phospholipids in plants

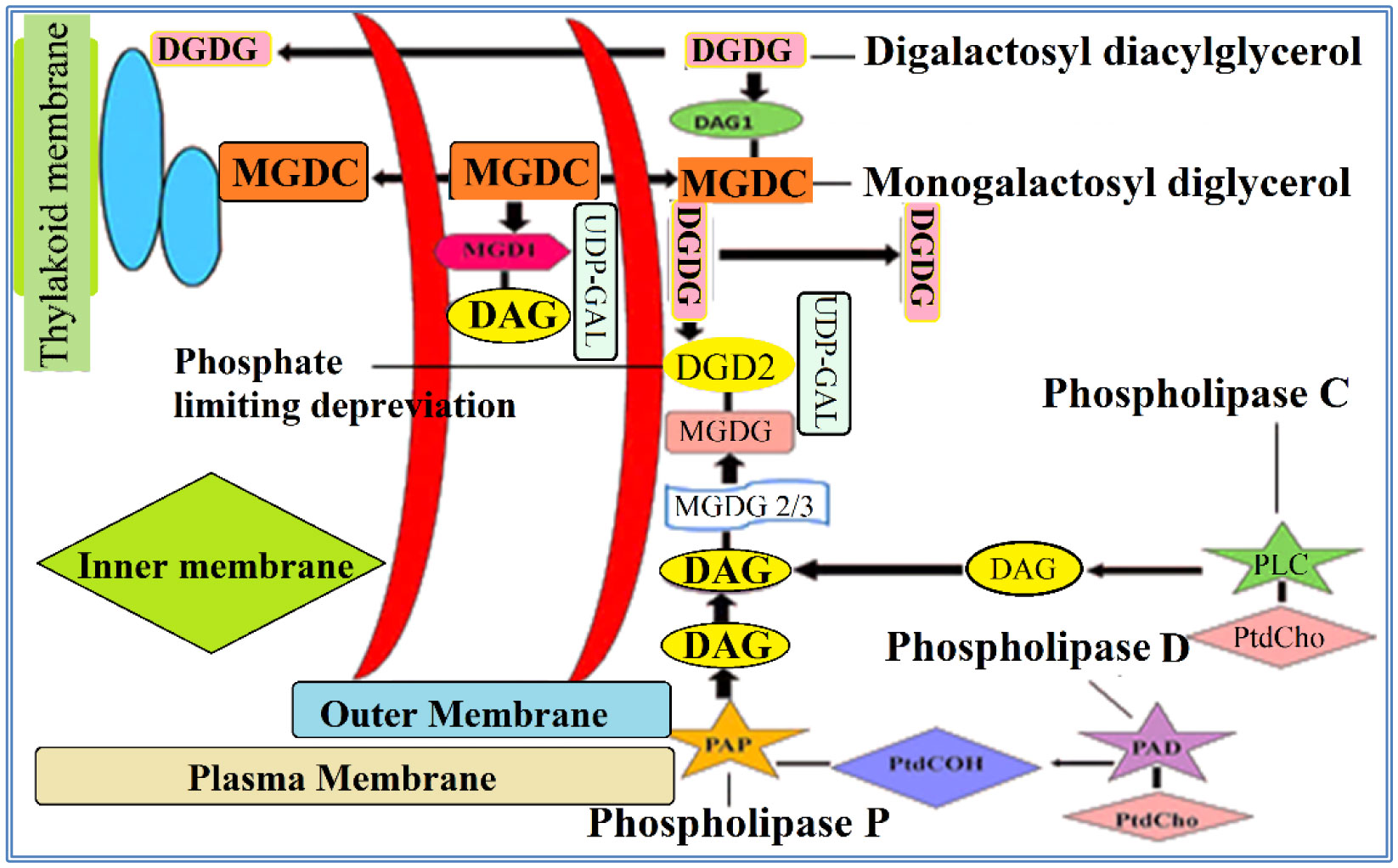
Plants are one of the richest sources of lipids and phospholipids. As shown in Table 2, there are four types of major phospholipids in plants. The phospholipids play a vital role in major life activities of plants, like photosynthesis, signal transduction, membrane trafficking and growth regulation. In plants, the photosynthetic membrane contains many galactolipids such as monogalactosyl diacylglycerol (MGDG) and digalactosyl diacylglycerol (DGDG) [80]. In chloroplast, these derivatives are essential for the photosynthetic light responses. About 80% of lipids are similar to monogalactosyl diacylglycerol and digalactosyl diacylglycerol [81]. Remarkable lipid remodeling occurs and saves phosphates, which are limiting for other cellular processes. The part of galactolipids for cellular membrane remodeling under phosphate limiting deprivation leads to galactolipid synthesis, which has essential significance for the occurrence of this process in plants [82]. Phosphate limiting deprivation was a response to lipid remodeling in Arabidopsis. The plasma film is drawn as one of a few conceivable extra plastidic layers that are redesigned taking after phosphate limiting deprivation.

Table 2.  Types of lipids and their contents present in oil-producing plants.

S. No.	Plants	Lipid%
		A	B	C	D	E
1	Arabidopsis thaliana seeds	4	19	27	20	21
2	Coconut	3	6	2	<1	80
3	Cocoa butter	35	35	3	<1	<1
4	Palm	4	38	10	<1	2
5	Olive	2	76	8	1	2
6	Canola	2	59	21	10	3
7	Peanut	2	48	34	<1	6
8	Sesame	4	41	43	<1	<1
9	Corn	2	25	61	1	<1
10	Soya bean	4	24	54	7	1
11	Sunflower	3	21	69	<1	<1
12	Cotton seed	2	18	54	<1	2
13	Safflower	2	12	78	<1	1
14	Flax	5	26	18	46	<1
15	Chia	3	7	21	61	<1

---

A: Monogalactosyl diacylglycerol; B: Digalactosyl diacylglycerol; C: Sulfoquinovosyl diacylglycerol; D: α-Linolenic acid; E: Others.

 | Show Table

DownLoad: CSV

MGD2/MGD3 and DGD2 are the other UDP-GAL subordinate galactosyltransferases of Arabidopsis prompted taking place after phosphate limiting deprivation (Figure 5) [83]. There are two proposed pathways for the turnover of phospholipids, one of it includes PLC and the other one PLD and PAP. These two pathways does not take place simultaneously in the same cell, but rather may be enacted relying upon the tissue of the plant. Phospholipase D (PLD)-mediated phosphatidylcholine (PtdCho) hydrolysis is the major source of both DG and PtdOH during the late signaling phase [84].

Sulfolipids are a class of lipids that have sulfur as the functional group. The most widely recognized constituents of sulfolipids are sulfoquinovose, it helps to form sulfoquinovosyl diacylglycerol. In plants, sulfolipids are essential intermediates in the sulfur cycle [85]. Sulfoquinovosyl diacylglycerol is the main sulfur-containing anionic glycerolipid and it is the low-dominant segment of the lipid membrane. Around 8%–34% of polar lipids in chloroplast are characterized by sulfoquinovosyl-diacylglycerol [86].

Figure 5.  Lipid remodeling in response to phosphate limiting deprivation. Three areas shown are Thylakoid Membrane, inner membrane, and outer membrane. The dark red and blue Foundation highlights the principal pathway of galactoglycero-lipid biosynthesis intervened by UDP-Gal-subordinate galactosyltransferases MGD1 and DGD1 in Arabidopsis, which give galactoglycero-lipids to the thylakoid membrane. The yellow circle foundation (DGD2) demonstrates the phosphate limiting deprivation incited responses prompting the redesigning of layers in the cell. MGDC: Monogalactosyl diacylglycerol; DGDG: Digalactosyl diacylglycerol; DAG: Diacylglycerol.

DownLoad: Full-Size Img PowerPoint

6.1.   Role of Phospholipids in plants signal transduction

In the plant cell, phospholipids act as second messengers. PLs are generated due to stimuli through the activation of lipid kinase. These lipid kinases are involved in membrane docking proteins, which contain the suitable lipid-binding domain i.e., throughout the signaling of lipid, a protein downstream involved in signaling cascade can move from the cytosol to membrane sites [87]. By combining signaling protein at micro-location interaction is elevated and is helpful for activating further transmission of signals [88],[89]. For example, a protein kinase could phosphorylate another kinase in the pathway or phospholipases could hydrolyze membrane lipids to deliver another round of lipid signaling. Signal transduction may inertly stimulate by expanding enzyme concentration at the docking sites yet the lipid can assume a more dynamic part by affecting a change in conformation that upgrades enzyme activity [90]. PL and their catabolites [91],[92] induce the changes in physical properties of the membrane such as raising the rate of ion flux or else decreasing the amount of ion flux, vesicle development, and membrane transportation. The PL act as plant growth regulators. There is evidence that in plant development, individual phospholipids play a major role and the most prominent of them is phosphatidic acid stress lipid signaling [93],[94].

7.   Phospholipids in animals

The animal cell membrane consists of plasma membrane along with various intracellular membranes that characterize compartments with specific activation, and variation in both membrane lipids content (Table 3) [95]. Few lipids are dispersed unevenly in the plasma membrane; for example, in the red blood cell, internal membranes are enriched in phosphatidylethanolamine and phosphatidylserine, whereas external membrane mostly contain phosphatidylcholine and sphingomyelin [96]. The foremost part of an animal cell is surrounded by phospholipid bilayer with embedded cholesterol and protein molecules [97]. Cholesterol was typically discovered as scattered in differing degrees in entire cell membrane, in the unpredictable spaces between the hydrophobic tail of the membrane lipids, where it contributes to hardening and reinforcing of the membrane [98]. The fuse ring arrangement of cholesterol implies that it is more inflexible than another layer of lipids [99]. It also acts as an essential part of membrane lipids, and is the metabolic precursor of steroid hormones. During moderate temperature, cholesterol decreases the fluidity level of the membrane by diminishing the movement of phospholipid. While at low temperature, it prevents disrupting to harden the regular packing of phospholipids [100].

The protein to lipid proportion additionally varies from different bio-membranes, 80% of lipids is present in the myelin sheath that protects nerve cells, and 20% of lipids in the internal membrane of mitochondria [101]. The structure of the membrane plays a role in signal transduction and cellular recognition. For example, erythrocytes contain phosphatidylserine in the outer leaflet of the plasma membrane, which increases the cell adherence to the vascular cell wall and acts as a signal for recognition of macrophage and phagocytosis [102]. These recognition methods are generally involved in the normal process of red cell turnover in the spleen [62],[100]. A free hydroxyl (three of five) group of phosphatidylinositol can be phosphorylated in cells [103],[104]. Altogether, among distinguished phosphorylated subsidiaries of phosphatidylinositol, one of derivatives phosphatidylinositol 3,4,5-triphosphate has not been found in plant cells [36],[37]. Phosphoinositide is agammaegately denoted as inositol phospholipids. They mainly participate in signal transduction pathway, which is activated by stimuli such as growth factors, hormones, and neurotransmitters [105].

Table 3.  Types of lipids and their contents present in the different animal cells.

S. No.	Animal source	Lipid% [121]
		A	B	C	D
1	Human erythrocyte	80	77	20	<4
2	Mouse erythrocyte	85	50	20	0
3	Rat erythrocyte	100	62	20	6
4	Monkey erythrocyte	82	67	13	0
5	Human platelet	93	45	20	9
6	Pig platelet	91	40	34	6
7	Mouse erythroleukemia cell	80	45	50	15
8	Rabbit intestinal brush border	63	32	34	44
9	Rabbit kidney brush border	80	35	23	15
10	Rat cardiac sarcolemma	93	43	25	0
11	Krebs ascites cell	47	52	45	19
12	Bile canalicular surface	65	85	50	0
13	Sinusoidal surface	65	85	55	0

---

A: Sphingomyelin; B: Phosphatidylcholine; C: Phosphatidylethanolamine; D: Phosphatidylserine.

 | Show Table

DownLoad: CSV

8.   Applications of phospholipids

8.1.   Bioleaching—a standard tactic for metal extraction

Some extremophiles have the capacity to oxidize and reduce the heavy metals that are found in the environment and make utilization of them as an electron acceptor in their energy production process, which is referred as bioleaching [106]. Bioleaching is usually done under a condition where the aseptic environment is not well-maintained because of the occurrence of extremophiles usually in one or more species groups, and these associations expand their productivity during the bioleaching of mines [107]. Being an oxidizing agent, PLs play a key role in bioleaching too. In the understanding of mechanism of action of bioleaching process, it is mandatory to learn/study the membrane fluidity and its relevant structural components such as fatty acids, lipids, and protein associated structures of a bacterial species [108]. Membrane kinetic analysis largely supports in increasing the biological products, where appropriate engineering of such will favor the large yield with minimal substrate level.

8.2.   Monitoring of ecological stress

Bacteria present in the soil are unimaginably delicate even to slight ecological changes. Expanded globalization has led to the diminished horticultural efficiency, adverse changes in the atmosphere, hazardous pollution and declined condition of the environment and ecosystems [109]. Soil microflora has defeated these impacts by corroding the toxins and preserving the cyclic change of the environmental substance [110]. Phospholipid fatty acid (PLFA) profiles provide sensitive reproducible measurements for characterizing the numerically prevailing part of soil microbial communities, without cultivating the organisms. The technique gives estimates of both microbial community composition and its biomass size, and results represent in situ conditions in the soil. PLFA analysis has been used to detect various environmental stresses in the soil and was found to be more discriminatory than other methods [111].

8.3.   Clinical applications

Lipids are used as carrier molecule of anticancer drugs namely paclitaxel and doxorubicin; hence, lipid components are in large demand in pharmaceutical industry. These solid lipid nanoparticles (lipid components) help in the controlled arrival of the particular drug [4]. Docosahexanoic acid (DHA) containing phospholipids find application in medicine, for example in promoting cell differentiation in leukemia [112]. The immune function was improved by using altered PL fatty acid, and the phospholipids play an important role in apoptosis [113]. Structured triacylglycerols containing medium-chain fatty acids play an important role in nitrogen balance, promoting immune function and better lipid clearance from the bloodstream [114]. Different fatty acids incorporated in PLs structure can offer intense and balanced nutrition for human beings as functional foods or pharmaceuticals.

Oxidized phospholipids are mainly utilized as biomarkers for the finding of cardiovascular illness [115]. They also agammaegate throughout the arteriosclerotic or thrombotic condition that produces an inflammatory signal. These signal transduction processes are useful tools for cardiovascular disease diagnosis [116]. Wide-range of phospholipids are worldwide being utilized as the enrolled pharmaceutical excipient, due to their physiological process, very much endured, toxicology safe and suitable for different organization of course. The composition of fatty acid and polar head group nature defines the physico-chemical properties of phospholipids. In pharmaceutical innovation, phospholipids are utilized as emulsifiers, carriers, for enhanced permeation, solubilizers, wetting and coating agents [117]. Finding the best phospholipid excipient for any medication substance, to suit its expected use and properties, requires an adequate comprehension of the properties of the phospholipids [15].

8.4.   Application of phospholipids in food industries

The mixtures called lecithin consist of different phospholipids extracted and purified from different sources. The phospholipids present in liquid lecithin are phosphatidic acid (PA, 5–12%), phosphatidylethanolamine (PE, 10–15%), phosphatidylinositol (PI, 10–15%) and phosphatidylcholine (PC, 14–16%). Lecithin is commonly used as a preservative in food, cosmetics, and pharmaceuticals [118],[119]. It acts as emulsifier, wetting, viscosity modifier, extrusion aid, separating agent, anti-dusting agent, and nutritional supplement. It is also utilized for assembling the biodegradable material [120]. Lecithin is also being used in textile and leather industries as calming and softening of the textile and leather fabrics. Furthermore use of lecithin helps in dispersing dyes used in coloring throughout the fabric, by immobilizing dyes within material, which encourages a controlled discharge and avoids the wastage of dyes [121].

9.   Conclusion

The new era of phospholipids are yet to come because it holds the secret key to unlock novel drug delivery system, medicines, food industry, emulsifiers etc. All biological processes are directly or indirectly linked to phospholipids. Fatty acid synthesis is the most energy-intensive process in phospholipids synthesis, and these biochemical mechanisms are key elements of bacterial physiology. The research focus on fatty acid has led to introduce modifications on the chain-length and unsaturation-degree of acyl groups. Structured PLs with a defined fatty acid profile and polar head groups can be produced by enzyme-catalyzed reactions, including hydrolysis, trans-esterification, and trans-phosphatidylation that employ according to the specificities of different phospholipases and lipases. PL, in addition, has their significance in membrane fluidity kinetic studies. Creation of a new database will certainly help to study all types of phospholipids in the biological systems. Profiling of phospholipid certainly contributes to different applications in many fields, such as cosmetics, food, nutrients, and pharmaceuticals. Further research in Phospholipids would pave the way for new advancements and applications in various other fields.