Anti-HIV lectins and current delivery strategies

1.   Introduction

With the incredible success of neural networks in the field of machine learning tasks, including image recognition, computer vision, natural speech processing, and cognitive science as well as the prospect of harnessing the great computing power of specialized hardware, there has been much interest in investigating their suitability also for high-performance computing tasks. The result is now an exciting new research field known as scientific machine learning, where techniques such as deep neural networks and statistical learning are applied to classical problems of applied mathematics. Thanks to the general approximation property of the neural network, it is natural to consider using the neural network to obtain the approximate solution for governing PDEs. As the predominant method nowadays for data-driven problems, deep neural networks (DNN) are used as surrogate models of PDE solvers to accelerate optimization. DNN is generally adopted as training a supervised machine learning task to establish the nonlinear mapping from input to output data pairs ^{[1,2,3,4,5,6]}, that is, learning a specific model from training data and the algorithm defined in advance structure, its quality is closely related to training data or distribution. Such models have yielded remarkable success in data-rich domains, yet in many fields of physics and engineering, the training data is often implied some prior knowledge, such as the flow field data of fluid mechanics problems need to satisfy the conservation of mass and momentum, and this part of prior knowledge is not utilized in the classic machine learning algorithms.

Physics-informed neural networks (PINNs) ^[6,7], which combine data-driven machine learning and the advantages of physical models, can train models that automatically satisfy physical constraints with a small amount of training data. The PINN algorithm has better generalization performance and can predict the important physical parameters of the model. The PINN can accurately solve the forward problems by minimizing the mean squared error loss function, such that one can get the numerical solutions of the PDEs by soving optimization problem which requires that the loss is close to zero. The loss function of PINN contains initial and boundary loss term as well as the residual from the governing equation given by the physics-informed part. It should be noted that different boundary condition setting methods used in PINN training have a significant impact on the training results. Usually, the boundary loss term is set by soft boundary in the loss function, and the weight of boundary loss term is controlled by penalty coefficient to accelerate the convergence of optimization problem. Furthermore, the selection of penalty coefficient often depends on experience to adjust, improper penalty coefficient is easy to lead to abnormal solution. Wang et al. ^[8] proposed an adaptive learning rate annealing algorithm, which utilizes the back-propagated gradient statistics during model training to assign appropriate weight to each term in the composite loss functions, that aims to balance the interplay between data-fit and regularization. This empirical parameter adjustment technique does not explain why some times PINNs fail to train. To investigated this question, Wang et al. utilized the neural tangent kernel (NTK) in their subsequent work ^[9], and proved that NTK of PINNs converges to a deterministic kernel that stays constant during training in the infinite width limit of fully-connected networks. They developed a novel adaptive training strategy that exploits the eigenvalues of the NTK to adaptively calibrate the convergence rate of the total training error. When using PINN to solve stiff ODE systems, Ji et al. ^[10] noticed that stiffness could cause the failure of the regular PINN. Thus he developed stiff-PINN approach which applies PINN to non/mild-stiff systems obtained by employing quasi-steady-state-assumptions (QSSA) to reduce the stiffness.

The neural networks can be regarded as a combination of linear transformation and nonlinear transformation, in which the activation function only determines the nonlinear approximation effect of the neural networks. The activation function plays an important role in the PINN training process as a result of the dependence of the derivative of the loss function on optimization parameters, in fact, depends on the derivative of the activation function. In the PINN algorithm various activation functions such as tanh, sin etc are used to solve various problems. There is no unified selection criterion for the activation function since it is often related to the specific problem. For ordinary neural networks, lots of literature ^[11,12] have confirmed that well-designed adaptive activation function can accelerate the convergence process. Jagtap et al. ^[13] introduced a scalable hyper-parameter in the activation function, which can be optimized and updated synchronously with neural networks parameters, and could dynamically adjust the derivative value of the activation function. Compared with the fixed activation function, this method can significantly accelerate the convergence rate and improve the accuracy of PINN training. To further accelerate the training convergence rate, different scalable parameters are introduced into the activation function of each neural layer/neuron separately in PINN ^[14]. Lu et al. ^[7] developed a Python library for PINN, i.e., DeepXDE, which can solve forward problems with initial and boundary conditions, as well as inverse problems. DeepXDE contributes to the rapid popularization and extensive applications of PINN, such as in the fields of fluid mechanics ^[15], biomedicine ^[16], cardiovascular flow ^[17] and so on. For more applications, the interested readers are referred to the review ^[18]. In ^[16], Sahli et al. improved diagnostic predictability in diagnosing atrial fibrillation by using PINN to solve an nonlinear wave dynamics equation satisfied by cardiac activation mapping. Kissas et al. ^[17] trained the PINN model on noisy and scattered clinical data of flow and wall displacement to predict blood flow in the cardiovascular system. In addition to the applications mentioned above, PINN is actively explored and improved in localized wave solutions^[19,20], high-dimensional integrable systems ^[21], porous flow ^[22], seepage equation ^[23] and so on.

The partial differential equation governs several important phenomena in physics, engineering and biology, and has a wide range of applications in the fields of epidemiological transmission^[24], tumor growth and wound healing ^[25,26], bacterial aggregation ^[27,28], the cardiomyocyte potential propagation model ^[29,30] and other fields. As the fundamental equation in such areas, Hamilton-Jacobi equations are numerically solved by many high-order accurate numerical methods. These works include, but are not limited to, central schemes ^[31,32], Godunov-type central schemes ^[33,34,35], WENO schemes ^[36,37,38]. Using neural networks to represent the viscosity solution of certain Hamilton-Jacobi (HJ) PDEs is not by itself a new idea, and some neural network architectures have led to promising results ^[39,40]. Graber et al. ^[39] presented optimal control problems on generalized networks that the controllability assumptions are not satisfied around the junctions, the Value Function is characterized as the unique solution to a system of HJ equations in a bilateral viscosity sense. In ^[40], the high-dimensional Hamilton-Jacobi-Bellman (HJB) PDEs is solved by Deep Galerkin Method which approximates the solution by a deep neural network trained to satisfy the differential operator, boundary condition, and initial conditions. The adaptive deep learning networks is proposed to model semi-global solutions for high-dimensional HJB PDEs in ^[41]. In ^[42,43], the authors proposed shallow neural network architectures to express the viscosity solution of certain HJ PDEs with particular form of convex initial data and specific Hamiltonians, where physical constraints that satisfy certain conditions are naturally encoded into the neural networks. Moreover, ^[43] investigated that two network architectures exactly represent the Lax-Oleinik formula solution of certain HJ PDEs whose initial data and convex Hamiltonian satisfy certain assumptions. Note that the Lax-Oleinik formula solution is given as the viscosity solution of the Hamiltonian which does not depend on the state variable $ {x} $ and the time variable $ {t} $. However, the performance of PINN is not yet fully investigated in solving HJ PDEs which have non-convex Hamiltonian. It sparks our interest to utilize the PINN algorithm to solve more fundamental HJ PDEs.

The paper is structured as follows. In Section 2, we will discuss the problem setup for HJ PDEs. Section 3 explores the generality of the PINN training algorithm for solving HJ equations, exactly embedding Dirichlet or periodic boundary conditions and physical constraints in neural networks architecture. To further improve the predictive accuracy, a physics-informed neural networks based on adaptive weighted loss functions (AW-PINN) is trained to solve unsupervised learning tasks for HJ PDEs with fewer training data while physical information constraints are imposed during the training process. In Section 4, we demonstrate the effectiveness and convergence of the AW-PINN training algorithm for convex and non-convex Hamiltonian. The series of numerical experiments illustrate that the proposed algorithm effectively achieves noticeable improvements in predictive accuracy and the convergence rate of the total training error. A comparison between the proposed algorithm and the original PINN algorithm for HJ equations indicates that the proposed AW-PINN algorithm can train the solutions more accurately with fewer iterations. Finally, we summarize and discuss our results.

2.   Hamilton-Jacobi equations

We consider the time-dependent Hamilton-Jacobi (HJ) equations

with Dirichlet or periodic boundary conditions on $ \partial\Omega $. The partial derivative with respect to $ t $ and the gradient vector with respect to $ \boldsymbol{x} $ of solution $ \varphi(\boldsymbol{x}, t) $ are denoted by $ \varphi_t $ and $ \nabla_{\boldsymbol{x}} \varphi(\boldsymbol{x}, t) = \left(\frac{\partial\varphi(\boldsymbol{x}, t)}{\partial x_1}, \dots, \frac{\partial\varphi(\boldsymbol{x}, t)}{\partial x_n} \right) $, respectively. The Hamilton $ H $ depends on $ \nabla_{\boldsymbol{x}} \varphi(\boldsymbol{x}, t) $ and possibly on $ x $ and $ t $. The solution of an HJ equation may have a discontinuity even when the initial data is smooth. As in conservation laws, the unique physically relevant solution can be singled out by the consideration of viscosity solutions which provides a consistent definition of a weak solution of Eq (2.1). Thus, we want to design a neural networks to approximate the viscosity solution of HJ equations from small training data. Here we draw motivation from the PINN algorithm ^[6,8,9] and some neural network architectures to solve some HJ PDEs ^[43]. We construct the PINN training method for HJ PDEs with different kinds of Hamiltonian and boundary conditions, and then optimize the weight coefficients to each term in the loss function such that their gradients during back-propagation are similar in magnitude. The problem of solving a PDE is converted into the multi-objective optimization problem where certain constraints are introduced in loss functional minimizing.

3.   Physics-informed neural networks based on adaptive weighted loss functions (AW-PINN)

3.1.   Network structure

We consider $ N^L:\mathbb{R}^{D_i} \rightarrow \mathbb{R}^{D_o} $ to be fully connected feed-forward neural networks of $ L $ layers and $ N_k $ neurons in $ k\text{th} $ layer $ \left(N_0 = D_i, \text{and}\; N_L = D_o\right) $. The input vector is denoted by $ \boldsymbol{z}\in \mathbb{R}^{D_i} $ and the output vector at $ k\text{th} $ layer is denoted by $ N^k(\boldsymbol{z}) $ and $ N^0(\boldsymbol{z}) = \boldsymbol{z} $. Each hidden layer of the network receives an output $ N^{k-1}(\boldsymbol{z})\in \mathbb{R}^{N_{k-1}} $ from the previous layer where an affine transformation of the form

is performed. The weight matrix and bias vector in the $ k\text{th} $ layer $ \left(1 \leq k \leq L\right) $ are denoted by $ \boldsymbol{W}^k \in \mathbb{R}^{N_k\times N_{k-1}} $ and $ \boldsymbol{b}^k \in \mathbb{R}^{N_k} $ respectively, which are initialized from independent and identically distributed samplings. Such a linear model is simple to solve but is limited in its capacity to solve complex problems. We should use a smooth nonlinear activation function, in order to efficiently compute arbitrary-order derivatives in the back propagation processe; in this study, we choose the hyperbolic tangent ($ tanh $). The nonlinear activation function $ \sigma(\cdot) $ is applied to each component of the transformed vector before sending it as an input to the next layer. Then the $ L $ layers fully connected feed-forward neural networks is defined as

The activation function is an identity function in the last hidden-layer. By taking $ \boldsymbol{\theta} = \{\boldsymbol{W}^k, \boldsymbol{b}^k\} $ as the collection of all weights and biases that represent the trainable parameters in the networks, We can write the neural network as follows

3.2.   Training data

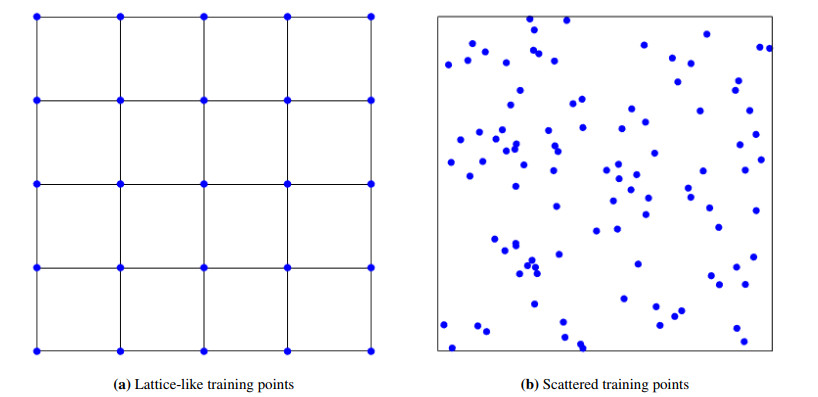
The distribution of training points has a certain impact on the flexibility of PINN. In unsupervised learning for solving PDEs, training data only consist of the initial and boundary conditions and the residual point locations in the domain, which is done without using true solution information. Figure 1 shows two different ways to select the residual point locations in the domain. The lattice-like training points are the same as the finite difference grid points, which are equispaced in the spatio-temporal domain. The scattered training points can be taken from certain quasi-random sequences, such as the Sobol sequences or the Latin hypercube sampling. The available sets of measurements can also be used to train the neural network model for some practical problems.

3.3.   Loss function and optimization algorithm

Let $ F(\boldsymbol{x}, t) $ denote the left-hand-side of the first equation in (2.1), i.e.,

Following the original idea of PINN in ^[6], we then approximate $ \varphi(\boldsymbol{x}, t) $ by the neural network denoted by $ \tilde{\varphi}(\boldsymbol{x}, t) $, in which the parameters $ \boldsymbol{\theta} $ consist of the weights $ \boldsymbol{W}^k $ and biases $ \boldsymbol{b}^k $. The schematic diagram for the neural network with multiple hidden layer is shown in Figure 2. The residual of (2.1) defines as

where the partial derivatives of the neural networks with respect to the space and time coordinates can be readily computed by automatic differentiation ^[44]. To learn a good set candidate parameters $ \boldsymbol{\theta} $ in neural networks $ \tilde{\varphi}(\boldsymbol{x}, t) $, we minimize the mean squared error via gradient descent for the following composite loss function in the general form

where $ \lambda_r $ and $ \lambda_i $ are hyper-parameters, which used to balance the interplay between the different loss terms. Here, $ L_r(\boldsymbol{\theta}) $ is a loss term that penalizes the PDE residual, and $ L_i(\boldsymbol{\theta}), i = 1, \dotsc, M, $ correspond to data-fit terms (e. g., measurements, initial or boundary conditions, etc.). For a typical initial and boundary value problem, these loss functions would take the specific form as

where $ \{(\boldsymbol{x}_0^i, 0), h(\boldsymbol{x}_0^i)\}_{i = 1}^{N_0} $ denotes the initial data, $ \{(\boldsymbol{x}_b^i, t_b^i), g(\boldsymbol{x}_b^i)\}_{i = 1}^{N_b} $ denotes the boundary data, and $ \{(\boldsymbol{x}_r^i, t_r^i), 0\}_{i = 1}^{N_r} $ denotes a set of collocation points that are randomly placed inside the domain $ \Omega $ in order to minimize the PDE residual. Consequently, $ L_r $ penalizes the equation for not being satisfied on a finite set of collocation points, which constitutes the physics-informed part of the neural networks. The loss terms $ L_0(\boldsymbol{\theta}) $ and $ L_b(\boldsymbol{\theta}) $ correspond to the initial and boundary data, which must be satisfied by the neural networks solution.

The resulting optimization problem leads to finding the minimum of a loss function by optimizing the parameters, i.e., we seek to find

One can solve this minimization problem by the stochastic gradient descent (SGD) algorithm which is widely used in the machine learning community, i.e.,

Here $ \eta > 0 $ is the learning rate and $ L(\boldsymbol{\theta}_{n}) $ is the loss function at $ n\text{th} $ iteration while the SGD methods can be initialized with some starting value $ \boldsymbol{\theta}_0 $. We see how the constants $ \lambda_r $ and $ \lambda_i $ can effectively introduce a rescaling of the learning rate corresponding to each loss term. In particular, the weights are updated as

The appropriate SGD optimizer such as Adam ^[45], AdaGrad ^[46] and L-BFGS ^[47] can be used according to the features of the neural networks.

3.3.1.   Adaptive weighted loss function

The weight coefficients of loss function play an important role in improving the trainability of NN, which can be user-defined or tuned automatically. One can obtain $ \lambda_i $ arbitrarily via a trial-and-error procedure, yet this manual hyperparameter tuning may not produce satisfying consequences. However, the optimal weights need to be reconstructed for different governing equations, which means we cannot find a fixed empirical formula that is transferable across different problems. Most importantly, the loss function needs to be tailored according to the form of PDEs. It is impractical to set the optimal weights for different loss terms without enough prior knowledge. Wang et al. have made some frontier exploration for adaptive weight by utilizing the back-propagated gradient statistics ^[8] and exploited the eigenvalues of the NTK during training ^[9]. Meer et al. introduced a scaling parameter as loss weight which balances the relative importance of the different constraints ^[48].

Here we draw motivation from the above research works and the Adam algorithm ^[45] to derive an adaptive estimate for choosing the weights during the training process. The Adam algorithm adaptively tunes the learning rate associated with each parameter in the $ \boldsymbol{\theta} $ vector, based on the track of the first- and second-order moments of the back-propagated gradients during training. Following a similar idea, our goal is to adaptively design appropriate weight to each loss term that their gradients are similar in magnitude during back-propagation. We define $ \lambda_r = 1 $ such that the residual loss generally dominate the other loss terms. For given initial and boundary loss terms $ L_i $, find $ \hat{\lambda}_i $ satisfying

where $ \bigl|\cdot\bigr| $ denotes the elementwise absolute value and the mean function denotes the average of all the elementwise value for $ \bigl|\nabla_{\boldsymbol{\theta}_n} L_i(\boldsymbol{\theta}_{n})\bigr| $. Therefore, it follows that

Then update the weight coefficients $ \lambda_i $ using the logarithmic mean ^[49] of the form

which include a numerically stable implementation and the details can be seen in Appendix 6. What's more, this updating method can also avoid the additional hyperparameter. This optimal choice of $ \lambda_r $ and $ \lambda_i $ leads to an adaptively weighted loss function

Thus, We propose the physics-informed neural networks based on adaptive weighted loss function, which adaptively assign appropriate weight to each term in the loss function during model training, an illustrative schematic is shown in Figure 2. Moreover, the logarithmic mean is employed in updating the weights, which can avoid the additional hyperparameter than learning rate annealing for PINN (LRA-PINN) ^[8].

As summarized in Algorithm 1, our proposed AW-PINN algorithm assigns appropriate weight to each term in the loss function such that the learning rate is adaptively tuned as shown in Eq (3.11), and the gradients of each term in the loss function are similar in magnitude. The proposed AW-PINN algorithm is a modification of the original PINN algorithm ^[6] and learning rate annealing for PINN ^[8]. we remark that one can update the adaptive weights according to the Eqs (3.14) and (3.15) either at every iteration of the gradient descent loop or at a frequency specified by the user. The proposed AW-PINN algorithm can be easily extended to loss functions consisting of multiple terms such as multiple boundary conditions for multivariate problems, while only the gradient statistics in Eqs (3.14) and (3.15) need to be calculated. Moreover, the AW-PINN algorithm can be used to compute the solution of HJ PDEs with different kinds of Hamiltonian $ H $, initial data, and boundary conditions, which further confirms the generality of physics-informed neural networks. Specifically, if take the adaptive weights $ \lambda_r, \; \lambda_i $ to be 1 in (3.6), then the AW-PINN becomes the conventional one, i.e.

Here we also explore the generality of the PINN algorithm for solving Hamilton-Jacobi equations, exactly embedding Dirichlet or periodic boundary conditions and physical constraints in neural networks architecture.

4.   Numerical experiments

In this section, we provide a series of numerical examples to capture the viscosity solution and illustrate the capacity of the proposed AW-PINN algorithm for solving HJ equations with both convex and nonconvex Hamiltonian. The original method introduced in ^[6] will also be explored in our experiments for comparison. For the sake of generality, only fully connected feedforward neural networks are considered. Unless otherwise stated, the proposed AW-PINN algorithm has the following set up of hyper-parameters: 4 hidden layers with 100 neurons in each layer, and the optimizing procedure is the Adam optimizer with an initial learning rate of 0.001 for 50000 iterations followed by the L-BFGS-B optimizer, in which training process would stop if the relative error between two neighboring training steps is less than $ \varepsilon = 10^{-8} $. The additional L-BFGS-B training process is used to accelerate the convergence rate during the training process. Moreover, the AW-PINN algorithm is initialized using the Glorot scheme ^[50] and implemented in TensorFlow.

4.1.   One dimensional case

For one dimensional case, unless otherwise stated, all randomly sampled collocation points inside the computational region are generated using a space filling Latin Hypercube Sampling strategy, such as Figure 3 for Example 4.1.1.

Example 4.1.1 Variable coefficient linear equation along with periodic boundary condition is given by

The exact solution is given as

Our goal here is to use this canonical benchmark problem to systematically analyze the performance of the AW-PINN algorithm. A neural networks $ \tilde{\varphi} $ approximating the solution of (4.1) can now be trained by minimizing the mean squared error loss

where $ L_0(\boldsymbol{\theta}) $ and $ L_r(\boldsymbol{\theta}) $ are defined by Eqs (3.7) and (3.9). The periodic boundary condition can strictly impose the periodicity requirement on the function and its derivative up to a finite order. Thus, the boundary loss term $ L_b(\boldsymbol{\theta}) $ for periodic boundary condition can be defined as

where $ \{x_b^i, t_b^i\}_{i = 1}^{N_b} $ denotes the boundary training data. The training point set consists of $ N_b = 50 $ boundary data randomly sampled from a uniform distribution $ \delta t = 0.01 $ in $ [0, 1] $, $ N_0 = 50 $ initial data randomly parsed from a uniform distribution $ \delta x = 0.01 $ in $ [0, 2\pi] $, as well as $ N_r = 2000 $ randomly sampled collocation points to enforce Eq (4.1) inside the solution domain. Figure 4 presents the approximate solutions obtained by the proposed AW-PINN algorithm with 50000 gradient descent iterations. The predicted solution obtained by the AW-PINN algorithm shown in Figure 4(b) is well consistent with the exact solution in Figure 4(a). From the comparison of the exact, PINN, LRA-PINN and AW-PINN solution at time $ t = 1 $ shown in Figure 4(c), it is observed that the predicted solutions obtained by the three algorithms agree well with the exact one. However, after 50000 Adam iterations and 9 L-BFGS-B iterations in about 1667.092 seconds, the relative error defined by $ \Vert{\varphi(x, t)-\tilde{\varphi}(x, t)}\Vert_{L^2}/\Vert\varphi(x, t)\Vert_{L^2} $ for our AW-PINN is 6.1164e-04 which is smaller than 1.4195e-02 for traditional PINN after 50000 Adam iterations and 278 L-BFGS-B iterations in about 852.0633 seconds as shown in Table 1. The LRA-PINN algorithm achieves the relative error of 1.4967e-03 after 50000 Adam iterations and 31 L-BFGS-B iterations in about 1994.6314 seconds. Figure 4(d) shows the loss history over the number of iterations, where the loss of the AW-PINN is decreasing faster than others. It can be deduced that the learning capabilities of AW-PINN are better as it improves greatly the convergence rate (accelerate the training), especially at the early stage. It is easy to see from Figure 5(a) that the weight coefficients $ \lambda_0 $ and $ \lambda_b $ adaptively changed with the iteration. Besides, from the evolution of loss terms $ L_0(\boldsymbol{\theta}), L_b(\boldsymbol{\theta}), L_r(\boldsymbol{\theta}) $ over the number of iterations shown in Figure 5(b), we obtain that all of the amplitude gradually decrease with iterations and the loss term of PDE residual is dominant. Table 2 summarizes our results with different methods and different neural network architectures. Evidently, the relative $ L^2 $ errors of the AW-PINN is smaller than the conventional PINN and LRA-PINN. In contrast, the proposed AW-PINN algorithm appear to be better robust with respect to network architectures.

Example 4.1.2 The strictly convex Hamiltonian is given by

with periodic boundary conditions. The singularity occurs at about $ t = 1/\pi^2. $ The change of variables, $ v = \varphi_x +1 $, transforms the Eq (4.5) into a conservation law, which can be easily solved via the method of characteristics ^[51]. Here we randomly choose initial training subset with $ N_0 = 50 $ from a uniform distribution with $ n_x = 201 $ in the space domain, boundary training subset with $ N_b = 50 $ from a uniform distribution with $ n_t = 101 $ in the time domain, and the collocation points with $ N_r = 2000 $ using a space filling Latin Hypercube Sampling strategy. Figure 6 shows the comparison of the exact solution and the predicted solution for the strictly convex HJ PDEs (4.5) trained by the conventional PINN, LRA-PINN and AW-PINN algorithms. Compared with the exact solution given in Figure 6(a), the neural networks presented in Figure 6(b) trained by our AW-PINN algorithm predict the solution very well. After the formation of the singularity at $ t = 1.5/\pi^2 $, the comparison of exact, conventional PINN, LRA-PINN and AW-PINN solutions is given in Figure 6(c), it can be seen that three algorithms accurately capture singularity of the solution. Table 3 contains the Iterations and relative errors of the approximations. Figure 6(d) shows the comparison of the loss history for the conventional PINN, LRA-PINN and AW-PINN algorithm, the loss of the AW-PINN algorithm converges faster to the global minimum after 20000 iterations without occasional large spikes occurring. Figure 7(a) provides a more detailed visual evolution of the adaptive weights $ \lambda_0 $ and $ \lambda_b $ used to scale the loss of initial and boundary conditions during the training procedure of the AW-PINN. Figure 7(b) shows the evolution of mean squared error loss terms $ L_0(\boldsymbol{\theta}), L_b(\boldsymbol{\theta}), L_r(\boldsymbol{\theta}) $ over the number of iterations, where all loss terms are convergent gradually. Evidently, the residual loss terms dominate the others.

Example 4.1.3 The one-dimensional Eikonal equation is given by

with periodic boundary conditions. Despite its origins in both geometric optics and wave propagation theory, the Eikonal equations are widely applied in science and engineering disciplines. For example, it is used to infer 3D surface shapes, calculate the distance fields, image denoising, segmentation in image processing and optimal path planning in robotics. As well, the Eikonal equation is used to compute geodesic distances in computer graphics and calculate travel time fields in seismology and is also used for etching, deposition, and lithography simulations in semi-conductor manufacturing. It is of great practical significance to study this equation. The viscosity solution to this equation has a shock forming in $ \varphi_x $ at $ x = \pi/2 $ and a rarefaction wave at $ x = 3\pi/2 $. The exact solution can be obtained via the Lax-Hopf formula ^[52]. Our training data is composed of the initial data $ N_0 = 50 $ randomly parsed from a uniform distribution with $ n_x = 201 $ in $ [0, 2\pi] $, the boundary points $ N_b = 50 $ randomly sampled from a uniform distribution with $ n_t = 101 $ in the time domain, as well as the collocation points $ N_r = 2000 $ using a space filling Latin Hypercube Sampling strategy. Figure 8 demonstrates the contour plot of the solution of the Eikonal equation on the $ x-t $ domain in the top row. Figure 8(c) provides a more detailed visual comparison of exact, conventional PINN, LRA-PINN and AW-PINN predicted solution at time $ t = 1 $. One can observe that the AW-PINN algorithm is able to capture the kink formed at $ \frac{\pi}{2} $ and the rarefaction wave at $ \frac{3\pi}{2} $. After 50000 Adam iterations and various number of L-BFGS iterations, the relative prediction error of AW-PINN is 7.6622e-03, improved by one order of magnitude compared to the conventional PINN (2.2495e-02) as shown in Table 4. Figure 8(d) shows that the loss of the AW-PINN algorithm converges faster towards global minimum, which indicates that the proposed AW-PINN algorithm seems to have the ability to train the superior solution more quickly, and have good stability also. Figure 9(a) provides the evolution process for the adaptive weights $ \lambda_0 $ and $ \lambda_b $ used to scale the initial and boundary conditions loss term during model training in the AW-PINN Algorithm. It can be seen that the weight $ \lambda_0 $ is larger than $ \lambda_b $ throughout the iterations and they all change more slowly after 20000 iterations. Figure 9(b) shows the mean squared error loss terms $ L_0(\boldsymbol{\theta}), L_b(\boldsymbol{\theta}), L_r(\boldsymbol{\theta}) $ over the number of iterations. Compared with the results obtained by the conventional PINN and LRA-PINN, the loss terms of the AW-PINN converge to a small deterministic number as the iterations increasing. Obviously, the proposed AW-PINN training algorithm can properly balance the interplay between the initial, boundary, and residual loss terms, and avoid oscillations at extreme points.

Example 4.1.4 The nonconvex Hamiltonian is given by

with periodic boundary conditions. We note that the exact solution can be given by $ \varphi(x, t) = -\cos(\pi x_0)+t[(v-1)\sin v+\cos v], v = 1+\pi \sin(\pi x_0) $ using characteristic methods. We approximate the solution by fully-connected neural networks $ NN(x, t;\boldsymbol{\theta}) $ of 8 hidden layers with 100 neurons in each layer. Here we choose randomly sampled training points with $ N_0 = 50 $, $ N_b = 50 $ and $ N_r = 2000 $ as the training set. The contour plot of the solution obtained by the AW-PINN algorithm shown in Figure 10(b) is well consistent with the exact solution in Figure 10(a). Figure 10(c) provides a more detailed visual comparison of the exact, conventional PINN, LRA-PINN and AW-PINN predicted solution at time $ t = \frac{1.5}{\pi^2} $. The predicted solution of the AW-PINN training algorithm outperforms the other two, and the $ L_2 $ relative error is 3.7065e-03, improved by one order of magnitude compared to the conventional PINN (5.9719e-02). The number of iterations and relative error of the three training algorithms are given in Table 5. In contrast, the proposed can train the solution more accurately with fewer iterations. The loss of the AW-PINN decreases faster and accelerates convergence as shown in Figure 10(d). Figure 11 illustrates the evolution process for the adaptive weights $ \lambda_0 $ and $ \lambda_b $, and the mean squared error loss terms $ L_0(\boldsymbol{\theta}), L_b(\boldsymbol{\theta}), L_r(\boldsymbol{\theta}) $. We can observe that the loss terms converge, and the residual loss term dominates the others. This example shows that the AW-PINN algorithm can approximate the solution even when the Hamiltonian is not convex.

Table 6 displays the relative $ L^2 $ error of the AW-PINN method for different examples, and for different neural architectures obtained by varying the number of hidden layers and the different number of neurons per layer. The proposed AW-PINN algorithm appear to be better robust with respect to network architectures and show a consistent trend in improving the prediction accuracy as the number of hidden layers and neural units is increased. As can be seen from Figure 4(d)–Figure 10(d) for the loss value over iterations, the loss trained in the first step are very large, the possible reason is the Xavier initialization. However, the loss decreases to a stable interval in a few steps. The numerical examples verify that our AW-PINN algorithm is stable, and the random initialization has tiny effect on numerical results.

4.2.   Two dimensional case

Example 4.2.1 The two-dimensional convex Hamiltonian is given by

with periodic boundary conditions on the domain $ \Omega = [0, 2\pi]\times[0, 2\pi] $. This problem can be reduced to a one-dimensional problem via the coordinate transformation $ \zeta = (x+y)/2, \eta = (x-y)/2 $, we can thus use the one-dimensional exact solution to analyze our predicted results. We approximate the solution by fully-connected neural networks $ NN(x, t;\boldsymbol{\theta}) $ of 5 hidden layers with 200 neurons in each layer. Small data set consists of the uniformly spaced grid points in the domain $ \Omega $ with the number of space and time grid points to be $ n_x = n_y = 41 $ and $ n_t = 41 $. Here we choose the randomly sampled collocation point with $ N_0 = 400, N_b = 4000 $ and $ N_r = 30000 $. We present the contour plot of the solution after the singularity formation in Figure 12. By using the same neural architecture hyperparameter, the trained solutions obtained by the AW-PINN and the conventional PINN algorithms are consistent with the exact one. However, the $ L_2 $ relative error 9.8475e-03 for the AW-PINN is smaller than 1.2731e-02 for the conventional PINN. What's more, the loss decreases faster and accelerates convergence as shown in Figure 12(d). Finally, Figure 13 presents the evolution process for the adaptive weights $ \lambda_0 $ and $ \lambda_b $, and the mean squared error loss terms $ L_0(\boldsymbol{\theta}), L_b(\boldsymbol{\theta}), L_r(\boldsymbol{\theta}) $ over iterations during the training of AW-PINN with 50000 iterations using the Adam optimizer. It can be seen from Figure 13(a) that although the weights $ \lambda_0 $ and $ \lambda_b $ trained in the first step are very large, they decrease to a stable interval in a few steps. Figure 13(b) shows that the residual loss term plays a dominant role in the total loss.

Example 4.2.2 The two-dimensional nonlinear equation is given by

with Dirichlet boundary conditions on the domain $ \Omega = [-\pi, \pi]^2 $. This is a genuinely nonlinear problem with a nonconvex Hamiltonian. The exact solution is given implicitly by $ \varphi(x, y, t) = -\cos(q)\sin(r)+\sin(q)+\cos(r) $ where $ x = q-t\sin(r) $ and $ y = r+t\cos(q) $. We approximate the solution by fully-connected neural networks $ NN(x, t;\boldsymbol{\theta}) $ of 5 hidden layers with 200 neurons in each layer. Small data set consists of the uniformly spaced grid points in the domain $ \Omega $, where the numbers of grid points are $ n_x = n_y = 41 $ and $ n_t = 41 $. Here we choose $ N_0 = 1681, N_b = 4000 $ and $ N_r = 30000 $ randomly sampled collocation points. We also present the detailed visual comparison of the exact solution, predicted solution using conventional PINN and AW-PINN at time $ t = 0.5 $ in Figure 14. Compared with the conventional PINN, the loss of the AW-PINN training algorithm decreases faster and accelerates convergence after 30000 iterations as shown in Figure 14(d). What's more, the $ L_2 $ relative error is $ 1.2702e-01 $, which is smaller than $ 1.2937e-01 $ for the conventional PINN. Finally, Figure 15 shows the evolution process for the adaptive weights $ \lambda_0 $ and $ \lambda_b $, and the mean squared error loss terms $ L_0(\boldsymbol{\theta}), L_b(\boldsymbol{\theta}), L_r(\boldsymbol{\theta}) $ for 50000 iterations. One can obtain that the variation range of the weights become smaller as the number of iterations increases and the residual loss term dominant the others.

Example 4.2.3 The shape-from-shading problem is given by

with $ \varphi(x, y, t) = 0 $ at the boundary of the domain $ \Omega = [0, 1]^2 $. Here I(x, y) is the brightness value with $ 0 < I(x, y)\leq 1 $, specifically, we take

The steady-state solution of equation (4.10) is the shape function, which has the brightness $ I $ under vertical lighting, see ^[53]. The shape-from-shading problem has multiple solutions to Eqs (4.10) and (4.11), and all satisfy the homogeneous boundary condition, according to ^[54]. Similar to traditional numerical methods ^[55], the additional "boundary conditions" are introduced at points where $ I(x, y) = 1 $. In our problem, we consider such "boundary conditions":

then the exact solution will be $ \varphi(x, y) = \sin(2\pi x)\sin(2\pi y) $. We approximate the solution by a fully-connected neural networks $ NN(x, t;\boldsymbol{\theta}) $ of 5 hidden layers with 200 neurons in each layer. Small data set consists of the uniformly spaced grid points in the domain $ \Omega $, where $ n_x = n_y = 41 $ and $ n_t = 161 $ are the number of space and time grid points. Here we take randomly sampled collocation points with $ N_0 = 1681, N_b = 4000 $ and $ N_r = 30000 $. We also show the detailed visual comparison of the exact solution, predicted solution using the conventional PINN and the AW-PINN at time $ t = 1 $ in Figure 16. The loss of AW-PINN training algorithm decreases faster and accelerates convergence after 30000 iterations as shown in Figure 16(d), and the $ L_2 $ relative error is $ 1.7686e-02 $, improved by one order of magnitude compared to the conventional PINN (1.5982e-01). Finally, Figure 17 presents the evolution process for the adaptive weights $ \lambda_0 $ and $ \lambda_b $, and the mean squared error loss terms $ L_0(\boldsymbol{\theta}), L_b(\boldsymbol{\theta}), L_r(\boldsymbol{\theta}) $ for 50000 iterations. For this problem, the residual loss term dominant the others as usual. However, to make the total loss decreases as the number of iterations increases, the weights for loss terms corresponding to the initial and boundary conditions change more frequently here.

5.   Summary and discussion

Although there are some very valuable works related to developing specific neural network architectures to solve some sets of HJ PDEs ^[42,43], whose Hamiltonian is convex and the viscosity solution can be defined by the Lax-Oleinik formula. The performance of physics-informed neural networks algorithm is not yet fully investigated in the literature in solving time-dependent HJ PDEs such as nonconvex Hamiltonian equations that can capture shock and rarefaction waves. The original PINN formulation ^[6] is trained to solve unsupervised learning tasks by minimizing the mean squared error loss with physics-informed constraint. This training method is suitable for solving certain types of problems, such as the curse of dimensionality problems. However, the original PINN also has difficulties in representing an accurate approximation for nonconvex Hamiltonian. To further improve the predictive accuracy, we have proposed the AW-PINN algorithm such that the weights for different loss terms can be adaptively updated, in which the residual loss terms keep dominating the others. This approach is an improvement of the learning rate annealing for physics-informed neural networks of Wang, Teng, Karniadakis ^[8], and updates the weights using the log average and provides better predictive accuracy for HJ PDEs. We examined our proposed training algorithm for solving time-dependent HJ PDEs, including variable coefficient linear equation, strictly convex Hamiltonian, Eikonal equation, nonconvex Hamiltonian, two-dimensional Burgers-type Hamiltonian, and two-dimensional nonlinear equation with a nonconvex Hamiltonian and the shape-from-shading problem. The series of numerical experiments show that the proposed algorithm effectively achieves noticeable improvements in predictive accuracy and increases the convergence rate. Although a series of numerical results have verified that this training algorithm can learn accurate approximation solutions of HJ PDEs, and yield practical improvements, the theoretical analysis of the proposed AW-PINN algorithm is worth further research. We will investigate many critical applications in computational science and engineering to better understand PINN. These numerical results may provide some inspiration for the subsequent theoretical research. And we notice that the AW-PINN algorithm can enforce exactly periodic boundary conditions by imposing the periodicity requirement on the function and all its derivatives. The neural network architecture can also be modified to exactly impose Dirichlet and periodic boundary conditions.

Acknowledgements

This work is supported by National Natural Science Foundation of China (Grant Nos. 11871399, 11901460) and China Postdoctoral Science Foundation (Grant No. 2022M712600), which are gratefully acknowledged.

Conflict of interest

The authors declare there is no conflict of interest.

Appendix A.   Logarithmic mean

The logarithmic mean of $ a $ is defined as

However, this is not numerically well-posed when $ a_l\to a_r $. To overcome this, let us write the logarithmic mean in another form. Let $ \zeta = \frac{a_l}{a_r} $, so that

where $ \ln(\zeta) = 2\Bigl(\frac{\zeta-1}{\zeta+1}+\frac{1}{3}\frac{(\zeta-1)^3}{(\zeta+1)^3}+\frac{1}{5}\frac{(\zeta-1)^5}{(\zeta+1)^5}+\frac{1}{7}\frac{(\zeta-1)^7}{(\zeta+1)^7}+o((\zeta-1)^9)\Bigr) $ is used to obtain a numerically well-formed logarithmic mean. The subroutine for computing the logarithmic mean is as following, let

and

so that $ a^{\ln}(l, r) = \frac{a_l+a_r}{2F} $ with $ \varepsilon = 10^{-2} $.