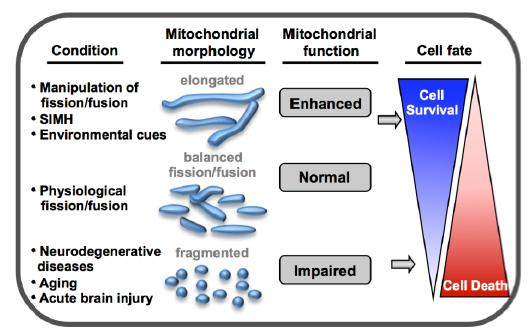
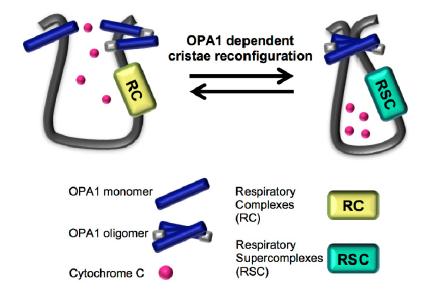
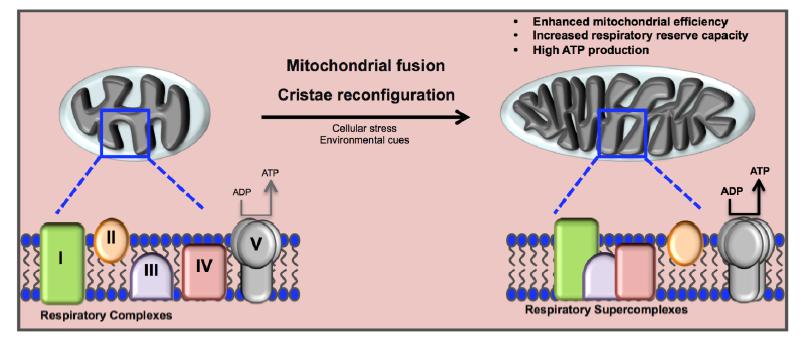
From Parkinson's disease to an ischemic stroke, a consistently reoccurring theme in the context of neuronal degeneration is the dysfunction of mitochondria as the underlying factor. Insight into the mechanistic basis for mitochondrial dysfunction in neurodegenerative disorders has allowed the theme of mitochondrial dynamics to be highlighted as a central player. The precise balance of mitochondrial dynamics is among the most critical features for the juxtaposed processes of cell death and survival. More recently, studies have allowed mitochondrial shape to emerge as a key regulator of respiratory efficiency that can enforce the bioenergetic status of cells and thereby determine cell fate. Here we review the most current advances that provide an explanation for the long-standing question of how mitochondrial shape can impact cellular metabolism. Furthermore, we discuss the implications of an imbalance in mitochondrial dynamics in neurodegenerative disorders.
1.
Introduction
Robots have the same fine manipulation capabilities as humans through visual perception and learning, which is of great significance in improving the robot's task adaptability and the efficiency of robot–human collaboration [1,2,3]. Grasping is an essential skill possessed by intelligent robots, and it enables them to autonomously engage in various forms of fine manipulation. The topic of grasp detection has garnered significant interest in recent years due to its practicality and indispensability in robotic applications. Nevertheless, the task of robotic grasping of stacked objects continues to encounter significant obstacles [4]. This task involves not only detecting of the object's orientation and grasping attitude but also coping with challenges caused by mutual occlusion. Therefore, grasping in stacked scenarios has become a prominent focus in current academic research.
Conventional approaches to robotic grasping often operate in a controlled setting where the object model is known [5,6]. However, this restricts its capacity to adapt to diverse objects and environments. A recent study has reported a tendency among individuals to perceive robotic grasping as an issue of object detection. The initial investigations into grasp detection predominantly employed analytical methods [7]. These methods relied on examining geometric and physical characteristics and incorporating manually engineered elements to achieve an optimal selection of grasp points. The advancements in deep learning techniques for image recognition and object detection have led to remarkable progress in grasp detection algorithms. These algorithms based on deep learning have displayed unprecedented performance on the Cornell grasping dataset. They have shown substantial enhancements in both detection accuracy and speed, as evidenced by the studies of Redmon and Angelova [8], Xu et al. [9], Cheng et al. [10], and Wu et al. [11]. Recently, Zuo introduced a novel approach called the "graph-based visual manipulation relationship reasoning network" to achieve stable and sequential grasping in stacked environments [12]. This approach directly generated object relationships and manipulation orders. Ge et al. [13] developed a visual strategy using the Mask-RCNN network to improve the capacity to grasp unoccluded objects in cluttered environments. This approach aimed to address the issue of instability in grasping induced by the presence of stacked objects. Li et al. [14] presented Key-Yolact, a new multitask real-time CNN model. This network addressed the challenges of object recognition, case segmentation, and multi-object key point detection in industrial stacked scenarios.
However, in practical applications, most of the objects in the lower layer of the stack are severely occluded. Consequently, the grasping sequence of objects inferred by the network is not completely consistent with the actual situation, resulting in a low success rate of robotic grasping. The robotic grasping in stacked scenarios is a complex task involving many factors, such as grasp pose detection, grasp planning, physical interaction, and force control. We mainly focused on grasp detection and categorized the detection task into two sub-tasks: stacked object detection and grasp pose prediction. We developed a two-step visual technique to pick up unobscured objects from the top layer of a stack, mitigating the shakiness of grasping that occurred when objects were stacked. Compared with prior research, grasp detection was conducted specifically on the properties of the object rather than on the entirety of the scenario. The perception associations were evaluated to determine the prioritization of object grasping. In conclusion, the primary contributions of this study are summarized as follows:
1) We presented a two-stage grasp detection algorithm framework to address the issue of sequential grasping by robots in stacked environments. A stacked dataset comprising 22 items from 10 categories was built to facilitate the training and evaluation of the algorithm.
2) In the context of the two-stage grasp detection technique, we developed a model called R-YOLOv3 to identify and locate the topmost object in stacking scenarios. Additionally, we introduced a network called G-ResNet50 to effectively determine the most suitable grasping pose.
3) We evaluated the performance of the network model in estimating grasp positions estimate through tests conducted on the publicly accessible Cornell grasping dataset. Furthermore, we effectively showcased our proposed methodology in a practical scenario involving picking up tasks in a real-world setting featuring a multi-object stacking environment, employing the UR5 robot.
The remaining manuscript is organized as follows. Section 2 briefly explains traditional methods for robotic grasping, deep learning for grasp detection, and robotic grasping of stacked objects. Section 3 discusses the proposed two-stage grasp detection method for stacked objects. Section 4 describes the experimental implementation, evaluates the performance of the proposed method, and also analyzes some problems encountered in the experiment. Section 5 concludes and anticipates forthcoming research.
2.
Related work
Significant progress has been achieved in estimating robotic grasp position through extensive research conducted during the last two decades. This section provides an overview of recent literature on the development of grasping techniques to address robotic manipulation challenges.
2.1. Traditional methods for robotic grasping
The primary focus of early grasping methods pertains to scenarios involving a solitary object inside organized surroundings. These methods encompass model analysis-based approaches and data-driven approaches for grasping. François et al. [15] demonstrated the use of analytic methodologies employing mechanical models to forecast grasping outcomes. Robotic grasp detection aims to select contact locations that ensure qualities such as force or form closure, as discussed in a previous study [16]. Abdeetedal and Kermani [17] proposed a measurement of the grasp quality used to assess the appropriateness of a grasp configuration. This measure was structured as a quasi-static grasping issue. However, background knowledge of the object and the manipulator is required to create such models and techniques. Saxena et al. [18] introduced a method for identifying the grasp point based on only RGB images, eliminating the need for prior information. The concept of employing rotated rectangles within a visual field to depict grasp areas was first introduced by Jiang et al. [19]. Despite the aforementioned studies offering potential methods for enhancing the dexterity of robotic grasping, it was evident that these methods heavily relied on the pre-existing knowledge and skill of the creators.
2.2. Deep learning for grasp detection
The deep learning strategy converts the grasp detection task into identifying five-dimensional vectors within an image. Lenz et al. [20] conducted a study at Cornell University demonstrating the feasibility of projecting the five-dimensional grasp model from RGB images into a three-dimensional spatial domain. Song et al. [21] introduced a solution for robotic grasp detection using an area proposal network in a single-stage framework. The proposed approach involved initially creating several reference anchors with certain orientations, which were then used for regressing and categorizing grasp rectangles.
Morrison et al. [22] created the generative grasping convolutional neural network (GG-CNN) to output grasp position and evaluation from depth images. This network was designed to accept depth images as the input and produce the grasp position along with the appropriate grasping evaluation as the output. Mahler et al. [23] used Dex-Net 2.0, a synthetic dataset, to train a Grasp Quality Convolutional Neural Network model that rapidly predicted grasp success from depth images to reduce the data collection time for deep learning of robust robotic grasp plans. The feature pyramid network was employed to provide predictions regarding the uncertainty of grasp for the RGB-D image, as discussed by Zhu et al. [24]. Yu et al. [25] developed a novel neural network architecture called Squeeze and Excitation ResUNet, specifically designed for grasp detection. The network integrated a residual module involving transfer attention. A cross-modal perception framework was introduced for grasp detection, aiming to accurately ascertain the position and posture of an item [26]. This framework incorporated a comprehensive multi-scale fusion of RGB and depth information. A previous study [27] introduced a hybrid deep architecture that integrated visual and tactile sensing for robotic grasp detection. Huang et al. [28] presented a new robotic grasping method called multi-agent TD3 with high-quality memory for successfully grasping objects that moved randomly in an unstructured environment. The ResNet50 model, a deep residual network, stands out among numerous models due to its depth and accuracy. It has been employed in robotic grasp pose prediction with remarkable success, as documented in previous studies [29,30]. These studies demonstrated that deep learning technology possessed significant benefits and possibilities addressing complex robotic grasping challenges.
The aforementioned methodologies demonstrated exceptional performance in both simulation trials and real-world experiments. Their academic endeavor offered definitive techniques and scientific support to address the challenge of grasping extremely complex multi-object stacking scenarios.
2.3. Robotic grasping of stacked objects
A large number of recent studies focused on the grasping of stacked objects. Ge et al. [31] introduced a novel 3D robotic grasp detection network that effectively mitigated the impact of varying camera orientations. Zhang et al. [32] proposed a multitask convolutional neural network (MT-CNN) as a solution for addressing occlusion issues in object stacking scenarios. The suggested MT-CNN aimed to facilitate the robot's ability to sequentially grasp the target item. Lin et al. [33] introduced a strategy for robotic grasping that used 3D vision guidance. The primary objective of this method was to address the issue of occlusion that arose when multiple items were present in a stacking scenario. Recent studies demonstrated that deep neural networks achieved impressive results in the field of visual relationship reasoning, as demonstrated in a previous study [34]. Zeng et al. [35] presented a robotic pick-and-place system capable of grasping and recognizing both known and novel objects in cluttered environments. The multifunctional gripper enabled quick and automatic switching between suction and grasping. Wu et al. [36] presented a model for robotic grasp detection in multi-object environments. This model effectively leveraged a hierarchy of characteristics to simultaneously learn object detection and pose estimation for robotic grasping. Hu et al. [37] proposed a novel grasps-generation-and-selection convolutional neural network (GGS-CNN), which was trained and implemented in a digital twin of intelligent robotic grasping. Significant advances were made in both the success rate and speed of grasp detection. Duan et al. [38] presented a novel two-stage multitask semantic mastery model called MSG-ConvNet to effectively identify associations between items and grasps in complex and stacked environments. Various multistage grasping strategies aimed at addressing the issues associated with grasping in stacked scenarios have emerged over time, as discussed in previous studies [39,40]. To address the complexity of the discussed methods, de Souza et al. [41] provided clear and standardized criteria for assessing robotic grasping methods, facilitating a transparent comparison among new proposals for researchers.
However, the applications face two primary challenges: 1) Occlusions among objects inside the stacked image pose challenges in effectively detecting them. 2) The cascade structure gives rise to several redundant calculations, such as the extraction of scenario elements, resulting in reduced processing speed.
Hence, we presented a novel approach for robotic grasp detection using a two-stage convolutional neural network in sequential robotic manipulation. Within the context of the two-stage grasp detection technique, a model called R-YOLOv3 was developed to identify and localize the topmost object in stacking scenarios. Additionally, a G-ResNet50 network was introduced to efficiently find the most suitable grasping pose. With the proposed framework, the robot could sequentially pick up objects from complex stacking scenarios one by one.
3.
Materials and methods
3.1. Method framework
The proposed robotic grasping method in the stacked scene mainly consisted of two parts: stacked scenario perception and grasp pose detection. As shown in Figure 1, the stacked multi-object scenario image obtained using the eye-in-hand camera was used as the input for the whole network. The R-YOLOv3 was used to detect the uppermost objects. Hence, the influencing factors for mutual occlusion among objects could be effectively avoided. The detected topmost object region was employed as the input of the grasp detection network during grasp pose detection. The estimation of multi-grasping candidate bounding boxes was performed using G-ResNet50. The candidate box exhibiting the highest score was selected as the optimum grasping pose.
Using the aforementioned networks, researchers could feasibly determine the category of the item and its grabbing posture in relation to the camera coordinate system. Providing the anticipated grasping pose as an input to the robot hand-eye conversion model was essential for executing the robotic grasping operation. This facilitated the derivation of grasping pose parameters within the robot coordinate system. The procedure was then repeated, with the grasping path for the topmost object in the stacked scenario being planned and executed. The grasping loop concluded when all objects in the stacked scene were successfully grasped.
3.2. Multi-object stacked dataset collection
The primary challenge in object grasping in stacked scenarios is the mutual occlusion problem. Humans can effectively address this issue using a grasping sequence, where the unobstructed object is grasped from the top. Inspired by this strategy, we designed a rotated object detection network R-YOLOv3 specifically tailored to detect only top-level objects. We trained R-YOLOv3 on a dataset annotated exclusively for the topmost object, enabling it to detect that object. In scenarios with multiple objects on the topmost layer, we prioritized the object with the highest confidence. To train this network, we built a corresponding dataset. The dataset was annotated using oriented bounding boxes. The label information in the dataset included only the position and classification attributes of the topmost object in the image. Oriented bounding boxes were applied to all unoccluded objects in the image, whereas occluded objects remained unlabeled. This dataset needed to adhere to the following principles:
1) The selected object must be graspable using the parallel gripper.
2) The number and placement of objects should be sufficient during the collection process.
3) The labeling information should pertain to the positional and categorical attributes of the object located on the uppermost layer of the stack depicted in the image.
In the laboratory, a Grasp-M dataset from University of Science and Technology of China (USTC) was created by randomly selecting 22 objects from 10 different categories. Several instances of the stacked dataset are illustrated in Figure 2.
The items included a wrench, a brush, a tape, a plastic, a mouse, sticks, pliers, a pen, a screwdriver, and a knife. We used a D415 camera to take $416 \times 416$ RGB pictures of the stacking scenario, while the objects were randomly placed on the platform. We captured 200 images of single-class objects randomly placed in various positions and orientations, 200 images of multiple-class objects randomly placed without stacking, and 800 images of multiple-class objects randomly placed with different stacking arrangements and orders to ensure scenario diversity and simulate realistic grasping scenarios. These 1200 images constituted the stacked object dataset. The inventory of items is presented in Table 1.
Various data augmentation approaches were used to increase the amount of data and diversify the range of samples to improve the overall generalization and robustness of neural networks. For instance, the augmented sample was established by simulating the scattered stacked characteristics. An example of the data augmentation process is shown in Figure 3.
Each image underwent a processing procedure, generating five augmented images to enhance the training set. From the existing labeled dataset, one to four sample objects were randomly selected each time, deducted from the original image, and placed in random positions in the new image sequentially. If the Intersection over Union (IoU) of the label frames of two objects was greater than 0.2, it was considered that the object placed first was occluded by the one placed later and would not be displayed in the final augmented label. The 800 images in the dataset were processed using the data augmentation method of simulated scattered object stacking proposed in this study. Finally, the training set contained 4000 images.
3.3. Stacked object detection model
3.3.1. Network architecture of R-YOLOv3
The process of detecting stacked objects involved determining the precise position of the boundary box and discerning the classification of the objects positioned on the uppermost layer of a stacked setting. It used a color image of a scenario with multiple stacked objects as input, and output the class and location box of the object(s) on the top layer without any occlusion. In addressing the robotic grasping challenge in a stacked scenario, we used the detection results obtained from the stacked object detection network as the primary objects for the robot to grasp, ensuring stability and safety during the grasping process. Therefore, identifying the location and class of objects on the top layer of a stack was regarded as an object detection task, offering a prioritized selection strategy for robotic grasping in a stacked scenario.
In stack scenarios, the stacking relationship between objects is considered a special visual semantic information. We used convolutional neural networks to construct a stack target detection network to detect objects on the top layer of the stack. The stack-grasping hierarchy concept was employed as a solution for addressing the challenge of recognizing objects and selecting appropriate grasping techniques for stacked scenarios. Building upon the YOLOv3 object detection network [42], we improved it to create R-YOLOv3 by adding angle prediction parameters into the feature dimension of the output, as shown in Figure 4. The original output form of the YOLOv3 network was changed, and the localization box was more closely wrapped around the objects on the top layer of the stack, reducing redundant background information.
The original YOLOv3 model output $ \left({x, y, w, h} \right) $ four-dimensional information. The R-YOLOv3 network incorporated an additional dimension into the output feature map to accommodate the diverse and unpredictable poses of identified targets. The additional dimension was employed for estimating the angle of rotation of the rectangle. The output $ \left({x, y, w, h, \theta } \right) $ of the localization bounding box is depicted in Figure 5.
We designated YOLOv3 with the output of the parameters of the rotated rectangular box $ \left({x, y, w, h, \theta } \right) $ as R-YOLOv3. Figure 6 illustrates the significance of the rotating rectangle $ \left({x, y, w, h, \theta } \right) $, where $ \left({x, y} \right) $ is the rotational frame's origin, $ w $ is its width, $ h $ is its height, and $ \theta $, in the range (0–180°), is an angle across the longest side and the X-axis's horizontal direction.
3.3.2. Loss function of R-YOLOv3
A six-dimensional vector parameter (x, y, w, h, θ, cls) was used to characterize items in stacked object detection. This vector accounted for the localization and recognition of the bounding box and object class in a scenario with numerous stacked objects. (x, y) represent the center coordinates of the bounding box, whereas (w, h) denote its width and height. The angle θ refers to the orientation of the bounding box in relation to the X-axis. Additionally, cls signifies the object class enclosed within the bounding box. The loss function for detecting stacked objects was calculated as follows:
The loss function of R-YOLOv3 comprised the following four components: localization loss $ {L_{(x, y, w, h)}} $, classification confidence loss $ {L_{conf}} $, classification loss $ {L_{class}} $, and angle loss function $ {L_\theta } $ for the rotating anchor box, expressed as:
In the aforementioned equations, the variable ${S^2}$ denotes the division of the feature map into $S * S$ grid units, with every single grid unit generating a B priori anchor box. The anticipated values of the positioning box are denoted as ${x_i}$, ${y_i}$, ${w_i}$, ${h_i}$, and ${\theta _i}$, whereas the corresponding true values of the positioning box label are represented by ${\hat x_i}$, ${\hat y_i}$, $ {\hat w_i} $, ${\hat h_i}$, and ${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } _i}$. The variables ${C_i}$ and ${\hat C_i}$ represent the estimated and actual values of the confidence, respectively. A sample with a target has a confidence label of 1, whereas a sample without a target has a confidence label of 0. The category's true and predicted values are ${P_i}(c)$ and ${\hat P_i}(c)$, respectively. A regression loss for the location box was assigned values ${\lambda _{{\text{c}}oord}} = 5$, ${\lambda _\theta } = 1.0$ to balance the contribution rate of different types of losses. Most of the predictions for a graph are based on grids that do not include targets. Hence, ${\lambda _{noobj}} = 0.5$ was set for balancing positive and negative samples to reduce the contribution of grids that did not contain targets to the loss.
3.4. Grasp pose detection
3.4.1. Robotic grasping descriptor
The robot needed information about the object's gripping position to successfully complete a grasping action. The grasp detection method identified a successful grab position G for each object based on RGB images. The formulation of the grasp pose was expressed as follows:
The vector $ \left({x, y, w, h, \theta } \right) $ was used to establish an oriented bounding box, as depicted in Figure 7. The image frame had five elements $ \left({x, y, w, h, \theta } \right) $ characterizing a particular grasp configuration. The focal point of the gripping position is denoted by $ \left({x, y} \right) $, whereas $ \left({h, \theta } \right) $ represents the gripper's opening width and grab angle. The size of the grasp region was dependent on the length $ w $ of the antipodal area.
The grasp poses, first represented in the image frame, were later transformed into the robot base frame. This transformed information was then transmitted to the robot controller for execution. $ T_{grasp}^{base} $, representing the transformation from the robot's grasping stance to the base coordinate system, was calculated using the following equation:
$ T_{eye}^{hand} $ could be determined using the traditional hand–eye calibration procedure. Robot forward kinematics yielded $ T_{hand}^{base} $. The conversion parameters $ T_{grasp}^{eye} $ related to the relationship between an image and a camera were derived using the intrinsic properties of the camera.
3.4.2. Network architecture of G-ResNet50
We leveraged an oriented anchor generator to obtain the preset bounding boxes to predict the grasp bounding box. Inspired by the Region Proposal Network (RPN) [43] and the prior study [29], we used K candidate-oriented bounding boxes with three scales and six angles for predicting shape adjustment at each anchor of the feature map. The three scales of the anchor box were obtained by K-means clustering on the annotation ground-truth bounding boxes. The angles $ \theta $ of the preset anchor box consisted of six empirical values, as depicted in Figure 8.
Then, the candidate anchor boxes were adjusted by the prediction network named G-ResNet50, which consisted of two primary components: a backbone feature extractor and a grasp pose predictor. As shown in Figure 9, ResNet50 was used as the feature extraction network, which comprised 16 convolutional residual blocks and exhibited robust capabilities for extracting features. The grasp prediction head consisted of a $3 \times 3$ convolutional layer and a $1 \times 1$ convolutional layer. The ResNet50 network was fed an RGB image with a resolution of $320 \times 320$ pixels, yielding a $10 \times 10 \times 2048$ feature map. A $10 \times 10 \times (7 \times {\text{k)}}$ three-dimension output could be obtained after the extracted feature map was fed into the grasp prediction head network. The preset anchor bounding box corresponding to the feature grid could be adjusted by the output of the G-ResNet50 network.
In this part, we exploited only ResNet50 as the backbone feature extraction network and design the own grasp prediction head network. Compared with the prior study [29], we simplified the structure of the feature extraction network while avoiding the need for multi-model prediction heads. Compared with another prior study [30], we adopted a more refined oriented anchor box generator, resulting in a clearer and more concise structure for G-ResNet50.
In the training stage, the preset anchor bounding boxes adjusted by the prediction needed to be categorized into positive and negative samples. The selection of positive samples should adhere to two principles to improve the prediction accuracy of the grasp bounding box: 1) The center points of the ground-truth box and predicted bounding box should be within the same feature grid cell. 2) The angle $ \theta $ between the ground-truth bounding box and the predicted bounding box cannot exceed ${{{{90}^ \circ }} / K}$. The former principle ensures similarity in position, whereas the latter principle maintains similarity in direction.
The five-dimensional vector $ ({x_a}, {y_a}, {w_a}, {h_a}, {\theta _a}) $ is used to depict the oriented anchor box, where $ ({x_a}, {y_a}) $ represents the center of the bounding box, $({w_a}, {h_a})$ represents the width and height of the bounding box, and ${\theta _a}$ indicates the angle of the bounding box with the X-axis. Similarly, $(x, y)$ and $(\hat x, \hat y)$ stand for the center of the predicted bounding box and the ground-truth bounding box respectively. The parameter $ ({t_x}, {t_y}, {t_w}, {t_h}, {t_\theta }) $ represents the difference between the actual and the predicted anchor boxes, whereas the parameter $ ({\hat t_x}, {\hat t_y}, {\hat t_w}, {\hat t_h}, {\hat t_\theta }) $ represents the difference between the actual and the labeled anchor boxes. Formula (8) was used to compute the disparity between the anticipated grasping anchor box and the directed anchor box.
3.4.3. Loss function of G-ResNet50
The categorization of training losses could be delineated into two separate types based on the arrangement of the output unit. The first component of the loss function pertained to the classification of the heatmap, whereas the second component involved the regression of the grasp parameters. Hence, the loss function of the grasping network consisted of the classification loss $ {L_{cls}} $ associated with the heatmap and the regression loss $ {L_{reg}} $ pertaining to the grasping box. The total loss function expression is shown in formula (9). A weight balance factor $ \lambda $ of 10 was used to achieve equilibrium between the two loss functions.
where N represents the quantity of the directed anchor box that corresponds to the anchor box of the actual label.
The graspability score was used to rank the unmatched preceding directed anchor box, and the top 3N boxes were chosen randomly to serve as negative samples. The cross-entropy loss was employed for categorizing graspable and ungraspable heatmaps. The classification loss $ {L_{cls}} $ of the heatmap was formally described as:
where $p_g^i$ is the confidence level of the accessibility score of the positive sample, and $p_u^i$ is the unattainable split confidence of negative samples.
The smoothL1 loss function is commonly employed in regression applications. The system maintains a uniform gradient in cases where the error surpasses the predetermined threshold while ensuring a dynamically adjusted gradient that is sufficiently small while the error is small. This study also used smoothL1 as the regression loss. The following equation defines the regression loss of the grasping box parameters:
where $ i \in Positive $, $ m \in \{ x, y, w, h, \theta \} $. The variable $ t_m^i $ represents the deviation of the network's prediction from the guided anchor box in the i-th sample. Further, ${t_m}$ and ${\hat t^{}}_m$ are the five parameter offset values representing the matching positive grasping anchor box, defined as in formula (8). The smoothL1 loss was calculated as follows:
4.
Experiments and results
4.1. Setup for grasping experiment
The computers were used to train and test the stacking object detection network R-YOLOv3 and the grasping position estimation network G-ResNet50. The computer system used for this study comprised Ubuntu 16.04 as the operating system, an Intel i7-7700K CPU processor, 64 GB of RAM, an NVDIA GTX TITAN XP 12G GPU, and the PyTorch 1.8 deep learning framework with NVDIA CUDA 10.2.
In this study, we employed the UR5 robot arm equipped with the gripper Robotiq-G85 to conduct a robotic grasping experiment. The repeat positioning accuracy of the robotic arm was ±0.03 mm, and its effective operating radius was 850 mm. The Robotiq-G85 gripper had a maximum clamping force of 220 N. The experiment used a D415 camera to acquire the RGB-D data, and the resulting stacked scenario had $416 \times 416$ picture pixels. Figure 10 depicts the experimental setup for the robot's grasping behavior.
We conducted three practical grasping experiments to enhance the credibility of our model design. 1) An experiment was conducted to recognize stacked objects. 2) An experiment was conducted to detect the stance for robotic grasping, using the Cornell grasping dataset as a basis. 3) A more complex experiment was conducted to evaluate multi-target grasping in real applications, specifically focusing on densely stacked objects.
4.2. Top-layer object detection in stacking scenarios
The object detection experiment in stacking scenarios involved using the R-YOLOv3 backbone network parameters. These parameters were initially pretrained on the voc2017 data and subsequently trained and tested on our self-built dataset, named the USTC Grasp-M dataset. The USTC Grasp-M dataset was randomly split into a test set and a training set in a ratio of 2:8. During training, the learning rate was initialized at 0.0001. The Adam optimizer was employed as the optimization algorithm, and a batch size of 8 was used. Following each round of data training, the learning rate was reduced by 10% until 60 training rounds were completed. We used average precision ($AP$) and picture processing speed (ms) as metrics to evaluate the model's performance so as to assess the impact of the proposed object recognition method for stacked objects.
where $Precision$ refers to precision and $Recall$ indicates the recall rate; $TP$ (true positives) represents the number of correctly predicted positive instances by the model; $FP$(false positives) is the number of labels that are actually negative but are judged to be positive by the model; and $FN$ (false negatives) is the number of labels that are actually positive but are incorrectly judged. The P–R curve was obtained by plotting the $ Recall $ value on the horizontal axis and the $Precision$ value on the vertical axis. $AP$ was calculated using formula (15), where $P$ is $Precision$ and $R$ is $Recall$.
The results of the experiments are presented in Table 2. The average accuracy ($AP$) of R-YOLOv3 exhibited a notable increase of 6.2% compared with that of the YOLOv3 model. A substantial improvement was observed in the precision and recall rates of R-YOLOv3. This was mainly because R-YOLOv3 added angle prediction information. Thus, R-YOLOv3 could better represent the bounding box of stack objects and filter out background information in the positioning box.
The experimental findings of item detection in an object stacked scenario are depicted in Figure 11. As shown in the figure, the stacking target detection model R-YOLOv3 suggested in this study could accurately detect and identify the position and category of objects on the uppermost layer of a stacking scenario and provide information support for the sequential robotic grasping decision.
We also conducted the ablation experiments on the top-level annotated and fully annotated datasets. As depicted in Table 3, the AP performance of R-YOLOv3 trained on the top-level annotated dataset was far superior to the AP performance of R-YOLOv3 trained on the fully annotated dataset.
4.3. Experiment on grasping pose estimation
In a previous study [20], the robotic grasp detection model was developed and tested using the Cornell grasping dataset. The dataset known as the Cornell grasping dataset comprised 1035 RGB-D images, each accompanied by corresponding depth information. These images encompassed a diverse range of 240 distinct items. Multiple photos of each object were captured in various orientations or attitudes. Every image was annotated with many positive and negative bounding boxes for grasping. The dataset that Cornell University provided was pre-divided into two subsets, with 80% of the data set aside for training and the remaining 20% set aside for testing. The training dataset comprised 708 photos, whereas the test dataset had 177 images.
In the experiments, the dataset was divided in two different ways. 1) Image-wise split: The photos were randomly divided into training and test datasets. This partitioning was intended to evaluate the capacity of the network model to generalize across various positions and orientations of identical objects. 2) Object-wise split: The photos depicting a particular object were grouped into a single set, ensuring that the two datasets did not overlap in terms of object representation. This methodology facilitated the evaluation of the network's ability to generalize to new objects.
The dataset had a limited number of images, which was inadequate for training a network that would yield satisfactory results. Data augmentation techniques were employed on the dataset to address this issue. A $320 \times 320$ area was obtained by center cropping the image. Then, 20–50 pixels were randomly selected in both the horizontal and vertical directions, and the colors were dithered while altering the brightness of the image in that area. The image subsequent to the aforementioned alteration was employed as the input for the grasp pose detection network.
In this study, the oriented bounding box stood in for the grasp stance. The rotation of the grab pose was just as crucial to a successful grasp as the position of the grasp stance. Therefore, the metric should consider not only the relative position but also the relative orientation between the ground truth and the prediction. Specifically, the Jaccard index needed to be higher than 25%, and the angle discrepancy between the prediction and the ground truth had to be less than 30 degrees. When the predicted grasping box satisfied the aforementioned two conditions, it was considered the correct grasping box. The Jaccard index was computed as follows:
where $ {g_p} $ is the grasping box that the network predicted and $ {g_t} $ is the real grasping box label.
Consistent with previous studies [28,41], we used the grasping prediction success rate (GPSR) metric to evaluate the performance of grasp pose detection. The GPSR metric served as a gauge for the effectiveness of the algorithm in generating proficient grasping poses from images. Table 4 presents the experimental findings, whereby the accuracy of two split approaches, namely image-wise split and object-wise split, was compared. This comparison was conducted assuming the matching Jaccard index threshold was set at 25%.
As indicated in the results presented in Table 4, the accuracy of the proposed method in this study was 96.6% for image-wise partitioning and 97.3% for object-wise partitioning, specifically for novel items. Compared with ResNet-50, the G-ResNet50 model proposed in our study directly regressed the angle, position, and size of the grasping box using the oriented anchor frame, resulting in an improvement of more than 0.6 and 1.2% in accuracy for image-wise and object-wise partitioning, respectively. Thus, the directed anchor box mechanism offered a more precise and efficient approach for grasp detection.
Each image of the Cornell grasping dataset had only one object. The experiment results presented in Table 4 compared the grasp detection network on the Cornell grasping dataset. The stacked detection network R-YOLOv3 was not used in this experimental scenario. Both our study and previous studies [29,30] used the ResNet-50 network backbone, however, the experimental outcomes exhibited variations. Our network model differed structurally from the models proposed in previous studies [29,30] in two notable aspects: 1) Our feature map had dimensions of $10 \times 10 \times 2048$, whereas the feature map mentioned in a previous study [29] had dimensions of $N \times 2048$ and the feature map mentioned in another previous study [30] had dimensions of $14 \times 14 \times 1024$. 2) Our method used convolutional layers as the final layers, whereas the method in a previous study [29] used fully connected layers as the final layers. In a previous study [30], ROI pooling and residual modules were concatenated after the feature map before applying fully connected layers as the final layer. The structural differences led to variations in feature extraction capabilities and receptive fields, resulting in distinct grasping prediction capabilities.
In a previous study [29], two ResNet-50 backbone networks were employed to extract the RGB features and depth features separately. We made significant progress toward implementing the approach described in a previous study [30], and our success rate in detecting grasping was nearly identical. We all used a ResNet-50 backbone network to extract multi-scale features, generating feature maps within the intermediate links. Our feature map had dimensions of $10 \times 10 \times 2048$, but the feature map mentioned in a previous study [30] had dimensions of $14 \times 14 \times 1024$. Furthermore, the grasping pose predictor we used was distinct. This affirmed the effectiveness of using the ResNet-50 backbone network for extracting multi-scale feature information from objects in RGB images. Additionally, it was crucial to develop a suitable grasping predictor compatible with the generated feature map.
Figure 12 displays the outcomes of the grasp pose detection for various items within the Cornell grasping dataset, using our G-ResNet50 network model. The first row of the image displays all grasp prediction boxes for which the network predicted output objects with a confidence value exceeding 0.5. The second row in the image displays the grasping boxes with the highest confidence score among the network's output for object grasping.
4.4. Grasp in a real-world environment
We opted to conduct tests in the context of stacked multi-object scenarios to assess the efficacy of our approach. As shown in Figure 10, a robotic grasping system comprised a UR5 robotic arm, a Robotiq-G85 gripper, and an Intel D415 depth stereo camera. The UR5 robot arm was equipped with a stationary camera. In this study, we employed the hand-eye open source code to calibrate the hands and eyes automatically, without needing any specialized gear.
In the experiments, we grasped all objects in the entire stacked scenario. The robot automatically detected the stacked objects and grasped them one by one in a top-to-bottom manner until all the objects in the scenario were grasped, using the proposed algorithm. The robotic grasping strategy in this experiment is shown in Algorithm 1.
After detecting the topmost object using R-YOLOv3, we obtained the position ${P_{top}}$ of the uppermost object. While detecting multiple topmost objects, we selected the parameters with the highest confidence. Subsequently, the pixel information from the ${P_{top}}$ region was input into G-ResNet50 to determine the grasping pose ${G_{top}}$. We calculated the Z-axis distance corresponding to the ${G_{top}}$ anchor box using aligned RGB images and depth information. ${Z_g}$ represents the average distance along the Z-axis of the four vertices of the ${G_{top}}$ bounding box. Finally, ${G_{top}}$ and ${Z_g}$ were transformed into parameters in the robot's workspace using the robot's hand–eye model. If the object underwent rotation solely around the Z-axis within the XOY plane, or if the working surface rotated around the Z-axis, the generated grasping anchor box by the grasping network autonomously adapted to the orientation. In cases where the table plane tilted significantly in relation to the XOY plane, exceeding an angle of 10°, it was advisable to realign the XOY plane to ensure its parallelism with the table plane.
The experimental approach entailed selecting a variable number of distinct entities, ranging from 2 to 8, and placing them on a flat surface. Subsequently, these entities were randomly stacked. The robot was then tasked with performing sequential grasping actions following the detected outcomes. Each time the target detection was correct and the grasping was completed, it was recorded as a successful experiment. Different kinds of objects were used to form stacked scenarios of two, three, four, five, six, seven, and eight objects, and the grasping experiment was carried out. Each set of experiments was repeated 40 times, resulting in 280 grasping experiments. We used the handling grasping success rate (HGSR) as our metric for grasping evaluation, following the assessment methodology used in previous studies [37,41]. A successful grasp was defined as the robot proficiently picking up the topmost object and accurately placing it in the designated position. A comprehensive set of 280 grasping experiments was conducted, wherein the robot successfully grasped 235 of them, resulting in an average HGSR of 83.93%. Table 5 depicts the robotic grasping results in real stacked multi-object scenarios.
The findings from the experiments conducted on multi-object stacking situations demonstrated that the algorithm proposed in this study effectively guided the robot in successfully detecting and sequentially grasping the stacked objects in the correct sequence. Figure 13 shows the process of the robotic grasping one by one in the stacking scenario. The experimental results demonstrated the effectiveness of our technique, demonstrating that the robotic system performed a high level of proficiency in completing the grasping task within the stacking scenario. This exemplified the efficacy and applicability of our approach.
Based on the statistics presented in Table 5, the robot achieved a maximum of 38 successful grasps when dealing with a scenario involving the stacking of 2 objects, resulting in a success rate of 95.0%. The success rate of robotic grasping rapidly diminished with the increase in the number and variety of stacked objects in the environment. In a given scenario with 8 kinds of objects stacked, the robot successfully grasped 29 objects, yielding a grasping success rate of 72.5%. Through data analysis and observation of the experimental process of grasping failures, we identified two primary factors contributing to the decline in the success rate of robotic grasping with the increase in the number of stacked objects: 1) The robot's capacity to perceive stacked objects diminished with the increase in the number of stacked objects, leading to a decline in its grasping capability. 2) The frequency of erroneous touches by the robot during grasping also increased with the increase in the number of stacked objects, significantly impeding the robot's ability to successfully grasp the objects. We defined "erroneous touches" as the unnecessary contact between the gripper and the target object or unintended contact with nontarget objects during the robot's execution of grasping tasks. Erroneous touches resulted in changes to the target pose or instability in the gripper's grasp.
Subsequently, we analyzed the occurrences and repercussions of erroneous touches during the robot's gripping process. When performing a grasping motion, the camera calculated the depth information along the Z-axis to determine the distance between the gripper and the target. The robot had a depth perception inaccuracy of ±1.5 mm along the Z-axis. Once the grasp pose anchor box for the top object was generated, the gripper's fingertips might inadvertently come into contact with these objects if additional objects were located beneath the anchor box. Such accidental contact could prevent the robot from achieving a successful grip. The inadvertent contact that occurred during robotic grasping was random, but it was influenced by the spatial relationship between the grasping anchor box of the target object and the stacking object, as depicted in Figure 14. All three grasping anchor boxes shown in Figure 14(a) could be accomplished accurately. Both anchor boxes 1 and 2 could be completed accurately (Figure 14(b)). Nevertheless, when anchor box 3 was activated (Figure 14(b)), the fingertips of the robot gripper might unintentionally come into contact with the brush positioned beneath the wooden stick, potentially resulting in a failure to grab. Anchor boxes 3 and 4 could be executed successfully (Figure 14(c)), but grasping pose anchor boxes 1 and 2 were affected (Figure 14(c)), making gripping difficult. Comparison among Figure 14(c), (d), and (e) revealed that, with the increase in the number of stacked objects, the grasping pose anchor boxes with more objects were affected when executed. Consequently, the robot's ability to grab the number of stacked objects decreased with the increase in the number of stacked objects.
Undoubtedly, enhancing the stacked object detection algorithm significantly enhanced the robot's ability to grasp objects in complex stacking scenarios. Furthermore, using 3D grasping techniques could improve the robot's ability to grab objects. The 3D grasping posture was estimated based on detecting the position and relative relationship of stacked objects in space. Also, all grasping poses that coincided with the occlusion point were prevented from being activated, thus efficiently avoiding unintentional contact between the robot and other objects during grasping. Additionally, employing a highly accurate stereo vision camera may enable exact regulation of the distance between the gripper's fingertips along the Z-axis, thereby minimizing the risk of inadvertent contact. These approaches can address the issue of the reduced capacity of the robot to grab stacked objects with the increase in their number. We plan to use these methodologies in our forthcoming study.
5.
Conclusions
In this study, we presented a novel approach for detecting grasping tasks in stacking scenarios, specifically designed for sequential robotic grasping. The proposed method involved a two-stage process, enabling the robot to identify the topmost object in stacking scenarios using R-YOLOv3 and estimate its optimal grasping pose one by one using G-ResNet50. We conducted comparative experiments for both the Cornell grasping dataset and real-world environments to showcase the efficacy of our model, exhibiting superior accuracy and generalization capabilities. The challenge of robotic grasping in a stacked environment could be addressed using a two-stage process involving stacked object detection and grasp detection.
Furthermore, we faced new challenges during the experiments in this study. The accuracy of detecting stacked objects reduced with the increase in the number of stacked objects, whereas the accuracy of robotic grasping decreased more significantly. We analyzed the causes behind this phenomenon and identified the consequences of the robot's inadvertent contact when the activated grasping anchor box aligned with the occlusion point. Therefore, addressing the challenge of robotic grasping requires addressing not only perceptual issues related to GPSR but also considering the physical interactions during the robot's gripping process. This includes managing potential instances of erroneous touches during grasping. Accurately detecting the grasping poses of stacked objects, effectively avoiding inadvertent contacts by the gripper, and simultaneously controlling appropriate gripping force to prevent slippage are all crucial factors in improving the success rate of robotic grasping in stacking scenarios. Resolving these issues may involve integrating advanced 3D grasping technology and improved stacked object detection methodologies in our forthcoming research to enhance the capability of robots in performing complex grasping tasks in stacking scenes more dexterously.
Use of AI tools declaration
The authors declare that artificial intelligence (AI) tools were not used in the design of this study.
Acknowledgments
This study received financial support from the Sichuan Provincial Natural Science Youth Fund Project (Grant Number: 2023NSFSC1442) and the 2023 Sichuan Provincial Key Laboratory of Artificial Intelligence Open Fund Project (Grant Number: 2023RYY05).
Conflicts of interest
The authors declare no conflicts of interest.










 DownLoad:
DownLoad: