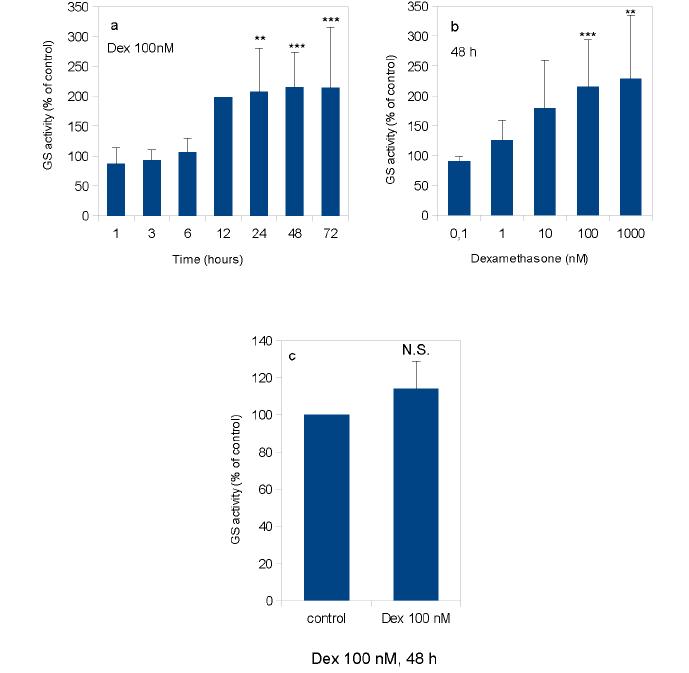
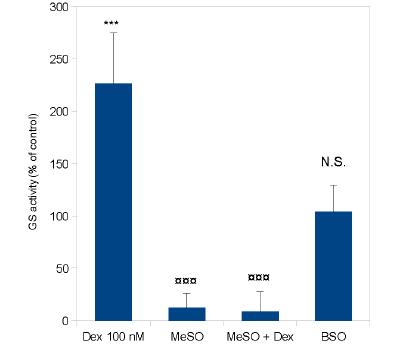
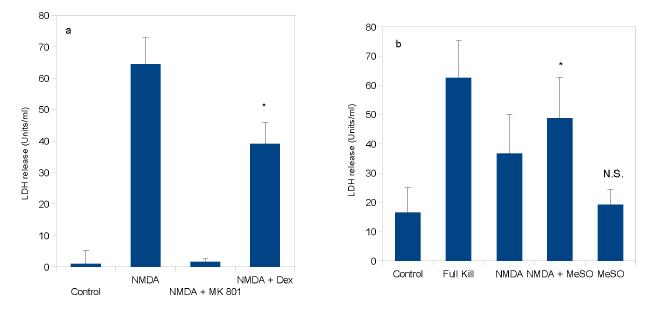
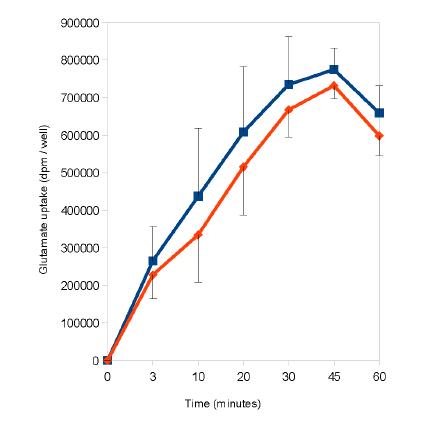
Astrocytes are claimed to protect neurons against excitotoxicity by clearing glutamate from the extracellular space and rapidly converting it into glutamine. Glutamine, is then released into the extracellular medium, taken up by neurons and transformed back into glutamate which is then stored into synaptic vesicles. Glutamine synthetase (GS), the key enzyme that governs this glutamate/glutamine cycle, is known to be upregulated by glucocorticoids. In the present work we have thus studied in parallel the effects of dexamethasone on glutamine synthetase activity and NMDA-induced neuronal death in cultures derived from the brain cortex of murine embryos. We showed that dexamethasone was able to markedly enhance GS activity in cultures of astrocytes but not in near pure neuronal cultures. The pharmacological characteristics of the dexamethasone action strongly suggest that it corresponds to a typical receptor-mediated effect. We also observed that long lasting incubation (72 h) of mixed astrocyte-neuron cultures in the presence of 100 nM dexamethasone significantly reduced the toxicity of NMDA treatment. Furthermore we demonstrated that methionine sulfoximine, a selective inhibitor of GS, abolished the dexamethasone-induced increase in GS activity and also markedly potentiated NMDA toxicity. Altogether these results suggest that dexamethasone may promote neuroprotection through a stimulation of astrocyte glutamine synthetase.
1.
Introduction
Lotka and Volterra introduced a system of differential equations known as the Lotka-Volterra equations, which have served as a foundation for studying predator-prey dynamics in ecology [1,2,3]. Intraguild predation, an ecological phenomenon where competition and predation coexist in the food web, has garnered significant attention for its profound influence on populations, impacting their abundance, distribution, and even evolution [4,5,6]. In a seminal paper, Polis et al. [7] initially introduced a concept involving a two-species predator system, where one species consumes the other while they compete for shared resources. Subsequent scholars have made substantial advancements in this area [8]. For instance, Hart [9] focused on marine ecosystems, investigating top-down and bottom-up characteristics in model food webs to explain outcomes observed in trophic cascade experiments in lakes. Moeller et al.[10] proposed a mathematical model demonstrating how two plankton species, acting as mixotrophs, can coexist through resource competition. Safuan et al. [11] developed an intraguild predation model where resources are shared among predators and prey, introducing a carrying capacity proportional to biological resources. Resource availability, impacted by both predators and prey, plays a crucial role in system behavior [12,13,14]. Abundant and high-quality resources lead to stability, while scarce or degraded resources result in chaotic dynamics, limit cycles, or even chaos [15,16].
External factors such as harvesting also influence this ecological interaction [17,18]. Harvesting's impact on resource and fishery management is significant both economically and ecologically [19,20]. Chaudhuri [21] examined harvesting in the context of two competing species, providing a detailed analysis of equilibrium solutions. Das et al. [22] explored bioeconomic fish extraction in predator-prey fishery models, while Ang and Safuan [23] considered independent harvesting strategies for predators and prey with their own economic values. To address limitations of the unit harvest concept, Clark introduced Michaelis-Menten-type harvesting [24]. Research on the combination of this harvesting type in ecological models has revealed various bifurcation behaviors [25,26,27]. Sharif and Mohd [28] conducted a comprehensive analysis of harvesting and enrichment effects on intraguild predator fishery ecosystems, highlighting diverse dynamic behaviors.
In predator-prey systems, factors like food digestion, gestation, disease transmission, capture, and defense involve time delays [29,30,31]. Time delay differential equations exhibit intricate dynamics, especially when delays exceed a critical threshold, leading to Hopf bifurcation and oscillations in population sizes [32,33]. For example, Li et al. [34] investigated spatial memory and Allee effects in prey-predator systems with time delays. Other researchers have explored various delays and analyzed local stability, Hopf bifurcation, and stability paths using methods like the center manifold and paradigm theory [35,36,37].
To our knowledge, prior research has not explored a double-delayed predator-prey model with a Michaelis-Menten-type harvesting. This article specifically focuses on gestation delays in prey and predator populations. In Section 2, we establish the model's framework. Section 3 examines equilibrium points and their local stability under varying time delays, including Hopf bifurcation analysis. Section 4 investigates conditions affecting bifurcation direction and stability factors crucial to Hopf bifurcation. In Section 5, we employ numerical simulations to explore the system's complex behavior. Finally, we summarize key findings, draw conclusions, and discuss the significance of our analytical results to conclude the paper in Section 6.
2.
Model description and equilibrium
Ang and Safuan in [27] presented an intricate ecological model that comprehensively captures the complex interplay among different species and their respective habitats:
This model not only elucidates the dynamics of predator and prey but also incorporates the dimension of human predation on the predator species, where $ X(t) $ and $ Y(t) $ denote the populations of a prey species and predator species over time, respectively. $ r_1 $ and $ r_2 $ represent the intrinsic growth rates of the prey, denoted as $ X $, and the predator, denoted as $ Y $, respectively. In this context, $ Z $ is used to signify a shared resource accessible to both prey and predator populations, with growth rates of $ m $ and $ n, $ respectively ($ 0 < m < 1 $, $ 0 < n < 1 $), satisfying the constraint $ m + n = 1 $. The parameter $ g $ characterizes the growth rate of biotic resources, and $ u $ and $ v $ represent the consumption rates of resources by prey and predator species, respectively. Furthermore, parameters $ a $ and $ b $ quantify the strength or intensity of the interaction between the prey and predator species. The catchability coefficient of predator fish is denoted as $ c $, while $ E $ represents the harvesting effort applied to predator fish, with $ d_1 $ and $ d_2 $ as positive constants.
The primary focus of this work centered on exploring the long-term behavior of the system, utilizing the harvest of predator fish as a bifurcation parameter and examining the associated economic implications using Pontryagin's maximum principle. The bistable behavior within the system was leveraged to derive the optimal threshold for predator harvest, aiming to strike a balance between maintaining fishery resources and maximizing economic profit. In this study, our objective was to delve into an unexplored aspect of system dynamics, with a particular emphasis on the impact of time delays. We have thoroughly investigated the predator-prey model within an intraguild setting, incorporating the Michaelis-Menten harvest style and introducing two significant time delays. A key highlight of our research lied in our careful consideration of the gestation time delays for both predator and prey. This approach represents a promising avenue for gaining deeper insights into ecological relationships and mechanisms that yields the following model:
Here, the constants $ T_1 $ and $ T_2 $ account for the gestation time delays of $ X $ and $ Y $, respectively. $ T_1 (T_2) $ represents the gestation delay in the presence of the prey (predator), i.e., after consuming the shared resource, the prey $ X $ (the predator $ Y $) takes some time to convert the shared resource $ Z $ into prey (predator) biomass [38]. Now, let's introduce dimensionless variables: $ x = anX/mr_2 $, $ y = aY/r_2 $, $ z = anZ/r_2 $, and $ t = r_2T $ so we obtain the following dimensionless system:
where the dimensionless parameters are $ \alpha = r_1/r_2 $, $ \beta = bm/an $, $ \delta = acE/d_2r_2 ^2 $, $ \rho = g/r_2 $, $ \varepsilon = mu/an $ and $ \mu = v/a $. To ensure that the system is biologically feasible, it is assumed that all the parameters are positive. By the biological senses, the initial conditions are chosen as
where $ \tau = \max\{\tau_1, \tau_2\}, (\phi_1(\theta), \phi_2(\theta), \phi_3(\theta)\in C([-\tau, 0], R^3_+) $ is a continuous vector function in the Banach space mapping $ [-\tau, 0]\rightarrow R^3_+ $ and $ R^3_+ = \{(x_1, x_2, x_3) : x_i\geq0, i = 1, 2, 3\} $.
Notice that in the absence of delays, i.e., $ \tau_1 = \tau_2 = 0 $, model (2.3) is reduced to the one considered by Sharif and Mohd in [28]. Since the presence of delays does not affect the number and existence of equilibria, we can have the following lemma (see [28] for details).
Lemma 2.1. For model (2.3) with $ \tau_1 = 0 $ and $ \tau_2 = 0 $, the following statements are true.
(a) If $ \mu\sigma+\rho-\delta\mu > 0 $, there is a prey-free equilibrium $ E_1 = \left(0, \frac{\rho}{\mu}, \frac{\rho(\mu\sigma+\rho)}{\mu(\rho+\mu\sigma-\delta\mu)}\right) $, which is locally stable provided $ \rho-\alpha\mu > 0 $ and $ (\rho+\mu\sigma)^2-\delta\mu^2\sigma-2\delta\mu\rho > 0 $ hold.
(b) There is always a predator-free equilibrium $ E_2 = \left(\frac{\rho}{\varepsilon}, 0, \frac{\rho}{\varepsilon}\right) $, which is locally stable provided $ \delta\varepsilon-\beta\rho\sigma-\varepsilon\sigma > 0 $ holds.
(c) Coexistence equilibrium $ E^* $ is given by the expression: $ E^* $$ = \left(\frac{\rho-\mu\hat{y}}{\varepsilon}, \hat{y}, \frac{\alpha(\mu\hat{y}-\rho)}{\varepsilon(\hat{y}-\alpha)}\right) $, where $ \hat{y} $ is the positive solution to the cubic equation $ A{\hat{y}}^3+B\hat{y}^2+C\hat{y}+D = 0 $, satisfying $ \rho-\mu\hat{y} > 0 $ and $ \alpha-\hat{y} > 0 $. Here,
It has been revealed in [28] that in the absence of delay, model (2.3) can have up to three possible equilibria and exhibit complex dynamics, including tri- or bistability phenomena and multi-type bifurcations. In this paper, we will turn our main attention to the investigation of the effects of delay on the dynamics of model (2.3).
3.
Local stability and Hopf bifurcation
In this section, we will explore the local stability of the equilibrium point/s of model (2.3), as well as investigate whether or not a Hopf bifurcation can occur at any arbitrary equilibrium point where coexistence is achieved. By linearizing model (2.3), we can derive the characteristic equation at the equilibrium point $ E_* (x_*, y_*, z_*) $. This equation determines the behavior of the system near the equilibrium point and provides insight into the stability properties of the system. The representation of the characteristic equation can be stated as follows:
According to (3.1), we first study the local stability of the prey-free equilibrium $ E_1 $ and the predator-free equilibrium $ E_2 $.
Theorem 3.1. Consider system (2.3) for any $ \tau_1 > 0 $ and $ \tau_2 > 0 $. We have
(i) If there exists a prey-free equilibrium $ E_1 $ (i.e., $ \mu\sigma+\rho-\delta\mu > 0 $), the prey-free equilibrium $ E_1 = \left(0, \frac{\rho}{\mu}, \frac{\rho(\mu\sigma+\rho)}{\mu(\rho+\mu\sigma-\delta\mu)}\right) $ is stable when $ \rho-\alpha\mu > 0 $ and $ 0 < \tau_1 < \tau_{2_0} $. Otherwise, it is unstable.
(ii) If $ \varepsilon\delta-\varepsilon\sigma-\beta\rho\sigma > 0 $ and $ 0 < \tau_1 < \tau_{1_0} $, the predator-free equilibrium $ E_2 = \left(\frac{\rho}{\varepsilon}, 0, \frac{\rho}{\varepsilon}\right) $ is stable. Otherwise, it is unstable.
Proof. (ⅰ) If the feasible criterion of $ \mu\sigma+\rho-\delta\mu > 0 $ is met, equilibrium $ E_1 $ always exists. The characteristic equation (3.1) at $ E_1 $ is of the form
Obviously, $ \alpha-\frac{\rho}{\mu} $ is one root of Eq (3.2). Let $ \mathfrak{G}(\lambda): = \lambda^2-\frac{\rho\delta\mu}{(\mu\sigma+\rho)^2}\lambda-\frac{\mu\sigma+\rho-\delta\mu} {\mu\sigma+\rho}(\lambda-\rho)e^{-\lambda\tau_2} $ and assume that $ \lambda = i\omega (\omega > 0) $ is a root of $ \mathfrak{G}(\lambda) = 0 $. Then it follows that
which leads to
Notice that when $ -\frac{(\mu\sigma+\rho-\delta\mu)^2\rho^2}{(\mu\sigma+\rho)^2} < 0 $, Equation (3.4) has a unique positive root $ \omega_0^2 = \frac{1}{2}\left[\left(\frac{\mu\sigma+\rho-\delta\mu} {\mu\sigma+\rho}\right)^2-\frac{\rho^2\delta^2\mu^2}{(\mu\sigma+\rho)^4}+\sqrt{\Delta_1}\right] $, where $ \Delta_1 = \left[\left(\frac{\mu\sigma+\rho-\delta\mu} {\mu\sigma+\rho}\right)^2-\frac{\rho^2\delta^2\mu^2}{(\mu\sigma+\rho)^4}\right]^2+\frac{4(\mu\sigma+\rho-\delta\mu)^2 \rho^2}{(\mu\sigma+\rho)^2} $. Substituting $ \omega_0^2 $ into Eqs (3.3), we obtain
Substituting $ \lambda(\tau_2) $ into the left-hand side of $ \mathfrak{G} = 0 $ and taking the derivative with respect to $ \tau_2 $, we have
which leads to
This suggests that the root crosses the imaginary axis from left to right at $ \tau_2 = \tau_{2_0} $, indicating that $ E_1 $ becomes unstable.
(ⅱ) The characteristic equation of system (2.3) at $ E_2 $ is
Obviously, $ \frac{\varepsilon\sigma+\beta\rho\sigma-\varepsilon\delta}{\varepsilon\sigma} $ is a characteristic root of Eq (3.7), which is positive if $ \varepsilon\sigma+\beta\rho\sigma-\varepsilon\delta > 0 $, indicating that $ E_2 $ is unstable. If $ \varepsilon\sigma+\beta\rho\sigma-\varepsilon\delta < 0 $, we only need to consider $ \mathfrak{T}(\lambda): = \lambda^2+(\alpha\lambda+\rho\alpha)e^{-\lambda\tau_1} = 0 $. Assume that $ \lambda = i\xi(\xi > 0) $ is a root of $ \mathfrak{T}(\lambda) = 0 $. Then we have
which leads to
Because $ -\alpha^2\rho^2 < 0 $, Equation (3.9) has a unique positive root $ \xi_0^2 = \frac{\alpha^2+\sqrt{\Delta_2}}{2}, \Delta_2 = \alpha^4+4\alpha^2\rho^2 $. Substituting $ \xi_0^2 $ into Eq (3.8), we obtain
Moreover, we can compute from $ \mathfrak{T}(\lambda) = 0 $ that
which leads to
This suggests that the root crosses the imaginary axis from left to right at $ \tau_1 = \tau_{1_0} $, indicating that $ E_2 $ becomes unstable. □
Next, let us delve into the local stability of $ E^* $$ (x^*, y^*, z^*) $ and explore the possible Hopf bifurcations at $ E^* $. $ E^* $ satisfies the equation
To simplify the analysis, let $ \bar{x}(t) = x(t)-x^*, \bar{y}(t) = y(t)-y^*, \bar{z}(t) = z(t)-z^* $, and still denote $ x(t), y(t), z(t) $, respectively. The linearized part of the system (2.3) at $ E^* $$ (x^*, y^*, z^*) $ is
Therefore, the corresponding characteristic equation of system (3.10) is given by:
where
In the following, we apply the method used in Ruan and Wei [39] to investigate the distribution of roots of the transcendental equation (3.14). As system (2.3) has two time delays, $ \tau_1 $ and $ \tau_2 $, we consider the following four cases.
Case 1: $ \tau_1 = \tau_2 = 0 $.
The characteristic equation (3.14) becomes:
where
By Routh-Hurwitz criterion, we can conclude that all of the roots of Eq (3.15) have negative real parts if and only if
$ \textbf{(H1)} $ $ m_{12} > 0, m_{10} > 0, \ m_{11}m_{12} > m_{10} $
are satisfied. Namely, when $ \tau_1 = \tau_2 = 0 $, the coexistence equilibrium $ E^* $ is locally asymptotically stable provided $ \textbf{(H1)} $ is satisfied.
Case 2: $ \tau_1 > 0, \ \tau_2 = 0 $.
The characteristic equation (3.14) becomes:
where
Assume that $ \lambda = i\omega_1 (\omega_1 > 0) $ is a root of Eq (3.16). By separating the real part and imaginary part, we obtain
which yields
where
Let $ \omega_1^2 = x $. Then Eq (3.18) becomes
We need only study the existence and number of positive roots for Eq (3.19). We can compute that
If $ \triangle = e_{22}^2-3e_{21}\leq0 $, we have $ \frac{ \rm{d}h(x)}{ \rm{d}x}\geq 0 $, and thus $ h(x) $ monotonically increases for $ x\in[0, +\infty) $. If $ \triangle > 0 $, Equation (3.20) has two different real roots:
Obviously, $ x_2^* < x_1^* $, and $ x_2^* $ and $ x_1^* $ are respectively the local maximum point and local minimum point. Notice the geometric characteristics of the cubic polynomial equation and also that $ h(0) = e_{20} $ and $ \lim\limits_{x\rightarrow +\infty}h(x) = + \infty $. We can make clear the number and existence of positive roots of Eq (3.19). The detailed analyses are provided in Appendix A. Without loss of generality, we assume the conditions in (H2) hold, that is,
(H2) $ e_{20} < 0 $, $ \Delta > 0 $ and $ x_2^* > 0 $; $ h(x_2^*) > 0 $ and $ h(x_1^*) < 0 $.
In this situation, Equation (3.18) has three positive roots denoted respectively by $ \omega_{1, i}, i = 1, 2, 3\ (\omega_{1, 1} < \omega_{1, 2} < \omega_{1, 3}) $. It then follows from Eq (3.17) that
from which we obtain that
for $ \kappa = 0, 1, 2, \cdots; i = 1, 2, 3 $.
Now we verify that the transversality condition holds. Differentiating both sides of Eq (3.16) with respect to $ \tau_1 $, we can obtain
Through some sophisticated calculations, we get
Lemma 3.2. Assume the conditions in (H2) hold. Then
Proof. 1) Based on (H2), we have $ h(0) = e_{20} < 0 $, $ h(x_2^*) > 0 $, and $ h'(x) > 0 \in [0, x_2^*] $. By the zero existence theorem, we know that there exists a unique $ \omega_{1, 1}^2\in (0, x^*_2) $, and, in addition, we have $ h'(\omega_{1, 1}^2) > 0 $.
2) From (H2), we may obtain $ h(x_2^*) > 0, h(x_1^*) < 0 $, and $ h'(x) < 0 \in [x_2^*, x_1^*] $. By the zero existence theorem, we know that there exists a unique $ \omega_{1, 2}^2\in (x_2^*, x_1^*) $, so $ h'(\omega_{1, 2}^2) < 0 $ is verified.
3) Finally, verify the symbol at $ h'(\omega_{1, 3}^2) $. By the zero existence theorem, $ h(x_1^*) < 0, \lim\limits_{x\rightarrow +\infty}h(x) = + \infty $, and $ h'(x) > 0 \in [x_2^*, +\infty) $, so we know that there exists a unique $ \omega_{1, 3}^2\in (x_2^*, +\infty) $, and in addition we have $ h'(\omega_{1, 3}^2) > 0 $. □
For the case when the characteristic equation (3.16) has three pairs of conjugate complex roots, the process of analyzing stability and switching phenomena can be relatively complex. As the time delay $ \tau_1 $ increases gradually and passes through the critical values of $ \tau_{1, 1}^{(\kappa)} $ and $ \tau_{1, 3}^{(\kappa)} $, the system may undergo a transition from stable to unstable, and as the time delay $ \tau_1 $ passes through the critical values of $ \tau_{1, 2}^{(\kappa)} $, the system may be switched from unstable back to stable. Thus, stability switch phenomena may occur and the specific situations of stabilizing switches depend on the relative positions of these critical time-delay values.
For the sake of narrative convenience, we reorder all the critical values $ \{\tau_{1, i}^{(\kappa)}\} $, $ i = 1, 2, 3; \kappa = 0, 1, 2, \cdots $ as $ \{\tau_{1}^{(\kappa)}\} $, $ \kappa = 0, 1, 2, \cdots $ such that $ 0 < \tau_1^{(0)} < \tau_1^{(1)} < \tau_1^{(2)} < \cdots $, and assume that the system undergoes a stability switch from stable to unstable and then from unstable to stable, and after finite times like this, the system becomes unstable eventually. We summarize these as the following theorem.
Theorem 3.3. For system (2.3) with $ \tau_1 > 0 $ and $ \tau_2 = 0 $, if (H1) and (H2) hold, then there exists a $ M \in \mathbb{N} $ such that when $ \tau_1\in(0, \tau_{1}^{(0)}) $ $ \bigcup(\tau_{1}^{(1)}, \tau_{1}^{(2)})\bigcup\cdots\bigcup $ $ (\tau_{1}^{(M-1)}, \tau_{1}^{(M)}) $, all the roots of Eq (3.16) have negative real part, and thus the system of (2.3) is locally asympotically stable; when $ \tau_1\in (\tau_{1}^{(0)}, \tau_{1}^{(1)})\bigcup $ $ (\tau_{1}^{(2)}, \tau_{1}^{(3)})\bigcup\cdots\bigcup(\tau_{1}^{(M)}, +\infty) $, at least one root of Eq (3.16) has a positive real part, and thus the system of (2.3) is unstable. In addition, the model undergoes a Hopf bifurcation at $ E^* $ when $ \tau_1 = \tau_{1}^{(\kappa)}, \kappa \in \mathbb{N}. $
Case 3: $ \tau_2 > 0, \tau_1 = 0 $.
Analyzing similarly as in Case 2, we have the following theorem.
Theorem 3.4. For system (2.3) with $ \tau_2 > 0 $ and $ \tau_1 = 0 $, the equilibrium $ E^* $ may undergo a finite number of stability switches, that is there is a $ N\in \mathbb{N} $ such that it is locally asymptotically stable for $ \tau_2\in(0, \tau_{2}^{(0)})\bigcup(\tau_{2}^{(1)}, \tau_{1}^{(2)})\bigcup\cdots\bigcup (\tau_{2}^{(N-1)}, \tau_{2}^{(N)}) $; and when $ \tau_2\in (\tau_{2}^{(0)}, \tau_{2}^{(1)})\bigcup (\tau_{2}^{(2)}, \tau_{2}^{(3)})\bigcup\cdots\bigcup(\tau_{2}^{(N)}, +\infty) $, the equilibrium point $ E^* $ is unstable. Additionally, model (2.3) undergoes a Hopf bifurcation at $ E^* $ for each $ \tau_2 = \tau_{2}^{(\kappa)}, \kappa\in \mathbb{N} $.
Case 4: $ \tau_1 > 0, \tau_2 > 0 $.
In this case, we choose $ \tau_1 $ as the bifurcation parameter and $ \tau_2 $ in one of its stable intervals, say $ (0, \tau_2^{(0)}) $ (the same below). Assume that $ \lambda = i\omega_{1}^*(\omega_{1}^* > 0) $ is a characteristic root of Eq (3.14), then we can obtain
where
Then, adding the squares of the above two equations, we obtain
where
It is difficult to discuss the roots of Eq (3.27). To get the main conclusion, we assume that Eq (3.27) has a finite number of positive real roots $ \omega_{1, i}^{*}(i = 1, 2, \cdots, h) $ and that for each $ \omega_{1, i}^{*} $, there is a series of $ \{\tau_{1, i}^{(\zeta)}| i = 1, 2, \cdots, h; \zeta = 0, 1, 2, \cdots\} $ satisfying Eq (3.27), where
Let $ \tau_{10}^{*}(\tau_2) = \min\{\tau_{1, i}^{(\zeta)}(\tau_2)|\; i = 1, 2, \cdots, h; \zeta = 0, 1, 2, \cdots\} $. When $ \tau_1 = \tau_{10}^{*}(\tau_2) $, Equation (3.28) has a pair of purely imaginary roots $ i\omega_{10}^{*} $ for $ \tau_2 $ in its stable intervals. Of course, we should verify the transversality condition. Taking the derivative on both sides of Eq (3.14) with respect to $ \tau_1 $ and substituting $ \lambda = i\omega_{10}^{*} $, we get
where
We make the following hypothesis:
$ \textbf{(H3)} $ $ sign{\left\{{\left[\frac{\rm{d}(\Re\lambda)}{(\rm{d}\tau_1)}\right]}^{-1}\right\}_{\lambda = i\omega_{10}^{*}} = R_1R_2+M_1M_2\neq0} $.
Using the same logic as above, model (2.3) can exhibit the phenomenon of stability switches. For convenience, here we assume that once $ E^* $ loses its stability, it will be unstable forever. Then we will see the following results.
Theorem 3.5. For model (2.3) with $ \tau_1 > 0 $ and $ \tau_2 $ in its stable intervals, if (H1) and (H3) hold, then the equilibrium $ E^* $ is asymptotically stable when $ \tau_1\in(0, \tau^*_{10}(\tau_2)) $ and unstable for $ \tau_1\in(\tau^*_{10}(\tau_2), +\infty) $. Moreover, model (2.3) undergoes a Hopf bifurcation at the equilibrium $ E^* $ for each $ \tau_1 = \tau_{10}^*(\tau_2) $.
4.
Direction and stability of the Hopf bifurcation
In this section, we shall discuss the direction and stability of the Hopf bifurcation periodic solution of system (2.3) with respect to $ \tau_1 $ and $ \tau_2\in[0, \tau_2^{(0)}) $. Using the normal method of Hassard [40] and the center manifold theory, for $ \tau_2\in[0, \tau_2^{(0)}) $, we derive explicit formulas to determine the properties of the Hopf bifurcation at the critical value $ \tau_1 = \tau_{10}^* $. For the readability of the article, we defer the detailed derivation to Appendix B.
Using Hassard's method [40], we can calculate $ g_{21} $ and compute the following values determining the qualitative behavior of the bifurcating periodic solutions at $ \tau = \tau_{10}^* $:
where $ \mu_2 $ determines the direction of the Hopf bifurcation: if $ \mu_2 > 0 $ $ (\mu_2 < 0) $, then the Hopf bifurcation is supercritical (subcritical). The stability of the bifurcating periodic solutions is determined by the sign of $ \beta_2 $: if $ \beta_2 < 0 $ $ (\beta_2 > 0) $, the bifurcating periodic solutions are stable (unstable). The period of the bifurcating periodic solutions is determined by the sign of $ T_2 $: if $ T_2 > 0 $ $ (T_2 < 0) $, the bifurcating periodic solutions increase (decrease).
5.
Numerical examples and simulations
Based on the results of the stability analysis and bifurcation discussed in Sections 2 and 3, we will conduct numerical simulations to examine the impact of time delays on the stability and periodic solutions of system (2.3). These simulations will allow us to observe the effect of delay on the behavior of the system and the effect of changes in harvest rate on latency. By studying these aspects, we can better understand the dynamics of the system in different situations [41,42].
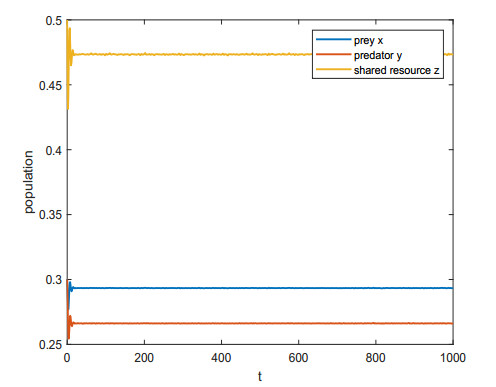
Let the parameters of system (2.3) be $ \alpha = 0.7 $, $ \beta = 0.08 $, $ \delta = 0.215 $, $ \sigma = 0.2 $, $ \rho = 1.165 $, $ \varepsilon = 0.75 $, and $ \mu = 3.55 $. (If more data details are required, please refer to [27]), then we can get the following prey-free equilibrium $ E_1 = (0, 0.32817, 0.55347) $, predator-free equilibrium $ E_2 = (1.6643, 0, 1.6643) $ and the coexistence equilibrium $ E^* $$ = (0.293, 0.2704, 0.4774) $. By Theorem 3.1, because $ \alpha-\frac{\rho}{\mu}\approx0.3718 > 0 $, and $ \varepsilon\sigma+\beta\rho\sigma-\varepsilon\delta\approx0.0074 > 0 $, we know prey-free $ E_1 $ and predator-free $ E_2 $ are unstable. For $ \tau_1 = 0, \tau_2 = 0 $, under the above parameters, we can check that the conditions in (H1) are satisfied, and therefore the coexistence equilibrium $ E^* $ of system (2.3) is asymptotically stable (see Figure 1).
When the time delay $ \tau_1 $ is within the range $ [0, \tau_{1}^{(0)}) $, the coexistence equilibrium $ E^* $ is still asymptotically stable (see Figure 2). However, once $ \tau_1 $ surpasses the critical value $ \tau_{1}^{(0)} = 2.7415 $ (at this point $ \omega_{1, 1} = 0.5618 $), the coexistence equilibrium $ E^* $ becomes unstable, leading to a Hopf bifurcation. This bifurcation results in the emergence of a family of periodic solutions originating from the coexistence equilibrium $ E^* $. In summary, the stability of $ E^* $ changes at $ \tau_{1}^{(0)} $, and this change triggers the appearance of periodic solutions (see Figure 3).
Similarly, we have $ \omega_{1, 2} = 0.8895, \tau_{2}^{(0)} = 0.5856 $, and the corresponding figures are Figures 4 and 5.
For $ \tau_1 > 0, \tau_2 = 0.2\in(0, \tau_{2}^{(0)}) $, we have $ \omega_{10}^* = 0.1269, \tau_{10}^* = 0.2885 $. According to Theorem 3.5, $ E^* $ is asymptotically stable when $ \tau_1\in [0, 0.2885) $ (see Figure 6) and unstable when $ \tau_1 > \tau_{10}^* $. After the computation of formula (4.1), we can obtain $ c_1(0) = -0.2225+1.3699i $, $ \beta_2 = -0.4449 < 0 $, $ \mu_2 = 3.2038 > 0 $, and $ T_2 = -0.5009 < 0 $. The Hopf bifurcation is characterized as a supercritical bifurcation, where the periodic solutions are stable. This can be visually represented in Figure 7.
For an intraguild predator-prey fishery model, a stable positive equilibrium indicates a balance among the prey, predators, and the resource they are competing for. This essentially means the fishery resources are being used in a sustainable way. On the flip side, when the positive equilibrium $ E^* $ loses its stability, it will lead to an emergence of a stable periodic solution.
Next, we consider the effect of the predator harvest parameter $ \delta $ on the dynamics of the system. We can see from Figure 8 that the predator harvest parameter $ \delta $ can have a significant effect on the sizes of two species and the quantity of resources, and meanwhile it can also affect the critical values of two delays: as $ \delta $ increases, $ x^* $ and $ z^* $ increase, and $ y^* $ decreases, suggesting that the degree of depredation by the predator changes the numbers of predators and prey. Keeping $ \tau_2 = 0.2 $ constant, the higher the degree of predator capture, the smaller the corresponding $ \tau_1 $ critical value $ \tau_{10}^* $ will be, indicating that the degree of capture destabilizes the corresponding system (2.3).
6.
Conclusions
In this paper, we have explored an intraguild prey-predator model (2.3) featuring two delays and a Michaelis-Menten-type harvesting. First, we analyzed the corresponding characteristic equation and discussed the stability of the prey-free equilibrium $ E_1 $ and the predator-free equilibrium $ E_2 $. According to the Hopf bifurcation theorem, we investigated the conditions for equilibrium stability and the existence of Hopf bifurcations. We employed the normal form theory and the center manifold theorem and obtained some explicit results. Specifically, when $ \tau_2 \in[0, \tau_2^{(0)}) $, we explored the stability and direction of Hopf bifurcations for varying values of $ \tau_1 $. Finally, we validated our theoretical findings through numerical simulations.
In ecological systems, the predator, the prey, and the shared resources are expected to persist within a given set of parameters. The local bifurcation observed in such systems has ecological significance. This means that changes in the parameters can result in ecologically relevant shifts in the population dynamics of the predator and prey, along with their interactions with shared resources. In addition, when both delays surpass their critical values, they can have a significant impact on the stability of the system and cause various changes in its properties and behaviors. An increase in predator harvesting parameter $ \delta $ may lead to unstable behaviors and phenomena that will influence the efficient use of shared resources by prey and predators, even if the number of predators has decreased.
To maintain sustainable fishing practices without depleting resources or driving predator species to extinction, it is crucial to employ qualitative analysis and numerical simulations in research. These methods provide insights into the dynamic behavior of ecosystems, enabling us to set limits and strike a balance. In essence, they help determine the level of fishing that is sustainable without harming the ecosystem. Overfishing can disrupt marine ecosystems, so selecting an appropriate value for $ \delta $ to achieve a balance between resource sustainability and maximizing benefits in the presence of time delays is a critical concern, which we leave for future research to address.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The authors would like to thank the National Natural Science Foundation of China (11671260; 12071293) for supporting this work.
Conflict of interest
The authors announce that there are no conflicts of interest. Sanling Yuan and Tonghua Zhang are the editorial board members for Mathematical Biosciences and Engineering and were not involved in the editorial review or the decision to publish this article.
Appendix
A. Detailed analysis on the positive root distribution of Eq (3.19)
1) If $ e_{20} > 0 $, then we have
(a) If $ \Delta\leq 0 $, then Eq (3.19) has no positive roots.
(b) If $ \Delta > 0 $, then we have
● when $ x_1^*\leq 0 $, then Eq (3.19) has no positive roots.
● when $ x_1^* > 0 $ and $ h(x_1^*) > 0 $, then Eq (3.19) has no positive roots.
● when $ x_1^* > 0 $ and $ h(x_1^*) = 0 $, then Eq (3.19) has one positive double root (i.e., $ x_1^* $).
● when $ x_1^* > 0 $ and $ h(x_1^*) < 0 $, then Eq (3.19) has two different positive roots.
2) If $ e_{20} = 0 $, then we have
(a) If $ \Delta\leq 0 $, then Eq (3.19) has no positive roots.
(b) If $ \Delta > 0 $, then we have
● when $ x_1^*\leq 0 $, then Eq (3.19) has no positive roots.
● when $ x_2^*\leq 0 < x_1^* $, then Eq (3.19) has one positive root.
● when $ x_2^* > 0 $ and $ h(x_1^*) > 0 $, then Eq (3.19) has no positive roots.
● when $ x_2^* > 0 $ and $ h(x_1^*) = 0 $, then Eq (3.19) has one positive double root (i.e., $ x_1^* $).
● when $ x_2^* > 0 $ and $ h(x_1^*) < 0 $, then Eq (3.19) has two different positive roots.
3) If $ e_{20} < 0 $, then we have
(a) If $ \Delta\leq 0 $, then Eq (3.19) has one positive root.
(b) If $ \Delta > 0 $, then we have
● when $ x_2^*\leq 0 $, then Eq (3.19) has one positive root.
● when $ x_2^* > 0 $ and $ h(x_1^*)h(x_2^*) > 0 $, then Eq (3.19) has one positive root.
● when $ x_2^* > 0 $, $ h(x_2^*) = 0 $ (respectively, $ h(x_1^*) = 0 $), then Eq (3.19) has one positive double root $ x_2^* $ (respectively, $ x_1^* $) and one positive root.
● when $ x_2^* > 0 $, $ h(x_2^*) > 0 $ and $ h(x_1^*) < 0 $, then Eq (3.19) has three positive roots.
To summarize, we can have the following results on Eq (3.18).
Lemma A.1. The following statements are true.
1) If one of the following four conditions holds, Equation (3.18) will have on positive roots.
(i) $ e_{20}\geq 0 $ and $ \Delta\leq 0 $;
(ii) $ e_{20}\geq 0 $, $ \Delta > 0 $ and $ x_1^*\leq 0 $;
(iii) $ e_{20} > 0 $, $ \Delta > 0 $ and $ \min\{x_1^*, h(x_1^*)\} > 0 $;
(iv) $ e_{20} = 0 $, $ \Delta > 0 $ and $ \min\{x_2^*, h(x_1^*)\} > 0 $.
2) If one of the following three conditions is satisfied, Equation (3.18) will have only one positive root.
(i) $ e_{20} = 0 $, $ \Delta > 0 $ and $ x_2^*\leq 0 < x_1^* $.
(ii) $ e_{20} < 0 $, $ \Delta > 0 $ and $ x_2^*\leq 0 $.
(iii) $ e_{20} < 0 $, $ \Delta > 0 $ and $ \min\{x_2^*, h(x_1^*)h(x_2^*)\} > 0 $.
3) If either of the following two conditions is satisfied, Equation (3.18) will possess two positive roots:
(i) $ e_{20} > 0 $, $ \Delta > 0 $ and $ x_1^* > 0 $ and $ h(x_1^*) < 0 $;
(ii) $ e_{20} = 0 $, $ \Delta > 0 $ and $ x_2^* > 0 $ and $ h(x_1^*) < 0 $;
4) Equation (3.18) has three positive roots provided the following conditions hold:
(H2) $ e_{20} < 0 $, $ \Delta > 0 $, $ x_2^* > 0 $, $ h(x_2^*) > 0 $, and $ h(x_1^*) < 0 $.
5) Equation (3.18) has one double positive root provided one of the following two conditions holds:
(i) $ e_{20} > 0 $, $ \Delta > 0 $, $ x_1^* > 0 $, and $ h(x_1^*) = 0 $; (ii) $ e_{20} = 0 $, $ \Delta > 0 $, $ x_2^* > 0 $, and $ h(x_1^*) = 0 $;
6) Equation (3.18) has two positive roots (a single root and a double root) provided the following conditions hold:
$ e_{20} < 0 $, $ \Delta > 0 $, $ x_2^* > 0 $, and $ h(x_2^*) = 0 $ (or $ h(x_1^*) = 0 $).
B. Computation of the Coefficients $ \mu_2 $, $ \beta_2 $, and $ T_2 $
Let $ \tau_1 = \tau_{10}^{*}+\mu, \mu\in R $, then $ \mu = 0 $ is the Hopf bifurcation value of the system. Let $ t = s\tau_1 $, $ x(s\tau_1) = \widehat{x}(s) $, $ y(s\tau_1) = \widehat{y}(s) $, $ z(s\tau_1) = \widehat{z}(s) $, and denote $ x = \widehat{x}(s) $, $ y = \widehat{y}(s) $, $ z = \widehat{z}(s) $, and $ t = s $, then system (2.3) can be written as a functional differential equation in $ C = C([-1, 0], R^3) $:
where $ X(t) = (x(t), y(t), z(t))^T\in R^3 $, $ X_t (\theta) = X(t+\theta) = (x(t+\theta), y(t+\theta), z(t+\theta))^T\in C $, and $ L_{\mu}:C\rightarrow R^3 $, $ F : R\times C\rightarrow R^3 $ are given by
and
where
where
By the Riesz representation theorem, there exists a $ 3\times3 $ matrix function $ \eta(\theta, \mu) $ of bounded variatation for $ \theta \in [-1, 0] $, such that
In fact, we can choose
where $ \delta(\theta) $ is the Dirac delta function.
For $ \phi\in C([-1, 0], R^3) $, define
and
Then this can be transformed into the following operator equation
which is a functional differential equation in $ C([-1, 0];R^3) $.
Denote $ \mathscr{A} = \mathscr{A}(0) $,
and
where $ \psi\in C^*([0, 1], (R^3)^*) $. Then $ \mathscr{A}^* $ are adjoint operators of $ \mathscr{A} $. If $ \pm i\omega_{1k}\tau_{1k} $ are eigenvalues of $ \mathscr{A} $, they are eigenvalues of $ \mathscr{A}^* $. Suppose that $ q(\theta) = (1, q_2, q_3)^T e^{i{\omega_{10}}^*{\tau_{10}}^*\theta} $ is the eigenvector of $ \mathscr{A} $ corresponding to $ i\omega_{10}^{*}\tau_{10}^{*} $, that is $ \mathscr{A}q(\theta) = i\omega_{10}^*\tau_{10}^*q(\theta) $. Then we can obtain that
Let $ q^*(s) = D(1, q_2^*, q_3^*)e^{i\omega_{10}^*\tau_{10}^*s} $ be an eigenvector of $ \mathscr{A}^* $corresponding to $ -i\omega_{10}^*\tau_{10}^* $, then we have
For this equation, we can get
Thus, one can choose $ D $ as
which satisfies $ < q^*(s), q(\theta) > = 1 $.
In the rest of this section, applying the methods from [40] along with similar computational procedures should enable us to ascertain the coefficients for determining both the Hopf bifurcation's direction and the stability of the bifurcating periodic solutions.
However,
Here $ M_1 = (M_1^{1}, M_1^{2}, M_1^{3})^{T}\in R^3 $ and $ M_2 = (M_2^{1}, M_2^{2}, M_2^{3})^{T}\in R^3 $ are also constant vectors and can be determined by the following equations, respectively.
with









 DownLoad:
DownLoad: