Biological control for predation invasion based on pair approximation

1.   Introduction

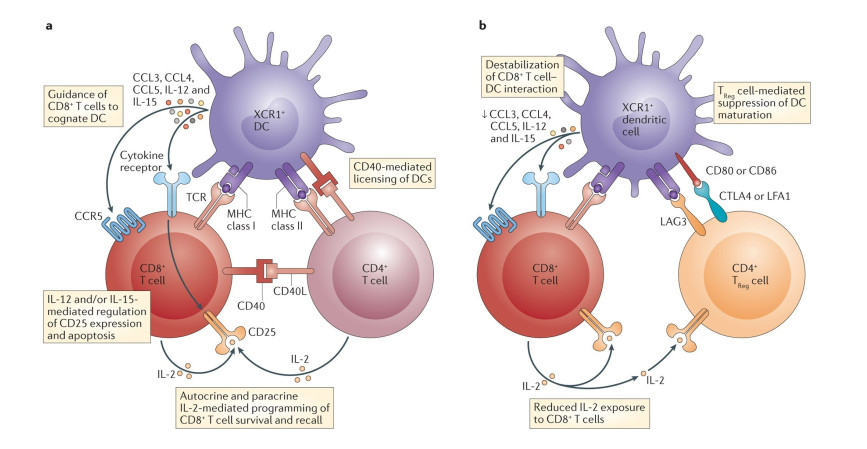
Diverse viral outbreaks, including those engendered by the human immune compromised virus (HIV) ^[1], ebola virus ^[2], acute respiratory syndrome Coronavirus‐2 (SARS‐CoV‐2) ^[3], dengue virus ^[4], nipah virus ^[5], HBV ^[6], etc., have been researched utilizing mathematical formulas to describe the within-host nonlinear versatile tendencies. In typical latent infection systems, uncontrolled infections, vulnerable tissues, and attacked cellular responses interact. Additionally, several researchers highlight the phenomenon of incubation by mentioning persistent contamination. The recipient defensive mechanism responds to viral infestation via inherent and monoclonal antibody immunogenicity. Both kinds of reactions can be roughly classified into lytic and nonlytic parts. While nonlytic responder processes prevent viremia by aqueous molecules, lytic responder strategies eliminate afflicted organisms. Innate mechanisms include the ability of autonomous assassin systems to destroy intracellular pathogens and the nonlytic inhibition of viral multiplication by cytokines released by cellular functions. Cytotoxic T lymphocytes (CTLs), which are allergen antibodies, destroy intracellular pathogens while autoantibodies deactivate dispersed viral proteins and prevent the transmission of bacteria to infected macrophages. Furthermore, CD4+ and CD8+ T lymphocytes can produce chemicals that inhibit infectious proliferation (e.g., IFN- and TNF-), (see Figure 1).

These discrepancies are not necessarily easy to make, though. For instance, cytokines like interferon and tumour necrotic signal have been shown to promote apoptosis in some circumstances, in addition to inhibiting infectious multiplication ^[7]. Eichelberger et al. ^[8] investigated whether the pathogen can be eradicated by the CD4+ T-cell-dependent antigen reaction in the absence of CD8+ T cells, (see Figure 2). Topham et al. ^[9] demonstrated that CD8+ T lymphocytes can eliminate the pathogen by a lytic process that is either regulated by complement activation or Fas. In terms of explaining the four distinct HCV scenarios quantitatively, Pan et al. ^[10] addressed the HCV infectious system, which incorporates the pathways of contamination and propagation, such as infectious agent and cell-to-cell dissemination patterns.

Chronic infestations result when the pathogen weakens and suppresses the innate immunity. An immunological reaction has occurred whereby, upon a bacteria's penetration into the system, the immunological mechanism identifies the onslaught and communicates this information to the defensive components, which then generate lymphocytes to eradicate the infection. Additionally, the responsive immunological mechanism is very important in regulating the virus replication. When an infection propagates in a person, the cells respond in two ways: first, a host antibody immune reaction is triggered by the B-cell, and then a cytotoxic immunological reaction is induced by the Cytotoxic T Lymphocyte (CTL). According to earlier investigations, the autoimmune disease seems to be more robust than the intracellular immunological defences. Elaiw et al. ^[11] addressed the production of antibodies, particular nonlinear prevalence rate expression, and behavioural features of viral transmission scenarios, including insidiously viral particles. Luo et al. ^[12] analyzed a nonlinear prevalence, cell-to-cell dissemination, and host immune protection framework for diffusive pathogen infectious diseases. Wang et al. ^[13] investigated the infectious patterns of a system of persistent HIV transmission that included multiple latencies, B-cell immunological responses, and the Beddington-DeAngelis occurrence criterion. Hattaf ^[14] presented a generalised virus-induced framework with several delayed and immune regulatory components that exhibit global stability and Hopf bifurcation. Rajivganthi and Rihan ^[15] presented the stochastic analysis of viral infection model involving latently infected cells. Olaide et al. ^[16] presented a novel metaheuristic algorithm named ebola optimization search algorithm (EOSA) based on the propagation mechanism of the ebola virus disease. For further investigations on optimization and epidemics, we refer the readers ^{[17,18,19,20,21,22,23,24,25]}.

Fractional calculus (FC) is a subfield of mathematics that was created by applying integer derivatives to differential equations (DEs) involving fractional-orders ^{[26,27,28,29,30,31]}. Since many considerable anomalies in digital circuits, phonics, physio-chemical processes, special relativity, photo-catalysis, transport phenomena, stretchability, and optoelectronics can be characterized by fractional DEs, this field, which deals with classical derivatives and fractional-order, has gained popularity in the last three decades. Additionally, FC is currently an essential strategy for simulating complicated events as well as electron mobility that occurs in permeable heterogeneity environments ^{[32,33,34,35,36]}. In order to analyze FDEs, scientists require a powerful toolset, yet it might be challenging to identify precise alternatives to these kinds of computations. Therefore, it is vital to designing appropriate quantitative strategies to address these issues ^[37]. However, quantitative approaches for FDEs create mathematical challenges that are not present in the evaluation of integer-order models. Because certain of the advantageous aspects of the conventional approximation operators are compromised, there are certain systemic problems in performing simulations of the fractional derivatives. During the last decade, the Atangana-Baleanu fractional operator has made recent advancements in fractional DEs approximation, ^[38]. Atangana ^[39] proposed a revolutionary nonlocal formulation that combines fractional-order and fractal-dimension: fractal-fractional (FF) differential and integral operators. To examine intricate real-world situations that can never be modelled using classical and fractional derivative/integral formulations of single order, the F-F technique has been expounded as a valuable technique in numerous scientific and epidemiological fields. Versaci et al. ^[40] presented a fuzzy similarity-based approach to classify numerically simulated and experimentally detected carbon fiber-reinforced polymer plate defects. The present scheme can be further formulated with the method proposed by ^[40].

However, the fractional-order and integer-order mathematical models have been developed to analyze a large number of randomized order derivatives, providing an additional level of flexibility in selecting; see ^{[41,42,43,44]}. The stochastic DEs might offer a significant level of reliability, and when linked to deterministic systems, they encompass the comprehensive spectra of an individual cohort and produce a highly precise result as compared to a classical model. We need to execute the simulations repeatedly and detect commonalities in the projected scenarios because the results of every inquiry in a stochastic procedure differ from the preceding ^[46,47,48]. According to several researchers, a non-linear recurrence projection for stochastic processes is one of the epidemiological techniques that has been examined for stability evaluation. In fact, random events are prevalent worldwide. Systems frequently experience random disturbances. Various studies have been conducted on stochastic dynamics; for example, a wide range of scientific theories, including meteorology, accounting, biology, and telecommunication systems, frequently exhibit randomized fluctuations with long-term dependency. In order to analyze fractional stochastic processes, fractional Brownian motion (BM) employing the Hurst index $H(1/2, 1)$ has been proposed as an alternative to classical BM ^[49]. Kerboua et al. ^[50] looked into stochastic fractional DEs with perturbed regulatory frameworks that involved fractional BM. Pei and Xu ^[51] investigated the non-Lipschitz stochastic DEs driven by fractional BM. In 2021, authors ^[52] presented a novel notion for analyzing and predicting the transmission of COVID-19 throughout Africa and Europe using stochastic and deterministic methods. Alkahtani and Koca ^[53] contemplated the fractional stochastic SIR system within the fractional calculus technique. Rashid et al. ^[54] contemplated the stochastic fractal-fractional tuberculosis model via a non-singular kernel with random densities.

Owing to the aforesaid propensity, we intend to suggest a novel fractal-fractional stochastic immune effector response to viral infections while taking the notion of a fluctuating population with white noise into consideration. We intend to divide the entire population into five distinct groups based on the severity of viral infection. Furthermore, several qualitative analyses are conducted, such as the existence and distinctiveness of the positive solution in the stochastic immune effector responses considering a Holling type II functionality reaction. Perceptions from these systems are distilled in this assessment, which also contrasts them with test findings. Numerical results are presented by employing the revolutionary technique proposed by Atangana and Araz ^[52] in the fractal-fractional derivative sense. Graphical illustrations are presented with low random densities, incorporating the fractal-dimension and fractional-order. In a nutshell, we presented the simulation findings with and without control.

The rest of this paper is structured as follows. Section 2 gives some foundational information on F-F operators in the ABC sense, formulations of stochastic perturbation and the fractional viral infection model construction. In Section 3, we demonstrate the model's configuration. Section 4 exhibits the solution's existence-uniqueness, as well as ergodicity and conducts a stationary distribution study on the proposed model. The unique result for the F-F viral model is established utilizing the Atangana-Baleanu sense and standard Brownian motion in Section 5. Furthermore, the discussion of numerical simulations utilizing the novel numerical scheme is provided to analyze the behaviors of the considered model. Finally, we give the conclusion of our paper in the last section.

2.   Preliminaries

Before advancing on to the formal description, it is imperative to study certain fundamental F-F operator concepts. Take into account the parameters provided in ^[39] as well as the functional $\mathbf{v}(\mathbf{t}_{1})$, which is continuous and fractal differentiable on $[c, d]$ with fractal-dimension $\wp$ and fractional-order $\alpha$.

Definition 2.1. (^[39]) The FF operator of $\mathbf{v}(\bar{\mathbf{t}})$ involving the index law kernel in the perspective of Riemann–Liouville (RL) can be described as follows for $\bar{\mathbf{t}}\in[0, 1]$:

where $\frac{d\mathbf{v}(\mathbf{w})}{d\mathbf{w}^{\wp}} = \lim\limits_{\bar{\mathbf{t}}\mapsto \varkappa}\frac{\mathbf{v}(\bar{\mathbf{t}})-\mathbf{v}(\varkappa)}{\bar{\mathbf{t}}^{\wp}-\varkappa^{\wp}}$ and $\mathbf{u}-1 < \alpha, \wp\leq \mathbf{u}\in\mathbb{N}.$

Definition 2.2. (^[39]) The FF operator of $\mathbf{v}(\bar{\mathbf{t}})$ involving the exponential decay kernel in the terms of RL can be described as follows for $\alpha\in[0, 1]$:

such that $\mathbb{M}(0) = \mathbb{M}(1) = 1$ containing $\alpha > 0, \; \wp\leq \mathbf{u}\in\mathbb{N}.$

Definition 2.3. (^[39]) The FF operator of $\mathbf{v}(\bar{\mathbf{t}})$ involving the generalized Mittag-Leffler kernel in the perspective of RL can be described as follows for $\alpha\in[0, 1]$:

such that $\mathbf{ABC}(\alpha) = 1-\alpha+\frac{\alpha}{\Gamma(\alpha)}$ involving $\alpha > 0, \; \wp\leq 1\in\mathbb{N}.$

Definition 2.4. (^[39]) The corresponding F-F integral formulae of $(2.1)$ is described as:

Definition 2.5. (^[39]) The corresponding F-F integral formulae of $(2.2)$ is described as:

Definition 2.6. (^[39]) The corresponding F-F integral formulae of $(2.3)$ is described as:

Definition 2.7. (^[38]) Let $\mathbf{v}\in H^{1}(\mathbf{c}, \mathbf{d}), \; \; \mathbf{c} < \mathbf{d}$ and the Atangana-Baleanu fractional derivative operator is described as:

where $\mathbf{ABC}(\alpha)$ represents the normalization function.

Definition 2.8. (^[55]) The Gaussian hypergeometric function $\, _{2}\mathcal{F}_{1}$, characterized as

where $\mathbb{B}(y_{1}, y_{2}) = \frac{\Gamma(y_{1})\Gamma(y_{2})}{\Gamma(y_{1}+y_{2})}$ and $\Gamma(y_{1}) = \int\limits_{0}^{\infty}\exp(-\bar{\mathbf{t}})\bar{\mathbf{t}}^{y_{1}}d\bar{\mathbf{t}}$ is the Gamma function.

3.   Model configuration

Here, the immunological mechanism is necessary for the highly contagious viral replication. If infectious processes are adequately described, the infection and the therapeutic medications employed to address it can be comprehended. Lymphocytes are vicariously liable for specialization and retention in responsive immunological systems. B cells and T cells are the two primary categories of lymphocytes. T cells have the ability to identify and eliminate contaminated organisms, whereas B cells are responsible for producing antigens that can neutralize pathogens. Immune systems, including CTL and antigen-response, have been examined in terms of their impact ^[56,57]. The impact of CTL reactions and cytoplasmic latencies has been considered by a few other scientists as well ^[58]. Murase et al. ^[59] presented the mathematical framework that shows how adaptive immunity affects viral transmission as follows:

The system (3.1) based on unrestricted infections $\mathbf{F}(\bar{\mathbf{t}})$, unaffected target cells $\mathbf{U}(\bar{\mathbf{t}})$, productively infectious specific cells $\mathbf{A}(\bar{\mathbf{t}})$ and antibodies/B tissue $\mathbf{Q}(\bar{\mathbf{t}}).$ The productivity $\Lambda$ of the infectious organisms $\mathbf{U}(\bar{\mathbf{t}})$ and fatality rate $\varsigma$ are both constant. The incidence of the disease by uncontrolled pathogen is $\lambda_{11}$, and uncontrolled bacteria become constructively contaminated at a rate of $\lambda_{22}$ for each of the two individuals. The percentage of viral components that died at $\delta, \nu_{2}$ and $\zeta$ released pathogens, antibodies, and B tissues, respectively. When tissues are actively infested, individual viral particles are created at a speed of $\varphi$, where is the ratio $\xi$ at which responses can eliminate the pathogen. The frequency of responses that are active versus the pathogen is $\chi$.

However, the persistent infectious factor is applied to framework (3.1) in this article as an improvement. We suppose that the incidence at which a Holling type II functioning reaction develops is that the unaffected cell $\mathbf{U}(\bar{\mathbf{t}})$ becomes contaminated by a neutral pathogen $\mathbf{F}(\bar{\mathbf{t}})$ or by virus is transmitted organism $\mathbf{A}(\bar{\mathbf{t}})$ at the rate $\frac{\lambda_{1}\mathbf{U}(\bar{\mathbf{t}})\mathbf{F}(\bar{\mathbf{t}})}{1+\mathbf{F}(\bar{\mathbf{t}})}+\frac{\lambda_{2}\mathbf{U}(\bar{\mathbf{t}})\mathbf{A}(\bar{\mathbf{t}})}{1+\mathbf{A}(\bar{\mathbf{t}})}$ response. The rates of pathogen to tissue infection and tissue to cell propagation are indicated by $\lambda_{1} > 0$ and $\lambda_{2} > 0,$, respectively, see ^[60]. We further estimate that the amounts of contamination that result in response times and efficiency are $1-\phi$ and $\phi\in(0, 1),$ respectively. In addition, we included the effect of unpredictability within the host by injecting nonlinear disturbances on the spontaneous mortality rate, employing white noise throughout each expression in an attempt to depict a more accurate state of pathogen progression. As a result, the modified framework is specified:

subject to initial conditions (ICs) $\mathbf{U}(0) > 0, \; \mathbf{S}(0) > 0, \; \mathbf{A}(0) > 0, \; \mathbf{F}(0) > 0, \; \mathbf{Q}(0) > 0.$ Moreover, the term $\mathbf{S}(\bar{\mathbf{t}})$ stands for the concentrations of contaminated tissues in the predictive phase at time $\bar{\mathbf{t}}.$ $\nu_{1}$ be the death rate of $\mathbf{S}(\bar{\mathbf{t}}),$ the underlying contamination becomes prolific at the rate $\sigma.$ Also, $\rho_{\iota}^{2}, \; \; \iota = 1, ..., 5$ are intensities of standard Gaussian white noise and $B_{\iota}, \; \; \iota = 1, ..., 5$ are independent standard Brownian motion (BM). The underlying ideas of probability theory and stochastic differential equations are described as: let $(\Omega, \mathfrak{F}, \{\mathfrak{F}\}_{\bar{\mathbf{t}}\geq0}, P)$ be a complete probability space using filtration such that $\{\mathfrak{F}\}_{\bar{\mathbf{t}}\geq0}$ admits the basic requirements. For further information on Itô's technique, see ^[61]. However, the deterministic model has certain limitations because it cannot consider demographic stochasticity, which are important features of any natural system. Due to the influence of environmental noise, population density usually does not stabilize at a fixed value, but fluctuates around a certain average value. Nowadays, stochastic biological modeling has attracted great interest from researchers all over the world ^[20,21,22].

4.   Existence-uniqueness of non-negative solution

In what follows, we provide the accompanying result to identify the stochastic model's (3.2) existence and uniqueness.

Theorem 4.1. For $\chi < \xi < \zeta, \; \lambda_{1}\varphi < \nu_{2}+\chi, 1+\lambda_{2} < \frac{\delta}{\varphi},$ the solution of the system $(3.2)~~ (\mathbf{U}(0), \mathbf{S}(0), \mathbf{A}(0), \mathbf{F}(0), \mathbf{Q}(0))$ is unique for $\bar{\mathbf{t}}\geq0$ underlying ICs $(\mathbf{U}(0), \mathbf{S}(0), \mathbf{A}(0), \mathbf{F}(0), \mathbf{Q}(0))\in\mathbb{R}_{+}^{5}.$ Also, the solution will probably stay in $\mathbb{R}_{+}^{5}$ having unit probability, i, e., $(\mathbf{U}(0), \mathbf{S}(0), \mathbf{A}(0), \mathbf{F}(0), \mathbf{Q}(0))\in\mathbb{R}_{+}^{5}, \; \forall\; \bar{\mathbf{t}} > 0$ almost surely (a.s).

Proof. Briefly, if the local Lipschitz criterion is fulfilled by the components of the scheme (3.2). Thus, (3.2) has an unique local solution $(\mathbf{U}(\bar{\mathbf{t}}), \mathbf{S}(\bar{\mathbf{t}}), \mathbf{A}(\bar{\mathbf{t}}), \mathbf{F}(\bar{\mathbf{t}}), \mathbf{Q}(\bar{\mathbf{t}}))$ on $[0, \tau_{e}],$ where $\tau_{e}$ is the exposition duration. Then, we illustrate that $\tau_{e} = \infty.$ Let us apply the same methodology used in ^[48] to prove the result. Our intention is to define a non-negative mapping $\mathbb{C}^{2}$ as $\mathcal{H}:\mathbb{R}_{+}^{5}\mapsto\mathbb{R}_{+}$ such that $\lim\limits_{\eta\mapsto\infty}(\mathbf{U}(\bar{\mathbf{t}}), \mathbf{S}(\bar{\mathbf{t}}), \mathbf{A}(\bar{\mathbf{t}}), \mathbf{F}(\bar{\mathbf{t}}), \mathbf{Q}(\bar{\mathbf{t}}))\in\mathbb{R}_{+}^{5}\backslash\Upsilon_{\eta}\inf\mathcal{H}(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q}) = \infty$ and $\mathbb{L}\mathcal{H}(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})\leq\Bbbk,$ where $\Upsilon_{\eta} = \big(1/\eta, \eta\big)\times\big(1/\eta, \eta\big)\times\big(1/\eta, \eta\big)\times\big(1/\eta, \eta\big)\times\big(1/\eta, \eta\big)$ and $\Bbbk$ is non-negative constant.

Now, considering two positive constants values $\epsilon$ from $(0, 1)$ and $\mathbb{T}$ must exist such that

Introducing a mapping $\mathcal{H}:\mathbb{R}_{+}^{5}\mapsto\mathbb{R}_{+}$ as:

This stored procedure non-negativity is shown by examining at $\varrho-1\ln\varrho, \; \forall\varrho > 0.$ Suppose that $\Bbbk_{0}\leq\Bbbk$ and $\mathbb{T} > 0.$ The Itô's formula can be used to acquire

It follows that

Utilizing the given hypothesis, there exists a non-negative constant $\eta$ such that $\mathbb{L}\mathcal{H} < \eta.$

Therefore,

Inserting $\Omega_{\eta} = \{\tau_{\eta}\leq\mathbb{T}\}$ for $\eta\geq\eta_{1}$ and by (4.1) we have $P(\Omega_{\eta})\geq\epsilon.$ Observe that for every $\omega$ from $\Omega_{\eta}$ there exist at least one $\mathbf{U}(\tau_{\eta}, \omega), \mathbf{S}(\tau_{\eta}, \omega), \mathbf{A}(\tau_{\eta}, \omega), \mathbf{F}(\tau_{\eta}, \omega), \mathbf{Q}(\tau_{\eta}, \omega)$ that yields $1/\eta\; or\; \eta.$ Consequently, $\mathcal{H}\big(\mathbf{U}(\tau_{\eta}), \mathbf{S}(\tau_{\eta}), \mathbf{A}(\tau_{\eta}), \mathbf{F}(\tau_{\eta}), \mathbf{Q}(\tau_{\eta})\big)\geq\Big(1/\eta-1+\ln\eta\Big)\wedge\mathbb{U}(\eta-1-\ln\eta).$

In view of (4.1) and (4.5), we can express

The indicating mapping of $\omega$ is denoted as $1_{\Omega_{(\omega)}}$ that approaches to $\infty,$ the contradiction

reveals itself, proving that $\tau_{\infty} = \infty.$

4.1.   Ergodicity and Stationary distribution (ESD)

Now, we review and examine the model's (3.2) stationary distribution outcomes, which show that the infections are eliminated or enduring.

Suppose there be a regular Markov technique in $\mathbb{R}_{+}^{\mathfrak{n}}$ for which the behaviour is as below:

The diffusion matrix takes the form

Lemma 4.1. (^[62]) Suppose there is a unique stationary distribution technique $\Phi(\bar{\mathbf{t}}).$ If there is a bounded region involving regular boundary such that $S, \bar{S}\in\mathbb{R}^{d}\bar{S}$ closure $\bar{S}\in\mathbb{R}^{d}$ satisfies the following:

(a) The smallest eigenvalue for $\mathbb{A}(\bar{\mathbf{t}})$ is bounded away from $(0, 0)$ for the open region $S$ having neighbourhood.

(b) For $\psi\in\mathbb{R}^{d}S,$ the mean time $\tau$ is bounded and for every compact subset $K\subset\mathbb{R}^{\mathfrak{n}}, \; \sup_{\psi\in\Bbbk}S^{\psi}\tau < \infty.$ Therefore, $f_{1}(.)$ is an integrable mapping containing measure $\pi,$ then

Theorem 4.2. For $\hat{\sigma} = \nu_{1}+\sigma+\frac{\rho_{2}^{2}}{2}, \; \hat{\delta} = \delta+\frac{\rho_{3}^{2}}{2}, \; \hat{\nu_{2}} = \nu_{2}+\frac{\rho_{4}^{2}}{2},$ then assume that $\mathbb{R}_{0}^{s}: = \frac{\Lambda\sigma \varphi\lambda_{1}(1-\phi)}{\varsigma\hat{\delta}\hat{\sigma}} > 1,$ then for any ICs exists in $\mathbb{R}_{+}^{5},$ the system has a unique ESD $\pi(.).$

Proof. The diffusive matrix for system (3.2) is computed as follows:

This proves that the criteria (a) in Lemma 4.1 is applicable for any compact subset of $\mathbb{R}_{+}^{5}$. In view of mapping $\mathbb{C}^{2}$ defined as $\mathcal{H}:\mathbb{R}_{+}^{5}\mapsto\mathbb{R}_{+}.$ Thus, we have

where $\theta\in[0, 1], \; \ell_{1} = \frac{\Lambda\lambda_{1}\sigma \varphi(1-\phi)}{\hat{\sigma}^{2}\hat{a}\hat{\nu_{2}}}, \; \ell_{2} = \frac{\Lambda\lambda_{1}\sigma \varphi(1-\phi)}{\hat{\sigma}^{2}\hat{a}^{2}\hat{\nu_{2}}}, \; \ell_{3} = \frac{\Lambda\lambda_{1}\sigma \varphi}{\hat{\sigma}\hat{a}\hat{\nu_{2}}^{2}}$ fulfilling $c-\frac{\theta}{2}(\rho_{1}^{2}\vee\rho_{2}^{2}\vee\rho_{3}^{2}\vee\rho_{4}^{2}\vee\rho_{5}^{2}) > 0$ and $\mathcal{M} > 0,$ admitting the assumption $-\mathcal{M}\nu_{2}+N_{1}\leq-2$ and $\nu_{2} = \varsigma(\mathbb{R}_{0}^{s}-1) > 0.$

This shows that $\mathcal{H}(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})$ is continuous as well as it tends to $\infty.$ So that $(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})$ approaches to $\mathbb{R}_{+}^{5}$ and $\|(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})\|\mapsto\infty.$ Also, $\mathcal{H}$ have ICs that lies in $\mathbb{R}_{+}^{5}.$

Again, in view of mapping $\mathbb{C}^{2}$ defined as $\mathcal{H}:\mathbb{R}_{+}^{5}\mapsto\mathbb{R}_{+}.$ Thus, we have

Considering Itô's technique $\mathbb{L}$ on the mappings $\mathcal{H}_{1}, ..., \mathcal{H}_{6}$ and utilizing the given hypothesis such that $c = \max\{\varsigma, \nu_{1}, \delta, \nu_{2}, \zeta\},$ we have

Analogously, we have

where $\mathcal{N}_{2} = \sup\limits_{(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})\in\mathbb{R}_{+}^{5}}\Big\{\Lambda(\mathbf{U}+\mathbf{S}+\mathbf{A}+\mathbf{F}+\mathbf{Q})^{\theta}-\frac{1}{2}\Big(c_{1}-\frac{\theta}{2}(\rho_{1}^{2}\vee\rho_{2}^{2}\vee\rho_{3}^{2}\vee\rho_{4}^{2}\vee\rho_{5}^{2})\Big)(\mathbf{U}+\mathbf{S}+\mathbf{A}+\mathbf{F}+\mathbf{Q})^{\theta+1}\Big\} < \infty.$

Utilizing (4.7) and (4.8), we have

For $\epsilon > 0,$ we construct the following set

We can validate Lemma 4.1 in order to demonstrate that $\mathbb{L}\bar{\mathcal{H}}\leq-1$ for $(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})\in\mathbb{R}_{+}^{5}\backslash\mathbb{D}\; and\; \mathbb{R}_{+}^{5}\backslash\mathbb{D} = \bigcup_{\iota = 1}^{10}\mathbb{D}_{\iota},$ where

Case (a) If $(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})\in \mathbb{D}_{1},$ then by (4.9), we find

If we choose a sufficiently small $\epsilon > 0,$ then we get $\mathbb{L}\bar{\mathcal{H}} < 0$ for each $(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})\in\mathbb{D}_{1}.$

Case (b) If $(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})\in \mathbb{D}_{2},$ then by (4.9), we find

If we choose a sufficiently small $\epsilon^{5} > 0,$ then we get $\mathbb{L}\bar{\mathcal{H}} < 0$ for each $(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})\in\mathbb{D}_{2}.$

Case (c) If $(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})\in \mathbb{D}_{3},$ then by (4.9), we find

If we choose a sufficiently small $\epsilon^{2} > 0,$ then we get $\mathbb{L}\bar{\mathcal{H}} < 0$ for each $(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})\in\mathbb{D}_{3}.$

Case (d) If $(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})\in \mathbb{D}_{4},$ then by (4.9), we find

If we choose a sufficiently small $\epsilon > 0,$ then we get $\mathbb{L}\bar{\mathcal{H}} < 0$ for each $(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})\in\mathbb{D}_{4}.$

Case (e) If $(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})\in \mathbb{D}_{5},$ then by (4.9), we find

If we choose a sufficiently small $\epsilon > 0,$ then we get $\mathbb{L}\bar{\mathcal{H}} < 0$ for each $(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})\in\mathbb{D}_{4}.$

Case (f) If $(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})\in \mathbb{D}_{6},$ then by (4.9), we find

If we choose a sufficiently small $\epsilon > 0,$ then we get $\mathbb{L}\bar{\mathcal{H}} < 0$ for each $(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})\in\mathbb{D}_{6}.$

Case (g) If $(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})\in \mathbb{D}_{7},$ then by (4.9), we find

If we choose a sufficiently small $1/\epsilon^{5} > 0,$ then we get $\mathbb{L}\bar{\mathcal{H}} < 0$ for each $(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})\in\mathbb{D}_{7}.$

Case (h) If $(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})\in \mathbb{D}_{8},$ then by (4.9), we find

If we choose a sufficiently small $1/\epsilon^{2} > 0,$ then we get $\mathbb{L}\bar{\mathcal{H}} < 0$ for each $(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})\in\mathbb{D}_{8}.$

Case (i) If $(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})\in \mathbb{D}_{9},$ then by (4.9), we find

If we choose a sufficiently small $1/\epsilon^{3} > 0,$ then we get $\mathbb{L}\bar{\mathcal{H}} < 0$ for each $(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})\in\mathbb{D}_{9}.$

Case (j) If $(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})\in \mathbb{D}_{10},$ then by (4.9), we find

If we choose a sufficiently small $1/\epsilon > 0,$ then we get $\mathbb{L}\bar{\mathcal{H}} < 0$ for each $(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})\in\mathbb{D}_{10}.$\\As a result of the foregoing explanation, a $\epsilon > 0$ exists such that $\mathbb{L}\bar{\mathcal{H}}(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q}) < 0$ $\forall$ $(\mathbf{U}, \mathbf{S}, \mathbf{A}, \mathbf{F}, \mathbf{Q})\in\mathbb{R}_{+}^{5}$. The unique ESD of the system (3.2) is predicated on Lemma 4.1. This completes the proof.

4.2.   Extinction of the model

This part defines the objectives for a virus's systemic elimination (3.1). Before proving the key findings, let's take a closer look at a key premise. Suppose

Theorem 4.3. Suppose there is a solution of the system $(3.1) ~~(\mathbf{U}(\bar{\mathbf{t}}), \mathbf{S}(\bar{\mathbf{t}}), \mathbf{A}(\bar{\mathbf{t}}), \mathbf{F}(\bar{\mathbf{t}}), \mathbf{Q}(\bar{\mathbf{t}}))$ having ICs lies in $\mathbb{R}_{+}^{5}.$ If

almost surely.

Proof. Under the hypothesis of Theorem 4.1, model (3.2) has non-negative solution,

Assume the stochastic DE of the aforementioned system

we have $\lim\limits_{\bar{\mathbf{t}}\mapsto\infty}\frac{1}{\bar{\mathbf{t}}}\int\limits_{0}^{\bar{\mathbf{t}}}\mathbf{U}(\varpi)d\varpi\leq\frac{\Lambda}{\varsigma} \; (a.s).$

Applying the result of ^[48], gives $\mathbf{U}(\bar{\mathbf{t}})\leq\mathbf{U}_{1}(\bar{\mathbf{t}})\; (a.s).$ Then

For $\varphi < \delta$ and introducing $\ln(\mathbf{S}(\bar{\mathbf{t}})+\mathbf{A}(\bar{\mathbf{t}})+\mathbf{F}(\bar{\mathbf{t}}))$ and implement the Itô's technique, we have

Applying integration from $0$ to $\bar{\mathbf{t}}$ and dividing by $\bar{\mathbf{t}},$ we have

that yields $\lim\limits_{\bar{\mathbf{t}}\mapsto\infty}\mathbf{S}(\bar{\mathbf{t}}) = 0, \; \lim\limits_{\bar{\mathbf{t}}\mapsto\infty}\mathbf{A}(\bar{\mathbf{t}}) = 0, \; \lim\limits_{\bar{\mathbf{t}}\mapsto\infty}\mathbf{F}(\bar{\mathbf{t}})\; (a.s).$

5.   Numerical experiment for fractal–fractional system

The modeling framework helps us understand and interpret experimental data on immune responses against viral infection model (5.1). The role of the fractal-fractional operator in the Atangana-Baleanu fractional derivative sense and antibodies for the resolution of viral infection is debated by utilizing the scheme proposed in ^[52]. Studies of the acute phase of the infection showed that humans who cleared the virus from their blood developed strong and sustained CTL responses ^[57]. Here, we illustrate the fractal-fractional derivative for the classical derivative formulation stated in (3.1). The fractal-fractional version in the sense of a generalized Mittag-Leffler function is described as

For ${t_{\mathfrak{n}+1}} = (\mathfrak{n}+1)\Delta \bar{\mathbf{t}},$ then we transform these mappings by their polynomials as follows:

where

Also,

6.   Results and discussion

To exemplify the theoretical outcomes of the suggested framework, numerical computations were performed in this part. We accomplish this using the stochastic complete numerical technique proposed by Atangana and Araz ^[52]. Moreover, we compute the fractal-fractional model (3.2) for Atangana-Baleanu-Caputo sense when both fractional-order $\alpha$ and fractal-dimension $\wp$ are distinct.

Figures 3–5 illustrate the effects of uninfected $\mathbf{U}(\bar{\mathbf{t}})$, latently infected $\mathbf{S}(\bar{\mathbf{t}})$, actively infected $\mathbf{A}(\bar{\mathbf{t}})$, free virus $\mathbf{F}(\bar{\mathbf{t}})$, and antibodies $\mathbf{Q}(\bar{\mathbf{t}})$ at various fractional-orders and fixed fractal-dimensions. We assign the following parameter values: $\Lambda = 10, \; \varsigma = 0.1, \; \lambda_{1} = 2, \; \lambda_{2} = 2, \; \phi = 0.5, \; \nu_{1} = 0.5, \; \sigma = 5, \; \delta = 10, \; \varphi = 2, \; \nu_{2} = 10, \; \xi = 3, \; \chi = 2, \; \zeta = 4.$ To demonstrate the system's dynamical behaviour, we input various white noise levels (5.1). We first take into account the white noise components $\rho_{1} = 0.9, \; \rho_{2} = 0.9, \; \rho_{3} = 0.7, \; \rho_{4} = 0.9$ and $\rho_{5} = 0.8,$ where the distinctive stationary distribution sensitivity criterion $\mathbb{R}_{0}^{s} > 1$ is attained. As the virus spreads through the community, the class diminishes over time and eventually affects all other categories in the structure. This classification corresponds rapidly at low orders and slowly at higher orders, which displays a consistent tendency.

Figures 6–8 display the temporal patterns of $(\mathbf{U}(\bar{\mathbf{t}}), \mathbf{S}(\bar{\mathbf{t}}), \mathbf{A}(\bar{\mathbf{t}}), \mathbf{F}(\bar{\mathbf{t}}), \mathbf{Q}(\bar{\mathbf{t}}))$ of the stochastic system (5.1) involving white noise $\rho_{1} = 0.9, \; \rho_{2} = 0.9, \; \rho_{3} = 0.7, \; \rho_{4} = 0.9$ and $\rho_{5} = 0.8,$ respectively. The solution varies at white noises, having a corresponding stochastic mean. The affected cells $\mathbf{S}(\bar{\mathbf{t}})$ exhibit a rapid decline in behaviour over time, similar to the behaviour of uninfected cells $\mathbf{U}(\bar{\mathbf{t}})$ at various fractal-fractional orders.

Figures 9–11 show the impacts of uninfected $\mathbf{U}(\bar{\mathbf{t}})$, latently infected $\mathbf{S}(\bar{\mathbf{t}})$, actively infected $\mathbf{A}(\bar{\mathbf{t}})$, free virus $\mathbf{F}(\bar{\mathbf{t}})$, and antibodies $\mathbf{Q}(\bar{\mathbf{t}})$ at various fractal-dimension and fixed fractional-orders. The corresponding attributed values: $\Lambda = 10, \; \varsigma = 0.1, \; \lambda_{1} = 2, \; \lambda_{2} = 2, \; \phi = 0.5, \; \nu_{1} = 0.5, \; \sigma = 5, \; \delta = 10, \; \varphi = 2, \; \nu_{2} = 10, \; \xi = 3, \; \chi = 2, \; \zeta = 4.$ Then, by increasing the white noise intensities to $\rho_{1} = 3.9, \; \rho_{2} = 3.7, \; \rho_{3} = 3.9, \; \rho_{4} = 3.9$ and $\rho_{5} = 3.8,$ we are able to satisfy the elimination criterion $\tilde{\mathbb{R}}_{0}^{s} < 1$ in Theorem 4.3 and validate the findings. Figures 9–11 demonstrate that as the white noise intensity escalates, contaminated lymphocytes $\mathbf{S}(\bar{\mathbf{t}})$, productively infested cells $\mathbf{A}(\bar{\mathbf{t}})$, and uncontrolled pathogen $\mathbf{A}(\bar{\mathbf{t}})$ can all perish and settle at a variety of fractal dimensions and fixed fractional-order. This shows that white noise concentration can effectively eradicate all insidiously, proactively, and freely virally infested cells, dramatically reduce the quantity of virally affected cells, and prevent the proliferation of contaminated nuclei.

Figures 12–14 predict the behaviour of uninfected $\mathbf{U}(\bar{\mathbf{t}})$, latently infected $\mathbf{S}(\bar{\mathbf{t}})$, actively infected $\mathbf{A}(\bar{\mathbf{t}})$, free virus $\mathbf{F}(\bar{\mathbf{t}})$, and antibodies $\mathbf{Q}(\bar{\mathbf{t}})$ at various fractal-dimension and fractional-orders. The corresponding attributed values: $\Lambda = 10, \; \varsigma = 0.1, \; \lambda_{1} = 2, \; \lambda_{2} = 2, \; \phi = 0.5, \; \nu_{1} = 0.5, \; \sigma = 5, \; \delta = 10, \; \varphi = 2, \; \nu_{2} = 10, \; \xi = 3, \; \chi = 2, \; \zeta = 4.$ Then, by increasing the white noise intensities to $\rho_{1} = 3.9, \; \rho_{2} = 3.7, \; \rho_{3} = 3.9, \; \rho_{4} = 3.9$ and $\rho_{5} = 3.8,$ and $\tilde{\mathbb{R}}_{0}^{s} < 1.$ This shows that the stochastic noise is demonstrated to be suppressed by the massive boom. The infectious populace is disappearing more significantly when both fractional-order and fractal-dimension are changed simultaneously in an infectious system in comparison to fractional systems, which leads to fascinating and biologically more plausible findings.

Figures 15–17 demonstrate the effect of uninfected $\mathbf{U}(\bar{\mathbf{t}})$, latently infected $\mathbf{S}(\bar{\mathbf{t}})$, actively infected $\mathbf{A}(\bar{\mathbf{t}})$, free virus $\mathbf{F}(\bar{\mathbf{t}})$, and antibodies $\mathbf{Q}(\bar{\mathbf{t}})$ at fixed fractal-dimension and fractional-orders with and without control, respectively. Considering an inadequate CTL reaction, we examine how virus replication affects the patterns of HCV and immunological reactions from acute infection through the chronic stage. This is accomplished using a mix of analytical and numerical techniques. Since the target cell restriction prevents the penetration of new viral variations in the case of severe liver damage, virus development is predicted to come to an end.

As a result of these pictorial outcomes, we draw the conclusion that by using this novel fractal-fractional operator concept, it is possible to detect more precise outcomes and to offer a wider insight of problems that arise in engineering and science as well as in the reality.

7.   Conclusions

In this article, we examined the variations in cellular complexities of a novel randomized fractal-fractional virus transmission system considering latently diseased tissues and a Holling type II functionality reaction. We discovered the existence of non-negative solutions to the examined system by accounting for environmental noise and the fractal effects of vaccination. In view of Itô's technique and Lyapunov candidate, we established the necessary assumptions of the stochastically permanence of the virus transmission scenario and the elimination of chronically diseased, productively contaminated cells and independent pathogen fragments. Ultimately, in order to create the suggested system, we employed the F-F calculus notion in the ABC context. Additionally, numerical simulations are provided to understand the tendencies of our theoretical model's analysis. We determine that increasing the noise strength will eventually render the virus obsolete. The illustration analysis shows that the fractal-fractional notion outperforms the integer-order and classical derivatives in terms of effectiveness and biological dependability. Upcoming research on viral infections, particularly the novel COVID-19, monkey pox and lumpy virus can confidently implement the revolutionary modelling methodology termed as the fractal-fractional operator.

Conflict of interest

The authors declare there is no conflict of interest.