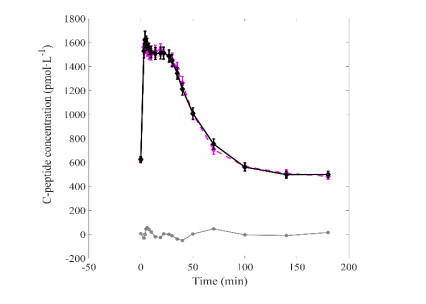
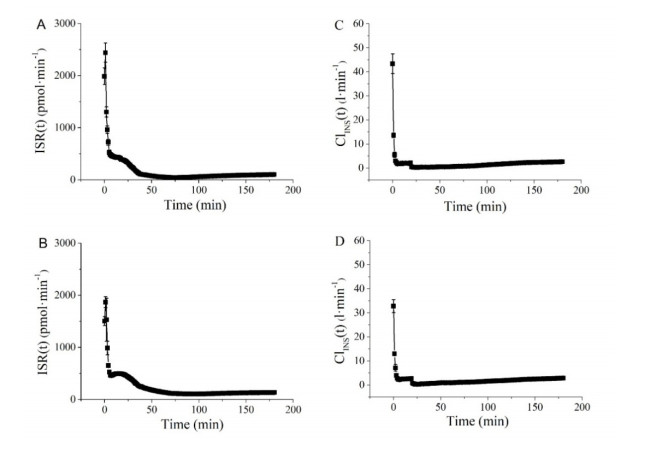
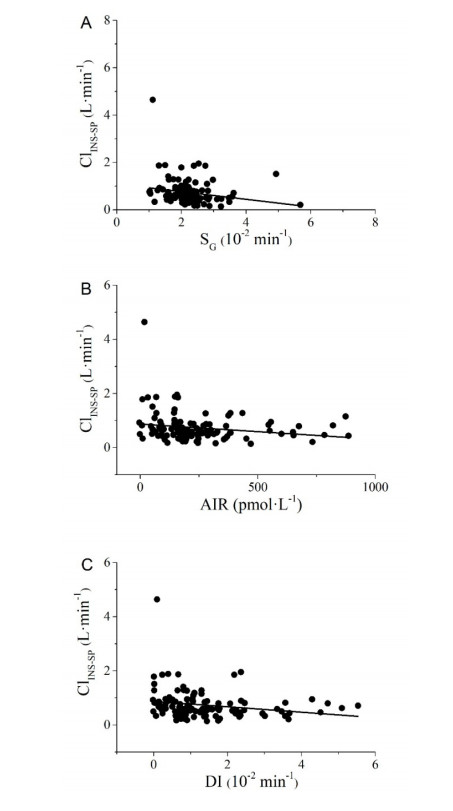
Women with a previous history of gestational diabetes mellitus (GDM) have increased risk of developing GDM in future pregnancies (i.e. recurrent GDM) and also Type 2 Diabetes (T2D). Insulin clearance represents one of the processes regulating glucose tolerance but has been scarcely investigated for its possible impairment in high-risk subjects. The aim of this study was to identify possible determinants of insulin clearance in women with a previous history of GDM. A detailed model-based analysis of a regular 3-hour, insulin-modified intravenous glucose tolerance test (IM-IVGTT) has been performed in women with a previous history of GDM (pGDM, n = 115) and in women who had a healthy pregnancy (CNT, n = 41) to assess total, first-phase and second-phase insulin clearance (ClINS-TOT, ClINS-FP and ClINS-SP) and other metabolic parameters (insulin sensitivity SI, glucose effectiveness SG, beta-cell function and disposition index DI). CLINS-SP was found increased in pGDM with respect to CNT and was found significantly inversely linearly correlated with SG (r = -0.20, p = 0.03, slope: -16.2, 95% CI -30.9 to -1.4, intercept: 1.1, 95% CI 0.7–1.4) and also with DI (r = -0.22, p = 0.02, slope: -10.0, 95% CI -18.5 to -1.6, intercept: 0.9, 95% CI 0.7–1.3). Disposition index, accounting for the combined contribution of insulin sensitivity and beta-cell function, and glucose effectiveness were identified as possible determinants of insulin clearance in women with a previous history of GDM. This may be of relevance for more accurate estimation and prevention of the risk for recurrent GDM and T2D.
1.
Introduction
Attachments and relationships are fundamental to human well-being during the course of evolution [1]. Humans are engrossed in webs of connections with fellow members through the cooperative formation of families, cultures and civilizations. Social behaviour is the mainspring in the evolution of human nature. Attachments and social bonds cannot be simply defined as these are completely hypothetical constructs and no one can directly measure them. However, attachments and social bonds are characterized by cognitive attraction or physical contact to a preferred partner [2]. The neurobiology of attachment and social bonds is very much dependent on the neuroendocrine substrates. Benefits of attachments and social bonds may be attributed to a few physiological processes which are supported by a few specific chemical pathways involving two neuropeptides, oxytocin and vasopressin [3],[4]. Exposure to oxytocin and vasopressin can retune the nervous system and thereby regulate emotions, social bonding, attachment, agammaession, healthy behaviour and mental health [1].
The neuropeptides oxytocin and vasopressin are the most interesting molecules for social neuroscience and there is a considerable genetic and structural resemblance between these structures [5]–[7]. Structural aspects indicate that two amino acids discriminate oxytocin and vasopressin and both of the neuropeptides have evolved from a common ancestral molecule, presumed to be vasotocin [8]. Oxytocin and vasopressin are synthesized in the somas of two groups of neurons which are situated in the paraventricular and supraoptic nucleus of the hypothalamus [9],[10]. This is followed by their transport along axons that project to the posterior pituitary [11]. They are ultimately released into the circulation playing the role of hormones on peripheral targets [6],[7]. According to Loup et al., in 1991, oxytocin and vasopressin act as neuromodulators or neurotransmitters within the brain apart from their well-documented peripheral actions [12]. The peripheral actions include uterine contraction and milk ejection in case of oxytocin whereas antidiuresis and vasoconstriction in case of vasopressin [11],[13]. In brain, they play the role of neuromodulators mainly via dendritic release in order to regulate complex social cognition and behaviours including attachment as it is evident that the dendrites of many neural populations transmit information back to their synaptic inputs by releasing neuroactive substances [14],[15].
Oxytocin and vasopressin were isolated and synthesized by Vincent du Vigneaud in 1953. This was the work for which he received the Nobel Prize in Chemistry in 1955 with the citation: “for his work on biochemically important sulphur compounds, especially for the first synthesis of a polypeptide hormone” [16]. In this mini-review, focus will be on these two wonder molecules oxytocin and vasopressin, “peptides of love and fear”. They play beneficial roles in social interactions, in maternal care and closeness, development of general trust and cooperation [17],[18]. The multi-dimensional roles of these two molecules also include breastfeeding, regulation of blood pressure (as peripheral effects) and social recognition, sexual behaviours and response to stress (as central effects) [17]. The exact relationship between central and peripheral oxytocin concentrations is not well known. A few research studies conducted on animals indicate that the central release from the hypothalamus and the peripheral release via the posterior pituitary is coordinated whereas other findings do not support this research study [18],[19]. In humans, a mixed result has been obtained. Some of the results are consistent with the related levels of central and peripheral endogenous oxytocin whereas a few reports show no significant associations. On the other side of the spectrum, it has been well established that vasopressin not only plays the role of a peripheral hormone with antidiuretic and pressor activities but is also a neurotransmitter/neuromodulator with numerous functions, found in many parts of the central nervous system [19].
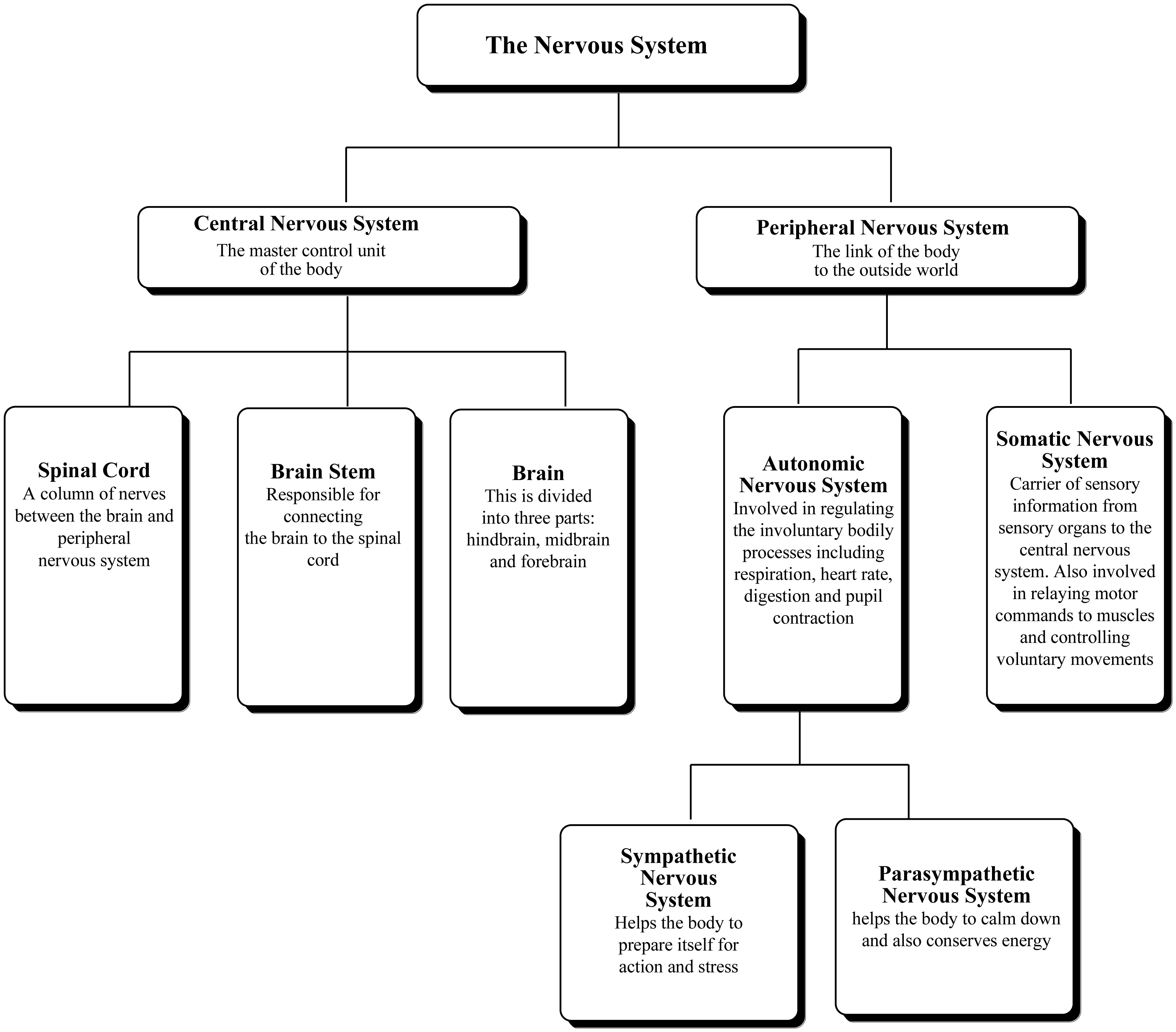
In this aspect, it is important to discuss that several regions of the brain play different roles which are socially and psychologically relevant [7]. The superior temporal sulcus is linked to the detection of biological motion. The medial prefrontal cortex and midline cortical structures have been attributed to self-related processing and awareness as well as in perspective taking. The temporal pole and amygdala are responsible for social scripts, emotions and judgments. The temporoparietal junction along with medial prefrontal cortex and temporal poles play an important role in mentalization of immediate goals and desires. As we all know, throughout the brain, prediction and predictive coding are thought to be central to information representation in multiple neural circuits. There are also evidences for specific systems representing expectations [7],[12]. Ventromedial prefrontal cortex and dorsolateral prefrontal cortex are the key regions playing significant roles in decision-making and instruction effects. Effects of expectation on perceptual decision-making have been shown to involve the hippocampus. Figure 1 represents a delineation of the nervous system scheme.
Oxytocin and vasopressin have made a noteworthy impact on modulation of fear and response to anxiety by regulating the hypothalamic-pituitary-adrenal axis (a complex set of direct influences and feedback interactions among three components namely the hypothalamus, the pituitary gland and the adrenal glands) and amygdala activity (a component of the limbic system, supposed to play important roles in emotion and behaviour) through its projections to the brain stem and hypothalamic structures [10],[14].
2.
Neurohormones share characteristics with both neurotransmitters and hormones: a brief idea
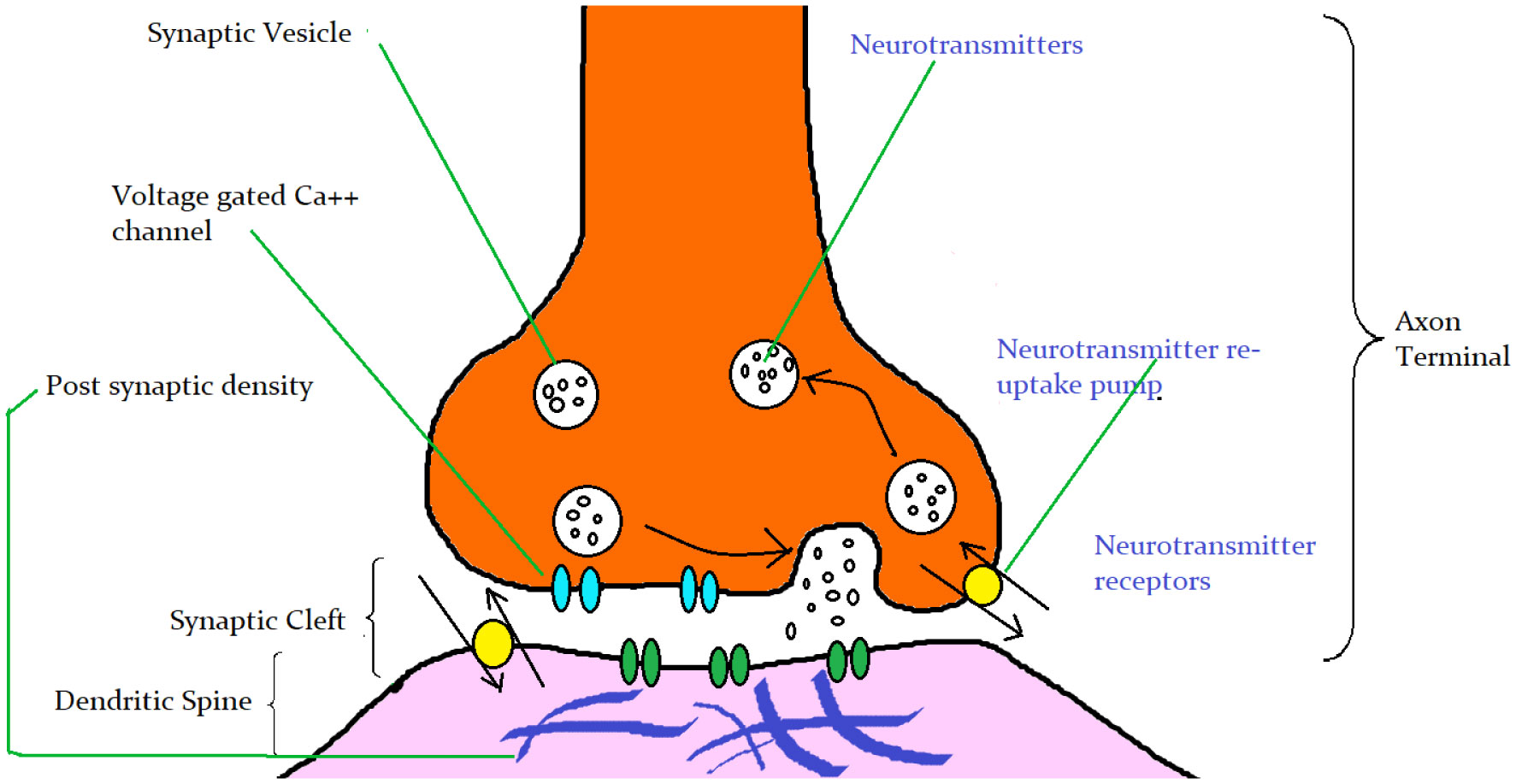
Neurotransmitters are chemical substances made by the nerve cells which are used by the neurons for the purpose of communications through the process of synaptic transmission often known as neurotransmission. They are specifically used for transmission of a message from a nerve cell across the synapse to a target cell in the form of another nerve cell, a gland cell and a muscle cell [20]. These are synthetized in and released from synaptic vesicles in synapses into the synaptic cleft. Consequently receptor proteins present in the cellular membrane of the target cells bind to such neurotransmitters thereby generally exciting target tissues often inhibiting or functionally modifying them [20],[21]. Neurons need to be capable of communicating with one another to transmit signals thereby sending messages throughout the body but the concern is that they are not simply connected to each other. The small space created at the end of each neuron is called synapse and this small space is needed to be crossed by the signal in order to communicate with the next cell. The process responsible for this is neurotransmission [22],[23]. A neurotransmitter is generally released from the axon terminal after an action potential has reached the synapse. As soon as an electrical signal reaches the end of a neuron, the release of vesicles or sacs containing the neurotransmitters takes place. The vesicles or sacs spill the neurotransmitters into the synapse and gradually move across the synaptic gap toward the adjacent cells. Neurotransmitters bind to the receptors present in these cells and induce changes in the concerned cells. After its release, the neurotransmitter gets attached to the receptor site in the forms of either exciting or inhibiting the receiving neuron depending on the nature of the neurotransmitter [24]. Importantly, the relationship between receptors and neurotransmitters are like a lock-and-key system. A specific neurotransmitter will only bind to a specific receptor. Excitatory property of neurotransmitters lies in the fact they can often bind to such receptors which cause an electrical signal to be transmitted down the cell whereas inhibitory property is manifested when a neurotransmitter blocks the signal from continuing thereby preventing the signal to carry on [23],[24].
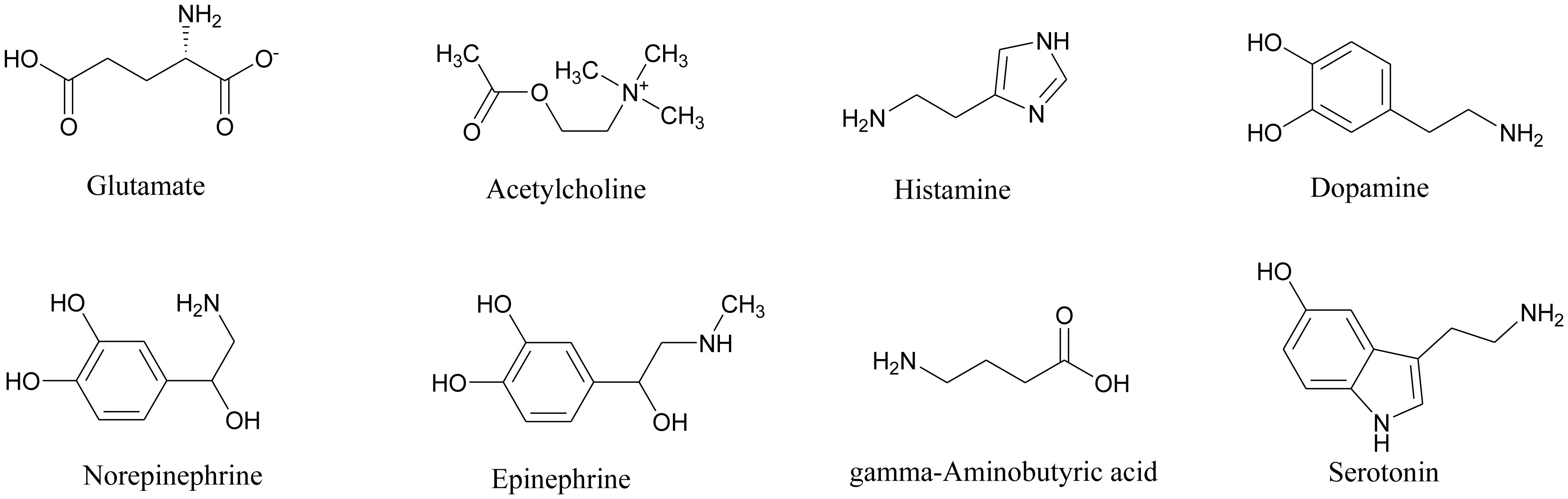
In order to manage everything from our breathing to our heartbeat and to keep our brains functioning, billions of neurotransmitter molecules continuously work. Psychological functions in the forms of pleasure, joy and fear are also affected by these chemical substances. Neurotransmitters are also essential to the function of complex neural systems and are synthesized from simple precursors like amino acids [25],[26]. Till now over two hundred unique neurotransmitters have been identified and most importantly they can be broadly divided into four different categories: excitatory neurotransmitters [Glutamate, Acetylcholine, Histamine, Dopamine, Norepinephrine (or Noradrenaline), Epinephrine (or Adrenaline)], inhibitory neurotransmitters [gamma-Aminobutyric acid, Serotonin and Dopamine], neuromodulators [Dopamine, Serotonin, Acetylcholine, Histamine, Norepinephrine] and neurohormones [Oxytocin, Vasopressin] (structures of the neurotransmitters are given in Figure 2 and their mode of action are given in Table 1) [27]–[30]. Figure 3 is given to represent the mechanism of action of neurotransmitters.
Hormones, on the other hand by definition, a chemical messenger molecule secreted by endocrine cells within endocrine glands and released into the bloodstream and travels throughout the body to find its target cells which may be within blood vessels or most commonly have target cells in tissues outside of the blood vessels [31]. Hormones can be eicosanoids, polypeptides and proteins, steroids, amino acid derivatives, fatty acid derivatives. They aid the communication between different parts of the body by sending chemical signals from one to the other. They play an important role in communicating between organs and tissues for physiological regulation. Apart from such active physiological roles, they play an important role in regulating the behavioural activities like respiration process, digestion, sensory perception, functioning of tissues, sleep control, induction of stress, excretion, lactation, metabolism, growth and development, reproduction and mood manipulation [32]. Hormones bind to specific receptor proteins in the target cell and regulate its functioning. This binding also results in the activation of a signal transduction pathway that in turn activates gene transcription thereby causing an increased expression of target proteins. However, non-genomic effects, being more rapid, can play in a cooperative way with genomic effects. Although many tissues are responsible for the secretion of hormones, endocrine glands are the key examples [33].
Before moving into the details of this mini-review, let us shed some light on the mode of actions of neurotransmitters and hormones. Both the chemicals, neurotransmitters and hormones play an important part in the body's physiology. The two different chemicals carry signals from one end of the body to another and are responsible for controlling a variety of physical and psychological functions like mood fluctuations, eating patterns, sleep cycles and many others [24],[26],[31]. They have certain differences along with a few striking similarities. However, the key difference between the two is that neurotransmitters are produced by the nervous system whereas the hormones are produced by the endocrine glands. Neurotransmitters after being released from the presynaptic nerve terminal move across the synaptic cleft followed by further movement to the next neuron where they bind to specific receptors and make changes in the electrical properties of target cells. Generally, neurotransmitters work locally, their actions are short-lived but very fast. Contrary to such characteristics of neurotransmitters, hormones on the other side are usually secreted from the endocrine system and then released into the bloodstream where they find their targets of action at some distance from its origin. They act on distant target cells for a longer period of time [24],[32].
Importantly, neurohormones share characteristics with both neurotransmitters and hormones. Just like neurotransmitters, neurohormones are released by neurons and similar to that of hormones, they travel in the bloodstream [33]. The best examples are the hypothalamic releasing hormones oxytocin and vasopressin (the antidiuretic hormone). In short, a neurohormone is a hormone that is produced and released by neuroendocrine cells into the blood. They are chemical messenger molecules synthesized in neurons but enter the bloodstream which carries them to distant tissues. Oxytocin and vasopressin are the only two well-known hormones released by the human posterior pituitary gland to act at a distance [34],[35].
Paraventricular and supraoptic nuclei in the hypothalamus are the major sites for the vasopressin production. However, vasopressin and its receptors are found in several brain nuclei and peripheral tissues. The physiological roles of vasopressin are mediated through both the peripheral and central mechanisms obviously including the regulation of blood pressure and fluid homeostasis [4],[5],[9]. It must not be forgotten that vasopressin is an important component of the endocrine stress response by means of its action in the posterior pituitary gland. In the pituitary gland, vasopressin promotes the secretion of Adrenocorticotropic Hormone (ACTH). V1a, V1b, and V2 are the three receptor subtypes where V2 receptors mediate the fluid regulating actions of vasopressin in the periphery. On the other hand, in the brain, V1a and V1b receptors are chiefly responsible for the behavioural and the central endocrine functions of vasopressin along with the central control of cardiovascular activity [12],[16].
Oxytocin on the other hand is released both into the central nervous system (CNS) and peripheral circulation from the neurosecretory cells in the paraventricular (PVN) and supraoptical (SON) nuclei of the hypothalamus. Anatomically, central and peripheral compartments of the oxytocin are separated by the blood-brain barrier. Oxytocin is involved in a range of social behaviours and social cognitive functions primarily through its central action. While the social cognitive effects of oxytocin are attributed to central mechanisms, oxytocin concentrations have typically been sampled in peripheral fluids like blood plasma, saliva and urine. Peripheral oxytocin concentrations can be correlated with psychological phenotypes or psychiatric disorder status [17],[34].
As mentioned earlier, oxytocin and vasopressin are produced in the overlapping regions of the hypothalamus, chiefly in large magnocellular neurons. These magnocellular neurons, which are situated in the supraoptic and paraventricular nuclei project their axons to the posterior pituitary. In the posterior pituitary, peptides are stored in small vesicles till the action potentials trigger their release into the peripheral circulation. Example includes labor and imbalance of water homeostasis. Oxytocin and vasopressin molecules which have been released in this way are mostly prevented from re-entering the central nervous system via the blood brain barrier [4],[5]. Often it is observed that a very small amount of the peripherally administered peptides cross over the cerebrospinal fluid. Oxytocin and vasopressin molecules play a significant role in the central nervous system as indicated by the observation that the concentrations of these molecules can be up to 1000 times higher in the brain than the peripheral blood. The central and peripheral release are mostly coupled but can also occur independently [6],[7].
3.
The chemistry of oxytocin and vasopressin
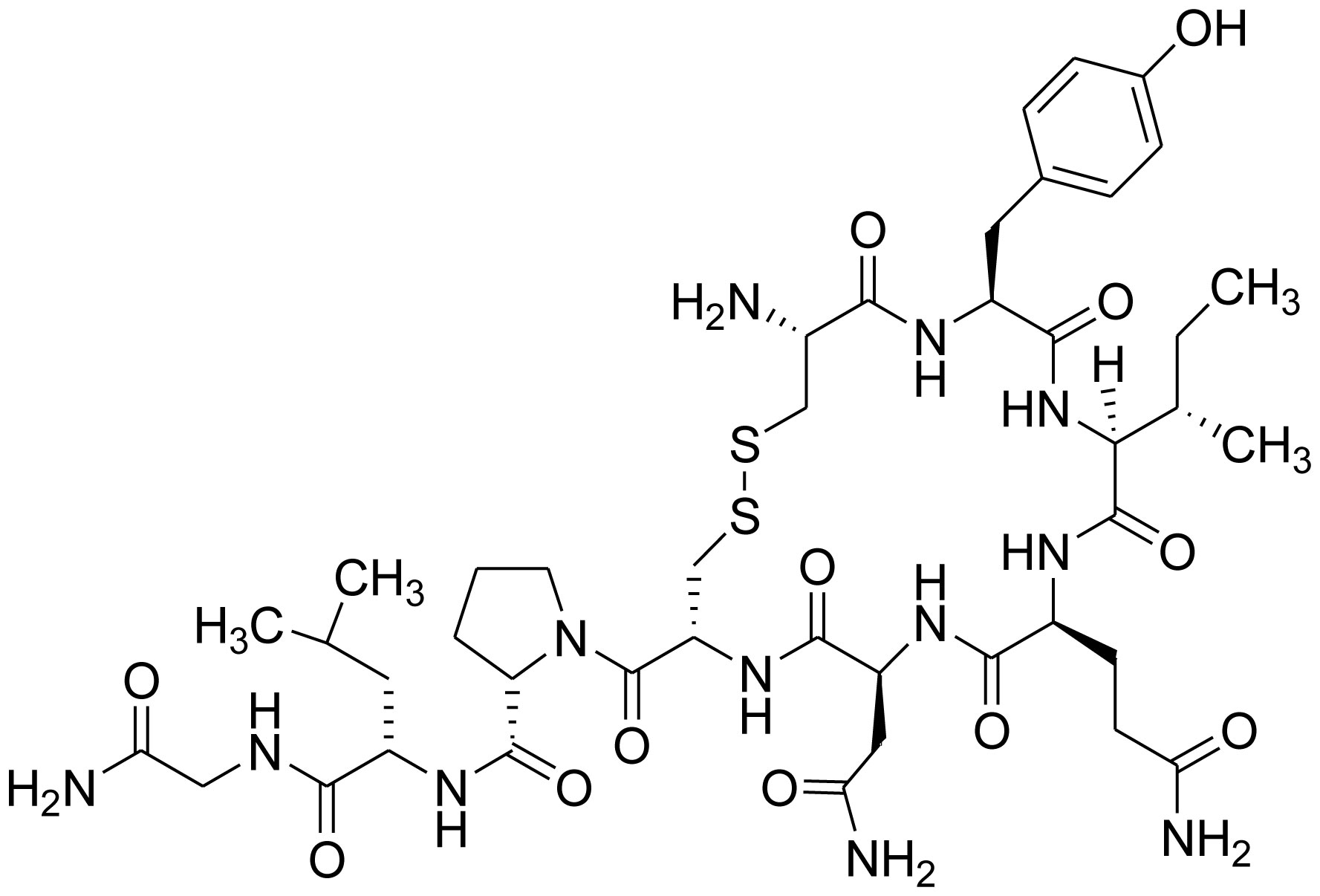
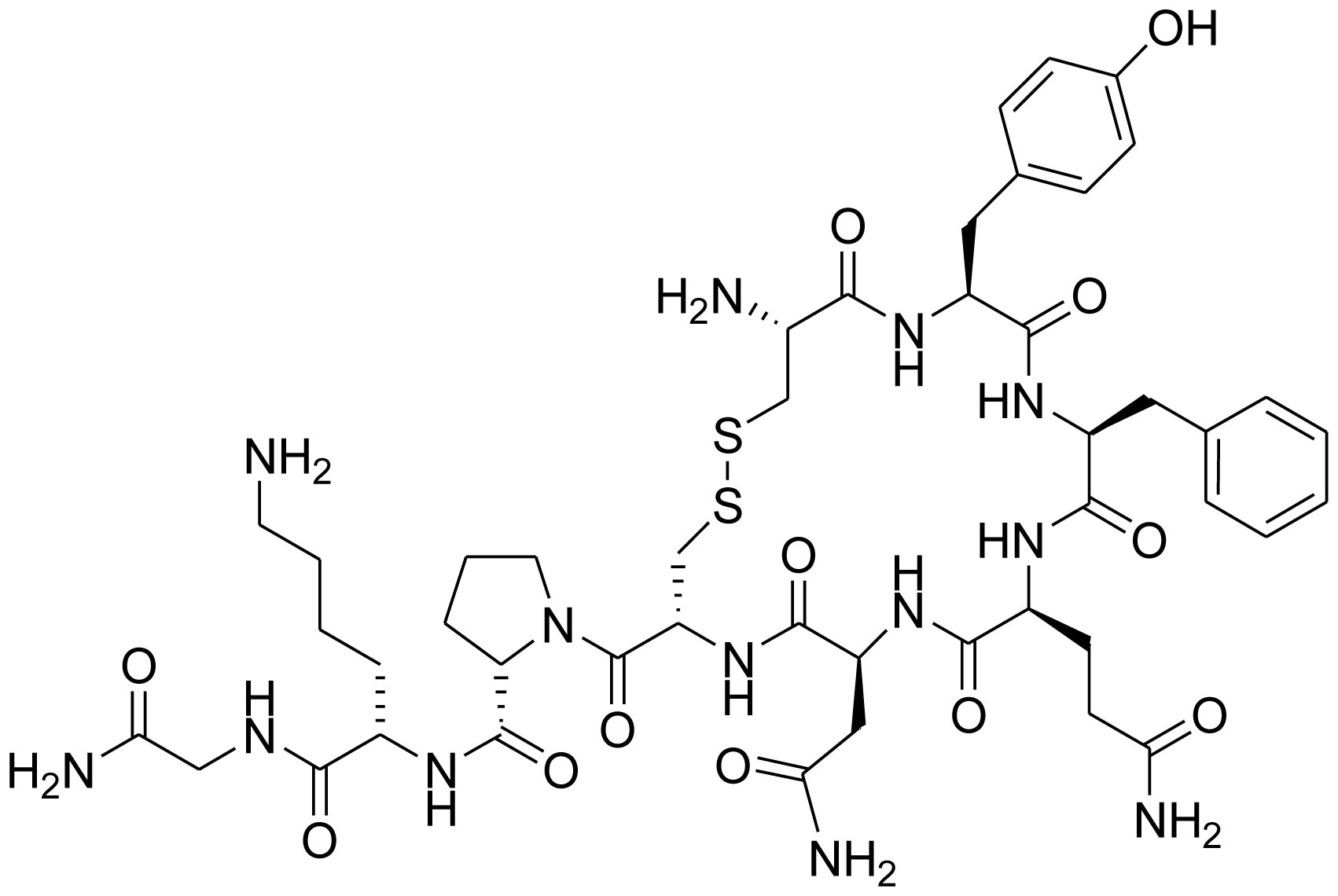
Oxytocin is generated in magnocellular neurosecretory cells in the supraoptic nucleus and paraventricular nucleus of the hypothalamus and it is discharged into the blood from the posterior lobe of the pituitary gland. Some neurons in the paraventricular nucleus that project to other parts of the brain and to the spinal cord are also responsible for the generation of oxytocin. Oxytocin was discovered by Henry Dale in 1906 [36]. However, its molecular structure (molecular formula: C43H66N12O12S2) was discovered in 1952. Oxytocin, a nonapeptide contains the sequence Cys-Tyr-Ile-Gln-Asn-Cys-Pro-Leu-Gly-NH2 (CYIQNCPLG-NH2) (Figure 4). C-terminal amino acid, glycine has been converted to a primary amide and a disulfide bridge is formed by the cysteine residues. Molecular mass of oxytocin is approximately 1007 daltons [37]. Oxytocin neurons make other peptides, including corticotropin-releasing hormone (CRH) and dynorphin but they act locally. It is worthwhile to mention that magnocellular neurons that make oxytocin are adjacent to magnocellular neurons that make vasopressin, and are similar in many respects. The biologically active form of oxytocin is octapeptide oxytocin disulfide, the oxidized version. However, oxytocin also exists as a reduced straight-chain dithiol nonapeptide called oxytoceine. Oxytoceine may be oxidized to oxytocin through the dehydroascorbate/ascorbate redox couple thereby showing the role of free radical scavenger [38],[39].
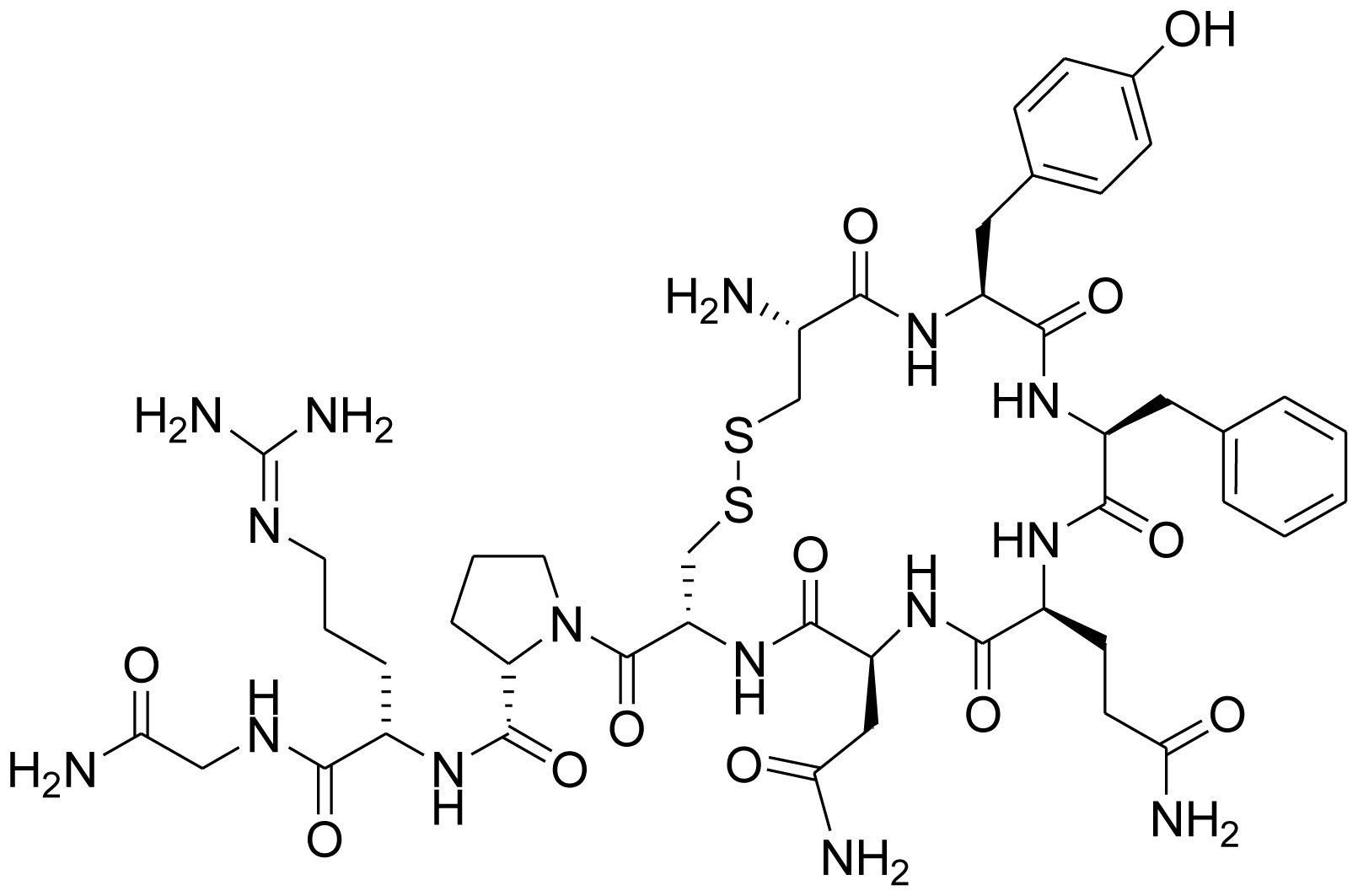
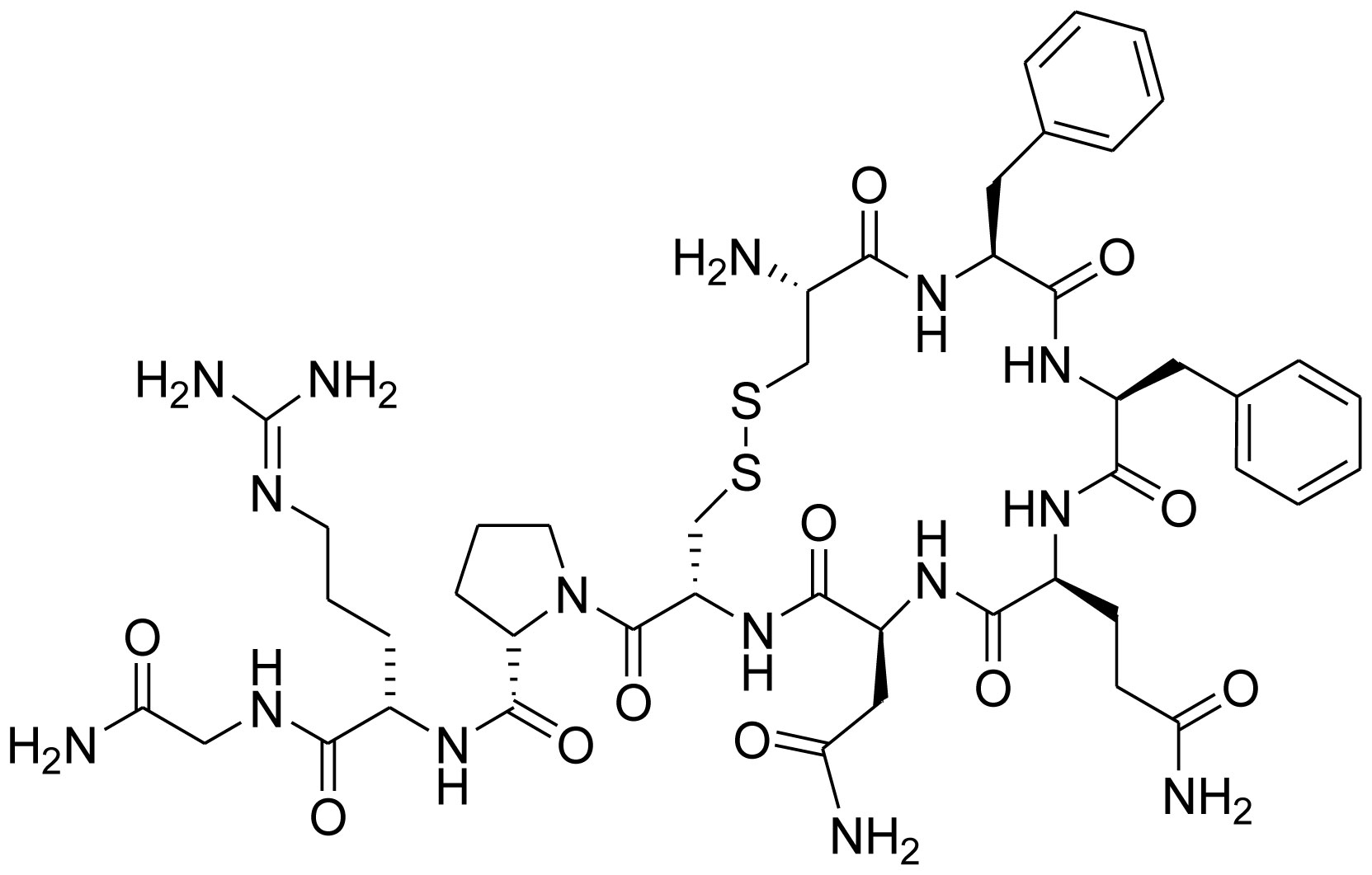
Vasopressin (C46H65N15O12S2), a nonapeptide is synthesized in neurons in the hypothalamus as a peptide prohormone and is converted to arginine vasopressin (AVP). It is derived from a preprohormone precursor that is synthesized in the hypothalamus, from which it is liberated during transport to the posterior pituitary [40],[41]. AVP contains the amino acid sequence Cys-Tyr-Phe-Gln-Asn-Cys-Pro-Arg-Gly-NH2 (Figure 5), where the cysteine residues forming a disulfide bond and the C-terminus of the sequence is converted to a primary amide. Lysine is placed in the position of Arginine at the eighth position of Lysine vasopressin often called lypressin (Figure 6), usually found in pigs and some related animals. Phenypressin is observed in some marsupials and the sequence is Cys-Phe-Phe-Gln-Asn-Cys-Pro-Arg-Gly-NH2 (Figure 7) [42].
The neuropeptides oxytocin and vasopressin possess a considerable structural resemblance. Both of them are phylogenetically conserved nonapeptide (in a six amino acid ring, formed by disulfide bridge involving two cysteines) and a three amino acid tail (with a terminal amine group) though their sequence of amino acids differ at two positions [43]–[45]. We have discussed that the structure of AVP is Cys-Tyr-Phe-Gln-Asn-Cys-Pro-Arg-Gly-NH2 whereas the structure of Oxytocin is Cys-Tyr-Ile-Gln-Asn-Cys-Pro-Leu-Gly-NH2, a distinct difference in the chemical structure of oxytocin and AVP with respect to 3rd and 8th position. The amino acid sequence of oxytocin includes an isoleucine and a leucine at the third and eighth position, respectively while in the corresponding positions, the structure of AVP contains a phenylalalanine and an arginine. Interestingly, in most species, both the genes are located on the same chromosome and they are separated by distance of approximately less than 15,000 bases and are transcribed in opposite directions. The two genes originated from a gene duplication event [44],[45].
The precursors for oxytocin and vasopressin consist of 12 amino acids. They are synthesized and released in combination with Neurophysins, the carrier proteins. Neurophysin-I is the carrier protein for oxytocin. Vasopressin, on the other hand, is analogously bound and transported by Neurophysin-II. Later, the precursors are cleaved into the “mature” versions of these peptides. The magnocellular neurons responsible for the secretion of vasopressin and magnocellular neurons responsible for the secretion of oxytocin are quite adjacent. This is responsible for their similarity in many respects especially with respect to cross-reactions. For example, oxytocin causes a slight antidiuretic function whereas uterine contractions are often caused due to high levels of AVP [46].
4.
The social and psychobiological importance of oxytocin
In this section, let us discuss the cause of some most important feelings in mankind: love, trust and attachment. Nothing can be better responsible for these except oxytocin. The word oxytocin was coined from the term oxytocic. Greek oxys, and, tokos, meaning “quick birth”. As we have already discussed, oxytocin, a peptide hormone and a neuropeptide, produced by the paraventricular nucleus of the hypothalamus and released by the posterior pituitary also acts as a neurotransmitter in the brain. Oxytocin is typically considered for the consequence it has on prosocial behaviours, such as its role in facilitating faith and attachment between individuals [1],[47]. Consequently, oxytocin is often incorrectly labelled by some of us as the “love hormone” as it is often associated with good feelings and emotions. But its role in the body is much more multifaceted than that since it plays a role in social bonding, sexual reproduction in both sexes [47]–[49]. Oxytocin is released into the bloodstream as a hormone in response to stretching of the cervix and uterus during labor and with stimulation of the nipples from breastfeeding. It is very much responsible in birth, bonding with the baby and obviously milk production. It is important to note in this aspect that oxytocin also finds applications as an important medication to facilitate childbirth. From a psychobiological viewpoint, oxytocin has been implicated in the etiology of autism, with one report suggesting autism is linked with genomic deletion of the gene containing the oxytocin receptor gene (OXTR) [48]–[50]. Just like in humans, oxytocin plays an important role in social behaviours in many species. In a 2003 study, both humans and dog oxytocin levels in the blood rose after five to 24 minutes of a petting session [51]. This probably plays a role in the emotional bonding between humans and dogs. Often maternal behaviour commences due to oxytocin. Female rats given oxytocin antagonists after giving birth do not exhibit typical maternal behaviour. On the other hand, virgin female sheep show maternal behaviour towards alien lambs upon cerebrospinal fluid infusion of oxytocin, which they would not do otherwise [52]. Nevertheless, oxytocin has a more multifaceted role than exclusively enhancing prosocial behaviours [53]. Oxytocin does not directly elicit fear or anxiety. Nasally administered oxytocin has been reported to decrease fear, possibly by inhibiting the amygdala (which is thought to be accountable for fear responses) [54]. Some researchers have argued oxytocin has a general enhancing outcome on all social emotions, since intranasal administration of oxytocin also amplifies envy and schadenfreude [55]. Individuals who receive an intranasal dose of oxytocin recognize facial expressions of disgust faster than persons who do not receive oxytocin [52],[55]. Oxytocin produces antidepressant-like effects in animal models of depression and a scarcity of it may be involved in the pathophysiology of depression in humans. The antidepressant-like effects of oxytocin are not blocked by a selective antagonist of the oxytocin receptor suggesting that these effects are not mediated by the oxytocin receptor [56]. It has been shown that oxytocin differentially affects males and females. Females who are administered oxytocin are overall faster in responding to socially relevant stimuli than males who received oxytocin. Additionally, after the administration of oxytocin, females show increased amygdala activity in response to threatening scenes. However, males do not show increased amygdala activity [57]. It has also been shown that testosterone directly suppresses oxytocin in mice. Serious methodological questions have arisen, however, with regard to the role of oxytocin in trust, faith and generosity [58]. Empathy in healthy males has been shown to be increased after intranasal oxytocin. Trust is increased by oxytocin. Disclosure of emotional events is a sign of trust in humans. When recounting a negative event, humans who receive intranasal oxytocin share more emotional details and stories with more emotional significance. Some studies vividly indicate that high levels of plasma oxytocin have been associated with romantic attachment. For instance, if a couple is separated for a long period of time, anxiety can increase due to the lack of physical affection. Oxytocin may assist romantically attached couples by lessening their emotions of anxiety when they are separated [59]. Sex is one of our biggest obsessions—causing thrills, anguish and downright confusion. But until recently, exactly what happens in the brain for the duration of sex was something of a mystery to scientists [60],[61]. A dose of the oxytocin may make people's orgasms more intense as suggested by a new study from a German research group. However, Oxytocin had no consequence on sex drive or arousal for either men or women nor did it affect the ability to accomplish an erection for men or vaginal lubrication for women [60],[62],[63].
5.
The social and psychobiological importance of vasopressin
Arginine vasopressin (AVP), often called argipressin travels down the axon of the cell and gets released from vesicles into the circulation in response to extracellular fluid hypertonicity. AVP plays significant roles in terms of increasing the amount of solute-free water reabsorbed into the circulation from the filtrate in the kidney tubules of the nephrons, thus regulating the tonicity of body fluids [64]. Concentration of urine and reduction of urine volume are the consequences of this renal reabsorption of water. It also helps in tightening the arterioles, which increases peripheral vascular resistance thereby raising the arterial blood pressure by inducing moderate vasoconstriction. Research suggests though it has a half-life (18–22 minutes), AVP may also be released directly into the brain from the hypothalamus, thereby playing an important role in sexual drive, social behaviour and pair bonding [65]. Vasopressin receptor 1A (V1AR) or arginine vasopressin receptor 1A (officially called AVPR1A) in prairie vole ventral forebrain regions facilitates and coordinates the reward circuits during partner preference formation, critical for pair bond formation. The role of AVP is involved in memory formation, delayed reflexes and social behaviour. AVP gets released into the brain during sexual activity and is also involved in initiating and sustaining patterns of activity that support the pair-bond between the sexual partners [66].
The physiological role of AVP includes the regulation of fluid homeostasis and blood pressure. These are mediated both through peripheral and central mechanisms. Besides, AVP due to its actions in the posterior pituitary gland, also plays an important role in the endocrine stress response. V1a, V1b and V2 are the three receptor subtypes for AVP. Among the three receptor subtypes, in the periphery, the fluid regulating actions of AVP are mediated by V2 receptors. However, in the brain, the V1a and V1b receptors mediate the behavioural and central endocrine functions of AVP. This is worthwhile to mention that these receptors are also involved in the central control of cardiovascular activity [65],[66].
AVP has several peripheral and central functions. Impact of AVP on human memory has been investigated and it has been observed that AVP is not primarily responsible for the control of attention in human beings. Animal research regarding the effects of AVP in humans shows that the mediation of behavioural effects of vasopressin relies primarily on hippocampal and related limbic structures [67],[68]. AVP is concerned to improve declarative memory formation in humans and intrinsically involved in both memory consolidation and memory retrieval. This effect concentrates on the memory encoding processes. The role of AVP in the central nervous system chiefly depends on the region where it is released. However, modulation of agammaessive behaviour is also involved. The effects of AVP have been found to be concerned with social behaviours that are usually labelled masculine like combativeness, pair-bond formation, scent marking and courtship. AVP is responsible for raising an individual's anxiety through its expression in the hypothalamic paraventricular nucleus. Generally speaking, AVP can be said to influence or enhance vigilance, anxiety, arousal and activation [69]–[71].
ASD, autism spectrum disorder, a brain disorder characterized by social impairments from the onset of childhood. ASD is diagnosed behaviourally due to the lack of the discovery of biomarkers. Emerging evidence indicates that low cerebrospinal fluid concentration of the AVP, the ‘social’ neuropeptide is a marker of social impairment in children with autism and this is significantly lower in pediatric ASD cases with respect to controls [72]–[74].
6.
A brief idea about the oxytocin-vasopressin pathway
Oxytocin and vasopressin are components of an integrated pathway where oxytocin and vasopressin interact dynamically with their respective receptors, the oxytocin receptor (OTR) and vasopressin receptor (V1aR) are termed as the Oxytocin-Vasopressin pathway. Both the peptides can bind to both the receptors, OTR and V1aR in vitro. Social engagement and defensive behaviours are affected through this pathway. Many instances can be cited where oxytocin acts in combination with vasopressin via vasopressin receptor (V1aR) often through the effects on both the receptors in order to regulate the capacity to form selective social behaviours [75]. Adaptation to highly emotional situations and the development of selective attachments are controlled by the Oxytocin-Vasopressin pathway. The presences of both the peptides along with the molecules like dopamine are responsible for such experiences. The effects of oxytocin and vasopressin interact dynamically to alter and influence the perception of fear and safety. In the evolutionary context, vasopressin is the older molecule with apparently the older receptors. Vasopressin is involved in mobilized behaviours including self-defence. Oxytocin and vasopressin both are necessary along with their receptors in manifesting sexual behaviour, paternal behaviour and pair bonding [76],[77].
7.
Oxytocin and vasopressin as medicine
Pitocin and Syntocinon are the common trade names in which synthetic oxytocin are often sold. In the gastrointestinal tract, oxytocin is destroyed therefore oxytocin must be administered by injection or as nasal spray [78]. Synthetic oxytocin is frequently prescribed nowadays in maternity care around the world as it speeds up labor and prevents postpartum haemorrhage even occasionally it is life-saving for both mothers and babies. In order to induce labor and to support labor in case of non-progression of parturition injected oxytocin analogues are often used. It has replaced ergotamine as the most important agent to increase uterine tone in acute postpartum haemorrhage. Oxytocin is also administered just after birth to prevent postpartum hemorrhage if the uterus does not continue to contract and stop bleeding [79],[80]. Oxytocin has a half-life of typically about three minutes in the blood. Oxytocin, when given intravenously, does not generally enter the brain in considerable quantities as it is primarily excluded from the brain by the blood-brain barrier. Often to stimulate breastfeeding and to increase milk production, oxytocin nasal sprays have been used but the efficacy of this approach is uncertain. Atosiban (Tractocile), the tocolytic agent performs the role of an antagonist of oxytocin receptors. Nowadays, in many countries, this drug is registered to suppress premature labor between 24 and 33 weeks of gestation as side-effects are lesser for this drug than the drugs previously used for this purpose in the form of salbutamol, ritodrine and terbutaline. When used at recommended doses, oxytocin is relatively safe. However, potential side effects may comprise: seizures, subarachnoid hemorrhage in central nervous system; blood pressure, increased heart rate, systemic venous return, cardiac output and arrhythmias in cardiovascular system; pelvic hematoma, impaired uterine blood flow, tetanic uterine contractions, uterine rupture, postpartum hemorrhage in genitourinary organs [80],[81].
Vasopressin, on the other hand is an endogenous hormone that is responsible principally for osmoregulation and blood volume control. Vasopressin is also used as a medication under the trade name of Pitressin or Pressyn [82]. The use of Vasopressin in cranial diabetes insipidus and variceal bleeding is well-established. It shows antidiuretic action by increasing the reabsorption of water by the renal tubules and contraction of muscle of the gastrointestinal tract along with all parts of the vascular beds. Evidence shows that in asystolic cardiac arrest, vasopressin in all probability is more effective than epinephrine in restoring cardiac output [83]. Desmopressin, a synthetic analogue of arginine vasopressin has 10 times antidiuretic action compared to that of vasopressin, though vasoconstrictor action is 1500 times less. Terlipressin, an analogue of vasopressin used as a vasoactive drug in the management of low blood pressure. Terlipressin has been found to be effective when norepinephrine does not work. Terlipressin plays a significant role in preventing urination [83],[84].
Septic shock is a potentially fatal medical condition that occurs when sepsis takes place. Septic shock is a consequence of a systemic infection that is characterized by hypotension unresponsive to fluid resuscitation. Maintenance of the mean arterial pressure is needed for the patients with septic shock along with suitable antimicrobial therapy. However, as a second line therapy in septic shock patients, vasopressin infusions can be used especially for those who are not responding to fluid resuscitation or infusions of catecholamines (e.g., dopamine or norepinephrine) [85].
Oxytocin in the central nervous system influences social cognition and behaviour, making it a potential candidate for treating clinical psychiatric disorders such as schizophrenia, post-traumatic stress disorder, borderline personality disorder and autism in light of research using both single and chronic administration etiquettes. Intranasal oxytocin has been shown to facilitate the encoding, consolidation and recognition of social stimuli in various contexts along with its important role in the treatment of inflammation and pain, dementia, controlling weight, and ageing-related neurocognitive decline [86]. Intranasal administration of oxytocin has been proposed as a probable delivery route to central nervous system. Several studies have revealed that intranasal administration of oxytocin has been found to enhance peer recognition and bonding behaviour across numerous mammalian species. In adult humans, improvement of eye gaze, emotion recognition and development of trust have been observed by intranasal administration of 24 International Units (IU) of oxytocin [87],[88]. Even in adults with autism, a single dose of oxytocin put a significant effect on acute symptoms. Intranasal administration has been preferred owing to it its well tolerability and its ease of use. A research work on this aspect has indicated that administering oxytocin using either intranasal spray or a nebulizer to 15 primates (Macaca mulatta) has increased the oxytocin concentration in the cerebrospinal fluid as well as in blood [89].
A comparative survey between intranasal and intravenous oxytocin administration clearly indicates that administration of intranasal oxytocin directly travels to the brain. The social-cognitive effects of intranasal oxytocin are not primarily due to effects on peripheral oxytocin receptors. It has been observed that in spite of having comparable peripheral oxytocin levels after intravenous and intranasal administration, neural and social cognitive effects are only observed after intranasal administration. Results also indicate that increasing peripheral oxytocin level via intravenous administration does not influence the social cognition and neural activity via activation of peripheral oxytocin receptors, at least with a 1 IU intravenous dose. It has also been observed that it is intranasal rather than intravenous, oxytocin administration increases the release of central endogenous oxytocin.
8.
Conclusions
This mini-review showcases the chemistry, the social and the psychobiological importance of oxytocin and vasopressin. Oxytocin, vasopressin, and their receptor systems provide neural substrates that are responsible for positive social responses toward partners. Vasopressin is the evolutionarily older one compared to oxytocin and is implicated in mobilized behaviours including defence of self and the family. Vasopressin system is also associated with anxiety, response to stress and/ or traumatic events. On the other hand, oxytocin and activation of the oxytocin receptor is of special significance with respect to adaptations involving high levels of sociality and psychological safety. The combined effects of two neuropeptides assist to permit optimal parental and sexual responses. Although many studies are needed regarding the mode of action of oxytocin and vasopressin in biological systems, this mini-review attempts to highlight a few important facts about the two wonder molecules of immense social and the psychobiological relevance.









 DownLoad:
DownLoad: