Disturbance observer based fixed time sliding mode control for a class of uncertain second-order nonlinear systems

1.   Introduction

Owing to its remarkable robustness in handling systems with parameter uncertainties and external disturbances, sliding mode control (SMC) has been widely applied across various fields ^{[1,2,3,4,5,6]}, including mobile robotics, missile guidance, unmanned aerial vehicles (UAVs), and industrial automation. The design of a sliding mode controller involves two primary steps: first, constructing a sliding mode surface that accurately characterizes the system state's behavior on this surface; and second, formulating a control law based on the system's state equations to drive the system state toward and maintain it on the sliding surface. Despite the switching function's contribution to SMC's robustness, the high-frequency switching associated with the discontinuous control law introduces a chattering problem. To address this issue, numerous methods have been developed. Shen et al. ^[7] proposed a higher-order sliding mode control (HOSMC) scheme, in which the discontinuity term is embedded into the higher-order derivatives of the sliding mode surface, effectively eliminating the chattering observed in lower-order sliding mode surfaces. In ^[8], Bartolini et al. introduced the super-twisting algorithm (STA), where the control input is derived from an integral term, thus avoiding high-frequency switching and consequently reducing system chattering. Furthermore, ^[9] presented a continuous sliding mode control law for robotic systems equipped with flexible actuators, which successfully eliminates system chattering.

Conventional linear sliding mode control (LSMC) only ensures that the system state asymptotically approaches zero ^[10]. For example, Pan et al. ^[11] developed a time-varying linear sliding surface, achieving exponential convergence for quadrotor states. However, LSMC guarantees only exponential asymptotic convergence of the system error, meaning the system error converges to zero as time approaches infinity. To address this limitation, terminal sliding mode control (TSMC) was introduced, which ensures finite-time convergence. In ^[12], TSMC was applied to manipulator tracking control, enabling the output tracking error to converge to zero within a finite time. In ^[13], a multi-input fast non-singular terminal sliding mode control (FNTSMC) strategy was adopted for trajectory tracking in UAVs, ensuring singularity-free finite-time stability and robustness. However, the convergence rate of TSMC is slower compared to LSMC. To achieve faster convergence speeds, a fast terminal sliding mode (FTSM) structure combining LSMC and TSMC was developed ^[14,15]. It should be noted that the upper bound function for convergence time in finite-time sliding mode control is a complex nonlinear equation dependent on system states and controller parameters. Therefore, when the initial state of the system is uncertain, an accurate upper bound for convergence time cannot be determined. For fixed-time convergence, the convergence time of the system state is independent of the initial conditions. Compared to finite-time convergence, fixed-time stability offers various superior performance characteristics and has garnered significant attention. Polyakov et al. ^[16] proposed a fixed-time sliding mode control scheme for nonlinear systems, ensuring that the stabilization time is independent of the initial state. In ^[17], fixed-time sliding mode control schemes were utilized to solve the adaptive fixed-time attitude stabilization problem for rigid spacecraft. However, a common shortcoming of many fixed-time sliding mode controllers is the introduction of negative exponential coefficients, which can lead to singularity issues. To address this challenge, several mature solutions have been proposed. Zhao et al. ^[18] introduced a control scheme with switchable sliding surfaces to avoid the singularity problem. Wang et al. ^[19] resolved the singularity issue by replacing the fractional power term with a quadratic polynomial function. In ^[20], an exponential non-singular terminal sliding mode was proposed to eliminate singularities and enhance the convergence rate. Although these control schemes effectively solve the singularity problem, they often involve multiple controller parameters, complicating the parameter tuning process. Therefore, developing a non-singular fixed-time sliding mode controller with a simpler structure remains a valuable area for further investigation. Additionally, system parameter uncertainties and external disturbances significantly affect the tracking accuracy of the controller. To mitigate these effects, disturbance observers have been widely applied in various control systems ^{[21,22,23,24]}. Xiao et al. ^[25] proposed an asymptotically stable disturbance observer. Unlike the work documented in ^[26], the disturbance observer presented in ^[25] does not assume that the disturbance is smooth or that its time derivative decays over time. However, when the time derivative of the disturbance does not converge, the estimation error will converge to a region near the origin, failing to guarantee the asymptotic stability of the estimation error.

Based on the aforementioned problems, this paper develops a non-singular and chattering-free fixed-time sliding-mode control surface that features a simple structure (i.e., it does not require many controller parameters for adjustment). Additionally, a fixed-time disturbance observer is introduced. With the help of this disturbance observer, a novel fixed-time sliding mode control scheme is proposed, which achieves high-performance trajectory tracking for a second-order nonlinear system. The primary contributions of this paper can be summarized as follows:

(1) This paper introduces a novel fixed-time sliding mode controller based on a sine function. Unlike traditional controllers that employ piecewise functions to avoid singularities due to power function differentiation, our approach using a sine function effectively mitigates these issues. In contrast, our method requires fewer control parameters for adjustment, simplifying the tuning process.

(2) This paper proposes a fixed-time disturbance observer to enhance the accuracy of the sliding mode controller. Compared with existing methods ^[25,26], the designed observer relaxes the assumptions on the disturbance: it does not require the total disturbance to be continuously differentiable or its derivative to be zero. This enables the observer to estimate rapidly changing disturbances. Furthermore, by estimating the higher-order derivatives of the system states, the requirements for using the observer are reduced, thereby extending its applicability.

2.   Problem statement

2.1.   Preliminaries

Consider the nonlinear system described by:

where $x \in \mathbb{R}$ represents the system state, $f: \mathbb{R}_+ \times \mathbb{R} \to \mathbb{R}$ is a known nonlinear function of time and state, $b$ is a known scalar input coefficient, $u(t) \in \mathbb{R}$ denotes the control input, and $d(t, x, \dot{x})$ represents the uncertain term, which encompasses parameter uncertainties and external disturbances.

Definition 2.1. The equilibrium of system (2.1) is said to be finite-time stable if it is Lyapunov stable and achieves convergence in finite time. Specifically, for all $x \in \mathbb{R}$, there exists an upper bound convergent time function $T(x_0) \ge 0$ such that $\lim_{t \to T(x_0)} x(t) = 0$, and for all $t \ge T(x_0)$, $x(t) = 0$.

Definition 2.2. The equilibrium of system (2.1) is said to be fixed-time stable if it is globally finite-time stable and there exists an upper bound $T > 0$ for the convergence time function, where $T$ is independent of the system's initial condition.

Definition 2.3. The system (2.1) is said to be practical fixed-time stable if the system (2.1) is fixed-time stable and there exists a bounded region $\Omega \subseteq \mathbb{R}$ and a positive scalar $T \in \mathbb{R}$ such that the system state $x(t)$ converges to the bounded region $\Omega$ after the time $T$.

Assumption 2.1. It is assumed that the uncertainties and disturbances in the nonlinear system are unknown but bounded. Specifically, it is assumed that $|d| \le a$, where $a$ is a positive constant.

2.2.   Control objective

In this paper, the following second-order nonlinear system is considered:

where $\mathbf{x} = [x_1, x_2]^T \in \mathbb{R}^2$ is the system state vector, $f(t, \mathbf{x})$ represents a known nonlinear function, $b$ is a known scalar, $u(t) \in \mathbb{R}$ is the control input, and $d(t, \mathbf{x})$ denotes the uncertain term caused by parameter uncertainties and external disturbances.

For the nonlinear system (2.2), the tracking error is defined as:

where $x_r(t)$ is the reference trajectory.

Taking the time derivative of the tracking errors yields:

This study aims to design a fixed-time disturbance observer-based sliding mode controller to ensure that the tracking errors of the closed-loop system (2.3) converge to zero within a fixed time, independent of the initial conditions.

3.   Main results

3.1.   Fixed-time convergence

Consider the following nonlinear function:

where $k_1$, $k_2$, and $k_3$ are positive constants.

To ensure the continuity of the function $\Xi(y)$ in (3.1) and its derivative with respect to $y$ at $|y| = 1$, the following conditions must be satisfied:

From these conditions, we derive:

Clearly, the parameters satisfy the following conditions:

Property 3.1. For the function $\Xi(y)$, $y \in \mathbb{R}$ with parameters as in (3.2), the following holds:

Proof. The function $\Xi(y)$ in (3.1) is an even function with respect to $y$. Define $g(y) = \sin^2(y) + y + 1$. The minimum value of $g(y)$ in $0 \le y < 1$ equals the minimum value of $\sin^2(|y|) + |y| + 1$ in $|y| < 1$. Taking the derivative of $g(y)$ with respect to $y$, we have:

Thus, $g(y)$ monotonically increases in the interval $0 \le y < 1$. Therefore, $g(y) \ge g(0) = 1$.

Further, we obtain:

From (3.2), we know $k_1 > k_3 > k_2 > 0$, so $\min(k_1, k_2) = k_2$. Therefore, for $|y| < 1$, $\Xi(y) \ge k_2$. □

Theorem 3.1. Consider the following nonlinear system:

The system state approaches 0 within a fixed time, and the upper bound of the convergence time $T_0$ is estimated by:

Proof. Define the function $V_0(t)$ as:

Taking the derivative of $V_0(t)$ with respect to time, we have:

For $|y(t)| \ge 1$, according to Property 3.1 and (3.6), we have:

This can be rewritten as:

Solving the differential equation yields:

Since $|y(t)| \ge 1$ and (3.6), we have:

Further, we obtain:

Namely, for $t \ge t_{1}$, $|y(t)| \le 1$ is guaranteed, where $t_{1} = \frac{5}{k_3}$.

For $|y(t)| < 1$, according to Property 3.1, (3.3), and (3.6), we have:

This can be rewritten as:

Solving the differential equation yields:

Since $t \ge t_{1}$, $|y(t)| \le 1$ and (3.6), we have:

Finally, we obtain that for $t \ge T_0$, $y = 0$ holds. □

3.2.   Non-singular sliding mode controller design

In order to conveniently analyze the stability and fixed convergence time of the sliding mode controller, some theorems are given as follows.

Theorem 3.2. For the tracking error system (2.3), when the system state is on the designed sliding surface $S_1 = e_2 + \lambda_1 \text{sign}(e_1)\Xi(e_1)$, the system state converges to 0 within a fixed time $t_{s1}$, where $t_{s1} = \frac{1}{\lambda_1}\left(\frac{5}{k_3} + \frac{1}{k_2}\right)$.

Proof. When $S_1 = 0$, we have

Define $V_1 = \frac{1}{2}e_1^2$. Taking the derivative of $V_1$ yields

According to Theorem 3.1, when $t \ge t_{s1}$, $e_1 = 0$ holds. □

To ensure that $S_1 = 0$ can be realized within a fixed time, the control law is designed as

where $\lambda_1 > 0$, $\lambda_2 > 0$, and $\gamma$ is a positive constant that satisfies $\gamma > \frac{|d|}{k_2}$. The function $\dot{\Xi}(e_1)$ is given by

Next, we will discuss the fixed-time stability of system (2.3) with the control input (3.12) and sliding surface $S_1$.

Theorem 3.3. For the tracking error system (2.3) with the control input (3.12) and sliding surface $S_1$, for $t \ge t_1$, $e_1 = 0$ and $e_2 = 0$ always hold, where $t_1 = \left(\frac{1}{\lambda_1} + \frac{1}{\lambda_2}\right)\left(\frac{5}{k_3} + \frac{1}{k_2}\right)$.

Proof. First, we prove that all system states converge to the sliding surface within a fixed time $t_{r1}$, where $t_{r1} = \frac{1}{\lambda_2}\left(\frac{5}{k_3} + \frac{1}{k_2}\right)$.

Define $V_2 = \frac{1}{2}S_1^2$. The derivative of $V_2$ yields:

Substituting (2.3) and (3.12) into the equation, we obtain:

For the term $-\gamma \Xi(S_1)$, based on Property 3.1 and (3.3), we get:

Thus,

When $\gamma > \frac{|d|}{k_2}$, we have:

According to Theorem 3.1, for $t \ge t_{r1}$, $S_1 = 0$ holds, where $t_{r1} = \frac{1}{\lambda_2}\left(\frac{5}{k_3} + \frac{1}{k_2}\right)$. Further, according to Theorem 3.2, when $t \ge t_{s1}$, $e_1 = 0$ and $e_2 = 0$ hold. Therefore, when $t \ge t_{s1} + t_{r1} = \left(\frac{1}{\lambda_1} + \frac{1}{\lambda_2}\right)\left(\frac{5}{k_3} + \frac{1}{k_2}\right)$, $e_1 = 0$ and $e_2 = 0$ can be guaranteed. □

Remark 3.1. In fixed-time sliding mode controller design, the sliding mode surface is often designed as:

where $k_1 > 0$, $k_2 > 0$, $\gamma_1 > 1$, and $0 < \gamma_2 < 1$. To obtain the control law, the derivative of the sliding function $S$ is given by:

For the system (2.3), the control law can be developed as:

Since $0 < \gamma_2 < 1$, it follows that $1 - \gamma_2 < 0$. As $|e_1| \to 0$, $|e_1|^{\gamma_2 - 1} \to \infty$, leading to a singularity problem. In our controller, the sliding mode surface is designed to avoid the singularity issue in its derivative function.

3.3.   Improved fixed-time sliding mode controller and disturbance observer design

As $y \to 0$, we have $\lim_{y \to 0^+} \text{sign}(y)\Xi(y) = k_2$ and $\lim_{y \to 0^-} \text{sign}(y)\Xi(y) = -k_2$. This indicates that the terms $\text{sign}(s)\Xi(s)$ and $\text{sign}(e_1)\Xi(e_1)$ are discontinuous, leading to chattering in sliding mode control. To eliminate this issue, we will improve the controller by making these terms continuous.

Initially, we improve the function (3.1) to a new continuous function, which is given as:

Based on (3.1), $\Phi(y)$ and $\dot{\Phi}(y)$ are continuous at $|y| = 1$. In order to make them continuous at $|y| = \sigma$, the parameters $k_4$ and $k_5$ must satisfy the following equations:

Solving above equations gives:

By choosing parameters $k_1$ and $k_2$ in (3.3) $k_4$ and $k_5$ in (3.16), the new function (3.15) is continuous at $|y| = 1$ and $|y| = \sigma$.

Remark 3.2. By selecting appropriate values for $\sigma$ and $k_3$ and substituting them into Eqs (3.3) and (3.16), all parameters of the function $\Phi(y)$ can be determined. The improved function $\Phi(y)$ is a continuous even function that passes through the origin, that is $\Phi(0) = 0$. As $y$ approaches zero, we have: $\lim_{y \to 0^+} \text{sign}(y)\Phi(y) = \lim_{y \to 0^-} \text{sign}(y)\Phi(y) = 0,$ which indicates that $\text{sign}(y)\Phi(y)$ is a continuous odd function. By replacing the discontinuous terms $\text{sign}(\cdot)\Xi(\cdot)$ in the control input $u$ and sliding surface $s$ with $\text{sign}(\cdot)\Phi(\cdot)$, the modified sliding mode controller effectively eliminates the chattering effect.

Theorem 3.4. Considering the nonlinear system

the system state is practically fixed-time stable. Specifically, when $t \geq T_1$, $|y| \leq \sigma$. The time $T_1$ can be estimated by

Proof. According to Property 1, the function $\Phi(y)$ can be defined as

Similar to the proof of Theorem 3.1, we select the Lyapunov function $V = \frac{1}{2} y^2$. Taking the derivative of $V$ with respect to time, we obtain

For $|y| \geq 1$

Solving this differential inequality, we get

For $\sigma \leq |y| < 1$

Solving this differential inequality, we get

Therefore, when $t \geq \frac{5}{k_3} + \frac{1}{k_2}$, we have $|y| \leq \sigma$. □

Before designing the sliding mode controller, a fixed-time disturbance observer is proposed to mitigate the impact of external disturbances on the controller. Inspired by previous work ^[25], an auxiliary system is designed as:

where $\alpha > 0$ and $E = x_2 - \xi$. Following this, a fixed-time disturbance observer is introduced to estimate the external disturbance $d$:

The estimation of $\hat{E}$ is defined by

where $\tilde{E} = E - \hat{E}$ is the estimation error and $\beta > 0$.

Theorem 3.5. Under the action of the fixed-time disturbance observer (3.20) and (3.22), the disturbance observation error $\tilde{d}$ is practically fixed-time stable. Namely, $|\tilde{d}| < \frac{\sigma}{\alpha}$ holds when $t \geq T_{obs},$ where $T_{obs} = \frac{1}{\beta} \left(\frac{5}{k_3} + \frac{1}{k_2} \right).$

Proof. By combining Eqs (3.19) and (3.22), the equation for the state estimation error can be derived as:

According to Theorem 3.4, we can conclude that $\tilde{E}$ is practically fixed-time stable. When $t \geq \frac{1}{\beta}\left(\frac{5}{k_3} + \frac{1}{k_2} \right)$, we have $|\tilde{E}| \leq \sigma$. Therefore, under the action of the fixed-time disturbance observer, the estimation error $\tilde{E}$ converges to within the bound $\sigma$ in a fixed time.

Based on Eqs (2.2), (3.19), and (3.20), the disturbance estimation error can be calculated as:

Thus, it follows that when $t > T_{\text{obs}}$, we have: $|\tilde{d}| \leq \frac{\sigma}{\alpha}.$ □

Remark 3.3. The proposed observer in this paper differs from the disturbance observer in ^[25] and offers the following advantages: (1) it ensures that the estimation error converges to the origin within a fixed time, rather than asymptotically; (2) it relaxes the assumptions on the disturbance, enabling accurate estimation even when the first derivative of the disturbance is non-zero, making it not only suitable for systems with smooth disturbances but also particularly effective for nonlinear systems subject to abrupt disturbances; and (3) it addresses the challenge of directly measuring the higher-order derivative $\dot{x}_2$ by introducing (3.21), which eliminates the need for $\dot{x}_2$ information, thereby significantly improving its practical applicability.

Remark 3.4. When tuning the parameters of the disturbance observer, the following guidelines should be noted. Selecting a smaller value of $\sigma$ and increasing the value of $\alpha$ can improve the estimation accuracy of the observer. On the other hand, increasing the values of $\beta$ and $k_3$ can accelerate the convergence speed of the estimation error and reduce the convergence time. In practical applications, the parameters should be carefully chosen to ensure that the observer achieves accurate disturbance estimation within a short time.

Next, we improve the sliding mode controller to eliminate system chattering. The improved sliding surface and control input are represented as

where $\lambda_1 > 0, \lambda_2 > 0$, $\gamma$ is a positive constant that satisfies $\gamma > \frac{|\tilde{d}|}{k_2}$ and $\hat{d}$ denotes the estimation of disturbance. The function $\dot{\Phi}(e_1)$ is given by

Remark 3.5. In some recent works ^[27,28,29], to achieve fixed-time convergence, the sliding surface has been designed as the sum of two nonlinear terms and piecewise sliding surfaces have been adopted to avoid singularity issues. This undoubtedly increases the number of controller parameters, thereby complicating parameter tuning. Owing to the proposed piecewise function (3.15), the controller gains $k_1$ and $k_2$ depend on $k_3$ (see (3.2)), and the gains $k_4$ and $k_5$ depend on $\sigma$ (see (3.16)). Our sliding surface requires fewer parameters to be tuned, which simplifies parameter adjustment and is more suitable for engineering applications.

Theorem 3.6. For the nonlinear system (2.3), if the sliding mode surface is chosen as (3.24) and the control law is designed as (3.25), and the disturbance observer (3.20) is used to estimate external disturbances, then the sliding mode variable $S$ remains within the region $|S| < \sigma$ when $t \ge t_r$. Additionally, the system states converge to the region defined by $|e_1| < \sigma$ and $|e_2| < \sigma + \lambda_1 \left[k_2 \left(\frac{2}{\sigma} + 1\right) + k_4 k_5 \right] \sigma$ when $t \ge t_r + t_s+T_{obs}$, where: $t_r = \frac{1}{\lambda_2} \left(\frac{5}{k_3} + \frac{1 - \sigma}{k_2} \right),$ and $t_s = \frac{5}{\lambda_1 k_3 - \sigma} + \frac{1 - \sigma}{\lambda_1 k_2 - \sigma}.$

Proof. To begin, let us analyze the time required for the system state to reach the sliding mode surface. Define the Lyapunov function as $V_2 = \frac{1}{2}S^2$. The derivative of $V_2$ with respect to time is given by:

For $|S| \geq 1$, using Eqs (2.3), (3.15) and (3.25) and Property 3.1, we have

When choosing $\gamma > \frac{|d - \hat{d}|}{k_2}$, it follows that

According to Theorem 3.1, for $t \geq t_r = \frac{1}{\lambda_2}\left(\frac{5}{k_3} + \frac{1 - \sigma}{k_2}\right)$, the condition $|S| \leq \sigma$ holds.

For $|S| < \sigma$, consider the function $V_3 = \frac{1}{2}e_1^2$. The derivative of $V_3$ with respect to time yields:

For $|e_1| \geq 1$, based on Eq (3.15), we have

This can be rewritten as

Solving this differential inequality gives us

Therefore,

Given that $|e_1| \geq 1$, we obtain

Further simplifying, we get

Thus, for $t \geq t_{s1}$, where $t_{s1} = \frac{1}{\lambda_2}\left(\frac{5}{k_3} + \frac{1 - \sigma}{k_2}\right) + \frac{5}{\lambda_1 k_3 - \sigma}$, the condition $|e_1| \leq 1$ holds.

For $\sigma < |e_1| < 1$, according to Property 3.1, we have

This can be rewritten as

Solving this differential inequality gives

Therefore,

Given $\sigma < |e_1| < 1$, we obtain

Hence,

Therefore, when $t > t \ge t_r + t_s+T_{obs}$, the condition $|e_1| < \sigma$ holds. Based on Eq (3.24), for $|S| < \sigma$ and $|e_1| < \sigma$, we have

□

Remark 3.6. When tuning the controller parameters, the following issues should be noted: (1) increasing the values of $\lambda_1$, $\lambda_2$, and $k_3$ can accelerate the convergence speed of the system and reduce the convergence time; (2) although changing the value of $\sigma$ can adjust the convergence speed, it may also affect the tracking accuracy. Therefore, the controller parameters should be carefully selected to achieve the desired control performance.

The parameter selection procedure is as follows: Step 1, select $\sigma$ such that $0 < \sigma < 1$; Step 2, choose $k_3 > 0$ and set $\lambda_1 = \lambda_2 = 1$ to ensure system stability; Step 3, adjust the values of $\lambda_1$ and $\lambda_2$ to tune the system convergence time.

Remark 3.7. Although the proposed control scheme in this paper avoids the singularity and chattering issues commonly associated with sliding mode control and simplifies parameter tuning, there are still some limitations that need to be addressed. For example, in practical engineering applications, achieving fast fixed-time convergence requires larger control inputs, which may lead to actuator saturation and degrade the controller's performance. Additionally, the presence of unknown nonlinear terms in the system may limit the applicability of the proposed algorithm. In future work, we plan to integrate other control techniques, such as anti-windup control ^[30] and reinforcement learning-based control ^[31], to further improve the tracking performance of the proposed scheme.

4.   Simulation results and analysis

In this section, numerical simulation results are presented to demonstrate the performance of the proposed control algorithm. The dynamics of the one-link manipulator system is given by

where $q$, $\dot{q}$, and $\ddot{q}$ represent the position, velocity, and acceleration of the manipulator, respectively; $u$ denotes the control input; and $d$ represents an unknown disturbance.

Letting $e_1 = q - q_r$ and $e_2 = \dot{q} - \dot{q}_r$, we obtain:

The parameters for the manipulator system are as follows: $m = 1\, \text{kg}$, $b = 1\, \text{Nms/rad}$ and $n = 1\, \text{Nm}$.

The reference trajectory is $q_r = \sin(t)$.

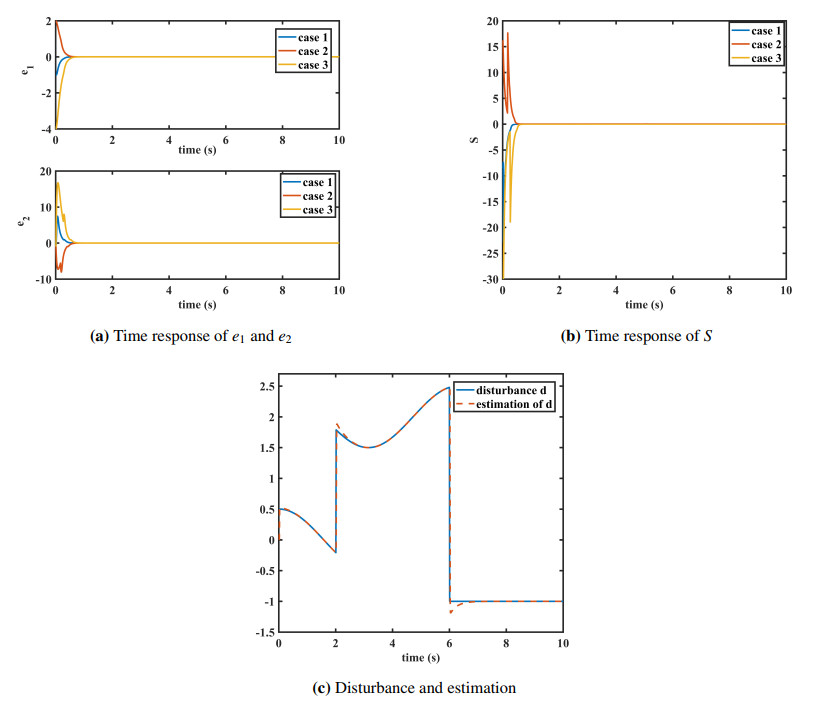
Example 1. In this experiment, to better demonstrate the superiority of the proposed non-singular sliding mode control scheme, simulations are conducted on a single-link manipulator with varying initial positions. An external disturbance with rapidly changing characteristics is introduced to test the performance of the disturbance observer. The controller parameters are as follows: $\lambda_1 = 3$, $\lambda_2 = 3$, $\sigma = 0.5$, and $k_3 = 2.5$. For the proposed observer, the parameters are configured with $\alpha = 10$, $\beta = 10$, $\sigma = 0.5$, and $k_3 = 4$. The initial positions of the manipulator are set at three different conditions: Case 1 with ${\mathbf{x}} = (-1, 0)^T$, Case 2 with ${\mathbf{x}} = (2, 0)^T$, and Case 3 with ${\mathbf{x}} = (-2, 0)^T$. The external disturbance is designed to have rapidly changing characteristics to test the disturbance observer's performance, defined as

As shown in the three subfigures of Figure 1, the simulation results are presented. Figure 1(a) illustrates the response curves of the trajectory tracking error and velocity tracking error for a single-link manipulator under different initial conditions. According to Theorems 3.4 and 3.6, the maximum stabilization time of the system is $T_{\text{max}} = 1.565$ seconds. The actual convergence times of the system are $0.62$ s, $0.66$ s, and $0.71$ s, respectively, all achieving stability within the fixed time. It is evident that, despite the different initial states, both the velocity error $e_1$ and the position error $e_2$ stabilize before the maximum stabilization time. This confirms that the convergence time of the system depends solely on the controller parameters and is independent of the initial system state. Figure 1(b) depicts the response curve of the sliding mode variable $S$. Despite the different initial values, it converges to zero before the maximum stabilization time. Additionally, as shown in the figure, the system exhibits no chattering, demonstrating the effectiveness of the proposed control strategy. Figure 1(c) presents the estimation curve of the disturbance observer. At $t = 2$ seconds, the disturbance abruptly changes from one smooth signal to another, and at $t = 6$ seconds, the disturbance becomes a constant. As can be observed from the figure, the observer accurately estimates the disturbance even during sudden changes. This highlights its robustness and superiority, as it is not only suitable for smooth disturbances but also effective for disturbances with abrupt changes.

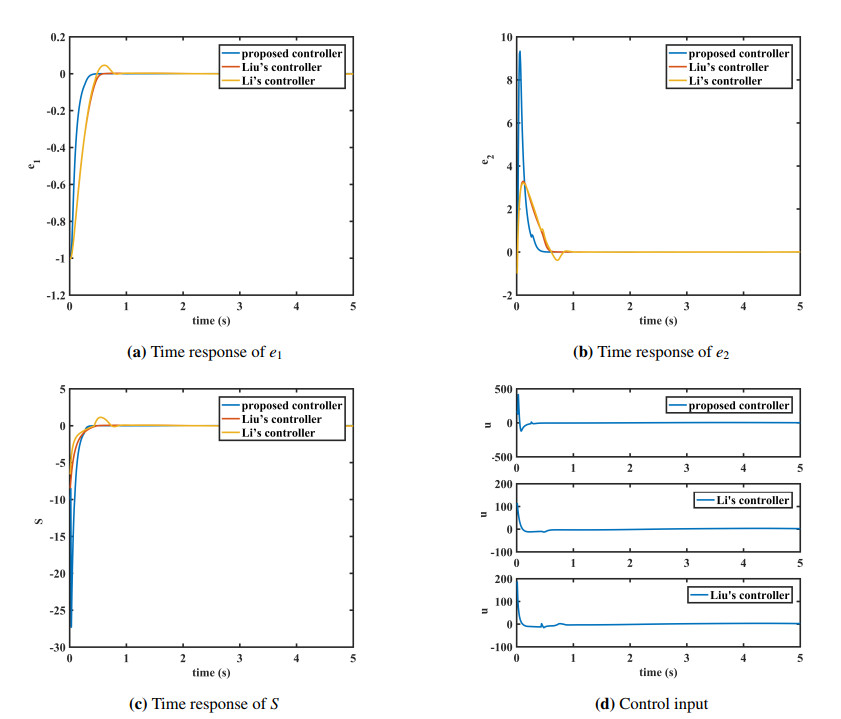
Example 2. In this section, we compare the proposed sliding mode controller with Li's controller (FTSMC) and Liu's controller (FNTSMC). The initial state of the single-link manipulator is the same as Case 1 in Example 1. The control parameters are shown in Table 1.

For Li's controller^[32]:

For Liu's controller^[33]:

The subfigures in Figure 2 present the simulation results. Based on calculations, the maximum convergence times for the three fixed-time controllers are $1.565$ s, $1.634$ s, and $1.741$ s, respectively. The simulation results show that the actual convergence times are $0.62$ s, $0.74$ s, and $0.83$ s. Figures 2(a) and 2(b) display the response curves of the robot tracking errors. It is evident that all three controllers ensure the system tracking errors converge to zero within the fixed time. Compared to the controllers proposed by Li and Liu, the controller presented in this paper exhibits faster convergence speed and shorter transient adjustment time. Notably, Li's controller demonstrates the largest overshoot. Figures 2(c) and 2(d) illustrate the curves of the sliding mode variable $S$ and the control input $u$ for different controllers, respectively. Clearly, all three controllers successfully avoid chattering phenomena. However, the proposed controller in this paper requires the largest control input.

To provide a more comprehensive comparison, we employ two performance indices: IAE (Integral of Absolute Error) and ISE (Integral of Squared Error). These metrics are defined as follows:

● Integral of absolute error (IAE):

● Integral of squared error (ISE):

where $e(t)$ is the position error signal at time $t$, and $T$ is the total simulation time.

As shown in Table 2, the proposed controller demonstrates lower values for both IAE and ISE compared to Li's and Liu's controllers. This indicates that the proposed controller has the least cumulative error and better suppression of instantaneous errors. In contrast, Li's controller shows higher cumulative and instantaneous errors, making it less effective in maintaining precision over time. Therefore, the proposed controller excels in improving tracking accuracy and enhancing disturbance rejection. These advantages make it particularly suitable for applications requiring high precision and rapid response.

5.   Conclusions

In this paper, a fixed-time non-singular sliding mode control scheme incorporating a disturbance observer is proposed for a class of second-order nonlinear systems. The primary advantages of this control strategy include ensuring fixed-time convergence of the system's tracking error while simultaneously avoiding the singularity problem. Additionally, enhancements to the proposed controller have successfully mitigated the chattering problem, guaranteeing the fixed-time convergence of the system states. The effectiveness and robustness of the proposed algorithm were demonstrated through simulations conducted in MATLAB using an example of a single-link manipulator. The results indicate that the proposed control scheme achieves superior performance in terms of both tracking accuracy and disturbance rejection compared to existing methods. These characteristics make the proposed approach particularly suitable for applications requiring high precision and rapid response.

Author contributions

Zhiqiang Chen: Formal analysis, Investigation, Conceptualization, Methodology, Writing-Original Draft; Alexander Yurievich Krasnov: Supervision, Writing-Review and Editing. All authors have agreed to and given their consent for the publication of this research paper.

Use of Generative-AI tools declaration

The authors declare they have used Artificial Intelligence (AI) tools in the creation of this article. DeepSeek was utilized to revise and improve the content, particularly in the "Introduction" and "Conclusions" sections, by enhancing language expression and logical structure.

Conflict of interest

All authors declare no conflict of interest in this paper.