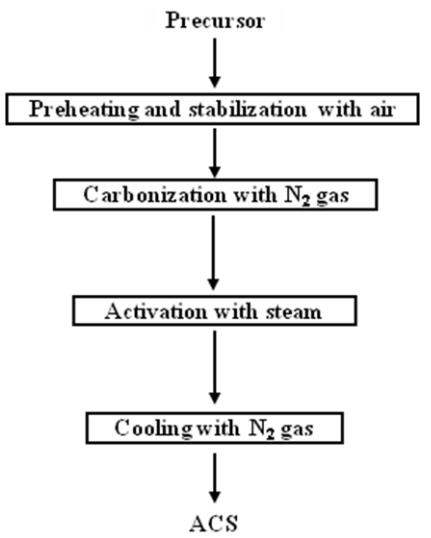
Activated or porous carbon is a carbonaceous material which has excellent adsorption capacity. Activated carbon has many applications including heavy metal and toxic gas removal as well as air and water filter applications. Microporous activated carbon in spherical shape (activated or porous carbon spheres) is a variant of activated carbon which has high compressive strength and low ash content. Pitch, polymeric (phenolic and sulfonated polystyrene resins) and other precursor materials (carbohydrate and seeds) have been generally used for production of activated carbon spheres employing carbonization and activation processes. Various parameters viz. carbonization temperature, heating rate, activation time and temperature, and activation media affected the performance and quality of end product. Generally activation by physical and chemical means is used for activated carbon spheres preparation. The use of polymeric precursors yielded better compressive strength and minimal ash content in comparison to other precursors. Activated carbon spheres produced using these processes has been successfully utilized as adsorbent materials for removal of heavy metals, organic dye, carbon dioxide, volatile organic chemicals, support for catalyst, gas and energy storage and also in chemical protective clothings. In present review, we discuss latest developments in activated carbon spheres and its use as adsorbent materials for removal of toxicants and various other applications.
Dedicated to Giuseppe Mingione on his 50th anniversary.
1.
Introduction
Minimizers of the variable exponent energy ∫|∇u|p(x)dx have been studied in hundreds of papers. In almost all cases, it is assumed that there exist constants c,C∈(1,∞) such that c⩽p(x)⩽C for all x. However, it is possible to use limiting procedures to study the borderline cases when p(x)=1 or p(x)=∞ for some points [34,35]. In recent years, minimizers of non-autonomous functionals
have been studied when φ has generalized Orlicz growth with tentative applications to anisotropic materials [57] and image processing [31]. Again, the upper and lower growth rates are usually assumed to lie in (1,∞). In this article we consider the case when the upper growth rate is allowed to equal ∞ in some points and the lower growth rate is greater than n, the dimension. We prove the Harnack inequality for minimizers of such energies.
Let us recall some information of the context by way of motivation. PDE with generalized Orlicz growth have been studied in many papers lately, both in the general setting and in particular special cases, such as the double phase case (e.g., [3,5,16,17,53]), perturbed variable exponent [52], Orlicz variable exponent [27], degenerate double phase [4], Orlicz double phase [6,10], variable exponent double phase [18,49,50], multiple-phase [7,22], and double variable exponent [56]. Our framework includes all these cases.
In the generalized Orlicz case it is known that solutions with given boundary values exist [15,28,33], minimizers or solutions with given boundary values are locally bounded, satisfy Harnack's inequality and belong to C0,αloc [9,36,37,55] or C1,αloc [38,39], quasiminimizers satisfy a reverse Hölder inequality [32], minimizers for the obstacle problem are continuous [41] and the boundary Harnack inequality holds for harmonic functions [12]. Some articles deal with the non-doubling [13] or parabolic [54] case as well as with the Gauss image problem [44]. We refer to the surveys [11,48] and monographs [14,30,42] for an overview. Advances have also been made in the field of (p,q)-growth problems [19,20,21,45,46,47].
In [8,9], the Harnack inequality was established in the doubling generalized Orlicz case for bounded or general solutions. In the current paper, we consider the effect of removing the assumption that the growth function is doubling thus allowing the upper growth rate to equal ∞. The approach is based on ideas from [35,43] involving approximating the energy functional. This is more difficult compared to the variable exponent case, since the form of the approximating problem is unclear as is the connection between solutions and minimizers. Additionally, the challenge in taking limits without the doubling assumption is to track the dependence of various constants on the parameters and to ensure that no extraneous dependence is introduced in any step. Nevertheless, we improve even the result for the variable exponent case.
Let us consider an example of our main result, Theorem 5.5. In the variable exponent case φ(x,t):=tp(x) we compare with our previous result [35,Theorem 6.4]. In the previous result, we assumed that 1p is Lipschitz continuous, but now we only need the more natural log-Hölder continuity.
Furthermore, the previous result applied only to small balls in which the exponent was (locally) bounded. The next example shows that the new result applies even to some sets where the the exponent is unbounded.
Example 1.1 (Variable exponent). Define p:B1→(n,∞] on the unit ball B1 as p(x):=2nloge|x|. Hence p(0)=∞ but p<∞ a.e. Assume that f∈W1,p(⋅)(B1) with ϱp(⋅)(|∇f|)<∞. If u∈f+W1,p(⋅)0(B1) is a minimizer of the p(⋅)-energy, then the Harnack inequality
holds for r⩽14. The constant C depends only on n and ϱp(⋅)(|∇f|). Note that Br we have, in the notation of Theorem 5.5, p−=2nloger and q∘=2nlog2er so that q∘p−=1+log2+log1rlog2+log1r is bounded independent of r.
In the double phase case we also obtain a corollary of Theorem 4.6 which improves earlier results in that the dependence of the constant is only on qp, not p and q. Note that the usual assumption of Hölder continuity of a is a special case of the inequality in the lemma, see [30,Proposition 7.2.2]. Also note that the "+r" in the Harnack inequality is not needed in this case, since the double phase functional satisfies (A1) in the range [0,K|B|] rather than [1,K|B|].
Corollary 1.2 (Double phase). Let Ω⊂Rn be a bounded domain, n<p<q and H(x,t):=tp+a(x)tq. Assume that f∈W1,H(Ω) and
for every x,y∈Ω. Then any minimizer u of the φ-energy with boundary value function f satisfies the Harnack inequality
The constant C depends only on n, qp and ϱH(|∇f|).
2.
Definitions and notation
We briefly introduce our definitions. More information on Lφ-spaces can be found in [30]. We assume that Ω⊂Rn is a bounded domain, n⩾2. Almost increasing means that there exists a constant L⩾1 such that f(s)⩽Lf(t) for all s<t. If there exists a constant C such that f(x)⩽Cg(x) for almost every x, then we write f≲g. If f≲g≲f, then we write f≈g.
Definition 2.1. We say that φ:Ω×[0,∞)→[0,∞] is a weak Φ-function, and write φ∈Φw(Ω), if the following conditions hold for a.e. x∈Ω:
● y↦φ(y,f(y)) is measurable for every measurable function f:Ω→R.
● t↦φ(x,t) is non-decreasing.
● φ(x,0)=limt→0+φ(x,t)=0 and limt→∞φ(x,t)=∞.
● t↦φ(x,t)t is L-almost increasing on (0,∞) with constant L independent of x.
If φ∈Φw(Ω) is additionally convex and left-continuous with respect to t for almost every x, then φ is a convex Φ-function, and we write φ∈Φc(Ω). If φ does not depend on x, then we omit the set and write φ∈Φw or φ∈Φc.
For φ∈Φw(Ω) and A⊂Rn we denote φ+A(t):=esssupx∈A∩Ωφ(x,t) and φ−A(t):=esssupx∈A∩Ωφ(x,t).
We next define the un-weightedness condition (A0), the almost continuity conditions (A1) and the growth conditions (aInc) and (aDec). Note that the constants Lp and Lq are independent of x even though p and q can be functions.
Definition 2.2. Let s>0, p,q:Ω→[0,∞) and let ω:Ω×[0,∞)→[0,∞) be almost increasing with respect to the second variable. We say that φ:Ω×[0,∞)→[0,∞) satisfies
(A0) if there exists β∈(0,1] such that φ(x,β)⩽1⩽φ(x,1β) for a.e. x∈Ω;
(A1- ω) if for every K⩾1 there exists β∈(0,1] such that, for every ball B,
(A1- s) if it satisfies (A1-ω) for ω(x,t):=ts;
(A1) if it satisfies (A1-φ);
(aInc)p(⋅) if t↦φ(x,t)tp(x) is Lp-almost increasing in (0,∞) for some Lp⩾1 and a.e. x∈Ω;
(aDec)q(⋅) if t↦φ(x,t)tq(x) is Lq-almost decreasing in (0,∞) for some Lq⩾1 and a.e. x∈Ω.
We say that (aInc) holds if (aInc)p holds for some constant p>1, and similarly for (aDec). If in the definition of (aInc)p(⋅) we have Lp=1, then we say that φ satisfies (Inc)p(⋅), similarly for (Dec)q(⋅).
Note that if φ satisfies (aInc)p with a constant Lp, then it satisfies (aInc)r for every r∈(0,p) with the same constant Lp. This is seen as follows, with s<t:
Condition (A1) with K=1 was studied in [30] under the name (A1′). The condition (A1-ω) was introduced in [8] to combine (A1) and (A1-n) as well as other cases. It is the appropriate assumption if we have a priori information that the solution is in W1,ω or the corresponding Lebesgue or Hölder space. The most important cases are ω=φ and ω(x,t)=ts, that is (A1) and (A1-s).
Definition 2.3. Let φ∈Φw(Ω) and define the modular ϱφ for u∈L0(Ω), the set of measurable functions in Ω, by
The generalized Orlicz space, also called Musielak–Orlicz space, is defined as the set
equipped with the (Luxemburg) quasinorm
We abbreviate ‖u‖Lφ(Ω) by ‖u‖φ if the set is clear from context.
Definition 2.4. A function u∈Lφ(Ω) belongs to the Orlicz–Sobolev space W1,φ(Ω) if its weak partial derivatives ∂1u,…,∂nu exist and belong to Lφ(Ω). For u∈W1,φ(Ω), we define the quasinorm
We define Orlicz–Sobolev space with zero boundary values W1,φ0(Ω) as the closure of {u∈W1,φ(Ω):suppu⊂Ω} in W1,φ(Ω).
In the definition ‖∇u‖Lφ(Ω) is an abbreviation of ‖|∇u|‖Lφ(Ω). Again, we abbreviate ‖u‖W1,φ(Ω) by ‖u‖1,φ if Ω is clear from context. W1,φ0(Ω) is a closed subspace of W1,φ(Ω), and hence reflexive when W1,φ(Ω) is reflexive. We write f+W1,φ0(Ω) to denote the set {f+v:v∈W1,φ0(Ω)}.
Definition 2.5. We say that u∈W1,φloc(Ω) is a local minimizer if
for every h∈W1,φ(Ω) with supph⋐Ω. We say that u∈W1,φ(Ω) is a minimizer of the φ-energy with boundary values f∈W1,φ(Ω), if u−f∈W1,φ0(Ω), and
for every v∈f+W1,φ0(Ω).
Let h∈W1,φ(Ω) have compact support in Ω, f∈W1,φ(Ω) and u∈f+W1,φ0(Ω) is a minimizer of the φ-energy. Then u+h∈f+W1,φ0(Ω) by the definition. By the φ-energy minimizing property,
the integrals over the set Ω∖supph cancel, and so u is a local minimizer. Hence every minimizer u∈W1,φ(Ω) of the φ-energy with boundary values f is a local minimizer.
3.
Auxiliary results
We denote by φ∗ the conjugate Φ-function of φ∈Φw(Ω), defined by
From this definition, we have Young's inequality st⩽φ(x,s)+φ∗(x,t). Hölder's inequality holds in generalized Orlicz spaces for φ∈Φw(Ω) with constant 2 [30,Lemma 3.2.13]:
We next generalize the relation φ∗(φ(t)t)⩽φ(t) which is well-known in the convex case, to weak Φ-functions. The next results are written for φ∈Φw but can be applied to φ∈Φw(Ω) point-wise.
Lemma 3.1. Let φ∈Φw satisfy (aInc)1 with constant L. Then
Proof. When s⩽t we use sφ(t)Lt−φ(s)⩽sφ(t)Lt⩽φ(t)L to obtain
On the other hand, by (aInc)1 we conclude that sφ(t)Lt⩽φ(s) when s>t, so the second term is non-positive and the inequality is established.
If φ∈Φw is differentiable, then
Thus φ satisfies (Inc)p if and only if tφ′(t)φ(t)⩾p. Similarly, φ satisfies (Dec)q if and only if tφ′(t)φ(t)⩽q. It also follows that if φ satisfies (Inc)p and (Dec)q, then
and so φ′ satisfies (aInc)p−1 and (aDec)q−1. We next show that the last claim holds even if only (aInc) or (aDec) is assumed of φ which is convex but not necessarily differentiable.
For φ∈Φc we denote the left and right derivative by φ′− and φ′+, respectively. We define the left derivative to be zero at the origin, i.e., φ′−(0):=0. Assume that φ satisfies (aInc)p with p>1, and let t0>0 be such that φ(t0)<∞. Then
Since φ′+ is right-continuous we also obtain that
Lemma 3.3. Let φ∈Φc satisfy (aInc)p and (aDec)q with constants Lp and Lq, respectively. Then
for every t⩾0, and φ′− and φ′+ satisfy (aInc)p−1 and (aDec)q−1, with constants depending only on qp, Lp and Lq.
Proof. Since φ is convex we have
for a proof see e.g., [51,Proposition 1.6.1,p. 37]. Let r∈[0,1). Since the left derivative is increasing, we obtain
Thus
where in the second inequality we used (aInc)p of φ. Choosing r:=(2Lp)−1/p we get
Writing h:=1p and x:=2Lp, we find that
where the inequality follows from convexity of s↦xs. Thus tφ′−(t)⩾p2ln(2Lp)φ(t).
Let R>1. Since φ′+ is increasing, we obtain
Thus
where (aDec)q of φ was used in the second inequality. With R:=1+1q we get
We have established the inequality of the claim.
We abbreviate cq:=1Lqe−1 and cp:=2ln(2Lp). Since φ is convex, we have φ′−⩽φ′+ and so
Thus we obtain by (aDec)q of φ for 0<s<t that
and (aDec)q−1 of φ′+ follows. The proof for (aInc)p−1 is similar as are the proofs for φ′−.
Before Lemma 3.3 we noted that limt→0+φ′+(x,t)=0, and hence
for z∈Rn. In light of this, we define
Theorem 3.4. Let φ∈Φc(Ω) satisfy (aInc)p and (aDec)q with 1<p⩽q. Denote φ′h:=φ′+χ{∇u⋅∇h⩾0}+φ′−χ{∇u⋅∇h<0}. If u∈W1,φloc(Ω), then the following are equivalent:
(i) u is a local minimizer;
(ii) ∫supphφ′h(x,|∇u|)|∇u|∇u⋅∇hdx⩾0 for every h∈W1,φ(Ω) with supph⋐Ω.
Proof. Let h∈W1,φ(Ω) with E:=supph⋐Ω be arbitrary. Define g:Ω×[0,1]→[0,∞] by g(x,ε):=|∇(u(x)+εh(x))|; in the rest of the proof we omit the first variable and abbreviate g(x,ε) by g(ε).
Note that g(ε)2=|∇u(x)|2+ε2|h(x)|2+2ε∇u(x)⋅∇h(x) and g⩾0. Thus in [0,1] the function g has a local minimum at zero for x∈Ω with ∇u(x)⋅∇h(x)⩾0 and a maximum otherwise. This determines whether we obtain the right- or left-derivative and so
for almost every x∈E.
Let us then find a majorant for the expression on the left-hand side of (3.5). By convexity,
for a.e. x∈E. Since ε∈[0,1] we have
By the triangle inequality,
Combining the estimates above, we find that
By Lemma 3.3, φ′+(x,t)t≲φ(x,t) for every t⩾0, so that
By (aDec),
Combining the estimates, we find that
The right hand side is integrable by [30,Lemma 3.1.3(b)], since |∇u|,|∇h|∈Lφ(Ω) and φ satisfies (aDec). Thus we have found a majorant. By dominated convergence and (3.5), we find that
Let us first show that (ⅰ) implies (ⅱ). By (ⅰ),
for ε∈(0,1], and hence (ⅱ) follows by (3.6).
Let us then show that (ⅱ) implies (ⅰ). For θ∈[0,1] and s,t⩾0 we have
so g(ε) is convex. Since t↦φ(x,t) and g(ε) are convex for almost every x∈E, and t↦φ(x,t) is also increasing, the composed function t↦φ(x,g(t)) is convex for a.e. x∈E. Thus
Since the above inequality holds for every ε∈(0,1), (3.6) implies that
which is (i).
We conclude the section by improving the Caccioppoli inequality from [8]; in this paper we only need the special case ℓ=1 and s=q, but we include the general formulation for possible future use. We denote by η a cut-off function in BR, more precisely, η∈C∞0(BR), χBσR⩽η⩽χBR and |∇η|⩽2(1−σ)R, where σ∈(0,1). Note that the auxiliary function ψ is independent of x in the next lemma. Later on we will choose ψ to be a regularized version of φ+B. Note also that the constant in the lemma is independent of q1.
Lemma 3.7 (Caccioppoli inequality). Suppose φ∈Φc(Ω) satisfies (aInc)p and (aDec)q with constants Lp and Lq, and let ψ∈Φw be differentiable and satisfy (A0), (Inc)p1 and (Dec)q1, p1,q1⩾1. Let β∈(0,1] be the constant from (A0) of ψ. If u is a non-negative local minimizer and η is a cut-off function in BR⊂Ω, then
for any ℓ>1p1 and s⩾q, where K:=8sq(Lqe−1)Lqln(2Lp)p(p1ℓ−1)(1−σ)+Lp.
Proof. Let us simplify the notation by writing ˜u:=u+R and v:=˜uβR. Since ∇u=∇˜u, we see that ˜u is still a local minimizer. By (A0) of ψ and v⩾1β, we have 0⩽ψ(v)−ℓ⩽1.
We would like to use Theorem 3.4 with h:=ψ(v)−ℓηs˜u. Let us first check that h is a valid test function for a local minimizer, that is h∈W1,φ(BR) and has compact support in BR⊂Ω. As ˜u∈Lφ(BR) and |h|⩽˜u, it is immediate that h∈Lφ(BR). By a direct calculation,
Note that ˜u∇v=v∇˜u. Since ψ is differentiable we may use (3.2) to get
For the third term in ∇h, we obtain |ψ(v)−ℓηs∇˜u|⩽|∇˜u|∈Lφ(BR). The term with ∇η is treated as h itself. Thus h∈W1,φ(BR). Since s>0 and η∈C∞0(BR), h has compact support in BR⊂Ω and so it is a valid test-function for a local minimizer.
We next calculate
The inequality p1ψ(t)⩽ψ′(t)t from (3.2) implies that ℓψ′(v)v−ψ(v)⩾(p1ℓ−1)ψ(v)>0. Since ˜u is a local minimizer, we can use the implication (i)⇒(ii) of Theorem 3.4 to conclude that
Since φ′−⩽φ′h⩽φ′+, we obtain 1q(Lqe−1))tφ′h(x,t)⩽φ(x,t)⩽2ln(2Lp)ptφ′h(x,t) from Lemma 2. Using also |∇η|˜u⩽21−σv, we have
Note that the constant in front of the integral can be estimated from above by K2Lq.
Next we estimate the integrand on the right hand side. By Young's inequality
where 1q+1q′=1. We choose ε:=LpKη(x)∈(0,1] and use (aInc)q' of φ∗ [30,Proposition 2.4.9] (which holds with constant Lq) and Lemma 3.1 to obtain
In the other term we estimate ε−1q′Lp⩽K1−1q′L1q′pε−1q′=η−1q′K and use (aDec)q of φ:
With these estimates we obtain that
The first term on the right-hand side can be absorbed in the left-hand side. This gives the claim.
The next observation is key to applications with truly non-doubling growth.
Remark 3.8. In the previous proof the assumption (aDec)q is only needed in the set ∇η≠0 since we can improve the estimate on the right-hand side integral to |∇η|˜u⩽21−σvχ{∇η≠0} and only drop the characteristic function in the final step.
4.
Bloch-type estimate for bounded supersolutions
The following definition is like [8,Definition 3.1], except φ+Br has replaced φ−Br. Furthermore, we are more precise with our estimates so as to avoid dependence on p and q.
Definition 4.1. Let φ∈Φw(Br) satisfy (aInc)p with p⩾1 and constant Lp. We define ψBr:Br→[0,∞] by setting
It is easy to see that ψBr∈Φw. Using that φ is increasing for the lower bound and (aInc)p for the upper bound, we find that
As in [8,Definition 3.1], we see that ψBr is convex and satisfies (Inc)p. If φ satisfies (A0), so does ψBr, since φ+Br≃ψBr. If φ satisfies (aDec)q, then ψBr is strictly increasing and satisfies (aDec)q, and, as a convex function, also (Dec) [30,Lemma 2.2.6].
We note in both the above reasoning and in the next theorem that constants have no direct dependence on p or q, only on Lp, Lq and qp.
Theorem 4.3 (Bloch-type estimate). Let φ∈Φc(Ω) satisfy (A0) and (A1). Let B2r⊂Ω with r⩽1 and φ|B2r satisfy (aInc)p and (aDec)q with p,q∈[n,∞). If u is a non-negative local minimizer, then
where C depends only on n, Lp, Lq, qp, the constants from (A0) and (A1), and ϱφ(|∇u|).
Proof. Let us first note that φ satisfies (aInc)n with the constant Lp. Let β be the smaller of the constants from (A0) and (A1). Denote v:=u+2r2βr and γ:=2Kβ, where K is from Caccioppoli inequality (Lemma 3.7) with ℓ=1, s=q and σ=12. Since p⩾n, we see that
When |∇u|>γv, we use (aInc)n to deduce that
for a.e. x∈Br. Rearranging gives |∇u|nvn≲φ(x,|∇u|)φ−B2r(γv). Since v⩾1β and γ⩾1, we obtain by (A0) that φ−B2r(γv)⩾1. If also φ−B2r(γv)⩽1|B2r|, then φ+B2r(βγv)⩽φ−B2r(γv) by (A1). Otherwise, (φ−B2r(γv))−1⩽|B2r|. In either case,
for a.e. x∈Br. When |∇u|⩽γv, we use the estimate |∇u|nvn⩽γn instead. Since u+r⩾12(u+2r)=βrv, we obtain that
It remains to bound the integral on the right-hand side.
Let ψB2r be as in Definition 4.1, let η∈C∞0(B2r) be a cut-off function such that η=1 in Br and choose ψ(t):=ψB2r(βγt). Then
where the second inequality follows from (4.2). We note that ψ satisfies (A0), (Inc)p and (Dec). Now we use the Caccioppoli inequality (Lemma 3.7) for φ and ψ with ℓ=1, s=q and σ=12 to get
the last inequality holds by (4.2) and γ=2Kβ since
We next show that the Bloch estimate implies a Harnack inequality for suitable monotone functions. We say that a continuous function u is monotone in the sense of Lebesgue, if it attains its extrema on the boundary of any compact set in its domain of definition. We say that φ∈Φw(Ω) is positive if φ(x,t)>0 for every t>0 and a.e. x∈Ω. If φ satisfies (aDec)q(⋅) for q<∞ a.e., then it is positive.
Lemma 4.4. If φ∈Φw(Ω) is positive, then every continuous local minimizer is monotone in the sense of Lebesgue.
Proof. Let u∈W1,φloc(Ω)∩C(Ω) be a local minimizer and D⋐Ω. Fix M>max∂Du and note that (u−M)+ is zero in some neighborhood of ∂D since u is continuous. Thus h:=(u−M)+χD belongs to W1,φ(Ω)∩C(Ω) and has compact support in Ω. Using that u is a local minimizer, we obtain that
Since φ(x,t)>0 for every t>0 and a.e. x∈Ω, it follows that ∇u=0 a.e. in supph. Thus ∇h=0 a.e. in Ω. Since h is continuous and equals 0 in Ω∖D, we conclude that h≡0.
Hence u⩽M in D. Letting M→max∂Du, we find that u⩽max∂Du. The proof that min∂Du⩽u in D is similar.
For x∈Ω we write rx:=12dist(x,∂Ω). Let 1⩽p<∞. In [43,Definition 3.6] a function u:Ω→R is called a Bloch function if
Note that if u is an analytic function in the plane and p=2, then by the mean value property
which connects this with Bloch functions in complex analysis. In the next theorem we assume for logu a Bloch-type condition. In the case p=n the next result was stated in [35,Lemma 6.3].
Lemma 4.5. Let u:Ω→(0,∞) be continuous and monotone in the sense of Lebesgue. If B4r⋐Ω, and
for p>n−1, then
for some C depending only on A, p and n.
Proof. Denote v:=logu. Since the logarithm is increasing, v is monotone in the sense of Lebesgue because u is.
As u is continuous and positive in ¯B3r⊂Ω, it is bounded away from 0. Thus v∈W1,p(B2r) is uniformly continuous in B3r. Mollification gives a sequence (vi)∞i=0 of functions in C∞(B2r)∩W1,p(B2r), such that v is the limit of vi in W1,p(B2r) and vi→v pointwise uniformly in B2r, as i→∞ [25,Theorem 4.1 (ii),p. 146]. By the Sobolev–Poincaré embedding W1,p(∂BR)→C0,1−n−1p(∂BR),
for every R∈(0,2r), where dS denotes the (n−1)-dimensional Hausdorff measure and the constant depends only on p and n (see, e.g., [26,Lemma 1], stated for the case n=p=3). Integrating with respect to R gives
Since vi→v uniformly, we obtain that (osc∂BRv)p=limi→∞(osc∂BRvi)p for every R. Using this and vi→v in W1,p(B2r), it follows by Fatou's Lemma that
As v is continuous and monotone in the sense of Lebesgue, we have that oscBrv⩽oscBRv=osc∂BRv for R∈(r,2r), and therefore
Since
it now follows that
We conclude this section with the Harnack inequality for local minimizers. The novelty of the next theorem, apart from the technique, is that the constant depends only on qp, not on p and q separately.
Theorem 4.6 (Harnack inequality). Let φ∈Φc(Ω) satisfy (A0) and (A1). We assume that B2r⊂Ω with r⩽1 and φ|B2r satisfies (aInc)p and (aDec)q with p,q∈(n,∞).
Then any non-negative local minimizer u∈W1,φloc(Ω) satisfies the Harnack inequality
when B4r⊂Ω. The constant C depends only on n, β, Lp, Lq, qp and ϱφ(|∇u|).
Proof. Let u∈W1,φloc(Ω) be a non-negative local minimizer. By Theorem 4.3,
where C depends only on n, Lp, Lq, qp, the constants from (A0) and (A1), and ϱφ(|∇u|). Since p>n, φ satisfies (aInc)p and u∈W1,φloc(Ω), u is continuous and Lemma 4.4 yields that u+r is monotone in the sense of Lebesgue. Thus we can apply Lemma 4.5 to u+r, which gives the Harnack inequality.
5.
Minimizers with non-doubling growth
Let us study minimizers with given boundary values.
Definition 5.1. Let p∈[1,∞), φ∈Φc(Ω) and define, for λ⩾1,
Note that since t↦φλ(x,t) is convex for a.e. x∈Ω, the left derivative φ′− exists for a.e. x∈Ω, and therefore the above definition makes sense.
Lemma 5.2. If φ∈Φc(Ω), then φλ∈Φc(Ω) satisfies φλ(⋅,t)≈tp with constants depending on λ. Furthermore,
for λ⩾1, φλ(x,t)⩽φΛ(x,t)+1λtp for any Λ⩾λ⩾1, and φλ→φ as λ→∞.
Proof. It follows from the definition that pλτp−1⩽φ′λ(x,τ)⩽p(1λ+λ)τp−1. Integrating over τ∈[0,t] gives φλ(⋅,t)≈tp. Let Λ⩾λ⩾1. Since the minimum in the integrand is increasing in λ, we see that
and thus lim supλ→∞φλ⩽φ. On the other hand, Fatou's Lemma gives
One of the terms in the minimum min{φ′−(x,τ),pλτp−1} is achieved in at least a set of measure t2. Since both terms are increasing in τ, this implies that
Since φλ(x,t)≈tp, it follows by [30,Proposition 3.2.4] that W1,φλ(Ω)=W1,p(Ω) and the norms ‖⋅‖φλ and ‖⋅‖p are comparable. However, the embedding constant blows up as λ→∞ unless φ also satisfies (aDec)p. This approximation approach is similar to that in [24]. Note in the next results that f is bounded by the Sobolev embedding in W1,p(Ω).
Lemma 5.3. Let q:Ω→(n,∞), and let φ∈Φc(Ω) satisfy (A0), (aInc)p and (aDec)q(⋅), p>n. Assume that f∈W1,φ(Ω) with ϱφ(∇f)<∞. Then there exists a sequence (uλk) of Dirichlet φλk-energy minimizers with the boundary value function f and a minimizer of the φ-energy u∞∈f+W1,φ0(Ω) such that uλk→u∞ uniformly in Ω as λk→∞.
Proof. Note that we use W1,φλ(Ω)=W1,p(Ω) and W1,φλ0(Ω)=W1,p0(Ω) several times in this proof. Let λ⩾p. Note that f∈W1,p(Ω) since tp≲φ(x,t)+1 by (A0) and (aInc)p. By [29,Theorem 6.2] there exists a minimizer uλ∈f+W1,p0(Ω) of
Fix λ⩾1. By Lemma 5.2 and tp≲φ(x,t)+1, we have tp≲min{φ(x,t2),λtp}+1≲φλ(x,t)+1. Also by the same lemma, φλ≲φ+1λtp≲φ+1. Since f is a valid test-function and uλ is a φλ-minimizer, we have
and hence {\varrho}_p(\nabla u_\lambda) is uniformly bounded. Note that the implicit constants do not depend on \lambda .
Since u_\lambda-f\in W^{1, p}_0(\Omega) , the Poincaré inequality implies that
Therefore, \|u_\lambda\|_p {\leqslant} \|u_\lambda-f\|_p + \|f\|_p {\leqslant} c and so \|u_\lambda\|_{1, p} is uniformly bounded. Since f + W_0^{1, p}(\Omega) is a closed subspace of W^{1, p}(\Omega) , it is a reflexive Banach space. Thus there exists a sequence (\lambda_k)_{k = 1}^\infty tending to infinity and a function u_\infty \in f + W_0^{1, p}(\Omega) such that u_{\lambda_k}\rightharpoonup u_\infty in W^{1, p}(\Omega) . Since p > n , the weak convergence u_{\lambda_k}-f\rightharpoonup u_\infty-f in W^{1, p}_0(\Omega) and compactness of the Sobolev embedding [1,Theorem 6.3 (Part IV),p. 168] imply that u_{\lambda_k}-f \to u_\infty-f in the supremum norm. Hence u_{\lambda_k} \to u uniformly in \Omega .
We note that the modular {\varrho}_{{\varphi}_\lambda} satisfies the conditions of [23,Definition 2.1.1]. Hence, it is weakly lower semicontinuous by [23,Theorem 2.2.8], and we obtain that
for fixed \lambda{\geqslant} 1 , where in the second inequality we used Lemma 5.2 and the fact that t^p \lesssim {\varphi}_\lambda(x, t) +1 . It follows by monotone convergence that
and hence |\nabla u_\infty| \in L^{\varphi}(\Omega) . Since p > n , \Omega is bounded and u_\infty -f \in W^{1, p}_0(\Omega) , we obtain by [58,Theorem 2.4.1,p. 56] that u_\infty - f\in L^\infty(\Omega) . Moreover, L^\infty(\Omega)\subset L^{\varphi}(\Omega) since \Omega is bounded and {\varphi} satisfies {\rm{(A0)}}. These and f\in L^{\varphi}(\Omega) yield that u_\infty \in L^{{\varphi}}(\Omega) . Hence we have u_\infty \in W^{1, {\varphi}}(\Omega) . Since u_\infty -f \in W^{1, p}_0(\Omega) and p > n , it follows that u_\infty-f can be continuously extended by 0 in \Omega^c [2,Theorem 9.1.3]. Then we conclude as in [40,Lemma 1.26] that u_\infty-f\in W^{1, {\varphi}}_0(\Omega) .
We conclude by showing that u_\infty is a minimizer. Suppose to the contrary that there exists u\in f+W^{1, {\varphi}}_0(\Omega) with
By {\varphi}_\lambda\lesssim {\varphi}+1 , {\varphi}_\lambda\to{\varphi} and dominated convergence, there exists \lambda_0 such that
for all \lambda{\geqslant} \lambda_0 . From the lower-semicontinuity estimate (5.4) we obtain k_0 such that
for all k{\geqslant} k_0 . By increasing k_0 if necessary, we may assume that \lambda_k{\geqslant} \lambda_0 when k{\geqslant} k_0 . For such k we choose \lambda = \lambda_k above and obtain that
This contradicts u_{\lambda_k} being a {\varphi}_{\lambda_k} -minimizer, since u \in f + W^{1, {\varphi}}_0(\Omega) \subset f + W^{1, {\varphi}_{\lambda_k}}_0(\Omega) . Hence the counter-assumption was incorrect, and the minimization property of u_\infty is proved.
We conclude this paper with the Harnack inequality for {\varphi} -harmonic functions. Here we use Remark 3.8 to handle the possibility that q could be unbounded and thus {\varphi} non-doubling, like in Example 1.1. This is possible since q^\circ is the supremum of q only in the annulus, not the whole ball.
Theorem 5.5 (Harnack inequality). Let p, q : \Omega \to (n, \infty) , and {\varphi} \in \Phi_{\mathit{\rm{c}}}(\Omega) be strictly convex and satisfy {\rm{(A0)}}, (A1), {({\rm{aInc}})_{p(\cdot)}} and {\left( {{\rm{aDec}}} \right)_{q(\cdot)}} with \inf p > n . Assume that f\in W^{1, {\varphi}}(\Omega) with {\varrho}_{\varphi}(|\nabla f|) < \infty . Then there exists a unique minimizer u of the {\varphi} -energy with boundary values f . Let B_{4r}\subset \Omega , p^-: = \inf\limits_{B_{2r}} p and q^\circ: = \sup\limits_{B_{2r}\setminus B_r} q . If \frac{q^\circ}{p^-} < \infty , then the Harnack inequality
holds for all non-negative minimizers with C depending only on n , \beta , L_p , L_q , \frac{q^\circ}{p^-} and {\varrho}_{\varphi}(|\nabla f|) .
Proof. By Lemma 5.3, there exists a sequence (u_k)\subset f+W^{1, p}_0(\Omega) of minimizers of the {\varphi}_{\lambda_k} energy which converge uniformly to a minimizer u_\infty\in f+W^{1, {\varphi}}_0(\Omega) of the {\varphi} -energy. Since {\varphi} is strictly convex, the minimizer is unique and so u = u_\infty .
From {\rm{(A0)}} and {\left( {{\rm{aInc}}} \right)_{{p^ - }}} we conclude that t^{p^-}\lesssim{\varphi}(x, t)+1 . It follows from Lemma 5.2 that {\varphi}_\lambda(\cdot, t)\simeq {\varphi}(\cdot, t)+\frac1\lambda t^{p^-} . Thus {\varphi}_\lambda satisfies {\rm{(A0)}} and {\rm{(A1)}} with the same constants as {\varphi} . Since u_k\to u in L^\infty(\Omega) and u is non-negative we can choose a sequence \varepsilon_k\to 0^+ such that u_k+ \varepsilon_k is non-negative. By Theorem 4.1 with Remark 3.8,
where C depends only on n , L_p , L_q , \frac{q^\circ}{p^-} , \beta from {\rm{(A0)}} and (A1), and {\varrho}_{{\varphi}_{\lambda_k}}(|\nabla u_k|) . Since u_k is a minimizer, {\varrho}_{{\varphi}_{\lambda_k}}(|\nabla u_k|){\leqslant} {\varrho}_{{\varphi}_{\lambda_k}}(|\nabla f|)\lesssim {\varrho}_{\varphi}(|\nabla f|)+1 . Thus by Lemma 4.5, we have
with C independent of k . Since u_k+ \varepsilon_k\to u_\infty uniformly, the claim follows.
Acknowledgments
Peter Hästö was supported in part by the Jenny and Antti Wihuri Foundation.
Conflict of interest
The authors declare no conflict of interest.














 DownLoad:
DownLoad: