1.
Introduction
Early adulthood is accompanied with several tasks including starting a business, managing a home and family affairs, civic responsibilities, starting a family, and learning to live with a marriage partner. On the other hands, the responsibilities of nursing roles, it can bring social challenges and conflicts for nursing students [1]. In the transition to student life, nursing students need to quickly adapt to new professional and social responsibilities [2],[3] and try to cope with the problems such as the strange environment of the university due to living away from family, the strange environment of the university, new relationships with colleagues, lack of welfare facilities, financial problems, increased individual responsibilities, need for independent decision-making, changing roles and expectations from family, friends and instructors endure a lot of stresses in life [4],[5]. Nursing students due to the nature of nursing work are more stressed than other students in addition to university stressors [6]–[8]. Pulido Martos et al. [7] stated the most perceived stress in nursing students are the fear of unknown situations, fear of mistake in patient care and the use of equipment. Also, Delprato [4] reported heavy workload, and lack of experience in clinical activities. In this regards, Mohammadinia [9] and Sadeghian [10] in Iran showed the fear of uncertain future, entering the clinical field and attending exams were the stressors for nursing students. Also, Lerdsamran [2] identified the financial and family problems as stressors in nursing students. What is known is that sometimes these stressors cause academic failure and dropouts in students [11],[12]. According to a study, every year, 15 to 20 percent of nursing students experience academic failure mainly because of their inability to adapt to new situations [13]. These stressful conditions have a negative impact on the dynamics of learning and put them at risk for depression, physical and behavioral problems such as smoking, drinking, inappropriate eating habits and poor educational performance [14],[15]. Given the information presented about the stressors and their impact on the life of nursing students, they should adopt stress management skills in order to achieve stability in their life. In any case, there is little evidence that show nursing student strategies in confronting with life challenges. Existing knowledge on this topic is mainly coping strategies for educational problems. However education is just one aspect of student life. In this qualitative study the researchers explore the perceived strategies of nursing students in confronting living challenges.
2.
Methodology
2.1. Design
This study is a qualitative conventional content analysis conducted in Iran from April 2017 to March of 2018.
2.2. Sampling
Nursing students from the universities of Tabriz and Khoy in Iran were selected through a purposive sampling. Single and married students, natives and non-natives, dormitory and non-dormitory students were selected to maximum variation sampling. A total of 18 undergraduate nursing students (9 male and 9 female students) were interviewed.
2.3. Data collection
The data were collected through in-depth unstructured and face-to-face interviews. Interviews were conducted by the first author Persian language. Interviews began with a general question “What do you do to confronting with life challenges?” And, and based on the responses of the participants, other questions were raised such as “How do you ask for help?”. The interviews were recorded, word-by-word and were transcribed in Microsoft office word (2007).
2.4. Data analysis
Data were continuously collected and analyzed simultaneously. Granhaym and Lundman method was applied to analysis. Each transcribed was read several times for a comprehensive understanding in abstracting process of data. Words, sentences, and paragraphs were compressed as meaning units according to the content. The codes according to their similarities and differences were categorized. Finally, the main theme was extracted as a hidden concept in the data. Data collection was stopped when no new information were not discovered in from further interviews.
2.5. Rigor and Trustworthiness
The rigor of this study was based on Guba and Lincoln criteria. Credibility was established by selecting nursing students with both genders; Azad University and public university, urban and rural, prolonged engagement with participants and checking data with research team. For reliability, two researchers outside of the research were asked to check the data separately. For transferability, the researchers used a detailed description of the field of study, the characteristics of the participants, the process of data analysis, and the provision of adequate quotes. Verifiability was supported by the systematic recording of all research steps.
2.6. Ethical considerations
This study was approved by the Ethics Committee of the Tarbiat Modares University Code of ethics: 9104/D52. Informed consent was obtained from participants. Participants were informed verbally of the aim of the study, voluntary participation, anonymity, confidentiality of information, and the right to withdraw from the research at the time of the request.
3.
Results
From the interviews 9 main categories were extracted: “Applying the problem-solving process”, “Self- Controlling in stressful pressures”, “Maintaining interpersonal relationships”, “Ask for help to remove obstacles”, “Relying on own abilities and beliefs”, “Organizing the financial situations”, “Avoid from unpleasant situations”, “Impulsive behavior with adverse conditions” and “Rule-based problem solving” (Table 1).
3.1. Applying the problem-solving process
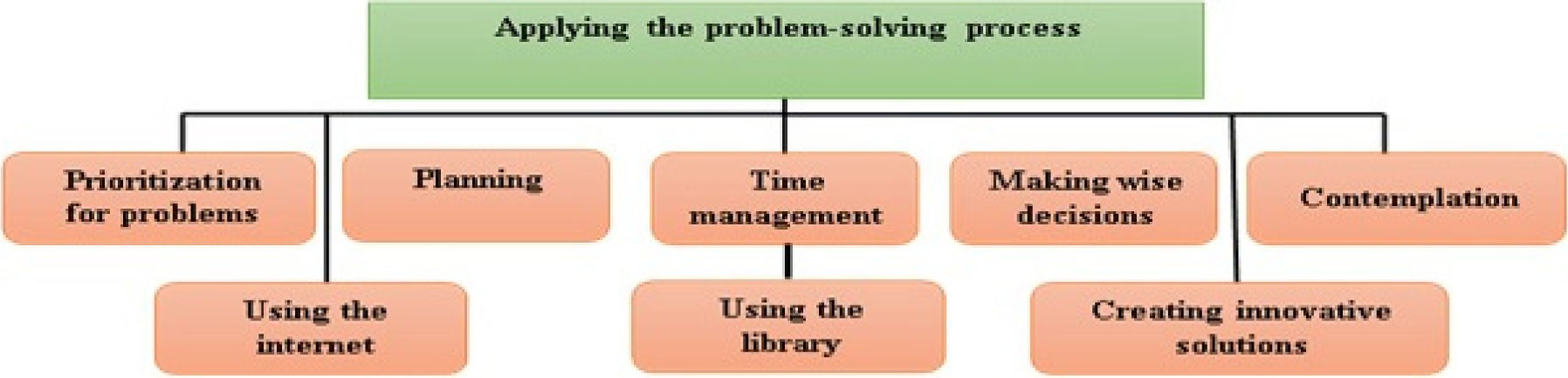
According to the students' statements, planning and prioritizing, estimating time, deciding, deep thinking, and comprehensive awareness of the problems, creating new solutions as well as the using the internet and library were nursing students' strategies for confronting with difficult conditions of life (Figure 1).
3.1.1. Planning
Nursing students used planning and setting goals in dealing with their living challenges. A 24-year-old male student says: “I set up goals not only for my lessons but also for my whole life. I have a multi-year, monthly, weekly, and daily plan for my life”.
3.1.2. Prioritization for problems
Nursing students used prioritizing life problems to solve their life challenges. A 24-year-old male student says: “I try to solve the most critical problem first. That is I prioritize”.
3.1.3. Time management
Accurate timing, time calculation and time- saving were another strategies among nursing students in dealing with problems in life. A 34-year-old female student says: “I have to take a bus every day at 5 am to reach the hospital. I tried to arrive early so that there was no problem with my educator”.
3.1.4. Making wise decisions
In difficult emotional situations, nursing students adopted a wise decision-making strategy. A 24-year-old female student says: “I always try to make decisions in difficult situations with a comfortable mental condition. In that case, the probability of fulfilling a decision is 90 percent and it is wise”.
3.1.5. Contemplation
Nursing students thoughtfully look in dealing with family and professional stressful problems described reflection behaviors. A 23-year-old female student says: “As for important events in my life, especially matters about my future destiny, I tried to think about it first and investigate”.
3.1.6. Using the internet
Nursing students also used the internet to increase their skills in problem solving. A 23-year-old female student says: “I usually solve my problems by searching in internet to get the necessary information”.
3.1.7. Using the library resources
Nursing students used the library for problem solving, especially on complex problems in their life. A 21-year-old female student says: “During exam whatever I studied, I would forget them on exam session. Then I noticed that by studying at the library I would learn more”.
3.1.8. Creating innovative solutions
Creating new strategies and using innovation in new situations were applied by students to problem solving during student life. A 24-year-old male student says: “For solving my problems, I have new ideas, and I use a creativity of mind because the teachers are not available always”.
3.2. Maintaining interpersonal relationships
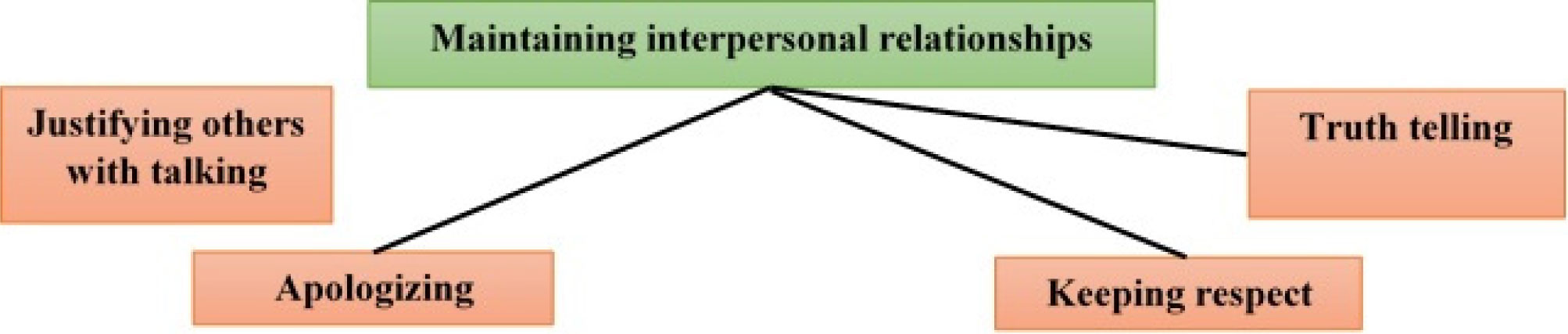
Nursing students tried to make the issues as transparent as possible to maintain interpersonal communications with others. Also, they apologize and respect others to gain satisfaction when a communication problem occurs. They are also in the face of annoying living conditions trying to prove the truth (Figure 2).
3.2.1. Justifying others with talking
Nursing students talked with people to justify and explain the causes of the events, behaviors, and their problems. A 24-year-old female student says: “I have recently been criticized by my friends saying that I am vindictive and proud. That made me sad. I explained to them the reason for my behavior and justified them, and all the doubt and possible grudges were resolved”.
3.2.2. Apologizing
Apologizing for unwanted events was another nursing student's strategy to maintaining and improving interpersonal communications. A 24-year-old female student says: “When I get into trouble with someone, I will apologize completely polite and without any shy”.
3.2.3. Keeping respect
Nursing students were respecting others to prevent possible excuses and conflicts in life. A 23-year-old female student says: “I have been extremely respectful and polite to my husband. Because whatever I did would change to a problematic subject for him”.
3.2.4. Truth telling
In dealing with annoying condition of life, nursing students took truth-telling in the description of the events to improve communications. A 23-year-old female student says: “If there are any problems related to the dignity and personality of me and it will affect my relationships, I will try to prove it”.
3.3. Self-control
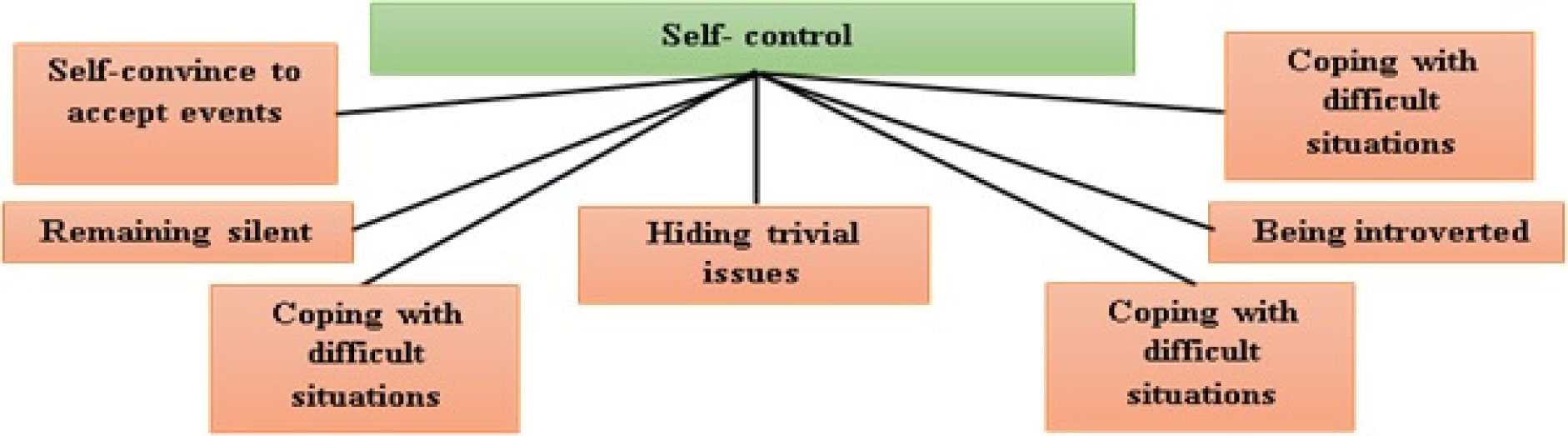
Nursing students tried to reduce the stresses by self-control their emotional stresses by convincing themselves to accept events, remaining silent, hiding trivial issues, being introvert, doing Spiritual Affairs, and mental relaxation strategies (Figure 3).
3.3.1. Self-convince to accept events
Convincing themselves against the events was strategy to self-control in nursing students. A 23-year-old male student says: “About my patient's death and my distress, I can say that by over time, I convinced myself that I was not guilty in my patient's death”.
3.3.2. Remaining silent
Participants tried to remain silent in the face of family problems, failure to persuade others, and insults. A 24-year-old female student says: “There were terrible conflicts and quarrels in my life between my family and my husband's family. I tried to keep silence for a while”.
3.3.3. Hiding trivial issues
Hiding issues of low importance was one of the strategies of nursing students were doing to handle difficult living conditions. A 24-year-old female student says: “when I went to the university, it was the first time that I came to town. I was stressed. I tried to hide it from others that I come from rural area”.
3.3.4. Being introverted
Not expressing and not conveying issues and events to others was a nursing student's strategy to reduce tension. A 24-year-old female student says: “I'm an introvert person because; it's not easy to say bad events to others. I have never told anyone”.
3.3.5. Coping with difficult situations
Nursing students to reduce their tension were trying to adapt themselves to recurrent problems. A 24-year-old male student says: “After the death of the child in hospital and a bad experience I had, I gradually adapted to my job. So, I did not hurt such events”.
3.3.6. Doing spiritual affairs
Resorting to God and praying were strategies of nursing students in difficulties. A 24-year-old male student says: “In troubles, or when I'm so upset, the only thing that can make me calm is talking to God and this will make me feel better”.
3.3.7. Doing mental relaxation
Nursing students used relaxation methods such as crying, listening to music, walking, and writing, participation in group and recreational activities and sleeping to distract their thoughts from stressful situations. A 24-year-old male student says: “I am entertaining myself with interesting things. Whether playing for fun or going to the gym, I try to distraction my thought. Truly, doing a group activity can be very effective”.
3.4. Ask for help to remove obstacles
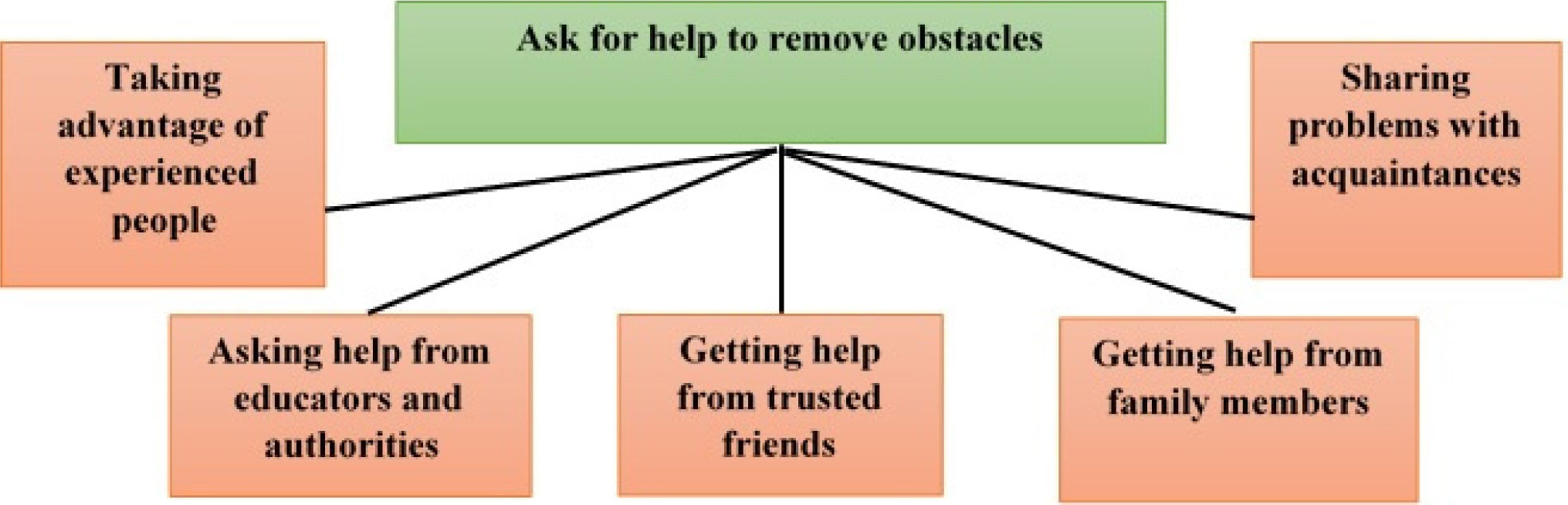
Asking for help from others was another strategy of nursing students to confronting with life challenges (Figure 4).
3.4.1. Taking advantage of experienced people
Taking advice from others such as experienced elders and informed people was another strategy of nursing students in difficulties. A 24-year-old male student says: “Sometimes I have a serious problem; I consult with one who is qualified and has more information than me in this field”.
3.4.2. Getting help from trusted friends
Asking help from intimate friends to do clinical activities and using their experiences in different aspects were a strategy of nursing students to manage difficult conditions. A 24-year-old male student says: “When there is a problem in a field or something is wrong with me, I talk about it with my friend, because I trust him. Then everything will be OK”.
3.4.3. Sharing problems with acquaintances
Consultation, sharing life issues and intermediation with family members (aunt, cousin) in disturbed situations to solve the problem was another strategy by nursing students. A 23-year-old female student says: “If there's a problem that I cannot share with my mom, I'll talk to my cousin (my mother's sister's daughter). I trust her a lot”.
3.4.4. Asking help from educators and authorities
Nursing students in the face of difficulties of educational-clinical situations would benefit from the help of educators and educational authorities. A 23-year-old female student says: “I was very stressed when I was taking blood from the patient. Then I got help from my educator.” A 22-year-old female student says: “In communication problems with my colleagues, head-nurse guided me a lot. She explained the professional behavior to me”.
3.4.5. Getting help from family members
Nursing students asked parents, siblings, and spouses for help in life and educational difficulties that was beyond their abilities. A 26-year-old male student says: “I had a financial problem and I get the most support from my parents and my brothers. They also agreed to pay some amount of money in this difficult condition”.
3.5. Relying on own abilities
Nursing students tried to rely on their own abilities, knowledge, risk-taking and imitating from others to solve their life problems (Figure 5).
3.5.1. Self-Reliance
These students believed that they would be able to solve life difficulties by self-dependence. A 23-year-old male student says: “I rely on myself instead of relying on others and I must solve my problems, not others”.
3.5.2. Taking risk in problem solving
Students tried to solve the problem immediately with risk taking in the uncertainty in the future. A 21-year-old male student talk about his own risk-taking experience in putting his personal belongings in an insecure condition: “The locker room was very unsafe, the lockers were not locked, I finally had to take risks and put my costumes there and go to the ward”.
3.5.3. Imitating from others
The imitation of others methods was another strategy used by nursing students to face with confused conditions. A 24-year-old female student says: “The first semester of the university was hard for me; it was the first time I was in the city. I was stressed. I tried to chase the other students and imitate their social behavior. And see how they commute and behave”.
3.6. Organizing the financial situation
Students tried to reduce their financial problems by obtaining loans, savings and student work (Figure 6).
3.6.1. Asking financial help from family
Participants asked for financial help from their family members to provide student expenses. A 23-year-old male student says: “My financial condition was bad the previous month. I went to my brother and asked for financial aid. He gave me money”.
3.6.2. Getting a job
Nursing students had to take a job to pay tuition and dormitory fees. A 24-year-old male student says: “I picked up student work this year. I don't like to be financially dependent on my father and brother.”
3.6.3. Getting a bank loan
In difficult financial situation, nursing students were using bank loans. A 26-year-old male student says: “I had a financial problem; I got an apartment with installments and got involved with it. I want to get a loan to see if I can fix my financial condition?”.
3.6.4. Economic saving
Nursing students were trying to managing their cost and salary. A 23-year-old male student says: “Some time I was a penniless, then I was trying to save as much as I could; I tried to use my salary until the end of the month Or I went to college from dormitory by bus”.
3.7.
Avoid from unpleasant situations
Nursing students were trying to get away from annoying situations (Figure 7).
3.7.1.
Get away from annoying problems
Not attending unpleasant situations and escaping problems were other student strategies for facing with educational or family constraints. A 27-year-old male student says: “With the childish and annoying thoughts of my classmates; I do not like to attend in classes”.
3.7.2.
Living alone
Nursing students were getting away from and reducing communications with others in the face of distressing situations of family life. A 23-year-old female student says: “Following all these family problems, I've now cut my communication with my husband's family. I do not have a relationship now, and now I feel better”.
3.7.3.
Not protracting the issues
Nursing students try to solve problems and reduce tension by shortening the quarrel and not discussing in turbulent social situations. A 23-year-old female student says: “Something I've experienced that you have to be patient with everyone and not protract the issue and say ‘yes’ you are right. In general, I do not discuss”.
3.8.
Impulsive behavior with adverse conditions
Nursing students, in response to unpleasent conditions and to resolve it, tried to protest in different metheds. Even in some circumstances, because of a problem in interpersonal communications they had to face fierce encounters (Figure 8).
3.8.1.
Protesting
Nursing students to solve and reduce the tensions of problems that arising from inappropriate performance of nursing staff, the discrimination between nursing students and medical students and inappropriate welfare conditions in the hospital, protesting in group. A 21-year-old male student said: “In the hospital's canteen, they were giving breakfast to medical students, but not to nursing students. To solve this problem, we wrote a letter of protest and we all signed the letter”.
3.8.2.
Quarreling
Dispute and harsh behavior were another nursing student's strategies in dealing with problems in interpersonal communications. A 24-year-old male student says: “I should say that it happened I quarreled in the college. If someone tells me a harsh word, I cannot be silent. Sometimes I have to have a kind of verbal or physical conflict with them”.
3.9.
Rule-based problem solving
The principle-oriented dealing with events and observing the rules in educational and daily living affairs are the most effective strategies in nursing students for managing their lives (Figure 9).
3.9.1.
Principled encounter
Nursing students were trying to use principled encounter with stressful events and overcome them. A 21-year-old male student says: “I think any problem can be solved. You just have to act in principle because you probably do not know what you're doing that moment because you might be stressed”.
3.9.2.
Observing the rules
Believing in the rule and observing the rules to accelerate problem solving were the nursing students' strategies in facing difficult situations in educational and life affairs. A 24-year-old male student says: “I follow the legal path in facing academic and administrative problems. Observing the rules has always advanced my affairs”.
4.
Discussion
The purpose of this study was to explore the undergraduate nursing student's strategies in confronting living challenges. According to the findings, nursing students used problem-solving methods. Many studies emphasize the importance of problem-solving to confront situational problems, and as an effective factor in reducing stress, increasing the person's ability to communicate with others [16],[17]. Because the problem-solving process differs by with the situations and cultural norms, it is expected that problem solving in Iranian students will also be different [18]. What is important in the findings is that students are trying to adjust their stressful situations with self-control and appropriate interaction with stress [19]. Different from this finding, Angulo [20] emphasizes that the lowest score of promotion program among nursing students is related to the self-control. Another finding was resort to God as a strategy in the most of nursing students. In explaining the cultural care process in nurses, it has been shown that Iranian nurses use spirituality based on their belief in divine destiny [21]. Findings show nursing students are trying to maintain communications with family, friends, teachers and their classmates to manage their living challenges. In a study by Bryan [22], nursing students have a weak to a moderate communication with their educators. Also, findings show nursing students asking help to remove obstacles by looking for social support and counseling from family, friends, university officials. In this regard, Wang [23] showed that nursing students are using optimistic actions and social support in deal with stressful situation. This finding is further enhanced by the high dependence of Iranian families. Financial Management was another strategy of nursing students; financial stress for students, almost always put emotional pressure on students especially in the costs of staying in a dormitory and studying. In many studies financial problems have always been considered as a serious challenge for nursing students [24],[25].
Trust in own abilities and beliefs in nursing students in this study was another strategy that they used to manage the stressful situations of education and family. In this regard, Mazloumi, et al [26] said that high self-esteem is an important factor in the health and well-being of the individual throughout his lifetime.
What can be considered in our study findings is that most students, with a multi-faceted strategies, were trying to moderate the adverse conditions caused by stressful issues in their comfort, Apart from strategies to avoid unpleasant events and impulsive reactions to unfavorable conditions, other methods adopted by the students suggest positive approaches to stress; what is seen in the technique of get away from unpleasant situations is the adoption of positive aspects of avoiding stressful situations. Shaban [18] and rafati [27] state avoidance is the most common mechanism in nursing students to cope with stress. Contrary to this finding, Al-Zayyat & Al-Gamal [28] and Chen & Hung [29] identified avoiding of the stressful situations is the least strategy used by nursing students. Some studies have shown escape-avoidance behavior such as drug abuse or unhealthy nutrition among students in confronting with stressful situations [25]. In our study, researchers believe that experiences that nursing students have learned from the community, family, friends or senior students helped them to cope effectively with stressors; therefore, they did not show avoidance behaviors. In line with our content analysis, Rafati [27], show nursing students were struggling to show principled encounter in dealing with stressful events and observe professional and life rules to speed things up which is the concept of Principle-oriented in the present study.
5.
Conclusion
In this study, finding show undergraduate nursing students are able to use empirically learned strategies to confront with educational and familial challenges. By knowing the problems and strategies of life management, nursing educational systems can arrange a curriculum to educate and develop these strategies for the student, education staff and even families. This program will be able to prepare nursing students for the daily life and professional future requiring more ability and promote the level of health and quality of their profession lives.









 DownLoad:
DownLoad: