1.
Introduction
In recent years moving boundary problems for rarefied gas dynamics have been extensively investigated in the connection with Micro-Electro-Mechanical-Systems (MEMS), see [4,10,11,16,22,24,25,29,30,31]. In micro scale geometries the mean free path is often of the order or larger than the characteristic length of the geometry, requiring the solution of kinetic equations. Usually, these flows have low Mach numbers, therefore, stochastic methods like DSMC are not the optimal choice, since statistical noise dominates the flow quantities. Moreover, when one considers moving rigid body, the gas domain will change in time and one has to encounter unsteady flow problems such that averages over long runs cannot be taken. Instead, one has to perform many independent runs in order to get smooth solutions. Although some attempts have been made to reduce the statistical noise, see, for example, [12], many works rather employ deterministic approaches for simplified models of the Boltzmann equation, like the Bhatnagar-Gross-Krook (BGK) model, see [10,22,30].
In this paper we are following deterministic approach to solve the BGK model and extend the semi-Lagrangian method suggested in [22] to two dimensions in physical space and three dimensions in velocity space. Since the rigid body moves in time, classical interpolation procedures near the rigid body become complicated and possibly inaccurate because of the arbitrary intersection of cells by the rigid body. We note that a cartesian cut cell method has been introduced in [11] to handle the moving object in the rarefied gas. A different technique has been used in [8], where the authors have used ghost point methods in a finite difference framework to treat moving boundaries. We refer also to the treatment of interfaces, for example, for multiphase flow problems in the framework of Lattice-Boltzmann schemes, see [18,23] for a review and further references.
We use an immersed boundary type approach [21] to simulate the fluid-rigid body interactions. However, at variance with the original immersed boundary method, which dealt with an incompressible fluid, here we treat the interaction of a rarefied gas with a rigid body, see [2,10] for immersed boundary approaches applied to kinetic equations. This means that we use a kinetic description of the gas, which is defined by a distribution function, and has therefore many more degrees of freedom than a (compressible or incompressible) fluid. The interaction with the boundary is based on mass conservation, and exchange of momentum and energy. About the energy exchange, we assume that the heat capacity of the solid is much larger than the one of the gas, so that the temperature of the solid object will be assumed constant in time. The approach is based on the combination between grid-based and mesh-free methods: the information about the distribution function is stored in an arbitrary fixed grid on a given domain. For this, the computational domain is discretized by a discrete set of fixed grid points which do not need to be regularly distributed. Moreover, the boundaries are also approximated by a discrete set of boundary points. On the boundary points we apply the boundary conditions. If boundaries move, the boundary particles also move with them.
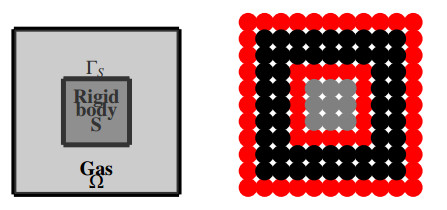
In the present approach the rigid body overlaps the gas grid points. We do not consider those gas-grid-points which are overlapped by the rigid body in the computation and define them as in-active points. The non-overlapped points are defined as active points. All boundary points are defined as active points (refer to Figure 1). Therefore, the distribution of the active grid points is not uniform in the vicinity of a rigid boundary, even if we use a regular lattice for the gas grid points. Moreover, it is varying over time as the rigid body moves. A moving least squares approach (later on referred as MLS) is a particularly suitable interpolation procedure in such a situation not requiring any special treatment. One only has to determine the overlapping and non-overlapping points and to update the kinetic distribution function from the active points with the help of the MLS-interpolation procedure. This process continues until the end of the simulation.
We finally note that in the present paper we restrict to a first order algorithm. Higher order methods are under construction.
The paper is organised as follows. In Section 2 we present the BGK model for the Boltzmann equation and the Newton-Euler equations for rigid body motions. In Section 3 we present the semi-Lagrangian scheme for the BGK model. Moreover, in the same section we present the moving least squares approximation, activating/deactivating grid points, boundary conditions and the coupling algorithm for the rigid body motion and rarefied gases. In Section 4 we present numerical results in one and two space dimensions. Finally, in Section 5 some conclusion and an outlook are presented.
2.
The model
We consider the BGK-model for rarefied gas dynamics and the Newton-Euler equations for the motion of the rigid body inside the gas.
2.1. BGK model for rarefied gas dynamics
Consider first the BGK equation for the distribution function of gas molecules denoted by f=f(t,x,v),t≥0,x∈Ω⊂Rd,(d=1,2) and v=(vx,vy,vz)∈R3. It is given by
with initial value f(0,x,v)=f0(x,v) and boundary conditions discussed later. For the numerical examples we consider one- and two-dimensional spatial geometries and use suitable reduction procedures for the BGK equation, see [9,14].
Here τ is the relaxation time and M[f] is the local Maxwellian given by
ρ,U,T are macroscopic quantities: Density, mean velocity and temperature, R is the universal gas constant.
These macroscopic quantities are computed from f(t,x,v) in the following way. Let ϕ(v)=(1,v,|v|22) be the collision invariants. The moments are defined by
E is the total energy density and it is related to the temperature through the internal energy
2.2. Newton-Euler equations for rigid body motion
The mechanical properties of the rigid body are uniquely defined by its mass and its moment of inertia, and its displacement is determined by the position of the center of mass and its orientation. The dynamics of the rigid body is determined by the Newton-Euler equations
where M is the total mass of the body S with center of mass Xc, V is the translational velocity of the center of mass, while ω denotes the angular velocity vector describing the rotation around an axis passing through Xc. F is the translation force, T is the torque and [I] is the barycentric moment of inertia.
The center of mass of the rigid body are obtained by
Finally, the velocity of the rigid body is given by Uw=V+(x−Xc)×ω,x∈S.
The force F and torque T are computed according to
where n is the unit boundary normal vector of the rigid body pointing towards the gas domain and φ is the pressure tensor given by
ΓS denotes the boundary of S, see Figure 1.
In this paper we limit to study one and two dimensional problems. In 1D the rigid body does not rotate, so the moment of inertia does not play any role. In 2D the center of mass is determined by two coordinates, Xc=(Xc,Yc), the only non zero component of the angular velocity vector is the out of plane z-component ω, and the barycentric moment of inertia is a scalar which can be computed from the mass distribution of the object:
In all our tests we assume the mass is uniformly distributed in the body of the object (which is a surface in 2D), therefore the moment of inertia depends only on the mass and the geometry of the object.
3.
Numerical methods
We describe a Semi-Lagrangian scheme with least squares interpolation for the BGK equation for three dimensional velocity space and two dimensional physical space.
3.1. Semi-Lagrangian scheme for BGK model
We consider a constant time step Δt, a uniform mesh in velocity space with mesh size Δv and a, in general, non-uniform mesh with average spacing Δx in physical space. The time discretization is denoted tn=nΔt,n=0,1,…. The space discretization is obtained by filling (regular or irregular) grid points xi=(xi,yi)∈Ω⊂R2,i=1,…,Nx, where Nx is the total number of grid points in physical space. We note that the Nx grid points include interior as well boundary points. The interior grid points are fixed and located inside the whole computational domain including the moving object. In contrast, the boundary points are fixed to the boundaries, that means moving on the boundaries of the moving object and fixed on the fixed boundaries. The interior grid points are distinguished according to whether they are overlapping with the moving body or not. In the first case they are called non-active points, otherwise active points. See Figure 1 for an illustration. Moreover, we consider an even number Nv of velocity grid points in each direction and a uniform velocity grid size Δv in all directions. We assume the distribution function is negligible for |vx,y,z|>vmax=NvΔv2. The uniform velocity grids are denoted by vj, vk and vl in x,y and z directions, respectively, where vj=−vmax+(j−1)Δv,j=1,…,Nv+1. Similarly, we define vk and vl for k,l=1,Nv+1.
Let fjkl=fjkl(t,x)=f(t,x,vj,vk,vl) and fijkl=fijkl(t)=f(t,xi,vj,vk,vl). The evolution equation of fjkl(t,x) along the characteristics between time steps n and n+1, i.e., for t∈[tn,tn+1], is calculated from the Lagrangian form of the discrete-velocity BGK model
with final conditions
together with appropriate boundary conditions for fjkl at boundary points.
Here Mjkl[f] is still the local Maxwellian having the moments of fjkl.
We consider the implicit Euler scheme for the above equations, which reads
and
for j,k,l=1…,Nv+1 and all active interior points.
The semi-Lagrangian method now consists of three steps:
(ⅰ) First, we determine ˜x and ˜y from the backward characteristics ˜x=xn+1i−vjΔt, ˜y=yn+1i−vkΔt. Then reconstruct the function ˜fnjkl at (˜x,˜y). At tn all values fnijkl are known for all active points and boundary points. At (˜x,˜y) we have to interpolate ˜fnijkl. One can use any interpolation formula. In this paper we use a least squares approximation for the reconstruction. This is presented in the next section.
(ⅱ) In the second step we obtain Mn+1ijkl. Since Mn+1i and fn+1i give the same conservative moments, we multiply the above discrete equation by the collisional invariants ϕ(v) and sum over all velocities. We get
Once the moments are known, we can compute the Maxwellian at the new time.
(ⅲ) Finally, we update the density function by
3.2. Time integration for the Newton-Euler equations
We solve the Newton-Euler equations by the explicit Euler method in time. The time step is the same as the time step of the BGK model. This means in particular, that the time step in the BGK model is chosen according to the stability requirements for the explicit Euler scheme for the Newton-Euler equations.
3.3. Moving least squares approximation
In this subsection we describe the least squares approximation of a function in a two-dimensional computational domain Ω∪Γ∈R2, where Γ is the boundary. As described above, we distinguish between the grid points on the boundary Γ and the interior grid points in Ω. The interior and boundary grid points are distinguished by assigning different flags, see Figure 1. Consider first the interior grid points (xi,yi) in Ω with average spacing Δx. They are chosen at the beginning of the calculation and are not moved. Those grid points overlapping with the moving body are non-active, the others are active.
Let f(x,y) be a scalar function and fi its values at (xi,yi). We consider the problem of approximating the function ˜f=f(˜x,˜y) at (˜x,˜y) from the values of its neighboring points. We associate a weight function such that nearby particles have more and far away particles have less influence. Therefore, one can choose any distance function as a weight function which decays as the distance goes to infinity. In this paper we have considered a Gaussian function, but other choices are possible (see for example [26,33] for other classes of weight functions). In order to limit the number of neighboring points we consider only the neighbors inside a circle of radius h with center (˜x,˜y). We choose as radius h some factor of the average spacing Δx, such that we have at least a minimum number of neighbors for the least-squares approximation, even next to the boundary. In case of regular grid and far from the boundary, one might consider using smaller values of h. Such adaptive choice of h has been considered, for example, in [17]. For the sake of simplicity, we have chosen a constant h=3.1Δx in this paper, which gives a sufficiently large number of neighbours even near concave boundaries (as is the case of the Example 6 in the last section). The use of adaptive values of h is left to future investigation. We sort the neighboring points from 1 to m with respect to distance, such that the neighbour index 1 is the nearest neighbor of (˜x,˜y). With a slight abuse of notation, let P(˜x,˜y;h)={(xj,yj),j=1,…,m(h)} denote the set of neighbor points of (˜x,˜y) inside the disc of radius h. We note that the number m of nighbours depends on (˜x,˜y) and h. In all calculations we have considered the following truncated Gaussian weight function
with α a user defined positive constant, chosen here as α=6, so that the the influence of far neighbor grid points is negligible. This choice has been suggested from previous experience [17,28]. It would be interesting to investigate what is the optimal choice of the parameters, or even to adopt a different class of weight functions. This is left to future investigation.
In order to approximate the function we consider the m Taylor's expansions of f(xj,yj) around (˜x,˜y)
for j=1,…,m, where ej is the error in the Taylor's expansion. We first assume that ˜f approximates the nearest point f1. In other words e1=0. The unknowns ˜f,∂˜f∂x,∂˜f∂y are computed by minimizing the error ej for j=2,…,m and setting the constraint e1 = 0. To solve this constraint least-squares problem, we use the constraint to rewrite the equations in the form
The system of equations can be written in matrix form as
where e=[e2,…,em]T, a=[∂˜f∂x,∂˜f∂y]T,b=[f2−f1,…,fm−f1]T and
For m>3, this system of equations is over-determined for two unknowns [∂˜f∂x,∂˜f∂y]T. The unknowns a are obtained from the weighted least squares method by minimizing the quadratic form
where W=wjδjk,k=2,…,m is the diagonal matrix. The minimization of J yields
Now from Eq. (3.10) with e1=0 for the closest point x1 we can compute the value of f(˜x,˜y) at (˜x,˜y) as
since ∂˜f∂x and ∂˜f∂y are now known. We note that higher order approximations are obtained by using higher order Taylor's expansion in (3.11). We refer to [28] for details.
In the above least-squares approximation a function is approximated at an arbitrary point from its neighboring points and the distribution of these points can be arbitrary. Such a straightforward least-squares approximation leads to a central difference scheme. In case of discontinuities in the solution, this will lead to numerical oscillations and one has to introduce additional numerical viscosity. This can be done in the least squares framework by adopting a suitably modified version of that approach using an upwind reconstruction.
Moreover, we note that for the stabalization of higher order approximations a WENO-type reconstruction can be used, see e.g., [1,32,33], where WENO approximations with least squares approaches have been developed for regular and irregular grids.
3.4. Activating/deactivating grid points
For the simulation of the interaction of the rigid body motion with the gas, we overlap the region defined by the rigid body and the region where the BGK model is computed. Those grid points in the gas phase which are overlapped by the rigid body during the motion are assigned as non-active grids and the others as active grids. The non-active grids are taken out of the numerical process and sorted out from the neighboring lists in the least-squares approximations. After the rigid body movement, some of the active grids will be overlapped by the rigid body and then redefined as non-active grids. In turn, some of non-active grids will be out of the overlapping zone of the rigid body and will be reactivated again for the numerical process. During this process we need to update the distribution function f(t,x,v) on the newly activated grid. This can be obtained from its neighboring active grid points using the least squares method from above.
3.5. Boundary conditions
On the solid boundary as well as on the moving rigid object boundaries we apply diffuse reflection boundary conditions. The boundary particles are sitting on the boundaries and all boundary points having contact with the gas phase are defined as active points. The boundary particles move with the boundary velocities. The boundary conditions are applied on the boundaries of the computational domain as well as on the surface of rigid body. Let ρw,Tw,Uw and n be the density, temperature, velocity and n unit normal of the wall and the surface of the rigid body. The wall normal vector n points towards the gas domain.
For (v−Uw)⋅n<0 we obtain the distribution function on the wall fn+1w from the evolution equation. For (v−Uw)⋅n>0 the distribution function is the Maxwellian with parameters ρw,Tw and Uw, which is given by
We note that the density ρw is not known and is determined by assuming the net flux across the wall or surface is zero. This means, we have
Hence, from (3.16) and (3.17) we obtain
3.6. Coupling rigid body motion and the rarefied gas
After calculation of the new density function fn+1j we first compute the pressure tensor (2.7) on all boundary points of the rigid body. Then we approximate the force and torque on the rigid body according to (2.6). We obtain the translational and rotational velocities and then move the boundary points and the center of mass accordingly. Finally, we update the normal vector n. The new velocity Uw is used to apply the boundary conditions for solving the BGK model. In summary, we use the following coupling algorithm:
(ⅰ) Generate initial grid points with flags as interior and boundary grids and prescribe the initial conditions in the gas as well as in the solid phases.
(ⅱ) Determine the active and non-active grids in the gas phase.
(ⅲ) Update newly activated grid points in the gas phase with the help of interpolations from its active neighbors.
(ⅳ) Solve the BGK model equation in the active grid points and apply boundary conditions on all boundary points.
(ⅴ) Compute the force and torque on the boundary points of the rigid body.
(ⅵ) Solve the Euler-Newton equations and then get new positions, velocity and the unit normal of the boundary points of the rigid body.
(ⅶ) Goto (ⅱ) and repeat until the final time is reached.
4.
Numerical results
In the following we consider numerical examples in one and two space dimensions and three velocity dimensions. The test cases are given in dimensionless form but can be interpreted in SI-units.
4.1. Example 1: 1D moving piston, one way coupling
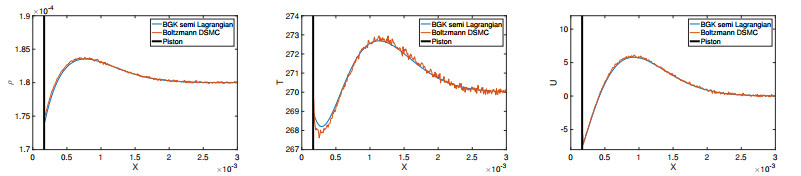
This problem has been considered in [10,22] in a larger domain. We consider the one-dimensional spatial domain Ω=[0,3×10−3]. Initially the piston is positioned at x=1.5×10−4. We considered the total number Nx=300 grid points in physical space and in Nv=30 grid points in every direction of velocity space. The left boundary moves with velocity
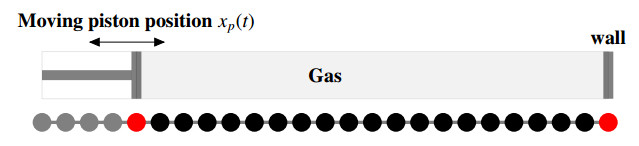
This is a one way coupling, since the motion of the piston is prescribed. We note that initially, some grid points less than x=1.5×10−4 are overlapped by the piston. They are non-active points and the piston position and the right boundary points are the active grid points, see Figure 2 for physical setup of the problem.
When the piston starts to move in time the process of activating and deactivating of grid points continues throughout the simulation. We have considered the final time tfinal=4×10−6. The time step is Δt=10−9. The minimum and maximum limit of the velocity are vmin=−1200 and vmax=1200. We have considered the Argon gas with diameter d=0.368×10−9, Boltzmann constant kb=1.3806×10−23 and the universal gas constant R=208. The initial temperature T0=270, initial density ρ0=0.00018 and the initial mean velocity U0=0. The corresponding Knudsen number is Kn=λ/L=0.215, based on the characteristic length L=3×10−3−1.5×10−4, where λ is the mean free path defined by
To validate the numerical results of the semi-Lagrangian scheme for the BGK model, we compare it with the results of a numerical solution of the full Boltzmann equation via the DSMC method [3,5,19]. For a proper comparison of the BGK model and the DSMC code for the Boltzmann equation we have to relate the relaxation time τ and the mean free path, see [7], as
where ˉC=√8RT0π. The corresponding relaxation time τ=2.0634×10−6. Nevertheless, by DSMC we solve the full Boltzmann equation, therefore differences in results may be due partially to the different models, and partially to the different numerical techniques adopted in the two cases.
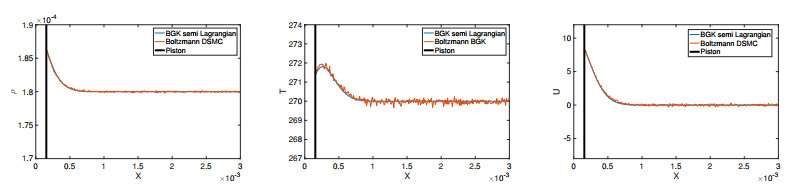
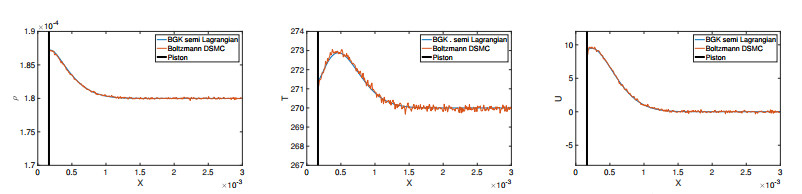
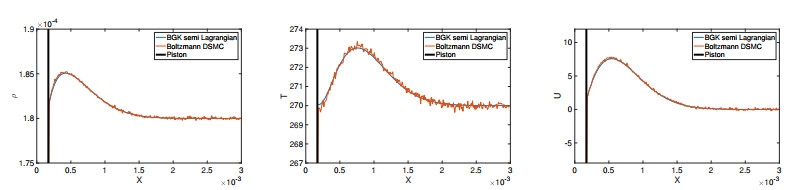
Initially, the piston and the gas are at rest. The piston starts oscillating in time and disturbs the gas phase. A wave is formed which eventually creates a shock. The flow is a low Mach number flow and the DSMC results show strong fluctuations. Since the flow is unsteady one cannot take time averages of the DSMC simulations. Therefore, one has to perform several independent runs. In the DSMC simulations we have considered the same number of cells as in the BGK model. To reduce the statistical noise, we have considered 10.000 gas molecules per cells initially. Moreover, we have performed 500 independent runs. In Figures 3–6 we have plotted the density, temperature and velocity of the gas determined from both numerical methods. We can observe that the BGK and the DSMC solutions have very good agreements at all times. We note, that the statistical noise for the DSMC simulations is still observed even after 500 independent runs.
In both methods we apply diffuse reflection boundary conditions on the piston with moving frame of reference Uw=(up,0,0), where up is the velocity of the piston, and the wall temperature Tw=T0. Similarly, we apply diffuse reflection boundary conditions with zero wall velocity and a wall temperature equal to the initial temperature on the right boundary.
4.2. Example 2: 1D moving plate, two way coupling
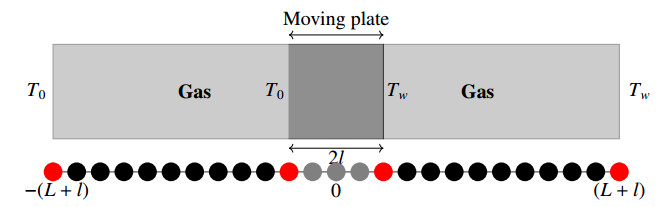
In Example 1, the gas flow was influenced by the motion of the piston, but there was no any influence of the gas flow on the motion of the piston. In this example, we consider a two way coupling of both phases. The force exerted on the rigid body from the surrounding gas influences the motion of the rigid body and vice versa. We again consider a one dimensional physical space and three dimensional velocity space. We consider the physical domain [−(L+l),(L+l)] as described in Figure 7 with L=1 and l=0.1, where 2l is the thickness of a plate which is driven by the pressure difference at its edges.
Initially the plate is located at (−0.1,0.1) with center of mass Xc=0, where the gas and the plate are at rest. This problem has been studied in [10]. We reconsider it as a benchmark problem since an analytical solution is available for the equilibrium state. We again consider a monatomic gas with parameters given in Example 1. The initial temperature is T0=270 and the initial pressures P0 are the same on both sides of the plate and are equal to 0.0386. The initial density ρ0 is obtained from the equation of state. The initial Knudsen number is 0.08 based on the characteristic length 2L and the relaxation time τ=5.398×10−4. Moreover, we have considered different density ratios of the gas and the plate. The other parameters are the same as in the Example 1. We prescribe a higher temperature Tw=330 on the right side of plate and on the right boundary of the computational domain. On the left boundary of the plate and on the left boundary of the computational domain the temperature is kept to T0. Due to the high temperature on the right walls, the pressure on the right hand side starts to increase and the plate starts to move to the left hand side. The motion of the plate is computed from the Euler-Newton equations, where only a translational force is computed for the one dimensional case. Since the plate has two opposite normals ±1, from Eq. (2.6) the total force is given as the difference of pressure
where A is the area of plate. The plate starts oscillating and finally reaches the equilibrium position [10]
The domain is discretized with Nx=300 cells. The velocity grid is given by Nv=20 cells for the BGK equations. The final time is 0.5. The time step is Δt=4×10−6. The other parameters are the same as in Example 1. The explicit Euler method with the same time step as the time step for the BGK model is used for time integration of the Newton-Euler equations.
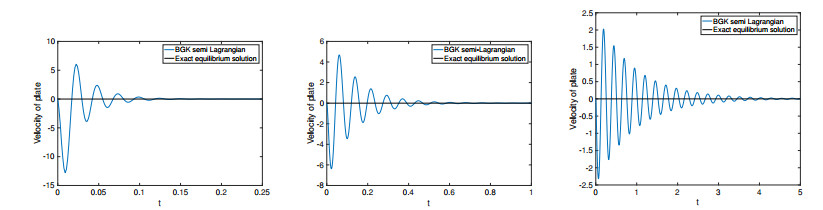
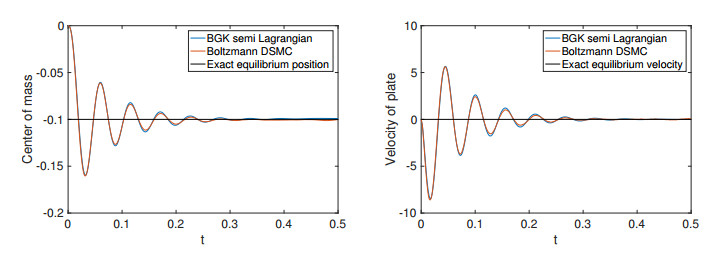
In this test case we have simulated a wide range of density ratios of gas and plate ranging from 1 to 10 up to 1 to 1000. In Figures 8 we have plotted the velocity of the plate with respect to time together with the exact equilibrium solution. One can observe, as expected, that a lower density plate reaches the equilibrium position earlier than the heavier plates. We remark, however, that the change of density ratio has been used just to change the mass of the plate. Indeed the dynamics depend only on the mass of the plate, not on its density. We choose to change the density just to allow a finite size of the plate (which is left unchanged in our simulations).
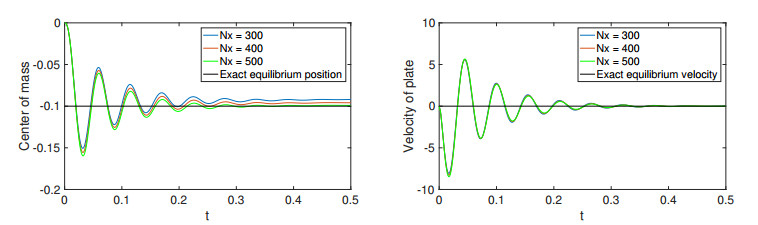
Additionally, we have performed a convergence study for the case of a density ratio 1 to 50. The results for the plate position and velocity are reported in Figure 9. We note that for Nx=300 we obtain an accurate approximation of the equilibrium value for the velocity, whereas, the equilibrium position still deviates from the analytical value. This is due to the first order error of the numerical scheme and an accumulation of very small numerical errors in velocity during the integration process. Increasing the number of grid points Nx in physical space, we obtain convergence towards the analytical equilibrium position. We remark that a velocity grid with Nv=30 gives almost the same results, see [27] for a numerical comparison.
We have further compared the solutions of the BGK model with the DSMC simulations for Nx=500. In the case of the DSMC simulations we have again considered 400 gas molecules per cell initially. The boundary conditions and other parameters are the same in both methods. We have performed 50 independent runs. In Figure 10 we have plotted the position of the center of mass and the velocity of piston vs time. We note that the time evolution of the the DSMC solutions and the solutions obtained from the BGK semi Lagrangian method are very close to each other.
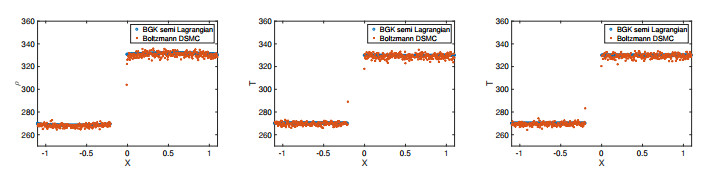
Furthermore, in Figure 11 we have plotted the temperature obtained from both methods for time t=0.1,0.2 and 0.4. We see that at time t=0.1 the temperature is not yet reaching equilibrium state, but after t=0.2 the temperature of the gas on the left reaches the left wall temperature and the temperature of the gas on the right reaches the right wall temperature.
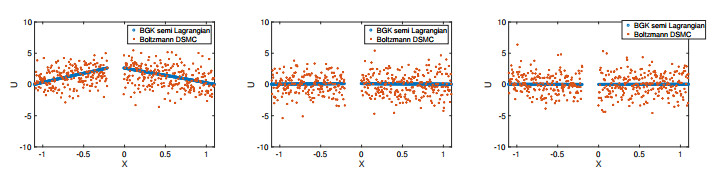
Similarly, we have plotted the velocity field of the gas on both sides of the plate in Figure 12 at different times for both methods. Here, we also observe, that the DSMC solutions fluctuate around the BGK solutions.
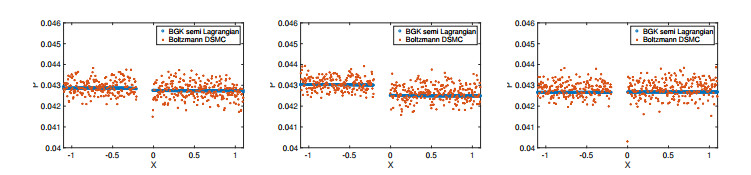
Finally, in Figure 13, we have plotted the pressure obtained from the BGK model and the DSMC simulations. In the beginning, the pressure on the right increases due to the increase of the temperature. When it reaches t=0.1 the pressure on the left is slightly larger than on the right side. At time t=0.2 the pressure on the left is still larger, which is clearly visible in the figure. It fluctuates and finally reaches the equilibrium state, where it is equal on both sides. The relative error of the computation versus the analytical solution [10] is approximately 0.7% for pressure and 0.6% for density in the stationary state for the finest discretization Nx=500.
4.3. Example 3: 2D driven cavity problem
Here, we consider a spatially 2-dimensional problem with three-dimensional velocity space. The flow in a cavity driven by the velocity on the top is a widely used benchmark problem for testing and comparing numerical methods. We consider a micron size square cavity. The top wall has velocity
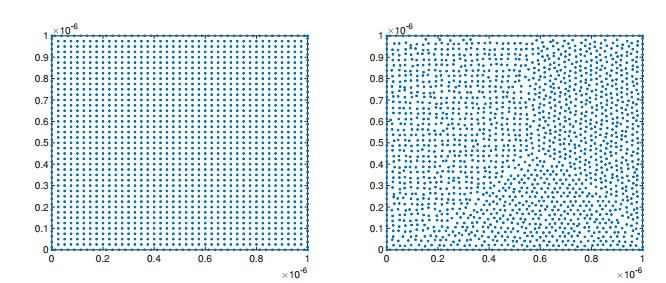
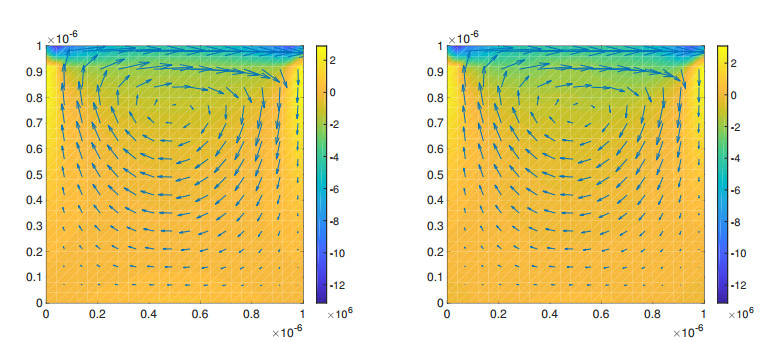
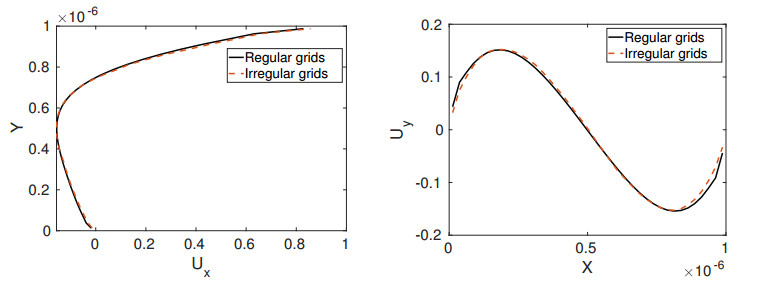
and on the other three walls we have Ux=Uy=0. The temperature is kept constant at T0=270 on all walls, the initial density is ρ0=1, the wall velocity uw=1 and the gas constant is R=208. The gas is again monatomic with parameters given as in the Example 1. The Knudsen number Kn=0.1 is based on the characteristic length given by the size of the wall. Diffuse reflection boundary conditions are applied on all walls. In Figure 14 we have plotted the regular and irregular gridpoints used for the simulation. Figure 15 shows the velocity fields and the vorticity obtained from the BGK equation for regular as well as irregular grid points. We use 50×50 gridpoints and approximately the same number of irregular grid points is generated. The time step is chosen as 5×10−11. The simulation was stopped after time t=4×10−7. Moreover, Figure 16 compares the x- and y-velocity components along the center lines in y- and x-direction, respectively. We observed that the solutions obtained from the regular and irregular grids are almost the same.
Moreover, we compare the semi-Lagrangian scheme for the BGK model with DSMC simulations for the Boltzmann equation for this example. The mean free path and the relaxation time are chosen according to Eq. (4.2). First, we choose the velocity of the upper wall as uw=1 in positive x-direction. In the DSMC simulations we have taken the same time step and the same number of cells as in the BGK model. For the DSMC simulations we have also applied diffuse reflection boundary conditions on all walls. The time steps and the gas parameters are the same as in the BGK model. In this case we look at the steady state solution. Therefore, unlike in the earlier two examples, we do not perform independent runs, but time averages.
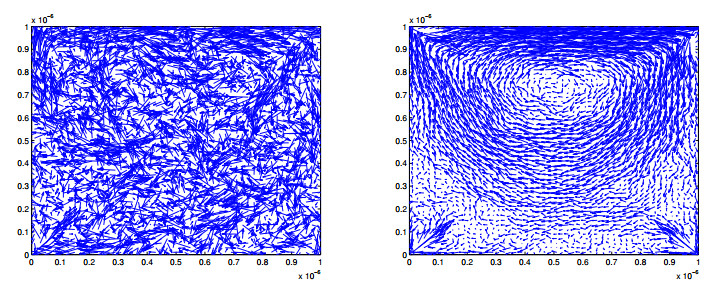
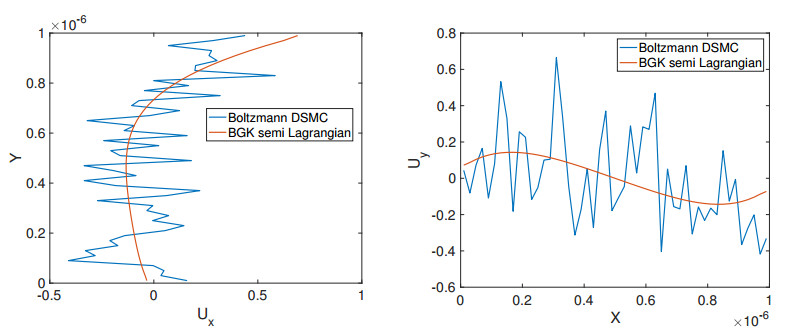
In Figure 17 on the left we have run the DSMC simulation up to 105 time steps, where the last 9×104 time steps are used for the averaging over the samples. In this case the fluctuations dominate the flow field. In Figure 17 on the right 3×106 time steps are used for the averaging over the samples.
In Figure 18 we have plotted the x-velocity component Ux along the central vertical line as well as the y-velocity component Uy along the central horizontal line for the case with 9×104 samples. We observe again the highly oscillating DSMC results compared to the BGK solutions.
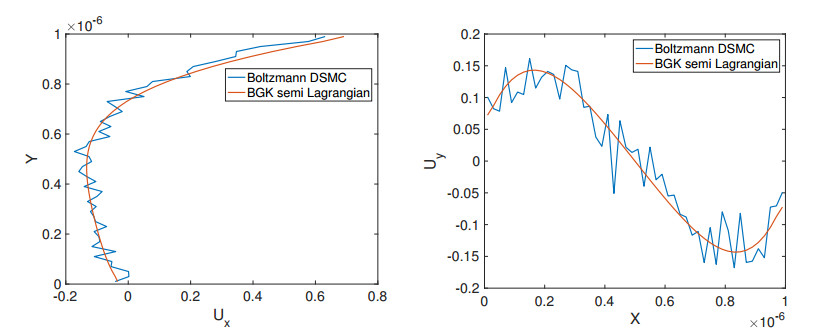
Similarly, in Figure 19 we have plotted the x-velocity component Ux along the central vertical line as well as y-velocity component Uy along the central horizontal line for 3×106 samples. The DSMC results are improving, but still fluctuating around the BGK solutions.
4.4. Example 4: Moving a 2d rigid body in rarefied gas
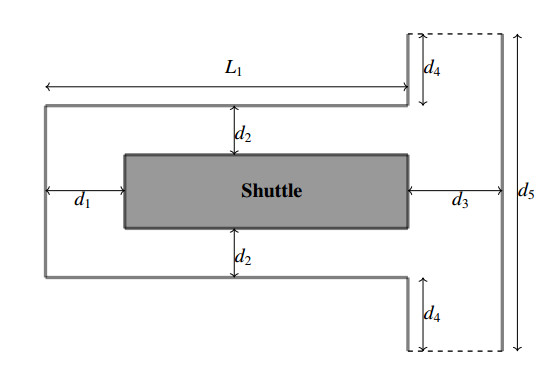
This example is the direct extension of Example 1 into two space dimensions. Here we have used a Chu reduction [9,14] to reduce the dimension of the velocity space from three to two. We have taken this problem from the paper by Frangi et al. [13], where the authors have studied the biaxial accelerometer produced by STMicroelectronics with a surface micro-machining process. The authors have analysed the problem by considering a two-dimensional simplification. In Figure 20 we have sketched the computational domain in details. The shuttle lies initially in the middle of the domain. In the rest of the domain a gas flow is taking place. The shuttle oscillates with the velocity cos(2πf0t), where f0 is the frequency. The parameters mentioned in the Figure 20 are L1=19.2×10−6,d1=4.2×10−6,d2=2.6×10−6,d3=5×10−6,d4=3.9×10−6,d5=18.8×10−6. In [13] the frequency has been taken f0=4400 Hz, but with this frequency, the shuttle crosses the upper and lower boundaries. Therefore, we have chosen f0=40×4400 Hz such that the maximum amplitude of the shuttle is half of the distance d2. The initial pressure of the gas is equal to 0.1 bar, which corresponds to initial density ρ0=0.1641. The initial distribution f0 of the gas is the Maxwellian with zero mean velocity, initial temperature T0=293 and initial density ρ0. The diffuse reflection boundary condition with wall temperature T0 is applied on the solid lines and a far field boundary condition f0 is applied on the dotted lines. We note that here, we solve the real motion of the shuttle, while in [13] the authors solve the stationary equations with assigned non zero velocity on the boundary.
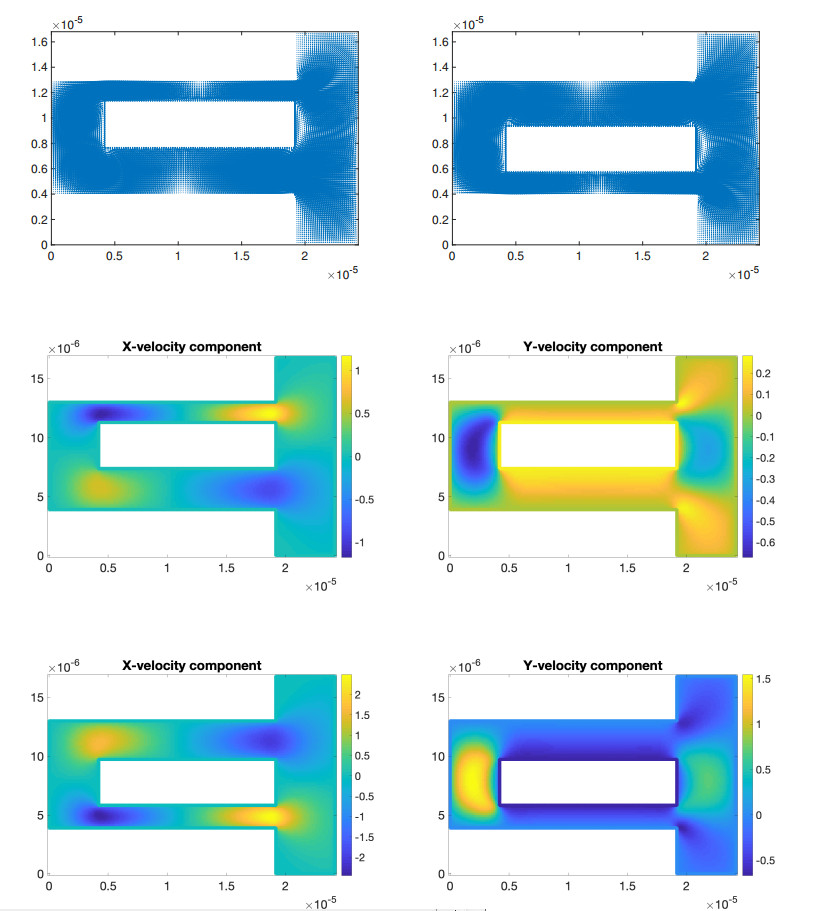
In Figure 21 we have plotted the velocity vector fields as well as x- and y- components of the velocity at times t=1.2×10−6 and t=3.6×10−6.
4.4.1. Convergence study
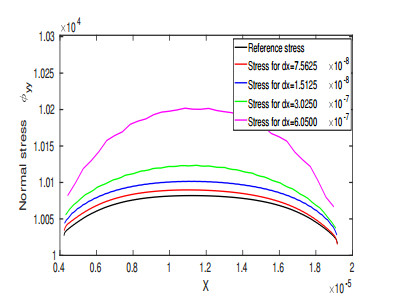
In Figure 22 we have plotted the normal stress tensor on the top wall of the shuttle at time t=1.2×10−6. As a reference solution we consider the one obtained at the finest resolution with cell size 4.84×10−8, which corresponds to 111.709 grid points including boundary points. The time step Δt=3.20×10−11, which corresponds the CFL number equal to 0.92. For the convergence study we have considered the other coarser grids with sizes 7.5625×10−8, 1.5125×10−7, 3.025×10−7 and 6.050×10−7 and changed the time steps keeping the constant CFL number equal to 0.92.
In Figure 22 we have plotted the normal stress tensor on the top of the shuttle at time t=1.2×10−6 for different resolutions. In order to estimate the error, we have generated the fixed number of points with N=100 in equal distance. On this grid points we have interpolated the stress tensors from different resolutions including the reference solutions and then defined the relative errors as
We note that ϕrefyy,i is the interpolated reference solution and ϕΔxyy,i is the interpolated solution for grid size Δx. In Table 1 we have presented the relative error of the normal stress tensor φyy at the same time. The errors in the table show the first order convergence of the scheme.
4.5. Example 5: Circular body motion in a driven cavity
Consider a circle immersed in a monoatomic gas in a micro square. We consider a 2D spatial and 3D velocity domain. Like in Example 3, the top wall has constant velocity in the positive x-direction. The initial and boundary conditions are the same as in Example 3. Initially, gas and rigid body are at rest. The rigid body is located at the center of the cavity.
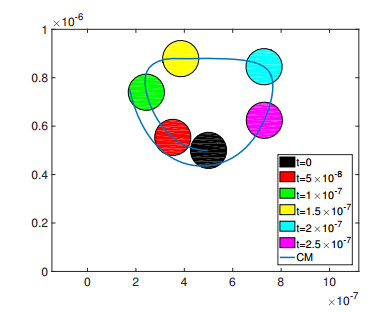
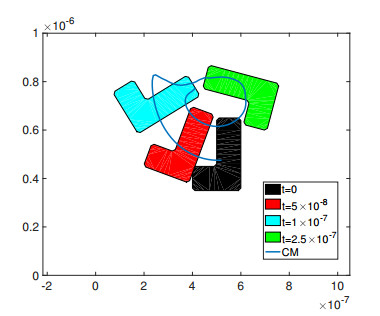
We proceed as in Example 2. The force and the torque are computed according to Eq. (2.6). The density of the rigid body is 10 times larger than the density of gas. We have performed the simulations for different density ratios. We experienced that if the density of the rigid body is at least ten times smaller than the density of the gas, instabilities occur in the present set up. A more quantitative comparison of the trajectories for objects with different densities requires a more accurate scheme, and will be performed in a future paper. Again, we use the explicit Euler scheme for the time discretization of the Euler-Newton equations and the same time step for the BGK model. The upper wall moves with velocity uw=30. We simulate up to the final time tfinal=4.4×10−7. In Figure 23 we have plotted the path of the center of mass of the body and its positions at different times.
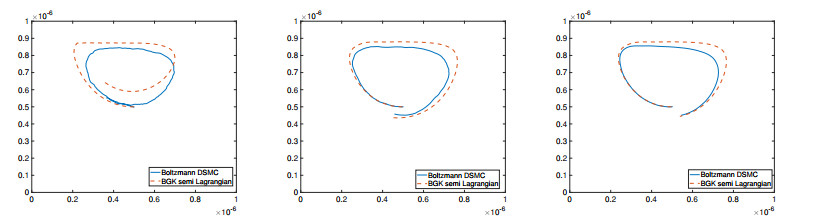
Since there are no analytical or experimental results to validate the numerical solutions, we validate our solutions with DSMC simulations for the Boltzmann equation. We use the same initial and boundary conditions and the same parameters for both schemes. First, we consider uw=10,20 and 30 for the DSMC simulation. As we have seen in earlier examples, the DSMC results are dominated from the statistical noise for smaller Mach number flows. In Figure 24 we have compared the trajectories of the center of mass obtained from both methods. We observe that increasing the wall velocity uw gives a better agreement between the numerical solution of the BGK model and the DSMC solution. In Figure 24 we have plotted the center of mass obtained from the BGK model and DSMC simulations. In the case of DSMC simulations 10 independent runs are carried out. For larger uw the BGK solutions and DSMC solutions are getting closer.
4.6. Example 6: Rigid body with arbitrary shapes in a driven cavity
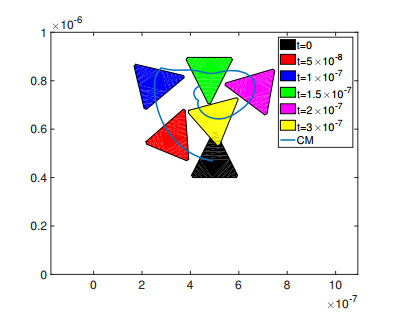
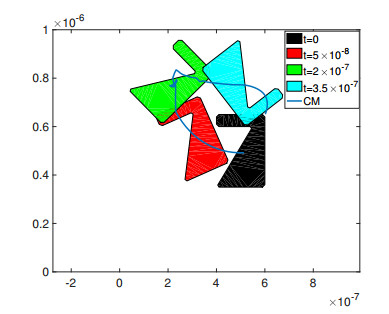
To show that the scheme is able to simulate the interaction of the gas with an arbitrary shaped rigid body, we have considered a 2D spatial and 2D velocity domain and three different types of bodies, which are triangular, L-shaped and chiral particles. For these three shapes, rotational effects are clearly observed. The initial and boundary conditions are as in Example 5. The density of the rigid bodies is again 10 times larger than the density of the gas. The upper wall has velocity uw=30 and the simulations are stopped after time 4.4×10−7 for all cases. All rigid bodies are initialised at the center of the cavity. In Figures 25–27 we have plotted the positions at different times together with the trajectories of triangle, L-shaped and chiral particles, respectively. In all cases we see that the rigid bodies follow the flow path. We mention here that in [24] a general method for the simulation of arbitrary shaped object in a rarefied gas has been presented. In that paper the gas satisfies the Boltzmann transport equation, which is effectively solved by DSMC.
5.
Conclusions and Outlook
In this paper, we have presented a mesh free method for the simulation of moving rigid bodies immersed in a rarefied gas flow. The motion of the rigid body is obtained by solving the Newton-Euler equations. The force and the torque are computed from the surrounding gas. The Newton-Euler equations are solved by an explicit Euler method. The rarefied gas is simulated by solving the BGK model of the Boltzmann equation. A semi-Lagrangian method is used to solve the BGK model, where a first order least squares approximation is used for the interpolation scheme. Several numerical tests are performed in order to validate the method, both in one and two space dimensions. In particular, in 1D we consider the case of a moving plate immersed in a rarefied gas. In a first test we assume the motion of the plate is prescribed (one way coupling), while in a second test the motion of the plate is computed from Newton's equations (two way coupling). In both cases we compared the results with those obtained by DSMC solution of the Boltzmann equation. Notice that DSMC results required to take the average of a lot of runs in order to decrease statistical fluctuations. In two space dimensions we considered several test problems: some in which the motion of the object is prescribed, such as the classical driven cavity (and compared the results with DSMC) and the motion of the shuttle in a 2D model of a Micro Electro Mechanical System (and results are compared with others available in the literature [13]). Finally, some tests are performed with a rigid body of arbitrary shape immersed in a gas and driven by the flow (two way coupling). In some cases the results are compared with those obtained by DSMC. In the regimes we investigated there is a good qualitative agreement between the solutions obtained by BGK and by the full Boltzmann equation simulated by DSMC. Of course accurate DSMC solutions require a computational time which is several orders of magnitude higher than the one needed by the numerical solution of the BGK model.
In this paper we consider a one way heat exchange: the temperature of the rigid body is assumed to be constant in space and time, which is equivalent to suppose that the heat capacity of the rigid body is much larger than the one of the gas. In future work we shall remove such an approximation and consider finite heat capacity of the rigid body. As a first step in this direction we assume a rigid body with infinite conductivity, which will make the temperature of the body constant in space. Later on we shall model heat diffusion in the solid as well.
Moreover, the scheme will be extended to the case of gas-mixtures [15] and to three space dimensions. An interesting application of the method will include the treatment of several bodies immersed in a rarefied gas. In this way it will be possible to model a collection mesoscopic particles dispersed in a rarefied gas, thus providing a quantitative tool that can be used to validate homogenised macroscopic models of suspensions.
From the methodological point of view, further research directions will include the use of on non-oscillatory higher order methods in space and time based on least squares approaches, see [1] for a combination of WENO and least squares approaches for fluid dynamic equations and high order approximation of boundary conditions.
Acknowledgment
This work is supported by the DFG (German research foundation) under Grant No. KL 1105/30-1 and by the ITN-ETN Marie-Curie Horizon 2020 program ModCompShock, Modeling and computation of shocks and interfaces, Project ID: 642768.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: