Fever is a extremely common symptom in infants and young children. Due to the lowresistance of infants and young, long-term fever may cause damage to the child’s body. Clinically,some children with long-term fever was eventually diagnosed with Kawasaki disease (KD). KD, anautoimmune disease, is a systemic vasculitis mainly affecting children younger than 5 years old. Dueto the delayed therapy and diagnosis, coronary artery abnormalities (CAAs) develop in children with KD, and leads to a high risk of acquired heart disease. Later, patients may have myocardial infarctionor even die a sudden death. Unfortunately, at present, the pathogenesis of KD remains unknownand KD lacks of specific and sensitive biomarkers, thus bringing difficulties to diagnosis and therapy.Therefore it is a highly focused topic to research on the mechanism of KD. Some scholars believethat KD is caused by the cross reaction of external infection and organ tissue composition, herebytriggering disorder of the immune system and producing a variety of cytokines. On the basis ofconsidering the cytokines such as vascular endothelial cells, inflammatory factors, adhesion factorsand chemokines, endothelial cell growth factors, put forward a kind of dynamic model of pathogenesisof KD by the theory of ordinary differential equation. It is found that the dynamic model can showcomplex dynamic behavior, such as the forward and backward bifurcation of the equilibria. This articlereveals the possible complexity of KD infection, and provides a theoretical references for the researchof pathogenic mechanism and clinical treatment of KD.
1.
Introduction
Autoimmune disease is the disease that the donor has an immune response to a certain part of its own, resulting in damage to the function of tissues and organs. Many autoimmune diseases have been found, and most of them are primary, but the pathogenesis of primary autoimmune disease is still controversial [1]. The unknown mechanism and the lack of biomarkers are a major problem in the study of autoimmune diseases. KD is a kind of primary autoimmune disease, also known as muco-cutaneous lymph node syndrome (MCLS). KD was first described by T. Kawasaki in 1967, which often associated coronary artery abnormalities (CAAs)[2].
Clinical features of KD usually includes long-time fever and generally more than thirty-nine degree centigrade, changes in the extremities, polymorphous exanthema, bilateral conjunctival injection, lesions of the lips and oral cavity and cervical lymphadenopathy [3]. There are many involved organs in KD, especially for organs which have rich capillaries. Due to a delayed diagnosis and therapy, CAAs develop in the part of children with KD, and leads to a high risk of acquired heart disease [4]. In many areas of China, the incidence rate of Kawasaki disease is rising year by year [5]. However, the lack of specific biomarkers and unclear pathogenic mechanism limit accuracy of diagnosis and timely treatment [6,7]. Currently, diagnosis criteria is established on fever and at least four of five clinical features of KD, but not all patients with KD have all been described symptoms in the standard, which is known as incomplete kawasaki disease [8]. In the treatment, although the lack of specific drugs for KD, intravenous immunoglobulin combined with aspirin is more effective for most of the patients, it is because that immunoglobulin can inhibit the activation of the immune cells, thereby inhibiting the production of inflammatory factors. However, there are some children who do not respond to immunoglobulin[9,10,11]. For these children with no reaction to immunoglobulin, it is possible to adopt new drugs such as glucocorticoid, infliximab and anti-tumor necrosis factor, but the curative effect has not been widely accepted, and some drugs are still in the stage of adaptation [9,12,13,14].
Most scholars believe that foreign viruses or bacterias are related to the pathogenesis of KD[15,16,17]. A. Harden et al first proposed that the etiology of KD is related with external infection[18]. Subsequently, some scholars found that Candida albicans was the pathogen of infected mice by establishing the animal model of KD[19]. Some scholars have also discovered that parvovirus and bacterial pathogens related to the etiology of KD through the polymerase chain reaction and DNA hybridization techniques[20]. So far, it is not possible to determine the pathogenic bacteria of KD, but the body immune system disorder because of these external infection, which triggered a series of inflammatory reaction.
Medium and small vessel vasculitis predominantly attack entire body of young children in pathogenesis of KD. Abnormal activated immune cells release a large number of inflammatory factors caused by immune system disorders in the body of patient with Kawasaki disease[21]. In the acute stage of KD, the level of inflammatory factors are significantly changed. For example, A large number of TNF-a and interleukin-6 produce in the patient's body. These inflammatory factors are directly related to the injury of vascular endothelial cells. TNF-a can directly damage vascular endothelial cells, promote necrosis and apoptosis of endothelial cells and damage the barrier function of endothelial cells, which can increase vascular permeability. On the other hand, it stimulates immune cells to produce more inflammatory factors by autocrine, which forms the waterfall effect of inflammation[22,23,24]. A large number of adhesion factors and chemokines is generated on the surface of injured endothelial cells, which cause waterfall growth of inflammatory factors. Because of chemotactic of chemokines and adhesion of adhesion factors, making abnormal activated immune cells in the lesion area increase[25]. At the same time, a large number of vascular endothelial growth factors (VEGF) is produced when endothelial cells injury, which promotes the proliferation of endothelial cells, thus changing vascular permeability[26]. VEGF also induces the expression of adhesion factors and chemokines on the surface of endothelial cells. This series of reactions cause vascular edema and agammaavating inflammation[9,26,27].
It is well-known that differential equations have played an important role in predicting extinction and persistence of population, infections of diseases, as well as growth of microorganism etc[28,29,30]. Differential equations have also been successfully applied to the modeling of viral infections and immune responses. They still play an important role in revealing some basic properties of immune selection, interactions between disease and related bio-markers, evolution relationships among healthy T-cells, free virus, infected T-cells and immune responses, as well as predicting outbreak of infectious disease etc. [31,32,33,34,35,36,37,38,39,40].
Based on the experimental literature of the pathogenesis of KD, in the paper, a class of differential equation model describing the interactions among the key elements of pathogenesis of KD has been constructed. Then, by analyzing stability properties of the equilibria of the differential equation model[28,41], we study the interaction mechanism among endothelial cells, endothelial growth factors, adhesion factors, chemokines and inflammatory factors, and finally provide some theory reference in clinical treatment of KD.
This paper is organized as follows. In the second section, we give differential equation model describing the interactions among endothelial cells, endothelial growth factors, adhesion factors, chemokines and inflammatory factors. In the third section, we consider global existence, uniqueness and nonnegativity of the solutions, and dissipation of the differential equation model. In the fourth section, first of all, we calculate the basic reproduction number of the differential equation model by the method of the next generation matrix[42,43], and then give the classification of the equilibria, and their stability analysis, further, we give some numerical simulations. Finally, in the last section, some discussions are given.
2.
Description of model
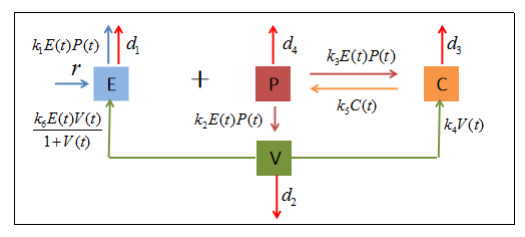
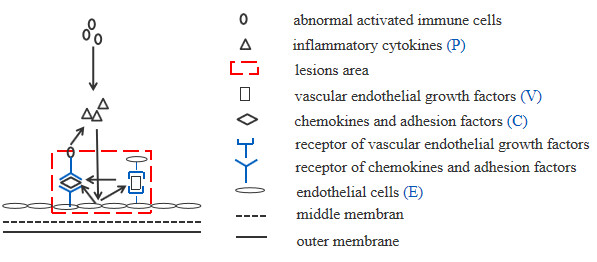
The following simplified Figure 1 of pathogenesis of KD visually demonstrates a series of inflammatory processes in lesions of patients after the disorder of the immune system, and describes the interactions between biomarkers in acute stage of KD.
Let the functions E(t), V(t), C(t), P(t) represent concentrations (pg/ml) of normal endothelial cells, vascular endothelial growth factors (VEGF), activated adhesion factors and chemokines, inflammatory factors, respectively, in the lesion area at time t in acute stage of KD. For each the function above, the derivative at time t indicates the rate of change of the corresponding concentration. Based on Figure 1, we have the block diagram Figure 2 which describes the interactions among E(t),V(t),C(t) and P(t). All the parameters r, di (i=1,2,3,4) and kj (j=1,2,⋯,6) in Figure 2 are assumed to be positive constants.
From the block diagram Figure 2, for each component of E,V,C and P, the corresponding rate of change follows the following rules:
(ⅰ) the rate of change of concentration (E) of normal endothelial cells = normal endothelial cells proliferation (r) + proliferation (k6VE/(1+V)) of normal endothelial cells promoted by vascular endothelial growth factors − loss (k1EP) of normal endothelial cells because of inflammatory factors − normal apoptosis (d1E);
(ⅱ) the rate of change of concentration (V) of vascular endothelial growth factors = damage of endothelial cells leading to production of vascular endothelial growth factors (k2EP) − normal proteolysis (d2V);
(ⅲ) the rate of change of concentration (C) of activated adhesion factors and chemokines = damage of endothelial cells leading to production of activated adhesion factors and chemokines (k3EP) + the production (k4V) of adhesion factors and chemokines induced by vascular endothelial growth factors − normal proteolysis (d3C);
(ⅳ) the rate of change of concentration (P) of inflammatory factors = the production of inflammatory factors induced by accumulation of abnormally activated immune cells induced by increasing of adhesion factors and chemokines (k5C) − normal proteolysis (d4P).
Based on the above rules, we have the following four-dimensional differential equation model, which describes the interaction among endothelial cells, vascular endothelial growth factors, adhesion factors, chemokines and inflammatory factors,
We would like to mention here that, in Figure 2 and the model (1), Holling-Ⅱ functional response (k6VE/(1+V)) is used to denote the growth of normal endothelial cells promoted by vascular endothelial growth factors. This is because that the proliferation of endothelial cells promoted by vascular endothelial growth factors does not always satisfy proportional relationship, and with the increasing of vascular endothelial growth factors, the amount of endothelial cells will approach saturation state.
The biological meanings, units of all the parameters and fixed value of parameters in model (1) are shown in Table 1. Here, the unit of time is depicted by day because of a long time in the disease state of patients with kawasaki disease.
3.
Global existence, uniqueness, nonnegativity and boundedness of solutions
Taking into account biological significance of the model (1), the initial condition is given as follows,
where, E0,V0,C0,P0 represent the initial concentrations of normal endothelial cells, vascular endothelial growth factors, adhesion factors and chemokines and inflammatory factors in lesion area.
Throughout of the paper, in order to ensure that the model (1) is dissipative, it is always assumed that the condition
(H)k6<d1
holds.
For global existence, uniqueness, nonnegativity and boundedness of the solutions of the model (1), we have the following result.
Theorem 3.1. The solution (E(t),V(t),C(t),P(t)) of the model (1) with the initial condition (2) is existent, unique, nonnegative, and ultimately bounded in [0,+∞).
Proof. In fact, global existence, uniqueness and nonnegativity of the solutions easily follows from standard theorems on the existence, uniqueness and continuation of the solutions of differential equations[28,41]. Let us consider ultimate boundedness. According to the first equation of the model (1), we have that for t≥0,
Hence, it follows from the condition (H) that lim supt→+∞E(t)≤r/(d1−k6). Define the function
We have that for t≥0,
where μ=min{d1−k6,d2/2,d3}. Thus, lim supt→+∞N(t)≤r/μ, which implies that
Finally, from the last equation of the model (1), we easily have
The proof of Theorem 3.1 is completed.
From the biological point of view, ultimate boundedness of the solutions shows that the concentrations of normal endothelial cells, vascular endothelial growth factors, adhesion factors, chemokines and inflammatory factors in the lesion area are always limited within some limited ranges at any time rather than suddenly erupt or tend to infinity.
4.
Existence of the equilibria and their dynamics analysis
The types of the equilibria of the model (1) and their asymptotic behaviors can be used to predict the evolution of endothelial cells, vascular endothelial growth factors, adhesion factors and chemokines, inflammatory factors in the lesion area over time, so as to provide some feasible control strategies for the treatment of KD.
4.1. The basic reproductive number
Firstly, we derive the expression of the basic reproduction number of the model (1) by the method of the next-generation matrix[42,43]. Obviously, the model (1) always has the inflammatory factors-free equilibrium Q0=(E0,0,0,0), where E0=r/d1. Let
Then the model (1) can be rewritten as
where
Jacobian determinant of F(x) and V(x) at the inflammatory factors-free equilibrium Q0 is
Let
FV−1 is the next-generation matrix for the model (1), and its spectral radius is
Hence, we get the basic reproduction number of the model (1) as follows,
where
It is noted that 1/d1, 1/d2, 1/d3 and 1/d4 is the average survival time of normal endothelial cells, endothelial growth factors, adhesion factors and chemokines and inflammatory factors, respectively. k2 is the growth rate of endothelial growth factors. k3 is the rate at which inflammatory factors cause the growth of adhesion factors and chemokines. k4 is the rate at which the endothelial growth factors causes the growth of adhesion factors and chemokines. k5 is the growth rate of inflammatory factors.
Therefore, R1 represents the amount of endothelial cells damage that a damaged endothelial cell eventually causes in the average survival period when the endothelial growth factor causes the growth of adhesion and chemokines in the acute phase of KD. R2 represents the amount of endothelial cells damage that a damaged endothelial cell eventually causes in the average survival period when the inflammatory factors increases the adhesion factors and chemokines in the acute phase of KD. R0 is expressed as the number of endothelial cells damaged by an injured endothelial cell in the acute phase of KD. It is worth noting that r and d1 are intrinsic values of endothelial cells.
If the ratio of k2/d2, k4/d3, k5/d4, or k3/d3 increases, then the value of R0 will increase. From a biological point of view, the concentration of inflammatory factors, endothelial growth factors, and adhesion factors and chemokines will rise and the degree of inflammation will increase. Conversely, if the ratios of k2/d2, k4/d3, k5/d4 and k3/d3 are reduced, then the degree of vascular damage caused by inflammation will be reduced and KD will likely be to treated.
4.2. Classification of equilibria
Assume that (E,V,C,P) is any equilibrium of the model (1), then it satisfy the nonlinear algebraic equations:
As mentioned in Subsession 4.1 that the model (1) always has the inflammatory factors-free equilibrium Q0=(E0,0,0,0).
From the biological point of view, the existence of the inflammatory factors-free equilibrium Q0 indicates that, under certain conditions, the concentrations of vascular endothelial growth factors, adhesion factors, chemokines and inflammatory factors in the lesion area of patients with KD may tend to zero, while the concentration of endothelial cells may tend to the value E0=r/d1. These indicate that the body will tend to normal state and inflammation caused by KD is controllable under certain conditions.
When V>0, the following relationship can be obtained from (6):
Then bring (7) to the first equation of (6) to get the following algebraic equation about V,
And then we get
where,
We have the following two cases to be considered.
(a) rk2(d1−k6)≥rd1k2−d1d2k1, i.e., rk2k6≤d1d2k1.
If R0>1, then there is a unique positive root V=V1≡V∗ in (9). And then we can get the unique inflammatory factors-existent equilibrium Q∗=(E∗,V∗,C∗,P∗) from (7).
If R0≤1, it is easy to have that the model (1) does not have any inflammatory factors-existent equilibrium.
(b) rk2(d1−k6)<rd1k2−d1d2k1, i.e., rk2k6>d1d2k1.
If R0≥1, then there is a unique positive root V=V1≡V∗1 in (9). Similarly, the unique inflammatory factors-existent equilibrium Q∗1=(E∗1,V∗1,C∗1,P∗1) can be obtained.
Next, let us discuss the case of R0<1. In this case, in order to ensure that the equation (8) has a positive root, its symmetry axis must be positive. Hence, it should has rk2(d1−k6)−(rd1k2−d1d2k1)R0<0, i.e.,
Based on Δ in (9), let us consider the function,
Let
It has from F(x)=0 that
By simple computations, it has
Moreover, notice
We have
If R0=ω, the two roots of (8) are equal, that is V=V1=V2≡V∗ω, and further, from the relationships between the roots and the coefficients of (8), we have
Similarly, the unique inflammatory factors-existent equilibrium Q∗ω(E∗ω,V∗ω,C∗ω,P∗ω) can be obtained.
If ω<R0<1, then both roots in (9) are positive, that is V=V1≡V∗1,V=V2≡V∗2. Hence, we can have the two inflammatory factors-existent equilibria Q∗1(E∗1,V∗1,C∗1,P∗1) and Q∗2(E∗2,V∗2,C∗2,P∗2). Furthermore, from (7), we also have the following relationships,
If 0<R0<ω, it is easy to see that the model (1) does not have any inflammatory factors-existent equilibrium.
Therefore, we have the following results.
Theorem 4.1. The model (1) always has the inflammatory factors-free equilibrium Q0=(E0,0,0,0). In addition, there are also the inflammatory factors-existent equilibria:
(i) If rk2k6≤d1d2k1 and R0>1, then the model (1) has a unique inflammatory factors-existent equilibrium Q∗(E∗,V∗,C∗,P∗).
(ii) If rk2k6>d1d2k1, then there are three cases:
(ii)1 if R0≥1, then the model (1) has a unique inflammatory factors-existent equilibrium Q∗1(E∗1,V∗1,C∗1,P∗1).
(ii)2 if ω<R0<1, then the model (1) has two inflammatory factors-existent equilibria Q∗1(E∗1,V∗1,C∗1,P∗1) and Q∗2(E∗2,V∗2,C∗2,P∗2).
(ii)3 if R0=ω, then the model (1) has a unique inflammatory factors-existent equilibrium Q∗ω(E∗ω,V∗ω,C∗ω,P∗ω).
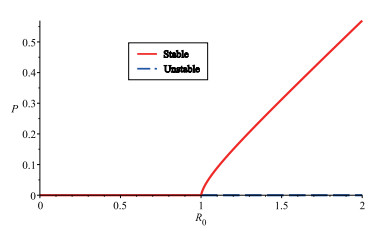
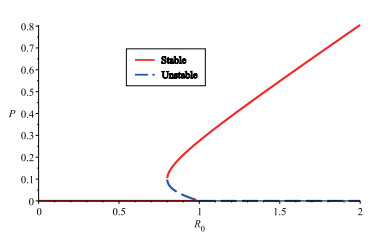
The case (i) in Theorem 4.1 indicates that the equilibria of the model (1) exhibit a forward bifurcation, and the cases (ii) in Theorem 4.1 indicate that the equilibria of the model (1) exhibit a backward bifurcation. Figure 3 and 4 are bifurcation diagrams for the equilibria of the model (1) under appropriate parameter values.
From the biological point of view, the existence of inflammatory factors-existent equilibria of the model (1) indicates that the concentrations of endothelial cells, endothelial growth factors, adhesion factors and chemokines, and inflammatory factors may tend to be some constants, which indicates that inflammation will continue to exist in lesion area of bodies with KD under certain conditions over time. In addition, the characteristics of the backward bifurcation mean that there are multiple equilibria. This shows that the disease may persist even when R0<1, which reveals the complexity of the pathogenesis of KD.
It is worth noting that R0 is independent on the parameter k6. According to the classification of the equilibria in Theorem 4.1, if the parameters r, d1, d2, k1 and k2 are fixed, then k6 is a very important bifurcation parameter. In addition, there is no k5 in the expression of ω, and R0 and k5 are proportional when all other parameters are fixed except k5. Hence, we could change the value of k5 to control R0.
4.3. Local dynamics of inflammatory factors-free equilibrium
For the local stability of the inflammatory factors-free equilibrium Q0=(E0,0,0,0), there are the following results.
Theorem 4.2. If R0<1, the inflammatory factors-free equilibrium Q0 is locally asymptotically stable; If R0>1, the inflammatory factors-free equilibrium Q0 is unstable; If R0=1, the inflammatory factors-free equilibrium Q0 is linear stable.
Proof. The corresponding linearization system at any equilibria Q(E,V,C,P) is
The corresponding Jacobian matrix is
The characteristic equation at the inflammatory factors-free equilibrium Q0 is
where
Obviously, λ=−d1 is a negative real root of (13). If R0<1, then, a2>0 and a3>0. Furthermore, it is clear that a1a2−a3>0 for R0<1. According to Routh-Hurwitz criterion, all the roots of (13) have negative real parts. Hence, the inflammatory factors-free equilibrium Q0 is locally asymptotically stable.
If R0>1, then, a3<0. Hence, there is a positive real root of (13), i.e., the inflammatory factors-free equilibrium Q0 is unstable.
If R0=1, then, a3=0. It is easy to get that λ=0 is a root of (13), and all other roots of (13) have negative real parts. Thus, the inflammatory factors-free equilibrium Q0 is linear stable. This proves Theorem 4.2.
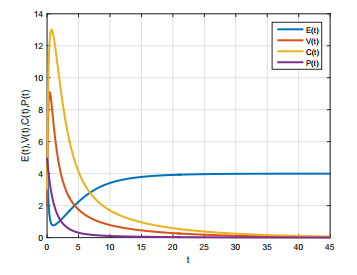
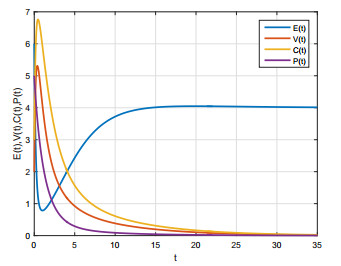
The condition R0<1 in Theorem 4.2 is equivalent to r/d1⋅k2/d2⋅k4/d3⋅k5/d4+ r/d1⋅k3/d3⋅k5/d4<1. Taking into account the biological meanings of the parameters, the local asymptotic stability of the inflammatory factors-free equilibrium Q0 and the above inequality indicate that, under certain initial conditions, if the proliferation rate (r) of normal endothelial cells, the growth rates (k2, k3, k4, k5) of endothelial growth factors caused by inflammatory factors, activated abhesion factors and chemokines caused by inflammatory factors, activated abhesion factors and chemokines caused by endothelial growth factors, abhesion factors and chemokines caused by endothelial growth factors are sufficiently small, or the rates (d1, d2, d3, d4) of proteolysis are large enough, then the concentration of normal endothelial cells will tend to a stable value r/d1 and the concentrations of endothelial cell growth factors, adhesion and chemokines, and inflammatory factors will tend to zero over time. This reveals that, by controlling the corresponding parameters of the interactions of each element in this model so that R0<1, the inflammation will be relieved or even cured over time. Therefore, the ratio of k5/d4 can be reduced by the monoclonal antibody of anti inflammatory factors, and the effects of adhesion and chemotaxis can be reduced by the competitive inhibitor of adhesion factors and chemokines, so that the ratio of k5/d4 can also be reduced. Because inflammatory factors, adhesion factors and chemokines, and endothelial growth factors are cytokines, the rate of proteolysis can be increased through regulation, thus reducing the value of R0.
Figures 5 and 6 are the solution curves of the model (1) with the initial value (6,2,3,5), and the values of the parameters are shown in Tables 1 and 2.
4.4. Local dynamics of inflammatory factors-existent equilibria
From (12), it has that, at any inflammatory factors-existent equilibrium Q(E,V,C,P), the corresponding Jacobian matrix can be rewritten as
From the first and second equations of (6), we can have
Hence,
Hence, we have the following lemma which will be used in considering the local stability of the inflammatory factors-existent equilibria.
Lemma 4.1. For any inflammatory factors-existent equilibrium Q(E,V,C,P), there is V<rk2/d2k1.
For the local stability of the inflammatory factors-existent equilibrium, there are the following theorem.
Theorem 4.3. Assume rk2k6≤d1d2k1 (the case of forward bifurcation). If R0>1, then the inflammatory factors-existent equilibrium Q∗ is locally asymptotically stable.
Proof. The characteristic equation of Jacobian matrix (14) can be written as the following form,
where,
At the inflammatory factors-existent equilibrium Q∗(E∗,V∗,C∗,P∗), it is obviously A1>0. To determine the sign of A4, consider the function
When x>0, G(x) is a monotonically increasing function about x. From the relations between the roots and coefficients of the algebraic equation (8), we have
Hence,
Thus, A4>0. According to Lemma 4.1, we have
Therefore,
Thus, A2>0 and A3>0.
Now, let us show that Δ2=A2A3−A1A4>0 and Δ3=A1Δ2−A23>0.
By suitable computations, Δ2 can be rewritten as the form, Δ2=Δ21+Δ22, where,
Notice
We have from (18) and (19) that Δ21>0 and Δ22>0.
Δ3 can be rewritten as the form, Δ3=A1Δ2−A23=A1(Δ21+Δ22)−A23, where
From Lemma 4.1, we have
Hence, from (19) and (20), we have
Therefore, Δ3=A1(Δ21+Δ22)−A23>A1Δ21−A23>0. Furthermore, we have Δ4=A4Δ3>0.
By Routh-Hurwitz criterion, we have that the inflammatory factors-existent equilibrium Q∗ is locally asymptotically stable. This completes the proof of Theorem 4.3.
Theorem 4.4. Assume rk2k6>d1d2k1 (the case of backward bifurcation). If R0≥1, then unique inflammatory factors-existent equilibrium Q∗1 is locally asymptotically stable; If ω<R0<1, the inflammatory factors-existent equilibrium Q∗1 is locally asymptotically stable, and the inflammatory factors-existent equilibrium Q∗2 is unstable; If R0=ω, unique inflammatory factors-existent equilibrium Q∗ω is linear stable.
Proof. Similar to the proof of Theorem 4.3, when the inflammatory factors-existent equilibrium Q∗2 exists, we have
Hence,
which implies L(0)=A4<0. Since limλ→+∞L(λ)=+∞, we have from the intermediate value theorem of continuous functions that the equation L(λ)=0 has at least one positive root. This shows that the inflammatory factors-existent equilibrium Q∗2 is unstable.
When the inflammatory factors-existent equilibrium Q∗1 exists, V∗ in (16)-(20) can be replaced by V∗1. Similar to the proof of Theorem 4.3, we can also prove that the inflammatory factors-existent equilibrium Q∗1 is locally asymptotically stable.
When R0=ω, there exists unique inflammatory factors-existent equilibrium Q∗ω. According to (10), we have G(V∗ω)=0, i.e., A4=0. By using similar method in the proof of Theorem 4.3, we can get Δ2>0, Δ3>0 and Δ4=0. We can easily to check that λ=0 is a simple root of (15), and that all other roots of (15) have negative real parts. Therefore, the inflammatory factors-existent equilibrium Q∗ω is linear stable. This completes the proof of Theorem 4.4.
In Theorem 4.3, when rk2k6≤d1d2k1 and R0>1, or in Theorem 4.4, when rk2k6>d1d2k1 and R0≥1, unique inflammatory factors-existent equilibrium Q∗ or Q∗1 of the model (1) is locally asymptotically stable. This indicates that, if the proliferation rate (r) of normal endothelial cells, the growth rates (k2, k3, k4, k5) of endothelial growth factors caused by inflammatory factors, activated abhesion factors and chemokines caused by inflammatory factors, activated abhesion factors and chemokines caused by endothelial growth factors, abhesion factors and chemokines caused by endothelial growth factors are large enough, or the rates (d1, d2, d3, d4) of proteolysis are small enough, then the concentrations of normal endothelial cells, endothelial cell growth factors, adhesion and chemokines, and inflammatory factors will tend to some constants over time. This reveals that inflammation will not disappear in a certain condition of the amount of the various elements of the pathogenesis in the acute phase of KD, but will tend to stable state, which means that KD will continue to exist in patients.
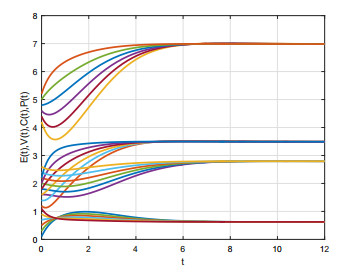
Figures 7 and 8 are the numerical simulations of the solution curves of the model (1) with the initial values (0.1,1.2,4.2,1.6), (0.3,1.4,4.4,1.8), (0.5,1.6,4.6,2.0), (0.7,1.8,4.8,2.2), (0.9,2.0,5.0,2.4) and (1.1,2.2,5.2,2.6), The parameters are shown in Tables 1 and 3.
When rk2k6>d1d2k1 and ω<R0<1, the situation is different from the previous case, and there exits a backward bifurcation. In addition to the inflammatory factors-free equilibrium Q0(E0,0,0,0), there are two inflammatory factors-existent equilibria Q∗1(E∗1,V∗1,C∗1,P∗1) and Q∗2(E∗2,V∗2,C∗2,P∗2). In this situation, it has from Theorems 4.2 and Theorem 4.4 that both the inflammatory factors-free equilibrium Q0(E0,0,0,0) and the inflammatory factors-existent equilibrium Q∗1(E∗1,V∗1,C∗1,P∗1) are asymptotically stable, and the inflammatory factors-existent equilibrium Q∗2(E∗2,V∗2,C∗2,P∗2) is unstable. The means that the treatment of KD cannot be judged only by the size of the basic reproduction number and 1. The development trend of KD related to the initial concentrations (E0, V0, C0, P0) of each element in the model.
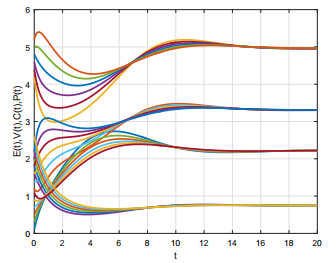
In biology, when the initial concentration of the inflammatory factors is higher, then the initial concentration of the corresponding endothelial cell growth factors is also higher, and the change of the permeability of the blood vessel is larger, so that the vascular injury is serious, then the concentration of elements of the model may approach constant over time. On the contrary, when the initial concentration of the inflammatory factors is lower, then the initial concentration of the corresponding endothelial cell growth factors is also lower, and the change of the permeability of the blood vessel is smaller, then the concentration of elements of the model may approach zero over time under certain conditions. That is to say that inflammation will be alleviated or even cured with time. Bistability reveals the complexity of the pathogenesis of KD. The severity of the disease may depend on the initial concentrations of endothelial cells, endothelial growth factors, adhesion factors and chemokines, cell inflammatory factors. So we have found a crucial parameter (ω) for controlling disease and we not only need to control the basic reproduction number less than one, but also further control less than ω to ensure that inflammation can be eliminated.
Figure 9 is the numerical simulations of the solution curves of the model (1) with the initial values (4.0,0.6,0.6,0.6), (3.0,0.4,0.4,0.4), (2.0,0.3,0.2,0.2), (1.0,0.2,0.1,0.1) and (0.8,0.1,0.05,0.05). We take k5=0.16, k6=0.45, and the other parameters are the same as those in Figure 6 of Table 2.
5.
Conclusion and prospect
In this article, we establish the dynamic model (1) of the interactions between various factors in the pathogenesis of KD, and then study the existence and local stability of the inflammatory factors-free equilibrium and the inflammatory factors-existent equilibria by using the stability theory of differential equations.
Theorem 4.1 gives the conditions for the existence of the equilibria in the model (1). The analysis shows that the equilibria of the model (1) exhibit forward bifurcation and backward bifurcation. Then, we obtain the expression of the reproduction number R0 by the method of next generation matrix. Studies have shown that the inflammatory factors-free equilibrium Q0 is locally asymptotically stable, unstable, and linear stable when R0<1, R0>1 and R0=1, respectively. If rk2k6≤d1d2k1 (the case of forward bifurcation) and R0>1, or rk2k6>d1d2k1 (the case of backward bifurcation) and R0≥1, the model (1) has a unique inflammatory factors-existent equilibrium Q∗ or Q∗1, and it is locally asymptotically stable. However, if rk2k6>d1d2k1 (the case of backward bifurcation) and ω<R0<1, then the model (1) has two inflammatory factors-existent equilibria Q∗1 and Q∗2. We have shown that the inflammatory factors-existent equilibrium Q∗1 is locally asymptotically stable, but the inflammatory factors-existent equilibrium Q∗2 is unstable. Interestingly, there is bistable, i.e., the inflammatory factors-free equilibrium Q0 and the inflammatory factors-existent equilibrium Q∗1 is locally asymptotically stable.
Note that when rk2k6≤d1d2k1 (the case of forward bifurcation), R0<1 is equivalent to rk5(k2k4+k3d2)<d1d2d3d4. The proliferation rate (r) of normal endothelial cells and its apoptotic rate (d1), the rates of proteolysis of endothelial growth factors, adhesion factors and chemokines and inflammatory factors (d2, d3 and d4) are considered as relatively fixed parameters. The local stability of the inflammatory factors-free equilibrium Q0 indicates that if the growth rate (k2) of endothelial growth factors caused by inflammatory factors, the growth rate (k3) of activated abhesion factors and chemokines caused by inflammatory factors, the growth rate (k4) of activated abhesion factors and chemokines caused by endothelial growth factors and the growth rate (k5) of abhesion factors and chemokines caused by endothelial growth factors are small enough, then whether KD is eliminated or not can be determined by the reproduction number R0<1.
Contrary to the above situation, i.e., when rk2k6>d1d2k1 (the case of forward bifurcation), if the growth rates (k2, k3, k4 and k5) are large enough, it is necessary to control the reproduction number R0 such that R0<ω<1 to eliminate KD. Furthermore, when ω<R0<1, there are two inflammatory factors-existent equilibria. This shows the complexity of the pathogenesis of KD.
In the study of clinical treatment of KD, the development of KD can be controlled by controlling the corresponding parameters. In model (1), due to adhesion of adhesion factors and chemotaxis of chemokines, activated immune cells are greatly increased, which leads to an increase in inflammatory factors.
We know from the expressions of R1 and R2 that R1 and R2 are positively proportional to the parameter k5. We could reduce the value of k5 through the effective biological method such that the value of R0 is reduced. In clinical research, monoclonal antibodies of anti inflammatory factors can be used to reduce the rate of production of cytokines, so that the parameter k5 decreases. It is also possible to use the competitive inhibitor of adhesion factors and chemokines to regulate the number of abnormally activated immune cells, which produced by adhesion and chemotaxis, leading to the rate of growth of inflammatory factors decrease. In addition, it is also possible to regulate the rate of hydrolyzation of endothelial growth factors, adhesion factors and chemokines, and inflammatory factors without affecting other proteins in the body, making the values of the parameters d2, d3 and d4 increase. By adjusting the above parameters, it can reduce the value of the basic reproductive number R0.
In addition to the adhesion factors and chemokines, other factors can also lead to produce a large number of inflammatory factors, such as inflammasome. However, the pathogenesis of Kawasaki disease is unclear, and adhesion factors and chemokines have obvious influence on production of inflammatory factors. Therefore, only the influence of adhesion factors and chemokines have been considered in the model (1). In fact, inflammation is more complex and serious in the actual clinical settings.
Finally, through numerical simulations, we give some problems which may be worth of further discussions.
(ⅰ) When rk2k6≤d1d2k1 (the case of forward bifurcation) and R0<1, or rk2k6>d1d2k1 (the case of backward bifurcation) and R0<ω, the inflammatory factors-free equilibrium Q0 is likely to be globally asymptotically stable.
(ⅱ) When R0>1, then the inflammatory factors-existent equilibria Q∗ and Q∗1 may also be globally asymptotically stable.
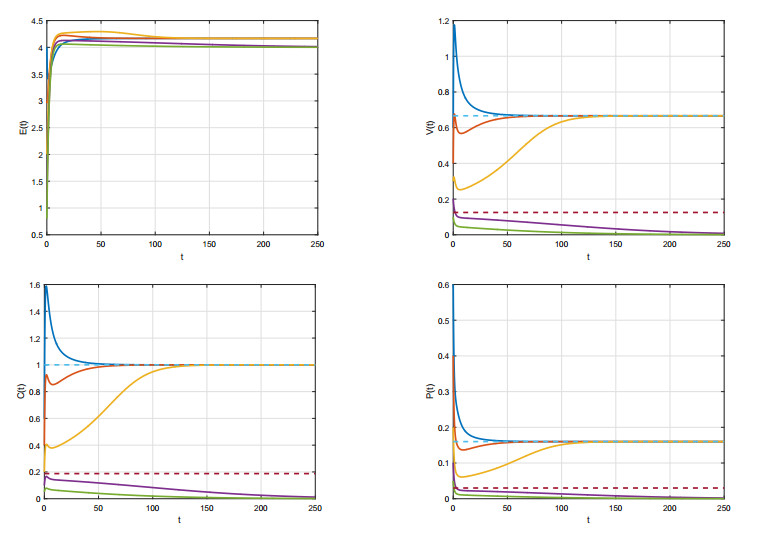
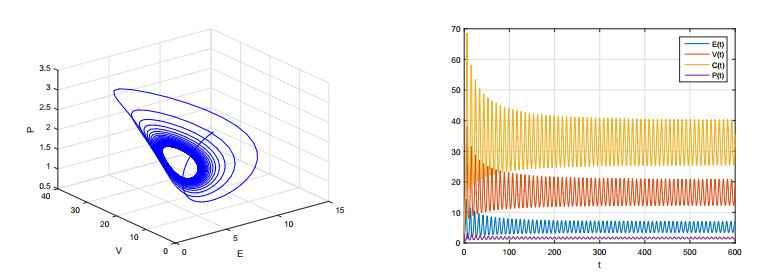
(ⅲ) In addition, throughout of this paper, we have assumed the condition (H) k6<d1 in order to ensure the dissipativeness of the model (1). However, Figure 10 suggest that, if k6≥d1, the model (1) is also likely dissipative, and it maybe exhibits more complicated dynamic phenomena.
Acknowledgments
The research is partly supported by National Key R&D Program of China (2017YFF0207401) and the NNSF of China (11471034) for W. Ma.
Conflict of interest
The author declares no conflicts of interest in this paper.









 DownLoad:
DownLoad: