1. Introduction
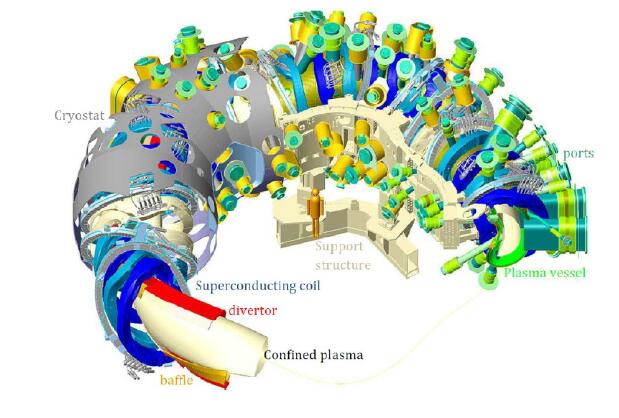
Wendelstein 7-X (W7-X), the world's largest modular nuclear fusion experiment of stellarator type, is currently operating (Figure 1) [1]. A hydrogen plasma is confined in a magnet field, generated with external superconducting coils, which allows the plasma to be heated up to fusion temperature without overheating the surrounding structure. The water-cooled Plasma Facing Components (PFC) protect the plasma vessel (PV) against radiative and convective heat from the plasma. Depending on the expected heat loads, four types of PFCs are basically used (Figure 2):
1) highly loaded divertors, made of water cooled CuCrZr fingers covered with carbon reinforced carbon tiles;
2) moderately loaded heat shields and moderately loaded baffles, both made of CuCrZr heat sinks brazed on water cooled steel pipes and covered with bolted graphite tiles. The heat shields are flexibly supported with a few pins onto the PV whereas the baffles are supported with rigid steel structures;
3) lowly loaded wall panels, which consist of two parallel steel plates welded together and filled with water cooling.
High stresses develop in coils, superconducting cables [2] and supporting structure when the coils are charged, due to the EM Lorentz forces. In Ref [3,4] several cracks were investigated in a Lateral Support Element (LSE) of the conducting coils of W7-X: the crack-growth assessment was obtained using a coupled FEM-DBEM approach [5,6,7,8], in order to take advantage of the higher accuracy and flexibility of DBEM when handling three-dimensional cracks under mixed-mode conditions [9,10,11]. In Ref [3,4] the choice of the initial crack geometry was driven by repair experience (the crack depth cannot be determined by the dye penetration tests) and it was found that such depth is typically less than half the superficial crack length.
In this paper, several cracks, discovered in the baffle modules of W7-X, are judged to be potentially critical and, consequently, the SIFs distribution along the crack front was calculated by using the proposed FEM-DBEM numerical approach.
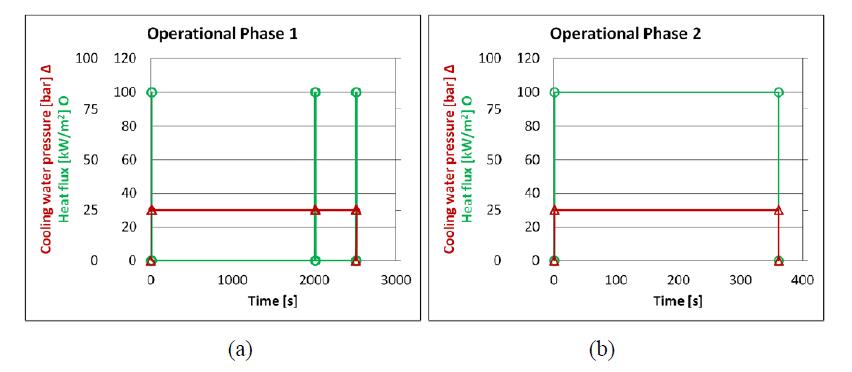
Two different Operational Phases are basically designated for the Wendelstein 7-X: the first is represented by Operational Phase 1 (OP1) consisting of different consecutive heat flux pulses applied on the graphite tiles and without refrigeration, whereas, the second by Operational Phase 2 (OP2) consists of a steady-state heat flux, again applied on the graphite tiles but with refrigeration.
ABAQUS [12] and BEASY [13] commercial codes are adopted for FEM and DBEM analyses respectively (the automatic data exchange between the two software is provided by an interface routine embedded in BEASY suite).
2. Theoretical Aspects of Crack Growth with DBEM
The present work is concerned with the numerical implementation of the DBEM to the three-dimensional analysis of crack-growth problems examined through the linear elastic fracture mechanics. The DBEM, a particular variant of the BEM, has successfully been applied to the incremental analysis of crack-extension problems.
The J-integral technique, based on a path-independent integral, is adopted for the stress intensity factor evaluation. A procedure, based on the decomposition of the elastic field into its respective symmetric and antisymmetric mode components, is used to decouple the stress intensity factors of a mixed-mode problem [14,15].
An incremental crack-extension analysis can be performed when to determine the crack path. And remeshing is just necessary close to break through points because the crack extension is discretised by just adding new boundary elements. For each increment of the analysis, in which the crack extension is modelled with new boundary elements, the DBEM is applied for the stress analysis and for the SIF evaluation. The incremental analysis is based on a prediction-correction technique to define the direction of the crack-extension increment.
2.1. DBEM Equations
The dual boundary element method allows to analyse general crack problems to be performed through a single-region boundary element formulation. The dual equations, on which the DBEM is based, are the displacement and the traction boundary integral equations (Eqs. (1) and (2)). Throughout this work, the Cartesian tensor notation and Einstein's summation convention are used. In the absence of body forces, the boundary integral representation of the displacement components ui at a source point x' on the boundary is given by
|
${c_{ij}}\left( {x'} \right){u_j}\left( {x'} \right) + \int\limits_\Gamma {{T_{ij}}} \left( {x',x} \right){u_j}\left( x \right)d\Gamma \left( x \right) = \int\limits_\Gamma {{U_{ij}}} \left( {x',x} \right){t_j}\left( x \right)d\Gamma \left( x \right)$
|
(1)
|
where cij(x') is a coefficient depending on the geometry in the source point, and the integral on the left side is calculated in the Cauchy principal-value sense. Uij(x', x) and Tij(x', x) are the Kelvin fundamental solutions. The traction components tj are given by
|
$\frac{1}{2}{t_j}\left( {x'} \right) + {n_j}\left( {x'} \right) + \int\limits_\Gamma {{S_{ijk}}} \left( {x',x} \right){u_k}\left( x \right)d\Gamma \left( x \right) = {n_i}\left( {x'} \right)\int\limits_\Gamma {{D_{ijk}}} \left( {x',x} \right){t_k}\left( x \right)d\Gamma \left( x \right)$
|
(2)
|
where ni denotes the i-th component of the unit outward normal to the boundary at the source point. The integral on the left side is to be considered in the Hadamard sense whilst that on the right side in the Cauchy principal-value sense. Equations (1) and (2) constitute the basis of the DBEM as described in [16].
2.2. Crack Modelling
The necessary conditions for the existence of the principal-value integrals obtained in the derivation of the dual boundary integral equations impose restrictions on the discretisation. Consider that both geometry and boundary field variables are described by a piece-wise continuously differentiable approximation and the collocation process is always performed with the source point at the boundary element nodes.
Under these considerations, the continuity requirements of the Cauchy principal-value integral in the displacement equation can be satisfied by any Lagrangian continuous or discontinuous boundary element. However, in the traction equation the continuity requirements of the Hadamard principal-value integral are satisfied only by discontinuous elements, since all the nodes are internal points of the element where a continuously differentiable approximation is defined. Moreover, the requirement of the smoothness of the geometry at a collocation point in the traction equation is implicitly satisfied by the discontinuous element. Furthermore, discontinuous traction fields can be modelled by discontinuous elements, since the tractions must satisfy Hölder continuity only at the nodes. It is important to realise that, if the element approximation does not satisfy these necessary continuity requirements, then the finite-part integrals do not exist. For the sake of efficiency and to keep the simplicity of the standard boundary elements, the present formulation uses discontinuous quadratic elements for crack modelling.
The general modelling strategy, developed by Portela, Aliabadi & Rooke [16], can be summarised as follows:
1) The traction Eq. (2) is applied for collocation on one of the crack boundaries;
2) The displacement Eq. (1) is applied for collocation on the opposite crack boundary and remaining boundaries;
3) The crack boundaries are discretised with discontinuous quadratic elements;
4) Continuous quadratic boundary elements are used along the remaining boundaries of the problem domain, except at the intersection between a crack and an edge, where discontinuous or semi-discontinuous elements are required, in order to avoid nodes at the intersection.
This simple strategy is robust and allows the DBEM to effectively model general edge or embedded crack problems. Crack tips, crack-edge corners and crack kinks do not require a special treatment, since they are not located at nodal points where the collocation is carried out.
2.3. Mesh Sensitivity Issues
When introducing a crack in the DBEM model an automatic remeshing is operated to adapt the original mesh to the inserted crack mesh. Even if the original mesh of the uncracked model were based on linear elements it is a good practice to enhance to quadratic the polinomal order of newly added elements, being the latter located in an area sourrounding the crack front and consequently undergoing strong stress gradients (alternatively a huge mesh refinements would be needed with linear elements).
As previously said the crack mesh is based on discontinuous elements and, again, it is higly recommendable (for accuracy reasons) to have them with quadratic polinomial order. Moreover, even if as an overall the crack mesh is made of triangular and quadrilateral elements, it is important to enforce just quadrilateral elements along the crack front in order to facilitate an accurate assessment of J-integral (numerical instabilities can arise if the J-path is connected to a triangular element).
3. Problem Description
The heat shields and baffles are manufactured by brazing the heat sinks onto the cooling pipes and then bending the pipes in the desired form to match the shape of the PV. Afterwards, it has been found that the bending process had triggered crack growth in the brazing and sometimes into the cooling pipes at the end of the brazed connection (Figure 3). Due to heat gradients occurring in each plasma pulse, thermal stresses are generated in the heat sinks, brazes and cooling pipes, that encourage cyclic crack-growth through the pipe thickness, with consequent potential risks of water leaks (such event would be catastrophic due to vacuum conditions in the PV).
The objective of this study is to predict the most critical crack configurations in the baffles undergoing OP1 or OP2, under the worst case assumption that cracks, similar to those discovered in the analysed simple components (clearly such highly damaged components were not assembled on the W7-X), are present in W7-X. Namely, cracks are introduced in areas judged prone to crack nucleation by Max Planck Institute personell, based on their experience coming from analysis of discarded cracked components (Figure 3) and based on stress analysis of uncracked components (as shown in the following). Notably, the worst cracks were observed in the baffle segments, as the corresponding cooling pipes were among the most strongly bent and twisted in the assembly phase (such assembly operation was devised as responsible of crack initiation), consequently the study focuses on the baffle segments.
4. FEM Analysis
4.1. FEM Global Model
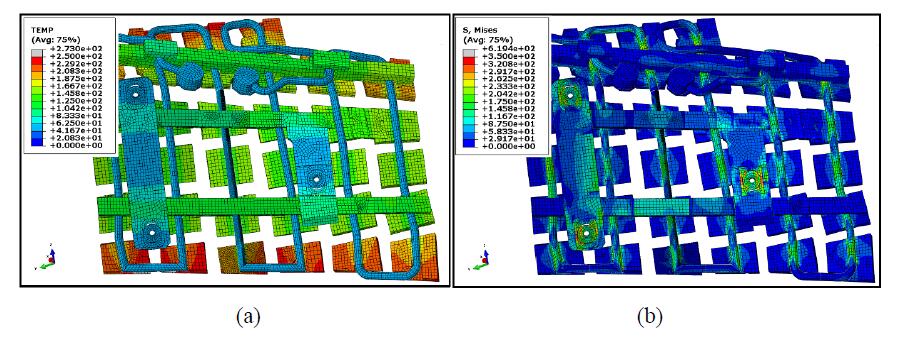
A FEM model involving the whole investigated Baffle Module 7v (BM-7v) is produced (Figure 4): it includes the CuCrZr heat sinks connected to the steel pipes and covered with graphite tiles, all supported with a rigid steel structure.
In this paper, the Operational Phases (OP1 and OP2), designed for W7-X operation, are used to extract two distinct load cases for FEM analyses. Such load cases are built considering the contribution of the cooling pipe internal pressure (equal to 25 bar) and the heat flux cycle, with maximum magnitude equal to 100 kW/m2, applied to the graphite tiles: in particular, 3 heat flux pulses are sequentially applied when considering OP1 as shown in Figure 5a, or, alternatively, a 360 s steady-state heat flux is applied when considering OP2 (Figure 5b). In OP1, even if present, the refrigerating fluid is not recirculated and consequently no refrigeration is modelled.
Both FEM analyses, related to OP1 and OP2, are split in two consecutive parts:
1) a thermal analysis, in which the heat flux pulses are applied on the graphite tiles in order to compute the temperature distribution on the baffle;
2) a thermomechanical analysis, in which the previously calculated temperature field, in addition to the internal pipe pressure and boundary constraints, is used to assess the stress field.
The FEM mesh is based on nearly 50,000 3D 8-node linear isoparametric elements for the thermomechanical analysis, whereas the meshes for the thermal analyses are based on 50000 and 305000 linear elements DC3D8 for respectively OP1 and OP2.
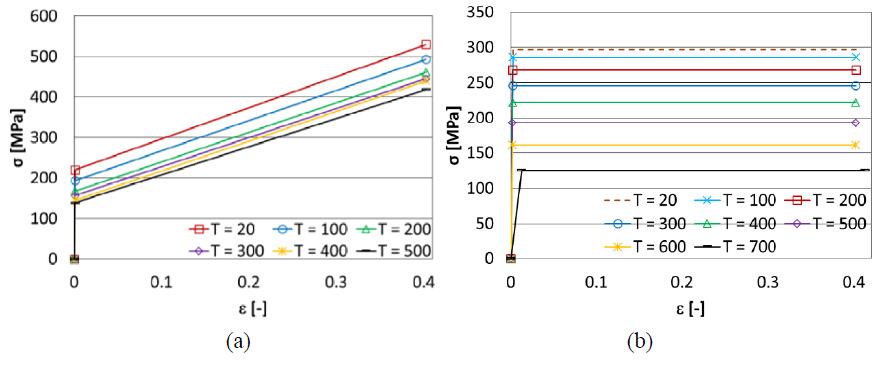
In this FEM global analysis, an elastic-plastic constitutive model is adopted for both CuCrZr and SS 316L alloys: in Tables 1 and 2, the thermal and linear-elastic properties are listed (as available from Max Planck Institute database), whereas, Figure 6 shows the adopted temperature-dependant elastic-plastic curves.
Table 1. SS 316 L material properties.
| T[°C] | 20 | 200 | 400 | 600 | 800 |
| E[GPa] | 200 | 184 | 168 | 152 | 126 |
| α[1/°C] | 1.59E−5 | 1.68E−5 | 1.78E−5 | 1.88E−5 | - |
| K[kW/m/°C] | 0.015 | - | 0.021 | - | - |
| cp[J/kg/°C] | 472 | - | 520 | - | - |
| ρ[kg/mm3] | 7.96E−6 | - | - | - | - |
| y | 220 | 167.2 | 145.2 | | |
Table 2. CuCrZr material properties.
| T[°C] | 20 | 200 | 400 | 600 | 800 |
| E[GPa] | 130 | 120 | 110 | 95 | 10 |
| α[1/°C] | 1.59E−5 | 1.68E−5 | 1.78E−5 | 1.88E−5 | - |
| K[kW/m/°C] | 0.379 | 0.357 | 0.356 | 0.366 | - |
| cp[J/kg/°C] | 388 | - | - | 473 | - |
| ρ[kg/mm3] | 8.92E−6 | - | - | - | - |
| y | 297 | 268 | 222 | 161 | |
4.2. FEM Submodels
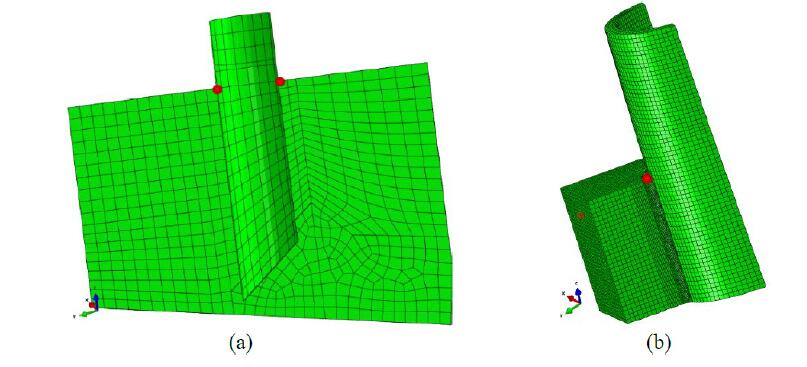
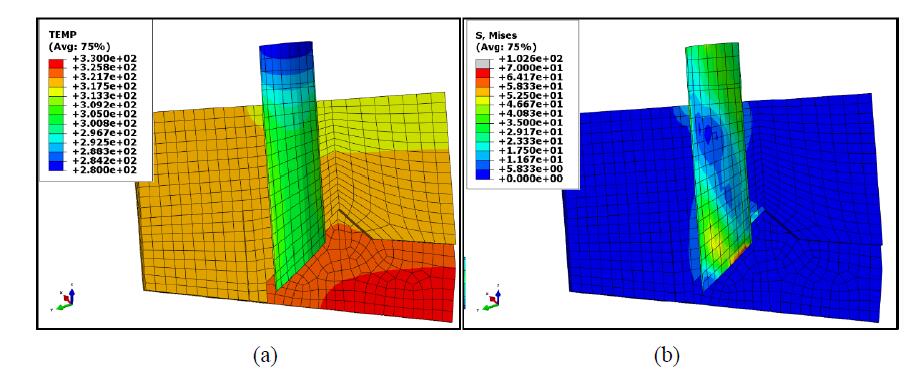
Two different FEM submodels were developed as an intermediate step to obtain two corresponding DBEM submodels; as a matter of fact it would have been too demanding from a computational point of view the extraction of DBEM submodels directly from the FEM global model (the interface routine, operating between BEASY and ABAQUS, would take a huge amount of time). One FEM submodel (Figure 7a) is representative of a whole CuCrZr plate with part of the brazed cooling pipe, whereas, the other (Figure 7b), is obtained by just taking half of the former submodel and further refining the mesh.
The larger and smaller FEM submodels are respectively built with nearly 3200 elements (Figure 7a), rather than nearly 36000 elements (Figure 7b); the latter explicitly models the braze with consequent sharp increase of degrees offreedom (dofs). Both submodels are made of 3D 20-node quadratic isoparametric elements.
4.3. FEM Results from the Global Model and from Submodels
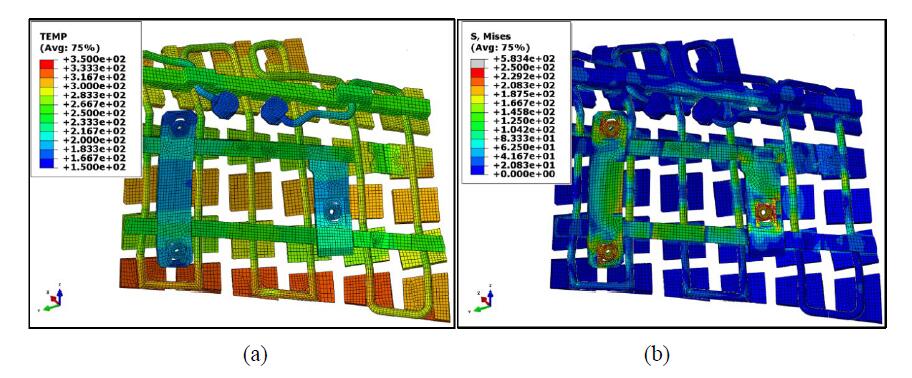
A transient thermal analysis is needed to compute the temperature field during the heat flux application phase (OPx in Figure 5). Subsequently, a thermal-stress analysis computes the stress-strain field. In Figures 8 and 9, temperatures and von Mises stress fields are shown as obtained at the end of application (in such instant the most severe stresses are produced) of the OP1 and OP2 load cases respectively.
The global model results are used to define the boundary conditions for the FEM submodel analyses. Temperature and von Mises stress fields are shown in Figures 10 and 11 for both FEM submodels: in particular the larger FEM submodel was used for calculations related to OP1, but such preliminary results highlighted the need for a more accurate analysis, so that a smaller submodel with a highly refined mesh was produced and adopted for the more critical load case OP2 (OP2 produces higher stresses and will be the load case applied for most part of the W7-X life).
5. DBEM Analyses
5.1. DBEM Submodel from the Larger FEM Submodel
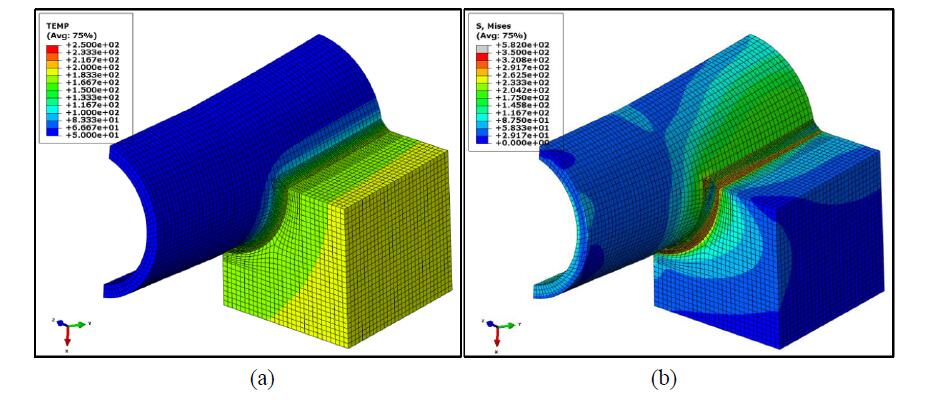
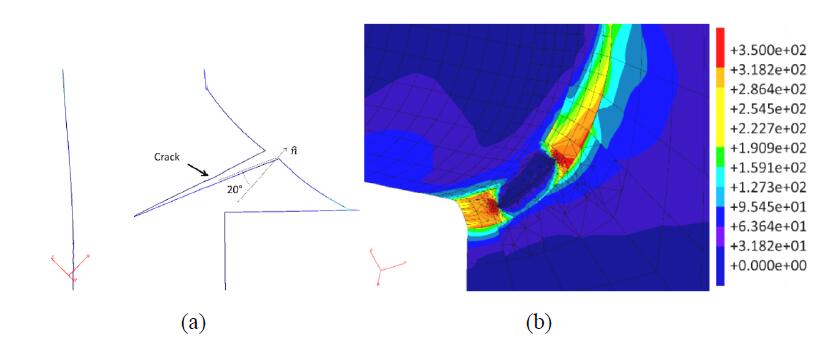
A DBEM submodel is extracted from the larger FEM submodel (Figure 7a) and, after crack introduction, is used for the fracture analysis of various crack configurations (Figure 12), in order to assess their criticity against the OP1 load case.
The DBEM submodel boundary conditions are built by interpolation of the FEM displacements and temperatures of those nodes distributed on the cutting surfaces (submodel boundaries). The interpolation is automatically operated by a routine available in BEASY suite: for each DBEM node the routine searches the 4 closest FEM nodes whose displacement/temperature are averaged, with weight coefficients proportional to their distance from the DBEM node itself, to provide the DBEM corresponding value of displacement/temperature. Displacements at the submodel cutting surfaces turn out to be continuous as, in this case, the DBEM mesh is continuous (with DBEM it is also possible to use “discontinuous elements” so renouncing to diplacement continuity but with no prejudice of the method convergence capabilities). Stresses, on the contrary, can exhibit a certain level of discontinuity on the cutting surfaces, also depending on the polinomial order of the adopted elements.
Cracks were mostly observed in the brazed area of the baffle segments as these cooling pipes were severely bent (and torque) after the brazing process (Figure 3c), so, in the DBEM model, it is necessary to explicitly model the braze root where to introduce the crack (the braze is not modelled in the FEM submodel).SIFs are evaluated using the J-integral approach [14,15].
Due to the limited heat fluxes magnitude considered in these analyses, the level of stresses do not produce appreciable plastic strains in the submodel domain, so that the materials can be considered to behave as linear-elastics in the DBEM submodel analysis. Moreover, uniform thermal-mechanical properties are considered in the analysed domain, as evaluated at the average temperature of the submodel: the temperature in the DBEM submodel at the considered instant of the transient analysis, has a limited variation, between 280 °C and 320 °C, so that such hyphotesis produces a negligible impact on the solution accuracy.
In case the applied heat flux were increased over a certain amount (nearly 100 kW/m2 in this case) an Elastic-Plastic analysis would be mandatory also for the submodels.
Boundary conditions applied on DBEM submodel are the temperature and displacement fields obtained in the FEM submodel analyses at the end of the applied load cases, in addition to the pipe internal pressure equal to 2.5 MPa.
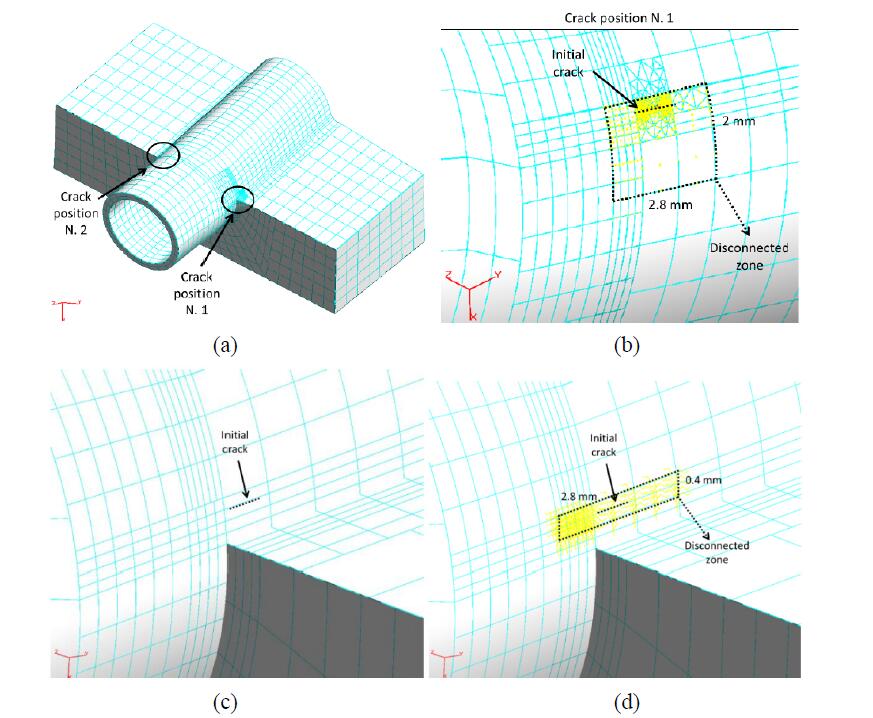
Various potentially critical crack configurations (Figure 13) have been analysed in order to assess the most dangerous scenario. The considered initial crack for all the analysed configurations, imported from the BEASY crack library, is a semi-circular part-through crack with radius equal to 0.3 mm (the cooling pipe thickness is 1 mm). In addition, internal springs of negligible stiffness are applied on some elements at the interface between pipe and heat sink: such boundary conditions allow to duplicate and disconnect the interface elements in order to simulate a separation between pipe and heat sink (e.g., in Figure 3c) as a consequence of braze local failure as highlighted by repair experience.
The considered configurations are:
1) two cracks and a disconnected area of 2.8 mm × 2 mm (Figure 12a) to highlight which side is most critical;
2) a single crack, on the most critical side, and a disconnected area of 2.8 mm × 2 mm (Figure 12b);
3) a single crack without modelling of the braze root (Figure 12c);
4) single crack, on the most critical side, and a disconnected area of 2.8 mm × 0.4 mm (Figure 12d).
As previously said, configuration A with two cracks is just used to detect the most critical crack position between the N. 1 and N. 2 (Figure 12a), where to model a single crack scenario for the subsequent analyses (Figures 12b-12d). Then, once the critical crack position is pointed out, the remaining configurations (b, c and d) are considered to assess the impact on SIFs of different disconnected area sizes.
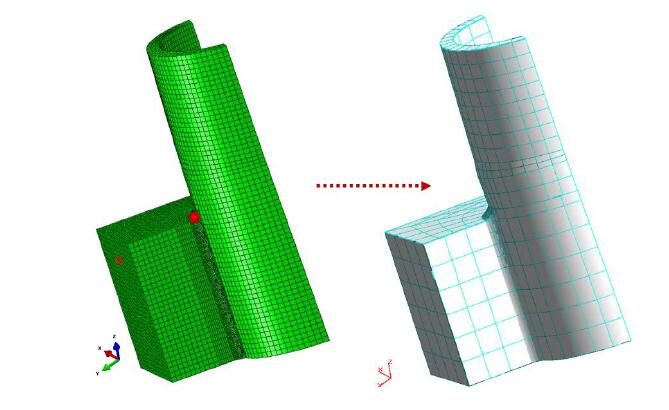
5.2. DBEM Submodel from the Smaller FEM Submodel
A DBEM submodel is created (Figure 14) and solved in order to evaluate SIFs for the investigated baffle BM-7v built in the PV.
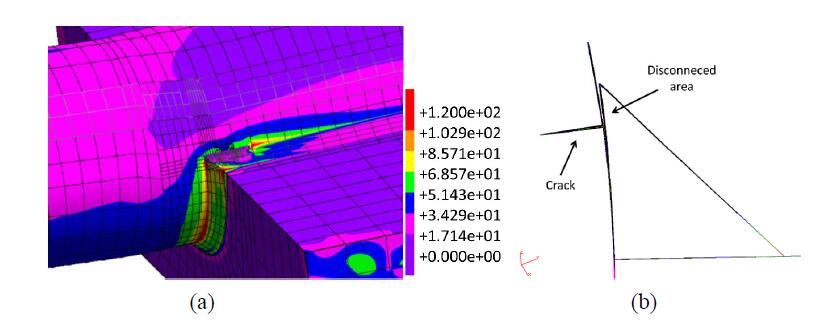
In order to simulate a crack crossing the braze root and prolonging into the pipe thickness, the modelling of a single zone involved by the crack propagation, with homogeneous material properties was needed (introducing an element of approximation), due to limitations of the adopted DBEM code concerning a crack crossing different materials. In particular, the braze root have been attributed the same properties of the pipe material and no interface between pipe and braze root has been modelled as shown in the following (e.g., Figures 21, 22 and 25).
Again, the boundary conditions applied on the DBEM submodel comes from the corresponding solved smaller FEM submodel, in terms of FEM temperature and displacement fields obtained at the end of the heat flux application phase and cooling water pressure applied on the pipe internal elements.
6. DBEM Results
6.1. DBEM Submodel Results with OP1
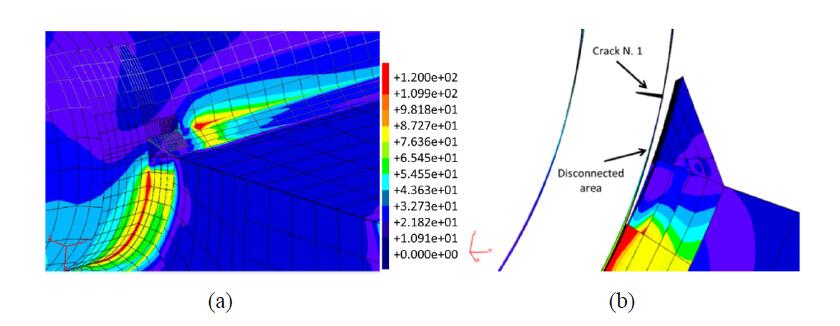
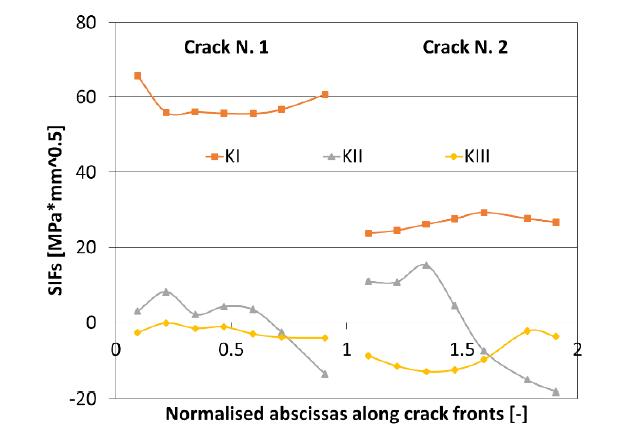
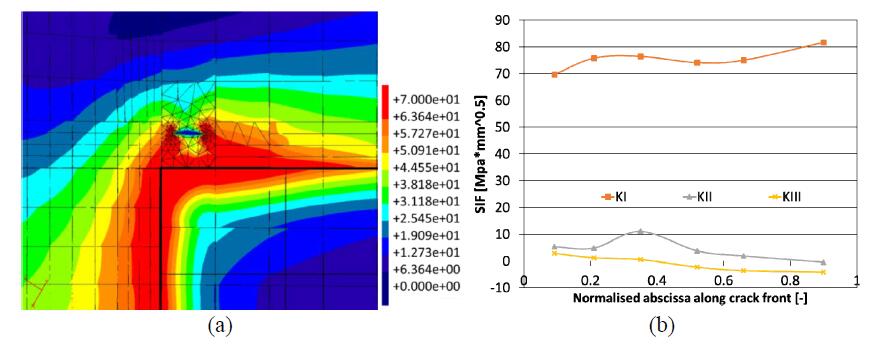
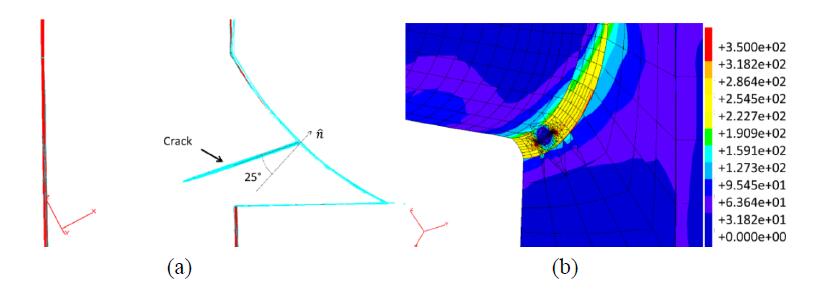
With reference to configuration A (Figure 13a), two semi-circular cracks have been inserted into the DBEM submodel: the stress-strain fields and SIF values along both crack fronts have been calculated. Analysing the von Mises stresses (Figure 15), it is possible to observe negligible yieldings with consequent validation of the linear elastic hyphotesis under which the DBEM analysis is deployed. SIFs are shown in Figure 16: crack position N. 1 turned out to have higher K values than the crack located in position N. 2, therefore additional analyses were devoted just to the analysis of this crack position.
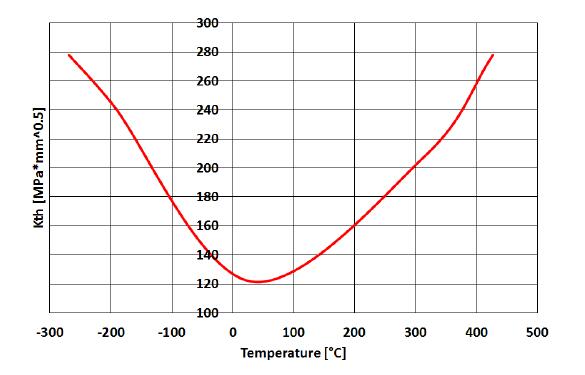
Although the crack N. 1 is more critical than the crack N. 2, both cracks present ∆K values (the stress ratio considered here is R = 0) lower than ∆Kth ≈ 208 MPa•$\sqrt {{\rm{mm}}} $ so that no crack propagation is expected under OP1 load case. Such value of ∆Kth can be retrieved from the graph in Figure 17 (available from Max Plack Institute database) at the average temperature of nearly 300 °C in the crack insertion area (Figure 10).
For OP1 load case KI is dominant (Figure 16) and is much lower than threshold so, for comparison, there is no need to calculate a ∆Keff by a combination of mode I, II and III SIFs.
The considered crack sizes are sufficiently long to allow a comparison with Kth valid for long cracks (small cracks have lower threshold SIF than long cracks). As a matter of fact, considering the El Haddad correction [17], used to allow for short crack effects on Kth, it is possible to show that the correction factor (a/a+a0)0.5 ≈ 1 being the intrinsic (or transition) crack length a0 = 0.0381, as provided by the NASGRO 2 database. Such intrinsic crack length is related to the average grain size of the considered material that ranges between 50 µm and 80 µm for SS 316 L [18] (actually higher values up to 100 µm could be obtained but only with specific heat treatments).
A further analysis (configuration C) is performed without considering the modelling of the braze root (the idea is that the braze is nearly destroyed by multiple spread cracks and consequently with no load carrying capacity anymore). For such configuration, the previously considered semi-circular crack is inserted and von Mises stresses with related initial SIFs are shown in Figures 18a and 18b, respectively.
Finally, configuration D is analysed. Such configuration is created inserting the crack in the position N. 1 and disconnecting a smaller area in the surroundings of the crack, now with dimensions of 2.8 mm × 0.4 mm (Figure 13d). The related von Mises stresses in the surroundings of the crack with highlight of the disconnected area and the SIF values along crack front are shown in Figures 19 and 20, respectively.
In all the analysed crack configurations SIFs were lower than threshold and consequently with no risk of increasing damage due to fatigue load.
6.2. DBEM Submodel Results with OP2
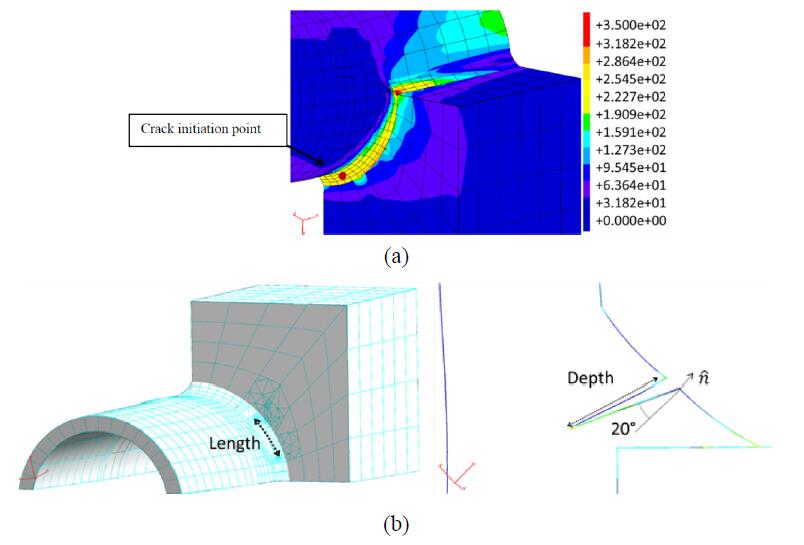
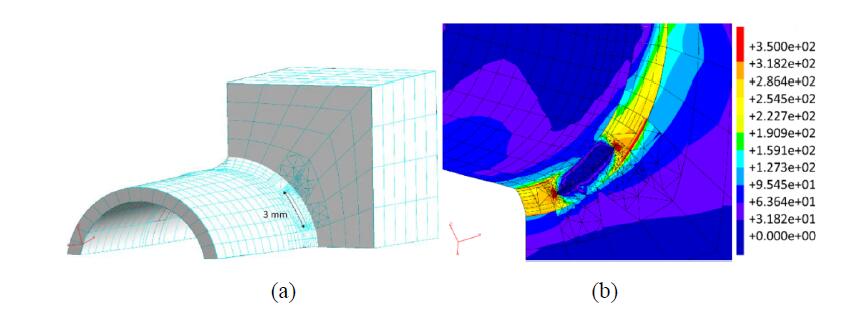
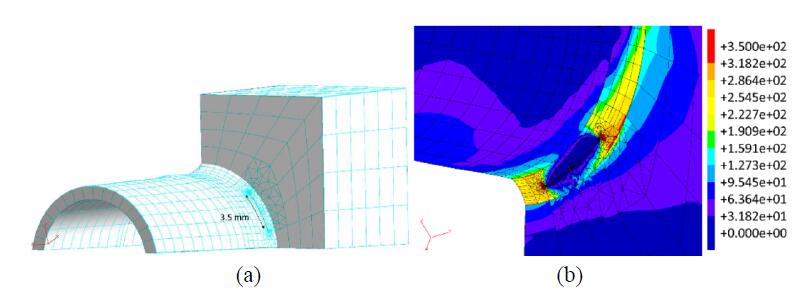
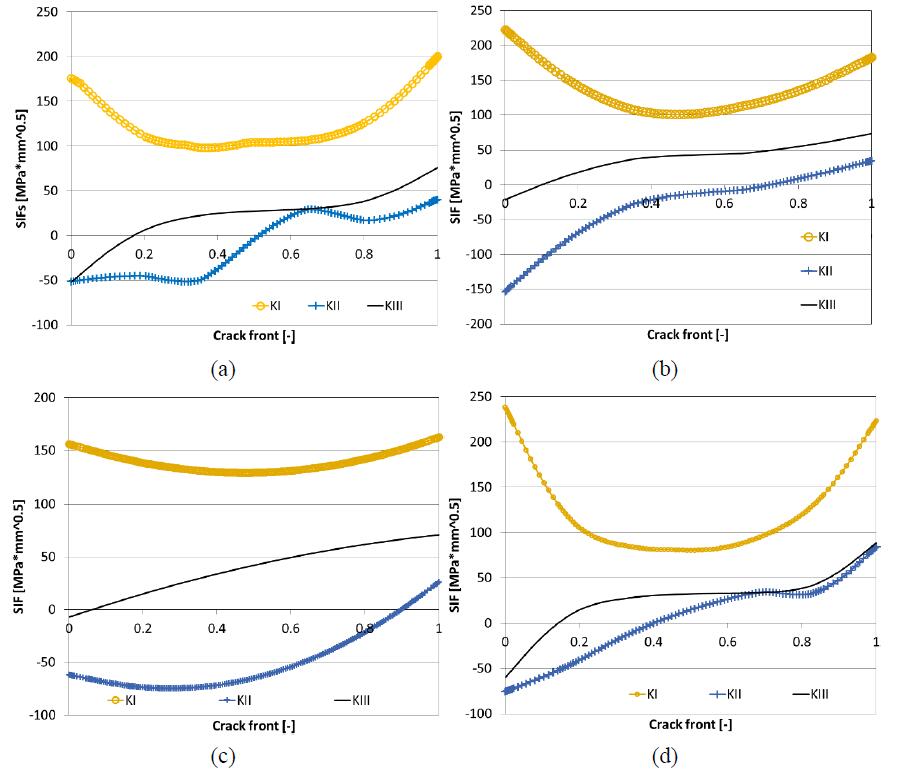
Four crack sizes have been considered, as representative of the cracks detected in the BM-7v. The modelled cracks differ in the initial crack size but have the same crack initiation point, chosen considering the zone of the submodel with highest values of Max Principal Stress (Figure 21). The initial crack shape is semi-elliptical and the different considered sizes are listed in Table 3.
The load condition is corresponding to the end of the steady-state heat flux application (most stressed time during the OP2 phase).
Table 3. Considered crack sizes.
| Case1 | Case2 | Case3 | Case4 |
| Length[mm] | 1.3 | 3 | 3.5 | 3 |
| Depth[mm] | 0.65 | 0.65 | 0.65 | 1 |
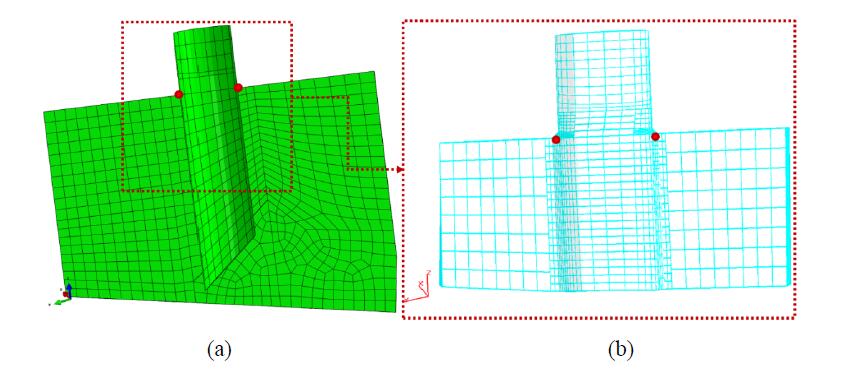
The cracks to be analysed have been inserted at the selected crack insertion node of the uncracked DBEM model (Figure 21a), with consequent remeshing in the surrounding area (Figure 21b). Then, the stress-strain fields are recomputed for the DBEM cracked domains and eventually J-integral are calculated at the J-paths positioned along the crack front.
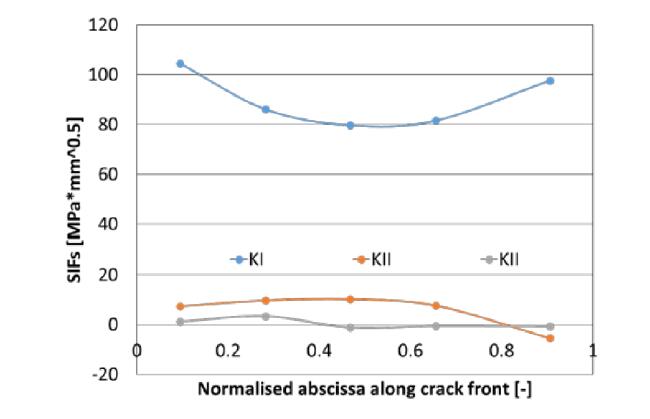
Figures 22-25 show the DBEM cracked model with the related Max Principal Stress plots, whereas Figure 26 shows the SIF variations along the crack fronts for the four considered cracks: in all the analysed configurations the ∆Kth ≈ 140 MPa·$\sqrt {{\rm{mm}}} $, in correspondance of an average temperature of nearly 150 °C in the crack insertion area (Figures 10 and 17) was overcome in those parts of crack front close to break through points. Such parts would be extended if considering that a moderate mixed mode condition was obtained along the crack front with consequent need to calculate an equivalent SIF (Keff), by an appropriate combination of KI, KII and KIII, to compare with Kth. Anyway the information obtained are sufficient to assess the need of a crack propagation simulation to check the residual fatigue life.
7. Discussion
Several crack configurations have been assumed as representatives of cracks observed into PFCs of W7-X. Two different FEM and DBEM submodels have been used in order to refine the evaluation of the FEM global stress-strain fields coming from the two scheduled OPs for W7-X. Subsequently, various crack shapes and dimensions and position in the component have been considered into the DBEM environment allowing for a comparative fracture mechanics assessment.
Regarding the OP1, four different critical configurations have been proposed for simulating the observed scenarios. For all of them, a fixed radius of 0.3 mm for the initial semi-circular crack has been assumed; then, the differences were only related to the extension of the disconnected brazed material at interface between CuCrZr plates and steel pipes. In addition, a further analysis was aimed at assessing the impact of braze root modelling on SIFs.
A first analysis (configuration A) was aimed at detecting the most critical crack insertion location between the two positions with the highest stresses as visible from the global stress plots. Then, in order to simulate the braze-pipe disconnection observed for the real damaged components, special boundary conditions (internal springs with negligible stiffness) have been applied on the DBEM submodel in order to duplicate and separate the elements in the zone of interest.
SIF values turned out to be increasing along with the reduction of braze/pipe disconnected area. However, although the considered initial crack had a considerable depth (they crossed the whole braze section and prolonged for 0.3 mm through the pipe thickness), SIFs evaluated in correspondance of OP1 were substantially lower than the threshold value (ΔKth) in all the considered configurations, showing non propagating crack scenarios and consequently safe configurations.
Regarding the OP2, four further crack configurations have been proposed. All the assumed cracks were positioned in the most stressed area as observed in the FEM stress plots and cracks had different sizes. In this case SIFs turned out to be higher than threshold, as expected due to the higher level of stresses in comparisono to OP1, suggesting the need for a crack propagation simulation.
8. Conclusion
Several cracks have been observed in the braze roots between pipes and heat sinks of Plasma Facing Components of Wendelstein 7-X. In order to assess the possibility of cooling water leakage due to cyclic crack-growth through the pipe thickness, several crack locations and dimensions have been numerically simulated undergoing both the scheduled Operational Phases 1 and 2 designed for the W7-X operation.
The adopted FEM-DBEM approach permitted to simulate various potential crack configurations by taking at the same time the advantage of FEM and DBEM methods: the FEM code has been used to solve the main global transient thermal-stress analyses considering the various loads and boundary conditions applied on the entire Baffle Module, whereas, the fracture mechanic assessment has been completely demanded to the DBEM code due to the the higher flexibility of DBEM when facing fracture problems.
Further developments could be oriented to setting up a DBEM implementation with more efficient computational alghoritms like those resorting to Fast DBEM [19], in order to make more appealing the use of DBEM also for larger and more complex submodels, embending larger parts of the cracked pipe.
Conflict of Interest
The authors declare that there is no conflict of interest regarding the publication of this manuscript.









 DownLoad:
DownLoad: