A Rao-Blackwellized particle filter for joint parameter estimation and biomass tracking in a stochastic predator-prey system

1.   Introduction

It is well established that the breadth of equilibrium fluid phases exhibited by relevant soft matter, such as globular protein solutions and colloidal suspensions, extends well beyond a macroscopic liquid-vapor phase separation, giving rise to inhomogeneous fluids phases composed of clusters or patterned morphologies ^[1].

At the microscopic level, the origin of such structures is commonly ascribed to the presence of competing interactions acting on different length scales: the propensity to form equilibrium clusters phases — heralding the development of patterned morphologies — stems from the competition between a short-range attraction, favouring agammaegation, and a long-range repulsion, frustrating a complete phase separation ^[2]. Model potentials of this kind are usually referred to as SALR (Short-range Attractive and Long-range Repulsive) interactions ^[3].

A flourishing literature clarified many aspects of the physics of SALR models (see e.g. ^{[4,5,6,7,8,9,10,11,12,13,14,15,16,17]}), including a broad assessment of their accuracy in describing general aspects of structure and thermodynamics of real protein solutions and colloidal suspensions, see e.g. ^{[18,19,20,22,21,23]}. The large interest on this topic is witnessed by several recent reviews ^{[24,25,26,27]}.

At the structural level, a ubiquitous indication to detect the presence of agammaegates is provided by a peak in the static structure factor $ S(q) $, located at a wavenumber $ q_{\rm c} $ well below the position of the main diffraction peak, see e.g. ^{[28,29,30,31]}. Nonetheless, a live debate concerns the correct relationship between such a low-$ q $ peak and the effective microscopic arrangement taking place in the fluid. Initially, this feature was related to the specific existence of equilibrium clusters, as observed both in colloid-polymer mixtures and in protein solutions ^[28]. However, the presence of such clusters was questioned by other experiments on similar systems ^[32,33,34]. Later on, a series of coupled dynamical and structural experiments on lysozyme solutions suggested the low-$ q $ peak in $ S(q) $ to arise from the formation of a generic Intermediate-Range Order (IRO) taking place in the fluid ^[22,21,23]. Such a situation, to be contrasted with the more specific formation of clusters, corresponds to a less distinct, locally non-homogeneous microscopic arrangement characterized by the presence of agammaegates with sizes ranging from dimers, trimers on, with a fast decrease of associated probability distribution ^[35,36]. This picture turns back to prior conclusions about the onset of a "medium–range order'' in models for covalently-bonded non-crystalline materials ^[37,38]. Therein, the presence of the low-$ q $ peak was ascribed to a local icosahedral order in the fluid. The original investigations in ^[22,21,23] prompted most recent studies, investigating dynamical properties of SALR fluids ^[39,40].

Two different criteria, based on the property of the low-$ q $ peak, were proposed to discriminate between IRO and genuine clustering in model SALR fluids. In the first scheme ^[36], it is argued that clusters (at low density) or cluster-percolated states (at higher densities), are signaled by a height of the low-$ q $ peak rising over $ \sim 2.7 $. This empirical observation closely recalls the Hansen-Verlet criterion for the freezing of simple fluids ^[41]. As for the second criterion, it is argued in ^[42] that clustering occurs as far as the thermal correlation length encoded in $ S(q_{\rm c}) $ becomes larger than the typical length-scale associated with the long-range repulsion. Recently, we addressed the same issue by using Monte Carlo simulation for a common SALR model, focusing on correlations in the real space, as described by the local density $ \rho (r) $ ^[43,44]. We have shown that, as the attractive strength increases, a threshold is crossed, whereupon a portion of $ \rho(r) $ experiences, at long distance, a tiny peculiar rearrangement, consisting in a reversal of trend. In coincidence, $ S(q_{\rm c}) $ rapidly rises, in such a way that it goes almost discontinuously well over the threshold $ S(q_{\rm c}) $$ \approx 2.7 $ (in agreement with the criterion of ^[36]), with the simultaneous appearance of a shoulder in the cluster-size distribution. Based on all such evidence, we argued that modifications observed in real-space correlation and onset of clustering are tightly linked.

In this work, we extend our previous investigation ^[43,44], to ascertain the worth of Integral Equation Theories (IETs) of the liquid state to study the onset of clustering. The possibility to discriminate on the basis of purely structural indicators the underlying arrangement of SALR fluids, coupled with the use of effective theoretical tools, turns to be especially advantageous in all those cases in which microscopic data are not readily available. Theoretical tools are also beneficial for a wide investigation of clustering conditions in different SALR models upon disparate thermodynamic conditions, a task prohibitively costly to bear by simulations only. We have organized the paper as follows: after introducing our SALR model and IETs (Section 2), we present and discuss our main findings in Section 3. Concluding remarks and perspectives follow in Section 4.

2.   Model and theory

Theoretical calculations concern a standard SALR model, constituted by hard spheres of diameter $ \sigma $ interacting via a potential formed by the sum of two Yukawa contributions of opposite sign (hard-sphere two-Yukawa, HS2Y). Hence, the total interaction between a pair of spheres, $ v(x) $ — with $ x = r/\sigma $ as the (reduced) interparticle distance — reads:

where $ \beta = 1/k_{\mathrm{B}}T $, with $ T $ and $ k_{\mathrm{B}} $ as the temperature and the Boltzmann constant, respectively. Positive parameters $ \varepsilon $ and $ A $ determine the strength of attractive and repulsive contributions respectively, while $ z_{ \mathrm{a}} $ and $ z_{\mathrm{r}} $ (with $ z_{\mathrm{a}} > z_{\mathrm{r}} $), determine their corresponding ranges. We focus on a particular set of HS2Y parameters, widely adopted in previous studies ^{[2,8,9,15,45]}: we have fixed $ z_{\mathrm{a}} = 1 $, $ z_{\mathrm{r}} = 0.5 $, $ A = 0.5 $ and let $ \varepsilon $ move from 0.9 to 1.6. Within our choice, the Mean Spherical Approximation predicts the occurrence of a microphase separation ^[2], the liquid-vapor coexistence taking over only for $ \varepsilon \gtrsim 5 $.

We carry out our study at fixed reduced density $ \rho\sigma^3 = 0.6 $, while the temperature is included in the definition of $ v(x) $, see Eq 1. Our choice for such a relatively high density allows the fluid to develop spatial correlations extending over relatively large distances. In this way, we observe under optimal conditions the tiny structural rearrangements at the heart of our findings, to be discussed in the next section.

We determine the pair structure of our model by means of two thermodynamically self-consistent integral equations, namely the hybrid mean spherical approximation (HMSA), derived by Zerah and Hansen ^[46], and the Self-Consistent Integral Equation (SCIE) derived by two of us ^[47,48,49]. Both approaches provide a closure to the Ornstein–Zernike equation ^[1], relating the pair correlation function $ g(x) $ to the direct correlation function $ c(x) $. Thermodynamically self-consistency is ensured by enforcing the equality of compressibilities obtained by two different routes from structure to thermodynamics ^[1], thank to the mixing parameter $ f $, i.e.:

where $ \chi _{\mathrm{T}} = -1/\rho \, (\partial P/\partial \rho)^{-1} $ is the isothermal compressibility and $ P $ is the pressure calculated via the virial theorem ^[1]. In order to calculate the total correlation function $ h(x) = g(x)-1 $ and the structure factor $ S(q) $, both theories are solved numerically by the iterative Newton–Raphson method ^[50], over an extended grid of $ 2^{14} $ points with a fine mesh of $ \Delta x = 0.005 $. Convergence is assumed when a difference smaller than $ 10^{-8} $ is reached between two consecutive iterations. The mixing parameter $ f $ is determined so that Eq 2 is satisfied to within less than one percent.

We also study the onset of clustering in terms of the entropy of the fluid ^[51]. An approximation for such a property is provided by the pair entropy $ s_{2} $, which involves only $ g(x) $:

This expression derives from the expansion of the configurational entropy in terms of multi-body correlations involving two, three and successively more particles ^[52,53,54]. In simple fluids, the leading term $ s_{2} $ is generally found to account for about 90% of the configurational entropy ^[54,55,56].

3.   Results and discussion

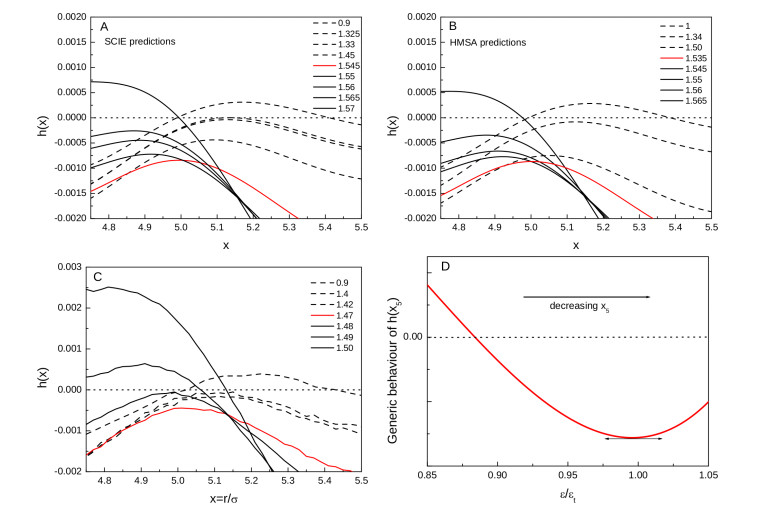
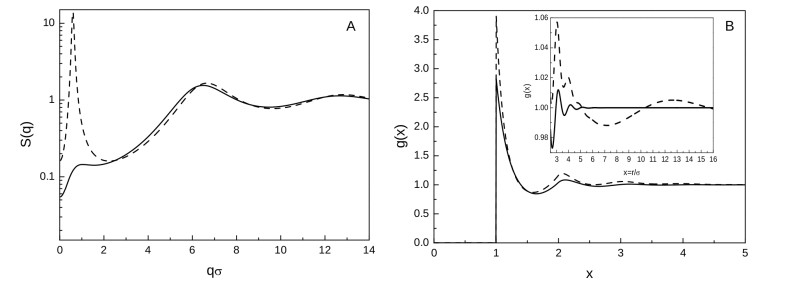
In Figure 1, we show SCIE structural predictions for two different attractive strengths, namely $ \varepsilon = 0.9 $ and $ 1.6 $. A low-$ q $ peak is visible in the $ S(q) $ (A) and becomes more and more pronounced as $ \varepsilon $ increases. According to ^[36], an IRO state takes place for $ \varepsilon = 0.9 $ [where $ S(q_{\rm c})\approx 0.2 $], while a more ordered clustered state occurs for $ \varepsilon = 1.6 $ [where $ S(q_{\rm c}) > 10 $]. As for $ g(x) $, in Figure 1B, the amplitude of the first four coordination shells — and apparently of the fifth one — increases with $ \varepsilon $, while the corresponding position shifts to slightly lower distances. In contrast, for $ \varepsilon = 1.6 $, $ g(x) $ no longer oscillates around one below $ x = 5 $ and, as shown in the large view in the inset, next distant neighbors eventually merge into a single oscillation of wavelength $ \approx 9\sigma $.

Figure 1.  SCIE $ S(q) $ (A) and $ g(x) $ (B) for $ \varepsilon = 0.9 $ (full lines) and $ \varepsilon = 1.6 $ (dashed lines). Inset: overview of $ g(x) $ at intermediate/long interparticle separations: as $ \varepsilon $ increases, a long-wavelength oscillation rises.

DownLoad: Full-Size Img PowerPoint

Since SCIE correctly predicts the typical structural features we documented by MC ^[43], the question naturally arises so as to whether IETs are able to discriminate — on the basis of local, real-space properties — between a generic intermediate-range order and the more specific onset of clustering. To this purpose, we examine now in detail the structural modifications undergone by $ h(x) $, as predicted by SCIE and HMSA, for intermediate attractive strengths. We recall that in^[43] we identified the MC clustering threshold as falling at $ \varepsilon_{\rm t} = 1.47 $. In Figures 2A and 2B we focus on the amplitude of the fifth neighbor peak of $ h(x) $, denoted as $ h(x_5) $; therein, we see that the behavior of $ h(x_5) $ contrasts with that of the first four coordination shells in that it does not monotonically increases with $ \varepsilon $. Specifically, in Figure 2A SCIE predicts that (i) $ h(x_5) $ starts to decrease from positive values as $ \varepsilon $ increases till, for $ \varepsilon = 1.33 \equiv \varepsilon_0 $, it turns negative and goes on decreasing, pointing to an increase of inhomogeneity in the fluid; apparently, since the fifth shell of neighbors seems to behave as next ones do, one may argue that it is about to merge into the heralding long-range oscillation. However, (ii) for $ \varepsilon = 1.545 \equiv \varepsilon_{\rm t} $, $ h(x_5) $ reaches a minimum and starts rising, going over zero for higher $ \varepsilon $ values; in this way, the fifth coordination shell eventually contributes to the overall stabilization of the structure formed by the first four shells. This scenario remains unchanged within HMSA in Figure 2B, but for slightly different $ \varepsilon_0 $ (1.375) and $ \varepsilon_{\rm t} $ (1.535) and, as shown in Figure 2C, it faithfully reproduces the MC data ^[43]; the little anticipation of the MC threshold $ \varepsilon_{\rm t} = 1.47 $ does not impair, in our opinion, the quality of our theoretical predictions.To summarize, whatever the method used, a generic behavior of $ h(x_{5}) $ can be drawn in Figure 2D. Therein, a threshold value $ \varepsilon _{t} $ is identified, whereupon $ h(x_{5}) $ reaches a minimum, leading to the local property:

Figure 2.  Portion of $ h(x) $ corresponding to the fifth coordination shell, for a series of $ \varepsilon $ (see legends), as obtained from SCIE (A), HMSA (B) and MC ^[43] (C). Dashed lines are for $ \varepsilon < \varepsilon_{\rm t} $, red lines for $ \varepsilon = \varepsilon_{\rm t} $, full lines for $ \varepsilon > \varepsilon _{\rm t} $. (D) Generic picture of $ h(x_{5}) $ vs $ \varepsilon $: theories and simulation predict that $ h(x_5) $ passes through a minimum at $ \varepsilon = \varepsilon_{\rm t} $.

DownLoad: Full-Size Img PowerPoint

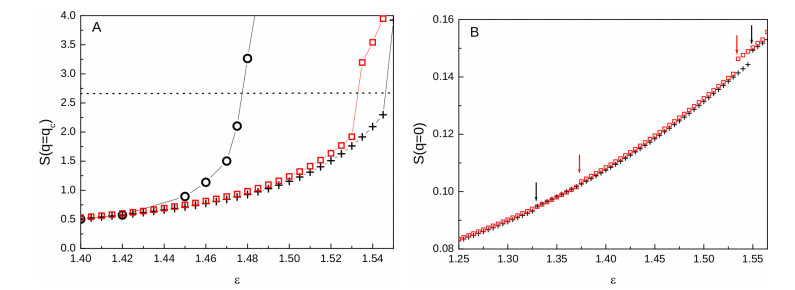
The consequences of our findings on the low-wavevector portion of the structure factor can be clearly appraised from Figure 3. In 3A we see that, as $ \varepsilon $ approaches $ \varepsilon_{\rm t} $, the height of the low-$ q $ peak, $ S(q_{\rm c}) $, slowly grows, with the fluid initially characterized by an intermediate-range order, then becoming progressively more structured. At $ \varepsilon = \varepsilon_{\rm t} $, $ S(q_{\rm c}) $ abruptly rises, exactly in correspondence with the real-space evidence that the fifth coordination shell correlates with the preceding ones. In agreement with our MC results ^[43], at this point the nature of the fluid changes, almost discontinuously, into a clustered state characterized by $ S(q_{\rm c}) > 2.7 $ ^[36]. We see in the Figure that SCIE and HMSA results closely agree, and appear slightly delayed with respect to the MC datum ^[43]; also, theories predict a sharp increase of $ S(q_{\rm c}) $ whereas MC shows a more rounded growth of this property. Since $ S(q = 0) $ is roughly proportional to $ S(q_{\rm c}) $ ^[8], also this property turns to discontinuously rise, as visible from Figure 3B; therein we see moreover that both SCIE and HMSA predict smaller jumps to occur also at $ \varepsilon_0 $.

Figure 3.  $ S(q_{\rm c}) $ (A) and $ S(q = 0) $ (B) vs $ \varepsilon $, as obtained by SCIE (crosses) and HMSA (squares). In (A) MC data ^[43] are also shown (circles); the dotted line represents the clustering threshold according to ^[35,36]. In (B), arrows indicate $ \varepsilon_0 $ and $ \varepsilon_{\rm t} $ as predicted by both theories, whereupon jumps occur, witnessing successive rearrangements within the fluid as the attractive strength increases.

DownLoad: Full-Size Img PowerPoint

The moderate increase of compressibility witnesses the development of larger and larger density fluctuations, as the system progresses within an increasingly inhomogeneous arrangement, heralding the onset of clustering.

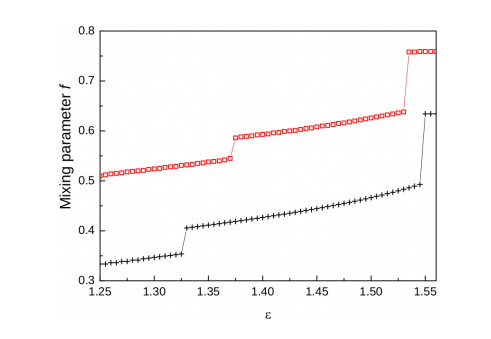
If we recall Eq 2, we conclude that structural rearrangements within the fluid taking place at $ \varepsilon_{0} $ and $ \varepsilon_{\rm t} $ involve corresponding changes in the isothermal compressibility $ \chi_{\rm T} $. Based on all evidence reported so far, both in real-space and reciprocal-space, we conclude that the observed atypical reversal of trend in the pair correlation faithfully witnesses the onset of clustering. The overall phenomenology observed by MC simulations is positively reproduced by IETs.

In agreement with our MC results ^[43], refined IETs predict a discontinuity in $ S(q_{\rm c}) $ at $ \varepsilon = \varepsilon_{\rm t} $. At this stage, an interesting issue concerns the origin, within the theoretical framework, of the observed discontinuities. Indeed, as seen in Figure 4, successive steps in the gain of inhomogeneity, observed at $ \varepsilon_{0} $ and $ \varepsilon_{\rm t} $, are marked by clear-cut jumps in the mixing parameter $ f $. Consequently, it is the very fulfillment of the thermodynamic consistency condition (Eq 2) — enforced by any refined IET — that allows us to identify the observed structural changes. In the case $ f = 1 $, both SCIE and HMSA reduce to the thermodynamically inconsistent HyperNetted chain (HNC) approximation. We refer the reader to our recent work ^[44] for an extended analysis of HNC predictions concerning the HS2Y model of Eq 1 within various parameterizations including the one employed in this work. We simply note here that, consistently with the assumption of a constant $ f $ value, HNC is unable to capture the discontinuous changes in the structural properties documented by MC ^[43].

Figure 4.  Mixing parameter $ f $ vs $ \varepsilon $ for SCIE (crosses) and HMSA (squares). When clustering is underway, inherent structural changes, occurring at $ \varepsilon_{0} $ and $ \varepsilon_{\rm t} $, are marked by clear-cut jumps in $ f $. Lines are guides to the eye.

DownLoad: Full-Size Img PowerPoint

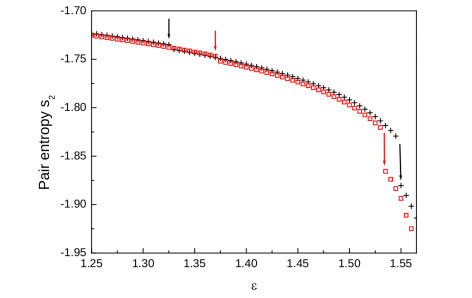
We finally turn to the pair entropy $ s_{2} $ of (Eq 3), a global property found to be a fingerprint to distinguish between liquid-like and solid-like environments on the one hand, and between different crystal structures on the other hand ^[57]. More generally, in simple liquids $ s_{2} $ decreases as the system becomes progressively more structured. As seen from Figure 5, this statement holds also for our model, during the clustering process. In facts, as $ \varepsilon $ increases, the formation of a further coordination shell contributes to the overall stabilization of the local environment around a given particle, provided by the existing shells of neighbours; as we have seen, this structural rearrangement abruptly triggers the clustering process, with the consequence that a drastic reduction of available configurational states affects all those particles forming agammaegates. This mechanism is exactly reflected in the rapid, almost discontinuous decrease of pair entropy visible in Figure 5. As $ \varepsilon $ increases, both structural rearrangements affecting $ h(x) $ at $ \varepsilon_{0} $ and $ \varepsilon_{\rm t} $ have visible effects on $ s_{2} $: a first discontinuity is followed, by further increasing the attractive strength, by a second discontinuous jump observed at $ \varepsilon = \varepsilon_{\rm t} $ to be ascribed to the entropy change related to the onset of clustering. In a previous study ^[14], we identified a possible signature of the arising IRO peak in HS2Y models, as a jump in the entropy, based on chemical potential calculations ^{[58,59,60,61]}; therein, we surmised that the loss of available space within the clusters is tempered by a gain of accessible space between clusters, mitigating overall the decrease of the total entropy due to the decrease of the main contribution provided by $ s_2 $. In general, the search for thermodynamic signatures of clustering could greatly help our understanding of these systems, favouring as well our capability of experimentally identifying agammaegation processes.

Figure 5.  SCIE (crosses) and HMSA (squares) pair entropy. Arrows indicate $ \varepsilon_0 $ and $ \varepsilon_{\rm t} $ as predicted by both theories, whereupon jumps occur, witnessing successive rearrangements within the fluid as the attractive strength increases.

DownLoad: Full-Size Img PowerPoint

4.   Conclusion

Refined thermodynamically self-consistent integral equations are shown to reproduce a mechanism, previously unearthed by MC ^[43], governing the clustering process in a model SALR fluid. Refined IETs, designed a priori for the study of the liquid state, are able to capture the structure of such a system across the clustering threshold. In a previous study ^[14], we documented the existence of small simultaneous discontinuities of several thermodynamic and structural properties of the same pair potential (but within different parameterizations), under physical conditions close to the early development of an intermediate-range order in the fluid. In comparison, discontinuities presently observed when passing from an IRO to a clustered state are neater. We speculate that in model colloids with competing interactions, the present mechanism is a generic feature intrinsic to the clustering process.

Possibly due to the fact that the scale at which our effect shows up is rather small, this process was overlooked in other studies using the same HS2Y model with identical parameters, but for those we already published ^[43,44]. As for the experimental side, the pair potential adopted in this work provides a reasonable description of dispersions of charged colloidal particles in the presence of a depletant, e.g. non-adsorbing polymer-coils, in which $ \varepsilon $ is proportional to the polymer concentration, the radius of gyration governs $ z_{\mathrm{a}} $, and the parameters entering the long-range repulsion depend on the electrostatic properties of the mixture ^[62]. Hence, an experimental realization of our setup, to gauge our findings against, would consist of a colloidal suspension, where all chemical and physical conditions are held fixed, but for the concentration of the polymer, so as to control the depletion potential strength. Similarly to what observed for simulations, also in experiments the process could be difficult to be traced in the neighborhood of the fifth coordination shell. Nevertheless, this limitation could be overcome since we have preliminary evidence that, for lower densities, the formation of clusters is signaled by reversals of trend occurring at shorter distances, making them easier to be detected.

Acknowledgments

The authors wish to thank Prof. Jean-Pierre Hansen, Prof. L. Lloyd Lee and Prof. Gerhard Kahl for their advices on the manuscript and fruitful discussions. We gratefully acknowledge the computer time made available at the Pôle Messin de Modélisation et Simulation (PMMS) and within the PO-FESR 2007-2013 MedNETNA (Mediterranean Network for Emerging Nanomaterials) Project.

Conflict of interests

All the authors declare no conflict of interest regarding the publication of this article.