CSR reporting in banks: does the composition of the board of directors matter?

Abbreviations:

$\Omega$: Constant angular velocity [ms^-1]; $\mu$: Dynamic viscosity [$kg\;{m}^{-1}{s}^{-1}$]; $(u, \, \, v, \, \, w)$: Velocity Components [ms^-1]; $\sigma$: Electrical conductivity [$S\;{m}^{-1}$]; $(r, \varphi, z)$: Cylindrical coordinates [m]; ${\left(\rho c\right)}_{p}$: Heat capacity of nanoparticle$\left[J{K}^{-1}\right]$; ${L_1}$: Velocity slip coefficient; ${L_2}$: Thermal slip coefficient; ${L_3}$: Concentration slip coefficient; ${\rho _f}$: Fluid density $\left[kg\;{m}^{-3}\right]$; ${\left(\rho c\right)}_{f}$: Heat capacity of liquid $\left[J{K}^{-1}\right]$; $v( = \frac{\mu }{{\rho }_{f}})$: Kinematic viscosity $\left[{m}^{2}{s}^{-1}\right]$; $T$: Fluid temperature $\left[K\right]$; $k$: Thermal conductivity $\left[W{m}^{-1}{K}^{-1}\right]$; ${B}_{0}$: Magnetic field $\left[Nm{A}^{-1}\right]$; $\alpha$: Velocity slip parameter; ${\alpha _m}$: Thermal diffusivity $\left[{m}^{2}{s}^{-1}\right]$; $Q$: Heat generation/absorption coefficient; $\beta$: Thermal slip parameter; ${D_T}$: Thermophoretic diffusion coefficient $\left[{m}^{2}{s}^{-1}\right]$; $\delta$: Heat generation/absorption parameter; ($x, \, y, \, z$): Directions; $\gamma$: Concentration slip parameter; ${C}_{\infty }$: Ambient fluid concentration; ${T}_{\infty }$: Ambient fluid temperature; $\sqrt {{{{{\rm{Re}}} }_r}} {C_f}$: Skin-friction co-efficient; ${T_w}$: Temperature at surface [K]; ${C_w}$: Concentration at surface; $nf$: Nanomaterial; ${D_B}$: Brownian diffusivity $\left[{m}^{2}{s}^{-1}\right]$; $f$: Base fluid; $p$: Nanoparticle; $Ha$: Hartman number; $Nt$: Thermophoresis parameter; $Nb$: Brownian motion parameter; Sc: Schmidt number; $\Pr$: Prandtl number; ϕ: Concentration distribution; $f'$: Non-dimensional velocities; ${\rm{Re}}_{r}^{\frac{-1}{2}}Sh$: Sherwood numbers; $g$: Non-dimensional velocities; $\theta$: Temperature field; $\eta$: Dimensional distance; $\frac{{{N_u}}}{{\sqrt {{{{{\rm{Re}}} }_r}} }}$: Local Nusselt number; ${{{\rm{Re}}} _r}$: Rotational Reynold number; MHD: Magnetohydrodynamics; NN: Neural Networks; AE: Absolute error; LM: Levenberg-Marquardt; MSE: Mean square error; AI: Artificial intelligence; MLP: Multilayer perceptron; BLMS: Backpropagation Levenberg-Marquardt Scheme

1.   Introduction

In the fields of mathematics and computers, non-linear least squares problems are resolved using the Levenberg-Marquardt (LM) scheme, which is sometimes referred to as the damped least-squares approach. In particular, these minimization issues arise in the least square curve fitting. In several software programs, the LM is employed to address general curve-fitting issues. First-order algorithms frequently converge more slowly than the Gauss-Newton algorithm ^[1]. It should be noted that, similar to other iterative optimization techniques, the LM just locates a local minimum, and not necessarily the global minimum. Parker developed upon it and subsequently resurrected it ^[2]. An innovative method in artificial intelligence (AI) is the use of (artificial neural networks (ANNs). ANNs can change during the learning process according to the data passing through the network, whether it comes from external or internal sources. ANNs enhance the performance of a multilayer perceptron (MLP) network by simultaneously training it using the backpropagation (BP) technique. It is the most popular, practical, and understandable model for intricate multilayer networks.

The Levenberg-Marquardt scheme (LMS) is a novel technique that offers numerical solutions to a range of fluid flow issues while guaranteeing a convergent dependability in ANNs. In recent years, various researchers have used this technique to explore the flow of non-Newtonian fluid systems and their mass and heat transfer characteristics. Neural networks were created by Akbar et al. ^[3] to investigate heat transport and magnetohydrodynamics (MHD) in a 2-phase model of nanofluid flow with thermal radiation. Neural networks were used by Shoaib et al. ^[4] to numerically explore a rotating MHD hybrid nanofluid flow with heat radiation across a stretched sheet. Khan et al. ^[5] used the Bayesian-LMS (BNN-LMS) to study the heat transfer across two porous parallel plates of steady nanofluids, thereby focusing on thermophoresis and Brownian effects. In order to represent the third-order non-linear Emden-Fowler equation, Sabir et al. ^[6] used computational intelligence techniques and the backpropagation neural network LMS. Yasmin et al. ^[7] employed a stochastic numerical technique based on ANNs to explore heat transfer in Maxwell nanofluid flow across a vertically moving surface with MHD. Using intelligent networks, Al-Sawalha et al. ^[8] studied the MHD fluid flow across coaxial flexible rotating disks in a thermal stratification medium.

The applications of MHD in engineering and the industrial sector have led to an increased interest in the study of heat transfer and boundary layer flow. Among other applications, magneto nanofluids have been utilized in the following areas: magnetic cell separation, biomedicine, hyperthermia, optical modulators, silk drift separation, optical grids, optical switches, and nonlinear optical materials. The flow and heat transfer of a system can be regulated by MHD, which is the movement of an electrically conducting fluid inside a magnetic field. Originally, MHD was utilized to address astrophysical and geophysical problems. In 1974, Pavlov et al. ^[9] conducted research on the MHD boundary layer flow of an electrically conductive fluid in an ever-present transverse magnetic field. Aldhafeeri and Yasmin et al. ^[10] investigated the computational study of heat transfer and friction drag in an unsteady MHD radiated Casson fluid flow across a stretching/shrinking surface. Chakrabarti and Gupta ^[11] extended this study in 1979 by examining hydromagnetic flow and heat transfer. Khan and Mao ^[12] deduced the numerical solution of the MHD radiative flow of an Oldroyd‐B nanofluid toward a porous stretched surface that contained gyrotactic microorganisms. Yasmin ^[13] investigated the flow of the MHD of a Sisko nanofluid in the presence of an applied magnetic field, which was triggered by the surface's bidirectional stretching. The anisotropic behavior of magnetic nanofluids (MNFs) during filmwise condensation across a vertical plate exposed to a uniform, variable-directional magnetic field was examined by Heysiattalab et al. ^[14]. Yasmin ^[15] compared the dual solutions of the problem which described the magnetized motion of a Newtonian and second‐grade fluid induced by a curved stretching/shrinking surface using the associations of a homogeneous-heterogeneous reaction and the Cattaneo-Christov model. Hayat et al. ^[16] investigated the 3D MHD flow of a nanofluid across a convectively heated nonlinear stretched surface. Additionally, they investigated the doubly stratified flow of a thixotropic nanofluid under the action of a magnetic field ^[17]. Khan et al. ^[18] studied the numerical analysis of heat transfer and friction drag related to the effect of Joule heating, viscous dissipation, and heat generation/absorption in an aligned MHD slip flow of a nanofluid. Malvandi et al. ^[19] observed the thermal characteristics of hydromagnetic nanofluid flows within an inclined micro-annular tube. Aldhafeeri and Yasmin ^[20] studied computer simulations of the magnetized effects of Cattaneo-Christov double diffusion models on the heat and mass transport behavior of a second-grade nanofluid flowing in two dimensions across a curved stretching and shrinking surface. A recent analytical solution for the MHD 3D flow of an Oldroyd-B nanofluid that took heat absorption and production into account was presented by Hayat et al. ^[21].

The useful features of nanomaterials are attracting the attention of researchers in the technical sciences and applied physics. Nanofluids have garnered a lot of interest lately ^[22,23]. Given that nanofluids have substantially better thermal conductivities than conventional fluids, they are widely employed in the field of heat transfer to improve the efficiency. The creation and research of a nanofluids' thermal conductivity have been prompted by the restricted heat transmission capacities of traditional fluids. Yasmin et al. ^[24] analyzed the potential uses of nanofluids in solid-state lighting, electronic devices, cancer treatments, safer surgical procedures, and nuclear reactors all of which were gained from an enhanced heat transfer for more efficient cooling made this field of study especially intriguing. In 1995, Choi and Eastman ^[25] introduced the idea of suspending nanoparticles in a base fluid. Khan et al. ^[26] considered the heat transfer in a dissipative nanofluid that passed by a convective stretching/shrinking cylinder near the stagnation point. Ali et al. ^[27] investigated the effects of nanoparticle aggregation aligned to thermal radiation with the prescribed heat flux. The Cattaneo-Christov heat flux (non-Fourier) and mass flux (non-Fick's) approaches in the optimized Buongiorno's model have been used to analyze the nanofluid magneto-transport mechanisms over the surface impacted by the gyrotactic behavior of microbe dispersion. Raza et al. ^[28] analyzed the influential study of novel microorganisms and nanoparticles during heat and mass transport in Homann flow of visco-elastic materials. Sheikholeslami et al. ^[29] concluded that heat transfer rates were significantly influenced by the thermal and viscosity characteristics of nanofluids. Alqahtani et al. ^[30] studied the impact of thermal radiation and viscous dissipation on the stagnation point flow of a copper-water nanofluid across a convective stretching/shrinking cylinder. Jan et al. ^[31] investigated the influence of heat generation inside homogeneous and heterogeneous reactions, as well as the thermal radiation between the two squeezing plates in the flow dynamics. Ali et al. ^[32] studied the significant role of Darcy-Forchheimer and thermal radiation on a Casson fluid flow that was subjected to a stretching surface in the dusty fluid. Common nanoparticles found in nanofluids include carbides, oxides, metals, and carbon nanotubes. In several fields, including computer microprocessors, biomedicine, manufacturing and nuclear reactor cooling, nano-fluids are employed to increase the heat transfer rates ^[33,34]. Ali et al. ^[35] investigated the optimization of heat transfer in a thermally convective micropolar-based nanofluid flow by the influence of the nanoparticle's diameter and nanolayer via a stretching sheet. Ahmad et al. ^[36] investigated the influential study of novel microorganisms and nanoparticles during heat and mass transport in the Homann flow of visco-elastic materials. Ali et al. ^[37] investigated the crucial features of aggregation in a TiO₂-water nanofluid aligned of chemically comprising microorganisms using the finite element method (FEM) approach. According to research performed on a novel kind of nanofluid by Nadeem et al. ^[38], nanoparticles can either have a tabular or a rod-like structure. Ali et al. ^[39] investigated the entropy generation on the dynamics of a volume fraction of nanoparticles and coriolis force impacts on a mixed convective nanofluid flow with a significant magnetic effect.

For many years, researchers have concentrated on studying the fluid flow over a rotating disk due to its various uses in aeronautical sciences and engineering. These applications include thermal power generating systems, rotating machinery, air cleaning machines, computer storage devices, crystal growth processes, medical equipment, electronic devices, and gas turbine rotors ^[40,41,42]. A significant early contribution in this area was made by Von Karman ^[43], who utilized the momentum-integral approach to analyze the fluid flow over a rotating disk. Cochran ^[44] later asymptotically solved the Von Karman problem, while Ackroyd ^[45] explored the effects of suction and injection, thereby offering a series solution with exponentially decaying coefficients. An isothermal disk's heat transfer process was investigated by Millsaps and Pohlhansen ^[46], whereas partial slip features were investigated by Miklavčič and Wang ^[47]. In the setting of MHD nano-fluid stagnation point flows through a cylinder contained in a permeable media, Alizadeh et al. ^[48] examined the thermodynamic and mixed convection irreversibility. Heat transmission in MHD nanofluids was numerically analyzed by Shah et al. ^[49]. The flow of the fluid behavior across a spinning disk submerged in a permeable zone was analyzed by Attia ^[50] using the Crank-Nicolson technique. Turkyilmazoglu and Senel ^[51] used a porous disk inside a rotating frame to study the flow of viscous liquids and heat/mass transfers. Shah et al. ^[52] investigated a ferrofluid flow using a Cattaneo heat flux and a thermal conductivity model. When Mustafa et al. ^[53] investigated a nanofluids flow caused by a stretching disk, they found that the influence of the uniformly stretching disk lowered the thickness of the boundary layer. Entropy production in the revolving disk of a MHD viscous liquid flow was investigated by Rashidi et al. ^[54]. The flow fluid across a rotating disk was studied by Hayat et al. ^[55], thereby considering nanoparticles, magnetic fields, and slip effects. Then, they expanded their investigation to include carbon nanotubes and Darcy-Forchheimer flow ^[56].

The second-grade fluid is one of the most challenging non-Newtonian fluid models. It is a viscous non-Newtonian fluid that is widely used in a variety of industries, including biomechanics, improved oil recovery, and polymer manufacturing. Water is critical to our health, and is essential for numerous bodily activities, including delivering nutrition to cells, eliminating waste, protecting joints and organs, and controlling body temperature. Bio-convection is a natural phenomenon characterized by the random movement of microorganisms in the form of either single cells or colonies of cells. Different bio-convection systems are based on the directed motion of various types of microorganisms. Gyrotactic microorganisms are those that move against gravity in still water, and their upward swimming is denser in the top section of the suspension than in the lower section. When volume concentrations are sufficiently high, overturning convection occurs; however, once bio-convection occurs, their swimming direction is determined by the balance of two physical torques caused by gravity and the viscous drag that acts on an asymmetric distribution of mass within the organism. The importance of bio-convection may be seen in a variety of bio-microsystems, such as enzyme biosensors and biotechnologies that improve mass movements and mixing. Several articles have proposed theoretical bio-convection models for a variety of motile bacteria. The bioconvection flow of a modified second-grade nanofluid including gyrotactic bacteria and nanoparticles was studied by Waqas et al. ^[57]. Siddique et al. ^[58] developed a biofuel application using the bioconvection of MHD second-grade fluid that transported nanoparticles across an exponentially expanding sheet. In their work, Shafiq et al. ^[59] simulated bioconvection in a suspension of a second-grade nanofluid that contained gyrotactic bacteria and nanoparticles. Zuhra et al. ^[60] analyzed the simulation of bioconvection in a suspension of a second-grade nanofluid that contained nanoparticles and gyrotactic microorganisms. Abbas et al. ^[61] studied the bio-convection flow of a fractionalized second-grade fluid through a vertical channel with Fourier's and Fick's laws. Hayat et al. ^[62] analyzed the heat transfer in a bio-convection second grade nanofluid with the Cattaneo-Christov heat flux model.

It might be difficult to obtain an accurate analytical solution to this issue; therefore, researchers employed various numerical and semi-numerical methods, such as the Keller box technique ^[63], the homotopy perturbation method (HPM) ^[64], the Galerkin finite element method ^[65], and the spectral relaxation method ^[66]. Most of the literature on nanofluid flows in various systems were created using these methods; however, due to their benefits and effectiveness, intelligent numerical computing models are crucial for an MHD nanofluid flow over a revolving disk through heat absorption/generation and slip effects. Computational intelligence techniques are utilized to solve differential equations in stochastic numerical solutions associated with ANNs, thus demonstrating varied capacities under different conditions. All these inspiring characteristics motivated scholars to utilized accurate and reliable AI-based numerical mathematical models to analyze non-Newtonian nanofluids. Graphical and numerical evaluations have been used to investigate the effects of numerous parameters on the velocity, concentration, and temperature profiles. To enhance the numerical accuracy, the Mathematica and MATLAB software packages are commonly used. This paper proposes a model to achieve the statistical results, including MSE, testing, validation, training, Mu, and a regression analysis, and to examine influences of several parameters on the velocity, concentration, and temperature profiles.

The innovation contributions of the present study for backpropagation networks for two phase models are highlighted as follows:

● A numerical computation is designed through neural networks with the backpropagation Levenberg-Marquardt scheme (NNB-LMS) for a comparative study of the impact of an MHD nano-fluid flow over a rotating disk (MHD-NRD) with heat generation/absorption and slip effects.

● A governing mathematical model of the impact of an MHD nano-fluid flow over a rotating disk (MHD-NRD) with heat generation/absorption and slip effects represented with nonlinear PDEs is reduced to a nonlinear system of ODEs by the competency of similarity adjustments.

● A reference data of the designed networks is effectively constructed for variants of MHD-NRD which demonstrate the scenarios for the velocity slip parameter, Hartman number, thermal slip parameter, heat generation/absorption parameter, concentration slip parameter, and Prandtl number by applying the RK4 method.

● The Mathematica software is used to compute the dataset for the designed NNB-LMS for the variation of the velocity slip parameter, Hartman number, thermal slip parameter, heat generation/absorption parameter, concentration slip parameter, and Prandtl number.

● The MATLAB software is used to interpret the solution and absolute error analysis plots of MHD-NRD.

● The training, testing, and validation-based process block structure of NNB-LMS is exploited to calculate the approximate solutions of MHD-NRD, and comparative study is conducted to validate the consistent accuracy.

● The worthy performance of the designed network is established by a learning curve on the MSE based fitness, histograms, and regression metrics.

The rest of this paper is organized as follows: the scheme and outcomes of the model MHD-NRD problem are bestowed in Section 2; Section 3 presents the solution approach and discusses the effects of the suggested NNB-LMS on various MHD-NRD solutions; and finally, the last unit includes the final remarks and future research directions.

2.   Model development

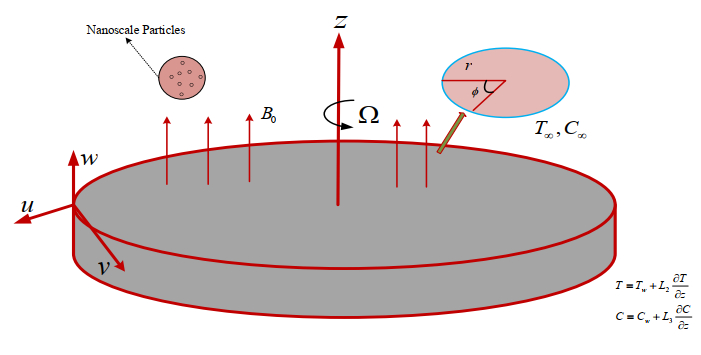
Consider the 3D MHD flow of a viscous nano-liquid through a rotating disk with partial slip effects and heat generation/absorption. At $z = 0$, the rotating disk has a constant angular velocity. The magnetic field with the strength ${B_0}$acts along the z-direction. The Brownian diffusion and thermophoresis are discussed. The existence of a magnetic field is ignored due to the assumption of a low magnetic Reynolds number ^[67]. The velocity components represented by ($u, v$, $w$) are increasing in the direction of $(r, \varphi, z)$, respectively. We can express the boundary layer equations as follow:

With consideration to the boundary conditions,

where$(\, u, \, \, v, \, \, w\, )$denote the velocities of the flow in the increasing directions of $(\, r, \, \, \phi, \, \, z\, )$respectively, ${\rho }_{f}$represents the base liquid density, $\mu$represents the dynamic viscosity, and $v( = \frac{\mu }{{\rho }_{f}})$represents the kinematic viscosity, respectively. $\sigma$represents the electrical conductivity. ${\left(\rho c\right)}_{f}, k, {\left(\rho c\right)}_{p}$and ${\alpha }_{m} = \frac{k}{{\left(\rho c\right)}_{f}}$represent the liquid heat capacity, the thermal conductivity, the effective heat capacity of the nanoparticles, and the thermal diffusivity, respectively. ${L}_{1}$indicates the velocity slip coefficient, ${L}_{2}$represents the thermal slip coefficient, and ${L}_{3}$represents the slip coefficient, ${D}_{T}$represents the thermophoretic diffusion coefficient, ${D}_{B}$represents the Brownian diffusivity, $T$represents the fluid temperature, ${C}_{\infty }$represents the ambient fluid concentration, ${T}_{\infty }$represents the ambient fluid temperature, and $Q$represents the heat generation/absorption coefficient. Choosing

Using Eq (1) satisfied, and Eqs (2)–(8) are reduced as follows:

With appropriate boundary conditions,

Here, $Ha$represents the Hartman number, while $\alpha$, $\beta$, $\gamma$, and $\delta$indicate the velocity slip, thermal slip, concentration slip, and heat generation/absorption parameters, respectively. Sc and Pr represent the Schmidt and Prandtl numbers, respectively $Nb$and $Nt$represent the Brownian motion parameters and thermophoresis, respectively. The following forms can be used to express all of these non-dimensional parameters:

The dimensionless coefficient forms of the skin fraction, and local Nusselt and Sherwood numbers are as follows:

where ${{Re} _r} = \frac{{2r(\Omega r)}}{v}$presents the local rational Reynolds number.

3.   Solution approach and consequences evaluation

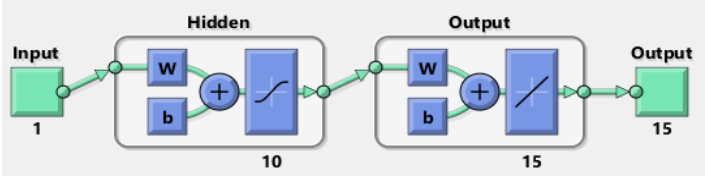
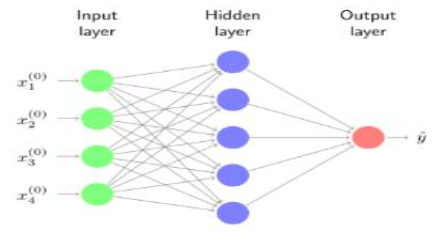
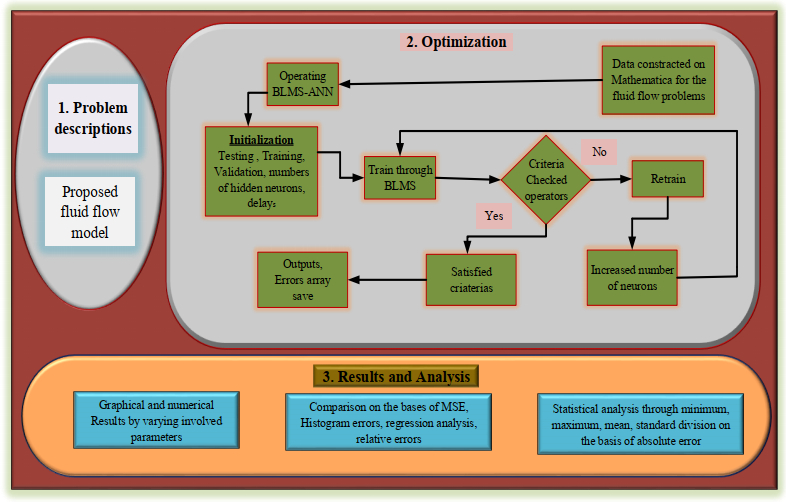
The comparative solutions (i.e., the NNB-LMS dataset) are determined using the Mathematica programming packages and the RK4 method. The suggested NNB-LMS consists of a combination of the structure of multi-layer neural network and the computation with backpropagation by LMS. Figure 1 is flow diagram of the given model. The proposed NNB-LMS is implemented in the Matlab software package via the 'nftool' neural network toolbox routine, which is a method for fitting neural network tools, thereby using appropriate hidden neuron settings, training data, validation data, testing data, and learning methodology. The proposed NNB-LMS within the framework of neural networks is illustrated in Figure 2. The Levenberg-Marquardt back-propagation scheme is employed to define the weights of the neural networks. Figure 3 depicts the NNB-LMS model, while Figure 4 illustrations the complete flow design.

Figure 1.  Flow diagram.

DownLoad: Full-Size Img PowerPoint

Figure 2.  Neural network architecture of the MHD-NRD model.

DownLoad: Full-Size Img PowerPoint

Figure 3.  A particular neuron paradigm is configured.

DownLoad: Full-Size Img PowerPoint

Figure 4.  The suggested workflow method for NNB-LMS in the MHD-NRD model.

DownLoad: Full-Size Img PowerPoint

Here, the numerical experiment implemented for NNB-LMS is presented for the MHD flow of the viscous nano-liquid model shown in Eqs (10)–(15). The deliberate NNB-LMS is effected for six scenarios, thereby varying the $\alpha$, $Ha$, γ, $\beta$, $\delta$, and $\mathrm{P}\mathrm{r}$, with 3-cases of the model MHD-NRD each, as shown in Table 1.

Table 1.  Depicts three different cases and all six possibilities for the MHD-NRD model.

Scenarios	Case	Physical quantities of interest
		$\alpha$	$Ha$	$\gamma$	$\beta$	$\delta$	$\Pr$	$Nb$	$Sc$	$Nt$
S1	1	0.3	0.2	0.4	0.4	0.1	1.0	0.3	1.0	0.1
	2	0.5	0.2	0.4	0.4	0.1	1.0	0.3	1.0	0.1
	3	0.7	0.2	0.4	0.4	0.1	1.0	0.3	1.0	0.1
S2	1	0.4	0.4	0.4	0.4	0.1	1.0	0.3	1.0	0.1
	2	0.4	0.7	0.4	0.4	0.1	1.0	0.3	1.0	0.1
	3	0.4	1.0	0.4	0.4	0.1	1.0	0.3	1.0	0.1
S3	1	0.4	0.2	0.4	0.4	0.1	1.0	0.3	1.0	0.1
	2	0.4	0.2	0.7	0.4	0.1	1.0	0.3	1.0	0.1
	3	0.4	0.2	1.0	0.4	0.1	1.0	0.3	1.0	0.1
S4	1	0.4	0.2	0.4	0.4	0.1	1.0	0.3	1.0	0.1
	2	0.4	0.2	0.4	0.5	0.1	1.0	0.3	1.0	0.1
	3	0.4	0.2	0.4	0.6	0.1	1.0	0.3	1.0	0.1
S5	1	0.4	0.2	0.4	0.4	0.0	1.0	0.3	1.0	0.1
	2	0.4	0.2	0.4	0.4	0.1	1.0	0.3	1.0	0.1
	3	0.4	0.2	0.4	0.4	0.2	1.0	0.3	1.0	0.1
S6	1	0.4	0.2	0.4	0.4	0.1	1.0	0.3	1.0	0.1
	2	0.4	0.2	0.4	0.4	0.1	1.3	0.3	1.0	0.1
	3	0.4	0.2	0.4	0.4	0.1	1.6	0.3	1.0	0.1

---

 | Show Table

DownLoad: CSV

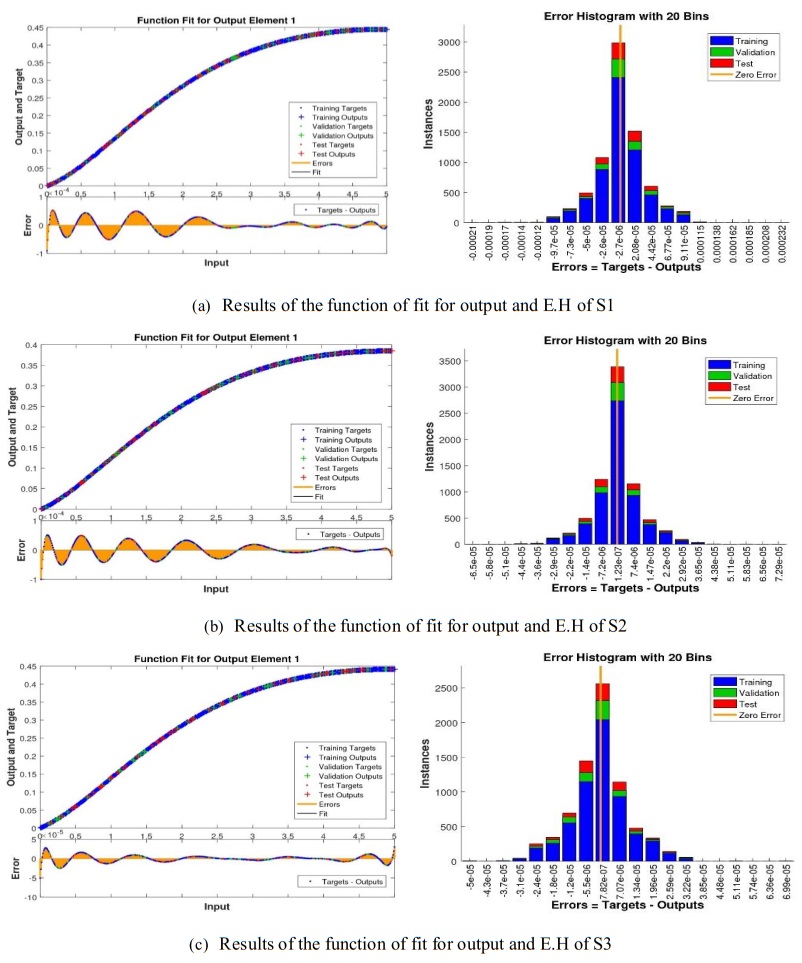
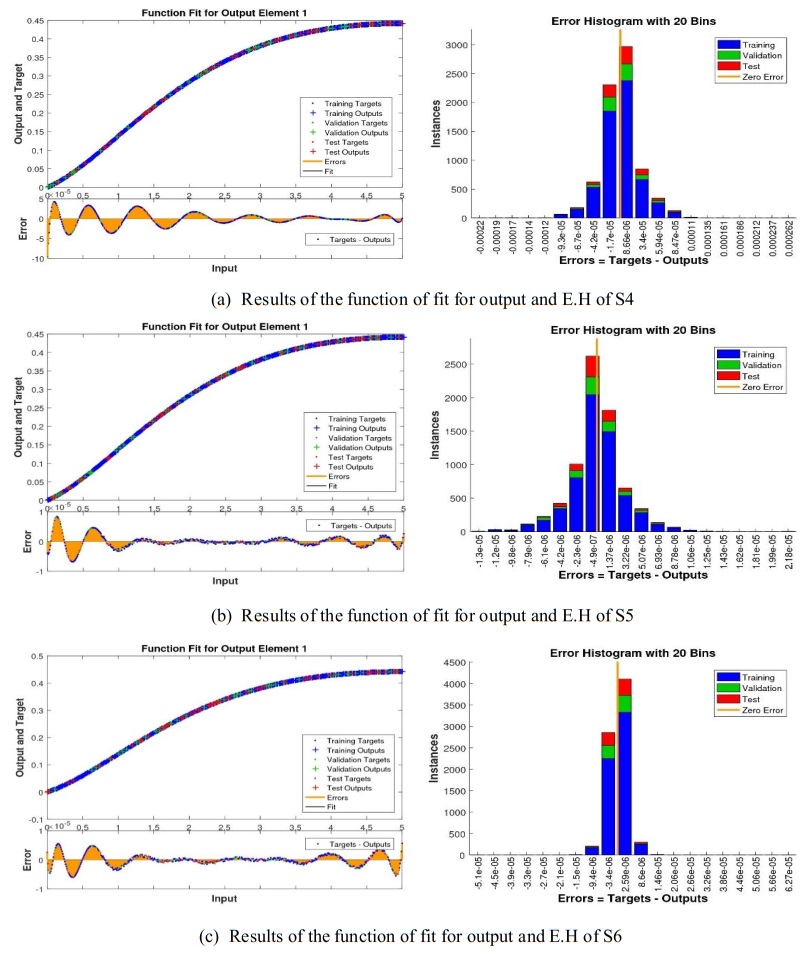
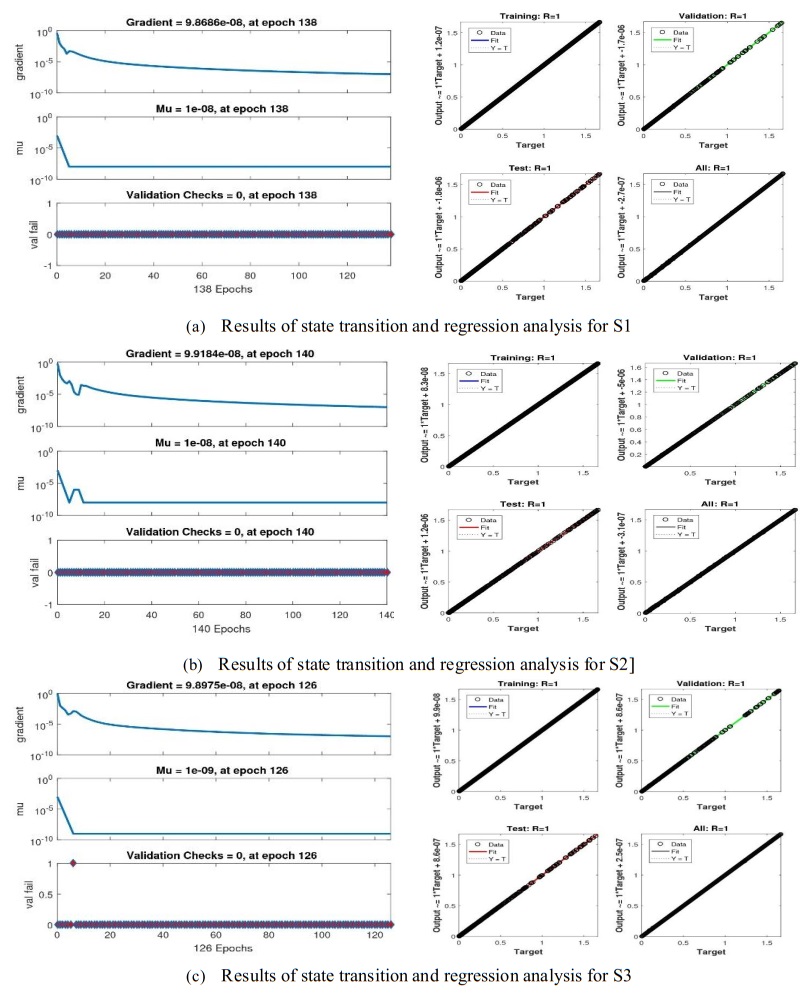
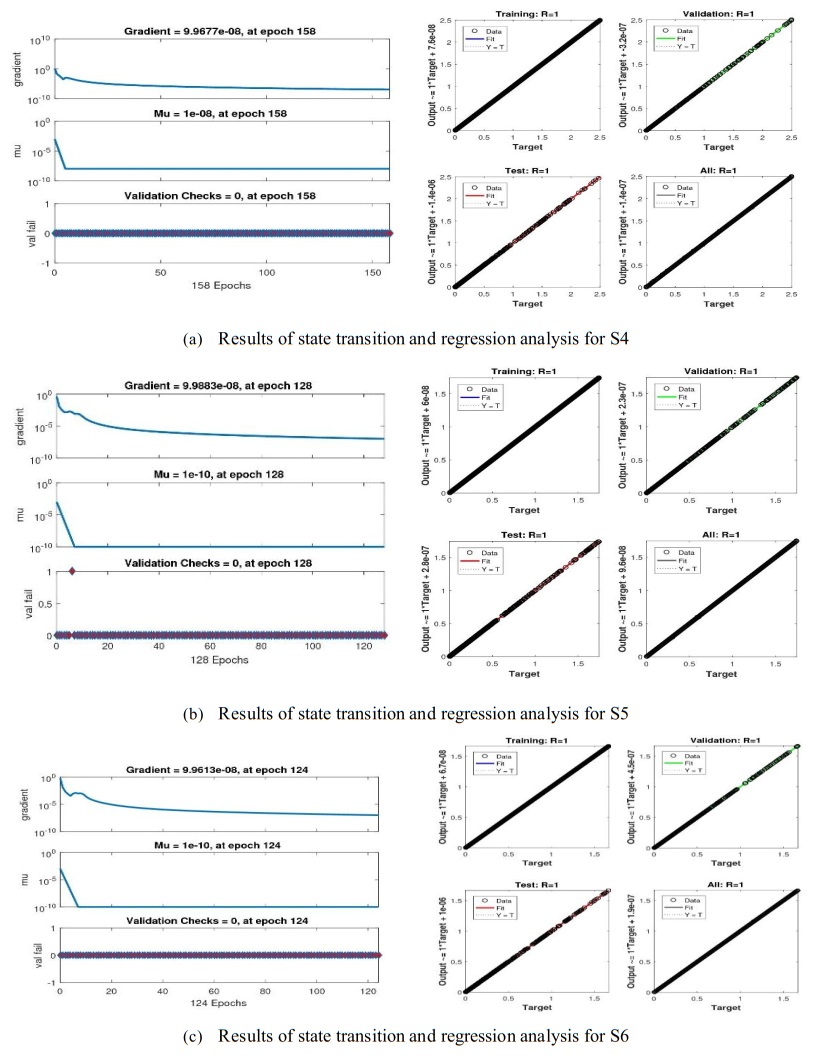
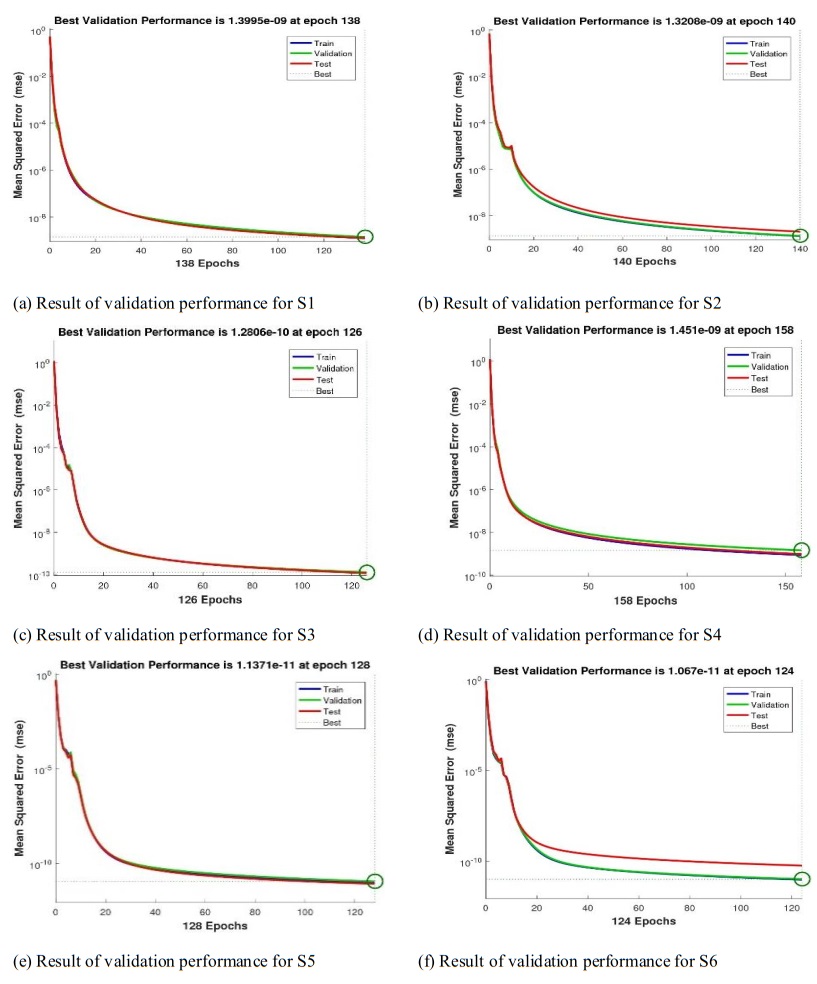
The effects of the NNB-LMS on the MHD-NRD model for situations 1–6 are shown in Figures 5–9. The function fitting and error histogram diagrams for all of the six scenarios are displayed in Figures 5 and 6. Figures 7 and 8 show the state transitions and regression analyses for each of the six situations. Figure 9 shows the validation performance analyses for the chosen MHD-NRD model scenarios. Furthermore, for every MHD-NRD model, Table 2 shows the parameters that were reached for convergence, such as the MSE, execution time, performance duration, backpropagation, and temporal complexity measures, for scenarios 1–6. Figures 5 and 6 show the output goal and error histogram progressions for the test procedures for scenarios 1–6 of the MHD-NRD model. In addition to the error histograms shown in Figures 5 and 6, each input point's error dynamics and outcomes for different scenarios are analyzed. When comparing the average value of the error-bin to the zero line, an error is seen close to $- 2.7 \times {10^{ - 06}}$, $1.23 \times {10^{ - 07}}$, $7.82 \times {10^{ - 07}}$, $8.66 \times {10^{ - 06}}$, $- \, 4.9 \times {10^{ - 07}}$, and $2.59 \times {10^{ - 06}}$of the fluid flow model for all six distinct scenarios, respectively. Figures 7 and 8 demonstrate the compactly [$9.87 \times {10^{ - 08}}, \, \,$$9.92 \times {10^{ - 08}}, \,$$\, 9.90 \times {10^{ - 08}}, \,$$\, 9.97 \times {10^{ - 08}}, \, \,$$9.99 \times {10^{ - 08}}\,$and $9.96 \times {10^{ - 08}}$] and [${10^{ - 08}}, \, \,$${10^{ - 08}}, \, \,$${10^{ - 09}}, \, \,$${10^{ - 08}}, \, \,$${10^{ - 10}}$and ${10^{ - 10}}$] with respect to the values of the gradient and Mu of Levenberg-Marquardt. However, the analysis inside the regression analyses is frequently classified using correlation analyses. The consequences of linking scenarios 1–6 of the MHD-NRD are demonstrated in Figure 9. The values of the correlation are frequently nearby to one, showing how well NNB-LMS resolves the MHD-NRD model and suggesting the ideal numbers for training, validation, and testing for exact modeling.

Figure 5.  For scenarios S1–S3, the recommended NNB-LMS's fitness and error histogram are solved in order to solve the MHD-NRD model.

DownLoad: Full-Size Img PowerPoint

Figure 6.  For scenarios S4–S6, the recommended NNB-LMS's fitness and error histogram are solved in order to solve the MHD-NRD model.

DownLoad: Full-Size Img PowerPoint

Figure 7.  Solution of state transition and regression analysis of Proposed NNB-LMS for solving fluid flow model for 1–3.

DownLoad: Full-Size Img PowerPoint

Figure 8.  Solution of state transition and regression analysis of Proposed NNB-LMS for solving the fluid flow model of 4–6.

DownLoad: Full-Size Img PowerPoint

Figure 9.  MSE validation achievement of the suggested NNB-LMS for solving MHD-NRD model of S1–S6.

DownLoad: Full-Size Img PowerPoint

Table 2.  NNB-LMS consequences for scenarios of the fluid flow model (MHD-NRD).

Scenarios	MSE			achievement	Gradient	Mu	Epoch	Time
	Training	Validation	Testing
$\alpha$	$1.22689\times {10}^{-09}$	$1.39949\times {10}^{-09}$	$1.25486\times {10}^{-09}$	$1.23\times {10}^{-09}$	$9.87\times {10}^{-08}$	$1.00\times {10}^{-08}$	$138$	$3$
$Ha$	$1.29401\times {10}^{-09}$	$1.32083\times {10}^{-09}$	$2.01454\times {10}^{-09}$	$1.29\times {10}^{-09}$	$9.92\times {10}^{-08}$	$1.00\times {10}^{-08}$	$140$	$3$
$\gamma$	$1.19098\times {10}^{-10}$	$1.28055\times {10}^{-10}$	$1.16143\times {10}^{-10}$	$1.19\times {10}^{-10}$	$9.90\times {10}^{-08}$	$1.00\times {10}^{-09}$	$126$	$3$
$\beta$	$8.72778\times {10}^{-10}$	$1.45104\times {10}^{-09}$	$9.67075\times {10}^{-10}$	$8.37\times {10}^{-10}$	$9.97\times {10}^{-08}$	$1.00\times {10}^{-08}$	$158$	$3$
$\delta$	$9.62085\times {10}^{-12}$	$1.13711\times {10}^{-11}$	$8.53623\times {10}^{-12}$	$9.62\times {10}^{-12}$	$9.99\times {10}^{-08}$	$1.00\times {10}^{-10}$	$128$	$3$
$\Pr$	$9.86760\times {10}^{-12}$	$1.06701\times {10}^{-11}$	$5.89417\times {10}^{-11}$	$9.87\times {10}^{-12}$	$9.96\times {10}^{-08}$	$1.00\times {10}^{-10}$	$124$	$2$

---

 | Show Table

DownLoad: CSV

Figure 9 demonstrates the MHD-NRD model's effectiveness by analysing the generated results of six different scenarios, with inputs ranging from 0 to 1 and a 0.01 step range. The error dynamics plot is validated by comparing the produced results to the reference numerical results of the RK4 method and the related outcomes. The greatest errors for the test, train, and validation statistics obtained through the suggested NNB-LMS for all six scenarios of the proposal model are less than $1.34\times 1{0}^{-09}$, $2.01\times 1{0}^{-09}$, $1.28\times 1{0}^{-10}$, $9.67\times 1{0}^{-10}$, $1.14\times 1{0}^{-11}$, and $5.89\times 1{0}^{-11}$, respectively. Furthermore, of the various MHD-NRD model situations (1–6), the associated numerical numbers in Tables 2 indicate that the MSE performance for the proposed NNB-LMS approach is close to ${10}^{-12}$. Moreover, the numerical results within Table 2, indicate that NNB-LMS effectively functions when solving the MHD-NRD model. The best performance of the network is achieved when the MSE is close to $1.23\times 1{0}^{-09}$, $1.29\times 1{0}^{-09}$, $1.99\times 1{0}^{-10}$, $8.37\times 1{0}^{-10}$, $9.62\times 1{0}^{-12}$, and $9.87\times 1{0}^{-12}$, respectively. The lower the MSE value, the more exact and effective the performance of the proposed approach. For different scenarios of the MHD-NRD model, the consequences and graphical representations indicate that NNB-LMS is efficient, accurate, and convergent.

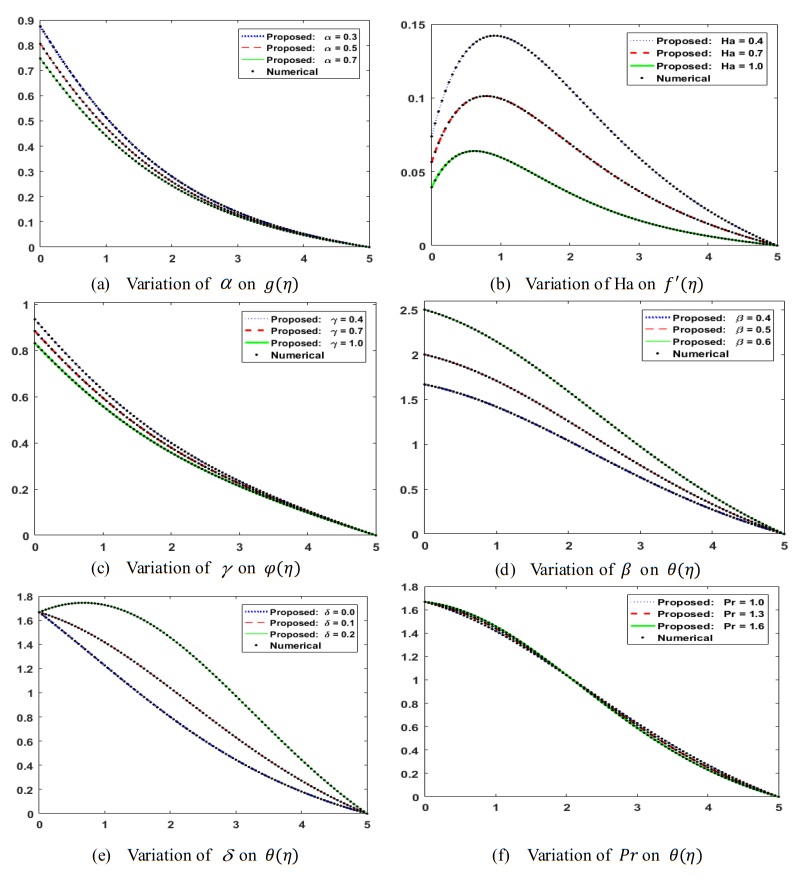
The NNB-LMS consequences are verified for the velocity profiles $g(\eta), \, \, \, f'(\eta)$, the concentration profile $\phi (\eta)$, and the temperature profile $\theta (\eta)$of the model MHD-NRD for all six scenarios of paradigm, and are shown in Figures 10 and 11. In Figure 10(a,b), the impact of the velocity profiles $g(\eta), \, \, \, f'(\eta)$is quantified for the variation of the velocity slip $\alpha$and the Hartman number $Ha$for scenarios 1-2 of the MHD-NRD model. Figure 10(a) depicts the variant in the velocity slip for velocity distribution. The purpose of the drawing in Figure 10(a) is to investigate the relationship between the velocity field $g(\eta)$and the velocity slip parameter $\alpha$fluctuation. The velocity field $g(\eta)$exhibits a declining tendency as the α values increase. The change in the velocity field ${f}^{\text{'}}\left(\eta \right)$for different Hartman numbers Ha is seen in Figure 10(b). A decrease in the velocity field ${f}^{\text{'}}\left(\eta \right)$is associated with an increase in the Hartman number Ha. In this scenario, a hydrodynamic flow is represented by the Hartman number Ha = 0, whereas a hydromagnetic flow is shown by the Hartman number Ha≠0. Figure 10(c) depicts the variation in the concentration velocity slip for the velocity distribution. It illustrates how a bigger concentration slip parameter results in a smaller concentration distribution. Figure 10(d) shows the effect of the thermal slip parameter $\beta$on the distribution of the temperature $\theta \left(\eta \right)$. An enhancement in the thermal slip parameter $\beta$expositions the reducing performance for the profile of the temperature $\theta \left(\eta \right)$and the associated thickness of the thermal layer. The temperature distribution $\mathit{\theta }\left(\mathit{\eta }\right)$is influenced by the heat generation/absorption parameter $\delta$, as shown in Figure 10(e). In terms of the temperature distribution for the heat generation/absorption parameter $\delta > 0$, it can be seen that $\delta > 0$represents heat generation and $\delta < 0$describes heat absorption. Figure 10(f) depicts the fluctuation in the temperature field $\theta \left(\eta \right)$as the Prandtl number Pr changes. The Prandtl number Pr has been shown to reduce the temperature. Moreover, the Prandtl number Pr refers to the physical ratio of momentum diffusivity to thermal diffusivity. Greater Pr values result in a reduced thermal diffusivity, which is correlated with a reduction in the thermal layer's thickness.

Figure 10.  Assessment of suggested numerical effects using suggested NNB-LMS for MHD-NRD model scenarios 1–6.

DownLoad: Full-Size Img PowerPoint

Figure 11.  Suggested NNB-LMS evaluation with outcomes from absolute error analysis of reference data set for MHV-RPD model scenarios 1–6.

DownLoad: Full-Size Img PowerPoint

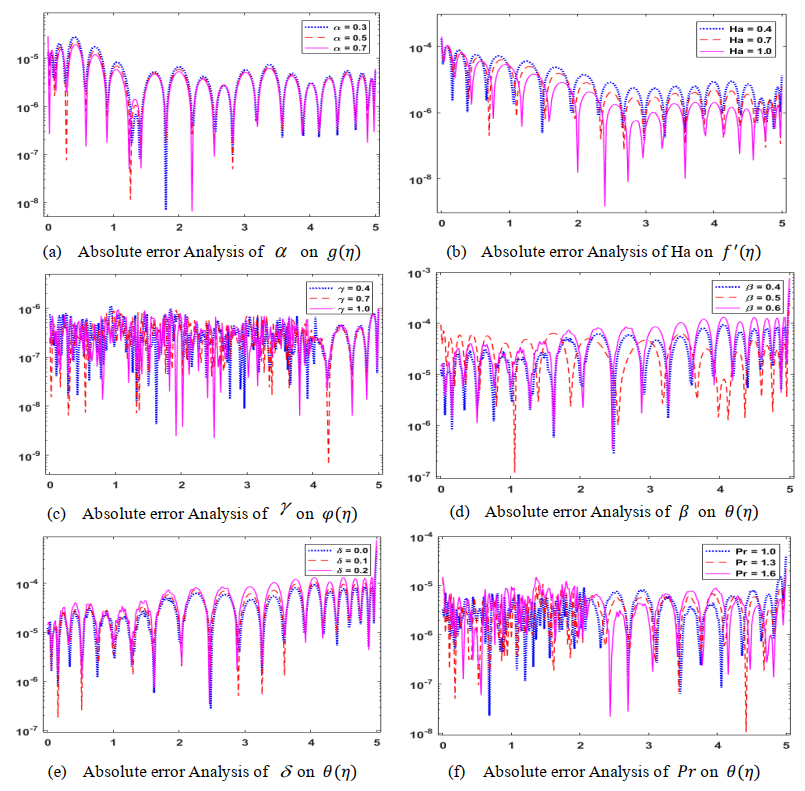
In Figure 11(a,b), the values of the absolute error achieved for the velocities distributions of scenarios 1-2 are ${10^{ - 08}}$to ${10^{ - 05}}$and ${10^{ - 08}}$to ${10^{ - 04}}$, respectively. For the concentration and temperature profiles in Figure 11(c,d), the absolute error values for scenarios 3-4 are approximately ${10^{ - 09}}$to ${10^{ - 06}}$and ${10^{ - 07}}$to ${10^{ - 03}}$, respectively. For the temperature profiles in Figure 11(e,f), the absolute error values for scenarios 5-6 are approximately ${10^{ - 07}}$to ${10^{ - 03}}$and ${10^{ - 08}}$to ${10^{ - 04}}$, respectively. In all of these graphical and numerical examples, the NNB-LMS calculating method solves the MHD-NRD model variations with a sufficient convergent and vigorous production.

All the above discussed parameters have a wide range of applications in real-world physics, which are briefly addressed below. In many fluid flow scenarios, the slip velocity is defined as the difference between the average velocities of two separate fluids flowing through a pipe. Velocity is a measure of motion that begins in one location and continues to another. There are numerous practical uses of velocity; however, one of the most prevalent is to calculate how soon you (or anything in motion) will arrive at a destination from a particular point. As the velocity slip parameter increases, the flow resistance reduces, and therefore the skin friction coefficient drops. It was found that when the velocity slip parameter increased, the velocity profile reduced, as did the skin friction and heat transfer; however, the mass transfer increased. Increasing the thermal slip parameter reduces the heat and mass transfer rates. Sometimes the frictional grip between the belts and pulleys becomes insufficient, thus causing the driver to go ahead without the belt. This is termed belt slip, and subsequently decreases the system's velocity ratio. The Hartmann Number, or Ha, is a key parameter in MHD that expresses the ratio of the induced electrodynamic (magnetic) force to the hydrodynamic force of the viscosity. It describes the effects of a magnetic field on the flow of a viscous, electrically conducting fluid. The Hartmann number is a dimensionless quantity that describes the balance of Lorentz and viscous forces in diffusive magnetic layers generated at the interfaces of materials with varying electric characteristics in the presence of a magnetic field. Physically, increasing the thermal slip parameter increases the rate of the heat transfer. Thermal slip is the relative motion of a fluid and a solid surface in relation to the temperature. Similar to the velocity slip, the no-slip condition is frequently assumed for temperatures at the solid boundary in classical heat transfer issues. A thermal analysis curve is interpreted by correlating the observed property versus the temperature data to chemical and physical processes in the sample. The heat generation/absorption parameter is non-dimensional and is determined by the quantity of heat either created or absorbed in the fluid. Heat is created as a result of current passing through metals, such as electrical conductors and heat produced by the fission and fusion reactions of nuclear fuel. Plants use the thermal energy from sunlight to transform carbon dioxide and water into glucose and oxygen. Cooking an egg involves absorbing heat energy from the pan. Darker hues tend to absorb more light. Because light is energy, absorption raises a material's temperature. Hence, darker materials become more effective heat radiators. It's necessary to remember that an item appears black if it absorbs all colors and white if it reflects them all. The contribution of conduction a heat transfer to the emission of thermal radiation is described by the radiation parameter. It goes without saying that raising the radiation parameter causes the boundary layer's temperature to rise. The primary mechanism that regulates the world's general temperature is the balance between heating brought on by solar thermal radiation entering the globe and cooling brought on by thermal radiation exiting the planet from the earth. As a result, radiation is the only form of heat transfer that does not need the passage of heat via a medium. In heat transfer issues, the Prandtl number determines the relative thickness of the momentum and thermal boundary layers. The Prandtl number is a dimensionless value that represents the ratio of momentum diffusivity to thermal diffusivity, thus demonstrating the significance of fluid movement vs heat transmission in a given issue. It is independent of the kind of flow or flow geometry, yet the flow regime or geometry might have an indirect impact on its analysis. The Prandtl number does not greatly change with pressure; however, it does fluctuate with temperature due to a temperature-dependent kinematic viscosity and thermal diffusivity. The Prandtl number in a boundary layer flow establishes a relationship between the thermal and velocity boundary layer thicknesses. A larger thermal boundary layer results from the thermal diffusion occurring more quickly than the momentum diffusion, as shown by a lower Prandtl number. In thermal equipment, the Lorentz force affects both the temperature field and the velocity magnitude. The mathematical formulas and the physical significance of forces acting on charged particles traveling through an electric and magnetic field-filled environment are explained by Lorentz's force. This is exactly why the Lorentz force is so important. The Lorentz force is applied in the following ways: Lorentz force is used in cyclotrons and other particle accelerators; and Lorentz force is used in a bubble chamber to generate the graph that shows the paths of charged particles. Viscous dissipation is the process by which a fluid's mechanical energy is turned into heat through internal frictional forces. This phenomenon is crucial in high-speed fluid flows because it may have a major impact on the system's temperature distribution and energy balance.

4.   Conclusions

This paper examined the MHD of a viscous nano-liquid flow across a spinning disk with slip effects and heat generation/absorption. At the boundary, slip conditions related to the temperature, concentration, and velocity were enforced and made use of an applied magnetic field. The problem formulation used boundary layer approximations and a low magnetic Reynolds number. The neural network backpropagation with the Levenberg-Marquardt scheme (NNB-LMS) produced numerical solutions. The following is a summary of the study's main findings:

• By employing neural networks, the solution of a mathematical model that exhibited (MHD-NRD) a slip effect was studied using backpropagation with Levenberg-Marquardt approach (NNB-LMS) and an adjustment of certain conditions (scenarios).

• The data set for the (MHD-NRD) model was generated using the RK4 methodology.

• The model was comprised of a range of physical measures, including the Prandtl number, concentration slip parameter, thermal slip parameter, velocity slip parameter, Hartman number, and heat generation/absorption parameter.

• Lower velocities $f'(\eta)$and $g(\eta)$were caused by an increase in the Hartman number Ha and the velocity slip parameter.

• A higher thermal slip value $\beta$was associated with a lower temperature profile; however, a bigger heat generation/absorption parameter $\delta$displayed the reverse tendency.

• As the Prandtl number Pr rose, the temperature field $\theta (\eta)$and the corresponding thickness of the thermal layer decreased.

• A weaker concentration profile was represented by a larger concentration slip parameter.

• A number of variants of the dataset were modified using NNB-LMS for testing, validation, and training, thereby utilizing 10%, 10%, and 80%, of the data set, respectively, to create the MHD-NRD reference dataset.

• The scheme's aptitude received a rating between a ${10}^{-9}to{10}^{-12}$for both the suggested and the reference consequences.

• Furthermore, we obtained some statistical data of the model using the NNB-LMS scheme including the mean square error, gradient, performance, and Mu.

Author contributions

Y.J. and H.Y Conceptualization, W.U.J; formal analysis, A.A. investigation, M.M.A. project administration, A.A. validation, visualization, H.Y. writing-review & editing; M.M.A; Data curation, H.Y. resources, Y.J; validation, H.Y. software, H.Y. visualization, W.U.J; resources, H.Y. project administration, H.Y. writing-review & editing, H.Y. funding. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (KFU242319).

Acknowledgments

This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (KFU242319).

Conflict of interest

The authors declare that they have no conflicts of interest.