Weighted energy method and long wave short wave decomposition on the linearized compressible Navier-Stokes equation

1.   Introduction

A cyber-physical system (CPS) is a sophisticated, multi-layered system that combines computing, networking, and the physical environment ^[1]. By leveraging the integrated collaboration features of computation, communication, and control (3C) technology, it is possible to achieve real-time monitoring, control, and information services for large-scale engineering systems ^[2]. The applications of a CPS are wide-ranging. In study ^[3], the existing research on insider threat detection in a CPS is thoroughly reviewed and discussed. In ^[4], the problem of observer-based adaptive resilient control for a class of nonlinear CPSs is studied, taking the sensors that are vulnerable to deception attacks into account. The study in ^[5] focuses on the challenge of security control for CPSs subjected to aperiodic denial-of-service attacks. To reduce the need for explicit communication, the semantic knowledge within a CPS is leveraged, especially the use of physical radio resources to transmit potential informative data ^[6]. As discussed in ^[7], CPSs are vulnerable to numerous attacks and their attack surface continues to expand. To summarize, there are two key features of a CPS ^[8]: (ⅰ) large-scale, intricate systems focused on physical, biological, and engineering domains; (ⅱ) a network core that includes communication networks and computing resources for monitoring, coordinating, and controlling these physical systems. A CPS closely integrates these two essential components, enabling analysis and design within a unified framework.

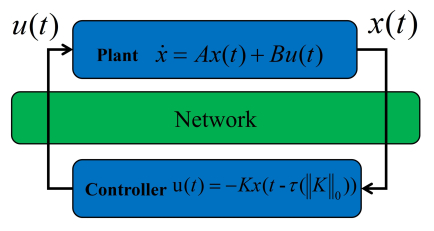
Over the past two decades, extensive research has been conducted on control theory related to the CPS. Traditional CPS control designs, however, often produce dense feedback matrices, with the optimal controller relying on all the information within the feedback matrix ^[9]. In extensive networks, implementation costs can be considerable, and the computational load required for communication between the controller and the dynamical system can be heavy ^[10]. Two idealistic assumptions are embedded in traditional CPS control designs: communication costs are infinite, and the communication network is solely reserved for control purposes ^[11]. In reality, however, network operators typically prefer sparse communication topologies to reduce costs, and the shared usage of the communication network by various users commonly leads to feedback delays ^[12]. To address this issue, we propose a CPS system with a static state feedback controller $ u(t) = -Kx(t-\tau) $, where $ K\in \mathbb{R}^{m\times n} $ and $ \tau $ represents the delay, which can be either constant or variable, and is introduced by the communication process between the state $ x $ and the computation of the input $ u $ ^[2]. The network control design presented in this paper aims to achieve a balance between two primary objectives: (ⅰ) system performance, represented by the traditional cost function $ J^{0}(K) $, and (ⅱ) the sparsity of the communication network. Thus, in this paper, we seek to solve the following problem: for a given CPS system, identify a feedback matrix $ K $ that balances system performance with controller sparsity.

Sparsity refers to a situation where the majority of elements in a vector or matrix are zero. The sparsity of a vector or matrix is characterized by its $ l_{0} $-norm. Sparsity is crucial in large-scale optimization problems, such as sound field reconstruction ^[13]. Employing sparsity not only minimizes storage requirements but also cuts transmission costs through vector compression. It streamlines a complex problem by extracting and using only the essential information from large datasets. In the absence of consideration for network topology, maximizing the sparsity of the feedback matrix typically has several reasons: (ⅰ) A sparse feedback matrix means that the controller only focuses on a small subset of variables in the system. This can significantly reduce the computational load and improve the responsiveness of real-time control, especially in large-scale systems. (ⅱ) Sparse control strategies can decrease the number of required sensors and actuators, thus reducing the overall system cost and energy consumption. This is particularly important in resource-constrained environments. (ⅲ) Sparse matrices often lead to simpler and more understandable control decisions. This can help designers more easily analyze and comprehend control strategies, making debugging and optimization processes more effective. (ⅳ) Sparsity may enhance the system's tolerance to failures of certain components. If some sensors or actuators fail, the system can still maintain functionality through other effective connections. (ⅴ) In some cases, sparse control strategies can exhibit better robustness to noise and disturbances, as they rely only on key parts of the system, reducing sensitivity to the overall system state.

Currently, sparse optimization has been extensively applied in various fields such as blade tip timing ^[14], robotic machining systems ^[15], and perimeter control ^[16,17]. Sparse optimization models can be generally categorized into two types ^[18]: (ⅰ) $ l_{0} $-regularization optimization problems modifying the traditional objective function by incorporating the $ l_{0} $-norm into a new objective function, and (ⅱ) sparse constrained optimization problems including the $ l_{0} $-norm within the constraints. However, both types of problems are NP-hard. In earlier studies, methods for solving the $ l_{0} $-norm minimization problem are typically categorized into model transformation techniques and direct processing techniques. The common feature of the model transformation method is to approximate the $ l_{0} $-norm with the $ l_{1} $-norm ^[19]. In terms of algorithms, several methods have been studied, including the iterative hard-thresholding algorithm (IHTA) ^[20], fast iterative shrinkage-thresholding algorithm (FISTA) ^[21], augmented method (ALM) ^[22], and alternating direction method of multipliers (ADMM) ^[23].

IHTA has two advantages as follows ^[20]: (ⅰ) It is straightforward to implement, making it accessible for various applications; and (ⅱ) it effectively promotes sparsity in solutions, which is beneficial in many signal processing and statistical tasks. There exists two disadvantages for IHTA as follows ^[20]: (ⅰ) It can converge slowly, especially for large-scale problems; and (ⅱ) it may struggle with nonsmooth functions, limiting its applicability in some optimization scenarios. FISTA offers two key benefits ^[21]: (ⅰ) It significantly accelerates the convergence compared to IHT by using Nesterov's acceleration, making it suitable for large datasets; and (ⅱ) it can handle a variety of loss functions and regularization terms, providing versatility in applications. FISTA has two drawbacks, outlined below ^[21]: (ⅰ) The implementation is more complex than IHT, requiring careful tuning of parameters; and (ⅱ) it may require more memory for storing additional variables, which could be a concern for very large problems. ALM has two notable benefits, listed below ^[22]: (ⅰ) It is effective for problems with constraints, making it a good choice for constrained optimization; and (ⅱ) it generally exhibits robust convergence properties, especially for nonconvex problems. ALM presents two notable drawbacks, detailed below ^[22]: (ⅰ) The performance heavily depends on the choice of parameters, which can be challenging to optimize; and (ⅱ) the method can be computationally intensive, particularly for high-dimensional problems. ADMM offers two key advantages, as outlined below ^[23]: (ⅰ) It allows large problems to be decomposed into smaller subproblems, which can be solved more easily; and (ⅱ) it handles a wide range of objective functions and constraints, making it versatile for various applications. ADMM comes with two significant downsides, as outlined below ^[23]: (ⅰ) While it has good convergence properties, it can sometimes converge slowly compared to other methods; and (ⅱ) like ALM, the performance can be sensitive to the choice of parameters, requiring careful tuning.

Optimal sparse control theory is now well developed. In ^[24], it explores the optimal control problem involving sparse controls for a Timoshenko beam, including its numerical approximation using the finite element method and its numerical solution through nonsmooth techniques. In ^[25], the study is focused on sparse optimal control for continuous-time stochastic systems using a dynamic programming approach, analyzing the optimal control through the value function. In ^[26], the study aims to develop a sparse tube-based robust economic model predictive control scheme. In ^[27], a novel sparse control strategy for acidic wastewater sulfidation is presented to ensure the continuous and safe HSS process. In ^[28], the construction of an eigenfunction vector of the Koopman operator is based on the sparse control strategy. However, for the CPS system with varying delay, these methods in ^{[24,25,26,27,28]} are not sufficient to determine an optimal sparse control policy. In this paper, we first demonstrate the existence of the partial derivatives of the system state with respect to the elements of the feedback matrix, and then use this to show that the gradient of the cost function can be computed by solving the state system and a variational system forward in time. In this case, our optimal control policy would be more straightforward and efficient for real-world applications compared to the methods in ^[24,25] depending on the numerical approximation, which could introduce a gap between the real and the approximated control policy.

Many existing optimal sparse control theories for the CPS assume constant delays, which can oversimplify the dynamics of a CPS where delays are often variable and unpredictable. This can lead to suboptimal control strategies that do not account for the true nature of system behavior. Sparse control with feedback delay plays a vital role in the CPS. (ⅰ) Effective control strategy design is essential in the CPS. Sparse control can optimize input signals, particularly when there are limited sensors and actuators or when energy efficiency is a priority. It is also important to account for feedback delays in the control algorithms to prevent potential instability. (ⅱ) The CPS generally requires immediate responses, but feedback delays necessitate that control strategies be equipped to mitigate their effects. By simplifying control signals, sparse control can improve responsiveness while ensuring that performance remains stable despite these delays. (ⅲ) Additionally, sparse control can help minimize the need for computational power and communication bandwidth in the CPS environments. The optimal control of communication networks described previously only considers the system cost. However, network operators frequently opt for sparse communication topologies to lower costs. With this in mind, to determine the optimal feedback control matrix $ K $, we propose a sparse optimal control (SOC) problem based on the CPS system with varying delay, aiming to minimize the sparsity of the controller subject to a maximum allowable compromise in system cost. A penalty method is employed to convert the SOC problem into a problem that is constrained only by box constraints. A smoothing technique is applied to approximate the nonsmooth component in the resulting problem. Subsequently, an analysis of the errors introduced by the smoothing technique is conducted. The gradients of the objective function with respect to the feedback control matrix are determined by solving both the state system and a variational system forward in time. Building upon the piecewise quadratic approximation ^[29], an optimization algorithm is developed to address the resulting problem. Finally, the paper provides the outcomes of the simulations.

The rest of the paper is organized as follows. We first describe the SOC problem based on the CPS system in Section 2. In Section 3, we develop an optimization algorithm to solve the SOC problem. Finally, a numerical example is given in Section 4.

2.   Problem formulation

2.1.   CPS modeling

Let $ I_n $ be the set of $ \{1, 2, ..., n\}. $

2.1.1.   Linear time-invariant system

We consider the following linear time-invariant (LTI) system ^[2]:

where $ x\in \mathbb{R}^{n} $ is the state and $ u\in \mathbb{R}^{m} $ is the control input. $ A\in \mathbb{R}^{n\times n} $ and $ B\in \mathbb{R}^{n\times m} $. Assume that $ (A, B) $ is controllable.

2.1.2.   Feedback control system with varying delay $ \tau(\|K\|_{0}) $

Two idealistic hypotheses are involved in conventional CPS control designs: that communication costs are unlimited and that the communication network is exclusively allocated for control purposes. In practice, however, network operators often favor sparse communication topologies to minimize costs, and the shared use of the same communication network by multiple users frequently results in feedback delay.

After the sparsity level of matrix $ K\in \mathbb{R}^{m\times n} $ is achieved, the bandwidth $ c $ is equally redistributed among the remaining links. Assume that the communication network follows frequency division multiplexing. Then, delay $ \tau $ can be defined by ^[2]:

where $ \|K\|_{0} $ denotes the number of nonzero elements in $ K $, and $ \kappa: \mathbb{R}\rightarrow \mathbb{R} $ is a positive function. Eq (2.1) implies that $ \tau $ will change as $ \|K\|_{0} $ changes. This change is captured by the function $ \mathcal Z(\cdot):\mathbb{R}\times \mathbb{R}\times \mathbb{R}\rightarrow \mathbb{R} $. The transmission of state $ x_l $ for the computation of input $ u_i $ is anticipated to encounter a delay denoted as $ \tau_{il} $ (expressed in seconds), $ i\in I_m, l\in I_n. $ This delay comprises two distinct components: $ \tau_{il} = \tau_{p_{il}} +\tau_{t_{il}} $, where $ \tau_{p_{il}} $ denotes the propagation delay, and $ \tau_{t_{il}} $ represents the transmission delay. The parameter $ \tau_{p_{il}} $ is characterized as the quotient of the link length divided by the speed of light, assumed to possess a uniform value denoted as $ \tau_{p} $ across all pairs $ i, l $. Our assumption posits an equal allocation of bandwidth for the communication link connecting any $ l_{th} $ sensor to any $ i_{th} $ actuator. Consequently, this implies that $ \tau_{t_{il}} $ maintains a uniform value across all $ i, l $ pairs ^[2]. Henceforth, we denote $ \tau_{il} $ uniformly as $ \tau $ across all pairs $ i, l $. In practice, potential deviations of $ \tau_{il} $ from the designated $ \tau $ due to variations in traffic and uncertainties within the network are acknowledged.

This controller will be deployed in a distributed manner utilizing a communication network, as depicted in Figure 1. This figure presents the CPS represented by a closed-loop system architecture. The $ i $th control input is written as $ u_i(t) = -\sum_{l = 1}^nK_{il} x_l(t-\tau(\|K\|_0)), i\in I_m. $ Then accordingly the closed-loop system is written as:

where $ \nu\in \mathbb{R}^{n} $ is a given vector, where each of its elements is assumed, without loss of generality, to be 0.5; and $ \tilde{x}(t) $ denotes $ x(t-\tau(\|K\|_0)) $. Let $ x(\cdot|K) $ be the solution of system (2.2) corresponding to the feedback matrix $ K\in \mathbb{R}^{m\times n} $.

2.2.   Problem statement

2.2.1.   Traditional optimal control problem

With reference to the delay mentioned above, we introduce the corresponding system cost as given below ^[30]:

where $ T $ is the final time, the matrix $ W\in \mathbb{R}^{m\times m} $ is symmetric positive definite, the feedback controller $ u = -Kx(t-\tau(\|K\|_0)) $, and the matrices $ S\in \mathbb{R}^{n\times n} $ and $ Q\in \mathbb{R}^{n\times n} $ are symmetric positive semidefinite.

We now present the feedback optimal control problem as follows.

where $ J^0(K) $ is given by (2.3).

2.2.2.   Sparse optimal control problem

Gradient-based optimization methods ^[31] can be used to solve Problem $ \mathbf{P_{1}} $. Let $ K_1^{*}\in \mathbb{R}^{m\times n} $ be the optimal feedback matrices for Problem $ \mathbf{P_{1}} $. However, these matrices tend to be rather dense, and for large networks, the implementation cost will be expensive. Furthermore, the computation burden of the controller will be high because the state information is required to be transmitted through the communication network. Thus, we introduce the following Problem $ \mathbf{P_{2}} $ given by

where $ \|K\|_{0} $ denotes the number of nonzero entries of the feedback matrix $ K\in \mathbb{R}^{m\times n} $, $ J^0(K) $ is given by (2.3), and $ J^{0}(K_1^{*}) $ is the benchmark optimal system cost obtained through solving Problem $ \mathbf{P_{1}} $. $ \varepsilon $ is a small number that is used to ensure that the system cost is not greatly affected during the sparsity process of the feedback matrix $ K\in \mathbb{R}^{m\times n} $.

Obviously, Problem $ \mathbf{P_{2}} $ balances system performance and the sparse level of the the feedback matrix $ K\in \mathbb{R}^{m\times n} $.

3.   Computational approaches

3.1.   Preconditioning algorithm: the approximation of $ \|\mathrm{K}\|_{0} $

The feedback matrix $ K $ is decomposed as $ n $ column vectors, i.e., $ K = (K^{1}, K^{2}, \ldots, K^{n}) \in \mathbb{R}^{m\times n} $. Note that $ \|K^{l}\|_{0}, l\in I_n, $ regularization is NP-hard. Thus, it is difficult to solve. In the past two decade, many approximation methods, such as $ \|K^{l}\|_{1} $ and $ \|K^{l}\|_{q}^{q}\ (0 < q < 1) $ have been proposed. In ^[29], the $ l_{0} $-norm of the vector is approximated by a piecewise quadratic approximation (PQA) method. In this paper, we shall extend PQA to spare the feedback matrix $ K $.

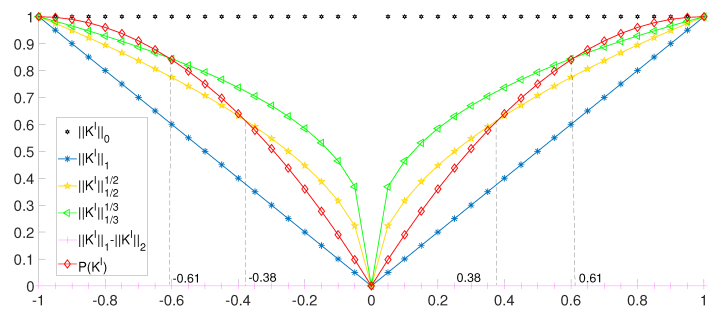
Remark 1. We shall illustrate that $ P(K^{l}), l\in I_n, $ performs better than other common approximations of $ \|K^{l}\|_{0}, l\in I_n, $ on $ [-e, e] $, $ e = \{1, 1, \ldots, 1\}\in \mathbb{R}^{m} $.

For $ l\in I_n, $ Figure 2 shows the approximation effects of $ \|K^{l}\|_{1} $, $ \|K^{l}\|_{1/2}^{1/2} $, $ \|K^{l}\|_{1/3}^{1/3} $, $ \|K^{l}\|_{1}-\|K^{l}\|_{2} $, and $ P(K^{l}) $ for the one-dimensional case in [–1, 1] ^[29]. Obviously, for $ l\in I_n, $ $ P(K^{l}) $ is superior to $ \|K^{l}\|_{1} $ for approximating the $ l_{0} $-norm when $ |K_i^{l}|\leq 1, i\in I_m. $ For $ l\in I_n, $ when $ 0.38 \leq |K_i^{l}| \leq 1, i\in I_m, $ $ P(K^{l}) $ gives a better approximation for $ \|K^{l}\|_{0} $, and when $ 0.61 \leq |K_i^{l}| \leq 1, i\in I_m, $ $ P(K^{l}) $ is better than $ \|K^{l}\|_{1/3}^{1/3} $. Also, for $ l\in I_n, $ $ P(K^{l}) $ is superior to $ \|K^{l}\|_{1}-\|K^{l}\|_{2} $, which is identically equal to 0 and has a large gap with $ \|K^{l}\|_{0} $ in [–1, 1].

On this basis, we use the piecewise quadratic function ^[29] to approximate $ \|\mathrm{K}^{l}\|_{0} $ over $ [-e, e] $.

If we choose $ f(K^{l}) = -\|\mathrm{K}^{l}\|^{2}_{2} $ and $ g(K^{l}) = 2\|\mathrm{K}^{l}\|_{1} $, then

where $ g $ is a proper closed convex and possibly nonsmooth function; $ f $ is a smooth nonconvex function of the type $ C^{1, 1}_{L_{f}}(\mathbb{R}^{n}) $, i.e., continuously differentiable with Lipschitz continuous gradient

with $ L_{f} > 0 $ denoting the Lipschitz constant of $ \nabla f $.

Based on the piecewise quadratic approximation ^[29], Problem $ \mathbf{P_{2}} $ can be approximated as given below:

where $ J^0(K) $, $ J^{0}(K_1^{*}) $, and $ \varepsilon $ are defined in Problem $ \mathbf{P_{2}} $.

3.2.   Smoothing the objective function $ F(K) $

Since the objective function $ F(K) $ is nonsmooth, it is difficult to solve $ \rm{Problem} \mathbf{\; P_{3}} $ by using gradient-based algorithms. To overcome this difficulty, we aim to find a smooth function for the objective function $ F(K) $ described in $ \rm{Problem} \mathbf{\; P_{3}} $.

First, we introduce the following notation: for $ x, y, z\in \mathbb{R}^{m} $,

Lemma 1. If we define that $ p(K^{l}_i) = \max\{K^{l}_i, 0\} $ and $ q(K^{l}_i) = \max\{-K^{l}_i, 0\} $, then the following properties are satisfied:

(1) $ K^{l}_i $ = $ p(K^{l}_i)-q(K^{l}_i) $, $ i\in I_m, l\in I_n; $ and

(2) $ \|K^{l}\|_{1} = \sum^{m}_{i = 1}[p(K^{l}_{i})+q(K^{l}_{i})] $, $ l\in I_n $.

Proof. (1) For $ l\in I_n $, and $ i\in I_m $, we have

which imply that $ K^{l}_{i} = {p(K^{l}_{i})-q(K^{l}_{i})}, i\in I_m, l\in I_n $.

(2) For $ l\in I_n $, and $ i\in I_m $, we get

which prove that $ \|K^{l}\|_{1} = \sum\limits^{m}_{i = 1}|K^{l}_{i}| = \sum\limits^{m}_{i = 1}[p(K^{l}_{i})+q(K^{l}_{i})] $.

Based on Lemma 1, we obtain

Then $ \rm{Problem} \mathbf{\; P_{3}} $ is equivalent to the following problem:

where

Clearly, the function $ \max\{x, 0\} $ is nondifferentiable with respect to $ x $ at $ x = 0 $. Thus, in order to smooth it, a smooth function $ \phi(x, \sigma) $ ^[32] is introduced as follows:

where $ \sigma > 0 $ is an adjustable smooth parameter.

Lemma 2. For any $ x\in R $ and $ \sigma > 0 $, the smooth function $ \phi(x, \sigma) $ has the following properties:

(1) $ \lim_{\sigma\rightarrow0^{+}}{\phi(x, \sigma)} = \max\{x, 0\} $,

(2) $ \phi(x, \sigma) > 0 $,

(3) $ 0 < \phi^{\prime}(x, \sigma) = \frac{1}{2}\Big(\frac{x}{\sqrt{x^{2}+4\sigma^{2}}}+1\Big) < 1 $,

(4) $ 0 < \phi(x, \sigma)-\max\{x, 0\}\leq\sigma $.

Lemma 2 shows that the function $ \phi(x, \sigma) $ is an effective smooth approximation for the function $ \max\{x, 0\} $, and the approximation level can be controlled artificially by adjusting the value of smooth parameter $ \sigma $.

Therefore, $ \rm{Problem} \mathbf{\; P_{4}} $ can be approximated by the following problem:

where

Note that the function $ F_{2}(K) $ is continuously differentiable. Thus, $ \rm{Problem} \mathbf{\; P_{5}} $ is a constrained optimal parameter selection problem, which can be solved efficiently by using any gradient-based algorithm.

3.3.   The relationship between Problem $ \mathbf{P}_4 $ and Problem $ \mathbf{P}_5 $

Theorem 1 presents that the optimal solution of $ \rm{Problem} \mathbf{\; P_{5}} $ is also the optimal solution of $ \rm{Problem} \mathbf{\; P_{4}} $ as long as $ \sigma\rightarrow0 $ and an error estimation between the solutions of $ \rm{Problem} \mathbf{\; P_{4}} $ and $ \rm{Problem} \mathbf{\; P_{5}} $ is given.

Lemma 3. For any $ \sigma > 0 $, one has

Proof. By using Lemma 2, one has

and

Thus,

This completes the proof of Lemma 3.

Theorem 1. Let $ K_{4} $ and $ K_{5} $ be the optimal solutions of $ \rm{Problem} \mathbf{\; P_{4}} $ and $ \rm{Problem} \mathbf{\; P_{5}} $, respectively. Then, we have

Proof. By using Lemma 3, one has

Note that $ K_{4} $ is the optimal solution of $ \rm{Problem} \mathbf{\; P_{4}} $. Then, we have

which indicates that

Note that $ K_{5} $ is the optimal solution of $ \rm{Problem} \mathbf{\; P_{5}} $. Then, we have

which indicates that

Then, we have $ 0 < F_{2}(K_{5})-F_{1}(K_{5})\leq F_{2}(K_{5})-F_{1}(K_{4}) \leq F_{2}(K_{4})-F_{1}(K_{4})\leq4mn\sigma $, which implies that

This completes the proof of Theorem 1.

Remark 2. Theorem 1 shows that the optimal solution of Problem $ \mathbf{\; P_{5}} $ is an approximate optimal solution of Problem $ \mathbf{\; P_{4}} $, as long as the adjustable parameter $ \sigma $ is sufficiently small.

3.4.   Penalty function method

The inequality constraint $ |J^{0}(K)-J^{0}(K_1^{*})|\leq \varepsilon $ is equivalent to

and equivalent to

and

Then, by using the idea of the penalty function method described by ^[31], the equality constraints (3.1) and (3.2) are appended to the objective function of $ \rm{Problem} \mathbf{\; P_{5}} $ to form an augmented objective function. Thus, a penalty problem can be defined as follows:

where

with $ \gamma_{1} $ and $ \gamma_{2} $ being the penalty parameters. It is important to note that violations of the equality constraints in Eqs (3.1) and (3.2) are addressed through the integral term $ G^{0}(K) $ in $ \rm{Problem} \mathbf{\; P_{6}} $. It can be demonstrated that by selecting sufficiently high values for $ \gamma_{1} $ and $ \gamma_{2} $, any minimizer of $ G^{0}(K) $ in $ \rm{Problem} \mathbf{\; P_{6}} $ within the region defined by $ \gamma_{1} > \gamma^* $ and $ \gamma_{2} > \gamma^* $ (where $ \gamma^{*} $ denotes the threshold for the penalty parameters) will also satisfy the feasibility conditions of $ \rm{Problem} \mathbf{\; P_{5}} $. Therefore, a feasible solution to $ \rm{Problem} \mathbf{\; P_{5}} $ can be effectively found by minimizing $ G^{0}(K) $ in $ \rm{Problem} \mathbf{\; P_{6}} $ with appropriately chosen penalty values for $ \gamma_{1} $ and $ \gamma_{2} $.

By adopting the function $ \phi(x, \sigma) $ to approximate the function $ \max\{x, 0\} $ again, $ \rm{Problem} \mathbf{\; P_{6}} $ can be written as the following problem:

where

Note that the function $ G(K) $ is continuously differentiable. Thus, $ \rm{Problem} \mathbf{\; P_{7}} $ is an unconstrained optimal parameter selection problem, which can be solved efficiently by using any gradient-based algorithm.

3.5.   The relationship of Problem $ \mathbf{P_5} $, Problem $ \mathbf{P_6} $, and Problem $ \mathbf{P_7} $

Theorem 2 shows that the optimal solution of $ \rm{Problem} \mathbf{\; P_{7}} $ is also the optimal solution of $ \rm{Problem} \mathbf{\; P_{6}} $ as long as $ \sigma\rightarrow0 $ and an error estimation between the solutions of $ \rm{Problem} \mathbf{\; P_{5}} $ and $ \rm{Problem} \mathbf{\; P_{7}} $ is given.

Definition 1. A control input $ K_{7} $ is $ \sigma $-feasible to Problem $ \mathbf{P_7} $, if the control input $ K_{7} $ satisfies the following inequality constraint:

Lemma 4 and Theorem 2 are the variations of Lemma 3 and Theorem 1, respectively.

Lemma 4. For any $ \sigma > 0 $, one has

where $ 0 < \gamma_{1} $ and $ \gamma_{2} < 1 $ are the penalty parameters.

Proof. By using Lemma 2, we have

and

Thus, we have

This completes the proof of Lemma 4.

Theorem 2. Let $ K_{6} $ and $ K_{7} $ be the optimal solutions of $ \rm{Problem} \mathbf{\; P_{6}} $ and $ \rm{Problem} \mathbf{\; P_{7}} $, respectively. Then, we have

Proof. By using Lemma 4, one has

Note that $ K_{6} $ is the optimal solution of $ \rm{Problem} \mathbf{\; P_{6}} $. Then, we have

which indicates that

Note that $ K_{7} $ is the optimal solution of $ \rm{Problem} \mathbf{\; P_{7}} $. Then, we have

which indicates that

Then, $ 0 < G(K_{7})-G_{0}(K_{7})\leq G(K_{7})-G_{0}(K_{6}) \leq G(K_{6})-G_{0}(K_{6})\leq(\gamma_{1}+\gamma_{2})\sigma $, which implies that

This completes the proof of Theorem 2.

Remark 3. Theorem 2 shows that the optimal solution of $ \rm{Problem} \mathbf{\; P_{7}} $ is an approximate optimal solution of $ \rm{Problem} \mathbf{\; P_{6}} $, as long as the adjustable parameter $ \sigma $ is sufficiently small.

Then, we can obtain the following theorem.

Theorem 3. Let $ K_{6} $ and $ K_{7} $ be the optimal solutions of $ \rm{Problem} \mathbf{\; P_{6}} $ and $ \rm{Problem} \mathbf{\; P_{7}} $, respectively. If $ K_{6} $ is feasible to $ \rm{Problem} \mathbf{\; P_{5}} $ and $ K_{7} $ is $ \sigma- $feasible to $ \rm{Problem} \mathbf{\; P_{5}} $, then we obtain

Proof. Note that $ K_{6} $ is feasible to $ \rm{Problem} \mathbf{\; P_{5}} $. Then, one has

and

Then, we have $ J^{0}(K)-J^{0}(K_1^{*})-\varepsilon\leq0 $ and $ -J^{0}(K)+J^{0}(K_1^{*})-\varepsilon\leq0 $. Note that $ K_{7} $ is $ \sigma $-feasible to $ \rm{Problem} \mathbf{\; P_{5}} $ in Definition 1 and the smooth function $ \phi(x, \sigma) $ is strictly monotone increasing (the first derivative is positive, see Lemma 1(3)). Thus, we obtain

and

By using Lemma 2(2) that $ \phi(x, \sigma) > 0 $, we obtain

Based on Theorem 2, we have

Thus, we get

This completes the proof of Theorem 3.

Remark 4. If $ \gamma_1 $ and $ \gamma_2 $ are greater than the threshold value $ \gamma^{*} $, the optimal solution of $ \rm{Problem} \mathbf{\; P_{6}} $ is the exact optimal solution of $ \rm{Problem} \mathbf{\; P_{7}} $ ^[31]. Furthermore, Theorem 3 provides an error estimation between the solutions of $ \rm{Problem} \mathbf{\; P_{5}} $ and $ \rm{Problem} \mathbf{\; P_{7}} $ as long as $ \gamma_1 > \gamma^{*} $ and $ \gamma_2 > \gamma^{*} $. Thus, the approximate optimal solution of $ \rm{Problem} \mathbf{\; P_{5}} $ can be achieved by solving $ \rm{Problem} \mathbf{\; P_{7}} $. Note that we have proved that the optimal solution of $ \rm{Problem} \mathbf{\; P_{5}} $ is also the optimal solution of $ \rm{Problem} \mathbf{\; P_{4}} $ as long as the adjustable smooth parameter $ \sigma $ is sufficiently small, and $ \rm{Problem} \mathbf{\; P_{4}} $ and $ \rm{Problem} \mathbf{\; P_{3}} $ are equivalent. Thus, the approximate optimal solution of $ \rm{Problem} \mathbf{\; P_{3}} $ can be achieved by solving $ \rm{Problem} \mathbf{\; P_{7}} $.

3.6.   Gradient formulae

Note that the cost function $ G(K) $ in Problem $ \mathbf{P_7} $ is continuously differentiable. Thus, $ \rm{Problem} \mathbf{\; P_{7}} $ is an unconstrained optimal parameter selection problem, which can be solved efficiently by using any gradient-based algorithm. Since the functionals depend implicitly on the feedback matrix $ K $ via system (2.2), it is important to derive an effective computational procedure for calculating the gradient of the cost function $ G(K) $ in Problem $ \mathbf{P_7} $.

3.6.1.   The gradients of $ x(\cdot|K) $ with respect to the feedback matrix

In this subsection, we investigate the gradients of $ x(\cdot|K) $ with respect to the feedback matrix. Define

Then, $ 0\in \Theta $ and $ \epsilon \in \Theta \Leftrightarrow K+\epsilon E_{i}^l \in \Theta. $ For each $ \epsilon \in \Theta $, define

and

Clearly,

Then we have the following lemmas.

Lemma 5. There exists a positive real number $ L_{1} > 0 $ such that for all $ \epsilon \in \Theta $, we have

Lemma 6. There exists a positive real number $ L_{2} > 0 $ such that for all $ \epsilon \in \Theta $, we have

The partial derivatives of the system state with respect to the feedback matrix are given in Theorem 4.

Theorem 4. Let $ t \in (0, T] $ be a fixed time point. Then $ x(t|\cdot) $ is differentiable with respect to $ K_{i}^l $ on [$ - $1, 1]. Moreover, for each $ K_{i}^l $, we have

where $ \Lambda_{i}^l(\cdot|K), i\in I_m, l\in I_n, $ is the solution of the following auxiliary system:

Proof. Let $ K_{i}^l\in[-1, 1], i\in I_m, l\in I_n, $ be arbitrary but fixed. For each $ \epsilon \in \Theta $, define the following functions:

where $ E_{i}^l $ denotes the matrix in which the elements in row $ i $ and column $ l $ are 1 and the rest are 0.

Based on Lemmas 5 and 6 and the continuous differentiability of the functions $ f $, we can obtain that there exist two constants $ M_{1} > 0 $ and $ M_{2} > 0 $ such that

where $ \|\cdot\| $ denotes the natural matrix norm on $ \mathbb{R}^{n\times n} $. In addition, by Lemmas 5 and 6, the following limits exist uniformly with respect to $ \eta\in[0, 1] $:

Thus, for each $ \delta > 0 $, there exists an $ \epsilon^{1} > 0 $ such that for all $ \epsilon $ satisfying $ |\epsilon| < \epsilon^{1} $,

and

Thus, it follows from Lemma 6 that

Now, let $ \delta > 0 $ be arbitrary but fixed and choose $ \epsilon \in \Theta $ such that $ 0 < |\epsilon| < \epsilon^{1} $. Then, by the chain rule, we have

Recall that $ t \in(0, T] $ is a fixed time point. Then, by the fundamental theorem of calculus, we get

Thus, the chain rule follows:

Note that we have

Substituting (3.5)–(3.7) into (3.4) gives

Note that

Then multiplying (3.8) by $ \epsilon^{-1} $, subtracting (3.9), taking the norm of both sides, and finally applying (3.3) yields

Also, we know that $ \varphi^{\epsilon}(t) = 0, t\leq0 $, $ \Lambda_i^l(s) = 0, s\leq0 $, and then the last integral term on the right-hand side of (3.10) can be simplified as follows:

Thus, (3.10) becomes

By the Gronwall-Bellman lemma, it follows that

which holds whenever $ 0 < |\epsilon| < \epsilon^{1} $. Since $ \delta $ is arbitrarily chosen, we conclude that $ \epsilon^{-1}\varphi^{\epsilon}(t)\rightarrow \Lambda_i^l(t|K) $ as $ \epsilon\rightarrow 0 $.

Then, we get

Because of

we obtain

thereby completing the proof.

We now present the following algorithm for computing the cost function of $ \rm{Problem} \mathbf{\; P_{7}} $ and its gradient at a given controller $ K $.

3.6.2.   The cost function with respect to the feedback matrix

Based on Theorem 4 and the chain rule, we have:

Theorem 5. The gradients of the cost function $ G(K) $ with respect to $ K_i^l, i\in I_m, l\in I_n, $ is given by

where

Then, $ \rm{Problem} \mathbf{\; P_{7}} $ can be solved efficiently by using any gradient-based algorithm based on Theorem 5.

4.   Numerical results

4.1.   Experiment design

In this section, all computational experiments are carried out in MATLAB R2021a on a computer with a 3.70 GHz Intel Core i9-10900K CPU243 and 32.0GB RAM. The Euler method is used to solve system (2.2) with a step size of $ 1/10 $, and the initial time and terminal time are $ 0 $ and $ 1 $, respectively. We consider the 10th-order.

We use the gradient-based methods described in ^[31] for solving Problem $ \mathbf{P_{1}} $ to obtain the optimal dense feedback matrix denoted by $ K_1^{*} $. Then, through the application of Algorithm 1, we solve Problem $ \mathbf{P_{7}} $ to obtain the optimal sparse feedback matrix $ K_2^{*} $.

To indicate the sparse level of the feedback matrix $ K $, we define the following indicator:

which represents the proportion of nonzero elements in the matrix. Obviously, a smaller value of $ r $ means a better sparse level of $ K $.

4.2.   Experiment 1

Based on empirical data, we consider a 10-th order LTI system with a state matrix

Assume that $ B = R = Q = E_{10} $, $ S = \mathbf{0}\in \mathbb{R}^{10\times 10} $, and $ \varepsilon = 0.1 $. The cost function is given by ^[30]:

where $ u = -Kx(t-\tau(\|K\|_0)) $.

4.3.   Experiment 2

Based on empirical data, we consider another 10th-order LTI system with a state matrix

Assume that $ B = R = Q = E_{10} $, $ S = \mathbf{0}\in \mathbb{R}^{10\times 10} $, $ \varepsilon = 0.1 $. The cost function is given by ^[30]:

where $ u = -Kx(t-\tau(\|K\|_0)) $.

4.4.   Experiment analysis

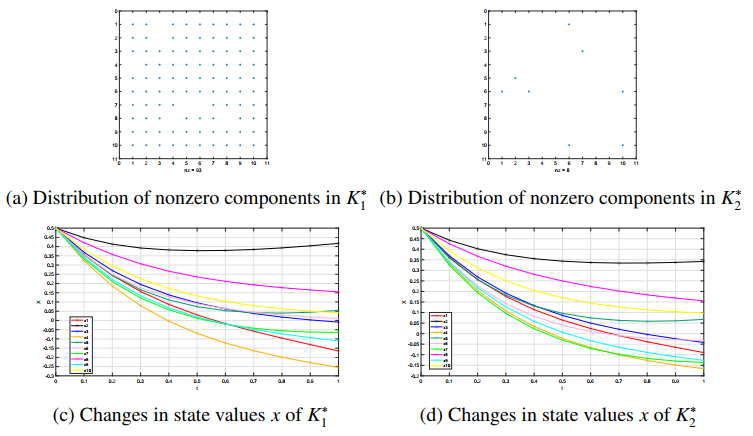
The distributions of nonzero components in the feedback matrices $ K^{*}_{1} $ and $ K^{*}_{2} $ and their corresponding state at each moment are displayed in Figures 3 and 4, where $ nz $ means the number of nonzero elements. Their corresponding optimal cost and sparsity levels are given in Tables 1 and 2. Figures 3 and 4 indicate that the feedback matrix $ K^{*}_{1} $ exhibits a high degree of density, while the feedback matrix $ K^{*}_{2} $ displays a notable level of sparsity. Furthermore, from Tables 1 and 2, it follows that the value of the cost function, specifically $ J^{0}(K^{*}_{2}) $, slightly exceeds that of $ J^{0}(K^{*}_{1}). $

We can see that the number of zero components in $ K^{*}_{2} $ increases rapidly with only a small increase in cost. Therefore, we can conclude that Algorithm 1 proposed in this paper can produce a better quality solution which balances the system performance and sparsity.

5.   Conclusions

In practical scenarios, network operators often choose sparse communication topologies to minimize costs, but the concurrent use of the network by multiple users often leads to feedback delays. Our goal is to determine the optimal sparse feedback control matrix $ K $. To achieve this, we formulate a SOC problem tailored to the CPS with variable delays, with the aim of minimizing $ ||K||_0 $ while adhering to a specified maximum compromise in system costs. We employ a penalty method to transform the SOC problem into one governed solely by box constraints. To handle the nonsmooth aspects of the resulting problem, we utilize a smoothing technique and subsequently analyze the errors it may introduce. The gradients of the objective function concerning the feedback control matrix are computed by simultaneously solving the state system and the associated variational system over time. An optimization algorithm is designed to tackle the resulting challenge, utilizing a piecewise quadratic approximation. The paper concludes with a discussion of the simulation results.

The innovation of the paper is stated as follows: (ⅰ) The innovative use of a penalty method transforms the problem into one constrained by box limits, simplifying the optimization process while still enforcing necessary control constraints; (ⅱ) the application of smoothing techniques to approximate nonsmooth components enables the derivation of gradients efficiently, facilitating the use of gradient-based optimization algorithms in sparse settings; (ⅲ) the method incorporates simultaneous solving of the state and variational systems, enhancing accuracy in gradient calculations and improving the overall performance of the control strategy; and (ⅳ) the development of an optimization algorithm based on piecewise quadratic approximation offers a computationally efficient way to navigate the optimization landscape, making the approach feasible for real-time applications.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported in part by the National Key Research and Development Program of China under Grant 2022YFB3304600, in part by the Nature Science Foundation of Liaoning Province of China under Grant 2024-MS-015, in part by the Fundamental Research Funds for the Central Universities under Grant 3132024196, and Grant DUT22LAB305, in part by the National Natural Science Foundation of China under Grant 12271307 and Grant 12161076, in part by the China Postdoctoral Science Foundation under Grant 2019M661073, and in part by the Xinghai Project of Dalian Maritime University.

Conflict of interest

The authors declare there is no conflicts of interest.