1.
Introduction
Sedentary behavior with low levels of physical activity is ubiquitous in the hospital or rehabilitation setting [1]–[3]. Sedentary behavior includes activities of low energy expenditure occurring in a seated, lying or reclined position (e.g., sitting or watching television) [4],[5], while physical activity encompasses a wide range of energy-expending actions, such as activities of daily living, household tasks, work-related activity, or exercise [6]. These concepts are distinct and may impact health outcomes via different mechanisms [7]. While bed rest was traditionally prescribed for recovery, recent evidence demonstrates that prolonged periods of reduced movement may lead to several adverse health outcomes in older adults, such as substantial loss of muscle mass [8], and increased frailty [9],[10]. Alternatively, better health outcomes may be gained with early mobilization during recovery: Literature from intensive care and other hospital settings suggest that early mobilization may prevent muscle atrophy [11], improve future functional outcomes [11], and support falls prevention [12]. Equally important to early mobilization, is to consistently break up prolonged periods of daily sedentary behavior throughout the recovery period.
Several factors may contribute to high periods of sedentary time for patients [13]: Reduced access to resources, falls-risk liabilities, patient perspectives, low staff-patient ratios, and physical aspects of the hospital environment. In particular, the indoor (built) environment can promote or hinder physical activity. In a recent Australian study, there were no statistical differences in sedentary behavior for two groups of patients: adults recovering from a stroke or adults recovering from an acute myocardial infarction despite their different (potential) capacities [14]. This study suggests environmental factors (beyond person-level factors) may also contribute to behavior [14], and warrants further investigation.
There are several studies describing the hospital indoor environment and person-level activity using behavioral mapping, an environmental scanning method used to systematically record and compare behaviors across time and locations [15]. An advantage of behavioral mapping is the ability to detect a lower threshold of activity, which can sometimes be missed due to the known limitations with pedometers and accelerometers for people with slow walking (gait) speed [16]. Further, behavioral mapping can provide important contextual information for activity [17]. However, most current behavioral mapping studies are limited to inpatients with dementia [15],[17] or after stroke [18]–[23]. Few studies, if any, relate to older adults admitted to an acute care of the elderly (ACE) hospital unit [24],[25]. These ACE units were “developed to disrupt the [unavoidable] trajectory of functional decline of geriatric patients who are admitted to acute hospital wards.” [25] page 219.
The ACE unit incorporates five key components—patient-centered, frequent medical review, early rehabilitation, environment, and enhanced discharge planning—to minimize the risk of older adults' functional decline during an acute hospital admission [26],[27]. Although rehabilitation is key to mitigate limited activity due to an acute illness, one or two therapy sessions/day leaves ample opportunity for prolonged sitting (and possibly provides an opportunity to reverse the benefits of therapy). Specifically, despite the many positive attributes of an ACE unit, it is also important to recognize the need for breaking up prolonged sitting with periods of light activity over the day (if possible). Light physical activity (e.g., activities of daily living, household tasks) provides health benefits [28]–[32], and may be perceived as more attainable, especially for an older adult who is hospitalized. The indoor environment may support older adults to be active in general [33], via destination rooms and or clear hallways with handrails, and benches or chairs for rest stops, for example. We wanted to understand these factors in an already enriched hospital (ACE) unit for older adults.
Our aim was to describe the indoor environment of geriatric hospital units, and patients' and visitors' behavior. Specifically, we used an environmental scan and behavioral mapping to characterize two ACE units to describe the, physical, therapeutic, and social opportunities for older adult inpatient mobility outside their hospital rooms. This contextual knowledge was an essential first step to understand older patients' activity patterns in the acute care setting, and is a foundation to develop interventions to maximize mobility recovery in older adults admitted to hospital.
2.
Methods
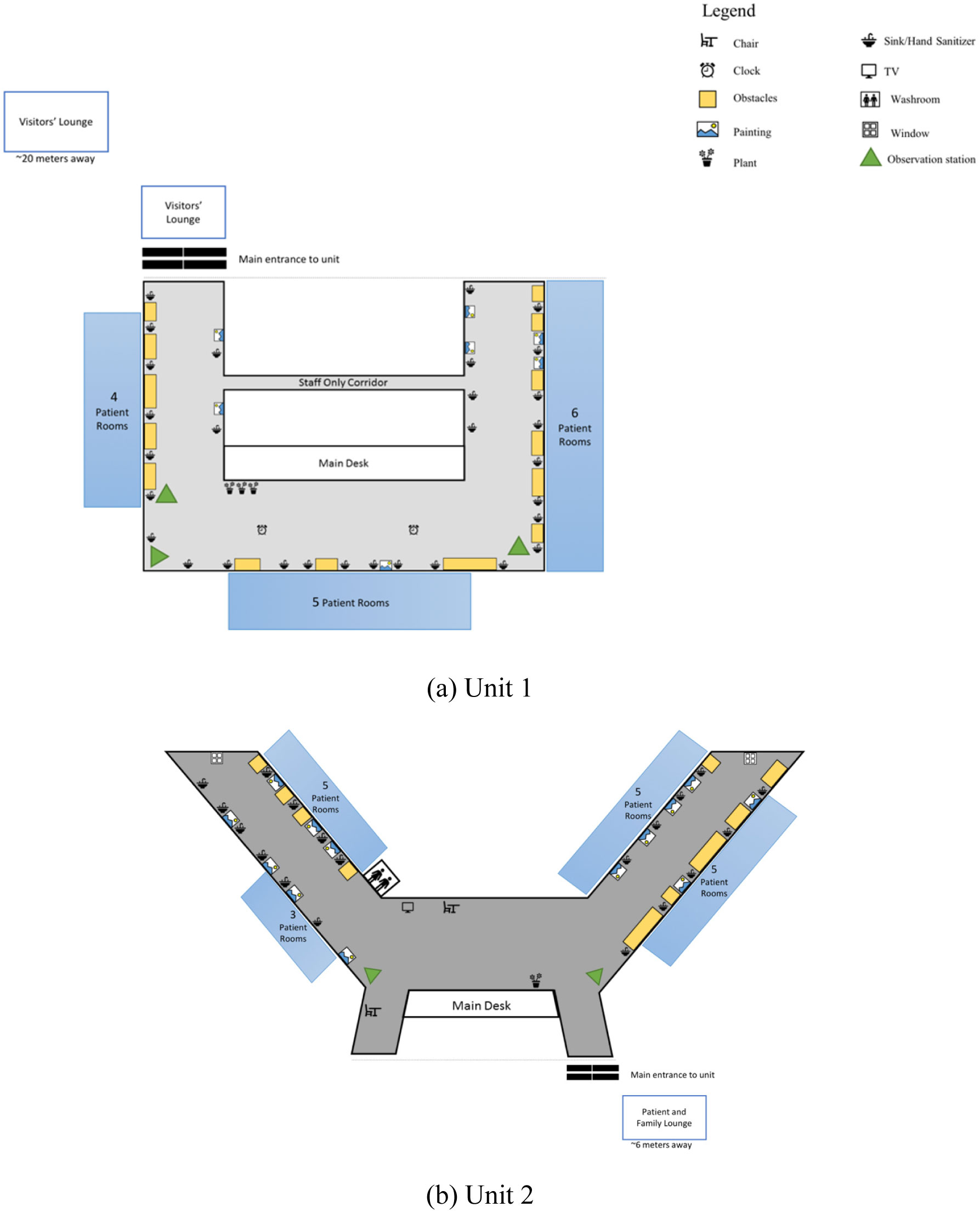
This was an observational inquiry of two inpatient units within a teaching hospital in Vancouver, Canada. We included two ACE units with patients (60 years and older). We also obtained minimal information on unit occupancy (number of patients, age and gender) during the data collection period. Please see Figure 1 for a visual description of both units. We documented the indoor environment and the behavior of patients and visitors (e.g., caregivers, friends, relatives). We used two data collection methods: First, we conducted an environmental scan to describe the indoor features and opportunities for movement in the unit, and second, we used behavioral mapping to describe the actions of people within unit environments during weekdays and weekends. We recognize the difference between gender and sex [34], however in this manuscript, we use gender-based terms, as we do not know the contribution of gender (“socially constructed roles”) or sex (biology) [34] for older adults' observed mobility whilst hospitalized. This study was approved by the university and hospital research ethics boards, and data were collected in September and October 2017.
2.1. Indoor environmental scan
We conducted an environmental scan of the two units to determine overall design and other key features that may (or may not) encourage physical activity. Specifically, we were interested in collecting information on environmental features that support or hinder safe physical activity, such as access to chairs, benches, and corridors with handrails [35], the color and texture of the floor material [36], noise and lighting [37],[38]. The same observer scanned each ward and recorded the environmental features, such as permanent structures (e.g., windows and bathrooms), and more transient items such as portable laundry carts. The observer recorded the information based on a checklist we created to assess the unit design, guided by the Evidence-Based Design conceptual framework [39]. In addition, the observer drew a map of each unit, and indicated the location of permanent and portable items.
2.2. Patient and visitor observations
Behavioral mapping is an observational research method to systematically record behavior within a specific environment [40]. We used standard methods [40] to observe activity every 15 minutes on each unit for two days (one week day/unit and one weekend/unit) from 8 am to 4 pm (except at 12 noon when we only recorded two sessions during lunch time). We specifically chose to look at weekend days as some hospitals generally have less therapy available on weekends. One trained observer, a combined-trained physiotherapist and occupational therapist, conducted the behavioral mapping over the four days. The observer moved in a predetermined pattern throughout each unit (in the public access areas only). Working with hospital staff, we identified two or three places on the unit (called “stations”), and one station in lounges, where the observer stopped for 5–10 seconds four times an hour for data collection. The identified lounges were immediately adjacent, but outside of the hospital units. During the observation period, the observer counted the number of patients and visitors (distinguished their role and posture/activity, and estimated the age and gender of patients) if they were in public areas of each unit (that is, the observer did not enter any rooms) to respect patient privacy. During the observation days, the observer also collected information on noise and lighting, because of the potential negative impact on patients' and staff's health and safety [37],[38].
2.3. Analysis
We describe the units (based on the environmental scan of the indoor environment), use frequencies (and percentages) to record the sum of people and activity over each hour in two units, and differentiate between week days and weekend days. One trained research assistant entered data, and reviewed it on multiple occasions for accuracy. We created summary tables, and met with hospital staff to discuss and situate our findings within the context of the hospital unit (member checking). We used the actual number and gender of patients admitted to hospital units on the observational days as the denominator for some calculations. We used Chi square tests to explore associations for observed number of patients (based on the total number of patients admitted) and (i) women and men for overall observations, (ii) women and men for weekdays, and (iii) women and men for weekend days. We conservatively applied a Bonferroni correction to account for multiple testing (p = 0.05/three analyses), and considered p < 0.017 as significant. We used SPSS Version 23 (IBM, Armonk, New York) for data description and analyses.
3.
Results
We completed the environmental scan and behavioral mapping protocol as planned. Tables 1 and 2 provide an overview of the units' environment features. The units differed in their floorplans, number of beds (23 vs 28), and an additional visitor lounge in Unit 2. Both units had a number of obstacles along the corridors and few handrails; but they also had pictures, plants and furniture placed outside hospital rooms (Figure 1). Flooring material differed in their color and design: Unit 1 had light colored floor materials perceived to better distinguish between the floor and adjacent items. Overall, lighting was sufficient, and there were moderate to low levels of noise observed in both units throughout the day (Table 2).
During the data collection period there were 22 patients (Wednesday) and 23 patients (Saturday) admitted on Unit 1, and 28 patients admitted on both days (Thursday and Sunday) for Unit 2. In Tables 2 and 3, we provide a summary of patient and visitor observations. There was consistency between observed and actual patient numbers, gender and age groups, with only one patient misclassified as younger than their actual age. Sitting was noted in 61% of the patients' observations. There was an equal distribution of upright and sitting postures for three days; the exception was a weekend day with considerably more observed sitting. There were more observations in Unit 1, but more visitor observations in Unit 2 (94 vs 134), especially on the weekend.
Table 3 provides a detailed description of observations by unit. In Unit 1 (weekday), there were 42 observations from 19 patients: This included five patients (one woman and four men) who were observed more than once (four patients had five or less observations, and one patient > five observations). For this same unit on the weekend day (23 observations from 14 patients), there were three participants observed (two women and one man) more than once (one patient < five observations, and two patients > five observations). In Unit 2, there was only one patient (woman) observed twice on the weekday (14 observations from 13 patients). For this same unit on the weekend day (38 observations from 14 patients), there were three patients (one woman and two men) observed multiple times (one patient < five observations, and two patients > five observations). In sum, for the patients observed in the public areas of the units, 24% of the patients in Unit 1 had more than one observation, compared with just 15% of patients in Unit 2 (overall average 20%). For all admitted patients, 10% of women (5/48) and 13% of men (7/53) had multiple observations.
There were no significant associations for women's and men's overall observations (Chi square = 1.04, p = 0.31). However, men were more commonly observed outside their rooms on weekdays, and the reverse effect was recorded for women's observations on the weekends. Specifically, there were significant associations for gender and observations on weekdays (men > women; Chi square = 17.01, p < 0.0001), and weekend days (women > men; Chi square = 6.11, p = 0.013).
4.
Discussion
Sedentary behaviors, such as prolonged sitting, lying or reclining, use very little energy expenditure [4],[5], and are ever-present throughout the hospital phase and subsequent recovery period [1],[2]. Studies indicate hospitalization can lead to the development of disability and loss of autonomy [41], and may mediate a change in residence upon discharge. Here, we describe the indoor environment for two ACE units with features that encourage more activity such as, low to moderate noise levels, adequate lighting, good esthetics (windows, pictures and plants), hallways for walking with rest stops (chairs), and destination rooms (visitor lounges). However, few handrails and the presence of items against walls in the hallways (perceived obstacles) were potential barriers to patients' mobility outside their rooms. Based on the behavioral mapping exercise, we observed about 60% of patients admitted to the ACE units left their room on at least one occasion, with 20% of patients with multiple observations. Sitting was noted in more than half of the observations. However, we recognize that patients may have engaged in routine rehabilitation (in their room or therapy department). Our work extends the literature to highlight an interesting finding related to gender and activity patterns. We observed significantly more older men outside their rooms during weekdays, and more older women outside their rooms on the weekend days: Concurrently, we recorded more visitor observations on the weekend. To our knowledge, our study is the first to observe activity patterns (using behavioral mapping) on an ACE unit, thus it is difficult to put our results into perspective. That is, older adults admitted to an ACE unit are generally considered frail, thus observing more than half of patients in the public areas of the units is encouraging. A laudable goal is to optimize physical activity for all older adults in the acute hospital setting, to avoid the cycle of prolonged sedentary behavior that can be difficult to change once discharged home. Therefore, these results serve as a baseline, and generate hypotheses for future testing to optimize the hospital experience for older adults.
The exploratory work presented here is an important first step to work collaboratively with key stakeholders. Behavioral mapping is a unique approach to provide contextual information on patients' mobility in the hospital setting. As there are few, if any, studies using behavioral mapping conducted within ACE units, we do not know if more patient observations lead to better health outcomes. However, other studies underscore that early [42]–[44] (and frequent) daily movement can be beneficial. The approach presented here provides a person-centered way to develop and test interventions to encourage safe mobility on the hospital unit and circumvent the post-hospital syndrome, a multifactorial phenomenon negatively impacting health and recovery [45]. As aptly stated by Professor Krumholz, “The hospitalization should not only address the urgencies of the acute illness, but also seek to promote health actively by strengthening patients and contributing to their physiological reserve.” [45] page 3. Hospital policies are generally developed for the health and safety of patients and staff. Although there has been a recent call to re-evaluate patients' activity in hospital vs. the risk of falls [13], there is an urgent need for solutions that promote mobility while minimizing harm. This is an important goal that would benefit from further clarification with empirical evidence.
Early mobilization is essential, however it is equally important to balance activity with restorative breaks, and develop skills, strategies and confidence with new or evolving mobility and health status. Technology advances could assist this change in focus by providing staff with real-time monitoring of patients' daily movement patterns [46]. Reduced self-efficacy (resulting from hospitalization) and or an increased fear of falling [47],[48] may result in older adults' hesitancy to mobilize. Support for activity and developing good health habits could begin through modeling within the hospital setting, while patients are still supervised by health care staff. It does not seem to be enough to “tell” people to be active once they are home. This can be an opportunity to develop positive health habits for longer term adoption outside of the hospital setting. Ultimately, the hospital experience is a complex, multi-dimensional issue that we need to better understand from different perspectives: Patients' families, hospital staff and policy makers. This comprehensive approach with a person-centered lens is ideal to develop and test possible solutions to minimize the risk for iatrogenic development of mobility disability and support in-hospital harm reduction.
We noted an interesting finding in our study: Older men were observed more in the unit during the weekdays and older women during the weekends. We do not know why this may have occurred but speculate that it may be a result of gender-based behaviors, the presence of family members (visitors), or by chance. It is possible that older men took a more traditional approach to the hospital admission and “worked” on their recovery during the weekdays: Older men (compared with older women) generally engage in more higher intensity physical activity [49]. Alternatively, maybe older men engaged in steps to gain back some control [50] (through exercise) when confronted with an acute hospital admission. Interestingly, based on our previous work at the same hospital, we noted there were more men who fell, compared with women [51] during a hospital admission: we do not know why they fell, but it is possible that older men may be at greater exposure for falls due to walking outside hospital rooms. There is other literature with similar observations for men in hospital [52],[53]. Conversely, there were slightly more visitors observed on the weekend, which may have encouraged women to leave their rooms. In a similar study by Prakash and colleagues [54], they noted that patients with stroke were more active (in hospital) when family was present, although there were no gender differences reported. We stopped data collection at 4 pm, so do not know whether visitors, such as family members, may have supported older women to leave their rooms on weekday evenings. These preliminary data generate hypothesis for future studies to disentangle the role of gender (if any) in the recovery period.
To address the current state of prolonged sedentary behavior in the hospital setting requires understanding factors at multiple levels: person, practitioner, policy and environment. The built environment is emerging as a key factor to support older adults' outdoor physical activity [55],[56], but, in general, less is known about older adults' physical activity and the indoor (home) setting [33]. Similar principles may apply to hospital settings, thus we used a framework to guide our research [39] and conducted an environmental scan of the hospital units. We noted several challenges within units which may account for patients' reduced activity. For example, handrails were missing on Unit 1, and for both units there were obstacles in the hallways, and no destination rooms within the unit (e.g., central dining room, small gym). In addition, we observed fewer patients in Unit 2; here the floor plan was more traditional, and flooring was darker (and possibly creating obstacles for older patients with low vision). These features may or may not have contributed to our findings, and it remains uncertain as there are no publications on barriers to activity in ACE units. Activity is most likely influenced by the interaction of the person within the physical and social environment. Within the stroke literature, Rosbergen and colleagues explored the effect of an “enriched environment” on activity for older adults with stroke [57]–[59]. In this controlled pre-post pilot study, they noted an increase in patients' activity, with no significant difference in adverse events compared with a control group [58]. This study is informative to guide future interventions for patients, staff, and hospital culture and policies.
We acknowledge the following limitations with this study. First, we only collected data in the public areas of the hospital units and are not able to account for activity participants engaged in within their room, or areas of the hospital outside of the unit. In particular, some ACE units have cycle ergometers for use in patient rooms. Second, we only collected data during the day for a few days, and cannot comment on any physical activity during the evenings. Nonetheless, we have detailed observations of patients' daily routines outside their rooms and can provide context to their patterns. Third, we observed low numbers of participants, and this may or may not represent typical behavior for older patients admitted to ACE units. Further, we do not have information on the health status of the patients on each unit, thus these factors could explain the observations (or lack thereof). We also did not use a direct measurement (e.g., accelerometry) of patients' activity patterns. However, given the low level of patients' observed physical activity, there is the possibility of missing data (due to slow gait speed) with accelerometry [60]. Conversely, in this study, an experienced physiotherapist-occupational therapist collected all data reducing the risk of missed activity. Finally, we do not know if the observed behaviors in hospital were associated with health outcomes post-discharge, but collectively, this valuable information is hypothesis-generating for our next research phase.
In conclusion, we describe the indoor environment for two ACE units, with features that can encourage mobility, but also noted potential barriers, such as few handrails, and obstacles in the hallways. We also describe older adults' physical activity patterns in the acute hospital units during a recent admission. We noted variability in observations (based on day and unit) for patients outside of their rooms, and sitting was observed over half of the time. Emerging evidence supports early activity, but to date, many older adults engage in prolonged periods of sedentary behavior as a hospital inpatient. A recent international consensus on older adults and sedentary behavior [61] includes a recommendation for more research to reduce prolonged sitting during hospitalization. Our exploratory data is a beginning to advance the field and supports our next phase, the co-creation of safe and person-centered policies on inpatient mobilization.









 DownLoad:
DownLoad:








