Integrating research into clinical practice for hip fracture rehabilitation: Implementation of a pragmatic RCT

1.   Introduction

Mathematical forecasts are yet to gain its improvement in fighting the COVID-19 pandemic. The meteoric spread, the course of actions, and the methods concerned in the containment of the infection demand the soonest and quickest understanding in perceiving solutions in line along with the biological, physiological, environmental, and continual aspects of life with much better predictions by mathematical computerized modeling. Almost all the countries are still suffering from the infection and its destructiveness is ascending gradually. The disease has spread, and is spreading amongst different countries or regions mainly through air-travel mode ^[1]. The infection doesn't happen on its own and the present occurrence is possibly because of our ignorance or casual thinking and way of living ^[2]. As a matter of fact, there are many looming queries about COVID-19 spread, such as "number of individuals that will be infected in coming days", "time of appearance of rate of inflexion point of infection", "infections during the pinnacle period and number of individuals that are infected at that time", "effectiveness of present action to control the spread", etc. Usually, in analysis of epidemiology, virus causing diseases grow exponentially maintaining a determined rate of reproduction ^[3].

One of the most economical and efficient means to prevent and control the infection spread is mass vaccination. The world is now getting leaky vaccinated to reduce the infection as the vaccines obstruct signs and symptoms of lethal infections but do not put a stop to contamination or onward spread ^{[4,5,6,7,8,9,10,11]}. It is seen in India that the government is facing a huge challenge to attain preferable vaccination coverage in order for group immunity to be in effect ^[12]. Hysteresis loops can surface in social replica of dynamical behaviour of vaccination ^[13]. The impact of varying vaccine efficacies has been investigated in response to control the spread of disease ^[14,15,16]. The vaccine is effective (infection can be prevented) for $ \eta = 1 $ (here we denote $ \eta $ as vaccine efficacy), whilst the value $ \eta = 0 $ means the vaccine is ineffective to prevent the virus infection. In the bio-mathematics regime, fractional calculus is now one of the vital studies to elaborate precise cellular behavior, and many human disease's mathematical models have been described by various types of fractional-order derivative operators ^{[17,18,19,20]}.

FDEs (short for Fractional Differential Equation) are used to include the memory of the phenomenon in the system's dynamics. As per literature ^[21], there are multiple kinds of fractional derivative operators, amongst which we present the study of the model by fractional differential equation by CF (short for Caputo-Fabrizio derivative) and ABC (short for Atangana-Baleanu-Caputo derivative) sense. ODEs (short for Ordinary Differential Equation) are particular cases of FDEs. FDEs provide descriptions of the courses of endemics, epidemics, pandemics, and some other natural processes in a better way than the ODEs ^[22]. In reference to deterministic models of the contagiousness of any disease, ODE models are well-structured yet sometimes researchers use models using FDE ^[23,24]. Some recent research papers focusing on FDE for various real-life problems which are modelled mathematically to understand the problems and their solutions has been studied ^{[25,26,27,28,29,30,31,32,33,34,35,36]}.

As per the author's knowledge, the remark and application for vaccine efficacy, and the study and experimentation has not yet looked into comparison between the mentioned fractional derivative operators for the SEVR COVID-19 model with the memory effect. The quantitative analysis makes the two operators propitious choices in modeling the dynamics of the disease mathematically. In the upcoming segments, the model is formed with fractional differential equation by CF and ABC sense. This technique is used to find the course of action of the infection whilst vaccination program is on the go. Using Next Generation Matrix Method the expression for the basic reproduction number, $ \mathcal{R}_{n} $, is found and by dint of that local stability are investigated for the equilibrium points. The existence and uniqueness for the models are done using the Banach fixed-point theorem. Considering the course of events for beginning of the transmission to clinical recuperation and seriousness of illness, the appropriateness of utilizing the two operators, joined by relative similitudes, are examined just as their disparities. Lastly, the article is wrapped-up by scrutinizing the seriousness of the spread of infection in terms of CF and ABC, and depict their upcoming involvement for the growth of infection control policy at worldwide level to limit the spread amongst humans.

The follow-up sections deal with the essence of the manuscript. In Section 2, some preliminary requisite knowings of CF and ABC non-singular kernel fractional derivatives is done to get acquainted with customary notations. This section also has model formulation with a box diagram to have a glimpse on the transmission dynamics. The parameters are broadly described with proper justification. The equilibrium points are evaluated and also $ \mathcal{R}_{n} $ is calculated. The stability analysis for the infection-free equilibrium has been done in regard to $ \mathcal{R}_{n} $ and Jacobian matrix. In Section 3, the solutions of the CF and ABC systems are shown to exist and unique using Banach fixed-point theory and Lipschitz condition. Section 4 deals with discussion and numerical simulation of both the systems in terms of graphs, order of fractional derivative and $ \mathcal{R}_{n} $. At last, in Section 5, we draw the conclusions of the entire manuscript.

2.   Preliminaries

Here, the preliminary and primary definitions in terms of properties of the mentioned two fractional derivative operators with exponential and Mittag-Leffler kernels are presented.

2.1.   Properties of CF and ABC operators

Definition 1. ^[37] Consider $ f \in \mathcal{H}^{1}\left(c_{1}, c_{2} \right) $, $ c_{2} > c_{1} $, $ \alpha \in \left]0, 1 \right[$ then the CF fractional derivative is defined as:

where $ \mathfrak{N}(\alpha) $ is a normalization function satisfying $ \mathfrak{N}(0) = \mathfrak{N}(1) = 1 $ if $ f \notin \mathcal{H}^{1}\left(c_{1}, c_{2} \right) $ then

Definition 2. ^[37,38] Let us assume that $ 0 < \alpha < 1 $, then the integral of the fractional order $ \alpha $ for a function $ f(t) $ is defined as:

$ t \geq 0 $.

Definition 3. ^[39] Consider $ f \in \mathcal{H}^{1}\left(c_{1}, c_{2} \right) $, $ c_{2} > c_{1} $, $ \alpha \in \left]0, 1 \right[$ then the ABC is defined as:

where $ \mathcal{M}_{\alpha} $ represent the Mittag-Leffler function and $ \mathcal{N}(\alpha) $ is a normalization function satisfying $ \mathcal{N}(0) = \mathcal{N}(1) = 1 $ and $ \mathcal{N}(\alpha) = 1-\alpha + \dfrac{\alpha}{\Gamma (\alpha)} $.

Definition 4. ^[39] Let us assume that $ 0 < \alpha < 1 $, then the integral of the ABC, fractional order $ \alpha $ for a function $ f(t) $ is defined as:

$ t \geq 0 $.

2.2.   Model formulation

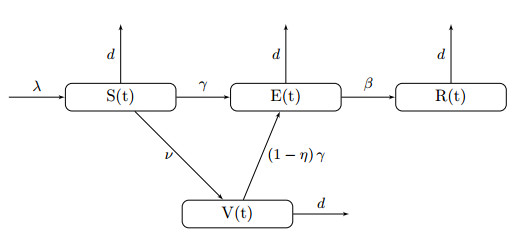
It is important to identify and then study the dynamical behaviour of unwanted results of COVID-19 disease on the populace growth and to predict what may occur. Keeping track of the infection has been a steadily tiring job and vaccination has been a usual approach for lessening the infection, day-to-day vaccination is currently supplied in all nations. It has been believed that the immune system will generate antibody against the virus after the vaccine doses. Even so, it may be not in a fully protective level. The memory effect is an important element in several biological phenomenons, which is included in the models. Hence, it is practicable to use fractional alternation, as fractional derivatives essentially involve the effect of memory. One of the best ways to tackle such issue is to put the fractional derivatives of order $ \alpha \in \left(0, 1 \right) $ for the state variables. The next step is to have some modification in the biological parameters such that for a FDE system the both sides of an equation must have dimension $ \frac{1}{\left(time \right)^{\alpha}} $. This can be done by raising each of the parameters by $ \alpha $ ^[40]. Motivated by these details, the SEV model presented Liu et al. ^[42] and Abuasad et al. ^[41], the updated SEVR model with vaccination by CF and ABC non-singular kernel fractional derivative operators are as follows:

and

The initial conditions for both the systems are $ S(0) = S_{0} > 0 $, $ E(0) = E_{0} \geq 0 $, $ V(0) = V_{0} \geq 0 $, and $ R(0) = R_{0} \geq 0 $. The virus spread method is considered amongst humans. In the models (2.1)–(2.4) and (2.5)–(2.8), $ S(t) $ denotes the fractions of susceptible individuals, $ E(t) $ denotes the fractions of virus effected individuals, $ V(t) $ denotes fractions of vaccinated individuals, and $ R(t) $ denotes fractions of individuals who have recovered from the disease, at any time $ t $. The explanation for the parameters (non-state variables) is as following:

$ {\rm{i)}} $ The parameter values involved in the aforementioned systems are considered to be non-negative, and $ \lambda > 0 $.

$ {\rm{ii}}) $ $ \lambda $: rate at which individuals are considered to be born susceptible.

$ {\rm{iii}}) $ $ d $: death rate of all the state variables.

$ {\rm{iv}}) $ $ \nu $: rate at which susceptibles are vaccinated.

$ {\rm{v}}) $ $ \gamma $: rate at which susceptibles are effected by the virus.

$ {\rm{vi}}) $ $ \left(1-\eta \right)\gamma $: rate at which vaccinated individuals are affected, which can be possible due to findings present in ^[43].

$ {\rm{v}}) $ $ \beta $: recovery rate of affected individuals but are open to infection again if proper medical and government guidelines are not followed.

The vaccine efficacy can be given a numerical value ^[44], and as per our knowledge the vaccine efficacy has not yet been modelled to any mathematical COVID-19 model. So for the solutions of system (2.1)–(2.4) and (2.5)–(2.8) we take two values of $ \eta $ in order to compare the solution trajectories. Next, one of the values for death rate of state variables, $ d $, is taken as 0.002 to have a view at the infection in terms of the basic reproduction number. The values of fractional order $ \alpha $ are taken arbitrarily. This section is followed by two other subsections dealing with finding the equilibrium points and the basic reproduction number along with stability analysis of the equilibrium points.

2.2.1.   Equilibrium points

Here, only two equilibrium points of the models given by the system (2.1)–(2.4) and (2.5)–(2.8) are presented with biological clarification. The points are as following:

$ {\rm{i}}) $ $ X_{0}\left(\dfrac{\lambda^{\alpha}}{d^{\alpha}+\nu^{\alpha}}, 0, \dfrac{\lambda^{\alpha}\nu^{\alpha}}{d^{\alpha}\left(d^{\alpha}+\nu^{\alpha} \right)}, 0 \right) $, which is named as "Infection-free equilibrium (IFE) point". This is the case where affected individuals are zero and individuals are in infection free state. The vaccination for this point is fruitful for both short and long run as the infection can be contained.

$ {\rm{ii}}) $ $ X^{*}\left(S^{*}, E^{*}, V^{*}, R^{*} \right) $, which is named as "Co-existing equilibrium (CoE) point". The point $ X^{*} $ satisfies the below mentioned system of the equations.

In this case, the affected individuals co-exist with susceptible individuals and this can be an alarming issue for the infection spread. The vaccination cannot be applied to the affected compartment for this situation as it will wreck havoc to the immune system, and also rate of positive infection will rise leading to indefinite death toll.

2.2.2.   Basic reproduction number, $ \mathcal{R}_{n} $

It is important information in the mathematical regime of infectious disease models as it helps in finding whether a pandemic will happen or not. The number $ \mathcal{R}_{n} $ resembles the expected cases of infections caused by an infectious individual inside susceptible populace. The next-generation matrix method ^[45] is used to find $ \mathcal{R}_{n} $ of the model presented in this article.

The Jacobian matrices $ \mathcal{F} $ and $ \mathbb{V} $ with the rate of appearance of new infections and rate of transfer of individuals into and out of compartments, respectively, at $ X_{0} $ are given by

Proceeding further, we get

The eigenvalues for the diagonal matrix $ \mathcal{F}\mathbb{V}^{-1} $ are the diagonal elements itself, and amongst them the dominant eigenvalue is $ \mathcal{R}_{n} = \dfrac{\gamma^{\alpha} \lambda^{\alpha} \left\lbrace d^{\alpha} + \left(1-\eta \right)\nu^{\alpha} \right\rbrace}{d^{\alpha} \left(d^{\alpha}+\beta^{\alpha} \right)\left(d^{\alpha}+\nu^{\alpha} \right)} $, which is the reproduction number for the proposed models.

The infection will self-annihilate if $ \mathcal{R}_{n} < 1 $, otherwise for $ \mathcal{R}_{n} > 1 $ the infection will conquer and begin to a pandemic or an epidemic until and unless the medical as well as government guidelines are not implemented amongst the mass.

2.2.3.   Stability analysis

The discussion will be for the case $ \mathcal{R}_{n} < 1 $, then the system (2.1)–(2.4) and (2.5)–(2.8) has IFE point $ X_{0} $ and it is globally asymptotically stable in an invariant region ^[41,42]

Now, to check local stablity the Jacobian of the models (2.1)–(2.4) or (2.5)–(2.8) at $ X_{0} $ is evaluated and it is given by the matrix

The characteristic equation for the matrix $ J(X_{0}) $ in variable $ \xi $ is given by

where $ a_{11} = -\left(d^{\alpha}+\nu^{\alpha} \right) $, $ a_{22} = \left(d^{\alpha}+\beta^{\alpha} \right)\left(\mathcal{R}_{n} - 1 \right) $, $ a_{33} = -d^{\alpha} $, and $ a_{44} = -d^{\alpha} $ are the eigenvalues. Therefore, the IFE point $ X_{0} $ of the models (2.1)–(2.4) and (2.5)–(2.8) is locally asymptotically stable for $ a_{22} < 0 $, implies that $ \mathcal{R}_{n} < 1 $. So, it can be stated in a theorem as following:

Theorem 1. For $ \mathcal{R}_{n} < 1 $, the IFE point $ X_{0} $ is locally asymptotically stable for the COVID-19 models (2.1)–(2.4) and (2.5)–(2.8).

The follow-up section is about two of the most essential parts of any system of equations viz, existence and uniqueness of solutions.

3.   Existence and uniqueness of solutions

Here, in this section, necessary theorems are provided and discussed thoroughly to support the existence and uniqueness of solutions of models (2.1)–(2.4) and (2.5)–(2.8) together with the initial conditions, by applying the Banach fixed-point theory.

3.1.   For the CF Model (2.1)–(2.4)

The findings for the system of equations of COVID-19 CF model using the fractional integral are as follows ^[38,46]:

The symbols, after arranged in the view of the problem, gives the following results:

For the sake of simplicity, we consider

Theorem 2. The Lipschitz condition and contraction are justified by the kernel

$ i) $ $ \mathcal{H}_{1} $ if $ 0 \leq \left(\gamma^{\alpha}\omega_{2}+d^{\alpha}+\nu^{\alpha} \right) < 1 $.

$ ii) $ $ \mathcal{H}_{2} $ if $ 0 \leq \left(\gamma^{\alpha}\omega_{1}+ \left(1-\eta \right)\gamma^{\alpha}\omega_{3}+ d^{\alpha}+\beta^{\alpha} \right) < 1 $.

$ iii) $ $ \mathcal{H}_{3} $ if $ 0 \leq \left(d^{\alpha}+\left(1-\eta \right)\gamma^{\alpha}\omega_{2} \right) < 1 $.

$ iv) $ $ \mathcal{H}_{4} $ if $ 0 \leq d^{\alpha} < 1 $.

Proof. Let us assume that the state variables present in the COVID-19 models are bounded, and therefore it can be said that $ \parallel S(t) \parallel \leq \omega_{1} $, $ \parallel E(t) \parallel \leq \omega_{2} $, $ \parallel V(t) \parallel \leq \omega_{3} $, and $ \parallel R(t) \parallel \leq \omega_{4} $ ^[46].

Let us consider $ S(t) $ and $ S'(t) $ be the two functions, and therefore

So, it can be mentioned now that

where $ \phi_{1} = \left(\gamma^{\alpha}\omega_{2}+d^{\alpha}+\nu^{\alpha} \right) $. Thus, the Lipschitz condition is achieved for kernel $ \mathcal{H}_{1} $ and $ 0 \leq \left(\gamma^{\alpha}\omega_{2}+d^{\alpha}+\nu^{\alpha} \right) < 1 $ ^[46] gives $ \mathcal{H}_{1} $, and also contraction is justified.

Like wise, contraction and the Lipschitz condition can be done and written for the kernels $ \mathcal{H}_{2} $, $ \mathcal{H}_{3} $, and $ \mathcal{H}_{4} $ as mentioned below;

where $ \phi_{2} = \left(\gamma^{\alpha}\omega_{1}+ \left(1-\eta \right)\gamma^{\alpha}\omega_{3}+ d^{\alpha}+\beta^{\alpha} \right) $, $ \phi_{3} = \left(d^{\alpha}+\left(1-\eta \right)\gamma^{\alpha}\omega_{2} \right) $, and $ \phi_{4} = d^{\alpha} $.

Taking the kernels $ \mathcal{H}_{1} $, $ \mathcal{H}_{2} $, $ \mathcal{H}_{3} $, and $ \mathcal{H}_{4} $ into consideration the following equations are obtained, which are as follows:

The following iterative formulae are now seen closely, which are as follows:

with the initial conditions of the COVID-19 model given in the system of Eqs (2.1)–(2.4). The upcoming expressions for the difference of sequential terms are written as:

It is evident that

Involving norm to $ \rho_{n}(t) $ then using triangle inequality, we get

It has been shown that the the Lipschitz condition is satisfied by the kernel $ \mathcal{H}_{1} $, therefore

Thus, it can be deduced that

In the same way, other results are followed as;

By taking the inequalities (3.13)–(3.16) into consideration the following theorem can be stated, which is:

Theorem 3. The system (2.1)–(2.4) has a solution if there exist a real number $ \tau_{0} $, satisfying

for all $ i = 1, 2, 3, 4 $.

Proof. Inequations (3.13)–(3.16) are considered along with the fact that the state variables are bounded and the kernels $ \mathcal{H}_{i} $ $ \left(i = 1, 2, 3, 4 \right) $ satisfy the Lipschitz condition. The following mentioned relations employ the iterative method ^[46]:

Thus, solutions of the system (2.1)–(2.4) exist, which are given by the functions (or inequalities) (3.17)–(3.20), and are also continuous. Let us now consider that

Taking $ \mathfrak{S}_{n}(t) $ into consideration, we now achieve

If this process is iterated then at $ \tau = \tau_{0} $, we get

Now, it is clear that $ \lim\limits_{n \rightarrow \infty} \parallel \mathfrak{S}_{n}(t) \parallel = 0 $. In the same manner it can be put that $ \mathfrak{E}_{n}(t) \rightarrow 0 $, $ \mathfrak{V}_{n}(t) \rightarrow 0 $, and $ \mathfrak{R}_{n}(t) \rightarrow 0 $ whenever $ n \rightarrow \infty $.

To clarify the uniqueness for the solutions of the system (2.1)–(2.4), we now assume that $ S'(t) $, $ E'(t) $, $ V'(t) $, and $ R'(t) $ are a distinct set of solutions for the said system, then

Let us consider that kernel $ \mathcal{H}_{1} $ justify the Lipschitz condition and taking the norm on the above equation, we get the inequality given below;

Similarly,

Theorem 4. For the system (2.1)–(2.4), a unique solution exists if the following inequalities holds good

for all i = 1, 2, 3, 4.

Proof. If we consider the assumption made, then from the inequalities given by (3.21)–(3.24), we get

This implies that $ S(t) = S'(t) $, $ E(t) = E'(t) $, $ V(t) = V'(t) $, and $ R(t) = R'(t) $. And this justifies the proof of COVID-19 model (2.1)–(2.4).

3.2.   For the ABC Model (2.5)–(2.8)

The system of equations of COVID-19 ABC model using the fractional integral ^[38,46], the findings involve the following:

The symbols, after arranged in view of the problem, give the following results;

For the sake of simplicity, we consider

Theorem 5. The Lipschitz condition and contraction are justified by the kernel

$ i) $ $ \mathcal{\bar{H}}_{1} $ if $ 0 \leq \left(\gamma^{\alpha}\bar{\omega}_{2}+d^{\alpha}+\nu^{\alpha} \right) < 1 $.

$ ii) $ $ \mathcal{\bar{H}}_{2} $ if $ 0 \leq \left(\gamma^{\alpha}\bar{\omega}_{1}+ \left(1-\eta \right)\gamma^{\alpha}\bar{\omega}_{3}+ d^{\alpha}+\beta^{\alpha} \right) < 1 $.

$ iii) $ $ \mathcal{\bar{H}}_{3} $ if $ 0 \leq \left(d^{\alpha}+\left(1-\eta \right)\gamma^{\alpha}\bar{\omega}_{2} \right) < 1 $.

$ iv) $ $ \mathcal{\bar{H}}_{4} $ if $ 0 \leq d^{\alpha} < 1 $.

Proof. Let us assume that the state variables present in the COVID-19 models are bounded, and therefore it can be said that $ \parallel S(t) \parallel \leq \bar{\omega}_{1} $, $ \parallel E(t) \parallel \leq \bar{\omega}_{2} $, $ \parallel V(t) \parallel \leq \bar{\omega}_{3} $, and $ \parallel R(t) \parallel \leq \bar{\omega}_{4} $ ^[46].

Let us consider $ S(t) $ and $ S'(t) $ be the two functions, and therefore

So, it can be mentioned now that

where $ \bar{\phi}_{1} = \left(\gamma^{\alpha}\bar{\omega}_{2}+d^{\alpha}+\nu^{\alpha} \right) $. Thus, the Lipschitz condition is achieved for kernel $ \mathcal{\bar{H}}_{1} $ and $ 0 \leq \left(\gamma^{\alpha}\bar{\omega}_{2}+d^{\alpha}+\nu^{\alpha} \right) < 1 $ ^[46] gives $ \mathcal{\bar{H}}_{1} $, and also contraction is justified.

Like wise, the Lipschitz condition and contraction can be performed and written for the kernels $ \mathcal{\bar{H}}_{2} $, $ \mathcal{\bar{H}}_{3} $, and $ \mathcal{\bar{H}}_{4} $ as mentioned below;

where $ \bar{\phi}_{2} = \left(\gamma^{\alpha}\bar{\omega}_{1}+ \left(1-\eta \right)\gamma^{\alpha}\bar{\omega}_{3}+ d^{\alpha}+\beta^{\alpha} \right) $, $ \bar{\phi}_{3} = \left(d^{\alpha}+\left(1-\eta \right)\gamma^{\alpha}\bar{\omega}_{2} \right) $, and $ \phi_{4} = d^{\alpha} $.

Taking the kernels $ \mathcal{\bar{H}}_{1} $, $ \mathcal{\bar{H}}_{2} $, $ \mathcal{\bar{H}}_{3} $, and $ \mathcal{\bar{H}}_{4} $ into consideration the following equations are obtained:

The following iterative formulae with the initial conditions of the COVID-19 model given in the system of Eqs (2.5)–(2.8) are now seen closely, which are as follows:

The upcoming expressions for the difference of sequential terms are written as follows:

It is evident that

Involving norm to $ \bar{\rho}_{n}(t) $ then using triangle inequality, we get

It has been shown that the Lipschitz condition is satisfied by the kernel $ \mathcal{\bar{H}}_{1} $, therefore

Thus, it can be deduced that

In the same way, other results are followed as:

Taking the inequalities (3.37)–(3.40) into consideration, the following theorem can be put forward:

Theorem 6. The system (2.5)–(2.8) has a solution if there exist a real number $ \tau_{0} $, satisfying

for all $ i = 1, 2, 3, 4 $.

Proof. The Inequations (3.37)–(3.40) are considered along with the fact that the state variables are bounded and the kernels $ \mathcal{\bar{H}}_{i} $ $ \left(i = 1, 2, 3, 4 \right) $ satisfy the Lipschitz condition. The following mentioned relations employ the iterative method ^[46]:

Thus, solutions of the system (2.5)–(2.8) exist, which are given by the functions (or inequalities) (3.41)–(3.44), and are also continuous. Let us now consider that

Taking $ \mathfrak{\bar{S}}_{n}(t) $ into consideration, we now achieve

If this process is iterated then at $ \tau = \tau_{0} $, we get

Now, it is clear that $ \lim\limits_{n \rightarrow \infty} \parallel \mathfrak{\bar{S}}_{n}(t) \parallel = 0 $. In the same manner it can be put that $ \mathfrak{\bar{E}}_{n}(t) \rightarrow 0 $, $ \mathfrak{\bar{V}}_{n}(t) \rightarrow 0 $, and $ \mathfrak{\bar{R}}_{n}(t) \rightarrow 0 $ whenever $ n \rightarrow \infty $.

To clarify the uniqueness for the solutions of the system (2.5)–(2.8), we now assume that $ S'(t) $, $ E'(t) $, $ V'(t) $, and $ R'(t) $ are a distinct set of solutions for the said system, then

Let us consider that kernel $ \mathcal{\bar{H}}_{1} $ justify the Lipschitz condition and taking norm on above equation, we get the following inequality given below as:

Similarly,

Theorem 7. For the system (2.5)–(2.8), a unique solution exists if the following inequalities hold good

for all $ i = 1, 2, 3, 4 $.

Proof. If we consider the assumption made, then from the inequalities given by (3.45)–(3.48),

This implies that $ S(t) = S'(t) $, $ E(t) = E'(t) $, $ V(t) = V'(t) $, and $ R(t) = R'(t) $. And this justifies the proof for the uniqueness of the solutions for COVID-19 model (2.5)–(2.8).

4.   Discussion and numerical results

The numerical simulation is done using Mathematica for both CF and ABC approach models (2.1)–(2.4) and (2.5)–(2.8), respectively. Next, the comparison and discussion of the following results are done. The dynamics of the novel COVID-19 infection-vaccination model are given by the system (2.1)–(2.4) and (2.5)–(2.8), respectively, for various values of $ \alpha $, randomly selected, are plotted in Figures 2–5. The parametric plot amongst the state variables of the SEVR model are plotted in Figures 6 and 7. The initial values of the state variables are taken as: $ S_{0} = 0.1 $, $ E_{0} = 0.05 $, $ V_{0} = 0.5 $, and $ R_{0} = 0 $ ^[41,46].

Due to lack of clinical evidence and support, it is not sure the precise death rate of individuals due to COVID-19 infection, and so we manipulate the value of $ d $ to understand the death dynamics. The numerical simulations' comparison of Figures 2(a)–(d), 3(a)–(d), 4(a)–(d), 5(a)–(d) and Figures 2(e)–(h), 3(e)–(h), 4(e)–(h), 5(e)–(h) for both the CF- and ABC approach, respectively, show that for same non-natural values of $ \alpha $, parameter values given in Table 1 and same initial conditions the SEVR model shows different trajectories. It is observed that susceptible populace decrease at a slower rate with the ABC approach as compared to the CF approach for the values of $ \alpha $ in Table 1, which can be clearly seen in Figure 2(e), (f) and 2(a), (b). But Figure 2(c), (d) and 2(g), (h) show that both CF- and ABC approach provides precisely same result. It is deduced from Figures 3(a), (b) vs. 3(e), (f) and 4(a), (b) vs. 4(e), (f) about comparisons that the ABC approach gives much variation in effected and vaccinated populaces than the CF approach, for $ d = 0.002 $ and $ \eta = 0.5 $, and $ 0.8 $. One more prominent aspect suggests that the effected and vaccinated populaces provide a sharp increase because of high spread of COVID-19 infection presented by Hellewell et al.^[47] and Gupta et al. ^[48]. But Figures 3(c), (d) vs. 3(g), (h) and 4(c), (d) vs. 4(g), (h) explain that both the CF- and ABC approach yields almost same outcome.

Moreover, on minute speculation of comparisons shown in Figure 3(a), (b), (e), (f) with Figure 5(a), (b), (e), (f) we see a difference between the peak of effected and recovered populaces, when $ d = 0.002 $. Be that as it may, it is noted that in Figure 3(c), (d), (g), (h) with Figure 5(c), (d), (g), (h) the difference between the decreasing peak points is approximately 5 days, calculated at $ d = 0.05 $. The gradient of curves for different values of $ \alpha $ share similarities with the findings. This shows that affected individuals are recovering very quickly by the ABC approach, whereas the CF approach shows almost a delay in the transfer of affected individuals to recover compartments.

In all this, we have come across that for almost any efficacy of vaccine, and for arbitrary chosen $ \alpha $ if the death rate $ d = 0.002 $, then affected individuals exhibits virulent characteristics. This may result in tending towards the co-existing equilibrium point $ X^{*} $. From the Table 2, it can be deduced mathematically that for any vaccine efficacy ranging between 50% to 80% effectiveness can bring stability to the susceptible individuals to fight against the virus. It would be interesting to see how some state variables of the SEVR model are responding to each other for the cases when $ \mathcal{R}_{n} > 1 $. Therefore, Figures 6 and 7 provide parametric plot between the state variables and it is noticeable that they experience a chaotic behaviour.

The virtue of the models (2.1)–(2.4) and (2.5)–(2.8), when contrasted, found remarkable differences under the parameter values given in Table 1. The reason is memory properties of the kernel in the fractional derivatives' definitions. The CF and ABC derivative has exponential kernel and generalized Mittag-Leffler kernel, respectively. The ABC type shows a power-law memory, and also partial exponential decay memory ^[49]. It is clear that the model lies upon the fractional order notably, for various values of $ \alpha $ it displays a clear difference and suggested models (2.1)–(2.4) and (2.5)–(2.8) explores new aspects at the fractional values of $ \alpha $.

5.   Conclusions

Infection-related contact ascends with a growth in the size of population. Thus, COVID-19 infection spread during vaccination program for non-integer order model is considered, using the CF and ABC sense. Numerical simulation output for the proposed fractional order models are shown with distinct fractional order values $ \alpha \in] 0, 1 [$ and briefly compared, discussed and investigated. The vaccine efficacy and the death rate for state variables plays a significant role in escaping the infection. Since COVID-19 virus biology is changing rapidly, so the precise estimation of death rate, $ d $, can unfold the appropriate time for vaccine administration and how effective it should be. The graphical results demonstrate the ABC approach provides better suitability for mild cases. Whereas, the CF approach provides superior and more flexible results for critical cases. The CF approach provided a guarantee for use in lenient cases, whereas the ABC approach has a notable impact on the dynamics of COVID-19 infection and has given new insight for its use as a device to further research in dynamics of the spread of the disease in critical cases. These results show that CF and ABC approach implementation in real life situations are both plausible and doable as per the severity of illness for patient management. The findings also underline that even incomplete vaccination can have delay positive repercussions in minding the symptoms and spread of the Coronavirus COVID-19. It is found from the analysis that proposed fractional order mathematical models yield better results than that of the classical ones. The entire manuscript deals with the solution of a dynamical system of COVID-19 model for various fractional order $ \alpha $ ranging in the interval $ \left[0, 1 \right] $.

For future research work the analysis of COVID-19 infection spread for different geographical areas can be achieved by examining the models with relevant parameter values as per data trends of the region, and also including quarantine and number of dosages of vaccines compartments. It is anticipated that this research will provide significance and will thus strengthen the research relevant to COVID-19 transmission dynamics, so that progressive disease control policies are formulated to provide patients with better medical care to all in need.

Acknowledgments

The researchers would like to thank the Deanship of Scientific Research, Qassim University for funding the publication of this project. We are also thankful to the editor and anonymous reviewers for their fruitful comments and suggestions that help to improve this manuscript.

Conflict of interest

The authors declare there is no conflict of interest as well as no known competing financial interests.