Robust tracking control of a flexible manipulator with limited control input based on backstepping and the Nussbaum function

1.   Introduction

Flexible manipulators, as autonomous robots, possess the capability to move and execute tasks independently without direct human intervention, as highlighted in references such as ^[1,2,3]. These robots are typically equipped with a range of functionalities, including autonomous navigation, environmental sensing, decision-making and execution capabilities. These features enable them to operate autonomously, navigate diverse environments, interact with their surroundings and accomplish predefined tasks. The applications of flexible manipulators are extensive, spanning various domains such as industrial automation, smart homes, agriculture, field management, exploration and search and rescue operations. They contribute to increased work efficiency, reduced labor requirements, and the ability to handle hazardous and challenging tasks effectively.

Attitude tracking control of flexible manipulators or nonlinear systems has always been a hot research topic ^[4,5,6]. To address these issues, researchers have proposed various methods in the control of flexible manipulators. In ^[7], a disturbance observer is designed to estimate the presence of external disturbances in a flexible manipulator. Additionally, they utilize ${H_\infty }$ control based on specified performance and iterative learning control techniques to address both the vibration and inertia uncertainties of the flexible manipulator while achieving good tracking performance. In ^[8], the study addressed the vibration suppression and angle tracking issues of a flexible unmanned aerospace system with input nonlinearity, asymmetric output constraints and uncertain system parameters. Utilizing inversion techniques, a boundary control scheme was developed to mitigate vibrations and adjust the spacecraft's angle. Simulations also demonstrated the strong robustness of this approach. In ^[9], researchers address the challenge of tracking desired motion trajectories within an underwater robot-manipulator system, particularly when direct velocity feedback is unavailable. To tackle this issue, a comprehensive controller-observer scheme is developed, leveraging an observer to estimate the system's velocity. This innovative approach not only achieves exponential convergence in motion tracking but also ensures a simultaneous convergence in estimation errors. Different from the References ^[7] and ^[9], Reference ^[10] proposes a finite-time trajectory tracking controller for space manipulators. In this context, a radial basis function neural network is utilized to both estimate and compensate for the uncertain model of the space manipulator, especially when dealing with the capture of unknown loads. An auxiliary system is designed to mitigate actuator saturation. In ^[11], a new adaptive control law is proposed to solve the terminal tracking problem of underwater robot-manipulator systems. In addition, using the unit quaternion to represent attitude overcomes the problem of kinematic singularity. The primary objective of this controller is to guarantee the convergence of tracking errors to zero, even in the presence of uncertainties. Furthermore, it is designed to maintain system stability and achieve satisfactory tracking performance, even when operating under underactuated conditions ^[12]. In essence, the proposed control strategy provides a robust and effective means to ensure precise tracking performance for the aerial manipulator system, even when facing uncertainties and underactuation challenges.

In practical control systems, one of the most common nonlinear challenges arises from the physical characteristics of actuators, specifically, their limited output amplitude. This issue is known as the input saturation problem ^{[13,14,15,16,17]}. Furthermore, limitations in actuator control inputs refer to the existence of input restrictions in the control system of the flexible manipulator system ^[18,19]. This means that the actuators of the flexible manipulator, such as motors or hydraulic cylinders, may have limitations and cannot provide an infinite amount of force or speed. This affects the response time and control accuracy of the flexible manipulator. In ^[18], under the constraints of external disturbance and asymmetric output, a boundary control law with disturbance observer is constructed to suppress vibration and adjust the position of the flexible manipulator. As we all know, due to the high-dimensional characteristics of the flexible manipulator and its complex modeling, many scholars often build the flexible manipulator into a dynamic model with partial differential equations (PDEs) ^[20,21]. In ^[22], the dynamic model of a three-dimensional flexible manipulator is established using the Hamiltonian principle, resulting in a set of PDEs. Moreover, the designed control algorithm enables joint angle control and manages external disturbances even when the controller becomes saturated. In ^[23], the study investigates the vibration suppression and angular position tracking problems of a robotic manipulator system composed of a rotating hub and a variable-length mechanical arm. To achieve precise dynamic responses, a PDE modeling approach is employed for the manipulator system. Furthermore, two boundary control laws are proposed to achieve vibration suppression and angular position tracking for the robotic arm system. This research methodology is quite novel and intriguing. Similar to ^[22], the dynamics of high-dimensional flexible manipulator is expressed by PDEs. In addition, ^[24] designs an adaptive law to compensate uncertainty and disturbance, while meeting physical conditions and input constraints. In ^[25], under the inverse control algorithm, a design scheme for adaptive fuzzy tracking control based on observers is proposed to address the issues of system saturation and nonlinearity in the operation arm of a single-link robot. The main contribution of ^[26] is the design of a controller based on disturbance observer to regulate the joint angular position and quickly suppress the vibration of the beam, considering the presence of input saturation in the robotic system. Theoretical analysis demonstrates the asymptotic stability of the closed-loop system, and numerical simulations validate the effectiveness of the proposed approach. In ^[27], this study addresses the problem of asymptotic tracking for high-order nonaffine nonlinear dynamical systems with nonsmooth actuator nonlinearities. It introduces a novel transformation method that converts the original nonaffine nonlinear system into an equivalent affine one. The controller design utilizes online approximators and Nussbaum gain techniques to handle unknown dynamics and unknown control coefficients in the affine system. It is rigorously proven that the proposed control method ensures asymptotic convergence of the tracking error and ultimate uniform boundedness of all other signals. The feasibility of the control approach is further confirmed through numerical simulations.

Taking inspiration from the references mentioned earlier, this paper seeks to achieve precise state tracking for a single-joint manipulator in the presence of external disturbances and constrained control inputs. To address these challenges, we introduce a novel control framework grounded in the backstepping methodology. Simultaneously, we employ the Nussbaum function method to effectively manage the limitations associated with control inputs. The primary contributions of this paper are the following:

1. Different from other control methods to deal with disturbance ^[28,29,30], in order to achieve accurate tracking of the system state and effectively combat external disturbances, we employ the backstepping method ^[31,32] as a central control strategy. This method aims to enhance tracking precision and resilience to disturbances.

2. Furthermore, recognizing the constraints imposed by control input limitations in the flexible manipulator's actuator control system, we introduce a design approach centered on the Nussbaum function ^[33,34]. This innovative method is implemented to overcome these limitations, enabling robust control even within these constraints.

3. Finally, the effectiveness and disturbance rejection capabilities of the proposed control strategy are substantiated through numerical comparative simulations conducted in MATLAB/Simulink. These simulations offer empirical evidence of the strategy's reliability, emphasizing its potential to address challenges related to external disturbances and control input limitations in the context of flexible manipulator control.

The subsequent sections of this paper are structured as follows: Section 2 establishes the dynamic model of the flexible manipulator and provides certain lemmas. Section 3 introduces the control algorithm based on the backstepping method and the Nussbaum function. In Section 4, we perform numerical comparative simulations using MATLAB/Simulink to further validate the robustness and disturbance rejection performance of the proposed control method. Finally, Section 5 serves as the conclusion of this paper.

2.   Model and problem description

2.1.   Dynamic model of flexible manipulator

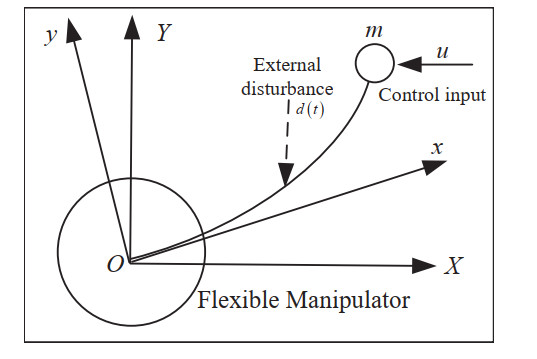
A single-joint flexible robotic arm consists of components including a transmission system, sensors, a controller, a power supply system and an outer casing with connecting elements. The controller serves as the intelligent core of the single-joint flexible robotic arm, enabling it to achieve bending, twisting and rotating motions, and it is used in various applications. The research object is a single-link flexible manipulator that moves horizontally, which as shown in Figure 1. From Figure 1, we can see that there is a $u(t)$ with limited input and external disturbances $d(t)$ at the end of the flexible manipulator. In the absence of gravitational effects, $XOY$ represents the inertial coordinate system, while $xOy$ serves as the follower coordinate system.

For the convenience of controller design, the single-joint flexible manipulator can be simplified as the following controlled object:

Let $x_1 = \theta$, $x_2 = \dot{\theta}$ and set $f(x) = -\frac{1}{I}\left(2 x_2+m g L \cos x_1\right)$, $\frac{1}{I} \tau(t) = u(t)$, then the controlled object can be written as:

where, $I$ is the moment of inertia, $u(t)$ represents the control input, $d(t)$ represents the disturbance and $F(x)$ represents the nonlinear function.

Remark 1: In this paper, the external disturbance $d(t)$ acting on the flexible manipulator is assumed to be equivalence bounded and satisfies $\left| {d\left(t \right)} \right| \le D$. In practical control systems of flexible manipulators, the existence of control input $u(t)$ constraints may lead to system divergence and loss of control. The control input constraint problem is a research focus. Therefore, the issue of control input constraints in the system will be investigated in the following sections.

2.2.   Useful assumptions and lemmas

Lemama 1 (see ^[35]): For a function $V:[0, \infty) \in \mathbb{R}$ and an inequality equation $\dot{V} \leqslant-\alpha V+f, t \geqslant t_0 \geqslant 0$, the solution is given by

where $\alpha$ is an arbitrary constant.

Lemama 2 (see ^[36]): Let $\Xi :\left[{\begin{array}{*{20}{c}} {\rm{0}} & \infty \end{array}} \right) \in R{\rm{ }}t \ge {t_0} \ge 0$, if $\dot \Xi \le - \varsigma \Xi + \wp$, then

where $\varsigma > 0$.

Lemama 3 (see ^[37]): For $k_{\mathrm{b}} > 0$, if the following inequality holds, then $|x| < c_b$:

Consider the following hyperbolic tangent smoothing function:

The function has the following four properties:

Remark 2: According to Figure 2, it can be observed that using a hyperbolic tangent smooth function can achieve bounded control input. For example, according to a Theorem in ^[38], using a hyperbolic tangent smooth function as a direct control law can achieve global asymptotic stability of the closed-loop system. However, this method is only suitable for the case when Eq (2.1) has $F(x) = 0$ and $d(t) = 0$. Building upon the work in ^[15,39], the following method presents a control algorithm for managing the input of a single-input single-output nonlinear system with the model structure given in Eq (2.1) when the control input is limited.

Remark 3: The Nussbaum function serves as a valuable mathematical tool for managing control input constraints, particularly in systems characterized by bounded control inputs. When compared to alternative methods for addressing control input saturation, such as saturation functions (as discussed in ^[40]), feedback linearization (as outlined in ^[41]) and dynamic output feedback (as explored in ^[42]), control laws based on the Nussbaum function offer the advantage of guaranteeing global asymptotic stability of the system. In simpler terms, regardless of the system's initial conditions, employing Nussbaum function-based control laws ensures that the system will converge to the desired equilibrium point, making it an ideal property in control systems. To sum up, the Nussbaum function provides an effective and robust approach for managing control input constraints, ensuring global stability and convergence of the control system, even when faced with bounded control inputs. Consequently, in order to address control input constraints in the context of robotic control systems, this paper has adopted an approach grounded in the Nussbaum function.

2.3.   Control objectives

This paper addresses challenges related to external disturbances and control input constraints in the context of a flexible manipulator control system. We propose a control strategy that combines the Nussbaum function and the backstepping method, as illustrated in Figure 3. This strategy is designed to ensure the stability of the system and to achieve accurate tracking of the system states, as represented by Eq (2.2). In this paper, let $y_d$ represent the reference signal, and the primary control objective is to guarantee that the control input $u(t)$ remains bounded, specifically $\left| {u\left(t \right)} \right| \le {u_{\max }}$. Additionally, as time $t$ tends toward infinity, our aim is for the system states $x_1$ to converge to $y_d$ and $x_2$ to converge to $\dot{y}_d$. This dual objective of input saturation control and asymptotic tracking is fundamental to our approach.

3.   Robust controller design based on backstepping

In order to satisfy $\left| {u\left(t \right)} \right| \le {u_{\max }}$, the control law is designed as follows

where ${u_{\max }}$ represents the maximum value of the control input $u(t)$.

Then, the design task of the control law is transformed into the design of $\wp \left(\chi \right)$, that is, the design of $\chi$.

The auxiliary system with stable design is

where $f(\Im) = {\chi _{\max }}\tanh \left({\frac{\Im }{{{\chi _{\max }}}}} \right)$, $\chi_{\max }$, $\chi$, $\Im$ and $U$ are auxiliary control signals.

Therefore, have

where $|\dot{u}(t)| \leqslant {\chi _{\max }}$ the design task of the control law is transformed into the design of $\Im$.

Remark 4: The advantage of backstepping control lies in its ability to handle nonlinear systems, unknown disturbances and parameter uncertainties, while exhibiting strong robustness and adaptability. Compared to other control methods, backstepping control offers design flexibility, robustness and adaptability to nonlinear systems. Therefore, in this paper, the control strategy based on backstepping is chosen to enhance the robustness against external disturbances.

Remark 5: Taking into account that the next controller design contains $y_d$ and its first to third derivatives ($\dot{y_d}, \ddot{y_d}, \dddot{y_d}$), the corresponding assumptions are made. In our work, we assume that $y_d$ and its first to third derivatives ($\dot{y_d}, \ddot{y_d}, \dddot{y_d}$) are bounded, and the exact values of these derivatives can be obtained. This assumption is to ensure that our controller design is feasible for practical application and can provide reliable performance.

The basic design steps of the inversion control method are:

Step 1: Define the position error as

Taking the derivative of Eq (3.5) with respect to time yields:

Define

Define virtual control quantity

where $b_1 > 0$.

Then

Select Lyapunov function as

Along with the trajectories of Eq (3.10), it can be shown that

Substituting the Eq (3.8) into the Eq (3.11), it can be obtained that

If $e_2 = 0$, then ${\dot L_1} \le 0$. To achieve this, the next step of the design is needed.

Step 2: Define the Lyapunov function as

Then

Remark 6: If we follow the traditional backstepping design method ^[43,44,45] for the control law designed based on the above equation, $u(t)$ can not be guaranteed to be bounded. In order to achieve bounded control input, we introduce a virtual term ${\tau _2}$ to design $u(t)$. Specifically, we let ${e_3} = \wp \left(\chi \right) - {\tau _2}$, which further leads to

Then

The virtual control law is defined as

where $b_2 > 0$.

Subsequently

Since $e_2 d \leqslant\left|e_2 d\right| \leqslant \eta_1\left|e_2\right|$, then

where

Therefore

From the ${\tau _2}$ expression, Eq (3.20) can be obtained

It can be seen that $\tau _2$ is a function of $x_1$, $x_2$, $y_{\mathrm{d}}$, $\dot{y}_{\mathrm{d}}$ and $\ddot{y}_{\mathrm{d}}$, then

where

From ${e_3} = \wp \left(\chi \right) - {\tau _2}$, we can get

Step 3: Define the Lyapunov function as

Then

Select

Then

Take

where $b_3 > 0$.

According to Eq (3.30), Eq (3.29) can be further rewritten as

with

According to Eq (3.20), we have

Then

Since

It can be seen that $\tau_3$ is $x_1$, $x_2$, $y_{\mathrm{d}}$, $\dot{y}_d$ and $\ddot{y_d}$, then

where

The Lyapunov function is defined as

Along with the trajectories of Eq (3.37), it can be shown that

Therefore, the design control law is

where $b_4 > 0$.

Substituting the Eq (3.39) into the Eq (3.38), we can further obtain

with

According to Eq (3.20), we have

Then

where $C_m = 2 \min \left\{b_1, b_2, b_3, b_4\right\}, \beta = \eta_1 k_u\left(\varepsilon_1+\varepsilon_2+\varepsilon_3\right)$.

According to Lemma 1, the solution of $\dot{V}_4 \leqslant-C_{\mathrm{m}} V_4+\beta$ can be obtained as

where

It can be seen that the final gain error of the closed-loop system depends on $C_{\mathrm{m}}$ and the upper bound of the disturbances $\eta_1$. In the absence of disturbances, $\eta_1 = 0$, $L_4(t) \leqslant \mathrm{e}^{-c_{\mathrm{m}} t} L_4(0)$ and $L_4(t)$ is exponentially convergent. In other words, $e_i$ is exponentially convergent. When $t \rightarrow \infty$, $x_1 \rightarrow y_{\mathrm{d}}$, $x_2 \rightarrow \dot{y}_d$.

Remark 7: In Section 3.1, a bounded control input method based on backstepping control is designed. In the control law Eqs (3.2) and (3.3), because of $\dot \Im = {\left({\frac{{\partial f(\Im)}}{{\partial \Im }}} \right)^{ - 1}}U$, when $\frac{\partial \wp}{\partial \chi}$ is very small, it is very easy to produce singular problems, which may usually lead to abnormal trajectory and even uncontrollable joint speed, bringing great damage to hardware equipment. Therefore, the design method of the Nussbaum function can be used to overcome this problem. In addition, the backstepping control method in Section 3.1 is still used.

From ${e_3} = \wp \left(\chi \right) - {\tau _2}$, we can get

where, $b$ is a constant and satisfies $b > 0$.

Design the auxiliary control signal as

Definition 1: If the function $N(X)$ satisfies the following conditions, then $N(X)$ is a Nussbaum function. A Nussbaum function satisfies the following bilateral characteristics ^[15]:

The Nussbaum function $N\left(X \right)$ and its adaptive law are defined as

where ${\gamma _X} > 0$.

Combined with Eq (3.44), we take

From Eqs (3.44) and (3.50), we can get

Selecting Lyapunov function as

Along with the trajectories of Eq (3.52), it can be shown that

Then

where

By further integrating the Eq (3.53), we can obtain

where

Remark 8: According to the theorem 1 analysis method in ^[15], the analysis is carried out by reduction to absurdity, and the conclusion that $X$ is bounded can be drawn by considering the two cases of $X$ having no upper bound and $X$ having no lower bound. Based on the boundedness of $X$, we know that $N\left(X \right)$ is bounded. According to the Eq (3.55), it can be known that $L_3(t)$ is bounded, so $e_1$, $e_2$, $e_3$, $\dot{e}_1$ and $\dot{e}_2$ are bounded. Based on Eq (3.55), we have ${C_1}\int_0^t {{L_3}} (\tau){\rm{d}}\tau {L_3}(t) - {L_3}(0) + \frac{1}{{{\gamma _X}}}w(t)$. Therefore, $\int_0^t {{L_3}} (\tau){\rm{d}}\tau$ is bounded. Furthermore, $\int_0^t {e_1^2(\tau)d\tau }$ and $\int_0^t {e_2^2(\tau)d\tau }$ are bounded. According to the Barbalat lemma, when $t \rightarrow \infty$, $e_1 \rightarrow 0$, $e_2\rightarrow 0$. Thereby we find that under the condition of $|u(t)| \leqslant u_{\mathrm{M}}$, $x_1 \rightarrow x_d$ and $x_2 \rightarrow \dot{x}_{\mathrm{d}}$.

4.   Simulation examples

4.1.   Two control methods for comparison

In this study, we performed simulations using MATLAB/Simulink, utilizing a simulation duration of 100 seconds and a time step of 0.001 seconds. This choice of parameters aims to enhance the validation process for the effectiveness of the robust backstepping control (RBSC) method. Furthermore, to ensure a fair comparison, we conducted simulations within an identical simulation environment and under the same external disturbance conditions, allowing us to contrast the simulation outcomes with those obtained using the robust sliding mode control (RSMC) method.

In addition, in order to verify the robustness and anti-disturbance performance of the control method (RBSC)} proposed in this paper, we chose the simulation verification under two kinds of disturbance (time-varying disturbance and constant disturbance). The time-varying disturbance and constant disturbance can be selected as:

Time-varying disturbance:

Constant disturbance

4.1.1.   RBSC method

In this section, we conducted numerical simulations using MATLAB/Simulink to validate the effectiveness of the control algorithm for a flexible manipulator under conditions of limited control input. The primary system program in Simulink, based on an S function, is illustrated in Figure 4. The flexible manipulator used as the controlled object is described by Eq (2.1), with a gravitational acceleration of 9.8 m/s$^2$, a manipulator mass of m = 1.66 kg, and a length of 1.20 m. The auxiliary signal $w$ is determined using Eq (3.45) through Eq (3.50), with parameters set as ${\gamma _\chi } = 1$, $b = 10$, ${b_1} = 10$, ${b_2} = 12$ and ${b_3} = 8$. The expression for the control input restriction is $\left| {{u_M}} \right| \le 18$. The simulation results are shown in Figures 5–8.

4.1.2.   RSMC method

In order to better verify the effectiveness and robustness of the precise tracking control proposed in this paper (RBSC method), we choose to compare it with the robust sliding mode control method (RBSC method)} in this paper. Aiming at the single-joint manipulator model (Eqs (2.1)–(2.2)), we choose a sliding mode function as

where, $c > 0$.

Furthermore, the angle tracking error of manipulator is defined as

We choose the Lyapunov function as

Taking the derivative of Eq (4.3) yields:

From Eq (4.4), the robust sliding mode controller is designed as follows

where $k > 0$.

4.2.   Simulation results

From Figures 5–8, it is evident that the precise tracking control of the manipulator's state and the overall system's stability can be achieved through the control strategy proposed in this paper. In Figure 5, } under the control method proposed in this paper, we use visual representations to highlight the performance of our controller. Specifically, the red solid line represents the ideal reference signal, while the blue dashed line illustrates the actual tracking of both the position and velocity of the manipulator. The key takeaway from this visualization is the successful tracking of the desired reference signal. Both the position and velocity profiles closely align with the ideal reference, indicating that our control method effectively guides the manipulator to achieve the desired trajectory. This visual confirmation of accurate tracking is significant because it demonstrates the practical applicability and efficacy of our control approach. Figures 6 and 8 depict the variations in $\chi$ and $X$. In Figure 7, we observe the response curve of the system's control input, even when subject to input limitations ($|u(t)| \leq u_{\mathrm{M}}$, where $u_{\mathrm{M}} = 18$). Remarkably, the Nussbaum function method proposed in this paper maintains system input stability under such constrained conditions. Figure 9 illustrates the response graph for angle and velocity tracking control of the manipulator, comparing the two control methods. It is evident from Figure 9 that the precise tracking control of the manipulator's angle and velocity can be effectively achieved using the control method presented in this paper.

Furthermore, Figure 10 displays the response graph of the control input under both methods, revealing the superior stability of the control method proposed in this paper.

Robustness is a crucial aspect of control system design. In order to further verify the effectiveness and robustness of the control method (RBSC method) in this paper, we refer to Figures 11 and 12. As can be seen from Figures 11 and 12, the angle and angular velocity of the manipulator can be well tracked under the control method (RBSC method) in this paper, and the control method (RBSC method) in this paper has stronger robustness and anti-disturbance performance.

5.   Conclusions

In summary, this study explores the challenges faced by flexible manipulators, versatile automated devices with a wide array of applications. These manipulators often encounter issues related to external disturbances and limitations in controlling their actuators, which significantly impact their tracking precision. To address these challenges, we have introduced a comprehensive control strategy. We employed the backstepping method to achieve precise state tracking and manage external disturbances effectively. Additionally, we utilized the Nussbaum function approach to tackle control input limitations, enhancing the robustness of the system.

For future work, we plan to further improve and expand this control strategy. This may include studying advanced control algorithms, exploring adaptive techniques to deal with various disturbances, and optimizing the design of methods based on the Nussbaum function. In addition, considering that the flexible manipulator model is easily disturbed and the controller design is complicated, the establishment of a flexible manipulator model based on PDE should be paid attention to.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

Science and technology project support of China Southern Power Grid Corporation (project number: [GDKJXM20201943]).

Conflict of interest

The authors declare there is no conflict of interest.