Multi-behavioral recommendation model based on dual neural networks and contrast learning

1.   Introduction

In recent years, with the rapid development of big data and mobile internet, people can access a lot of online content, such as movies, news and other goods, but a lot of information will make users at a loss, so filtering the data becomes an essential part. The recommendation algorithm can learn the user's interest and preference according to the user's attributes and historical behavior and select the items that the user may be interested in from the mass of information to recommend to the user ^[1,2,3]. Thus, it can improve the efficiency of information screening ^[4], solve the problem of information overload in the era of big data and improve the user experience.

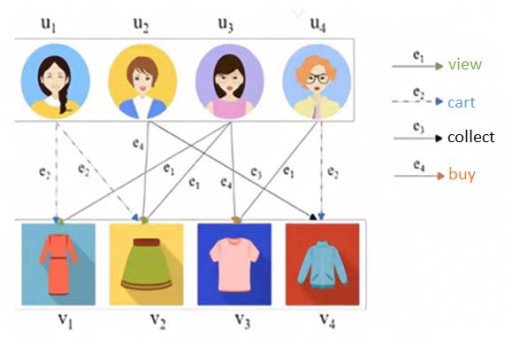
In all kinds of recommendation algorithms, the collaborative filtering algorithm ^{[17,18,19,20]} is the most widely used. However, traditional recommendation algorithms mainly utilize a single user interaction data and ignore the multiple behavior types of users and items in the real application scenario. Figure 1 is an example of user-item interaction for an online marketplace, where ${v}_{k}$ denotes item k, and ${v}_{i}$ denotes user i. ${e}_{1}, {e}_{2}, {e}_{3}$ and ${e}_{4}$ represent user behavior of viewing, carting, collecting and purchasing, respectively. Therefore, in-depth analysis of user item interaction, considering the behavior type of user interaction, can improve the accuracy of user item modeling and improve the accuracy and interpretability of recommendations.

In recent years, the recommendation algorithm based on deep learning framework has become a research hotspot and is the first choice of recommendation platform. Deep learning can effectively learn user and item characteristics through the user's interaction history and a variety of supporting information (such as text, images, etc.) to improve the effectiveness and accuracy of recommendations. At present, the multi-behavior recommendation algorithm based on deep learning is mainly based on graph neural network ^[12].

Graph neural network is one of the main methods of multi-behavior recommendation algorithm based on deep learning. It first constructs the interaction graph under multi-behavior and then uses the graph neural network to model the user's multi-behavior interaction graph. High-order cooperative information is captured, for example. The graph is a u-centered multi-behavior interaction graph, and the high-order domain information of ${u}_{1}$ is obtained by graph convolution. For example, MBGCN ^[5] and GHCF ^[6] both use graph convolution networks to handle multi-behavior interaction graphs. The recurrent neural network method is also widely used in the multi-behavior recommendation of deep learning ^[21–23]. First, it constructs the multi-behavior interaction sequence of the user. The temporal characteristics of multi-behavioral data are then obtained using recurrent neural network methods, such as DUPN ^[7] and DIPN ^[8], which utilize long-and short-term memory networks ^[9] and bidirectional gated cyclic units ^[10], respectively, to process multi-behavioral interaction sequences, getting the temporal characteristics of the data.

Although great progress has been made in the research of multi-behavior recommendation, the following problems still exist:

(1) Complex dependencies between user and item multi-actions have not been fully captured. Both MBGCN ^[5] and GHCF ^[6] emphasize that different behaviors have different degrees of importance and aggregate higher-order neighborhood information by assigning different weights to behaviors. However, this approach only learns the importance of behavior. KHGT ^[11] emphasizes not only that different behaviors have different degrees of importance but also that there are interactions between behaviors. Still, none of these approaches emphasizes the temporal nature of behavior. DUPN ^[7] and DIPN ^[8] emphasize the sequence of behavior occurrence and use the method of circular neural network to model the multi-behavior interaction sequence, which can effectively capture the temporal correlation of behavior, but it ignores the feature correlation of behavior. To sum up, both of the two multi-behavior recommendation methods have one-sidedness. In fact, capturing feature correlation and temporal correlation at the same time is beneficial to learning accurate user features.

(2) The relevance of behavioral characteristics to users and items is ignored. MBGCN uses a graph convolution network to learn a user's multi-behavior interaction graph and distinguish the learning weight of interaction number under different behavior, but it only considers the correlation between behavior and user. The GHCF sets independent behavior vectors that, when convoluted, aggregate weights for joint item information and behavior informatics habits but only considers the correlation of items with behavior. MBGMN ^[13] uses a graph convolution network to extract high-order neighborhood information of users and items and then sets up a trainable network to learn the effects of various behaviors on user preferences under target behaviors, but it does not take into account the relevance of behavior to users and items.

(3) The over-smoothing problem is caused by multi-layer convolution. MBGCN and GHCF both use graph convolutional neural networks to model multi-behavior interaction graphs, but neither of them takes into account the over-smoothing caused by multi-layer convolution. S-MBRec ^[14] and CML ^[15] used graph convolution to model the multi-behavior interaction graph, which mainly emphasized capturing the common characteristics of items under multi-behavior of users, ignored the differences between multi-behavior interactions of users and easily introduced redundant information, increasing over-smoothness. The MMCLR ^[16] emphasizes fine-grained differences between multi-behavioral interactions, considering only differences in interactions of different behavioral types and not differences in interactions at different times. To sum up, effectively distinguishing the differences of different user characteristics, the differences of user interaction characteristics and the differences of interaction characteristics at different times can effectively alleviate the problem of over-smoothing and improve recommendation performance.

Based on the research and analysis of multi-behavior recommendation algorithms, this paper summarizes two problems of current multi-behavior recommendation algorithms: First, they cannot fully capture the complex dependence relationship between users and item multi-behavior; the problem of over-smoothing is caused by multi-layer convolution. In order to solve the above problems, this paper proposes corresponding solutions.

First, in order to fully capture the complex dependencies between user and item, a multi-behavior recommendation model based on dual neural networks is proposed. First, in order to capture the user's behavior dependence, we set up different behavior vectors for each user, and use a graph convolution network to process the user item interaction graph under different behaviors. Then, the characteristics of users and items under different behaviors are input into the self-attention network, and the feature correlation between learning behaviors is analyzed. In this study, we input the user's recent interaction items and the corresponding behavior characteristics into the recurrent neural network according to the time sequence and then introduce the attention network to learn the temporal characteristics related to the items to be recommended. In order to improve the performance of the target behavior prediction model, behavior features and time series features are integrated into the prediction layer for learning.

Second, in order to alleviate the over-smoothing problem caused by multi-layer graph convolution in graph neural networks, the contrast learning method is introduced based on the multi-behavior recommendation model based on double neural networks. First, the distance between the current user and the similar user is shortened, and the distance between the current user and the different user is increased. Second, we can distinguish the differences between the products of different time interactions and learn more accurate user characteristics. The contrast learning task was used as an auxiliary task to enhance the prediction performance of the target task.

2.   The design of DNCLR model

In this study, a multi-behavior recommendation model based on dual neural networks and contrast learning is designed. The model frame is shown in Figure 3. The model mainly includes a multi-behavior graph convolution layer, a multi-behavior recurrent neural network layer and a prediction layer:

(1) Multi-behavior graph convolution layer: It convolves the interaction graph under multi-behavior separately, obtains the convolution weight by combining user, behavior and item features, aggregates higher-order information and obtains the user and item features under k behavior. Then, in order to reduce the problem of over-smoothing caused by graph convolution, the contrast learning method is introduced into the convolution layer of the multi-behavior graph. By narrowing the distance between current users and similar users, pushing the distance between different users, and filtering out the redundant information caused by the aggregation of multi-layer neighborhood information. Secondly, by distinguishing the interactive features of users under different behaviors, the effects of user similarity and different interaction behaviors on users are emphasized. Finally, the convolutional contrast loss of multi behavior graphs was introduced as an auxiliary task.

(2) Multi-behavior recurrent neural network layer: It inputs the behavior and item features of the user's recent interaction sequence into the long-term and short-term memory network to learn the context information of the multi-behavior interaction and obtains the temporal correlation of the multi-behavior. In order to obtain more accurate short-term preferences of users, the contrast learning method is introduced in the layer of the multi-behavior recurrent neural network. By making the characteristics of users' preferences closer to their near-term preferences and far away from their historical preferences, and emphasizing the impact of the time of occurrence of behaviors on users. A multi-behavior recurrent neural network was introduced to compare the loss as an auxiliary task.

(3) Prediction layer: It combines the user's multi-behavior feature correlation and time series correlation to obtain the user's final features and combines the user's personalized behavior vector to predict the user's probability of interacting with the recommended items under the target behavior. The loss of contrast learning is combined with the loss of model training.

The following sections, sections 2.1 and 2.2 and 2.3, detail the graph convolution layer, the multi-behavior recurrent neural network layer and the prediction layer.

2.1.   The multi-behavior graph convolution layer

2.1.1.   Multi-behavior graph convolution network

In this section, graph convolution networks are introduced to enrich user and item characteristics by aggregating higher-order neighborhood information. The input is a multi-behavior interaction graph G = {U, V, B}, where B represents the set of edges in the graph, and G = {U, V, Bk} represents the interaction graph under K behavior, and Bk represents the set of K-behavior edges. Considering that different users have different behavior characteristics, the user personalized behavior vector b_{u, k} is set. In the graph Gk convolution, (u, b_{u, k}, v_j) is treated as a triplet (head node, relation, tail node), and the relation weight is obtained by calculating the inner product of the three factors. Taking the user as an example, the aggregate weight is obtained by the inner product of the user u and (b_uk+v_j). Figure 4 shows the implementation of the multi-behavior diagram convolution layer. The specific formula for calculating the convolution weight is as follows:

where v_j denotes the interactive items of user u, ${\pi }_{u, {v}_{j}}^{{b}_{u, k}}$ denotes the preference weight of user u for item v_j under behavior k, and the higher the value of ${\pi }_{u, {v}_{j}}^{{b}_{u, k}}$ is, the more item v_j conforms to the characteristics of the user's interest under behavior k. ${N}_{u}^{k}$ represents the neighbor information of user u under k behavior. ${\stackrel{-}{\pi }}_{u, {v}_{j}}^{{b}_{u, k}}$ is the normalized weight.

According to the weighted values, the corresponding neighborhood features are weighted and summed to update the embedding representation of users and items under k behavior.

where ${\boldsymbol{u}}^{\boldsymbol{k}, \left(\boldsymbol{h}\right)}$ and ${\boldsymbol{v}}^{\boldsymbol{k}, \left(\boldsymbol{h}\right)}$ represent the representations of user u and v in layer h under behavior k, respectively. ${\boldsymbol{u}}^{\boldsymbol{k}, \left(0\right)}$ is the initial embedding u of the user, and where ${\boldsymbol{v}}^{\boldsymbol{k}, \left(0\right)}$ is the initial embedding v of the item. After propagation in the h layer, we get the representation of multiple users and items under a single action and merge these representations into the user and item representations under multiple actions, as in the case of the user representation under action k:

Then, the self-attention mechanism is used to learn the correlation between multiple behaviors, and a feedforward neural network (FNN) is used to fuse user interaction features under multiple behaviors to obtain user features related to behavioral features u_feature. u_feature captures the correlation of user features under multiple behaviors.

where ${\boldsymbol{w}}_{\boldsymbol{u}, \boldsymbol{k}}ϵ{R}^{d*d}$ is the trainable weight matrix.

2.1.2.   The convolution layer of multi-behavior graph introduces the contrast learning method

In the previous section, we introduced that multi-behavior graph convolution networks enrich the features of central nodes by aggregating the information of neighbor nodes, but they also face the problem of over-smoothing. Although the degree of over-smoothing is reduced by assigning values to edges, one still faces the problem of over-smoothing when aggregating multi-layer neighborhood features. Therefore, this section seeks from two angles to introduce a comparative learning method to further alleviate the smoothing problem. First, by closing the distance between the current user and the similar user and pushing the distance between the current user and the different user, the redundant information introduced by multi-layer image convolution can be filtered out, and the smoothing problem can be alleviated, to capture the differences among the user's own multi-behavior interaction features, strengthen the user's personalized features and further reduce the degree of over-smoothness.

This section uses the Jaccard similarity coefficient to calculate user-to-user similarity based on the user interaction history, with the following implementation formula:

where ${I}_{u}$ is the set of items that user u has interacted with, ${I}_{{u}_{i}}$ is the set of items that user ${u}_{i}$ has interacted with, ${I}_{u}\bigcup {I}_{{u}_{i}}$ is the intersection of two sets, ${I}_{u}\bigcap {I}_{{u}_{i}}$ is the union of two sets, and $J({I}_{u}, {I}_{{u}_{i}})$ is the ratio of the intersection size to the union size of the historical collection of user u and user ${u}_{i}$ interactions. The greater the similarity coefficient of Jaccard is, the more similar the historical interaction characteristics of two users are.

Figure 5 shows the changes before and after learning based on the user interaction history. The yellow dots represent the user, and the blue dots in the circle represent the user interaction items. After contrast learning, the distance between users with the same interaction is decreased, and the distance between users without the same interaction is greater.

In the multi-behavior recurrent neural network layer, the method of contrast learning is introduced, in which the user-based loss function of contrast learning is defined as

where ${\boldsymbol{u}}_{\boldsymbol{f}\boldsymbol{e}\boldsymbol{a}\boldsymbol{t}\boldsymbol{u}\boldsymbol{r}\boldsymbol{e}}$ represents user characteristics obtained from the convolution layer of the multi-behavior graph, ${u}_{{i}^{+}}$ represents users with high similarity to the user u history interaction set (Jaccard), and ${u}_{{i}^{-}}$ represents users who have not had the same interaction with user u. ${L}_{UserCL}$ decreases the distance between ${\boldsymbol{u}}_{\boldsymbol{f}\boldsymbol{e}\boldsymbol{a}\boldsymbol{t}\boldsymbol{u}\boldsymbol{r}\boldsymbol{e}}$ and users with similar preferences and increases the distance between users without similar preferences, thus filtering out the redundant information introduced by multi-layer graph convolution and enhancing the user's personalized characteristics, mitigating the smoothing problem.

Moreover, because the feedback information provided by the user is implicit, it usually takes the user's interactive goods as the positive sample of the user and the non-interactive goods as the negative sample of the user. In fact, not all of the items that have been interacted with in the user's multi-activity interaction data match the user's interests. For example, a user is directed to view an item but is not interested in the item after viewing it and therefore does not purchase it. Therefore, there are differences between multi-behavior interactions, and capturing the differences between interaction features under multi-behavior can help in learning more accurate user characteristics. This section classifies items that interact under multiple user actions into levels based on the type of behavior. For example, in an online store, users view unpurchased items that have not been purchased or added to a shopping cart with less priority than the purchased items. This section prioritizes the items that the user has interacted with. Items with higher priority are more in line with user preferences.

Figure 6 shows the priority of the item according to the type of behavior, with the lowest being view priority, and the goods under view priority are the goods that are only viewed, with nothing else being done. Cart and collect items are items that will only be added to the cart or collected but are not bought. Buy-first items are items that the user ultimately buys.

The goal of this section in prioritizing items based on the type of user behavior is to capture the differences between the user's multi-action interactions. By introducing the method of contrast learning, the similarity between users and high-priority items and the difference between users and low-priority items are maximized to enhance the learning of users' personalized characteristics. The item-based loss function of contrast learning is defined as

where ${v}_{j}^{k}$ denotes item ${v}_{j}$ that interacts under k behavior, ${v}_{j\text{'}}^{k\text{'}}$ denotes item ${v}_{j\text{'}}$ that interacts under other behavior k', and action k always takes precedence over action k'. The item ${v}_{j\text{'}}$ is interactive under k' behavior and not interactive under k behavior. For example, the priority will be divided into view, cart and collect and buy priorities. View priority is when the commodity is only viewed, without other operations; cart and collect items are items that will only be added to the cart or collected but are not purchased; purchase priority is the highest and refers to the end-user purchase of goods. The loss function is calculated according to the priority, taking the 3-level priority as an example, and the concrete implementation is formulated as follows:

Based on the users' contrast learning loss and the item-based contrast learning loss, the positive and negative samples are selected from two angles, and the two contrast learning losses are optimized at the same time, so that the distance between the users and the positive samples is lower, and the distance between the users and the negative sample is greater, strengthening the user personalized characteristics and reducing the degree of over-smoothness. The combined objective function of two comparative losses is formulated as follows:

2.2.   Multi-behavior recurrent neural network layer

2.2.1.   Multi-behavior recurrent neural network

In this section, we introduce a multi-behavior recurrent neural network layer in order to capture the temporal correlation between behaviors, so we can learn the context information of multi-behavior interaction and the temporal correlation of behavior. As shown in Figure 7, we select the recent T interactions of user u to form seq{${s}_{1}, {s}_{2}, ···, {s}_{t}, ···, {s}_{T}$}, where each interaction ${s}_{t}$ contains the behavior vector b_ut and the item vector v_t and input them to GRU in chronological order. The GRU gating mechanism is formulated as follows:

where ${r}_{t}$ and ${z}_{t}$ are reset door and update door at t time, respectively. The values of ${r}_{t}$ and ${z}_{t}$ are in the range of 0 ~ 1. ${r}_{t}$ controls the proportion of the former state information ${h}_{t-1}$ to ${h}_{t\text{'}}$. The smaller the ${r}_{t}$ is, the less information ${h}_{t-1}$ adds to ${h}_{t\text{'}}$. ${z}_{t}$ controls the amount of new information and historical information to retain, (1-${z}_{t}$) larger, ${h}_{t-1}$ more information to retain. ${h}_{t}$ is the output of data that has been selected to be forgotten and retained by updating the gate.

At the same time, in order to get the different behavior dependence when interacting with different items, we present the HT output of each hidden layer of GRU, the learning of the input attention mechanism and the historical interaction characteristics which have high correlation with the items to be recommended. First, we define Q $\in {R}^{d*d}$, K $\in {R}^{d*d}$, V $\in {R}^{d*d}$ in the attention mechanism and calculate the weight ${{\mathtt{β}}}_{v, {h}_{t}}$ of each interactive input value. ${{\mathtt{β}}}_{v, {h}_{t}}$ is determined by the inner product of the query value and the key value and is implemented as follows:

where ${{\mathtt{β}}}_{v, {h}_{t}}$ is the correlation score of memory ${h}_{t}$ at time t and items v to be recommended. The ${\boldsymbol{u}}_{\boldsymbol{t}\boldsymbol{i}\boldsymbol{m}\boldsymbol{i}\boldsymbol{n}\boldsymbol{g}}$ was obtained by weighted polymerization of normalized ${\stackrel{-}{{\mathtt{β}}}}_{v, {h}_{t}}$. ${\boldsymbol{u}}_{\boldsymbol{t}\boldsymbol{i}\boldsymbol{m}\boldsymbol{i}\boldsymbol{n}\boldsymbol{g}}$ captures temporal correlations between multiple behaviors.

2.2.2.   Multi-behavior recurrent neural network introduces contrast learning method

In addition to considering the item priority of interactions under multiple actions, we also need to consider the impact of the time of action on user preferences. Therefore, this section introduces contrast learning in the multi-behavior recurrent neural network layer and emphasizes the differences of interaction characteristics at different times. Since the user requirements are stable over time, this section assumes that the user has recently interacted with T items of the same category, and beyond T, the item that the user interacted with comes from another requirement. As shown in Figure 8, recently, the T interaction features of users tend to be demand for "Snack package, " while the T interaction features before the interaction are more inclined to other requirements. Therefore, the method of contrast learning is introduced to make the user features close to the user's recent interaction items and far away from the user's historical interaction features, so as to obtain more accurate recent user preference features. This section sets the recent interactions to positive ${v}_{{t}^{+}}$, and before the T interactions, it randomly selects T as negative ${v}_{{t}^{-}}$.

Based on the above analysis, a comparative learning method is introduced in the multi-behavior recurrent neural network layer, which emphasizes the influence of the time of behavior occurrence on the users by making the characteristics of the users' preferences closer to their recent preferences and far away from their historical preferences. The user-based loss function of contrast learning is defined as

where ${\boldsymbol{u}}_{\boldsymbol{t}\boldsymbol{i}\boldsymbol{m}\boldsymbol{i}\boldsymbol{n}\boldsymbol{g}}$ is a time-series-based user feature obtained by multi-behavior recurrent neural network layer in DNCLR model.

2.3.   Prediction layer

The convolution layer of the multi-behavior graph learns the user representation ${\boldsymbol{u}}_{\boldsymbol{f}\boldsymbol{e}\boldsymbol{a}\boldsymbol{t}\boldsymbol{u}\boldsymbol{r}\boldsymbol{e}}$ by capturing the feature correlation between the multi-behavior. The multi-behavior recurrent neural network layer learns the user representation ${\boldsymbol{u}}_{\boldsymbol{t}\boldsymbol{i}\boldsymbol{m}\boldsymbol{i}\boldsymbol{n}\boldsymbol{g}}$ by capturing the temporal correlation between the multi-behavior. Combine the two to get the final statement from user u:

At the same time, we get the ${\boldsymbol{v}}_{\boldsymbol{f}\boldsymbol{e}\boldsymbol{a}\boldsymbol{t}\boldsymbol{u}\boldsymbol{r}\boldsymbol{e}}$ of item v and then use the inner product to calculate the probability score of user u interacting with item v under k behavior:

The loss function is calculated according to the probability score obtained by the inner product and is defined as follows:

where K represents the total number of behavior types, and ${\lambda }_{k}$ is the hyperparameter. ${\lambda }_{k}$ can be adjusted for the data set to control the effect of K behavior on overall training, while $\sum _{k = 1}^{K}{\lambda }_{k}$ = 1.

Finally, taking advantage of the combined learning loss, in the training phase, this section uses the Adam algorithm to optimize the following objective functions:

3.   Experiment and analysis

This section mainly introduces the experimental data set, evaluation index, experimental benchmark, parameter setting, model performance evaluation and ablation experiment. Yelp, ML20M and Tmall were used in the experiment. Hit ratio (HR) and normalized discounted cumulative gain (NDCG) were used to evaluate the recommendation performance of the DNCLR model, and compared with three advanced multi-behavior recommendation algorithms to verify the recommendation performance of the DNCLR model.

3.1.   Experimental data

In this experiment, the performance of the model was tested using a public dataset of movie recommendations and music recommendations. The data comes from Last.FM, the online music platform, and contains music interactions for about 2,000 users, 20,000 friends and 10,000 triples of knowledge. Movielens-1M is one of the most widely used public datasets for movie recommendation scenarios, containing about one million user ratings, 40,000 friends and 20,000 triples of the knowledge graph. The dataset was randomly divided into the training set and the testing set in a ratio of 8:2. Detailed statistical results are shown in Table 1.

Yelp is a well-known US merchant review site, similar to our popular review. According to the data of users' comments and ratings, there are four behavior types: (1) The user comments on the merchant. (2) The user dislikes the user comments on the merchant, and the rating r ≤ 2. (3) Neutrality indicates that the user's rating of the merchant is 2 < R < 4. (4) Preference indicates that the user's rating of the merchant is R ≥ 4. Set {like} as the target behavior here.

ML20M: The MovieLens public data set stores user ratings of movies, which are widely used in recommendation systems. In this study, we select ML20M as an experimental data set and use the same classification criteria as Yelp according to user ratings. There are three behavior types, {dislike, neutral, like}, and we set {like} as the target behavior.

Tmall: This data set was obtained from the Heaven Lake platform. To ensure that each user has enough training data, users and items with fewer than five interactions are filtered out. The dataset contains four main behaviors {view, cart, collect, buy} and sets {buy} as the target behavior.

Table 1 shows the details of these datasets, where the bold font represents the target behavior.

3.2.   Evaluation indicators

Two commonly used metrics were used to evaluate model performance, namely, hit ratio (HR) and normalized discounted cumulative gain (NDCG).

HR represents the number of items in the test set that appear in the top-K recommendation list as a percentage of the total number of items in the test set. The higher the HR is, the higher the hit rate.

where GT is the total number of items in the test set, and Number of Hits@K is the number of test set items contained in the Top-K recommendation list.

The NDCG represents a comprehensive assessment score for the relevance and ranking of items in the test set in the Top-K recommendation list. The higher the NDCG value is, the better the sorting result.

where $re{l}_{i}$ denotes the correlation score of item i, and ${{\mathrm{D}}{\mathrm{C}}{\mathrm{G}}}_{u}@{\mathrm{K}}$ calculates the score of the first K items in the user's u recommendation list, taking into account both correlation and order factors. ${\mathrm{I}}{\mathrm{D}}{\mathrm{C}}{{\mathrm{G}}}_{u}@{\mathrm{K}}$ is the normalized result of ${{\mathrm{D}}{\mathrm{C}}{\mathrm{G}}}_{u}@{\mathrm{K}}$, and ${\mathrm{N}}{\mathrm{D}}{\mathrm{C}}{\mathrm{G}}@{\mathrm{K}}$ is the average of all users as the final score.

3.3.   Baseline model

In order to verify the effectiveness of introducing the method of contrast learning to strengthen the personalized recommendation model, three advanced multi-behavior recommendation algorithms based on contrast learning are selected in this section:

S-MBRec ^[14]: Using graph convolution networks to obtain the basic features of users and items, and set up adaptive monitoring tasks to learn the importance of different behaviors. Then, contrast learning is used to explore the commonalities between multiple behavioral interactions. Reduced the redundancy of auxiliary behavior data and extracted key information.

CML ^[15]: The graph neural network of behavior perception is used to acquire the user interaction features under the multi-behavior. Then, through the contrast learning paradigm, the contrast loss weight of each behavior is adaptively learned. Therefore, we can model the individual dependence relationship between different behaviors.

MMCLR ^[16]: Based on multi-view learning of user features, firstly, using the method of contrast learning to learn accurate user interaction features. Secondly, using the method of contrast learning to model the relationship between different behaviors. This method captures coarse-grained commonalities and fine-grained differences between multiple behavioral interactions.

3.4.   Parameter settings

In the experiment, the model is based on TensorFlow framework and optimized by Adam Optimizer. The settings of the three data sets are shown in Table 2. Epoch refers to the number of training sessions of the model, which is 120 for all three datasets; lr refers to the learning rate; batch_size refers to the batch size; d refers to the embedded dimension of user, item and behavioral characteristics; H refers to the level of graph convolution; and T represents the number of recent interactions. The weight parameters ${{\mathrm{\lambda }}}_{k}$ in Yelp, ML20M and Tmall datasets were set to [1/6, 1/6, 1/6, 3/6], [1/3, 1/3, 1/3], [1/4, 1/4, 1/4, 1/4]. The ${{\mathrm{\lambda }}}_{k}$ of each dataset is different because each task has a different impact on user and item feature optimization in different datasets. Moreover, in order to ensure the accuracy of the experimental results, the model and other comparison benchmarks are run under the same environment configuration. At the same time, the personalized recommendation based on behavior dependence and contrast learning mainly involves three important parameters. These three parameters are item priority of multi-behavior interaction, super-parameter ${{\mathrm{\alpha }}}_{1}$ of contrast learning weight based on multi-behavior and super-parameter ${{\mathrm{\alpha }}}_{2}$ of contrast learning weight based on time series, respectively. The range of values for ${{\mathrm{\alpha }}}_{1}$ and ${{\mathrm{\alpha }}}_{2}$ is [0.1, 0.05, 0.01, 0.005, 0.001]. The specific parameter settings are shown in Table 2.

3.5.   Model performance assessment

As shown in Table 3, the experimental results of DNCLR consistently outperformed the other three comparison benchmarks. First of all, DNCLR, S-MBRec and CML are optimized models based on graph convolution networks using contrast learning method. However, compared with S-MBRec, DNCLR increased HR@10 by 4.98%, 6.1% and 8.82%, respectively. The reason is that the S-MBRec model only studies the influence of auxiliary behavior on the target behavior and fails to consider the mutual influence of multi-behavior. It only considers the commonness among the characteristics of multi-behavior interaction, failing to account for differences in interaction characteristics at different times. It also shows that DNCLR can effectively improve recommendation performance by capturing the complex dependencies between user and item behaviors and considering the effect of behavior occurrence time on user preferences. In addition, the HR@10 results on the three CML data sets increased by 2.97%, 2% and 4.59%, respectively.

MMCLR uses multi-view modeling to learn user characteristics. Experimental results show that DNCLR improves HR@10 by 2.5%, 0.3% and 4%, respectively, compared with MMCLR on three data sets. Although the commonality of user behavior is captured in MMCLR, it fails to consider the impact of behavior timing on user preferences. According to MMCLR, the user's preference for interaction items under the target behavior is always greater than that for interaction items under other behaviors. In fact, the type of user interaction cannot completely determine the user's preference characteristics, and one also needs to consider the impact of behavior timing on user preferences.

3.6.   Ablation experiments

To verify the effect of graph convolutional neural network and recurrent neural networks on the performance of the DNCLR model, two variants of the DNCLR model, w/o GCN and w/o GRU, were compared on three data sets. The experimental results are shown in Table 4, in which w/o GCN indicates canceling the convolution layer of the multi-behavior graph, retaining the recurrent neural network, and w/o GRU indicates canceling the multi-behavior recurrent neural network layer, while the convolution layers of multi-behavior graphs are preserved.

Table 4 shows the results of the ablation experiments, with both variants showing a reduction in DNCLR results relative to the overall model. It can be concluded that the removal of any module in the model leads to the degradation of the recommendation performance of the model, which shows that capturing the complex dependencies between the user and the item in the model can improve the recommendation performance of the model.

To verify the effect of the introduction of a contrast learning method on the performance of the present model DNCLR, three variants of the DNCLR model, DNCLRGCNCL, DNCLRGRUCL and DNCLRWithoutCL, were compared on three data sets, and the experimental results are presented in Table 5. The DNCLRWithoutCL model does not introduce the contrast learning method, and DNCLRGCNCL indicates that it only introduces the contrast learning method in the convolution layer of the multi-behavior graph of the DNCLR model. DNCLRGRUCL indicates that the contrast learning method is only introduced in the multi-behavior recurrent neural network layer of the DNCLR model.

In addition, the experimental results show that HR@10 and NDCG@10 of DNCLRGCNCL and DNCLRGRUCL on the three data sets are always higher than those of DNCLRWithoutCL, which shows that the introduction of the contrast learning method can effectively improve the accuracy of recommendation. The experimental result of DNCLRGCNCL is higher than that of DNCLRWithoutCL, which shows that the introduction of contrast learning into the convolution layer of the multi-behavior graph can remove the redundant information introduced by the convolution layer and alleviate the over-smoothing problem. Thus, more layers of neighborhood information can be convolved to introduce more useful cooperative information to learn user characteristics. The experimental results of DNCLRGRUCL are higher than that of DNCLRWithoutCL, which shows that the introduction of contrast learning in the multi-behavior recurrent neural network layer emphasizes the influence of the time of occurrence of behavior on the users' preferences, and it learns more accurate features of the users' recent preferences. In addition, the experimental results of DNCLR are higher than those of DNCLRGCNCL and DNCLRGRUCL, indicating that the combined two-part comparative learning method can more accurately learn the characteristics of users and items, thus improving the performance of recommendation.

In order to verify whether the introduction of contrast learning in the convolution layer of the multi-behavior graph can effectively solve the over-smoothing problem, this section shows the HR@10 experimental results of DNCLRWithoutCL and DNCLR models with different convolution layers H set in the three data sets, as shown in Figure 9.

To sum up, the introduction of the contrast learning method in the convolution layer of the multi-behavior graph can effectively alleviate the over-smoothing problem and obtain efficient high-order cooperative information. By introducing the method of contrast learning into the multi-behavior recurrent neural network layer, the effect of behavior occurrence time on user preference can be captured effectively, and the learning of recent user interaction characteristics can be strengthened. The introduction of two-part information in DNCLR can improve the performance of recommendation effectively.

3.7.   Effect of hyperparameters on recommendation accuracy

3.7.1.   The effect of embedding vector dimension d on recommendation accuracy

To evaluate the effect of embedding vector dimension d on recommendation performance, this section presents experimental results of the DNCLR model with different embedding vector dimensions d in different data sets.

Moderate dimensions allow for effective learning of user and item characteristics, while too high a dimension can lead to over-fitting and high time complexity. In this paper, we set the user, item and behavior as the same embedding dimension and modify the dimension in the range of 8 to 32 to optimize the model result. As shown in Figure 10, the performance of the model increases with the increase of the embedding dimension. When the embedding dimension is 32, the model achieves better results, and when the embedding dimension is increased from 16 to 32, the performance improvement is small. In order to ensure the running efficiency of the model, the optimal embedding dimension of the three data sets is set to 32.

3.7.2.   The effect of convolution layer H on recommendation accuracy

To evaluate the effect of convolution layer H on recommendation performance, the experimental results of the DNCLR model with different convolution layers H in different data sets are presented in this section.

By aggregating multi-layer neighborhood node information in the user-item multi-behavior interaction graph, more abundant user and item features can be obtained, and higher-order cooperative information of users and items can be captured. As shown in Figure 11, the experimental results of the three datasets improve with the increase of the number of layers, and the experimental results of the three datasets reach the optimum when the number of convolution layers of the graph is 2. However, if the number of convolution layers continues to increase, when the neighborhood information of three layers is aggregated, the experimental results are lower than with two layers. Because the neighborhood information of multiple layers is aggregated, the obtained central node features contain too much neighborhood information, and the nodes become similar to each other, resulting in an over-smoothing problem, which cannot improve the performance.

3.7.3.   The effect of recent interaction number T on recommendation accuracy

To assess the impact of recent interaction number T on recommendation performance, this section presents the experimental results of the DNCLR model with different interaction numbers T in different data sets.

The average number of interactions was 70 for Yelp, 52 for ML20M and 34 for Tmall. Figure 12 shows that the model was optimal when the number of recent interactions T was 30, 20 or 15, respectively, for the three data sets. The experimental results gradually declined as the number of interactions T increased after reaching the optimal value. The results show that with the increase of T, the Yelp and ML20M data sets increase less, which is due to the weak temporal correlation between the multi-behavior interactions in the two data sets. The increase of the experimental results in the Tmall dataset is due to the strong temporal correlation between the multi-behavior interactions in the dataset. Besides the temporal correlation, the recurrent neural network layer can also capture the user's recent preferences.

4.   Conclusions

In this paper, we propose a multi-behavior recommendation model called Dual Neural Networks and Contrast Learning (DNCLR), which addresses the limitations of the current multi-behavior recommendation algorithms in capturing the complex dependence relationship between users and items. Our model divides the complex dependencies among multiple behaviors into feature correlation and temporal correlation. To capture the high-order cooperative information of a single behavior interaction graph, we use a graph convolution network to calculate the convolution weights by combining user, behavior and item characteristics, and the correlations among the three are learned. To enhance the learning of users' features, we introduce contrast learning into the graph convolution layer to distinguish the differences between a user's interaction history and multi-behavior interaction. Additionally, we capture the temporal correlation between behaviors using long-term and short-term memory networks. The temporal features of multiple behaviors related to the items to be recommended are captured using an attention mechanism. We also introduce contrast learning into the multi-cycle neural network layer to strengthen the short-term user preference learning by distinguishing short-term interaction features from historical interaction features. Finally, we combine the loss introduced by comparative learning in the prediction layer to more accurately predict the user interaction under the target behavior of the items to be recommended. We validate the effectiveness of the DNCLR model on Yelp, ML20M and Tmall datasets. The experimental results demonstrate that our proposed model can effectively capture the correlation between users and items and alleviate the over-smoothing problem caused by multi-layer graph convolution.

Although DNCLR can improve the performance of recommendation effectively, it needs a lot of time to train the model due to the introduction of multi-behavior data, and the model has many parameters, which need to be adjusted many times. Therefore, the next step is to improve the parameter setting scheme in the model and optimize the model to reduce the time complexity, so as to improve the training efficiency.

Use of AI tools declaration

The authors declare they have not used artificial intelligence (AI) tools in the creation of this article.

Acknowledgments

This work is supported by the Research and Innovation Project in Tianjin (special service industry project) [2022SKYZ315].

Conflict of interest

The authors declare there is no conflict of interest.