Mathematical modeling for solving fractional model cancer bosom malignant growth

1.   Introduction

Lung cancer is one of the most common cancers that endanger human health seriously, and approximately one million people die from it every year ^[1,2]. Lung adenocarcinoma (LUAD) is widely regarded as the most common histological subtype of lung cancer ^[3]. It is reported that the 5-year survival rate for LUAD patients in the United States is below 20% ^[4]. Over the past few decades, despite the progress has been made in the treatment of LUAD, the overall survival rate of this cancer is not evidently upgraded ^[5]. Recently, it has been proved that tremendous advance in cancer treatment has been obtained through immunotherapy, and immune checkpoint inhibitors are increasingly used to treat LUAD ^[6].

Evidence has indicated that targeting programmed cell-death protein 1/programmed cell death 1 ligand 1 (PD-1/PD-L1)-related pathways is an emerging concept in cancer immunotherapy ^[7]. PD-1 (also called PDCD-1) is expressed on both exhausted and activated T cells, which is an immune checkpoint molecular ^[8]. PD-1 blockade had remarkable efficacy against extensive advanced malignancies ^[9], and it also serves critical role in lung cancer. For example, Kagamu et al. ^[10] observed that many advanced lung cancer patients achieved long-term survival without disease progression after treatment with PD-1 blockade, suggesting that PD-1 blockade therapy could evidently improve the outcome of lung cancer patients. In addition, with the development of gene expression profiles, researchers have discovered several gene expression characteristics related to survival outcomes of various cancers. The constructed prognostic model may be helpful for early diagnosis of LUAD and personalized treatment ^[11]. For instance, Zhang et al. ^[12] constructed a risk model with four genes that could predict the overall survival of LUAD patients. Moreover, Sun et al. ^[13] established an immune prognostic model for LUAD, which could independently identify high-risk patients with poor survival. However, the PD-1 associated risk model that was used for predicting the prognosis of LUAD has not been constructed.

In the present study, we aimed to identify PD-1-related gene signature to predict the survival of LUAD patients. The gene expression data and clinical information related to LUAD were downloaded from the Gene Expression Omnibus (GEO) and The Cancer Genome Atlas (TCGA) databases. After a series of bioinformatics analysis, the genes related to both PD-1 expression level and immune cells were identified, and then Lasso Cox regression analysis was performed to obtain key genes to construct prognostic model. Furthermore, the predictive performance of this model was validated by using the data from an independent GEO and TCGA cohorts. Figure S1 shows the analysis process of the present study. This study will provide new insights into the mechanisms of PD-1 immune checkpoints and provide novel therapeutic targets for LUAD patients with poor prognosis.

2.   Materials and methods

2.1.   Source of data

The National Center for Biotechnology information (NCBI) GEO database ^[14] was used to search the gene expression profiles of LUAD with "lung adenocarcinoma" as a keyword. The search criteria were as follows: 1) the species was set to "Homo sapiens" 2) the clinical parameters of the samples in dataset must include prognostic information, 3) the sample size of cancer tissues in the dataset was at least 60. Finally, four datasets (GSE26939, GSE68465, GSE72094, and GSE68571) that met the requirements were obtained and included in this analysis.

Concretely, GSE26939 dataset included 116 LUAD samples, among which, one sample without prognostic information was removed. The platform was GPL9053 Agilent-UNC-custom-4X44K. GSE68465 dataset included 443 LUAD samples and 19 normal lung tissue samples. Of which, 442 samples with complete prognostic information were selected for further analysis. The platform was GPL96 [HG-U133A] Affymetrix Human Genome U133A Array. GSE72094 dataset included 442 LUAD samples. After filtering, 398 samples were enrolled for analysis. The platform was GPL15048 Rosetta/Merck Human RSTA Custom Affymetrix 2.0 microarray [HuRSTA_2a520709.CDF]. In addition, GSE68571 dataset included 86 LUAD samples, which were analyzed based on GPL80 [Hu6800] Affymetrix Human Full Length HuGeneFL Array platform.

2.2.   Data preprocessing

For these four datasets, standardized probe expression matrix and the corresponding annotation information were downloaded from GEO database. Then, probes that not matched to gene symbol were removed. If different probes mapped to the same gene symbol, the average value of these probes was applied as the final expression value.

2.3.   K-M survival analysis for each dataset based on the expression level of PD-1

Combined with the expression level of PD-1 in each sample and the corresponding survival information, K-M survival analysis was performed by using R package survminer (Version 0.4.3) to determine the optimal cutpoint. According to the optimal cutpoint, samples were divided into PD-1 low expression group (PD-1 expression level in sample < cutpoint) and high expression group (PD-1 expression level in sample > cutpoint). Next, survival analysis and log-rank test were used to compare the prognostic value of low and high expression groups by using the R package survival (Version 2.42-6).

2.4.   Association analysis of PD-1 and clinical characteristics

The distribution of clinical factors in each sample of the PD-1 low and high expression groups was counted and plotted using R package ggstatsplot (Version: 0.6.5). In addition, the difference in continuous variables between two groups was compared using Welch's t-test, and the difference in discrete variables between two groups was calculated using Chi-square test. Clinical factors with p-value < 0.05 were regarded as statistically significant.

2.5.   Functional enrichment analysis

R package gene set variation analysis (GSVA, Version: 1.36.2) ^[15] was applied to calculate the enrichment score of each Kyoto Encyclopedia of Genes and Genomes (KEGG) pathway in each sample to obtain a scoring matrix. Then, differential pathway between PD-1 low and high expression groups was identified by using R package limma ^[16] (Version 3.10.3). Then, Benjamini- Hochberg method was used to perform multiple test correction and obtained adjusted p-value (adj. p-value). The adj. p-value < 0.05 was considered as the cut-off criterion of significantly enriched pathway.

2.6.   Screening of differentially expressed genes (DEGs)

DEGs between PD-1 high expression and low expression groups were screened by using the Bayesian method provided by limma in R package. Further, Benjamini- Hochberg method was used for the adjustment of p-value. |log fold change (FC)| > 0.585 and adj. p-value < 0.05 were considered as statistically significant.

2.7.   Construction of weighted gene co-expression networks and Screening of PD-1 expression related modules

According to the expression matrix of all genes, variance analysis was adopted to find the TOP2000 genes with higher degree of variation among samples. Then, these genes were analyzed by using R package weighted gene co-expression network analysis (WGCNA) ^[17] (Versions 1.61 and modules closely related to PD-1 were identified. After that, R package clusterprofiler ^[18] (Version: 3.8.1) was used to perform KEGG pathway enrichment analysis of genes in these modules with the following parameters: pAdjustMethod = "BH" and pvalueCutoff = "0.05". P-value < 0.05 was the threshold value of significantly enriched results.

Subsequently, we narrowed down the range of candidate genes to obtain closely related genes. In brief, the above obtained DEGs and genes in modules were integrated, and then the overlapping genes were selected for further analysis.

2.8.   Screening of genes related to infiltrating immune cells

The gene sets used to label the type of each immune cell in tumor microenvironment (TME) were obtained from the study by Charoentong et al. ^[19]. Based on the ssGSEA algorithm in R package GSVA ^[20], the enrichment score of each immune cell in samples was calculated, which represented the relative abundance of each TME infiltrating cell in each sample. Then, based on the relative abundance, pheatmap package (Version: 1.0.12) was used to perform unsupervised clustering for samples, and the samples were clarified into high and low infiltrating immune groups. After that, DEGs between these two groups were screened using limma in R package. The threshold values of DEGs were |log FC| > 1 and adj. p-value < 0.05, and these genes were considered to be closely related to the immune microenvironment.

2.9.   Identification of PD-1 related immune genes

Genes related to PD-1 expression as well as immune cells were integrated, and the shared genes were obtained for further analyses. Next, Gene ontology (GO)-biological process (BP) ^[21] and KEGG ^[22] pathway analyses of these genes were performed using DAVID ^[23] (Version 6.8). Count ≥ 2 and p-value < 0.05 were regarded as statistically significant.

2.10.   Construction of prognostic model

Combined with the expression values of genes and the overall survival time of each sample, univariate Cox regression analysis was conducted. Genes with p-value < 0.05 were regarded as prognosis-related genes and included for the next analysis.

Then, based on these prognosis-related genes, a LASSO Cox regression was applied to identify key genes for the construction of prognostic models by using glmnet package ^[24] (Version 2.0-18). The 50-fold cross-validation was performed to determine the optimal value of Lasso penalty parameter. After that, multivariate Cox regression analysis of these key genes was conducted to construct prognostic risk model using the following formula: Risk score = β_gene1*expr_gene1 + β_gene2*expr_gene2 +... +β_geneN*expr_geneN (β represents correlation coefficient of prognostic gene and expr represents the expression value of the corresponding genes). According to the median value of risk score, the samples were divided into low risk group and high risk group. Next, K-M survival analysis of these two groups was performed using log-rank test.

2.11.   Independent analysis of risk score model

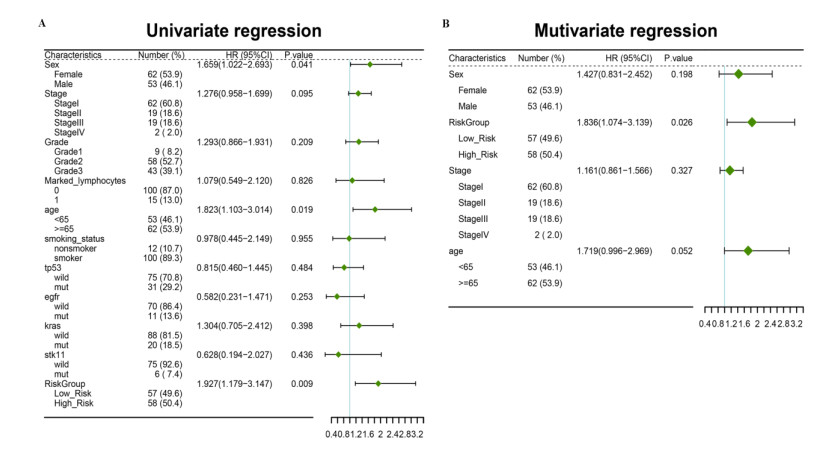
To determine whether the risks core model could be applied as an independent prognostic factor, the prognostic value of the risk score and other clinical parameters, including age, sex, stage, grade, marked lymphocytes, smoking status, TP53 mutation, EGFR mutation, KRAS mutation, and STK11 mutation, was evaluated with univariate and multivariate Cox regression analyses. Variables with p-value < 0.05 were regarded as independent prognostic factors in both analyses.

2.12.   Validation of the prognostic model

We used a microarray datasets GSE72094 to validate the stability and repeatability of prognostic model. At first, the expression value of model genes in each sample of GSE72094 was extracted. According to the prognostic coefficient obtained from the previous analysis, the risk score was calculated using the same formula. Then, the samples were divided into low risk group and high risk group based on the median, followed by K-M survival analysis. In addition to the GEO dataset, we also included data from TCGA to validate the prediction performance of the model. In brief, the RNA-seq data of LUAD and survival information of corresponding samples were downloaded from the UCSC Xena platform (https://toil.xenahubs.net). In the previous study, the samples with number "-01A", that is, the primary tumor samples were selected for subsequent analysis. Finally, a total of 497 samples were obtained. Based on the expression value of seven genes in model, the risk score was calculated using the same formula. Similarly, all samples were assigned to low-risk and high-risk groups according to the median value of risk score, followed by a survival analysis.

2.13.   Comparison between prognostic model and other PD-1 related biomarkers

Moreover, we compared the predictive ability of the seven-gene prognostic model with other molecular biomarkers such as PD-1 and PD-L1 in the GSE26939 dataset. Meanwhile, a 1-, 3-, and 5-year receiver operating characteristic (ROC) curves were plotted using the R package timeROC ^[25], and then the area under the curve (AUC) value of the survival ROC curves was calculated.

3.   Results

3.1.   K-M survival analysis of PD-1

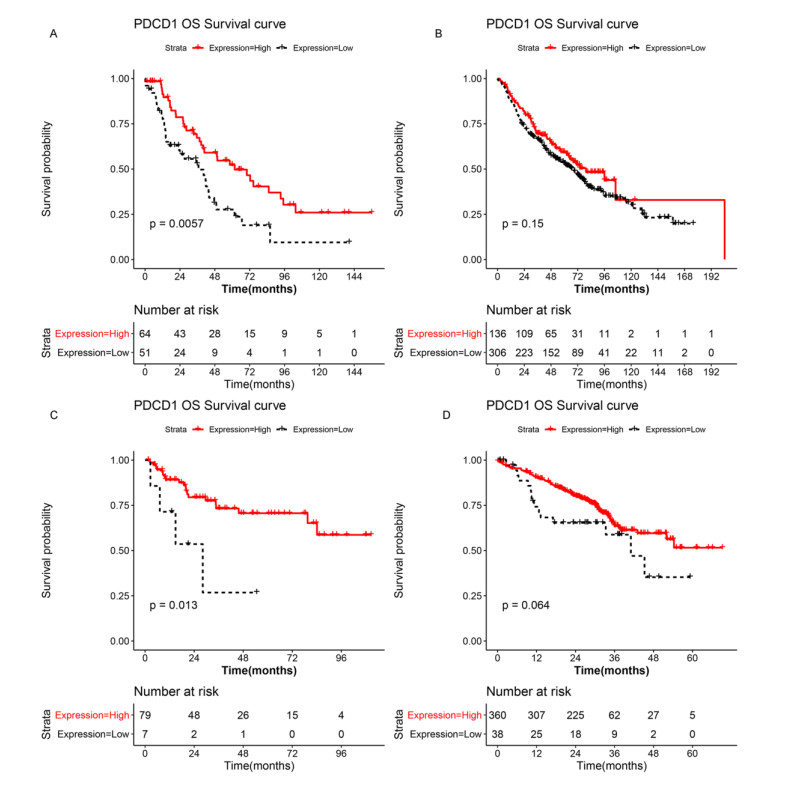
The clinical information of cases in four datasets is presented in Table S1. As shown in Figure 1, results showed that the survival probability of patients in the PD-1 high expression group was higher than that of low expression group. Despite there was no significant difference in survival time between PD-1 high expression group and low expression group in the GSE68465 and GSE72094 datasets, the overall trend was consistent.

3.2.   Association analysis of PD-1 and clinical characteristics

According to the analysis results in the previous step, we observed that the number of samples in the PD-1 low expression group of GSE68571 and GSE72094 was significantly lower than that in the high expression group. In order to reduce the impact of the imbalance of samples in the two groups on the results, we only selected samples in the GSE26939 and GSE68465 datasets for further analyses.

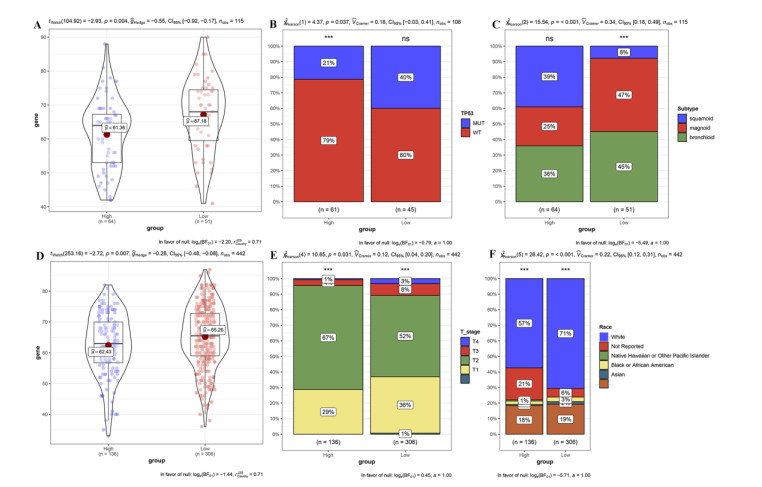
The distribution of different clinical factors in the PD-1 high and low expression groups in these two datasets was calculated, and factors with p-value < 0.05 were obtained. In brief, in GSE26939 dataset, the age of the PD-1 high expression group was evidently lower than that of the low expression group (Figure 2A, p value = 0.004); the high expression group had more TP53 wild type (Figure 2B, p-value = 0.037); and the PD-1 high expression group had more Squamoid subtype (Figure 2C, p-value ≤ 0.001). Meanwhile, in the dataset of GSE68465, the age of patients in the PD-1 high expression group was markedly younger than that of the low expression group (Figure 2D, p-value = 0.007); the high expression group had more T1-T2 samples and less T3-T4 samples than the low expression group (Figure 2E, p-value = 0.031); and PD-1 high expression group had fewer white people than low expression group (Figure 2F, p-value ≤ 0.001).

3.3.   Results of GSVA

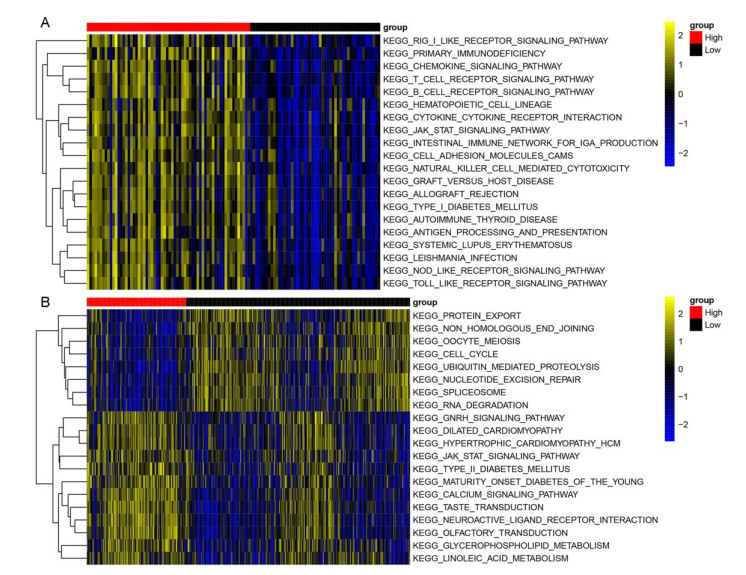
Afterward, GSVA was performed to explore difference in KEGG pathways between the PD-1 high expression and low expression groups from the GSE26939 as well as GSE68465 datasets. In total, there were 72 KEGG pathways enriched by samples in GSE26939 dataset and 137 KEGG pathways in GSE68465 dataset. The top20 pathways are presented in Figure 3. In the GSE26939 dataset, several pathways related to immunity were observed (Figure 3A), such as immunodeficiency, intestinal immune network for IgA production, and primary immunodeficiency. These pathways were increased in high expression group in comparison with that in low expression group. Meanwhile, in the GSE68465 dataset, 12 pathways were significantly higher in the PD-1 high expression group than in the low expression group, such as type II diabetes mellitus pathway and JAK-STAT-signaling pathway (Figure 3B). Notably, JAK-STAT-signaling pathway was evidently increased in the PD-1 high expression group of two GEO datasets.

3.4.   Screening of DEGs between PD-1 low expression and high expression groups

Combined with the results of the previous analyses, we found that the expression level of PD-1 in GSE26939 was significantly related to prognosis of LUAD, and samples in this dataset were mainly enriched in immune-related pathways. Therefore, GSE26939 dataset was retained for further analysis. According to the threshold (|log FC| > 0.585 and adj. p-value < 0.05), 822 DEGs (709 up-regulated and 113 down-regulated genes) were screened between PD-1 high expression group and low expression group. As shown in Figure S2, DEGs could distinguish the PD-1 low expression group from the high expression group, which proved initially that these DEGs were associated with the expression level of PD-1.

3.5.   Identification of modules related to PD-1 expression

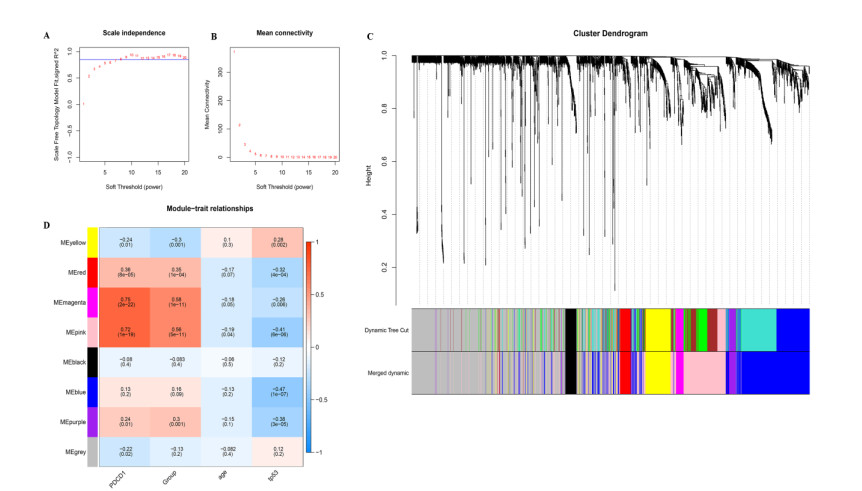
WGCNA was used to identify PD-1 expression related modules. This analysis was performed by a step-by-step method. First, soft threshold power of 8 was selected to calculate the adjacencies because it was the lowest power at which the scale-free topology fit index reached 0.85 (Figure 4A, B). Second, based on clustering and dynamic tree cut methods, the similar modules were clustered. Modules with correlation coefficient > 0.7 were selected and finally seven modules were obtained (Figure 4C). Next, the relationship between module and clinical characteristics (age, TP53 mutation status, PD-1 high- or low-expressed groups, and PD-1 expression level) was analyzed (Figure 4D). For the expression level of PD-1, magenta module, pink module, red module, and purple module represented evidently positive correlations (r > 0 and p-value < 0.05), while yellow module showed significantly negative correlation (r < 0 and p-value < 0.05). In addition, KEGG pathway enrichment analysis for genes in five modules showed that magenta module, pink module, red module, purple module, and yellow module were respectively enriched in 4, 39, 12, 52, and 8 pathways (Figure S3). For example, genes in magenta module, pink module, red module, purple module, and yellow module were mainly enriched in primary immunodeficiency, cytokine-cytokine receptor interaction, protein digestion and absorption, TNF signaling pathway, and cholesterol metabolism, respectively.

Furthermore, genes in the five models and DEGs in PD-1 low expression vs. high expression groups were intersected, and 388 overlapping genes were obtained (Figure S4), which were regarded as candidate genes for further analysis.

3.6.   Screening of immune infiltration-related genes

As presented in Figure S5A, the samples were divided into low immune infiltration group and high immune infiltration group according to the enrichment fraction of immune cells in each sample. We also observed that the high immune infiltration group was mainly composed of samples with high expression level of PD-1, and the low immune infiltration group was mainly contained samples with low expression level of PD-1. Furthermore, differential analysis was performed between high immune infiltration and low immune infiltration groups. A total of 467 DEGs were identified, including 445 up-regulated and 22 down-regulated genes.

3.7.   Further screening of PD-1 related immune genes

A total of common 237 genes were obtained via the intersection of 467 immune related genes and 388 PD-1 related genes. Thus, these 237 genes were considered as PD-1 related immune genes. To explore the biological function of these genes, GO_BP terms and KEGG pathways analyses were conducted. Results showed that these 237 genes were significantly enriched in 87 GO-BP terms (such as immune response and inflammatory response) and 38 KEGG pathways (such as cytokine-cytokine receptor interaction and rheumatoid arthritis). The top20 results are presented in Figure S5B.

3.8.   Construction of prognostic model

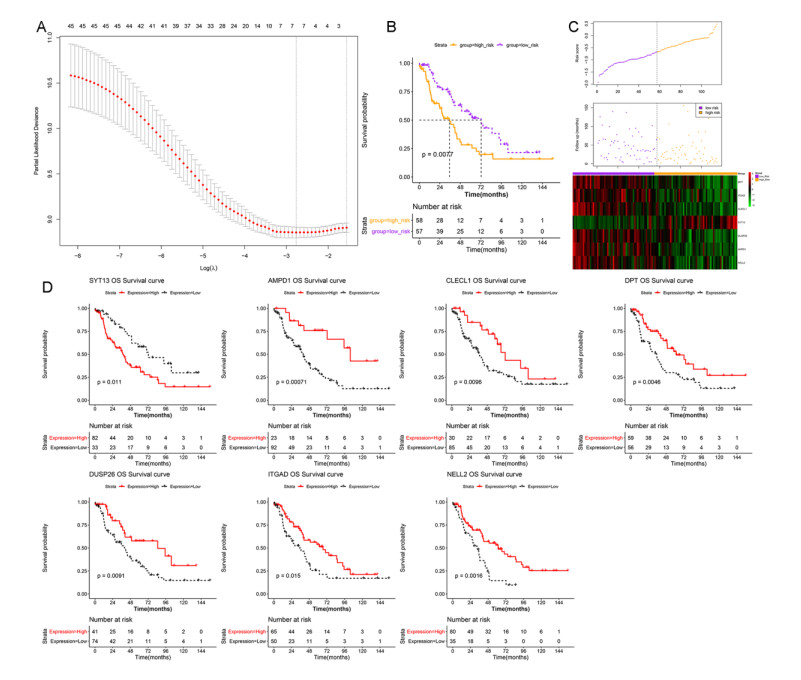
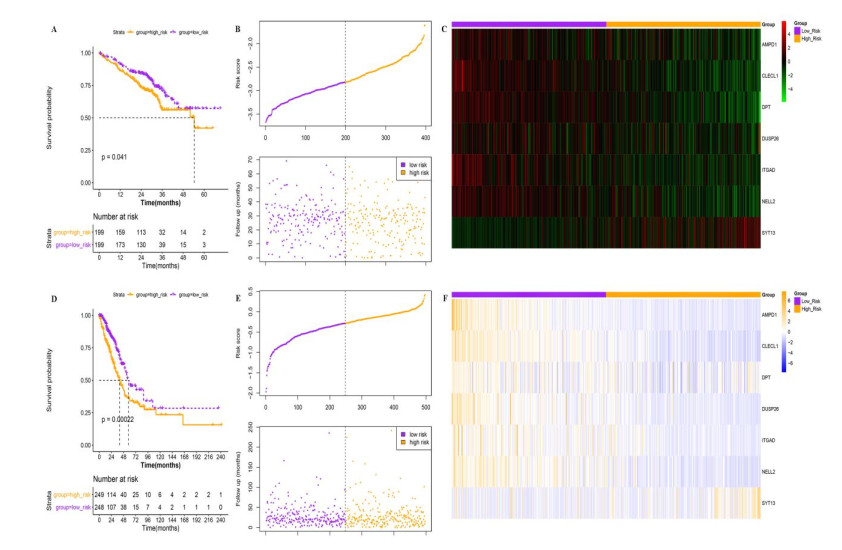
Based on the 237 PD-1 related immune genes, univariate Cox regression analysis was performed. A total of 47 genes that were significantly associated with overall survival of LUAD were obtained. Next, LASSO Cox regression analysis for these 47 genes was conducted to reveal the optimal modeling parameter (λ), and results showed λ = 7 was considered as optimum parameter (Figure 5A). Finally, a seven-gene (DPT, ITGAD, CLECL1, SYT13, DUSP26, AMPD1, and NELL2) signature was used to construct the prognostic model. Risk score was calculated by using the following formula: (-9.322*expr_AMPD1) + (-0.169*expr_CLECL1) + (-0.176*expr_DPT) + (-0.029*expr_DUSP26) + (-0.056*expr_ITGAD) + (-0.063*expr_NELL2) + (0.077*expr_SYT13). Based on the median of risk score, samples were divided into low risk group and high risk group. Patients in high risk group had significantly worse survival rate than those in low risk group (Figure 5B). Distributions of risk score, follow-up time, and seven-gene expression profiles are shown in Figure 5C. The expression level of SYT13 was up-regulated in the high risk group, and the expression level of the remaining six genes was down-regulated in the high risk group compared with the low risk group. In addition, K-M survival curve showed that the prognosis of patients with high expression of SYT13 was poor, and the prognosis of patients with low expression of the remaining 6 genes was worse (Figure 5D).

3.9.   Independent analysis of risk score model

Further, univariate and multivariate Cox regression analyses were performed to evaluate whether risk score could be used as an independent prognostic factor for LUAD. Several clinical factors were included in this analysis, including sex, age, stage, grade, marked_lymphocytes, smoking_status, and genetic mutation status (TP53, EGFR, KRAS, STK11). Univariate Cox analysis indicated that sex, age, and risk groups were significantly associated with prognosis of LUAD (Figure 6A). Next, multivariate analysis revealed that the risk score was an independent prognostic predictor (Figure 6B), suggesting that the constructed model could independently predict the prognosis of LUAD.

3.10.   Validation of the prognostic model by using GEO dataset

According to the seven-gene risk model, the risk score of the 398 LUAD patients from GSE72094 was calculated using the same formula. Then, these patients were classified into low and high risk groups according to the median of risk score. K-M survival curve presented that the prognosis of patients in high risk group was significantly worse than those in low risk group (Figure 7A). The risk scores distribution and follow up of the patients in these two groups were analyzed, indicating that the high risk score group had more mortality cases (Figure 7B). Moreover, the expression level of these seven genes in the two groups was consistent with the results of above analysis (Figure 7C). These findings suggested that the constructed prognostic model was reliable and efficient.

3.11.   Validation of the prognostic model by using TCGA data

To further determine whether the prognostic model was reliable in different populations, we executed the same formula and determined the cut-off value in the TCGA cohort. Next, patients were divided into low- or high-risk groups. Consistent with the results in the GSE72094, patients with high risk score had a lower overall survival than those with low risk score (Figure 7D). The distributions of risk score of LUAD patients as well as the relationship between risk score and follow up were visualized in Figure 7E. In addition, the expression level of SYT13 was up-regulated in the high risk group, and the level of the remaining six genes was down-regulated in the high risk group (Figure 7F), which was consistent with that in the GEO datasets.

3.12.   Comparisons between prognostic model and other molecular biomarkers

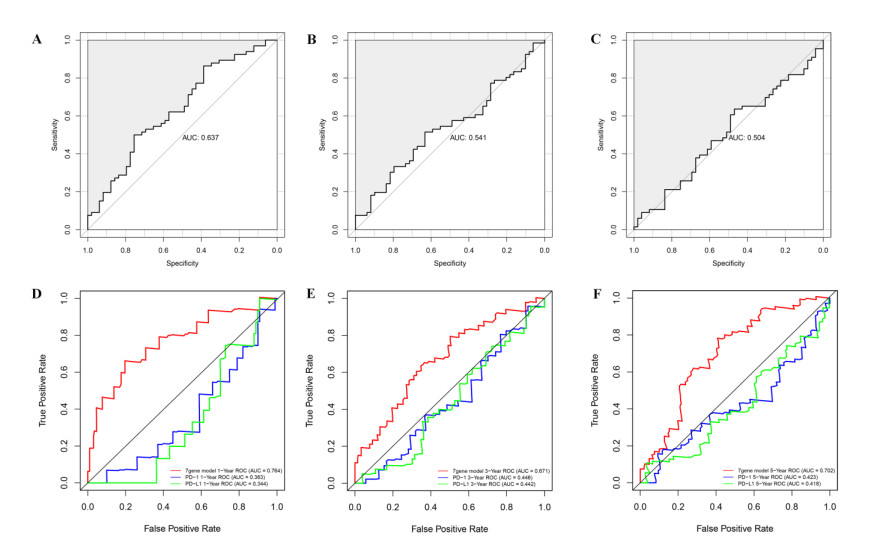
Next, we plotted the ROC curves for prognostic model, PD-1 and PD-L1, and then the AUC values were calculated. Results showed that AUC values for prognostic model, PD-1, and PD-L1 were respectively 0.637, 0.541, and 0.504 (Figure 8A–C), indicating that the predictive ability of prognostic model was better than that of PD-1 and PD-L1. In addition, the accuracy of these three biomarkers for survival of LUAD patients 1, 3, and 5 years were evaluated. The AUC values of the ROC curves for seven-gene, PD-1, and PD-L1 predicted the 1-year overall survival were 0.764, 0.363, and 0.344, respectively (Figure 8D); AUC values of ROC predicted the 3-year survival were 0.671, 0.446, and 0.442, respectively (Figure 8E); and AUC values of ROC predicted the 5-year survival were 0.702, 0.423, and 0.418, respectively (Figure 8F). These results further confirmed that the constructed model outperformed other biomarkers with superior predictive performance.

4.   Discussion

In the present study, a PD-1 expression-related immune prognostic model was constructed, which included seven genes (DPT, ITGAD, CLECL1, SYT13, DUSP26, AMPD1, and NELL2). All samples were divided into high-risk and low-risk groups based on the risk score for this model. Notably, the survival time of the patients in the high risk group was significantly lower than those in the low risk group. Meanwhile, this prognostic model was verified to be effective and reliable by other GEO dataset and TCGA cohort. In addition, survival analysis suggested that the prognosis of patients with higher expression level of SYT13 was poor, and the survival time of patients with lower expression level of the remaining 6 genes was worse. Our constructed PD-1-related prognostic model may be helpful for early diagnosis and treatment of LUAD in clinical practice.

DPT, a noncollagenous extracellular matrix (ECM) protein, is involved in ECM assembly activities and cellular adhesion. Yamatoji et al. ^[26] indicated that DPT played a significant role in tumor metastasis and invasiveness of oral squamous cell carcinomas (OSCCs), and might be a therapeutic target for the treatment of OSCCs. Guo et al. ^[27] suggested that DPT could suppress the proliferation of papillary thyroid carcinoma cells via repression of MYC. Some previous studies also suggested that DPT was differentially expressed in some other cancers, such as hepatocellular carcinoma ^[28]. ITGAD belongs to the beta-2 integrin family of membrane glycoproteins, and is expressed in the tissue and circulating myeloid leukocytes. Evidences demonstrated that ITGAD was associated with metastatic gastric carcinoma ^[29] and histiocytic sarcomas ^[30]. However, there was no previous research describing the association between ITGAD and LUAD or lung cancer. Another gene, SYT13, encodes a member of the large synaptotagmin protein family, and it is considered as a target for the treatment of peritoneal metastasis of gastric cancer ^[31]. Jahn et al. ^[32] identified SYT13 as a liver tumor suppressor gene. Meanwhile, silencing of SYT13 promoted apoptosis and suppressed proliferation of colorectal cancer cells and thus inhibited tumor growth ^[33]. The study of Zhang et al. ^[34] suggested that SYT13 was involved in the growth, invasion, migration, and apoptosis of LUAD. Together, these studies further highlighted that SYT13 was closely associated with the development of cancer. Recently, DUSP26 has been proved to be a potential therapeutic target for human cancer ^[35]. Bourgonje et al. ^[36] indicated that lower expression level of DUSP26 was correlated with poor prognosis of gliomas and overexpression of it in E98 glioblastoma cells could reduce tumorigenicity. In addition, the findings of Yu et al. ^[37] suggested that DUSP26 might be regarded as an oncogene in anaplastic thyroid cancer. For the NELL2, it encodes a glycoprotein containing several von Willebrand factor C domains and epidermal growth factor (EGF)-like domains. Study in mice has shown that the protein plays a role in the growth and differentiation of nerve cells and tumorigenesis ^[38]. Nakamura et al. ^[39] indicated that NELL2 played roles in the inhibition of cell migration of renal cell carcinoma. Meanwhile, Kim et al. ^[40] confirmed that NELL2 was involved in cancer development by the regulation of E2F transcription factor 1. Taken together, these studies suggested that genes such as DPT, ITGAD, SYT13, DUSP26, and NELL2 were involved in pathogenesis of cancers, and were associated with the prognosis of various cancers. Nevertheless, few studies reported the roles of CLECL1 and AMPD1 in cancer especially in the LUAD. Thus, we speculated that these genes also could predict the prognosis of LUAD.

In this analysis, we also explore the relationship between immune cells and genes. It is reported that altered cell adhesion played promoting roles in immune suppression of cancers ^[41], and DPT was involved in cellular adhesion ^[26], suggesting that DPT was associated with immunity in cancers. Integrin adhesion is required for aspects of immune function such as antigen presentation and migration in germinal centers, inflammation sites, and lymph nodes ^[42]. Synaptotagmin (SYT) is a large class of membrane transporters with 13 members, and is considered to be the main calcium sensor in the process of immune cell exocytosis ^[43]. Among these, SYT16 is reported to be correlated with immune infiltrates and a prognostic biomarker in glioma ^[44]. The member of dual-specificity phosphatases (DUSPs) family, such as DUSP1, DUSP2 DUSP4 DUSP10, and DUSP16 are important for immune response and metabolic homeostasis ^[45]. CLECL1 is involved in the regulating immunity ^[46], and AMPD1 plays a role in the immune function in sepsis patients ^[47]. These evidences indicated the indirect or direct relationship between genes in the model and immunity. Therefore, these genes may affect the prognosis of LUAD via regulating the immune microenvironment. However, the specific molecular mechanism still needs further experimental verification.

Importantly, a model composed of seven PD-1 related immune genes (DPT, ITGAD, CLECL1, SYT13, DUSP26, AMPD1, and NELL2) was constructed, which could distinguish LUAD patients and predict prognosis. After calculation of the risk score, results of survival analysis showed that the overall survival of patients in the high-risk group was significantly worse than those in the low-risk group. This model could be used as an independent prognostic factor for LUAD patients. According to our research, the models constructed from these seven PD-1 related genes can well predict the prognosis of patients with LUAD. We think that these seven genes are biomarkers for predicting the prognosis of LUAD patients, and may become new research targets. In short, our study provided a new method for evaluating the prognosis of LUAD patients.

Nevertheless, our results have to be interpreted in light of some limitations. First, the molecular functions of these identified genes in LUAD remain largely unknown, which require further studies in vivo and in vitro. Secondly, all genes in the constructed model were derived from the public databases (GEO and TCGA); therefore, more external samples from medical centers are needed to validate the predictive performance of the risk model.

5.   Conclusions

In summary, a PD-1 related seven-gene (DPT, ITGAD, CLECL1, SYT13, DUSP26, AMPD1, and NELL2) prognostic model was constructed, which could predict the overall survival of LUAD patients well. These seven genes help us to further understand the molecular mechanism of PD-1, and they may be potential biomarkers for the treatment of LUAD. However, the lack of experimental verification is a limitation of the present study, thus further researches are needed to verify the present results.

Acknowledgements

This study was supported by the Shanghai Minhang District Health Commission Research Project (No. 2020MW05).

Conflict of interest

The authors declare that they have no conflict of interest.