Figure 1.
Bibliometric indicator types.
Objective: Quantification of disease-disease association (DDA) enables the understanding of disease relationships for discovering disease progression and finding comorbidity. For effective DDA strength calculation, there is a need to address the main challenge of integration of various biomedical aspects of DDA is to obtain an information rich disease representation. Materials and Methods: An enhanced and integrated DDA framework is developed that integrates enriched literature-based with concept-based DDA representation. The literature component of the proposed framework uses PubMed abstracts and consists of improved neural network model that classifies DDAs for an enhanced literaturebased DDA representation. Similarly, an ontology-based joint multi-source association embedding model is proposed in the ontology component using Disease Ontology (DO), UMLS, claims insurance, clinical notes etc. Results and Discussion: The obtained information rich disease representation is evaluated on different aspects of DDA datasets such as Gene, Variant, Gene Ontology (GO) and a human rated benchmark dataset. The DDA scores calculated using the proposed method achieved a high correlation mainly in gene-based dataset. The quantified scores also shown better correlation of 0.821, when evaluated on human rated 213 disease pairs. In addition, the generated disease representation is proved to have substantial effect on correlation of DDA scores for different categories of disease pairs. Conclusion: The enhanced context and semantic DDA framework provides an enriched disease representation, resulting in high correlated results with different DDA datasets. We have also presented the biological interpretation of disease pairs. The developed framework can also be used for deriving the strength of other biomedical associations.
Citation: Karpaga Priyaa Kartheeswaran, Arockia Xavier Annie Rayan, Geetha Thekkumpurath Varrieth. Enhanced disease-disease association with information enriched disease representation[J]. Mathematical Biosciences and Engineering, 2023, 20(5): 8892-8932. doi: 10.3934/mbe.2023391
| [1] | Loris Nanni, Michelangelo Paci, Gianluca Maguolo, Stefano Ghidoni . Deep learning for actinic keratosis classification. AIMS Electronics and Electrical Engineering, 2020, 4(1): 47-56. doi: 10.3934/ElectrEng.2020.1.47 |
| [2] | Tamizhelakkiya K, Sabitha Gauni, Prabhu Chandhar . Modulation classification analysis of CNN model for wireless communication systems. AIMS Electronics and Electrical Engineering, 2023, 7(4): 337-353. doi: 10.3934/electreng.2023018 |
| [3] | Suriya Priya R Asaithambi, Sitalakshmi Venkatraman, Ramanathan Venkatraman . Proposed big data architecture for facial recognition using machine learning. AIMS Electronics and Electrical Engineering, 2021, 5(1): 68-92. doi: 10.3934/electreng.2021005 |
| [4] | Abdullah Yahya Abdullah Amer, Tamanna Siddiqu . A novel algorithm for sarcasm detection using supervised machine learning approach. AIMS Electronics and Electrical Engineering, 2022, 6(4): 345-369. doi: 10.3934/electreng.2022021 |
| [5] | Habib Hadj-Mabrouk . Analysis and prediction of railway accident risks using machine learning. AIMS Electronics and Electrical Engineering, 2020, 4(1): 19-46. doi: 10.3934/ElectrEng.2020.1.19 |
| [6] | Manisha Bangar, Prachi Chaudhary . A novel approach for the classification of diabetic maculopathy using discrete wavelet transforms and a support vector machine. AIMS Electronics and Electrical Engineering, 2023, 7(1): 1-13. doi: 10.3934/electreng.2023001 |
| [7] | J. Rajeshwari, M. Sughasiny . Modified PNN classifier for diagnosing skin cancer severity condition using SMO optimization technique. AIMS Electronics and Electrical Engineering, 2023, 7(1): 75-99. doi: 10.3934/electreng.2023005 |
| [8] | Deven Nahata, Kareem Othman . Exploring the challenges and opportunities of image processing and sensor fusion in autonomous vehicles: A comprehensive review. AIMS Electronics and Electrical Engineering, 2023, 7(4): 271-321. doi: 10.3934/electreng.2023016 |
| [9] | Amleset Kelati, Hossam Gaber, Juha Plosila, Hannu Tenhunen . Implementation of non-intrusive appliances load monitoring (NIALM) on k-nearest neighbors (k-NN) classifier. AIMS Electronics and Electrical Engineering, 2020, 4(3): 326-344. doi: 10.3934/ElectrEng.2020.3.326 |
| [10] | Abdul Yussif Seidu, Elvis Twumasi, Emmanuel Assuming Frimpong . Hybrid optimized artificial neural network using Latin hypercube sampling and Bayesian optimization for detection, classification and location of faults in transmission lines. AIMS Electronics and Electrical Engineering, 2024, 8(4): 508-541. doi: 10.3934/electreng.2024024 |
Objective: Quantification of disease-disease association (DDA) enables the understanding of disease relationships for discovering disease progression and finding comorbidity. For effective DDA strength calculation, there is a need to address the main challenge of integration of various biomedical aspects of DDA is to obtain an information rich disease representation. Materials and Methods: An enhanced and integrated DDA framework is developed that integrates enriched literature-based with concept-based DDA representation. The literature component of the proposed framework uses PubMed abstracts and consists of improved neural network model that classifies DDAs for an enhanced literaturebased DDA representation. Similarly, an ontology-based joint multi-source association embedding model is proposed in the ontology component using Disease Ontology (DO), UMLS, claims insurance, clinical notes etc. Results and Discussion: The obtained information rich disease representation is evaluated on different aspects of DDA datasets such as Gene, Variant, Gene Ontology (GO) and a human rated benchmark dataset. The DDA scores calculated using the proposed method achieved a high correlation mainly in gene-based dataset. The quantified scores also shown better correlation of 0.821, when evaluated on human rated 213 disease pairs. In addition, the generated disease representation is proved to have substantial effect on correlation of DDA scores for different categories of disease pairs. Conclusion: The enhanced context and semantic DDA framework provides an enriched disease representation, resulting in high correlated results with different DDA datasets. We have also presented the biological interpretation of disease pairs. The developed framework can also be used for deriving the strength of other biomedical associations.
In late 2019, the world witnessed one of the most severe health disasters that affected all countries [1,2,3,4,5,6]. Spotted in Wuhan City, Hubei Province, China, Covid-19 is a respiratory disease that is caused by the new coronavirus SARS-CoV-2 (Severe Acute Respiratory Syndrome Coronavirus 2) [7,8,9,10]. Coronavirus is a pathogenic disease that starts by attacking the respiratory tract and then directs itself into the cells using an enzyme called furin and impairs the immune system [10]. The primary signs and symptoms of COVID-19 include fever (38℃ or higher), dry cough, dyspnea, sore throat, tiredness, pains, and, in certain cases, diarrhea. Loss of taste and smell is reported as Covid-19 symptoms. Respiratory problems are observed in those developing more severe forms, and these can result in hospitalization in critical care as well as death [7,11,12,13]. The World Health Organization declared, on February 11, 2020, this new disease to be a pandemic after it took a few weeks to spread rapidly throughout the world [7]. While writing this review, the accumulated positive cases is 698,035,072, including 6,940,130 deaths, and 669,603,810 recovered [14] (Last updated: November 20, 2023, 17:56 GMT).
Faced with this complicated situation, many precautions have been taken to minimize the spread of Covid-19: Washing hands with soap frequently, using hydroalcoholic solution, keeping social distance (2 meters), covering mouth while sneezing, and wearing a mask [7,15,16]. The precautions taken did not stop there. Rather, movement between cities and countries was prevented, and a lockdown was imposed [17,18]. Due the demand to effective solutions of this disease and after deep research in laboratories, researchers developed Covid-19 vaccines. Indeed, different types of vaccines are available: BNT162 (Pfizer BioNTech, USA), ChAdOx1 (AstraZeneca, UK), mRNA1273 (Moderna, USA), Ad26.COV2-S (Johnson & Johnson, USA), BIBP-CorV (Sinopharm, China), CoronaVac (Sinovac, China), and Sputnik V (Gamaleya, Russia) [19,20,21,22].
Considered a gold standard to detect Covid-19, Reverse Transcription-Polymerase Chain Reaction (RT-PCR) can detect the virus's genetic material, offering high accuracy. However, the need for specialized equipment and well-trained personnel and the time to confirm the patients as well as its expensiveness are the considerable obstacles of its use for testing in this pandemic [10,23]. To overcome this issue, medical images analysis is used massively in this field and allows doctors and specialists to make accurate diagnoses and eliminate the need for laborious manual review processes [24]. Indeed, X-Ray and CT (Computed Tomography) images are the most used in processing of medical images. The utilization of these images required a very good expertise to detect Covid-19 which is taking a lot of time [8]. So, the necessity of new techniques allowing the detection of the virus effectively with minimal time is crucial. Hence, the combination of Deep Learning and Machine Learning methods with X-Ray and CT images is one of the solutions that helps to beat this problem [25]. In fact, Machine Learning and Deep Learning have recently played a major role for automated medical diagnostics by providing new solutions overcoming the shortcomings of the classical methods. Therefore, developing automated analysis system based on X-Ray and CT images using Machine Learning and Deep Learning techniques, that allow to detect the anomalies in the images, helped physicians and healthcare professionals to make accurate decision and save a lot of time [26].
We aim to focus on classification and detection of Covid-19 using X-Ray and CT images through Deep Learning and Machine Learning techniques. Based on a qualitative and quantitative analysis of published documents on this field and the use of new technologies to improve the diagnosis of Covid-19, we highlight the role of Deep Learning and Machine Learning methods on recognizing Covid-19 from medical images. Data analysis is used to get more insights from the data to determine some information's such as: The distribution of published papers in all used databases, and the most used techniques in the contributions. The participation of each country in terms of the number of published documents was considered as well as the type of publication. The rest of this paper is organized as follows. In Section 2, we describe the methodology of the bibliometric analysis employed, along with the tools used for this analysis. Section 3 delves into various aspects of bibliometric analysis, including the techniques used, annual trends, types of publications, geographic dispersion, leading authors, and predominant journals. Finally, Section 4 provides a detailed breakdown analysis for each database.
The first and the most important step in any bibliometric analysis is the selection of the relevant databases which pertain to the objectives of the study [27]. The scope of bibliometric analysis is limited by the type of accessible information [28]. It is therefore imperative that the information sources be trusted and adapted to conduct such an analysis and make the most efficient decisions [29]. For our study, we used six well known databases: IEEE Xplore, ACM, MDPI, PubMed, Springer, and ScienceDirect.
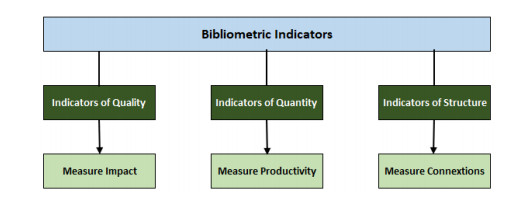
Once the databases have been selected, the second step is to pick out the appropriate indicators for evaluating the resulting samples. The published papers articles showcase a range of bibliometric measures [29]. We can distinguish three different types of bibliometric indicators: (1) Quality Indicators, which can measure the impact, (2) Quantity Indicators that allow us to measure the productivity, and (3) Structural Indicators that measure the connection [30]. Figure 1 shows the types of bibliometric indicators. In our study, we focused on quantity indicators.
Our purpose of this study is to investigate the research area of classification and detection based on X-Ray and CT images using Deep Learning and Machine Learning techniques. We conducted our review using IEEE Xplore, ACM, MDPI, PubMed, Springer, and ScienceDirect databases. In our bibliometric analysis, we covered the most prevalent areas of knowledge, the prolific authors, the journals and the most publications, the most productive countries, the number of citations, the trends of publications, document types, and countries or territories of origin. To carry out our research, we used the same advanced search string for all the selected databases:
("Covid" OR "Covid19" OR "Covid 19" OR "Covid-19" OR "Coronavirus" OR "Corona Virus") AND ("Classification" OR "Image Classification") AND ("Detection" OR "Image Detection") AND ("Deep Learning" OR "Deep Neural Networks" OR "DL" OR "Convolutional Neural Network" OR "CNN") AND ("X-Ray" OR "X-Ray Image" OR "CT" OR "Computed Tomography") AND ("Machine Learning" OR "Machine Learning Algorithms" OR "ML")
The methodology followed in our bibliometric analysis is described in Figure 2. First, it begins with selecting the databases (IEEE Xplore, ACM, MDPI, PubMed, Springer, and ScienceDirect). An advanced string search query is applied across these databases to gather research papers. Then, the results from this search undergo a cleaning process to refine the selection of documents. The specific counts of papers retrieved from each database are indicated: IEEE Xplore (128), ACM (58), MDPI (13), PubMed (35), Springer (217), and ScienceDirect (132). The bibliometric analysis software VOSviewer and Numpy, Pandas, and Matplotlib Python packages are used to conduct the data analysis and visualizations. The cleaning process involves eliminating duplicated documents and documents that do not address classification and detection of Covid-19 based on X-Ray and CT images.
After the cleaning process, we extracted the relevant information for each document and created an excel file to process the data analysis. In the excel file, we stored the following information: Title of the document, year of publication, first author, country (of the first author; in some documents, we found many authors with different countries), type of document (conference paper, journal article, and book chapter), publisher (title of conference or journal), database, number of citations (the last upgrade of number of citation was 6 November 2023), abstract, key words, and the technique used (Deep Learning, Machine Learning or Deep Learning and Machine Learning). The Excel file was used as a primary tool to conduct an initial analysis of the data, which helped us understand the dataset better. This preliminary analysis opened the point for more interpretation and advanced data visualization. With the help of Python and its powerful libraries such as Pandas, Numpy, and Matplotlib, we created detailed graphs and charts that helped us visualize our findings and understand complex patterns within the data more effectively.
The research resulted in 139, 80, 15, 39,239, and 161 documents in IEEE Xplore, ACM, MDPI, PubMed, Springer, and ScienceDirect, respectively. The cleaning process consists of removing duplicated and documents that do not exactly address the classification and detection of Covid-19 based on X-Ray and CT images using Deep Learning and Machine Learning. The total number of documents, after the cleaning process, for the databases IEEE Xplore, ACM, MDPI, PubMed, Springer, and ScienceDirect is 128, 58, 13, 35,217, and 132 documents, respectively. Figure 3 shows the distribution of total documents of each database over the years.
We used VOSviewer version 1.6.20 as bibliometric analysis software due to its efficiency in analyzing clustered search results. Indeed, VOSviewer is a software tool designed for creating and visualizing networks within bibliometric data. Such networks include journals, researchers, or individual publications, and are formed through various relationships such as citation, bibliometric coupling, co-citation, or co-authorship relations. It also provides text mining capabilities, allowing us to construct and visualize the patterns of the networks of important terms drawn from a body of scientific literature [31,32]. VOSviewer analyzes the text within abstracts and titles of published papers by segmenting the paragraphs into individual words and phrases and connecting them with the citation data of the corresponding papers. The outcomes are presented as a density map or term bubbles. As we can see in the figure below (Figure 4), the density map highlights key areas of research related to Covid-19, including terms like "Covid-19", "deep learning, " and "machine learning" as central nodes. These nodes are surrounded by related terms such as "classification", "computed tomography image", "lung detection, " and "chest x-ray, " suggesting they are common subjects of study in the field. This visualization helps to identify the most prominent topics and techniques addressed in the existing body of research on Covid-19.
To facilitate the bubble map, words/terms occurring at a minimum of 1 time in the publications were examined and visualized, and 148 keywords met the selected threshold. Figure 5 illustrates the obtained results that are in the form of network visualization and density diagrams. Different colors indicate thematic concentrations in the literature, and lines between terms depict the relationships and collaborative nature of these research areas. VOSviewer has generated 16 clusters of terms.
The total documents used in this review is 584 documents. While extracting the relevant information from the documents, we took into consideration the contribution of each document and the technique used by the authors for classification and detection of Covid-19 based on X-ray and CT image. As a result, authors have used three techniques: Deep Learning, Machine Learning, or the combination of these two techniques. Figure 6 illustrates the distribution of techniques applied within these documents. It reveals that most of the documents, precisely 378 or 64.7%, used Deep Learning techniques, highlighting the predominant role that this method plays in the field. Moreover, Deep Learning and Machine Learning techniques were jointly utilized in 135 documents. A total of 71 documents were reviewed that used Machine Learning alone, representing 12.2% of all documents reviewed. This distribution underscores how important it is for research trends to focus on advanced computational methods, especially Deep Learning.
Since the beginning of the Covid-19 pandemic in 2020, academic publications about the virus have increased significantly, especially those using Deep Learning and Machine Learning methods. Indeed, the trend shown by Figure 7 presents the yearly distribution of total documents categorized by the utilized techniques from 2020 to 2024. Deep Learning techniques demonstrated its presence with 39 documents, and a significant increase in 2021 (100 documents), 2022 (125 documents), 2023 (111 documents), and 6 documents have already been published as of 2024, even though we are in 2023. A modest count of 6 documents for Machine Learning in 2020 had a low increase for 2021, 2022, and 2023 with 22, 26, and 16 documents, respectively. During the observed period, the combination of Deep Learning and Machine Learning remains relatively stable, indicating a consistent integration of these two approaches in research practices. As the years progressed, the adoption of Deep Learning and Machine Learning continued to grow. This continual increase underlines the critical role that Deep Learning and Machine Learning have played in understanding and combating the Covid-19 pandemic through innovative research and analysis.
In our study, we carefully paid attention to the type of document, distinguishing three major categories: Conference paper, journal article, and book chapter. We were able, through this classification, to analyze and understand the dissemination patterns and academic impact of each type of publication within the research environment. Regularly, authors present their initial findings in conference papers and their detailed contributions to the body of knowledge in journal articles, while comprehensive insights into specific areas of study are typically reserved for book chapters. Figure 8 represents the distribution of different publication types. As we can see, with 337 (57.7%) of all publications being journal articles, they make up the majority and play a major role in publishing research findings. Conference papers contain 211 (36.1%) of the publications, which is a notable proportion, indicating their significance as a platform for showcasing preliminary research findings and promoting academic discussion. Although they are fewer in number, book chapters make up 6.2% (36) of the publication because they provide more in-depth analysis and discussion on field-related topics. This distribution demonstrates the variety of channels that the academic community uses to publish research findings.
We take the first author's country into account to determine the country of origin for the research contribution in our study. Geographic dispersion of documents across the globe is illustrated in Figure 9. India tops the countries with an impressive count of 196 documents, highlighting its robust research in the topic. Followed by China in second with 61 contributions, illustrates the volume of its academic output. Other notable contributions come from Turkey with 29 papers, and Pakistan and the USA, each contributed with 23 papers. Other noteworthy contributions come from Egypt and Bangladesh, with 21 documents each. A substantial representation of Middle Eastern nations come from Iran and Saudi Arabia with 18 and 15 articles, respectively. Morocco from north Africa contributed 14 documents. The rising forces in economy and technology have challenged the established powers' traditional dominance in the field of global research and are making significant contributions. These emergent forces are leading the way in both academic and practical advances because of their remarkable agility and innovation.
The top 5 authors who have made major contributions to the corpus of documents are the focus of this analysis. We explore the specifics of their contributions, looking at the geographical context of their affiliations as well as the volume of published works they have contributed. The number of papers published, the esteemed journals that have published their work, and the corresponding databases are used to gauge their impact. This allows us to recognize the depth of their academic impact and the size of knowledge they contribute to the forefront of their respective fields.
As mentioned in Figure 10, K. Shankar from India has published four important journal articles in three years. Shankar's research papers received 18 and 38 citations in 2021 when they were published in "ACM Transactions on Internet Technology" [32] and "Applied Soft Computing" [33], respectively, both published by ACM and ScienceDirect. His work continued to garner attention in "Multimedia Systems" [34] published by Springer the following year. Shankar's 2023 publication in "Cognitive Neurodynamics" [35] was also published by Springer. All these articles, which have appeared in respectable journals and databases, have accumulated 118 citations.
The Pakistani author Imran Ahmed published two articles in 2022: "Interdisciplinary Sciences: Computational Life Sciences" [36] published by Springer, and one in "Virtual Reality & Intelligent Hardware" [37] hosted on ScienceDirect. Imran made another significant contribution in 2023 when he published an article in "Computing" [38], which was also published by Springer. The total citation of Imran reached 63 citations.
Santosh Kumar, an Indian researcher, published two journal articles in 2022, having a total of 36 citations. One article was published in "Computer Methods and Programmes in Biomedicine" [39] which is indexed in PubMed Database. His second work was featured in "Computers and Electrical Engineering" [40] on ScienceDirect.
The Iranian author Mustafa Ghaderzadeh had a remarkable year in 2021. His research was published as a conference paper by ACM and presented at the 5th International Conference on Medical and Health Informatics in 2021 [41]. Furthermore, he published an article in the "Journal of Medical Internet Research" [42] that was indexed in PubMed. He received a total count of 59 citations.
In 2023, Aysen Degerli, from Finland, made a significant contribution by publishing one journal article in "Health Information Science and Systems" [43] indexed in Springer with 76 citations. In 2022, he published a conference paper in the IEEE International Conference on Image Processing (ICIP), which is indexed in the IEEE Xplore database and earned 9 citations [44].
The prominence of the rising academic forces is demonstrated by the four leading authors who are from India, Pakistan, and Iran. Indeed, this is demonstrated by showcasing the increasing intellectual talent of their respective nations. These researchers have highlighted an academic ascendancy trend in regions that have been strongly pushing the boundaries of innovation and research.
A comprehensive overview of the 20 most productive journals in this study with details of corresponding databases, total citations, and average citation per journal is presented in Table 1. The analysis showcases that "Multimedia Tools and Applications" (29 documents), "Computers in Biology and Medicine" (19 documents), and "Expert Systems with Applications" (13 documents) are the most top three journals within their corresponding databases (PubMed for the first journal and ScienceDirect for the two others). These articles earned total citations of 237, 3711, and 399, respectively. With their large number of citations, they established a standard for scholarly impact. A more thorough analysis identifies a trend of significant contributions on several platforms, including ScienceDirect, Springer, and IEEE Xplore. This trend across databases demonstrates how research publications are dynamic and how journals bear witness to how academic discourse is changing. These results highlight the critical role that highly regarded journals play in promoting knowledge advancement among the international research community.
| Journal Title | Database | Total Documents | Total Citation | Average Citation per Journal |
| Multimedia Tools and Applications | PubMed | 29 | 237 | 8.17 |
| Computers in Biology and Medicine | ScienceDirect | 19 | 3711 | 195.32 |
| Expert Systems with Applications | ScienceDirect | 13 | 399 | 30.69 |
| Applied Soft Computing | ScienceDirect | 12 | 632 | 52.67 |
| Biomedical Signal Processing and Control | ScienceDirect | 12 | 181 | 15.08 |
| Journal of Ambient Intelligence and Humanized Computing | Springer | 10 | 290 | 29.00 |
| Scientific Reports | Springer | 9 | 462 | 51.33 |
| Applied Intelligence | Springer | 8 | 1422 | 177.75 |
| IEEE Access | IEEE Xplore | 7 | 2637 | 376.71 |
| Informatics in Medicine Unlocked | ScienceDirect | 7 | 757 | 108.14 |
| Neural Computing and Applications | Springer | 7 | 106 | 15.14 |
| SN Computer Science | Springer | 5 | 78 | 15.60 |
| ACM Transactions on Multimedia Computing, Communications, and Applications | ACM | 4 | 132 | 33.00 |
| Computers and Electrical Engineering | ScienceDirect | 4 | 29 | 7.25 |
| Computer Methods and Programs in Biomedicine | PubMed | 4 | 615 | 153.75 |
| Procedia Computer Science | ScienceDirect | 4 | 39 | 9.75 |
| Neurocomputing | ScienceDirect | 4 | 48 | 12.00 |
| Pattern Recognition | ScienceDirect | 4 | 314 | 78.50 |
| Soft Computing | Springer | 4 | 185 | 46.25 |
| Knowledge-Based Systems | ScienceDirect | 3 | 74 | 24.67 |
DownLoad:
CSV
From Figure 11, we can notice that there is no clear trend indicating a direct proportionate relationship between the number of documents published and average citations. This implies that more publications do not necessarily lead to a higher average citation count per document.
The total documents that have been published in IEEE Xplore database is 128 documents. As depicted in Figure 12, most published papers used Deep Learning techniques, accounting for 77 documents of research, which is showing its significant role in studies. Machine Learning techniques and the combined use of Deep Learning and Machine Learning are almost in the same range with 23 and 28 documents, respectively.
For the distribution of publication type in IEEE Xplore, as shown in Figure 13, the first remark that we can raise is the absence of book chapters. Only conference papers, which are predominant, with 113 documents, and journal articles with 15 documents and are published. This distribution clearly highlights conference proceedings within the IEEE community, reflecting the typical patterns of academic distribution in the field.
The graph in Figure 14 represents the top 10 contributing countries to the IEEE Xplore database. India is in the lead with a substantial 51 documents, underscoring the country's significant research output. Indonesia came in second with 10 publications, while the USA, Bangladesh, and Canada each contributed 7 documents. With four publications, Turkey follows closely in demonstrating its scholarly presence. Notable contributors include Saudi Arabia, Qatar, Morocco, and the UK, each of which has three publications in the database.
For the IEEE Xplore Database, all authors have published one single document in the IEEE Xplore database. Indeed, Abbas Mazrouei Sebdani, from Iran, published a conference paper [45] on the 5th International Conference on Pattern Recognition and Image Analysis (IPRIA) in 2021. He proposed two classification algorithms of Covid-19 using Machine Learning. In 2020, the south Korean researcher, Abdul Waheed, has published a journal article [46] where he proposed a method to generate synthetic chest X-ray (CXR) images by developing an Auxiliary Classifier Generative Adversarial Network (ACGAN). Using a deep unsupervised framework to classify lung diseases from chest CT and X-ray images, Pooja Yadav (India) published in IEEE Access [47]. Oussama El Gannourm, from Morocco, presented a Deep Learning based system for the diagnosis of COVID19 disease at the IEEE 2nd International Conference on Electronics, Control, Optimization, and Computer Science (ICECOCS) [48]. Using Deep Learning and Machine Learning, a framework named CovFrameNet., which consist of a pipelined image pre-processing method and a deep learning model for feature extraction, classification, and performance measurement, has been published by Olaide Nathaniel Oyelade from South Africa on IEEE Access [49].
According to Table 2, "IEEE Access" is the prominent journal in IEEE Xplore with a total of 7 documents and an impressive total of 2637 citations. Followed by "IEEE Journal of Biomedical and Health Informatics", "IEEE Transactions on Engineering Management", and "IEEE Transactions on Medical Imaging" participating with 2 documents each with total citations of 72, 33, and 186, respectively. With only one document, "IEEE Transactions on Big Data" shows its weight in the field with 70 citations.
| Journal Title | Database | Total Documents | Total Citation | Average Citation per Journal |
| IEEE Access | IEEE Xplore | 7 | 2637 | 376.71 |
| IEEE Journal of Biomedical and Health Informatics | IEEE Xplore | 2 | 72 | 36.00 |
| IEEE Transactions on Engineering Management | IEEE Xplore | 2 | 33 | 16.50 |
| IEEE Transactions on Medical Imaging | IEEE Xplore | 2 | 186 | 93.00 |
| IEEE Transactions on Big Data | IEEE Xplore | 1 | 70 | 70.00 |
DownLoad:
CSV
58 documents have been published in ACM database. Figure 15 illustrates that most documents used Deep Learning technique (46 documents) while Machine Learning and combined Deep Learning and Machine Learning techniques are less used accounting for 8 and 4, respectively. This makes us conclude the importance of Deep Learning techniques in ACM platform.
For the ACM database (Figure 16), only conferences articles and journal articles have been published with a dominance of conference articles around 76% (44 documents) and only 24% (14 documents) for journal articles. This distribution highlights the dual focuses of ACM database, which are to contribute to the body of knowledge with journal articles and to promote the academic record through the conferences.
Figure 17 is demonstrating China's remarkable advantage with 14 documents. India comes in second with 9 documents, while the USA contributes 6 publications. Greece, Thailand, Taiwan, and Saudi Arabia participated with 4 documents. With 2 documents, the UK contributed to the publication, although Brazil and Canada marked their presence with 1 document. This data shows a geographically varied collection of contributions to the ACM database, illustrating the international scope and cooperative character of modern research initiatives among different countries.
As for the ACM database, we do not have duplicated authors. Indeed, the paper of Abhishek Kumar, from India, was published for the 13 Indian Conference on Computer Vision, Graphics, and Image Processing (ICVGIP) [50]. He presented a comparative analysis of the most well-known CNN models to classify X-Ray images. The 12th ACM Conference on Bioinformatics, Computational Biology, and Health Informatics was an opportunity for the Georgian Tarun Naren [51] to publish his work where he developed a new variant of Model-Agnostic Meta-Learning (MAML) algorithm, named MAML++, in order to classify X-Ray images. From Vietnam, Pham Ngoc Ha [52] in 2023, participated in the 8th International Conference on Intelligent Information Technology and published his paper. He used Vision transformer architecture to extract data characteristics and classify images. In 2020, a system for automatic detection of COVID-19 from CXR images using machine learning techniques was proposed by Phongsathorn Kittiworapanya [53] on the Eleventh International Conference on Computational Systems-Biology and Bioinformatics. The year 2023 was when Robert Hertel [54] published a hit paper in ACM Computing Surveys. He presented an in-depth review of deep learning techniques on the purpose of diagnosis and prognosis of COVID-19 patients.
Table 3 presents the top 5 Journals Ranked by Productivity for ACM database. Indeed, "ACM Transactions on Multimedia Computing, Communications, and Applications" stands out as the most productive journal in the ACM database with 4 papers and 132 citations overall, followed by "ACM Transactions on Management Information Systems" having 3 publications and a total of 47 citations. Publishing 2 documents, "ACM Transactions on Internet Technology" and "IEEE/ACM Transactions on Computational Biology and Bioinformatics" got overall citations of 33 and 957, respectively. "ACM Computing Surveys" has completed the list of the top five productive journals with one contribution totaling five citations.
| Journal Title | Database | Total Documents | Total Citation | Average Citation per Journal |
| ACM Transactions on Multimedia Computing, Communications, and Applications | ACM | 4 | 132 | 33.00 |
| ACM Transactions on Management Information Systems | ACM | 3 | 47 | 15.67 |
| ACM Transactions on Internet Technology | ACM | 2 | 33 | 16.50 |
| IEEE/ACM Transactions on Computational Biology and Bioinformatics | ACM | 2 | 957 | 478.50 |
| ACM Computing Surveys | ACM | 1 | 5 | 5.00 |
DownLoad:
CSV
Participating with only 13 documents in this study, MDPI possesses the smallest collection of documents. The distribution of published documents (Figure 18) according to the techniques used is that more than 61% (8 documents) of the techniques used are Deep Learning, and the mixture of Deep Learning and Machine Learning is highlighted in four documents (30.8%). The use of Machine Learning was used only in one document.
Journal articles make up 100% of the publications and are the only contributor. The complete dominance of journal articles across all 13 documents in the dataset suggests that the ACM database places a high value on formal, peer-reviewed articles. The focused nature of this collection is highlighted by the absence of other publication types like conference papers or book chapters.
The top 10 nations that have contributed to the MDPI database are shown in Figure 19. Turkey leads the count with 3 documents. Following with 2 contributions, China and Pakistan show that they are actively involved in academic publishing within MDPI. Additionally, Bangladesh, Egypt, Iraq, Jordan, Saudi Arabia, and South Korea, contributed one document each.
There was one contribution per author from the MDPI database. Indeed, Ali Tariq Nagi [55], from Pakistan, has a paper that involves an evaluation of the performance of deep learning models for COVID-19 diagnosis using chest X-ray images from a dataset containing the largest number of COVID-19 images ever used in the literature. The Iraqi, Awf Ramdhan [56] proposed an approach that uses image cropping methods and a deep learning technique that classifies three public datasets. In [57], Bayan Alsaaidah from Jordan conducted a comprehensive review of Deep Learning and Machine Learning methods for detection and classification of Covid-19. Using Deep Learning techniques, a computer-aided diagnostic system for chest X-ray and CT images for Covid-19 classification was developed by Heba M. Emara [58] from Egypt. A Turkish researcher, Jawad Rasheed [59], proposed a computer vision and artificial-intelligence-based hybrid approach aid in efficient detection and control of the COVID-19 disease.
The top 5 Journals Ranked by Productivity for the MDPI database are presented in Table 4. With 3 published documents, "Diagnostics" leads the 5 productive journals in the MDPI database, and having 10 citations, was followed by "Applied Sciences" and "Sensors" with a count of 2 documents and an overall of citation of 33 and 27, respectively. "Bioengineering" with 15 citations and "Cancers" had 6 citations as their publications, with one document each.
| Journal Title | Database | Total Documents | Total Citation | Average Citation per Journal |
| Diagnostics | MDPI | 3 | 10 | 3.33 |
| Applied Sciences | MDPI | 2 | 33 | 16.50 |
| Sensors | MDPI | 2 | 27 | 13.50 |
| Bioengineering | MDPI | 1 | 15 | 15.00 |
| Cancers | MDPI | 1 | 6 | 6.00 |
DownLoad:
CSV
In this study, 35 documents were selected in the PubMed database. Figure 20 displays the distribution of techniques used. Having almost 50% (17 documents), Deep Learning was used as a technique for detection and classification of Covid-19 in the PubMed database. Deep Learning and Machine Learning were utilized jointly with a count of 14 documents (40%). The use of Machine Learning as a technique appeared only 4 times with a percentage of 11.4%. This brings us to the superiority of the use of Deep Learning techniques in the PubMed database.
Same as for the ACM database, only journal articles were published in the PubMed database. With the absence of other publication types, such as book chapters or conference papers, we can underline that peer-reviewed articles are the focused nature of the PubMed database.
Leading the top 10 countries that contributed to publication, India published 8 documents, followed by the UK with 5 publications. Three published documents were the participation of China and Iran each. Not far from them is South Africa, with 3 published documents. Other countries include Pakistan and the USA with 2 publications, and Australia, Greece, and Italy contributed with 1 document each. Figure 21 displays the top 10 Countries that contributed to publications for the PubMed database.
As displayed in Figure 22, from Saudi Arabia, Mahmoud Ragad published 2 journal articles in 2021 and 2022. In his first paper [60], he presented an artificial intelligence-based ensemble model for detection and classification (AIEM-DC) that aims to accurately detect and classify the COVID-19 using an ensemble of DL models. In [61], Mahmoud Ragad proposed a new Quantum Seagull Optimization Algorithm with a DL-based COVID-19 diagnosis model, named the QSGOA-DL technique to detect and classify COVID-19 with the help of CXR images. Abdullah Alen, from Turkey, proposed a Residual Convolutional Neural Network (ResCNN) used as a deep learning method, with the assistance of machine learning algorithms and extracted features from images [62]. An effective COVID-19 detection and classification approach using the Shufflenet CNN by employing three types of images (chest radiograph, CT-scan, and ECG-trace images) was proposed by the Pakistani Naeem Ullah [63]. The main idea of Linh T Duong, from Vietnam, in [64] is exploiting cutting-edge Machine Learning techniques for the detection of Covid-19 from chest X-ray (CXR) and lung computed tomography (LCT) images. From Italy, Luca Saba [65] presented a comparative study between Deep Learning and Machine Learning algorithms for the detection of Covid-19 based on radiological computed tomography (CT) lung scans.
Table 5 displays the 5 most productive journals in the PubMed database. With 3 documents, "Diagnostics (Basel)" ranks first with 29 citations, followed by "Computational Intelligence and Neuroscience" with 2 published papers, which got 8 citations. "Mathematical Biosciences and Engineering", "Journal of Healthcare Engineering", and "Journal of Medical Internet Research" have participated in this field by publishing 1 article each with total citations of 8, 10, and 59, respectively.
| Journal Title | Database | Total Documents | Total Citation | Average Citation per Journal |
| Diagnostics (Basel) | PubMed | 3 | 29 | 9.67 |
| Computational Intelligence and Neuroscience | PubMed | 2 | 8 | 4.00 |
| Mathematical Biosciences and Engineering | PubMed | 1 | 8 | 8.00 |
| Journal of Healthcare Engineering | PubMed | 1 | 10 | 10.00 |
| Journal of Medical Internet Research | PubMed | 1 | 59 | 59.00 |
DownLoad:
CSV
Springer is the database that has the highest number of documents in this study by contributing 217 documents. With 148 journal articles, Deep Learning dominated the techniques used in Springer database with a percentage of 68.2%. Merged Deep Learning and Machine Learning techniques have been used in 55 documents, achieving 25.3% of all documents. Moreover, the use of Machine Learning techniques occurred only in 14 documents (6.5%). This distribution used techniques that signify the research trends and priorities within the Springer database. Figure 23 shows the distribution of techniques used for the Springer database.
With a percentage of 60.8% (132 documents), the publication type of published documents in Springer are journal articles with a huge part (see Figure 24). A considerable number of types of publications are conference papers, accounting for 54 documents or 24.9%. Book chapters got a significant part of publication type with 31 documents (14.3%). This means that springer is a database that opens all the opportunities to researchers to publish their works.
As we can see in Figure 25, Indian researchers lead the top 10 countries that contributed to publication with a very high number of documents (90 publications). This carries us to India's superiority in the field of scientific research in recent years. With a very big gap between India, China came second with 18 documents, followed by Pakistan, Egypt, and Turkey in the same range of published documents, with a count of 13, 11, and 10 documents, respectively. Morocco and the USA marked their presence with 8 publications each. Furthermore, Bangladesh, Iraq, and Algeria have participated with 5 documents each.
The top 5 researchers in Springer participated with 2 documents each. Indeed, an Indian researcher, K. Shankar, who came first with publications [66], presented a new metaheuristic-based fusion model for COVID-19 diagnosis using chest X-ray images using Weiner filtering for preprocessing, grey level co-occurrence matrix for feature extraction, and artificial neural network for classification. In 2023, an automated COVID-19 diagnosis process using Convolutional Neural Network (CNN) with a fusion-based feature extraction model (FM-CNN) was developed in his second paper [67]. In 2021, Sourabh Shastri, from India, designed a nested ensemble model using deep learning methods based on long short-term memory (LSTM) [68]. A CheXImageNet model has been introduced for detecting Covid-19 disease using digital images of Chest X-ray with the help of an openly accessible dataset in his second paper [69]. The work done by the Pakistani Kainat Khero in [70] was a review of ML and DL-based techniques for early detection of Covid using chest X-rays. A comparison study of 9 state-of-the-art CNN architectures through a transfer learning approach for detection of Covid-19 was presented in his second work [71]. Siddharth Gupta, from India, presented pre-trained CNN models (VGG16 and VGG19) that were used for transfer learning and several machine learning classifiers for the classification of images, such as Covid19 [72]. In [73], he employed DL-based automated techniques (VGG16, VGG19, and Inception V3) to process the chest X-ray images for the detection of Covid-19. The Indian author Ebenezer Jangam [74] proposed a stacked ensemble of heterogenous pre-trained computer vision models where 4 pre-trained DL models were considered (VGG19, ResNet101, DenseNet169, and WideResNet502). His second work [75] was about a novel multi-class classification framework that can minimize either false positives or false negatives, and is useful in computer aided diagnosis or computer aided detection, respectively.
Publishing 28 documents with a total citation of 222 citations, "Multimedia Tools and Applications" came out on top of the productive journal in Springer (see Table 6). With a considerable difference of 18 documents, "Journal of Ambient Intelligence and Humanized Computing" took the second rank, with 290 citations. "Applied Intelligence" and "Scientific Reports" have published 8 documents each with 1422 and 462 citations respectively. Six publications and 106 citations allowed "Neural Computing and Applications" to be in the top 5 productive journal in Springer.
| Journal Title | Database | Total Documents | Total Citation | Average Citation per Journal |
| Multimedia Tools and Applications | Springer | 28 | 222 | 7.93 |
| Journal of Ambient Intelligence and Humanized Computing | Springer | 10 | 290 | 29.00 |
| Applied Intelligence | Springer | 8 | 1422 | 177.75 |
| Scientific Reports | Springer | 8 | 462 | 57.75 |
| Neural Computing and Applications | Springer | 6 | 106 | 17.67 |
DownLoad:
CSV
With 132 collected documents, ScienceDirect comes in second of all the databases concerned in this study. From Figure 26, we can conclude that Deep Learning techniques are the most used with a total count of 81 documents, which is almost a huge portion of all technique used. The use of Deep Learning and Machine Learning together appeared in 30 (22.7%) papers while Machine Learning as type of technique occurred in 21 (15.9%) documents.
As illustrated in Figure 27, more than 96% (127 papers) of documents published in ScienceDirect are journal articles. This shows the total dominance of this type of publication, and it is the main way for researchers to publish their works in ScienceDirect. Even though they are less in number, book chapters make up 3.8% of all publications (5 documents).
Like almost all the databases, India tops the 10 countries that contributed to publications in ScienceDirect with 38 documents, which confirms its dominance in this study. India is followed by China, with a significant gab accounting for 21 published papers. Turkey maintained its presence among the countries contributing to publication in this database. Bangladesh and Iran contributed 8 documents, while Egypt and Pakistan h 7 and 5 times, respectively. South Korea, UAE, and Saudi Arabia insisted on being included among the countries with 3 documents each. Figure 28 displays the top countries that contributed to the publications for the ScienceDirect database.
The year 2021 was a special year for the Pakistani Saddam Hussain Khan when he published two papers (Figure 29). In [76], he proposed two new deep learning frameworks: Deep Hybrid Learning (DHL) and Deep Boosted Hybrid Learning (DBHL) for effective COVID-19 detection in X-ray dataset. He developed, in his second work [77], two novel custom CNN architectures (COVID-RENet-1 and COVID-RENet-2) for COVID-19 specific pneumonia analysis. The Indian researcher, Aakarsh Malhotra [78], presented a COVID-19 Multi-Task Network (COMiT-Net), which is an automated end-to-end network for COVID-19 screening and that can perform semantic segmentation of the regions of interest to make the model explainable. Originally from India, Sakthivel R [79] built an efficient hardware architecture based on an ensemble deep learning model to identify the COVID-19 using chest X-ray (CXR) records. Saeed Iqbal [80] suggested a technique allowing a class balancing algorithm to understand and detect lung disease signs from chest X-ray and CT images. He used Deep learning techniques to train and evaluate images, enabling the extraction of basic visual attributes. Roa'a Mohammedqasem [81], from Turkey, proposed a real-time detection system based on the Internet of Things framework. The system can collect real-time data from users to determine potential coronavirus cases, analyze treatment responses for people who have been treated, and accurately collect and analyse the datasets.
As presented in Table 7, the journal "Computers in Biology and Medicine" came in the top 5 productive journals with 19 published documents and accumulating a total of 3711 citations. With 13 papers having 221 citations, "Expert Systems with Applications" ranked in second place, followed by "Biomedical Signal Processing and Control" and "Applied Soft Computing" with 12 and 11 documents and receiving 181 and 622, respectively. "Informatics in Medicine Unlocked" announced its position within the productive journals with 7 documents accounting for a total of 757 citations.
| Journal Title | Database | Total Documents | Total Citation | Average Citation per Journal |
| Computers in Biology and Medicine | ScienceDirect | 19 | 3711 | 195.32 |
| Expert Systems with Applications | ScienceDirect | 13 | 221 | 17.00 |
| Biomedical Signal Processing and Control | ScienceDirect | 12 | 181 | 15.08 |
| Applied Soft Computing | ScienceDirect | 11 | 622 | 56.55 |
| Informatics in Medicine Unlocked | ScienceDirect | 7 | 757 | 108.14 |
DownLoad:
CSV
In this review, we highlighted the use of Deep Learning and Machine Learning techniques to detect and classify Covid-19 using X-Ray and CT images. The bibliometric analysis carried out for this study revealed a significant number of documents describing the importance of the use of Deep Learning in this field compared to Machine learning methods. Moreover, one conclusion we can draw from this study is the rising forces in economy and technology, especially India, China, Turkey, and Pakistan, which began to compete in the field of scientific research. Additionally, journal articles, as a publication type, dominated the type of publication compared to Conference Papers and Book Chapters. This means that authors prefer to publish their detailed contributions to the field of knowledge in journals than publish their initial findings in conference papers or their comprehensive insights into specific areas in Book Chapters. Furthermore, authors focused on the Springer database to submit their works for publication, which is explained by the high number of published documents in this database compared to other databases.
The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.
The authors declare that there are no conflicts of interest in this paper.
| [1] |
M. Žitnik, V. Janjić, C. Larminie, B. Zupan, N. Pržulj, Discovering disease- disease associations by fusing systems-level molecular data, Sci. Rep., 3 (2013), 1–9. https://doi.org/10.1038/srep03202 doi: 10.1038/srep03202
|
| [2] |
S. Bang, J. H. Kim, H. Shin, Causality modeling for directed disease network, Bioinformatics, 32 (2016), 437–444. https://doi.org/10.1093/bioinformatics/btw439 doi: 10.1093/bioinformatics/btw439
|
| [3] |
A. Suratanee, K. Plaimas, DDA: A novel network-based scoring method to identify disease-disease associations, Bioinform. Biol. Insights, 9 (2015), 175–186. https://doi.org/10.4137/bbi.s35237 doi: 10.4137/bbi.s35237
|
| [4] |
J. Yang, S. J. Wu, S. Y. Yang, J. W. Peng, S. N. Wang, F. Y. Wang, et al., DNetDB: The human disease network database based on dysfunctional regulation mechanism, BMC Syst. Biol., 10 (2016), 1–8. https://doi.org/10.1186/s12918-016-0280-5 doi: 10.1186/s12918-016-0280-5
|
| [5] |
J. Li, B. Gong, X. Chen, T. Liu, C. Wu, F. Zhang, et al., DOSim: An R package for similarity between diseases based on disease ontology, BMC Bioinformatics., 12 (2011), 1–10. https://doi.org/10.1186/1471-2105-12-266 doi: 10.1186/1471-2105-12-266
|
| [6] |
D. A. Davis, N. V. Chawla, Exploring and exploiting disease interactions from multi-relational gene and phenotype networks, PLoS One, 6 (2011), 22670. https://doi.org/10.1371/journal.pone.0022670 doi: 10.1371/journal.pone.0022670
|
| [7] |
Y. Li, P. Agarwal, A pathway-based view of human diseases and disease relationships, PLoS One, 4 (2009), 4346. https://doi.org/10.1371/journal.pone.0004346 doi: 10.1371/journal.pone.0004346
|
| [8] |
S. S. Deepika, T. V. Geetha, Pattern-based bootstrapping framework for biomedical relation extraction, Eng. Appl. Artif. Intell., 99 (2021), 104130. https://doi.org/10.1016/j.engappai.2020.104130 doi: 10.1016/j.engappai.2020.104130
|
| [9] |
C. A. Hidalgo, N. Blumm, A. L. Barabási, N. A. Christakis, A dynamic network approach for the study of human phenotypes, PLoS Comput. Biol., 5 (2009), 1000353. https://doi.org/10.1371/journal.pcbi.1000353 doi: 10.1371/journal.pcbi.1000353
|
| [10] |
X. Zhang, R. Zhang, Y. Jiang, P. Sun, G. Tang, X. Wang, et al., The expanded human disease network combining protein-protein interaction information, Eur. J. Hum. Genet., 19 (2011), 783–788. https://doi.org/10.1038/ejhg.2011.30 doi: 10.1038/ejhg.2011.30
|
| [11] |
Y. Hu, M. Zhou, H. Shi, H. Ju, Q. Jiang, L. Cheng, Measuring disease similarity and predicting disease-related ncRNAs by a novel method, BMC Med. Genomics, 10 (2017), 67–74. https://doi.org/10.1186/s12920-017-0315-9 doi: 10.1186/s12920-017-0315-9
|
| [12] |
L. M. Schriml, J. B. Munro, M. Schor, D, Olley, C. McCracken, V. Felix, et al., The human disease ontology 2022 update, Nucleic Acids Res., 50 (2022), 1255–1261. https://doi.org/10.1093/nar/gkab1063 doi: 10.1093/nar/gkab1063
|
| [13] |
S. Carbon, E. Douglass, N. Dunn, B. M. Good, N. L. Harris, S. E. Lewis, et al., The gene ontology resource: 20 years and still GOing strong, Nucleic Acids Res., 47 (2019), 330–338. https://doi.org/10.1093/nar/gky1055 doi: 10.1093/nar/gky1055
|
| [14] |
S. Köhler, M. Gargano, N. Matentzoglu, L. C. Carmody, D. Lewis-Smith, N. A Vasilevsky, et al., The human phenotype ontology in 2021, Nucleic Acids Res., 49 (2021), 1207–1217. https://doi.org/10.1093/nar/gkaa1043 doi: 10.1093/nar/gkaa1043
|
| [15] |
O. Bodenreider, The Unified Medical Language System (UMLS): Integrating biomedical terminology, Nucleic Acids Res., 32 (2004), 267–270. https://doi.org/10.1093/nar/gkh061 doi: 10.1093/nar/gkh061
|
| [16] |
D. L. Ngo, N. Yamamoto, V. A. Tran, N. G. Nguyen, D. Phan, F. R. Lumbanraja, et al., Application of word embedding to drug repositioning, J. Biomed. Sci. Eng., 09 (2016), 7–16, http://doi.org/10.4236/jbise.2016.91002 doi: 10.4236/jbise.2016.91002
|
| [17] |
P. T. Lai, W. L. Lu, T. R. Kuo, C. R. Chung, J. C. Han, R. T. H. Tsai, et al., Using a large margin context-aware convolutional neural network to automatically extract disease-disease association from literature: Comparative analytic study, JMIR Med. Inform., 7 (2019), 14502. https://doi.org/10.2196/14502 doi: 10.2196/14502
|
| [18] | R. O'Shea, Gextext: disease network extraction from biomedical literature, preprint, arXiv1911.02562. |
| [19] | M. V. Korff, B. Deffarges, T. Sander, Data mining in MEDLINE for disease-disease associations via second order co-occurrence, in 2015 IEEE Symposium Series on Computational Intelligence, (2015), 314–321, https://doi.org/10.1109/SSCI.2015.54 |
| [20] | A. L. Beam, B. Kompa, A. Schmaltz, I. Fried, G. Weber, N. Palmer, et al., Clinical concept embeddings learned from massive sources of medical data, Pac. Symp. Biocomput., 25 (2018), 295–306. |
| [21] |
A. B. Holmes, A. Hawson, F. Liu, C. Friedman, H. Khiabanian, R. Rabadan, Discovering disease associations by integrating electronic clinical data and medical literature, PLoS One, 6 (2011), 21132. https://doi.org/10.1371/journal.pone.0021132 doi: 10.1371/journal.pone.0021132
|
| [22] | S. Ghosh, P. Chakraborty, E. Cohn, J. S. Brownstein, N. Ramakrishnan, Characterizing diseases from unstructured text: A vocabulary driven Word2vec approach, preprint, arXiv.1603.00106. |
| [23] |
J. Park, K. Kim, W. Hwang, D. Lee, Concept embedding to measure semantic relatedness for biomedical information ontologies, J. Biomed. Inform., 94 (2019), 103182. https://doi.org/10.1016/j.jbi.2019.103182 doi: 10.1016/j.jbi.2019.103182
|
| [24] |
J. Z. Wang, Z. Du, R. Payattakool, P. S. Yu, C. F. Chen, A new method to measure the semantic similarity of GO terms, Bioinformatics, 23 (2007), 1274–1281. https://doi.org/10.1093/bioinformatics/btm087 doi: 10.1093/bioinformatics/btm087
|
| [25] | P. Resnik, Using information content to evaluate semantic similarity in a taxonomy, preprint, arXiv: cmp-lg/9511007. |
| [26] | D. Lin, An information-theoretic definition of similarity, in International Conference on Machine Learning, 98 (1998), 296–304. |
| [27] | S. Mathur, D. Dinakarpandian, Automated ontological gene annotation for computing disease similarity, Summit Transl Bioinform., (2010), 12–16. |
| [28] |
S. Mathur, D. Dinakarpandian, Finding disease similarity based on implicit semantic similarity, J. Biomed. Inform., 45 (2012), 363–371, https://doi.org/10.1016/j.jbi.2011.11.017 doi: 10.1016/j.jbi.2011.11.017
|
| [29] |
F. Z. Smaili, X. Gao, R. Hoehndorf, Onto2Vec: Joint vector-based representation of biological entities and their ontology-based annotations, Bioinformatics, 34 (2018), 52–60, doi: https://doi.org/10.1093/bioinformatics/bty259 doi: 10.1093/bioinformatics/bty259
|
| [30] |
L. Cheng, J. Li, P. Ju, J. Peng, Y. Wang, SemFunSim: A new method for measuring disease similarity by integrating semantic and gene functional association, PLoS One, 9 (2014), 99415. https://doi.org/10.1371/journal.pone.0099415 doi: 10.1371/journal.pone.0099415
|
| [31] |
S. Su, L. Zhang, J. Liu, An effective method to measure disease similarity using gene and phenotype associations, Front. Genet., 10 (2019), 1–8. https://doi.org/10.3389/fgene.2019.00466 doi: 10.3389/fgene.2019.00466
|
| [32] |
S. Jiang, W. Wu, N. Tomita, C. Ganoe, S. Hassanpour, Multi-Ontology Refined Embeddings (MORE): A hybrid multi-ontology and corpus-based semantic representation model for biomedical concepts, J. Biomed. Inform., 111 (2020), 103581. https://doi.org/10.1016/j.jbi.2020.103581 doi: 10.1016/j.jbi.2020.103581
|
| [33] | Z. Yu, B. C. Wallace, T. Johnson, T. Cohen, Retrofitting concept vector representations of medical concepts to improve estimates of semantic similarity and relatedness, preprint, arXiv.1709.07357. |
| [34] |
E. Nourani, V. Reshadat, Association extraction from biomedical literature based on representation and transfer learning, J. Theor. Biol., 488 (2020), 110112. https://doi.org/10.1016/j.jtbi.2019.110112 doi: 10.1016/j.jtbi.2019.110112
|
| [35] | Y. Peng, Z. Lu, Deep learning for extracting protein-protein interactions from biomedical literature, in Proceedings of the BioNLP 2017 workshop, (2017), 29–38. http://doi.org/10.18653/v1/W17-2304 |
| [36] |
C. Quan, L. Hua, X. Sun, W. Bai, Multichannel convolutional neural network for biological relation extraction, Biomed Res. Int., (2016), 1850404. https://doi.org/10.1155/2016/1850404 doi: 10.1155/2016/1850404
|
| [37] |
N. K. Rakhi, R. Tuwani, J. Mukherjee, G. Bagler, Data-driven analysis of biomedical literature suggests broad-spectrum benefits of culinary herbs and spices, PLoS One, 13 (2018), 1–20, doi: https://doi.org/10.1371/journal.pone.0198030 doi: 10.1371/journal.pone.0198030
|
| [38] |
J. Li, X. Zhu, J. Y. Chen, Building disease-specific drug-protein connectivity maps from molecular interaction networks and PubMed abstracts, PLoS Comput. Biol., 5 (2009), 1000450. https://doi.org/10.1371/journal.pcbi.1000450 doi: 10.1371/journal.pcbi.1000450
|
| [39] |
H. W. Chun, Y. Tsuruoka, J. D. Kim, R. Shiba, N. Nagata, T. Hishiki, et al., Extraction of gene-disease relations from medline using domain dictionaries and machine learning, Pac. Symp. Biocomput., 15 (2006), 4–15. https://doi.org/10.1142/9789812701626_0002 doi: 10.1142/9789812701626_0002
|
| [40] |
C. Perez-Iratxeta, P. Bork, M. A. Andrade, Association of genes to genetically inherited diseases using data mining, Nat. Genet., 31 (2002), 316–319. https://doi.org/10.1038/ng895 doi: 10.1038/ng895
|
| [41] |
S. Pletscher-Frankild, A. Pallejà, K. Tsafou, J. X. Binder, L. J. Jensen, DISEASES: Text mining and data integration of disease-gene associations, Methods, 74 (2015), 83–89. https://doi.org/10.1016/j.ymeth.2014.11.020 doi: 10.1016/j.ymeth.2014.11.020
|
| [42] |
J. Lee, S. Kim, S. Lee, K. Lee, J. Kang, On the efficacy of per-relation basis performance evaluation for PPI extraction and a high-precision rule-based approach, BMC Med. Inform. Decis. Mak., 13 (2013), 1–12. https://doi.org/10.1186/1472-6947-13-S1-S7 doi: 10.1186/1472-6947-13-S1-S7
|
| [43] |
M. Song, W. C. Kim, D. Lee, G. E. Heo, K. Y. Kang, PKDE4J: Entity and relation extraction for public knowledge discovery, J. Biomed. Inform., 57 (2015), 320–332. https://doi.org/10.1016/j.jbi.2015.08.008 doi: 10.1016/j.jbi.2015.08.008
|
| [44] |
L. Tari, J. Hakenberg, G. Gonzalez, C. Baral, Querying parse tree database of medline text to synthesize user-specific biomolecular networks, Pac. Symp. Biocomput., 98 (2009), 87–98. https://doi.org/10.1142/9789812836939_0009 doi: 10.1142/9789812836939_0009
|
| [45] |
B. Bhasuran, J. Natarajan, Automatic extraction of gene-disease associations from literature using joint ensemble learning, PLoS One, 13 (2018), 1–22. https://doi.org/10.1371/journal.pone.0200699 doi: 10.1371/journal.pone.0200699
|
| [46] |
Y. Zhang, Z. Lu, Exploring semi-supervised variational autoencoders for biomedical relation extraction, Methods, 166 (2019), 112–119. https://doi.org/10.1016/j.ymeth.2019.02.021 doi: 10.1016/j.ymeth.2019.02.021
|
| [47] |
N. Rosário-Ferreira, V. Guimarães, V. S. Costa, I. S. Moreira, SicknessMiner: a deep-learning-driven text-mining tool to abridge disease-disease associations, BMC Bioinformatics, 22 (2021), 1–12. https://doi.org/10.1186/s12859-021-04397-w doi: 10.1186/s12859-021-04397-w
|
| [48] | M. Asada, M. Miwa, Y. Sasaki, Extracting drug-drug interactions with attention CNNs, in Proceedings of the BioNLP 2017 workshop, (2017), 9–18. http://doi.org/10.18653/v1/W17-2302 |
| [49] | Y. Hsieh, Y. Chang, N. Chang, W. Hsu, Identifying rotein-protein interactions in biomedical literature using recurrent neural networks with long short-term memory, in Proceedings of the The 8th International Joint Conference on Natural Language Processing, (2017), 240–245. |
| [50] |
L. Hua, C. Quan, A shortest dependency path based convolutional neural network for protein-protein relation extraction, Biomed Res. Int., (2016), 8479587. https://doi.org/10.1155/2016/8479587 doi: 10.1155/2016/8479587
|
| [51] | X. Wang, L. Zhu, Z. Zheng, M. Xu, Y. Yang, Align and tell: Boosting text-video retrieval with local alignment and fine-grained supervision, IEEE Trans. Multimedia, (2022), 1–11. https://doi.org/10.1109/TMM.2022.3204444 |
| [52] | R. Xu, L. Li, Q. Q. Wang, DRiskKB: A large-scale disease-disease risk relationship knowledge base constructed from biomedical text, BMC Bioinformatics, 15 (2014) 105. https://doi.org/10.1186/1471-2105-15-105 |
| [53] |
D. Wei, T. Kang, H. A. Pincus, C. Weng, Construction of disease similarity networks using concept embedding and ontology, Stud. Health Technol. Inform., 264 (2019), 442–446. https://doi.org/10.3233/shti190260 doi: 10.3233/shti190260
|
| [54] |
S. V. S. Pakhomov, G. Finley, R. McEwan, Y. Wang, G. B. Melton, Corpus domain effects on distributional semantic modeling of medical terms, Bioinformatics, 32 (2016), 3635–3644. https://doi.org/10.1093/bioinformatics/btw529 doi: 10.1093/bioinformatics/btw529
|
| [55] | G. K. Mazandu, N. J. Mulder, Information content-based gene ontology semantic similarity approaches: Toward a unified framework theory, Biomed Res. Int., (2013). https://doi.org/10.1155/2013/292063 |
| [56] |
X. Song, L. Li, P. K. Srimani, P. S. Yu, J. Z. Wang, Measure the semantic similarity of go terms using aggregate information content, IEEE/ACM Trans. Comput. Biol. Bioinform., 11 (2014), 468–476. https://doi.org/10.1109/tcbb.2013.176 doi: 10.1109/tcbb.2013.176
|
| [57] |
Z. Teng, M. Guo, X. Liu, Q. Dai, C. Wang, P. Xuan, Measuring gene functional similarity based on group-wise comparison of GO terms, Bioinformatics, 29 (2013), 1424–1432. https://doi.org/10.1093/bioinformatics/btt160 doi: 10.1093/bioinformatics/btt160
|
| [58] |
C. Zhao, Z. Wang, GOGO: An improved algorithm to measure the semantic similarity between gene ontology terms, Sci. Rep., 8 (2018), 1–10. https://doi.org/10.1038/s41598-018-33219-y doi: 10.1038/s41598-018-33219-y
|
| [59] | Z. Wu, M. Palmer, Verb semantics and lexical selection, in Proceedings of the 32nd annual meeting on Association for Computational Linguistics, (1994), 133–138. https://doi.org/10.3115/981732.981751 |
| [60] | R. Richardson, A. Smeaton, J. Murphy, Using WordNet as a knowledge base for measuring semantic similarity between words, Tech. Rep. Work. Pap. 9 (1994). |
| [61] |
J. Cheng, M. S. Cline, J. Martin, D. Finkelstein, T. Awad, D. Kulp, et al., A knowledge-based clustering algorithm driven by Gene Ontology, J. Biopharm. Stat., 14 (2004), 687–700. https://doi.org/10.1081/bip-200025659 doi: 10.1081/bip-200025659
|
| [62] |
H. Wu, Z. Su, F. Mao, V. Olman, Y. Xu, Prediction of functional modules based on comparative genome analysis and Gene Ontology application, Nucleic Acids Res., 33 (2005), 2822–2837. https://doi.org/10.1093/nar/gki573 doi: 10.1093/nar/gki573
|
| [63] |
D. Wang, J. Wang, M. Lu, F. Song, Q. Cui, Inferring the human microRNA functional similarity and functional network based on microRNA-associated diseases, Bioinformatics, 26 (2010), 1644–1650. https://doi.org/10.1093/bioinformatics/btq241 doi: 10.1093/bioinformatics/btq241
|
| [64] |
G. K. Mazandu, N. J. Mulder, A topology-based metric for measuring term similarity in the gene ontology, Adv. Bioinformatics, (2012), 975783. https://doi.org/10.1155/2012/975783 doi: 10.1155/2012/975783
|
| [65] |
A. B. Kamran, H. Naveed, GOntoSim: A semantic similarity measure based on LCA and common descendants, Sci. Rep., 12 (2022), 3818. https://doi.org/10.1038/s41598-022-07624-3 doi: 10.1038/s41598-022-07624-3
|
| [66] |
J. Camacho-Collados, M. T. Pilehvar, R. Navigli, NASARI: Integrating explicit knowledge and corpus statistics for a multilingual representation of concepts and entities, Artif. Intell., 240 (2016), 36–64. https://doi.org/10.1016/j.artint.2016.07.005 doi: 10.1016/j.artint.2016.07.005
|
| [67] |
Z. H. Guo, Z. H. You, D. S. Huang, H. C. Yi, K. Zheng, Z. H. Chen, et al., MeSHHeading2vec: A new method for representing MeSH headings as vectors based on graph embedding algorithm, Brief. Bioinform., 22 (2021), 2085–2095. https://doi.org/10.1093/bib/bbaa037 doi: 10.1093/bib/bbaa037
|
| [68] |
X. Zhong, R. Kaalia, J. C. Rajapakse, GO2Vec: Transforming GO terms and proteins to vector representations via graph embeddings, BMC Genomics, 20 (2019), 918. https://doi.org/10.1186/s12864-019-6272-2 doi: 10.1186/s12864-019-6272-2
|
| [69] |
F. Z. Smaili, X. Gao, R. Hoehndorf, OPA2Vec: Combining formal and informal content of biomedical ontologies to improve similarity-based prediction, Bioinformatics, 35 (2019), 2133–2140. https://doi.org/10.1093/bioinformatics/bty933 doi: 10.1093/bioinformatics/bty933
|
| [70] |
J. Lee, D. Lee, K. H. Lee, Literature mining for context-specific molecular relations using multimodal representations (COMMODAR), BMC Bioinformatics, 21 (2020), 250. https://doi.org/10.1186/s12859-020-3396-y doi: 10.1186/s12859-020-3396-y
|
| [71] |
L. Deng, D. Ye, J. Zhao, J. Zhang, MultiSourcDSim: An integrated approach for exploring disease similarity, BMC Med. Inform. Decis. Mak., 19 (2019), 269. https://doi.org/10.1186/s12911-019-0968-8 doi: 10.1186/s12911-019-0968-8
|
| [72] |
P. Li, Y. Nie, J. Yu, Fusing literature and full network data improves disease similarity computation, BMC Bioinformatics, 17 (2016), 326. https://doi.org/10.1186/s12859-016-1205-4 doi: 10.1186/s12859-016-1205-4
|
| [73] |
C. H. Wei, A. Allot, R. Leaman, Z. Lu, PubTator central: automated concept annotation for biomedical full text articles, Nucleic Acids Res., 47 (2019), 587–593. https://doi.org/10.1093/nar/gkz389 doi: 10.1093/nar/gkz389
|
| [74] |
J. Piñero, J. M. R. Anguita, J. S. Pitarch, F. Ronzano, E. Centeno, F. Sanz, et al., The DisGeNET knowledge platform for disease genomics: 2019 update, Nucleic Acids Res., 48 (2020), 845–855. https://doi.org/10.1093/nar/gkz1021 doi: 10.1093/nar/gkz1021
|
| [75] |
L. E. Salnikova, E. V. Chernyshova, L. A. Anastasevich, S. S. Larin, Gene-and disease-based expansion of the knowledge on inborn errors of immunity, Front. Immunol., 10 (2019), 2475. https://doi.org/10.3389/fimmu.2019.02475 doi: 10.3389/fimmu.2019.02475
|
| [76] |
T. Pedersen, S. V. S. Pakhomov, S. Patwardhan, C. G. Chute, Measures of semantic similarity and relatedness in the biomedical domain, J. Biomed. Inform., 40 (2007), 288–299. https://doi.org/10.1016/j.jbi.2006.06.004 doi: 10.1016/j.jbi.2006.06.004
|
| [77] |
A. P. Davis, C. J. Grondin, R. J. Johnson, D. Sciaky, J. Wiegers, T. C. Wiegers, et al., Comparative Toxicogenomics Database (CTD): Update 2021, Nucleic Acids Res., 49 (2021), 1138–1143. https://doi.org/10.1093/nar/gkaa891 doi: 10.1093/nar/gkaa891
|
| [78] | S. Manchanda, A. Anand, Representation learning of drug and disease terms for drug repositioning, in 2017 3rd IEEE International Conference on Cybernetics (CYBCON), (2017), 1–6. https://doi.org/10.1109/CYBConf.2017.7985802 |
| [79] |
J. J. Lastra-Díaz, J. Goikoetxea, M. A. Hadj Taieb, A. García-Serrano, M. Ben Aouicha, E. Agirre, A reproducible survey on word embeddings and ontology-based methods for word similarity: Linear combinations outperform the state of the art, Eng. Appl. Artif. Intell., 85 (2019), 645–665. https://doi.org/10.1016/j.engappai.2019.07.010 doi: 10.1016/j.engappai.2019.07.010
|
| [80] | M. de Marneffe, C. D. Manning, Stanford typed dependencies manual, 2008. Available from: https://downloads.cs.stanford.edu/nlp/software/dependencies_manual.pdf |
| [81] | Y. Tsuruoka, J. Tsujii, Bidirectional inference with the easiest-first strategy for tagging sequence data, Proceedings of Human Language Technology Conference and Conference on Empirical Methods in Natural Language Processing (HLT/EMNLP), (2005), 467–474. http://doi.org/10.3115/1220575.1220634 |
| [82] | T. Mikolov, I. Sutskever, K. Chen, G. Corrado, J. Dean, Distributed representations of words and phrases and their compositionality, in Proceedings of the 26th International Conference on Neural Information Processing Systems, 2 (2013), 3111–3119. |
| [83] | S. Pyysalo, F. Ginter, H. Moen, T. Salakoski, S. Ananiadou, Distributional semantics resources for biomedical text processing, Proceedings of the 5th International Symposium on Languages in Biology and Medicine, 5 (2013), 39–44. |
| [84] | Y. Tang, Deep Learning using Linear Support Vector Machines, preprint, arXiv: 1306.0239. |
| [85] | E. Choi, M. T. Bahadori, L. Song, W. F. Stewart, J. Sun, GRAM: Graph-based attention model for healthcare representation learning, in Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, (2017), 787–795. https://doi.org/10.1145%2F3097983.3098126 |
| [86] | L. Song, C. W. Cheong, K. Yin, W. K. Cheung, B. C. M. Fung, J. Poon, Medical concept embedding with multiple ontological representations, in Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, (2019), 4613–4619. https://doi.org/10.24963/ijcai.2019/641 |
| [87] | Q. Le, T. Mikolov, Distributed representations of sentences and documents, preprint, arXiv: 1405.4053 |
| [88] |
A. Schlicker, F. S. Domingues, J. Rahnenführer, T. Lengauer, A new measure for functional similarity of gene products based on gene ontology, BMC Bioinformatics, 7 (2006), 302. https://doi.org/10.1186/1471-2105-7-302 doi: 10.1186/1471-2105-7-302
|
| [89] | M. Miwa, M. Bansal, End-to-end relation extraction using LSTMs on sequences and tree structures, in Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics, 1 (2016), 1105–1116. http://doi.org/10.18653/v1/P16-1105 |
| [90] | D. Zeng, K. Liu, S. Lai, G. Zhou, J. Zhao, Relation classification via convolutional deep neural network, in Proceedings of COLING 2014, the 25th International Conference on Computational Linguistics: Technical Papers, (2014), 2335–2344. |
| [91] |
J. Devlin, M. W. Chang, K. Lee, K. Toutanova, BERT: Pre-training of deep bidirectional transformers for language understanding, Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, 1 (2019), 4171–4186. http://doi.org/10.18653/v1/N19-1423 doi: 10.18653/v1/N19-1423
|
| [92] |
J. Lee, W. Yoon, S. Kim, D. Kim, S. Kim, C. H. So, et al., BioBERT: A pre-trained biomedical language representation model for biomedical text mining, Bioinformatics, 36 (2020), 1234–1240. https://doi.org/10.1093/bioinformatics/btz682 doi: 10.1093/bioinformatics/btz682
|
| [93] | J. Pennington, R. Socher, C. D. Manning, Glove: Global vectors for word representation, in Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), (2014), 1532–1543. http://doi.org/10.3115/v1/D14-1162 |
| 1. | Shaima Ibraheem Jabbar, Abathar Qahtan Omran Aladi, 2024, Fuzzy inference system for detection CT and X-Ray image’s edges, 979-8-3503-8753-7, 1, 10.1109/AICT61888.2024.10740426 |
Figures(9) / Tables(17)
Karpaga Priyaa Kartheeswaran, Arockia Xavier Annie Rayan, Geetha Thekkumpurath Varrieth. Enhanced disease-disease association with information enriched disease representation[J]. Mathematical Biosciences and Engineering, 2023, 20(5): 8892-8932. doi: 10.3934/mbe.2023391
| Journal Title | Database | Total Documents | Total Citation | Average Citation per Journal |
| Multimedia Tools and Applications | PubMed | 29 | 237 | 8.17 |
| Computers in Biology and Medicine | ScienceDirect | 19 | 3711 | 195.32 |
| Expert Systems with Applications | ScienceDirect | 13 | 399 | 30.69 |
| Applied Soft Computing | ScienceDirect | 12 | 632 | 52.67 |
| Biomedical Signal Processing and Control | ScienceDirect | 12 | 181 | 15.08 |
| Journal of Ambient Intelligence and Humanized Computing | Springer | 10 | 290 | 29.00 |
| Scientific Reports | Springer | 9 | 462 | 51.33 |
| Applied Intelligence | Springer | 8 | 1422 | 177.75 |
| IEEE Access | IEEE Xplore | 7 | 2637 | 376.71 |
| Informatics in Medicine Unlocked | ScienceDirect | 7 | 757 | 108.14 |
| Neural Computing and Applications | Springer | 7 | 106 | 15.14 |
| SN Computer Science | Springer | 5 | 78 | 15.60 |
| ACM Transactions on Multimedia Computing, Communications, and Applications | ACM | 4 | 132 | 33.00 |
| Computers and Electrical Engineering | ScienceDirect | 4 | 29 | 7.25 |
| Computer Methods and Programs in Biomedicine | PubMed | 4 | 615 | 153.75 |
| Procedia Computer Science | ScienceDirect | 4 | 39 | 9.75 |
| Neurocomputing | ScienceDirect | 4 | 48 | 12.00 |
| Pattern Recognition | ScienceDirect | 4 | 314 | 78.50 |
| Soft Computing | Springer | 4 | 185 | 46.25 |
| Knowledge-Based Systems | ScienceDirect | 3 | 74 | 24.67 |
DownLoad:
CSV
| Journal Title | Database | Total Documents | Total Citation | Average Citation per Journal |
| IEEE Access | IEEE Xplore | 7 | 2637 | 376.71 |
| IEEE Journal of Biomedical and Health Informatics | IEEE Xplore | 2 | 72 | 36.00 |
| IEEE Transactions on Engineering Management | IEEE Xplore | 2 | 33 | 16.50 |
| IEEE Transactions on Medical Imaging | IEEE Xplore | 2 | 186 | 93.00 |
| IEEE Transactions on Big Data | IEEE Xplore | 1 | 70 | 70.00 |
DownLoad:
CSV
| Journal Title | Database | Total Documents | Total Citation | Average Citation per Journal |
| ACM Transactions on Multimedia Computing, Communications, and Applications | ACM | 4 | 132 | 33.00 |
| ACM Transactions on Management Information Systems | ACM | 3 | 47 | 15.67 |
| ACM Transactions on Internet Technology | ACM | 2 | 33 | 16.50 |
| IEEE/ACM Transactions on Computational Biology and Bioinformatics | ACM | 2 | 957 | 478.50 |
| ACM Computing Surveys | ACM | 1 | 5 | 5.00 |
DownLoad:
CSV
| Journal Title | Database | Total Documents | Total Citation | Average Citation per Journal |
| Diagnostics | MDPI | 3 | 10 | 3.33 |
| Applied Sciences | MDPI | 2 | 33 | 16.50 |
| Sensors | MDPI | 2 | 27 | 13.50 |
| Bioengineering | MDPI | 1 | 15 | 15.00 |
| Cancers | MDPI | 1 | 6 | 6.00 |
DownLoad:
CSV
| Journal Title | Database | Total Documents | Total Citation | Average Citation per Journal |
| Diagnostics (Basel) | PubMed | 3 | 29 | 9.67 |
| Computational Intelligence and Neuroscience | PubMed | 2 | 8 | 4.00 |
| Mathematical Biosciences and Engineering | PubMed | 1 | 8 | 8.00 |
| Journal of Healthcare Engineering | PubMed | 1 | 10 | 10.00 |
| Journal of Medical Internet Research | PubMed | 1 | 59 | 59.00 |
DownLoad:
CSV
| Journal Title | Database | Total Documents | Total Citation | Average Citation per Journal |
| Multimedia Tools and Applications | Springer | 28 | 222 | 7.93 |
| Journal of Ambient Intelligence and Humanized Computing | Springer | 10 | 290 | 29.00 |
| Applied Intelligence | Springer | 8 | 1422 | 177.75 |
| Scientific Reports | Springer | 8 | 462 | 57.75 |
| Neural Computing and Applications | Springer | 6 | 106 | 17.67 |
DownLoad:
CSV
| Journal Title | Database | Total Documents | Total Citation | Average Citation per Journal |
| Computers in Biology and Medicine | ScienceDirect | 19 | 3711 | 195.32 |
| Expert Systems with Applications | ScienceDirect | 13 | 221 | 17.00 |
| Biomedical Signal Processing and Control | ScienceDirect | 12 | 181 | 15.08 |
| Applied Soft Computing | ScienceDirect | 11 | 622 | 56.55 |
| Informatics in Medicine Unlocked | ScienceDirect | 7 | 757 | 108.14 |
DownLoad:
CSV
| Journal Title | Database | Total Documents | Total Citation | Average Citation per Journal |
| Multimedia Tools and Applications | PubMed | 29 | 237 | 8.17 |
| Computers in Biology and Medicine | ScienceDirect | 19 | 3711 | 195.32 |
| Expert Systems with Applications | ScienceDirect | 13 | 399 | 30.69 |
| Applied Soft Computing | ScienceDirect | 12 | 632 | 52.67 |
| Biomedical Signal Processing and Control | ScienceDirect | 12 | 181 | 15.08 |
| Journal of Ambient Intelligence and Humanized Computing | Springer | 10 | 290 | 29.00 |
| Scientific Reports | Springer | 9 | 462 | 51.33 |
| Applied Intelligence | Springer | 8 | 1422 | 177.75 |
| IEEE Access | IEEE Xplore | 7 | 2637 | 376.71 |
| Informatics in Medicine Unlocked | ScienceDirect | 7 | 757 | 108.14 |
| Neural Computing and Applications | Springer | 7 | 106 | 15.14 |
| SN Computer Science | Springer | 5 | 78 | 15.60 |
| ACM Transactions on Multimedia Computing, Communications, and Applications | ACM | 4 | 132 | 33.00 |
| Computers and Electrical Engineering | ScienceDirect | 4 | 29 | 7.25 |
| Computer Methods and Programs in Biomedicine | PubMed | 4 | 615 | 153.75 |
| Procedia Computer Science | ScienceDirect | 4 | 39 | 9.75 |
| Neurocomputing | ScienceDirect | 4 | 48 | 12.00 |
| Pattern Recognition | ScienceDirect | 4 | 314 | 78.50 |
| Soft Computing | Springer | 4 | 185 | 46.25 |
| Knowledge-Based Systems | ScienceDirect | 3 | 74 | 24.67 |
| Journal Title | Database | Total Documents | Total Citation | Average Citation per Journal |
| IEEE Access | IEEE Xplore | 7 | 2637 | 376.71 |
| IEEE Journal of Biomedical and Health Informatics | IEEE Xplore | 2 | 72 | 36.00 |
| IEEE Transactions on Engineering Management | IEEE Xplore | 2 | 33 | 16.50 |
| IEEE Transactions on Medical Imaging | IEEE Xplore | 2 | 186 | 93.00 |
| IEEE Transactions on Big Data | IEEE Xplore | 1 | 70 | 70.00 |
| Journal Title | Database | Total Documents | Total Citation | Average Citation per Journal |
| ACM Transactions on Multimedia Computing, Communications, and Applications | ACM | 4 | 132 | 33.00 |
| ACM Transactions on Management Information Systems | ACM | 3 | 47 | 15.67 |
| ACM Transactions on Internet Technology | ACM | 2 | 33 | 16.50 |
| IEEE/ACM Transactions on Computational Biology and Bioinformatics | ACM | 2 | 957 | 478.50 |
| ACM Computing Surveys | ACM | 1 | 5 | 5.00 |
| Journal Title | Database | Total Documents | Total Citation | Average Citation per Journal |
| Diagnostics | MDPI | 3 | 10 | 3.33 |
| Applied Sciences | MDPI | 2 | 33 | 16.50 |
| Sensors | MDPI | 2 | 27 | 13.50 |
| Bioengineering | MDPI | 1 | 15 | 15.00 |
| Cancers | MDPI | 1 | 6 | 6.00 |
| Journal Title | Database | Total Documents | Total Citation | Average Citation per Journal |
| Diagnostics (Basel) | PubMed | 3 | 29 | 9.67 |
| Computational Intelligence and Neuroscience | PubMed | 2 | 8 | 4.00 |
| Mathematical Biosciences and Engineering | PubMed | 1 | 8 | 8.00 |
| Journal of Healthcare Engineering | PubMed | 1 | 10 | 10.00 |
| Journal of Medical Internet Research | PubMed | 1 | 59 | 59.00 |
| Journal Title | Database | Total Documents | Total Citation | Average Citation per Journal |
| Multimedia Tools and Applications | Springer | 28 | 222 | 7.93 |
| Journal of Ambient Intelligence and Humanized Computing | Springer | 10 | 290 | 29.00 |
| Applied Intelligence | Springer | 8 | 1422 | 177.75 |
| Scientific Reports | Springer | 8 | 462 | 57.75 |
| Neural Computing and Applications | Springer | 6 | 106 | 17.67 |
| Journal Title | Database | Total Documents | Total Citation | Average Citation per Journal |
| Computers in Biology and Medicine | ScienceDirect | 19 | 3711 | 195.32 |
| Expert Systems with Applications | ScienceDirect | 13 | 221 | 17.00 |
| Biomedical Signal Processing and Control | ScienceDirect | 12 | 181 | 15.08 |
| Applied Soft Computing | ScienceDirect | 11 | 622 | 56.55 |
| Informatics in Medicine Unlocked | ScienceDirect | 7 | 757 | 108.14 |
