1.
Introduction
The steam power system is composed of multiple equipment, which has strong interaction with each other. The operating state and equipment performance of the steam power system determine its safety and operation efficiency. As a complex steam power system widely used in the fields of electric power and navigation, it is of great significance to evaluate the operation state of the boiler system [1]. An accurate and reliable overall state assessment model for steam power systems can reduce the risk of technical development, shorten the development cycle, save research costs and provide a review basis for decision-makers. At the same time, after the boiler system or nuclear power system is built and officially put into operation, the state assessment model can be used to evaluate the real-time data, find problems in time, get the fault location, and judge the fault degree and trend. These functions provide reliable technical and management guarantees for the safe, stable, long-term, high-performance and high-quality operation of the steam power system. Therefore, how establishing an accurate and reliable evaluation model for the operational state of steam power system has always been the focus of scholars' research [2].
Decision and Evaluation Theory was put forward in the 1940s, and gradually developed the Fuzzy Evaluation Method, Gray Evaluation Method, Evaluation Method based on Rough Set Theory, Simulation Evaluation Method and other new methods by introducing Information Theory, Applied Mathematics, Computer Technology, Artificial Intelligence Technology and others [3]. In terms of evaluation theory, Dimitri et al. studied the performance evaluation criteria and methods of combat aircraft. Based on the performance standards of combat aircraft, such as affordability, mission performance, safety, availability, survivability and safety, considering their comprehensive impact on aircraft systems, Dimitri et al. completed the performance evaluation indicator system of combat aircraft by analyzing the above performance according to functional criteria, measurable criteria and purposeful criteria [4]. Oien et al. summarized the basic theory of indicator evaluation and defined indicators as directly measurable or indirectly measurable factors used to describe target attributes. The article divided the indicators into leading indicators and lagging indicators. The leading indicators were derived from factors affecting safety, while lagging indicators were derived from the specific manifestations of insecurity. The meaning of these two types of indicators was explained in combination with the safety indicators of nuclear power operation. It is concluded that the construction of indicator systems need be continuously improved by the proposal, practice and modification [5].
In terms of the status evaluation of the steam power system, Wan et al. proposed a comprehensive assessment method combining quantitative and qualitative analysis to assess the operation state of ship power plants [6]. Li et al. used AHP method to analyze the safety of civil nuclear power ships, established hierarchical models of primary and secondary systems of nuclear power plants, and formulated corresponding indicator evaluation criteria [7]. In order to prevent major accidents, Ivonne Andrade Herrera et al. put forward a set of safety indicators for potential unsafe factors. They not only explained the safety indicators but also analyzed how to select indicators. The safety performance indicator was described in the origin, development and selection criteria of the indicator, especially giving the indicator prediction performance. Zhu et al. combined AHP and VIKOR based on the rough number to solve the subjectivity and fuzziness in evaluation [8]. Saqib et al. discussed the safety performance indicators proposed by IAEA, analyzed the targets and limits of the safety performance indicators of nuclear power plants, gave the satisfaction values and allowable values of the underlying indicators, and verified them in combination with the power plants [9]. Shin et al. used the analytic hierarchy process to evaluate a power station in South Korea to prevent the occurrence of validation risks [10]. Srividya et al. used the AHP-FUZZY method to evaluate the maintainability of nuclear power plants. Among them, AHP is mainly used to determine the weight, select the criteria indicators, use the expert scoring method to quantify the indicators, and finally synthesize the FUZZY evaluation results [11]. There was Didcot A Power Plant installed with four 500MW coal-fired units are installed in, and Didcot B Power Plant installed with two 680MW gas combined cycle units. Both power plants of British National Power Company established power plant management grid systems that included the detection of operation processes of all units, the maintenance management procedures and the monitoring processes of auxiliary electrical equipment [12]. Singapore's New Energy Grid Co., Ltd. also implemented condition-based maintenance on electrical equipment, which has brought great benefits to New Energy Grid Co., Ltd. [13,14]. Tao [15] proposed a new comprehensive evaluation method for thermal power plants, namely, fuzzy comprehensive evaluation method, to avoid the shortcomings of complex empirical calculation and poor objectivity when evaluating the overall operation of thermal power plants [16].
Although a lot of research on the operation state evaluation of steam power systems was carried out, especially boiler systems, some problems still need to be solved. The linear weighting method based on a standardized function is applicable to the preliminary calculation in low precision and simple system. Without the influence of the fuzziness of a complex system, the calculation result is a specific value, which is questionable in reliability. The fuzzy evaluation method based on the membership degree considers the fuzziness of complex systems, but the final result is gotten by using the maximum membership degree principle, which can only get a rough grade classification, and cannot give a more detailed evaluation result. At the same time, these two methods do not take into account the impact of the specific state of the indicator parameters on the whole system. However, the impact has a huge impact on the accuracy of the assessment results.
The evaluation of steam power system operation status is a multi-attribute and multi-level work, which is also affected by subjective factors and indicator weight. At the same time, the impact of single indicator level changes on the overall system operation performance status is nonlinear rather than linear. In view of the above two problems, by introducing the deterioration degree and health value, this paper takes an experimental supercharged boiler system as the research object, and puts forward a new evaluation model algorithm based on the theory of the deterioration degree and health value. The new method takes into account the fuzziness of the complex system and the impact of the specific state of the indicator parameters on the entire system. The final results not only include the classification of health evaluation grades, but also give the specific quantitative health indicators. Firstly, the parameters are selected to establish the boiler system evaluation indicator system, and then the indicator parameters are standardized, in which the standardized function method and the deterioration method are used respectively in the normalization process. The weight assignment methods of various subjective and objective indicators are discussed, and the weight modification is carried out by introducing the variable weight theory method of the health value and the method based on expert experience. Finally, the linear weighting method based on standardized function, the fuzzy comprehensive evaluation method based on the membership degree and the comprehensive evaluation method based on the deterioration degree and health value are respectively used to evaluate the experimental supercharged boiler under normal and abnormal operation conditions, and the results are compared. The results show that, compared with other methods, the comprehensive evaluation method based on the deterioration degree and health value is applicable to the condition evaluation of the experimental supercharged boiler, and is more sensitive to minor abnormalities and faults of the experimental supercharged boiler. At the same time, the final results include specific quantitative health indicators. For the steam power system with nonlinear, strong parameter coupling, complex system and other characteristics such as supercharged boiler, the comprehensive evaluation method based on the deterioration degree and health value can help the operator more accurately and sensitively catch and judge the abnormal state of system operation.
2.
Criteria for constructing indicator system
In view of the relevant problems in the existing steam power system operation state evaluation research mentioned above, it is necessary to obtain the important parameter indicators that can be output by the detector according to the actual situation and evaluation needs, then the hierarchical relationship of the parameter indicators can be established, and the value of the parameter indicators can be quantified.
In order to accurately, timely and comprehensively reflect the operation performance of the steam power system and ensure the normal and reasonable development of the evaluation research, the selected indicator parameters should be able to directly reflect the direct impact on the operation status of the steam power system at a certain level. Therefore, the indicators of the indicator system in the evaluation study of the steam power system operation state should meet the following principles:
1) The indicators should cover the characteristics of each piece of equipment in the steam power system as much as possible [17].
2) The redundancy of evaluation parameters should be reduced as far as possible, and the operation performance of steam power system can be reflected concisely [18].
3) The evaluation indicator system should minimize subjective factors [19].
4) Indicator parameters that can be detected quantitatively should be selected as far as possible [20].
5) The parameters in the indicator system should not contradict each other in terms of evaluation methods [21].
For the selection of the evaluation indicators of the operation status of the experimental supercharged boiler system, this paper referred to the existing research and relevant safety operation guidance documents of various countries.
The structure of the evaluation indicator system for the operation status of a steam power system should be hierarchical and can include as many parameter indicators related to the operation performance as possible, so it is necessary to build the indicator system according to its own functions and system structure characteristics, combined with the evaluation focus.
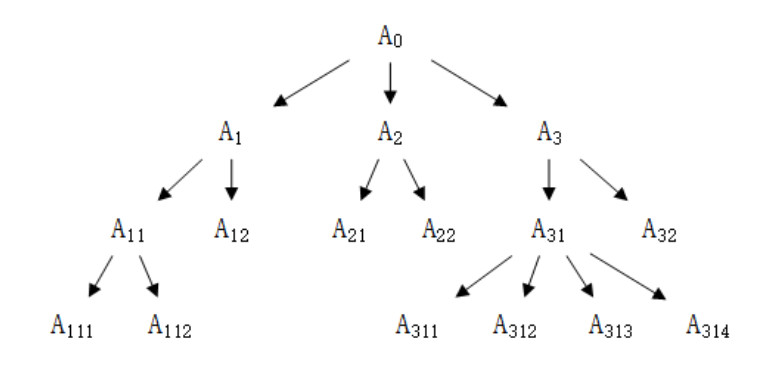
In the process of building the indicator system of the evaluation process, it is necessary to establish the hierarchy of the overall evaluation object in advance. The system can be divided into three or more layers. Although the increase in the number of layers will enhance the description clarity of the evaluation object, and can reflect the evaluation status of the overall goal more comprehensively and accurately, the increase in the number of layers will intuitively result in the expansion of the matrix magnitude and significantly improve the calculation difficulty. An example of the hierarchy of the evaluation indicator system is shown in Figure 1.
3.
Standardized method of evaluation indicators
The construction criteria for the evaluation indicator system of the steam power system operation state can be obtained in the existing research, but the actual values of each indicator cannot be directly used as the calculation benchmark based on the criteria because the existing underlying parameters had different physical characteristics on different physical scales and ranges. The indicators need to be standardized to solve the following problems before further analysis:
1) The dimensions of each indicator parameter are different, so it is impossible to aggregate the parameters of two different units.
2) The threshold and magnitude of each parameter indicator are different.
3) The value change trend of each indicator is different. The higher the value of some indicators, the better the system performance is. And the lower other indicators are, the better the system performance are. Besides, some indicators need to be in a certain range. Therefore, they should be processed according to different indicator characteristics.
3.1. Standardized function method
The standard function method is the most common parameter standardization method for evaluation indicators. The value of each parameter can be projected to the [0, 1] interval using the standardized function. Different standardized functions are selected to adapt to different indicator trends. However, this method has a high degree of fuzziness so that it cannot give an accurate evaluation value that is completely consistent with the actual situation. At present, the common standardized functions in the evaluation process include Linear Function, Gaussian Function, Γ Function, Cauchy Function and K Degree Parabola Function. See Table 1 for the calculation formulas of various standardized functions for different types of parameters. In the table, r represents the result of parameter standardization.
3.2. Deterioration degree and health value method
In the research on the evaluation of the operating state of the steam power system, the evaluation of the operating state of the system involves various attributes and multi-level evaluation, and the evaluation result is also affected by subjective factors and weight factors. At the same time, the impact of single level changes on the overall system operation performance state is nonlinear rather than linear. In view of the above two problems, this work introduced the concept of the deterioration degree to represent the relative the deterioration degree of the current actual operating state of an object at a certain level of the system compared with the fault state. The value range is the interval [0, 1] as the same as that of the standardized function method.
The deterioration indicates the difference between the actual value and the rated value of the indicator. The smaller the deterioration degree is, the farther the indicator is from the ideal working state. The deterioration method can be used to standardize quantitative indicators with rating and limit. The deterioration degree method also needed to be calculated according to different indicators.
For Cost Type Indicators, there is an obvious upper limit of parameters. If the upper limit is exceeded, the equipment will be damaged or cause failures. The deterioration degree of these parameters is calculated as shown in Formula (1):
In the formula:
α, Parameter value during normal operation of equipment;
β2, Upper alert limit value of parameter.
However, the characteristics of Benefit Type indicators are opposite to cost type indicators, and their operating performance parameters cannot be lower than a certain set value. Their deterioration degree is calculated as shown in Formula (2):
In the formula:
α, Parameter value during normal operation of equipment;
β1, Lower alert limit value of parameter.
For intermediate indicators, the parameters are required to be kept between the set upper and lower limits, and the deterioration degree calculation formula is as follows:
In the formula:
α1, Parameter lower limit normal operation value;
α2, Parameter upper limit normal operation value;
β1, Lower alert limit value of parameter;
β2, Upper alert limit value of parameter.
The definition of the deterioration degree is simple, and the value range is [0, 1], which is convenient for mathematical processing and calculation. However, this definition is contrary to the conventional intuitive habit. In order to more intuitively judge the health level of a sub indicator's operating state, the calculation method of the parameter's operating health value is mapped based on the definition of the deterioration degree:
When the parameter runs completely normally, its deterioration degree is 0, and the corresponding health value is 100. When the parameter reaches its alert limit, the deterioration degree is 1, and the corresponding health value is 60. The health value indicator will also serve as the theoretical and mathematical basis of the variable weight method based on health degree in the following article.
3.3. Standardization of the membership degree of indicator interval
As discussed in the previous standardization method of fixed value, a large number of fuzziness and uncertainty factors were introduced in the method of taking score as the final result. Therefore, in order to obtain more reasonable evaluation results, considering the fuzziness of steam power system operation performance evaluation, fuzzy comprehensive evaluation theory can be used for optimization. To calculate the result of the fuzzy comprehensive evaluation, the standardized indicator value needs to be processed by the membership function, and the score value is distributed in each evaluation grade interval to obtain the membership value in this interval.
To determine the membership degree, the corresponding evaluation set must be given first. Although there is no uniform standard for the classification of steam power system performance evaluation at present, it can be formulated according to expert opinions and the actual operating state characteristics of the steam power system. Table 2 below shows the evaluation set of steam power system operation state evaluation indicators divided into five grades: excellent, good, medium, pass and fail, and the corresponding meaning of the evaluation grade.
The membership degree standardization of quantitative indicators can directly process the standardized value of indicators with membership functions to obtain the corresponding membership degree of quantitative indicators. Common membership functions include the fuzzy triangular distribution function, Gaussian distribution function Γ Function, Cauchy distribution function and ridge distribution function. According to the distribution and change trend of specific indicator parameters, combined with parameter group threshold and satisfaction value, the appropriate specific membership function can be chosen.
4.
Indicator weight of steam power system operation status evaluation
In the evaluation process, the influence and importance of different parameter indicators in the indicator system are different on the overall operating performance or subsystem operating performance.
Combined with the characteristics of the steam power system, different indicators have different contributions to the overall system, and some indicators may have redundancy, while some indicators have a decisive influence on the operating state of the steam power system. The two types of indicators need to reflect the difference in the contribution degree through the weight method in the indicator system, that is, by giving different weights to determine the impact of an indicator on the superior indicators.
In this research, the methods of calculating indicator weight were divided into two categories, namely the constant weight method and the variable weight method.
4.1. Constant weight method for status evaluation of steam power system
For weights, our most commonly used weighted sum algorithm formula is:
In the formula, wi(i=1,...,n) is the weight value. When wi is a constant value, it is called as constant weight. Constant weight reflects the relative importance of each parameter indicator in the evaluation of the overall object to some extent, and is widely used in the evaluation field due to its simplicity and fixed value.
The constant weight method can be further subdivided into subjective weight method and objective weight method. The former is commonly used as the Analytic Hierarchy Process (AHP), while the latter is mainly represented by the entropy weight method.
The Analytic Hierarchy Process is a simple and flexible multi-dimensional criteria decision-making mathematical method proposed in the 1970s [22]. In the process of application, the object is firstly decomposed into a multi-layer structure, which is the indicator system structure in the study of steam power system state evaluation [23]. Then, the parameter indicators in each level are compared and scored according to the 1−9 score as the judgment ruler, and the decision judgment matrix in the corresponding level is obtained. The obtained judgment matrix is used for an eigenvalue solution and consistency test, and the weight values of this indicator relative to the previous level are calculated [24].
The entropy weight method is a typical objective weighting method [25]. Entropy itself is a term of thermodynamics, but it has been extended to the field of information theory to expand its connotation. It represents the average amount of information. The smaller the information entropy is, the smaller the degree of information disorder is. The more information it contains, the higher the utility value of the information. If the information entropy is larger, the opposite is true. The relative weight of the indicator is reflected through the judgment of this information entropy.
The specific calculation steps of entropy weight are as follows:
Firstly, the initial conditions are determined. There are n scheme values and m evaluation indicators, that is, {Xij} set, where i=1,2,...,n; j=1,2,...,m. Xij is the standardized value of the jth evaluation indicator of the ith scheme.
Then calculate the corresponding proportion of each indicator value:
Then calculate the information entropy of each indicator:
In the formula:
Then calculate the information redundancy:
Finally, the indicator weight is obtained:
In the above formula, set {Wj} is the calculated entropy weight.
In sum up, the subjective weighting method does not need indicator data, but can obtain weights only according to the indicator connotation and expert experience. However, it contains many human subjective factors, which may be erroneous. Although the objective weighting method does not include any subjective factors and emphasizes the characteristics of the indicator data itself, it is very easy to be affected by the characteristics of small sample data for equipment such as large and complex steam power systems that are difficult to obtain large amounts of data.
4.2. Variable weight method for state evaluation of steam power system
Corresponding to constant weight, if wi is a variable quantity, it is called variable weight. The variable weight is not always changing, so it can be understood as a transient constant weight. The influence of subjective and objective factors and the lack of a relevant knowledge base can be reduced through the change of weight value, so as to better approach the actual situation of the operating performance of the evaluated steam power system.
The subjective and objective comprehensive weight method combines the advantages of the subjective weighting method and the empirical ranking method, and considers the weight optimization method of data objectivity. This method requires subjective and objective weights as the data basis for calculation.
Let the number of indicators at a certain level be n, and the standardized value vector of the corresponding evaluation indicator after standardization is {z1,z2, ..., zj, ..., zn}.
According to the above subjective weighting calculation method, the subjective weight of indicators is:
In the formula: n∑j=1αj=1,αj⩾0(j=0,1,2,...,n)..
According to the above objective weighting calculation method, the objective weight of indicators is:
In the formula: n∑j=1βj=1,βj⩾0(j=0,1,2...,n)
The comprehensive weight of the indicator is:
In the formula: n∑j=1wj=1,wj⩾0(j=0,1,2...,n)
The comprehensive weight can reflect the degree of preference for subjective and objective weights by introducing preference coefficient μ. The larger the preference coefficient μ is, the more attention will be paid to the influence of subjective factors, that is, the more subjective weight will be favored. On the contrary, the more objective the weight is as the same. The value range of preference coefficient μ is [0, 1].
Therefore, the weight optimization decision model is established as follows:
In the formula: {wj>0n∑j=1wj=1.
When the sum of normalized vectors is greater than zero, there is a unique solution:
The value μ in the formula can be a fixed value, or it can be used as a function related to parameter value or time item, such as μ(Z,τ), and the specific method can be changed according to actual needs.
If some experts obtained the corresponding indicator weight scheme for the evaluation of the steam power system operation state through the corresponding weight assignment method during the evaluation process, the indicator weight scheme can be used as a direct criterion to introduce expert experience to modify the preference coefficient, then the weight value of the same system indicator that the operator or user needs to be weighted can be corrected, which was the variable weight method based on expert experience.
Above all, the method of modifying coefficient was used to adjust the existing weights to obtain the final weight value, but it did not involve the problems related to the indicator parameters. The changes in these weights were realized through the preference coefficient, rather than directly reflecting the parameter characteristics through the indicator parameter characterization.
Therefore, it is better than the variable weight model can maintain its main constant weight characteristics under normal operating conditions. When some parameter indicators deviate from the normal state obviously, the performance drops sharply, and the weight value will be rapidly increased as the subsequent faults and accidents happen. The parameter indicator state with possible faults will be fed back from the overall operational performance.
Combining the health value parameters in Section 3 of this paper, the following formula was obtained:
In the formula:
V, Simple weighted value of m indicators after weight change;
w(0)j, The original weight of the jth indicator;
xj, The health value of the jth indicator divided by 100;
wj, The variable weight value of the jth indicator.
The variable weight calculation formula was as follows:
With reference to the viewpoint of the equilibrium function [26], the variable weight calculation formula was improved. When the health value of a parameter in the evaluation object system significantly deviated from the normal range, it was an obvious "punishment" evaluation method to increase the weight and enlarge the proportion of weight. In general, when the health degree of a parameter indicator deviated from the normal operating value in the evaluation process, the proportion of the indicator and the overall evaluation value was reflected in the evaluation results.
The specific punitive equilibrium function formula was as follows:
Then optimize the variable weight model:
Under the operation requirements of the steam power system, the deviation of a single indicator would certainly affect the overall operation status. It was not allowed to arise the contradiction that some indicators were not qualified as well while the overall operation performance is still at a high level, which was obviously inconsistent with the actual situation. The parameter indicators deviating from the normal state played a great role in the overall operational performance. Therefore, in this study, punishment evaluation was used to deal with the deviation in the process of such evaluation.
The formula was as follows:
When α above tends to 1, the whole value will tend to the original weight value. On the contrary, the effect of penalty weight will be more emphasized when it approaches zero. α=0.2 was taken in this paper.
5.
Comprehensive evaluation method based on deterioration degree and health value
After the research on the evaluation indicator system, indicator standardization criteria and indicator weight method of the steam power system operation state, the theory and data basis of the steam power system operation state evaluation method were obtained. Common evaluation methods include linear weighting method based on standardized function and fuzzy comprehensive evaluation method based on the membership degree.
Although the linear weighting method based on the standardized function is simple and convenient, it does not take into account the fuzziness of the steam power system, and the final result is a specific value, which has the problem of credibility. It can only be used for the preliminary calculation of low-precision and simple systems. The fuzzy comprehensive evaluation method based on the membership degree considers the fuzziness of the steam power system and reflects the influence of fuzziness by using the membership degree in fuzzy mathematics, the final result criterion is to use the maximum membership degree principle, which can only obtain rough grade division. At the same time, the two methods mentioned above do not take into account the impact of the specific state of the indicator parameters on the overall system, that is, when some parameters significantly deviate from the normal operating state, the overall operating state of the steam power system will be degraded.
In view of the above problems, by introducing the deterioration-health value and health evaluation grade value, an evaluation model algorithm based on the deterioration degree and health value for the operating state of the steam power system were proposed to deal with the defects and applicability of the basic evaluation method.
The deterioration degree gave the difference between the actual value and the rated value. The smaller the value of the deterioration degree was, the farther the indicator was from the ideal working state. However, the definition of the deterioration degree was contrary to conventional intuitive habits. Generally speaking, the closer the indicator is to "1", the better the state is. Therefore, in order to judge the health level of a sub indicator more intuitively, the health value linked to the deterioration degree was introduced as the subsequent calculation criterion.
This health value was also related to the weight calculation of the variable weight method. It was a key parameter representing the health level of the indicator's operating state, and its value range was [60,100]. Then, the evaluation model algorithm steps were carried out. Finally, the health evaluation grade value was given for calculation, and the results with accurate refined health evaluation scores and corresponding health evaluation grades can be obtained.
The indicator system of the operation status of the steam power system was established, and the corresponding low-level indicators in the indicator system were calculated in order to obtain the corresponding standardized value and health value of the low-level indicators.
For all child nodes under the same indicator in a hierarchy, the standardized value set of the indicator after standardization was Ai={αi1,αi2,...,αim}, where m was the number of child indicators under the ith parent node.
The total set of standardized values of indicators for the evaluation indicator system of steam power system operation status:
The indicator health value set was Ki={ki1,ki2,...,kim}.
The total set of indicator health values for the evaluation indicator system of steam power system operation status:
Develop a set of health comments on steam power system operation status V={v1,v2,⋯,vm}.
Use the corresponding expert scoring or membership function method to obtain the fuzzy membership degree Ri=(ri1,ri2,...,rim)(i=1,2,...,n) of the ith indicator. The membership vector R1,R2,...,Rn of n indicators was obtained, and then the membership matrix R was formed:
Standardize the membership matrix R to obtain the normalized surrogate membership matrix ∼R :
The AHP analytic hierarchy process in the subjective weighting method was used to calculate the subjective weight, and the subjective weight was finally obtained after the consistency test:
In the formula: n∑j=1αj=1,αj⩾0(j=0,1,2...,n).
Use the entropy weight method in the objective weighting method to calculate the objective weight:
In the formula: n∑j=1βj=1,βj⩾0(j=0,1,2...,n).
The subjective and objective comprehensive weight method was used to calculate the comprehensive weight:
In the formula: n∑j=1wzj=1,wzj⩾0(j=0,1,2...,n)
μz was the subjective and objective preference coefficient, and the value range was [0, 1]. Use experience variable weight method to calculate expert experience weight:
In the formula: n∑j=1wsj=1,wsj⩾0(j=0,1,2...,n).
μs was the preference coefficient of expert experience correction, and the value range was [0, 1]. γ was the expert experience weight:
In the formula: n∑j=1γj=1,γj⩾0(j=0,1,2...,n).
γj can be obtained by the formula of the average value algorithm, or by the de tailed average value algorithm.
The variable weight method based on health degree was used to calculate the variable weight, and the penalty function was used to modify the variable weight formula:
In the formula:
xj, The health value of the jth indicator divided by 100;
wbj, Variable weight value of the jth indicator;
α, The influence of penalty weight is emphasized when the variable weight coefficient tends to zero;
Aggregate the indicator generation membership matrix and indicator variable weight value obtained above.
In the formula:
∘ is the evaluation aggregation operator.
In the membership fuzzy comprehensive evaluation algorithm based on variable weight of the deterioration degree and health value, the above formula can be equivalent to:
Finally, the result of the membership degree was obtained, that is, the membership degree vector:
Analyze the result of the membership degree, adopt the fuzzy mathematics theory, and use the maximum membership degree principle to obtain the final evaluation membership result under the condition that the result meets the following formula:
The evaluation set was specifically divided into five grades: health, good, attention, deterioration and failure to indicate the health level of the steam power system operation state, and the corresponding grade score value was given: health = 100, good = 90, attention = 80, deterioration = 70 and failure = 60.
Calculate the health score of steam power system operation status:
In the formula:
S, Health score value of steam power system operation status.
The final score between 50−60 was "failure", 60−70 was "deterioration", 70−80 was "attention", 80−90 was "good", and 90−100 was "health".
6.
Operation status evaluation and comparison for experimental supercharged boiler
This work took the experimental bench of experimental supercharged boiler system as the object to verify the feasibility and accuracy of the comprehensive evaluation method based on the deterioration degree and health value. The boiler model was SZS (Z) 1.5−1.27/350−Y, which was a natural circulation supercharged boiler using light diesel as fuel. The test equipment was shown in Figure 2.
With reference to the content in Section 2 of this paper, the operating status of the boiler system was divided into two main sub indicators: the operating status of the combustion system and the operating status of the steam and water system. Then, with reference to the relevant national guidance documents on safe operation, the indicator parameters were screened to form the final evaluation indicator system, as shown in Table 3.
According to the relevant test program and operation standards of the experimental supercharged boiler test bench, the evaluation criteria for the above indicators were shown in Table 4.
When the experimental supercharged boiler test bed ran stably and normally, the data of each indicator parameter was collected every second. The 4000 groups of data were collected in total, and the average value was taken as the evaluation indicator value. Since the evaluation indicator parameters were quantitative in nature, and belonged to intermediate parameters with a clear upper and lower limit and satisfactory values, the following result took the flue gas temperature of the third level indicator as an example for standardized calculation.
There are three indicator standardization methods, namely the standardized function method, the deterioration degree method and the membership degree method. In the standardized function method, linear functions were uniformly used for calculation. The average value of flue gas temperature measurement was greater than the satisfactory value, so the measured value was subtracted from the upper limit value, and then the difference between the above limit value and the satisfactory value is subtracted. The result was 0.906. The standardized results of the operation status evaluation indicators of the experimental supercharged boiler were shown in Table 6.
Using the same method, the deterioration degree and health value of the operating state indicators of the experimental supercharged boiler were calculated as shown in Table 7, which were used for the calculation of the comprehensive evaluation method based on the deterioration degree and health value in the following text.
After the indicators were standardized to obtain specific standardized values, the standardized values were subject to membership processing.
There were four commonly used membership functions such as fuzzy trigonometric function, Gaussian distribution function Γ Function, Cauchy distribution function and ridge distribution function. Among them, the distribution of the Gaussian distribution in the whole area was relatively smooth, which can better reflect the relationship between the standardized value and the evaluation grade interval. Therefore, in the following example calculation, the Gaussian distribution function was used to calculate the membership.
The Table 8 gave the subordinate degree results of the bottom indicators of the experimental supercharged boiler system operation state evaluation indicator system.
After the indicator standardization calculation was completed, the next step was the indicator weight calculation. The weight result of AHP with subjective weighting was given here.
Then the entropy weight method in the objective weighting method was used to calculate the objective weight value of the indicator.
After the subjective weight and objective weight were calculated above, the comprehensive weight was changed. In this paper, the preference coefficient of 0.5 was used for weight calculation. The following Table 11 was for the indicator weight results of comprehensive weighting method.
In the comprehensive evaluation model based on the health value of the deterioration degree, it was necessary to consider the impact of the deviation of the operating state parameters of the experimental supercharged boiler from the normal operating state on the overall operating state evaluation results. Therefore, the variable weight impact of the health value should be considered when calculating the weight.
The variable weight coefficient adopted here was 0.2, and the more this coefficient tended to zero, the more emphasis was placed on the weight penalty effect for deviating from the normal state. The weight calculation results of the health value variable weight algorithm were shown in Table 12.
The results of the linear weighting method based on the standardized function were shown in Table 13.
The results of the fuzzy comprehensive evaluation method based on the degree of membership were shown in Table 14 below:
According to the principle of maximum membership, the operation status of the experimental supercharged boiler system was evaluated as "excellent" (0.687).
The results of the comprehensive evaluation method based on the deterioration degree and health value were presented in the form of tables, as shown in Table 15.
The final score between 50–60 was "failure", 60–70 was "deterioration", 70–80 was "attention", 80–90 was "good", and 90–100 was "health". Finally, it was concluded that the health level of the experimental supercharged boiler system was "healthy". In this evaluation example, the conclusion of the three methods was that the experimental supercharged boiler system was in excellent or good operating condition, which verified the applicability of the evaluation criteria, evaluation process, and comprehensive evaluation method based on the deterioration degree and health value.
During the operation of the experimental supercharged boiler system, the disturbance to the bypass valve could simulate the abnormal boiler load caused by the slight fault at the load end during the actual use of the boiler, such as the fault of the turbine inlet valve and the control valve, which had practical significance. In the experiment, a step disturbance was applied to the bypass valve. At this time, the water level and pressure of the steam drum decreased significantly. The disturbance was shown in Figure 3.
The data collected within 1000 seconds after the disturbance was analyzed according to the above three methods, and the results were shown in Table 16.
To sum up, compared with the linear weighting method based on the standardized function and the fuzzy comprehensive evaluation method based on the membership degree, the comprehensive evaluation method based on the health value of the deterioration degree gave consideration to the fuzziness of the complex system and the impact of the specific state of the indicator parameters on the entire system. It could not only accurately determine the state of the experimental supercharged boiler system during normal operation, but also had higher sensitivity to the identification of minor abnormalities or faults. At the same time, the final results of the comprehensive evaluation method based on the deterioration degree and health value not only included fuzzy evaluation such as "attention", but also gave specific quantitative health indicators.
7.
Conclusions
Aiming at the defects of such evaluation methods as linear weighting method based on standardized function and fuzzy comprehensive evaluation method based on the membership degree, the new evaluation model algorithm based on the theory of the deterioration degree and health value is proposed in this paper. The evaluation indicator system of the boiler system is established by selecting parameters, and then the indicator parameters are standardized by using various methods. The weight assignment methods of various subjective and objective indicators are discussed, and the weight modification is carried out by introducing the variable weight theory method of health value and the method based on expert experience. Finally, the linear weighting method based on standardized function, the fuzzy comprehensive evaluation method based on the membership degree and the comprehensive evaluation method based on the deterioration degree and health value are respectively used to evaluate the experimental supercharged boiler under normal and abnormal operation conditions, and the results are compared. The results are as follows:
1) When using the data of normal operation of an experimental supercharged boiler system for evaluation, the conclusion of the comprehensive evaluation method based on the deterioration degree and health value is consistent with that of the other state evaluation methods, which proves the applicability and feasibility of the new method.
2) Compared with other methods, the comprehensive evaluation method based on the deterioration degree and health value is more sensitive to minor abnormalities and faults of the experimental supercharged boiler. When the bypass valve is disturbed and the other methods are evaluated as good, the comprehensive evaluation method based on the deterioration degree and health value can more accurately judge the abnormality and give a reminder.
3) The comprehensive evaluation method based on the deterioration degree and health value takes into account the fuzziness of the complex systems and the impact of specific status of indicator parameters on the whole system. At the same time, the final results not only include fuzzy evaluation such as "Attention", but also specific quantitative health indicators. For the steam power system with nonlinear, strong parameter coupling, complex system and other characteristics such as a supercharged boiler, the comprehensive evaluation method based on the deterioration degree and health value can help the operator more sensitively catch and judge the abnormal state of system operation.
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad:





