Monotonicity properties arising in a simple model of <i>Wolbachia</i> invasion for wild mosquito populations

Diego Vicencio; Olga Vasilieva; Pedro Gajardo; Diego Vicencio; Olga Vasilieva; Pedro Gajardo

doi:10.3934/mbe.2023053

Mathematical Biosciences and Engineering

2023, Volume 20, Issue 1: 1148-1175. doi: 10.3934/mbe.2023053

Previous Article Next Article

Research article Special Issues

Monotonicity properties arising in a simple model of Wolbachia invasion for wild mosquito populations

1.
Departmento de Matemática, Universidad Técnica Federico Santa María, Avenida España 1680, Valparaíso, 2390123, Chile
2.
Departmento de Matemáticas, Universidad del Valle, Cl. 13,100-00, Cali, Valle del Cauca 760032, Colombia

Received: 20 September 2022 Revised: 20 September 2022 Accepted: 11 October 2022 Published: 26 October 2022

In this paper, we propose a simplified bidimensional Wolbachia infestation model in a population of Aedes aegypti mosquitoes, preserving the main features associated with the biology of this species that can be found in higher-dimensional models. Namely, our model represents the maternal transmission of the Wolbachia symbiont, expresses the reproductive phenotype of cytoplasmic incompatibility, accounts for different fecundities and mortalities of infected and wild insects, and exhibits the bistable nature leading to the so-called principle of competitive exclusion. Using tools borrowed from monotone dynamical system theory, in the proposed model, we prove the existence of an invariant threshold manifold that allows us to provide practical recommendations for performing single and periodic releases of Wolbachia-carrying mosquitoes, seeking the eventual elimination of wild insects that are capable of transmitting infections to humans. We illustrate these findings with numerical simulations using parameter values corresponding to the wMelPop strain of Wolbachia that is considered the best virus blocker but induces fitness loss in its carriers. In these tests, we considered multiple scenarios contrasting a periodic release strategy against a strategy with a single inundative release, comparing their effectiveness. Our study is presented as an expository and mathematically accessible tool to study the use of Wolbachia-based biocontrol versus more complex models.

Keywords:

Citation: Diego Vicencio, Olga Vasilieva, Pedro Gajardo. Monotonicity properties arising in a simple model of Wolbachia invasion for wild mosquito populations[J]. Mathematical Biosciences and Engineering, 2023, 20(1): 1148-1175. doi: 10.3934/mbe.2023053

Related Papers:

[1]	Hakkee Jung . Analytical subthreshold swing model of junctionless elliptic gate-all-around (GAA) FET. AIMS Electronics and Electrical Engineering, 2024, 8(2): 211-226. doi: 10.3934/electreng.2024009
[2]	Hakkee Jung . Analysis of drain induced barrier lowering for junctionless double gate MOSFET using ferroelectric negative capacitance effect. AIMS Electronics and Electrical Engineering, 2023, 7(1): 38-49. doi: 10.3934/electreng.2023003
[3]	Hakkee Jung . Analytical models of threshold voltage and drain induced barrier lowering in junctionless cylindrical surrounding gate (JLCSG) MOSFET using stacked high-k oxide. AIMS Electronics and Electrical Engineering, 2022, 6(2): 108-123. doi: 10.3934/electreng.2022007
[4]	K Srilatha, B T P Madhav, J Krishna, Y V N R Swamy Banothu, Anil Badisa . Design of electromagnetic cloak with sequentially connected rectangular split ring resonators for S-band applications. AIMS Electronics and Electrical Engineering, 2022, 6(4): 385-396. doi: 10.3934/electreng.2022023
[5]	Tadele A. Abose, Fanuel O. Ayana, Thomas O. Olwal, Yihenew W. Marye . BER performance analysis of polar-coded FBMC/OQAM in the presence of AWGN and Nakagami-m fading channel. AIMS Electronics and Electrical Engineering, 2024, 8(3): 311-331. doi: 10.3934/electreng.2024014
[6]	Jeevani W. Jayasinghe . Application of Genetic Algorithm for Binary Optimization of Microstrip Antennas: A Review. AIMS Electronics and Electrical Engineering, 2021, 5(4): 315-333. doi: 10.3934/electreng.2021016
[7]	Habib Hadj-Mabrouk . Analysis and prediction of railway accident risks using machine learning. AIMS Electronics and Electrical Engineering, 2020, 4(1): 19-46. doi: 10.3934/ElectrEng.2020.1.19
[8]	Simona Miclaus, Delia-Bianca Deaconescu, David Vatamanu, Andreea Maria Buda, Annamaria Sarbu, Bogdan Pindaru . Peculiarities of the radiated field in the vicinity of a mobile terminal connected to 4G versus 5G networks during various applications usage. AIMS Electronics and Electrical Engineering, 2022, 6(2): 161-177. doi: 10.3934/electreng.2022010
[9]	Manisha R. Bansode, Surendra S. Rathod . A bandwidth enhanced multilayer electromagnetic bandgap structure to reduce the simultaneous switching noise. AIMS Electronics and Electrical Engineering, 2023, 7(4): 406-420. doi: 10.3934/electreng.2023021
[10]	Patrick Seeling . Augmented Reality Device Operator Cognitive Strain Determination and Prediction. AIMS Electronics and Electrical Engineering, 2017, 1(1): 100-110. doi: 10.3934/ElectrEng.2017.1.100

Abstract

1. Introduction

The planar-type MOSFETs are no longer available due to Short Channel Effects (SCEs), such as an increase in subthreshold swing, off-current, threshold voltage roll-off and Drain Induced Barrier Lowering (DIBL) as the transistor size decreases ^[1,2,3]. The FinFET structure, which is a tri-gate structure used to solve this problem, also has limitations in scaling, so a transistor with a new structure has been developed ^[4,5,6]. In particular, FinFET using ferroelectric was developed to solve the increase in power consumption, which is the most problematic due to the reduction in transistor size, which is indispensable for high-speed operation ^[7,8]. Also, a Gate-All-Around (GAA) FET is being developed as a next-generation transistor structure to overcome the limitations of FinFETs ^[9,10]. The GAA FET has a structure that maximizes the ability of the gate to control the channel carrier, and numerous studies are currently being conducted on these devices ^[11,12]. In particular, the junctionless structure ^[13,14], which makes the doping concentration of the channel and the source/drain region almost the same, is applied to the GAA FET structure as a structure that can solve the difficulty of manufacturing due to the reduction in transistor size ^[15,16,17].

In addition, to achieve low power consumption, it is also necessary to reduce the subthreshold swing (SS). To overcome the limit of 60 mV/dec for the SS, ferroelectric materials are used, for which Metal-Ferroelectric-Insulator-Semiconductor (MFIS) structures and Metal-Ferroelectric- Metal-Insulator-Semiconductors (MFMIS) are mainly used ^[18,19]. Compared to the MFMIS structure, the stability of the ferroelectric material in the MFIS structure is independent of the gate leakage current, but gate leakage is ignored in this paper, so an analytical model of subthreshold swing is presented for the junctionless GAA FET of the MFMIS structure with high on-current. Research has been conducted extensively on junction-based MFIS-structured GAA FETs ^[20,21], but little has been done on junctionless MFMIS-structured GAA FETs.

Rassekh et al. analyzed SCEs such as the SS and DIBL for a channel length of 100 nm for the MFMIS-structured double-gate junctionless FET with ferroelectric ^[22]. It was found that the change of SS for the ferroelectric thickness could not be observed in the deep subthreshold region when the channel length was about 100 nm. Pahwa et al. analyzed the threshold voltage roll-off, SS, DIBL, etc. up to 10 nm channel length for undoped channel double gate FETs with MFIS and MFMIS structures, but they only used numerical simulation ^[23]. Sakib et al. analyzed SCEs for ferroelectric GAA FETs, but only numerically simulated junction-based MFIS and MFMIS structures ^[24]. Choi et al. and Raut et al. analyzed SCEs for junctionless GAA FET using ferroelectric, but only used TCAD ^[25,26]. Mehta et al., Gaidhane et al. and Kim et al. analyzed the current-voltage characteristics of the ferroelectric MFIS structure, but analyzed only one-dimensionally for the channel radial direction of the long-channel, so the change of SS occurring in the short channel could not be interpreted ^[27,28,29]. It is necessary, however, to analyze not only the potential distribution along the radial direction of the channel but also along the channel length direction as the size of the transistor decreases. To this end, it is necessary to solve the two-dimensional Poisson equation in the GAA structure. In addition, in the junctionless GAA structure using ferroelectric, it is necessary to know how the charge in the ferroelectric changes according to the gate voltage to interpret the SS in the junctionless GAA FET with ferroelectric. Therefore, in this paper, we will find the solution of Poisson's equation two-dimensionally for the junctionless GAA FET of cylindrical structure with ferroelectric, and derive the drain current-gate voltage relationship using it. From the current-voltage relationship obtained in this way, we will find SS according to the definition of SS and compare it with the value of the analytical SS model presented. Ferroelectric will use the properties of HZO and will use the MFMIS structure, which has been proven in many experiments ^[30,31]. In addition, we will use the relationship between ferroelectric voltage, inner voltage and outer voltage by the LK (Landau-Khalatnikov) equation.

2. MFMIS junctionless GAA FET with ferroelectric

2.1. Structure of junctionless GAA FET with ferroelectric and ferroelectric charge

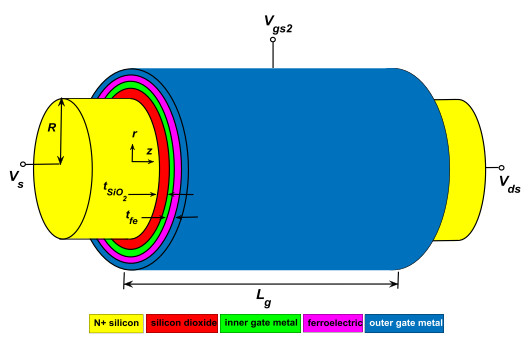
Figure 1 is the structure of the ferroelectric junctionless GAA FET used in this paper. As shown in Figure 1, the MFMIS structure was used and device parameters are shown in Table 1. Although not shown in Figure 1, V_gs1 is the voltage induced to the inner gate metal, and V_gs2 is the voltage applied to the outer gate metal.

Figure 1. Schematic view of junctionless GAA FET with ferroelectric.

DownLoad: Full-Size Img PowerPoint

Table 1. Device parameters for this analytical SS model.

Device parameter	Symbol	Value
Channel length	L_g	20~60 nm
Channel radius	R	5~10 nm
SiO₂ thickness	t_ox	1~2 nm
Doping concentration	N_d	10¹⁸/cm³
Ferroelectric thickness	t_fe	0~10 nm
Remanent polarization	P_r	15~30 ${\mathtt{μ}}$ C/cm²
Coercive field	E_c	0.8~1.5 MV/cm

| Show Table

DownLoad: CSV

To obtain the potential distribution within the channel of a MOSFET with a GAA structure, Li's two-dimensional potential model for the r and z directions was used ^[32]. In other words, the potential in the channel can be obtained as the sum of the one-dimensional solution ${\phi _1}(r)$ of Poisson's equation and the two-dimensional solution ${\phi _2}(r,z)$ of the homogeneous Laplace equation, as follows.

$\phi(r, z) = \phi_{1}(r)+\phi_{2}(r, z)$

${\phi _1}(r) = - \frac{{q{N_d}}}{{4{\varepsilon _{si}}}}{r^2} + {V_{gs}} - {\phi _{ms}} + \frac{{q{N_d}R}}{{2{C_{ox}}}} + \frac{{q{N_d}{R^2}}}{{4{\varepsilon _{si}}}}$

(2.1)

${\phi _2}(r,z) = \sum\limits_{n = 1}^\infty {\left[ {{C_n}\exp \left( {\frac{{{\alpha _n}z}}{R}} \right) + {D_n}\exp \left( { - \frac{{{\alpha _n}z}}{R}} \right)} \right]{J_0}\left( {\frac{{{\alpha _n}r}}{R}} \right)}$

(2.2)

where ${\alpha _n}$ is an eigenvalue that satisfies (2.3). Refer to the C_n and D_n in ^[32]

$R{J_0}({\alpha _n}) - \frac{{{\varepsilon _{si}}}}{{{C_{ox}}}}{\alpha _n}{J_1}({\alpha _n}) = 0$

(2.3)

To find the charge in the ferroelectric, the charge in the channel must first be obtained from the relational expression of (2.4).

${Q_{sc}} = - {C_{ox}}({V_{gs1}} - {\phi _{ms}} - {\phi _s})$

(2.4)

At this time, the surface potential ${\phi _s}$ can be obtained as the following (2.5) by substituting r = R into (2.1) and (2.2).

$\varphi_{s}(z) = \varphi_{1}(R)+\varphi_{2}(R, z)$

(2.5)

$\begin{align} & {{\phi }_{1}}\left( R \right) = -\frac{q{{N}_{d}}}{4{{\varepsilon }_{si}}}{{R}^{2}}+{{V}_{gs1}}-{{\phi }_{ms}}+\frac{q{{N}_{d}}R}{2{{C}_{ox}}}+\frac{q{{N}_{d}}{{R}^{2}}}{4{{\varepsilon }_{si}}} = {{V}_{gs1}}-{{\phi }_{ms}}+\frac{q{{N}_{d}}R}{2{{C}_{ox}}} \\ & {{\phi }_{2}}\left( R,z \right) = \sum\limits_{n = 1}^{\infty }{\left[ {{C}_{n}}\exp \left( \frac{{{\alpha }_{n}}z}{R} \right)+{{D}_{n}}\exp \left( -\frac{{{\alpha }_{n}}z}{R} \right) \right]}{{J}_{0}}\left( \frac{{{\alpha }_{n}}R}{R} \right) \\ & = \sum\limits_{n = 1}^{\infty }{\left[ {{C}_{n}}\exp \left( \frac{{{\alpha }_{n}}z}{R} \right)+{{D}_{n}}\exp \left( -\frac{{{\alpha }_{n}}z}{R} \right) \right]{{J}_{0}}\left( {{\alpha }_{n}} \right)} \\ \end{align}$

where ${\phi _{ms}}$ is the work function difference between the gate metal and semiconductor. Substituting (2.5) into (2.4), the charge in the channel Q_sc can be obtained as shown in (2.6) below.

${Q_{sc}} = {C_{ox}}\left\{ {\frac{{q{N_d}R}}{{2{C_{ox}}}} + \sum\limits_{n = 1}^\infty {\left[ {{C_n}\exp \left( {\frac{{{\alpha _n}z}}{R}} \right) + {D_n}\exp \left( { - \frac{{{\alpha _n}z}}{R}} \right)} \right]{J_0}\left( {{\alpha _n}} \right)} } \right\}$

(2.6)

Using (2.6), the ferroelectric charge Q can be obtained from (2.7).

$2\pi R{L_g} \times Q = - \int_0^{{L_g}} {\pi R{Q_{sc}}dz}$

(2.7)

Here, the ferroelectric charge can be derived as in (2.8).

$\begin{gathered} Q = - \frac{1}{{2{L_g}}}\int_0^{{L_g}} {{Q_{sc}}dz} \hfill \\ \,\,\,\,\, = - \frac{{q{N_d}R}}{4} - \frac{{{C_{ox}}}}{{2{L_g}}}\left[ {\sum\limits_{n = 1}^\infty {\left[ {{C_n}\exp \left( {\frac{{{\alpha _n}{L_g}}}{R}} \right) - {D_n}\exp \left( { - \frac{{{\alpha _n}{L_g}}}{R}} \right) - {C_n} + {D_n}} \right]\left( {\frac{R}{{{\alpha _n}}}} \right){J_0}\left( {{\alpha _n}} \right)} } \right] \hfill \\ \end{gathered}$

(2.8)

Using the ferroelectric charge Q, the ferroelectric voltage V_f can be obtained from the following (2.9) by Landau theory.

${V_f} = 2\alpha {t_f}Q + 4\beta {t_f}{Q^3} + 6\gamma {t_f}{Q^5}$

(2.9)

$\begin{gathered} \alpha = - \frac{{3\sqrt 3 }}{4}\frac{{{E_c}}}{{{P_r}}}\,\,(m/F) \hfill \\ \beta = \frac{{3\sqrt 3 }}{8}\frac{{{E_c}}}{{P_r^3}}\,\,({m^5}/F/{C^2}) \hfill \\ \gamma = 0 \hfill \\ \end{gathered}$

where P_r is the remanent polarization of the ferroelectric material and E_c is the coercive field. As shown in Table 1, the values of P_r and E_c were within the range derived from various papers in the case of HZO ^{[33,34,35,36]}. Using the ferroelectric voltage V_f derived in this way, the relationship between inner gate voltage V_gs1 and outer gate voltage V_gs2 can be expressed as in (2.10) below.

${V_{gs2}} = {V_{gs1}} + {V_f}$

(2.10)

Using (2.1) and (2.2), the relationship between drain current and gate voltage can be derived by the following (2.11).

${I_d} = \frac{{2\pi {N_d}{\mu _n}kT\left\{ {1 - \exp \left( {\frac{{ - q{V_{ds}}}}{{kT}}} \right)} \right\}}}{{\int_0^{{L_g}} {\frac{1}{{\int_0^R {r\exp \left\{ {\frac{{q\phi (r,z)}}{{kT}}} \right\}} dr}}} }}$

(2.11)

The relationship between drain current and gate voltage obtained using (2.11) is shown in Figure 2(a). As can be seen in Figure 2(a), it was found to be in good agreement with the ISE-TCAD result at t_fe = 0, and in Figure 2(b), it was observed that the SS decreased as the ferroelectric thickness increased. In this paper, we propose an analytical SS model consistent with the two-dimensional SS derived in Figure 2.

Figure 2. (a) Drain current vs. gate voltage curves with the ferroelectric thickness as a parameter and (b) subthreshold swing derived from the slope of drain current vs. gate voltage curves under the given conditions in the figure.

DownLoad: Full-Size Img PowerPoint

2.2. Analytical subthreshold swing of junctionless GAA FET with ferroelectric

To obtain the analytical SS model, the SS can be expressed in the following (2.12) by the definition of SS.

$SS = \frac{{\partial {V_{gs2}}}}{{\partial (\log {I_{ds}})}} = \ln (10)\left( {\frac{{kT}}{q}} \right){\left( {\frac{{\partial {\phi _{\min }}}}{{\partial {V_{gs2}}}}} \right)^{ - 1}} = \ln (10)\left( {\frac{{kT}}{q}} \right){\left[ {\frac{{\partial \phi (0,{z_{\min }})}}{{\partial {V_{gs2}}}}} \right]^{ - 1}}$

(2.12)

Here, r = 0 is substituted since most carriers move along the central axis of the channel in the junctionless structure, and z = z_min, which has the minimum potential value, is substituted ^[37]. In (2.12), the parenthesis of the last term is as follows.

$\begin{array}{l} \frac{{\partial \phi (0,{z_{\min }})}}{{\partial {V_{gs2}}}} = \frac{\partial }{{\partial {V_{gs2}}}}\left\{ {\sum {\left[ {{C_n}\exp \left( {{\alpha _n}{z_{\min }}/R} \right) + {D_n}\exp \left( { - {\alpha _n}{z_{\min }}/R} \right)} \right]{J_0}\left( 0 \right)} + {\phi _1}(0)} \right\} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{\partial }{{\partial {V_{gs2}}}}\left\{ {\sum {\left[ {{C_n}\exp \left( {{\alpha _n}{z_{\min }}/R} \right) + {D_n}\exp \left( { - {\alpha _n}{z_{\min }}/R} \right)} \right]} } \right\} + \frac{{\partial {\phi _1}(0)}}{{\partial {V_{gs2}}}}\,\,\,\,\,\,\,\,\left\{ {\because {J_0}\left( 0 \right) = 1} \right\} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{\partial {\phi _1}(0)}}{{\partial {V_{gs1}}}}\frac{{\partial {V_{gs1}}}}{{\partial Q}}\frac{{\partial Q}}{{\partial {V_{gs2}}}}\,\, + \sum {\left[ \begin{array}{l} \exp \left( {{\alpha _n}{z_{\min }}/R} \right)\frac{{\partial {C_n}}}{{\partial {V_{gs2}}}} + {C_n}\frac{\partial }{{\partial {V_{gs2}}}}\left\{ {\exp \left( {{\alpha _n}{z_{\min }}/R} \right)} \right\} \hfill \\ + \exp \left( { - {\alpha _n}{z_{\min }}/R} \right)\frac{{\partial {D_n}}}{{\partial {V_{gs2}}}} + {D_n}\frac{\partial }{{\partial {V_{gs2}}}}\left\{ {\exp \left( { - {\alpha _n}{z_{\min }}/R} \right)} \right\} \hfill \\ \end{array} \right]} \,\,\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{\partial {V_{gs1}}}}{{\partial Q}}\frac{{\partial Q}}{{\partial {V_{gs2}}}}\,\, + \sum {\left[ \begin{array}{l} \exp \left( {{\alpha _n}{z_{\min }}/R} \right)\frac{{\partial {C_n}}}{{\partial {V_{gs2}}}} + {C_n}\frac{\partial }{{\partial {V_{gs2}}}}\left\{ {\exp \left( {{\alpha _n}{z_{\min }}/R} \right)} \right\} \hfill \\ + \exp \left( { - {\alpha _n}{z_{\min }}/R} \right)\frac{{\partial {D_n}}}{{\partial {V_{gs2}}}} + {D_n}\frac{\partial }{{\partial {V_{gs2}}}}\left\{ {\exp \left( { - {\alpha _n}{z_{\min }}/R} \right)} \right\} \hfill \\ \end{array} \right]} \,\,\,\left\{ {\because \frac{{\partial {\phi _1}(0)}}{{\partial {V_{gs1}}}} = 1} \right\}\, \hfill \\ \end{array}$

(2.13)

The derivative of each term for V_gs2 in (2.13) can be obtained using the parametric differentiation method indicated in the Appendix. Using the formula in the Appendix, the SS can be obtained analytically.

To obtain the analytical SS model, the value of n = 1 had to be used when calculating the z_min value in the Appendix. To prove its validity, the deviation of SSs calculated for n = 1 and n = 32 (the number of n that satisfies (2.3) when the maximum of $\alpha$ is 100) is shown in Figure 3 according to the ratio of the channel length and radius, L_g/R. As shown in Figure 3, the deviation increased as the ratio of channel length and radius decreased, and the deviation was less than 1% regardless of the ferroelectric thickness for L_g/R > 3. In particular, it was found that it is sufficient to calculate only the case of n = 1 when calculating this analytical SS model as the ferroelectric thickness decreases. In general, it will be sufficient to calculate only the case of n = 1 since L_g/R > 2.

Figure 3. Deviation of SS for n = 1 and n = 32 for the ratio of channel length and radius with the ferroelectric thickness as a parameter under the given conditions in the figure.

DownLoad: Full-Size Img PowerPoint

3. Results and discussions

3.1. Verification of the analytical SS model

In Figure 4, the results of the analytical SS model in the case of n = 1 presented in this paper, the SS derived from the relationship between drain current and gate voltage in (2.11) and the 3D ISE-TCAD simulation value ^[32] calculated at t_fe = 0 nm were compared. As shown in Figure 4, it can be seen that the SS proposed in this paper is reasonable.

Figure 4. Comparison of SSs from this model and drain current vs. gate voltage curveand ISE-TCAD with the ferroelectric thickness as a parameter under the given conditions in the figure.

DownLoad: Full-Size Img PowerPoint

To compare the change of SS according to the ferroelectric thickness with the case of using the analytical SS model of this paper and the SS derived from the slope in the subthreshold region of the drain current and gate voltage curve of (2.11), the SSs are shown with the channel length as a parameter in Figure 5. At this time, to maintain the deviation of less than 1%, it was calculated for the case of L_g/R > 4. As can be seen in Figure 5, the SSs from the analytical SS model of this paper agree very well with the SSs derived from the curve of drain current and gate voltage using a 2D potential distribution. As can be observed in Figure 5, it can be seen that the difference between the two values increases as L_g/R decreases. As mentioned in Figure 2(b), the SS decreased as the ferroelectric thickness increased and the change in SS due to the change in ferroelectric thickness decreased as the channel length increased. In particular, SS < 60 mV/dec was exhibited when the channel length was 40 nm or more under the given conditions.

Figure 5. Comparison of SSs from this model and drain current vs. gate voltage curve with the channel length as a parameter under the given conditions in the figure.

DownLoad: Full-Size Img PowerPoint

To compare the change of SS with the change of channel radius, Figure 6 shows the change of SS while changing the channel radius R from 5 nm to 10 nm when the channel length is 30 nm under the given conditions. Based on Figure 6, it can be observed that the results of the 2D calculation and the analytical SS model are in good agreement. Since it is in the range of 3 < L_g/R < 6, even if n = 1 was used, the value could be obtained within the deviation range of less than 1%. As the channel radius R increases, SS increases, and it can be observed that the increasing rate $(\Delta SS/\Delta R)$ increases as R increases. In particular, it was found that the case of R = 5 nm, that is, the case of L_g/R = 6, matches very well. Therefore, the analytical SS model of this paper will be very useful.

Figure 6. Comparison of SSs from this model and drain current vs. gate voltage curve with the channel radius as a parameter under the given conditions in the figure.

DownLoad: Full-Size Img PowerPoint

3.2. SS for remanent polarization and coercive field

As shown in , it can be seen that SS > 60 mV/dec if L_g < 30 nm under the given conditions. This is the case of remanent polarization ${P_r} = 17\,\mu C/c{m^2}$ and coercive field E_c = 1.2 MV/cm, as shown in Figure 5. The remanent polarization and coercive field values are important factors that determine the hysteresis characteristics of ferroelectric materials, and it is known that the SS value is proportional to the absolute value |C_fe| of the capacitance of ferroelectric materials ^[38]. Figure 7 shows the contours of SS for the change of P_r and E_c when the channel length is 30 nm while keeping the device parameters the same as in Figure 5. The red dot in shows the SS value calculated under the conditions of . As can be seen in , the SS decreases as the remanent polarization decreases and the coercive field increases, and it can be observed that a region of SS < 60 mV/dec appears in the range of $15 \leqslant {P_r} \leqslant 16.8\,\mu C/c{m^2}$ and $1.34 \leqslant {E_c} \leqslant 1.5\,MV/cm$ . It can be seen that there is a relationship of |C_fe| $\propto {P_r}/{E_c}$ . Therefore, if P_r and E_c satisfying the condition of SS < 60 mV/dec are used, SS < 60 mV/dec can be obtained even if the channel length is shortened.

Figure 7. Contours of SSs for remanent polarization and coercive field at L_g = 30 nm under the given conditions in the figure.

DownLoad: Full-Size Img PowerPoint

As shown in Figure 5, the SS shows a relatively large value of SS > 70 mV/dec when the channel length is 20 nm. To obtain the condition of SS < 60 mV/dec, after reducing R = 3 nm and t_ox = 1 nm, the contour plot for P_r and E_c is shown in . As can be seen in , it can be observed that the SS < 60 mV/dec appears in the range of $15 \leqslant {P_r} \leqslant 23\,\mu C/c{m^2}$ and $0.95 \leqslant {E_c} \leqslant 1.5\,MV/cm$ . As such, it can be observed that if the channel radius R and the oxide thickness t_ox are reduced, device parameters satisfying the value of SS < 60 mV/dec can be obtained even when the channel length is about 20 nm. However, the models for the quantum and tunneling effect are required when the channel length is less than 10 nm or the channel diameter is reduced to 7 nm ^{[39,40,41,42,43]}, but further research on this should be conducted.

Figure 8. Contours of SSs for remanent polarization and coercive field at L_g = 20 nm under the given conditions in the figure.

DownLoad: Full-Size Img PowerPoint

Observing Figures 7 and 8, it can be seen that the contours have a relationship of P_r=aE_c (a is a proportionality constant) to maintain a constant SS value. That is, it can be seen that the SS according to a certain P_r/E_c value is constant. To observe this, Figure 9 shows the change of SS for the change of P_r/E_c value with the channel length as a parameter. As can be seen in Figure 9, it can be seen that the SS is plotted as a single value when P_r/E_c is determined in a given channel length. As mentioned in this section, the SS increases as the value of |C_fe| increases if P_r/E_c increases. It can be seen that the change of SS is relatively large according to P_r/E_c when the channel length is relatively short, 20 nm. As the channel length increased, the changing rate of SS for P_r/E_c decreased, and as P_r/E_c increased, the changing rate of SS for the channel length increased. Note that the SS is almost identical at P_r/E_c=10 pF/cm for channel lengths of 30 nm and 40 nm.

Figure 9. SSs for the ratio of the remanent polarization and coercive field P_r/E_c with the channel length as a parameter under the given conditions in the figure.

DownLoad: Full-Size Img PowerPoint

4. Conclusions

In this paper, an analytical SS model was presented to analyze the SS for junctionless GAA FET with ferroelectric. It has been found that the analytical SS model is valid since the SS value derived from the relation between drain current and gate voltage using a 2D potential distribution agrees well with the analytical SS model proposed here. In the case of the potential distribution represented by the Fourier-Bessel series in this paper, the case of n = 1 is dominant, so compared to the case of using n = 32, n = 1 could be used with a deviation of less than 1% according to the given conditions. As a result of SS analysis of junctionless GAA FET with ferroelectric using this analytical SS model, when the ferroelectric thickness increases at the same outer gate voltage, the voltage applied to the inner gate decreases as the voltage applied to the ferroelectric increases, and the flowing drain current decreases and SS also decreases. As the channel length increased, the change of SS according to the change of ferroelectric thickness relatively decreased. The decrease in channel radius results in a relatively greater ferroelectric thickness, resulting in a decrease in SS. As such, it can be seen that the SS value changes according to the relationship between the channel dimension and the ferroelectric thickness, and a result of SS < 60 mV/dec could be derived according to the device parameters when the ratio P_r/E_c between the remanent polarization P_r and the coercive field E_c decreases even in case of the channel length of 20 nm. In addition, it was found that the SS value was also constant at the given P_r/E_c. From the above results, it is judged that the analytical SS model presented in this paper can be used to analyze the SS of junctionless GAA FET with ferroelectric, and if the device parameters used in this paper are smaller, research on the quantum mechanical model should be conducted.

Supplementary: The derivative of each term

$\begin{array}{l} \frac{{\partial {C_n}}}{{\partial {V_{gs2}}}} = \frac{{\partial {C_n}}}{{\partial {V_{gs1}}}}\frac{{\partial {V_{gs1}}}}{{\partial Q}}\frac{{\partial Q}}{{\partial {V_{gs2}}}} \hfill \\ \frac{{\partial {D_n}}}{{\partial {V_{gs2}}}} = \frac{{\partial {D_n}}}{{\partial {V_{gs1}}}}\frac{{\partial {V_{gs1}}}}{{\partial Q}}\frac{{\partial Q}}{{\partial {V_{gs2}}}} \hfill \\ \frac{{\partial {C_n}}}{{\partial {V_{gs1}}}} = - \frac{{2{J_1}({\alpha _n})}}{{{\alpha _n}[J_1^2({\alpha _n}) + J_0^2({\alpha _n})]}}\frac{{\left[ {\exp \left( { - {\alpha _n}L/R} \right) - 1} \right]}}{{2\sinh \left( { - {\alpha _n}L/R} \right)}} \hfill \\ \frac{{\partial {D_n}}}{{\partial {V_{gs1}}}} = - \frac{{2{J_1}({\alpha _n})}}{{{\alpha _n}[J_1^2({\alpha _n}) + J_0^2({\alpha _n})]}}\frac{{\left[ {1 - \exp \left( {{\alpha _n}L/R} \right)} \right]}}{{2\sinh \left( { - {\alpha _n}L/R} \right)}} \hfill \\ \frac{{\partial {V_{gs1}}}}{{\partial Q}} = {\left( {\frac{{\partial Q}}{{\partial {V_{gs1}}}}} \right)^{ - 1}} = {\left[ { - \frac{{{C_{ox}}}}{{2{L_g}}}\left[ {\sum\limits_{n = 1}^\infty {\left[ {\frac{{\partial {C_n}}}{{\partial {V_{gs1}}}}\exp \left( {\frac{{{\alpha _n}{L_g}}}{R}} \right) - \frac{{\partial {D_n}}}{{\partial {V_{gs1}}}}\exp \left( { - \frac{{{\alpha _n}{L_g}}}{R}} \right) - \frac{{\partial {C_n}}}{{\partial {V_{gs1}}}} + \frac{{\partial {D_n}}}{{\partial {V_{gs1}}}}} \right]\left( {\frac{R}{{{\alpha _n}}}} \right){J_0}\left( {{\alpha _n}} \right)} } \right]} \right]^{ - 1}} \hfill \\ \frac{{\partial Q}}{{\partial {V_{gs2}}}} = \frac{1}{{2\alpha {t_{fe}} + 12\beta {t_{fe}}{Q^2} + 30\gamma {t_{fe}}{Q^4} + \frac{{\partial {V_{gs1}}}}{{\partial Q}}}} \hfill \\ \frac{\partial }{{\partial {V_{gs2}}}}\left[ {\exp \left( {{\alpha _n}{z_{\min }}/R} \right)} \right] = \frac{{{\alpha _n}}}{R}\exp \left( {{\alpha _n}{z_{\min }}/R} \right)\frac{{\partial {z_{\min }}}}{{\partial {V_{gs2}}}} \hfill \\ \frac{\partial }{{\partial {V_{gs2}}}}\left[ {\exp \left( { - {\alpha _n}{z_{\min }}/R} \right)} \right] = - \frac{{{\alpha _n}}}{R}\exp \left( { - {\alpha _n}{z_{\min }}/R} \right)\frac{{\partial {z_{\min }}}}{{\partial {V_{gs2}}}} \hfill \\ \end{array}$

Here, the z_min and derivative of z_min for V_gs2 can be obtained as the following.

$z_{\min } = \left(\frac{R}{2 \alpha_{1}}\right) \ln \left(\frac{D_{1}}{C_{1}}\right)$

$\begin{array}{l} \frac{{\partial {z_{\min }}}}{{\partial {V_{gs2}}}} = \left( {\frac{R}{{2{\alpha _1}}}} \right)\frac{\partial }{{\partial {V_{gs2}}}}\left( {\ln {D_1} - \ln {C_1}} \right) \hfill \\ = \left( {\frac{R}{{2{\alpha _1}}}} \right)\left( {\frac{{\partial \ln {D_1}}}{{\partial {V_{gs1}}}}\frac{{\partial {V_{gs1}}}}{{\partial Q}}\frac{{\partial Q}}{{\partial {V_{gs2}}}} - \frac{{\partial \ln {C_1}}}{{\partial {V_{gs1}}}}\frac{{\partial {V_{gs1}}}}{{\partial Q}}\frac{{\partial Q}}{{\partial {V_{gs2}}}}} \right) = \left( {\frac{R}{{2{\alpha _1}}}} \right)\left( {\frac{{\partial \ln {D_1}}}{{\partial {V_{gs1}}}} - - \frac{{\partial \ln {C_1}}}{{\partial {V_{gs1}}}}} \right)\left( {\frac{{\partial {V_{gs1}}}}{{\partial Q}}\frac{{\partial Q}}{{\partial {V_{gs2}}}}} \right) \hfill \\ \left( {\frac{R}{{2{\alpha _1}}}} \right)\left( {\frac{{\partial \ln {D_1}}}{{\partial {V_{gs1}}}} - \frac{{\partial \ln {C_1}}}{{\partial {V_{gs1}}}}} \right) = \left( {\frac{R}{{2{\alpha _1}}}} \right)\left( {\frac{{2{J_1}({\alpha _1})}}{{{\alpha _1}[J_1^2({\alpha _1}) + J_0^2({\alpha _1})]}}} \right)\left[ {\frac{{ - \left[ {1 - \exp \left( {{\alpha _1}L/R} \right)} \right]}}{{2{D_1}\sinh \left( { - {\alpha _1}L/R} \right)}} - \frac{{ - \left[ {\exp \left( { - {\alpha _1}L/R} \right) - 1} \right]}}{{2{C_1}\sinh \left( { - {\alpha _1}L/R} \right)}}} \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {\frac{R}{{4{\alpha _1}\sinh \left( { - {\alpha _1}L/R} \right)}}} \right)\left( {\frac{{2{J_1}({\alpha _1})}}{{{\alpha _1}[J_1^2({\alpha _1}) + J_0^2({\alpha _1})]}}} \right)\left[ {\frac{{\left[ {\exp \left( {{\alpha _1}L/R} \right) - 1} \right]}}{{{D_1}}} + \frac{{\left[ {\exp \left( { - {\alpha _1}L/R} \right) - 1} \right]}}{{{C_1}}}} \right] \hfill \\ \end{array}$

Use of AI tools declaration

The authors have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The author declares that there is no conflicts of interest in this paper.

References

[1]	A. Hoffmann, B. Montgomery, J. Popovici, I. Iturbe-Ormaetxe, P. Johnson, F. Muzzi, et al., Successful establishment of Wolbachia in Aedes populations to suppress dengue transmission, Nature, 476 (2011), 454–457. https://doi.org/10.1038/nature10356 doi: 10.1038/nature10356
[2]	C. McMeniman, R. Lane, B. Cass, A. Fong, M. Sidhu, Y.-F. Wang, et al., Stable introduction of a life-shortening Wolbachia infection into the mosquito Aedes aegypti, Science, 323 (2009), 141–144. https://doi.org/10.1126/science.1165326 doi: 10.1126/science.1165326
[3]	L. Moreira, I. Iturbe-Ormaetxe, J. Jeffery, G. Lu, A. Pyke, L. Hedges, et al., A Wolbachia symbiont in Aedes aegypti limits infection with dengue, chikungunya, and plasmodium, Cell, 139 (2009), 1268–1278. https://doi.org/10.1016/j.cell.2009.11.042 doi: 10.1016/j.cell.2009.11.042
[4]	T. Ruang-Areerate, P. Kittayapong, Wolbachia transinfection in Aedes aegypti: a potential gene driver of dengue vectors, Proc. Natl. Acad. Sci. U.S.A., 103 (2006), 12534–12539. https://doi.org/10.1073/pnas.0508879103 doi: 10.1073/pnas.0508879103
[5]	T. Walker, P. Johnson, L. Moreira, I. Iturbe-Ormaetxe, F. Frentiu, C. McMeniman, et al., The wMel Wolbachia strain blocks dengue and invades caged Aedes aegypti populations, Nature, 476 (2011), 450–453. https://doi.org/10.1038/nature10355 doi: 10.1038/nature10355
[6]	L. Almeida, Y. Privat, M. Strugarek, N. Vauchelet, Optimal releases for population replacement strategies: application to Wolbachia, SIAM J. Math. Anal., 51 (2019), 3170–3194. https://doi.org/10.1137/18M1189841 doi: 10.1137/18M1189841
[7]	C. McMeniman, S. O'Neill, A virulent Wolbachia infection decreases the viability of the dengue vector Aedes aegypti during periods of embryonic quiescence, PLoS Negl. Trop. Dis., 4 (2010), e748. https://doi.org/10.1371/journal.pntd.0000748 doi: 10.1371/journal.pntd.0000748
[8]	S. Ritchie, M. Townsend, C. Paton, A. Callahan, A. Hoffmann, Application of wMelPop Wolbachia strain to crash local populations of Aedes aegypti, PLoS Negl. Trop. Dis., 9 (2015), e0003930. https://doi.org/10.1371/journal.pntd.0003930 doi: 10.1371/journal.pntd.0003930
[9]	L. Almeida, A. Haddon, C. Kermorvant, A. Léculier, Y. Privat, M. Strugarek, et al., Optimal release of mosquitoes to control dengue transmission, ESAIM: Proc. Surv., 67 (2020), 16–29. https://doi.org/10.1051/proc/202067002 doi: 10.1051/proc/202067002
[10]	J. Schraiber, A. Kaczmarczyk, R. Kwok, M. Park, R. Silverstein, F. Rutaganira, et al., Constraints on the use of lifespan-shortening Wolbachia to control dengue fever, J. Theor. Biol., 297 (2012), 26–32. https://doi.org/10.1016/j.jtbi.2011.12.006 doi: 10.1016/j.jtbi.2011.12.006
[11]	M. Turelli, Cytoplasmic incompatibility in populations with overlapping generations, Evolution, 64 (2010), 232–241. https://doi.org/10.1111/j.1558-5646.2009.00822.x doi: 10.1111/j.1558-5646.2009.00822.x
[12]	D. E. Campo-Duarte, D. Cardona-Salgado, O. Vasilieva, Establishing wMelPop Wolbachia infection among wild Aedes aegypti females by optimal control approach, Appl. Math. Inf. Sci., 11 (2017), 1011–1027. https://doi.org/10.18576/amis/110408 doi: 10.18576/amis/110408
[13]	D. E. Campo-Duarte, O. Vasilieva, D. Cardona-Salgado, Optimal control for enhancement of Wolbachia frequency among Aedes aegypti females, Int. J. Pure Appl. Math., 112 (2017), 219–238.
[14]	D. Contreras-Julio, P. Aguirre, J. Mujica, O. Vasilieva, Finding strategies to regulate propagation and containment of dengue via invariant manifold analysis, SIAM J. Appl. Dyn. Syst., 19 (2020), 1392–1437. https://doi.org/10.1137/20M131299X doi: 10.1137/20M131299X
[15]	A. Fenton, K. Johnson, J. Brownlie, G. Hurst, Solving the Wolbachia paradox: modeling the tripartite interaction between host, Wolbachia, and a natural enemy, Am. Nat., 178 (2011), 333–342. https://doi.org/10.1086/661247 doi: 10.1086/661247
[16]	D. E. Campo-Duarte, O. Vasilieva, D. Cardona-Salgado, M. Svinin, Optimal control approach for establishing wMelPop Wolbachia infection among wild Aedes aegypti populations, J. Math. Biol., 76 (2018), 1907–1950. https://doi.org/10.1007/s00285-018-1213-2 doi: 10.1007/s00285-018-1213-2
[17]	J. Farkas, S. Gourley, R. Liu, A.-A. Yakubu, Modelling Wolbachia infection in a sex-structured mosquito population carrying West Nile virus, J. Math. Biol., 75 (2017), 621–647. https://doi.org/10.1007/s00285-017-1096-7 doi: 10.1007/s00285-017-1096-7
[18]	C. Ferreira, Aedes aegypti and Wolbachia interaction: population persistence in an environment changing, Theor. Ecol., 13 (2020), 137–148. https://doi.org/10.1007/s12080-019-00435-9 doi: 10.1007/s12080-019-00435-9
[19]	B. Zheng, M. Tang, J. Yu, Modeling Wolbachia spread in mosquitoes through delay differential equations, SIAM J. Appl. Math., 74 (2014), 743–770. https://doi.org/10.1137/13093354X doi: 10.1137/13093354X
[20]	A. Adekunle, M. Meehan, E. McBryde, Mathematical analysis of a Wolbachia invasive model with imperfect maternal transmission and loss of Wolbachia infection, Infect. Dis. Model., 4 (2019), 265–285. https://doi.org/10.1016/j.idm.2019.10.001 doi: 10.1016/j.idm.2019.10.001
[21]	L. Almeida, M. Duprez, Y. Privat, N. Vauchelet, Mosquito population control strategies for fighting against arboviruses, Math. Biosci. Eng., 16 (2019), 6274–6297. https://doi.org/10.3934/mbe.2019313 doi: 10.3934/mbe.2019313
[22]	P.-A. Bliman, M. S. Aronna, F. Coelho, M. da Silva, Ensuring successful introduction of Wolbachia in natural populations of Aedes aegypti by means of feedback control, J. Math. Biol., 76 (2018), 1269–1300. https://doi.org/10.1007/s00285-017-1174-x doi: 10.1007/s00285-017-1174-x
[23]	L. Xue, C. Manore, P. Thongsripong, J. Hyman, Two-sex mosquito model for the persistence of Wolbachia, J. Biol. Dyn., 11 (2017), 216–237. https://doi.org/10.1080/17513758.2016.1229051 doi: 10.1080/17513758.2016.1229051
[24]	J. Farkas, P. Hinow, Structured and unstructured continuous models for Wolbachia infections, Bull. Math. Biol., 72 (2010), 2067–2088. https://doi.org/10.1007/s11538-010-9528-1 doi: 10.1007/s11538-010-9528-1
[25]	I. Dorigatti, C. McCormack, G. Nedjati-Gilani, N. Ferguson, Using Wolbachia for dengue control: insights from modelling, Trends Parasitol., 34 (2018), 102–113. https://doi.org/10.1016/j.pt.2017.11.002 doi: 10.1016/j.pt.2017.11.002
[26]	H. Dutra, M. Rocha, F. Dias, S. Mansur, E. Caragata, L. Moreira, Wolbachia blocks currently circulating Zika virus isolates in Brazilian Aedes aegypti mosquitoes, Cell Host Microbe, 19 (2016), 771–774. https://doi.org/10.1016/j.chom.2016.04.021 doi: 10.1016/j.chom.2016.04.021
[27]	N. Ferguson, D. Kien, H. Clapham, R. Aguas, V. Trung, T. Chau, et al., Modeling the impact on virus transmission of Wolbachia-mediated blocking of dengue virus infection of Aedes aegypti, Sci. Transl. Med., 7 (2015), 279ra37–279ra37.
[28]	M. Woolfit, I. Iturbe-Ormaetxe, J. Brownlie, T. Walker, M. Riegler, A. Seleznev, et al., Genomic evolution of the pathogenic Wolbachia strain, wMelPop, Genome Biol. Evol., 5 (2013), 2189–2204. https://doi.org/10.1093/gbe/evt169 doi: 10.1093/gbe/evt169
[29]	H. Yeap, P. Mee, T. Walker, A. Weeks, S. O'Neill, P. Johnson, et al., Dynamics of the "popcorn" Wolbachia infection in outbred Aedes aegypti informs prospects for mosquito vector control, Genetics, 187 (2011), 583–595. https://doi.org/10.1534/genetics.110.122390 doi: 10.1534/genetics.110.122390
[30]	S.-B. Hsu, H. Smith, P. Waltman, Competitive exclusion and coexistence for competitive systems on ordered Banach spaces, Trans. Am. Math. Soc., 348 (1996), 4083–4094. https://doi.org/10.1090/S0002-9947-96-01724-2 doi: 10.1090/S0002-9947-96-01724-2
[31]	O. E. Escobar-Lasso, O. Vasilieva, A simplified monotone model of Wolbachia invasion encompassing Aedes aegypti mosquitoes, Stud. Appl. Math., 146 (2021), 565–585.
[32]	H. Smith, Monotone Dynamical Systems: An Introduction to the Theory of Competitive and Cooperative Systems, vol. 41 of Mathematical Surveys and Monographs, American Mathematical Society, Providence RI, USA, 1995.
[33]	J. Jiang, X. Liang, X.-Q. Zhao, Saddle-point behavior for monotone semiflows and reaction–diffusion models, J. Differ. Equ., 203 (2004), 313–330. https://doi.org/10.1016/j.jde.2004.05.002 doi: 10.1016/j.jde.2004.05.002
[34]	U. Boscain, B. Piccoli, Optimal syntheses for control systems on 2-D manifolds, vol. 43 of Mathématiques & Applications, Springer-Verlag, Berlin, Germany, 2004.
[35]	H. Sussmann, Regular synthesis for time-optimal control of single-input real analytic systems in the plane, SIAM J. Control Optim., 25 (1987), 1145–1162. https://doi.org/10.1137/0325062 doi: 10.1137/0325062
[36]	H. Sussmann, The structure of time-optimal trajectories for single-input systems in the plane: the $c^{\infty}$ nonsingular case, SIAM J. Control Optim., 25 (1987), 433–465. https://doi.org/10.1137/0325025 doi: 10.1137/0325025
[37]	H. Sussmann, The structure of time-optimal trajectories for single-input systems in the plane: the general real analytic case, SIAM J. Control Optim., 25 (1987), 868–904. https://doi.org/10.1137/0325048 doi: 10.1137/0325048
[38]	P.-A. Bliman, A feedback control perspective on biological control of dengue vectors by Wolbachia infection, Eur. J. Contr., 59 (2021), 188–206. https://doi.org/10.1016/j.ejcon.2020.09.006 doi: 10.1016/j.ejcon.2020.09.006
[39]	H. Aida, H. Dieng, T. Satho, A. Nurita, M. Salmah, F. Miake, et al., The biology and demographic parameters of Aedes albopictus in northern peninsular Malaysia, Asian Pac. J. Trop. Biomed., 1 (2011), 472–477. https://doi.org/10.1016/S2221-1691(11)60103-2 doi: 10.1016/S2221-1691(11)60103-2
[40]	D. Angeli, E. Sontag, Monotone control systems, IEEE Trans. Automat. Contr., 48 (2003), 1684–1698. https://doi.org/10.1109/TAC.2003.817920 doi: 10.1109/TAC.2003.817920
[41]	J. H. Arias-Castro, H. J. Martinez-Romero, O. Vasilieva, Biological and chemical control of mosquito population by optimal control approach, Games, 11 (2020), 62. https://doi.org/10.3390/g11040062 doi: 10.3390/g11040062
[42]	P.-A. Bliman, D. Cardona-Salgado, Y. Dumont, O. Vasilieva, Implementation of control strategies for sterile insect techniques, Math. Biosci., 314 (2019), 43–60. https://doi.org/10.1016/j.mbs.2019.06.002 doi: 10.1016/j.mbs.2019.06.002
[43]	M. H. Chan, P. S. Kim, Modelling a Wolbachia invasion using a slow–fast dispersal reaction–diffusion approach, Bull. Math. Biol., 75 (2013), 1501–1523. https://doi.org/10.1007/s11538-013-9857-y doi: 10.1007/s11538-013-9857-y
[44]	D. Cianci, J. Van Den Broek, B. Caputo, F. Marini, D. Torre, H. Heesterbeek, et al., Estimating mosquito population size from mark–release–recapture data, J. Med. Entomol., 50 (2013), 533–542. https://doi.org/10.1603/ME12126 doi: 10.1603/ME12126
[45]	P. Crain, J. Mains, E. Suh, Y. Huang, P. Crowley, S. Dobson, Wolbachia infections that reduce immature insect survival: Predicted impacts on population replacement, BMC Evol. Biol., 11 (2011), 290. https://doi.org/10.1186/1471-2148-11-290 doi: 10.1186/1471-2148-11-290
[46]	S. De Oliveira, D. Villela, F. Dias, L. Moreira, R. de Freitas, How does competition among wild type mosquitoes influence the performance of Aedes aegypti and dissemination of Wolbachia pipientis?, PLoS Negl. Trop. Dis., 11 (2017), e0005947.
[47]	H. Delatte, G. Gimonneau, A. Triboire, D. Fontenille, Influence of temperature on immature development, survival, longevity, fecundity, and gonotrophic cycles of Aedes albopictus, vector of chikungunya and dengue in the Indian Ocean, J. Med. Entomol., 46 (2009), 33–41. https://doi.org/10.1603/033.046.0105 doi: 10.1603/033.046.0105
[48]	J.-T. Gong, Y. Li, T.-P. Li, Y. Liang, L. Hu, D. Zhang, et al., Stable introduction of plant-virus-inhibiting Wolbachia into plant hoppers for rice protection, Curr. Biol., 30 (2020), 4837–4845. https://doi.org/10.1016/j.cub.2020.09.033 doi: 10.1016/j.cub.2020.09.033
[49]	L. Gouagna, J.-S. Dehecq, D. Fontenille, Y. Dumont, S. Boyer, Seasonal variation in size estimates of Aedes albopictus population based on standard mark-release-recapture experiments in an urban area on Reunion Island, Acta Trop., 143 (2015), 89–96. https://doi.org/10.1016/j.actatropica.2014.12.011 doi: 10.1016/j.actatropica.2014.12.011
[50]	L. Perko, Differential Equations and Dynamical Systems, Texts in Applied Mathematics, Springer, New York, USA, 2013.
[51]	A. C. Pimentel, C. S. Cesar, M. Martins, R. Cogni, The antiviral effects of the symbiont bacteria Wolbachia in insects, Front. Immunol., 11 (2021), 3690. https://doi.org/10.3389/fimmu.2020.626329 doi: 10.3389/fimmu.2020.626329
[52]	E. Pliego-Pliego, O. Vasilieva, J. Velázquez-Castro, A. Fraguela-Collar, Control strategies for a population dynamics model of Aedes aegypti with seasonal variability and their effects on dengue incidence, Appl. Math. Model., 81 (2020), 296–319.
[53]	H. Smith, Monotone dynamical systems: Reflections on new advances & applications, Discrete Contin. Dyn. Syst. Ser. A, 37 (2017), 485–504.
[54]	L. Styer, S. Minnick, A. Sun, T. Scott, Mortality and reproductive dynamics of Aedes aegypti (Diptera: Culicidae) fed human blood, Vector Borne Zoonotic Dis., 7 (2007), 86–98. https://doi.org/10.1089/vbz.2007.0216 doi: 10.1089/vbz.2007.0216
[55]	E. Suh, S. Dobson, Reduced competitiveness of Wolbachia infected Aedes aegypti larvae in intra-and inter-specific immature interactions, J. Invertebr. Pathol., 114 (2013), 173–177.

This article has been cited by:

1.	Analysis of Drain-Induced Barrier Lowering for Gate-All-Around FET with Ferroelectric, 2024, 14, 2226-809X, 189, 10.46604/ijeti.2023.12887
2.	Ibrahim Rahmani, Zohir Dibi, Hichem Farhati, Faycal Djeffal, Novel junctionless GAA negative capacitance FET based on gate engineering aspects: analytical modeling and performance assessment, 2025, 24, 1569-8025, 10.1007/s10825-024-02241-x
3.	F. Djeffal, I. Rahmani, H. Ferhati, Performance Assessment of a New Opto-ferroelectric-JL-FET IR Phototransistor: Impact of Negative Capacitance and Nanoparticle Plasmonics, 2024, 1557-1955, 10.1007/s11468-024-02728-0

Reader Comments

Your name:*

Email:*
© 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)