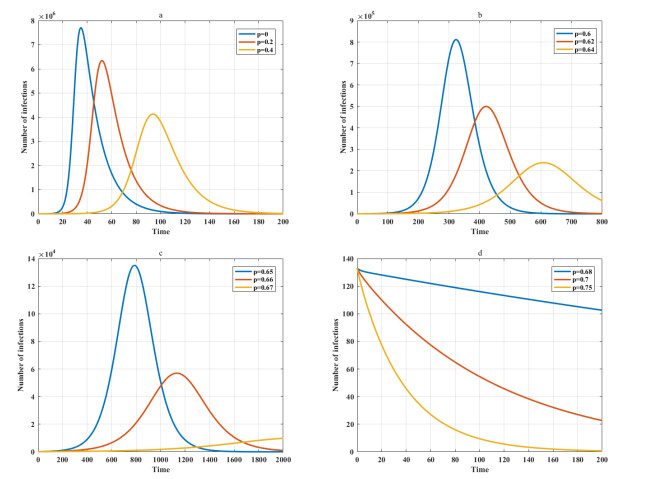
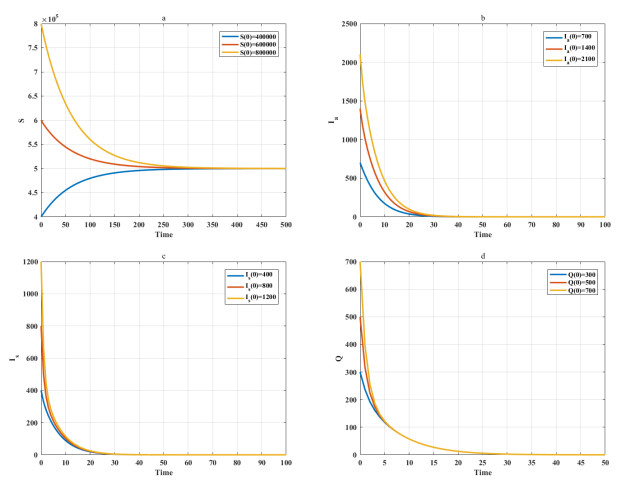
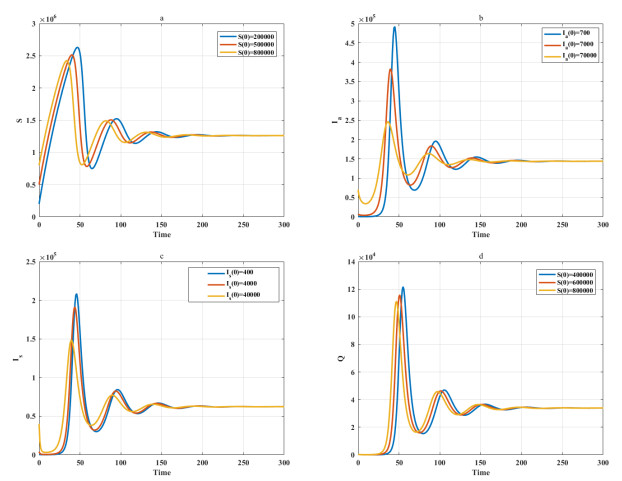
|
[1]
|
H. Wang, Z. Wang, Y. Dong, R. Chang, C. Xu, X. Yu, et al., Phase-adjusted estimation of the number of coronavirus disease 2019 cases in wuhan, china, Cell Discov., 6 (2020), 1–8. https://doi.org/10.1038/s41421-020-0148-0 doi: 10.1038/s41421-020-0148-0

|
|
[2]
|
D. Wang, M. Zhou, X. Nie, W. Qiu, M. Yang, X. Wang, et al., Epidemiological characteristics and transmission model of corona virus disease 2019 in china, J. Infect., 80 (2020), e25–e27. https://doi.org/10.1016/j.jinf.2020.03.008 doi: 10.1016/j.jinf.2020.03.008

|
|
[3]
|
F. S. Dawood, P. Ricks, G. J. Njie, M. Daugherty, W. Davis, J. A. Fuller, et al., Observations of the global epidemiology of covid-19 from the prepandemic period using web-based surveillance: A cross-sectional analysis, Lancet Infect. Dis., 20 (2020), 1255–1262. https://doi.org/10.1016/S1473-3099(20)30581-8 doi: 10.1016/S1473-3099(20)30581-8

|
|
[4]
|
C. Jiang, X. Li, C. Ge, Y. Ding, T. Zhang, S. Cao, et al., Molecular detection of sars-cov-2 being challenged by virus variation and asymptomatic infection, J. Pharm. Anal., 11 (2021), 257–264. https://doi.org/10.1016/j.jpha.2021.03.006 doi: 10.1016/j.jpha.2021.03.006

|
|
[5]
|
F. A. Engelbrecht, R. J. Scholes, Test for covid-19 seasonality and the risk of second waves, One Health, 12 (2021), 100202.
|
|
[6]
|
M. Yao, H. Wang, A potential treatment for covid-19 based on modal characteristics and dynamic responses analysis of 2019-ncov, Nonlinear Dyn., 106 (2021), 1425–1432. https://doi.org/10.1007/s11071-020-06019-1 doi: 10.1007/s11071-020-06019-1

|
|
[7]
|
P. Das, R. K. Upadhyay, A. K. Misra, F. A. Rihan, P. Das, D. Ghosh, Mathematical model of covid-19 with comorbidity and controlling using non-pharmaceutical interventions and vaccination, Nonlinear Dyn., 106 (2021), 1213–1227. https://doi.org/10.1007/s11071-021-06517-w doi: 10.1007/s11071-021-06517-w

|
|
[8]
|
K. Shah, Z. A. Khan, A. Ali, R. Amin, H. Khan, A. Khan, Haar wavelet collocation approach for the solution of fractional order covid-19 model using caputo derivative, Alex. Eng. J., 59 (2020), 3221–3231. https://doi.org/10.1016/j.aej.2020.08.028 doi: 10.1016/j.aej.2020.08.028

|
|
[9]
|
C. Han, Y. Liu, J. Tang, Y. Zhu, C. Jaeger, S. Yang, Lessons from the mainland of China's epidemic experience in the first phase about the growth rules of infected and recovered cases of covid-19 worldwide, Int. J. Disaster Risk Sci., 11 (2020), 497–507. https://doi.org/10.1007/s13753-020-00294-7 doi: 10.1007/s13753-020-00294-7

|
|
[10]
|
J. T. Machado, J. Ma, Nonlinear dynamics of covid-19 pandemic: modeling, control, and future perspectives, Nonlinear Dyn., 101 (2020), 1525–1526. https://doi.org/10.1007/s11071-020-05919-6 doi: 10.1007/s11071-020-05919-6

|
|
[11]
|
S. He, Y. Peng, K. Sun, Seir modeling of the covid-19 and its dynamics, Nonlinear Dyn., 101 (2020), 1667–1680. https://doi.org/10.1007/s11071-020-05743-y doi: 10.1007/s11071-020-05743-y

|
|
[12]
|
G. Stewart, K. van Heusden, G. A. Dumont, How control theory can help us control covid-19, IEEE Spectrum, 57 (2020), 22–29. https://doi.org/10.1109/MSPEC.2020.9099929 doi: 10.1109/MSPEC.2020.9099929

|
|
[13]
|
D. Fanelli, F. Piazza, Analysis and forecast of covid-19 spreading in china, italy and france, Chaos Solitons Fract., 134 (2020), 109761.
|
|
[14]
|
R. Li, S. Pei, B. Chen, Y. Song, T. Zhang, W. Yang et al., Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (sars-cov-2), Science, 368 (2020), 489–493.
|
|
[15]
|
W. O. Kermack, A. G. McKendrick, Contributions to the mathematical theory of epidemics. ii.—the problem of endemicity, Bull. Math. Biol., 138 (1932), 55–83.
|
|
[16]
|
C. Zheng, Complex network propagation effect based on sirs model and research on the necessity of smart city credit system construction, Alex. Eng. J., 61 (2022), 403–418. https://doi.org/10.1016/j.aej.2021.06.004 doi: 10.1016/j.aej.2021.06.004

|
|
[17]
|
Z. Zhao, L. Pang, Y. Chen, Nonsynchronous bifurcation of sirs epidemic model with birth pulse and pulse vaccination, Nonlinear Dyn., 79 (2015), 2371–2383. https://doi.org/10.1007/s11071-014-1818-y doi: 10.1007/s11071-014-1818-y

|
|
[18]
|
D. Saikia, K. Bora, M. P. Bora, Covid-19 outbreak in india: An seir model-based analysis, Nonlinear Dyn., 104 (2021), 4727–4751.
|
|
[19]
|
C. Xu, Y. Yu, Y. Chen, Z. Lu, Forecast analysis of the epidemics trend of covid-19 in the usa by a generalized fractional-order seir model, Nonlinear Dyn., 101 (2020), 1621–1634. https://doi.org/10.1007/s11071-020-05946-3 doi: 10.1007/s11071-020-05946-3

|
|
[20]
|
R. K. Upadhyay, A. K. Pal, S. Kumari, P. Roy, Dynamics of an seir epidemic model with nonlinear incidence and treatment rates, Nonlinear Dyn., 96 (2019), 2351–2368. https://doi.org/10.1007/s11071-019-04926-6 doi: 10.1007/s11071-019-04926-6

|
|
[21]
|
P. Yarsky, Using a genetic algorithm to fit parameters of a covid-19 seir model for us states, Math. Comput. Simulat., 185 (2021), 687–695. https://doi.org/10.1016/j.matcom.2021.01.022 doi: 10.1016/j.matcom.2021.01.022

|
|
[22]
|
N. ben Khedher, L. Kolsi, H. Alsaif, A multi-stage seir model to predict the potential of a new covid-19 wave in ksa after lifting all travel restrictions, Alex. Eng. J., 60 (2021), 3965–3974. https://doi.org/10.1016/j.aej.2021.02.058 doi: 10.1016/j.aej.2021.02.058

|
|
[23]
|
N. Piovella, Analytical solution of seir model describing the free spread of the covid-19 pandemic, Chaos Solitons Fract., 140 (2020), 110243.
|
|
[24]
|
S. J. Weinstein, M. S. Holland, K. E. Rogers, N. S. Barlow, Analytic solution of the seir epidemic model via asymptotic approximant, Physica D., 411 (2020), 132633–132633. https://doi.org/10.1016/j.physd.2020.132633 doi: 10.1016/j.physd.2020.132633

|
|
[25]
|
T. Britton, D. Ouédraogo, Seirs epidemics with disease fatalities in growing populations., Math. Biosci., 296 (2018), 45–59. https://doi.org/10.1016/j.mbs.2017.11.006 doi: 10.1016/j.mbs.2017.11.006

|
|
[26]
|
G. Lu, Z. Lu, Global asymptotic stability for the seirs models with varying total population size., Math. Biosci., 296 (2018), 17–25. https://doi.org/10.1016/j.mbs.2017.11.010 doi: 10.1016/j.mbs.2017.11.010

|
|
[27]
|
O. M. Otunuga, Estimation of epidemiological parameters for covid-19 cases using a stochastic seirs epidemic model with vital dynamics, Result. Phys., 28 (2021), 104664.
|
|
[28]
|
M. A. Abdelaziz, A. I. Ismail, F. A. Abdullah, M. H. Mohd, Codimension one and two bifurcations of a discrete-time fractional-order seir measles epidemic model with constant vaccination, Chaos Solitons Fract., 140 (2020), 110104.
|
|
[29]
|
A. A. Thirthar, R. K. Naji, F. Bozkurt, A. Yousef, Modeling and analysis of an si1i2r epidemic model with nonlinear incidence and general recovery functions of i1, Chaos Solitons Fract., 145 (2021), 110746.
|
|
[30]
|
L. Liu, D. Jiang, T. Hayat, Dynamics of an sir epidemic model with varying population sizes and regime switching in a two patch setting, Phys. A., 574 (2021), 125992.
|
|
[31]
|
S. S. Nadim, I. Ghosh, J. Chattopadhyay, Short-term predictions and prevention strategies for covid-19: a model-based study, Appl. Math. Comput., 404 (2021), 126251.
|
|
[32]
|
S. Khajanchi, K. Sarkar, Forecasting the daily and cumulative number of cases for the covid-19 pandemic in india, Chaos, 30 (2020), 071101.
|
|
[33]
|
D. K. Das, A. Khatua, T. K. Kar, S. Jana, The effectiveness of contact tracing in mitigating covid-19 outbreak: A model-based analysis in the context of india, Appl. Math. Comput., 404 (2021), 126207.
|
|
[34]
|
Y. Liu, K. Lillepold, J. C. Semenza, Y. Tozan, M. B. Quam, J. Rocklöv, Reviewing estimates of the basic reproduction number for dengue, zika and chikungunya across global climate zones, Environ. Res., 182 (2020), 109114.
|
|
[35]
|
Y. Zhou, W. Sun, Y. Song, Z. Zheng, J. Lu, S. Chen, Hopf bifurcation analysis of a predator–prey model with holling-ii type functional response and a prey refuge, Nonlinear Dyn., 97 (2019), 1439–1450. https://doi.org/10.1007/s11071-019-05063-w doi: 10.1007/s11071-019-05063-w

|
|
[36]
|
P. Van den Driessche, J. Watmough, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission, Math Biosci. 180 (2002), 29–48. https://doi.org/10.1016/S0025-5564(02)00108-6
|
|
[37]
|
M. Samsuzzoha, M. Singh, D. Lucy, Uncertainty and sensitivity analysis of the basic reproduction number of a vaccinated epidemic model of influenza, Appl. Math. Model., 37 (2013), 903–915. https://doi.org/10.1016/j.apm.2012.03.029 doi: 10.1016/j.apm.2012.03.029

|
|
[38]
|
S. Tchoumi, M. Diagne, H. Rwezaura, J. Tchuenche, Malaria and covid-19 co-dynamics: A mathematical model and optimal control, Appl. Math. Model., 99 (2021), 294–327. https://doi.org/10.1016/j.apm.2021.06.016 doi: 10.1016/j.apm.2021.06.016

|
|
[39]
|
B. Tang, X. Wang, Q. Li, N. L. Bragazzi, S. Tang, Y. Xiao, et al., Estimation of the transmission risk of the 2019-ncov and its implication for public health interventions, J. Clin. Med., 9 (2020), 462.
|
|
[40]
|
G. Rohith, K. Devika, Dynamics and control of covid-19 pandemic with nonlinear incidence rates, Nonlinear Dyn., 101 (2020), 2013–2026. https://doi.org/10.1007/s11071-020-05774-5 doi: 10.1007/s11071-020-05774-5

|
|
[41]
|
Wuhan Municipal Bureau of Statistics. Available from: http://tjj.wuhan.gov.cn.
|
|
[42]
|
G. Fan, H. Song, S. Yip, T. Zhang, D. He, Impact of low vaccine coverage on the resurgence of covid-19 in central and eastern europe, One Health, 14 (2022), 100402. https://doi.org/10.1016/j.onehlt.2022.100402 doi: 10.1016/j.onehlt.2022.100402

|
|
[43]
|
K. Adhikari, R. Gautam, A. Pokharel, K. N. Uprety, N. K. Vaidya, Transmission dynamics of covid-19 in nepal: Mathematical model uncovering effective controls, J. Theor. Biol., 521 (2021), 110680.
|
|
[44]
|
A. Ali, F. S. Alshammari, S. Islam, M. A. Khan, S. Ullah, Modeling and analysis of the dynamics of novel coronavirus (covid-19) with caputo fractional derivative, Results Phys., 20 (2021), 103669.
|
|
[45]
|
A. B. Gumel, E. A. Iboi, C. N. Ngonghala, E. H. Elbasha, A primer on using mathematics to understand covid-19 dynamics: Modeling, analysis and simulations, Infect. Dis. Model., 6 (2021), 148–168.
|
|
[46]
|
A. M. Salman, I. Ahmed, M. H. Mohd, M. S. Jamiluddin, M. A. Dheyab, Scenario analysis of covid-19 transmission dynamics in malaysia with the possibility of reinfection and limited medical resources scenarios, Comput. Biol. Med., 133 (2021), 104372.
|
|
[47]
|
Q. Fan, W. Zhang, B. Li, D. J. Li, J. Zhang, F. Zhao, Association between abo blood group system and covid-19 susceptibility in wuhan, Front. Cell. Infect. Microbiol., 10 (2020), 404. https://doi.org/10.3389/fcimb.2020.00404 doi: 10.3389/fcimb.2020.00404

|









 DownLoad:
DownLoad: