The number of COVID-19 clusters in healthcare and elderly care facilities averted by vaccination of healthcare workers in Japan, February–June 2021

1.   Introduction

Diabetes mellitus (DM) is an endocrine metabolic disease caused by the interaction of genetic, immune and environmental factors that lead to a defect in insulin secretion or a decrease in insulin sensitivity of the cells, resulting in disorders of blood glucose, carbohydrate, lipid and protein metabolism ^[1]. According to the World Health Organization, diabetes is one of the leading non-communicable diseases with the highest mortality rate worldwide ^[2]. It is one of the most common non-communicable diseases worldwide. Over the past 30 years, the prevalence of diabetes has increased annually and by 2021, there were approximately 537 million adults with diabetes worldwide ^[3]. According to projections by the International Diabetes Federation in 2021, the total number of diabetics worldwide will increase to 643 million by 2030 and to 783 million by 2045 ^[4]. The American Diabetes Association (ADA) classifies DM as type 1 diabetes, type 2 diabetes, gestational diabetes and specific types of diabetes ^[5]. Of these, type 1 diabetes accounts for about 5% and type 2 diabetes for 90% to 95% ^[6]. The main characteristics of DM are high fasting and postprandial glucose, and the common clinical manifestations are mainly polyhydramnios, polyuria, polyphagia and weight loss. Long-term elevated glucose can damage the body's cardiovascular and nervous systems, which can lead to chronic complications such as diabetic cardiovascular disease, diabetic nephropathy, diabetic retinopathy and peripheral neuropathy ^[7]. Similarly, recurrent episodes of hypoglycemia can easily damage the brain function of patients, accelerating the process of dementia and even brain death ^[8]. The disease has not yet been cured. The only way to control the progression of diabetes is through early diagnosis and timely treatment, which can be achieved by managing diet ^[9], reasonable insulin injections ^[10], active monitoring of blood glucose levels ^[11], etc., to maintain blood glucose levels within normal limits ^[12].

The artificial pancreas (also known as the closed-loop insulin delivery system) has been one of the breakthroughs pursued in the treatment of diabetes since the 19th century ^[13]. It consists of three main components: a continuous glucose monitoring device (CGM), an insulin pump (IP) and a closed-loop control algorithm (CA), which automatically monitors the blood glucose level of the diabetic patient through the CGM and controls the insulin pump to automatically deliver the right amount of insulin to the patient through the closed-loop control algorithm ^[14]. The closed-loop control algorithm is the most central and critical part of the artificial pancreas function ^[15]. However, most current CGM devices monitor glucose levels in interstitial fluid ^[16], which has a delay in real-time glucose levels in the blood, and there is a physiological lag, which requires closed-loop control algorithms to accurately predict glucose levels. With the continuous development of glucose prediction technology, numerous scholars have started to explore the performance of different types of models in glucose prediction ^{[17,18,19,20,21,22,23,24]}. Based on the published literature, two types of glucose prediction methods can be classified: physiology-based glucose prediction and data-driven glucose prediction ^[25,26]. The physiologically based blood glucose prediction model is a continuous dynamic model that relies on the basic physiological mechanism of the human body. However, since the regulation of the human body environment is a dynamic process, this prediction method depends on the physiological regulation mechanism of the individual. However, the blood glucose changes between different patients have significant variability, so it is difficult for the overall physiological model to guarantee the accuracy of different individuals. Moreover, due to the excessive factors to be considered in the construction of physiological models, the cost of modeling is high, and the practical application is low at present.

In recent years, with the widespread use of CGM, data-driven blood glucose prediction models have become a new hot topic of research, which usually use previous continuous blood glucose time series data to predict future blood glucose trends at some prediction horizon (PH), often using regression, machine learning and deep learning methods to build prediction models. In 2015, Georga et al. ^[27] used random forest algorithm and RReliefF to rank feature sets to obtain feature sets of blood glucose level, insulin dose, dietary intake, and physical activity, which were combined with regression models for blood glucose prediction. In 2019, Idriss et al. ^[28] proposed a deep learning neural network model (LSTMNN) based on a Long Short Term Memory Network (LSTM) layer and two hidden layers to predict blood glucose levels in diabetic patients, which predicted blood glucose levels with a mean RMSE of 12.38 mg/dL. In 2020, Teng et al. ^[29] proposed a prediction model using the GRU method to predict blood glucose time series data with RMSE and MAPE of 0.7612 mmol/L and 7.3427%, respectively, for a PH = 60 min. In 2021, Karim et al. ^[20] trained an artificial neural network with the bolus and basal insulin dosing and timing, baseline glucose levels, maximum glucose infusion rate and total carbohydrate content as parameters and predicted an RMSE of 1.72 mmol/L at PH = 120 min. Cichosz et al. ^[30,31] proposed that adding penalty weights could improve the clinical performance of CGM prediction models. In 2022, Koutny and Mayo ^[22] proposed a new low-complexity, interpretable method for blood glucose prediction using Meta-Differential Evolution to determine the parameters of the predictor, extending the prediction time by 5 min with a relative error of less than 30% for 95.8% of predicted blood glucose levels in all patients. In 2023, Yang et al. ^[23] proposed a short-term prediction method for blood glucose based on the Patients' Time Multiple Attention Mechanism for Diabetes (PBGTAM), with overall root mean square error of prediction, prediction accuracy and clinical accuracy of 20.57, 84.35 and 85.18%, respectively.

Due to the non-linearity and non-smoothness of CGM data, direct use of raw data to build prediction models often fails to meet the accuracy requirements. More researchers have applied relevant methods of signal analysis to pre-process CGM data in order to reduce its non-stationarity and improve the prediction accuracy. Rabby et al. ^[32] and Xu et al. ^[21] used Kalman filtering to smooth the CGM data in 2021 and 2022, respectively, but the Kalman filtering method can only process linear processes and the signal noise must obey a Gaussian distribution, and the smoothing effect of the Kalman filtering method on the data will be reduced when the nonlinear characteristics of the actual system are slightly stronger or the noise characteristics deviate from the Gaussian distribution. Carrillo-Moreno et al. ^[33] used a sliding average filter to deal with noise in CGM data. The advantage of this method is that it is simple to operate, but the size of the sliding window will have a large impact on the smoothing effect, and this filtering method will lose some of its accuracy when the real value within the sliding window changes a lot, and the filtering result is close to the average expectation of the real value. The larger the window is, the more serious the lag phenomenon is. The wavelet transform threshold denoising algorithm is not only able to retain more information about the signal at high frequencies, but also the signal at low frequencies is almost invisible to noise interference, and has a better smoothing effect for non-linear non-smooth signals. In 2022, Liang ^[34] and Peng ^[35] used the traditional wavelet transform threshold denoising algorithm to smooth CGM data, but did not study in depth the way the threshold of wavelet transform was selected and the influence caused by the threshold function on the smoothing effect of CGM data.

Therefore, in order to further improve the prediction effect of the blood glucose trend prediction model, this paper improves the wavelet transform threshold selection method and threshold function, improves the data smoothing effect while retaining the original characteristics of CGM data to the greatest extent so that the smoothed CGM data can be input to the GRU model to effectively improve the accuracy of blood glucose prediction and combines the characteristics of the fast running speed of the GRU model to build a blood glucose trend prediction model with high real-time capability and high accuracy. The rest of the paper is structured as follows: Section 2 introduces the data sources and relevant theoretical background, including the basic principles of wavelet transform and GRU. Section 3 describes in detail the improved method of using the wavelet transform threshold denoising algorithm and compares the SNR and MSE of the algorithm before and after the improvement applied to CGM data. Section 4 provides a detailed description of the data pre-processing steps and the parameters of the IWT-GRU model and the remaining control models. Section 5 compares the strengths and weaknesses of the IWT-GRU model and the other four models by means of model performance measures and verifies the actual performance of the models using Clarke Error Grid Analysis (CEGA). Section 6 concludes the research presented in this paper and provides an outlook on future developments in the field of glucose trend prediction.

2.   Relevant theories and data sources

2.1.   Wavelet threshold denoising principle and its basic steps

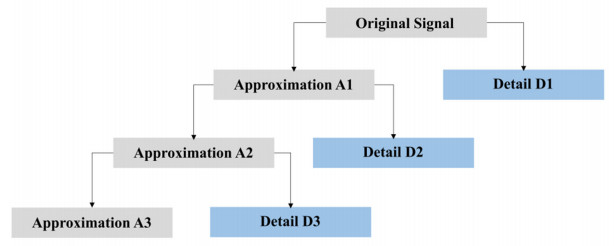
The wavelet transform inherits the idea of localization of the short-time Fourier transform, while overcoming the disadvantage of the window size not varying with frequency, providing a "time-frequency" window that changes with frequency, making it an ideal tool for time-frequency analysis and processing of signals ^[36]. The wavelet transform is highly de-data-dependent, concentrating the energy of the signal on some of the larger wavelet coefficients in the wavelet domain, while the white noise contained in the orthogonal basis of the transform is white noise, the wavelet transform distributes the noise energy over most of the unfolded coefficients in the wavelet domain. Therefore, the wavelet coefficients with larger amplitude after wavelet transform are generally dominated by the signal, while the coefficients with smaller amplitude are largely noise. Therefore, the coefficients with larger amplitude can be retained and the coefficients with smaller amplitude can be set to zero to obtain the estimated wavelet coefficients, and then the signal can be reconstructed to achieve the purpose of removing noise. Take the three-layer wavelet transform as an example, as shown in Figure 1 The signal is decomposed into three layers to obtain four wavelet coefficients (A3, D3, D2, D1). Approximation is the low frequency component of the signal and A1 is the approximate wavelet coefficient. Detail is the high frequency component of the signal and D1, D2 and D3 are the detail wavelet coefficients. After the three-layer decomposition, the amplitude of the wavelet coefficients of the original signal is larger than that of the noise and the number of signal wavelet coefficients is much smaller than that of the noise wavelet coefficients ^[37].

The first step of wavelet threshold denoising is to select a suitable wavelet basis function and the number of decomposition layers to carry out wavelet decomposition of the noisy signal. The commonly used wavelets are mainly dbN wavelet, symN wavelet, coifN wavelet, Haar wavelet, biorNr.Nd wavelet, etc. The number of decomposition layers is generally selected as 3−5 layers. The second step is to select a suitable threshold $\lambda$ and threshold function. If the selected threshold is too large, some of the original signal information will be lost, resulting in distortion of the reconstructed signal; if the selected threshold is too small, too much noise will be retained, resulting in poor denoising effect. The common threshold functions are mainly the hard threshold function (Eq (1)), soft threshold function (Eq (2)) and Garrote threshold function (Eq (3)). The third step is to perform a discrete wavelet transform on the processed wavelet coefficients to obtain the reconstructed denoised signal.

The flow of the wavelet transform threshold denoising algorithm is shown in Figure 2.

2.2.   Introduction to GRU theory

Artificial Neural Networks (ANNs) were inspired by the neural networks in the biological brain. ANNs consist of a large number of neural nodes that model the complex relationships between input data and output signals through connections between nerves ^[38]. In general, an ANN consists of an input layer, a hidden layer, and an output layer, and the parameters of data modelling are the structural information of the nerve and the weight values between the two nodes connected. In 1982, Hopfiled ^[39] first proposed Recurrent Neural Networks (RNNs), which, compared to traditional artificial neural networks, also connect neurons in a single layer to form a "loop" structure between neurons in a single layer, enabling the sharing of weights between layers, and the recurrent neural network transmits information through the "loop" structure, realizing the information sharing between layers. It can be used to model sequential data such as text statements, time sequences and biosignal sequences. If the input vector is $X = {({x}_{0}, {x}_{1}, {x}_{2}\dots, {x}_{p-1})}^{T}$, then the states of the layers at time t are

Where ${f}_{hh}$ and ${f}_{hy}$ are the activation functions from the hidden layer to the hidden layer and from the hidden layer to the output layer, respectively, and are generally Sigmoid functions or tanh functions; ${W}_{xh}$, ${W}_{hh}$, and ${W}_{hy}$ are connection weight matrices between input layer and hidden layer, hidden layer and hidden layer, and hidden layer and output layer, respectively. The structure of the RNN is shown in Figure 3(a).

Since the basic RNN uses the back-propagation through time (BPTT) algorithm for parameter tuning, there is the problem of gradient disappearance or gradient explosion, and the basic recurrent neural network is unable to remember information with long time steps. Based on this, two variants of the basic RNN emerged: the LSTM and the GRU, whose variations are shown schematically in Figure 3(d).

The LSTM uses long and short memory units to replace the activation functions in the basic RNN hidden layer. In addition to the original activation functions, the LSTM contains input gates, forgetting gates and output gates made up of Sigmoid functions, as well as a series of multiplication and addition operations. The input gate controls new information, ${X}_{t}$, merged into long-term memory, the forgetting gate controls the extent to which past unit states ${C}_{t-1}$. The input gate and the forgetting gate together determine the extent to which the cell state (${C}_{t}$) updates, and the output gate is based on the cell state ${C}_{t}$ and controls the hidden layer of ${H}_{t}$. The Sigmoid function transforms the data obtained from the linear transformation of the hidden layer information at the previous time point and the current input information into a numerical output between 0 and 1, which controls the degree of information memory on the one hand and solves the gradient disappearance and gradient explosion problems caused by the BP algorithm on the other. The internal structure of the LSTM is shown in Figure 3(b).

LSTM is widely used in the prediction of time series problems because of its good prediction performance, but its complex internal structure also leads to the slowdown of model training speed. GRU is a variant of LSTM, which does not have an explicit cell state, but uses a reset gate to implement the role of the forgetting gate and input gate in LSTM, and an update gate to control the update of the hidden layer state. This internal structure of GRU makes it inherit the advantages of LSTM on the one hand, and reduce the parameters required for model training on the other hand, thus reducing the model training time. The GRU hidden layer output is calculated as follows:

where ${X}_{t}$ is the input vector at moment t, ${R}_{t}$ is the reset guys vector at moment t, ${Z}_{t}$ is the update gate vector at time t, ${H}_{t}$ is the hidden layer output vector at time t, $\stackrel{-}{{H}_{t}}$ is the updated candidate vector and ${W}_{sh}$, ${W}_{sx}$, ${W}_{zx}$, ${W}_{zh}$, ${W}_{rx}$ and ${W}_{rh}$ are the weight matrices in each connection vector, respectively. $\sigma$ is the Sigmoid function. The internal structure of the GRU is shown in Figure 3(c).

2.3.   Data sources

The data for this study was obtained from a silicon-based kinetic glucose monitor that acquired patients' blood glucose data at 5-minute intervals, and raw CGM data from 80 patients were selected over 7 consecutive days. Table 1 presents baseline data for patients. Data are represented as means ± standard deviation. Figure 4 shows the blood glucose change curve (2016 blood glucose values) for a patient over a consecutive 7-day period.

3.   Improved wavelet transform threshold denoising algorithm and validation of the effect

3.1.   Threshold stratification selection method and improvement of traditional threshold function

The main wavelet denoising thresholds currently in use are based on unbiased likelihood estimation (rigsure), fixed thresholds (sqtwolog), heursure thresholds (heursure) and minimaxi thresholds (minimaxi). The choice of a suitable threshold is important for subsequent signal processing. If the threshold is chosen too small, there is a residual noise removal, and if the threshold is chosen too large, part of the signal is filtered out. Since the wavelet coefficient of noise decreases with the increase of decomposition layers, the threshold value of different decomposition layers should decrease with the increase of decomposition layers when denoising the signal. In this paper, we propose the threshold layer selection method, and the threshold layer selection equation is:

In the above equation, N is the number of corresponding wavelet transform coefficients, j is the corresponding number of layers of the wavelet transform and ${\sigma }_{n}$ is the variance contained in the noise, and since the noise variance is not known in practical use, it can be estimated from the wavelet decomposition coefficients of the first layer, i.e.,

The three traditional thresholding functions are often used in signal processing, but each of them has certain shortcomings. When using hard thresholding, the signal is better marginalized, but the function itself is discontinuous and may lead to unwanted oscillations in the reconstructed signal; soft thresholding has good continuity and the denoising result is smoother, but when the wavelet coefficients are large, there is a fixed deviation between the estimated wavelet coefficients and the original coefficients, resulting in a loss of the high frequency part of the signal, leading to the approximation degree of the reconstructed signal being poor compared with the original signal, which easily produces distortion. The Garrote thresholding function combines the advantages of soft and hard thresholding functions, with good signal continuity, and the fixed deviation tends to zero when the wavelet coefficients are large, effectively overcoming the shortcomings of soft and hard thresholding functions. However, it ignores the characteristics of noise decreases with increasing scale under wavelet transform, and for mutating signals, its denoising effect is still insufficient. The three traditional thresholding functions are shown in Figure 5.

As the three types of traditional threshold functions mentioned above all have their own shortcomings, a new threshold function is constructed under the premise of fully considering the respective advantages of these three types of functions, with the specific expression shown in Eq (12). The improved image of the threshold function is shown in Figure 6. By introducing the adjustment factors α and β, it retains the continuity of the soft threshold function and can rapidly approximate the hard threshold function, and the approximation speed of the function can be reasonably controlled by controlling the values of α and β, which is more applicable to different signals.

3.2.   Performance validation of the improved threshold function

In this paper, the CGM data of a patient was randomly selected from 80 patients, and three traditional threshold functions and the improved threshold function were adopted to denoise the signal. dB10 wavelets were selected to do 3-layer wavelet decomposition on the CGM signal, and the adjustment factors α and β were chosen as 0.5 and 2 respectively. The traditional three threshold functions adopt fixed threshold, and the improved threshold function adopts hierarchical threshold selection method. The signal-noise ratio (SNR) and mean square error (MSE) are used to quantify and compare their denoising effects. The SNR is an important measure of the denoising effect of the signal, and the higher the SNR, the better the signal extraction effect. The smaller the MSE between the denoised signal and the original signal, the smaller the distortion, the more complete the signal extraction and the better the denoising effect. The equations for SNR and MSE are shown in Eqs (13) and (14), where s(i) represents the original signal and y(i) represents the denoised signal.

When α and β are selected as 0.5 and 2 respectively, the model SNR and mean square error can obtain the best values. The relationship between α and β values and SNR and mean square error is shown in Figures 7 and 8. The effect of denoising the CGM data by the four methods is shown in Figure 9 and the comparison of SNR and MSE is shown in Table 1. From Table 2, it can be seen that the improved wavelet transform threshold denoising algorithm has a SNR of 24.8135 and an MSE of 0.2309, and the denoising effect is better than the three traditional methods.

4.   Blood glucose trend prediction model construction

4.1.   Data pre-processing and determination of optimal input sequence length

As the Dynamic Glucose Monitor from Silicon Motion has a data storage function, it does not have individual missing values if not for sensor damage, so there is no need to fill in the data and exclude user data that has not been continuously monitored for 7 days.

Due to the non-linearity and non-smoothness of the raw CGM data, the prediction accuracy of the model training directly using the raw data often fails to achieve good results, so the data needs to be smoothed. In this paper, the improved wavelet transform threshold denoising algorithm described in Section 3 is used to smooth the raw CGM data.

As the neural network model frameworks all have adapted input data scales, different input sequence lengths have a significant impact on the prediction results. Therefore, to better train the model, a linear normalization method is first used to scale the data to the (0, 1) interval. The normalized data is then divided using the data sliding window method, thus converting the dataset into a supervised learning type of data sample and enabling flexible transformation of data lengths. By adjusting the size of different windows, the model can use feature time series data with a previous time length of 5*m (min) to predict future blood glucose fluctuations with a total time length of 5*n (min).

4.2.   Predictive model and parameter design

In this paper, the RNN, LSTM, SVR, GRU and IWT-GRU algorithms are selected for modelling and training respectively, in which, except for the IWT-GRU model, the data smoothing algorithms of all the models adopt the general wavelet threshold denoising algorithm, i.e., the CGM data are smoothed using fixed threshold and soft threshold functions and the IWT-GRU model adopts the improved wavelet transform proposed in this paper. For the threshold denoising algorithm for data smoothing, wavelet basis is selected as sym8 and the number of decomposition layers is 3. In addition, the IWT-GRU model chooses MAE as the loss function, the learning rate is 0.0001, the optimizer chooses RMSProp, the number of samples included in each training is 64 and the maximum number of iterations is 200. The structure and parameters of the RNN, LSTM and GRU models are the same as those of IWT-GRU, and the SVR uses radial basis neural network as the kernel, C = 10, gamma = 0.1. The overall construction process of the blood glucose trend prediction model in this paper is shown in Figure 10.

5.   Results and analysis

5.1.   Model performance evaluation indicators

In this paper, root mean square error (RMSE), mean absolute percentage error (MAPE), coefficient of determination (${R}^{2}$) and running time are used as the evaluation metrics for model performance. The running environment of the code is Windows 10 operating system, and the CPU parameters are i5-11260H@2.60GHz. RMSE, MAPE and ${R}^{2}$ are calculated as shown in the following equations:

where n is the number of samples and ${x}_{i}$ is the actual value of the ith sample, the $\stackrel{~}{{x}_{i}}$ is the predicted value of the ith sample and $\stackrel{-}{{x}_{i}}$ is the mean value of the original data. In statistics, the smaller the value of RMSE and MAPE, the better the model predicts. ${R}^{2}$ is the ratio of the total regression sum of squares to the total deviation sum of squares, ranging from 0 to 1. Closer to 1 means a more significant fit of the model and better model prediction.

Tables 3−5 show the mean prediction performance of the IWT-GRU model for different prediction horizon when the length of the input data sequence is 30, 60 and 90 min, respectively. From Tables 3−5, it can be seen that for different input data sequence lengths, the model performance is better when the prediction horizon is 45 min than for the other prediction horizon. As the length of the input data sequence increases, the performance of the model at PH = 45 min shows a higher and then lower state. Overall, the IWT-GRU model performs best when the input sequence data length is 60 min and the prediction horizon is 45 min. Table 6 shows the comparison of the mean prediction results of the five models at an input sequence data length of 60 min and PH = 45 min. From Table 6, it can be seen that the GRU model performs best in terms of performance and running time under the same pre-processing method, while the performance of the IWT-GRU model processed with the improved wavelet transform threshold denoising algorithm has a significant improvement over the performance of the conventional GRU model, and the running time is only 0.9 seconds slower than that of the GRU model.

5.2.   Clark error grid analysis

In order to demonstrate the validity and accuracy of the model in a clinical setting, the Clarke Error Grid Analysis (CEGA), which is commonly used in clinical practice, was chosen to assess the difference between actual and predicted blood glucose values. This method has a target blood glucose control value of 3.9−10.0 mmol/L, with interventions required below 3.9 mmol/L or above 13.3 mmol/L. After converting the blood glucose values to mg/dL, a Clark error analysis grid was drawn using the CGM-value (without filtering) and the model predicted values as the horizontal and vertical axes of the grid, respectively. Zone A is the clinically accurate zone, representing ± 20% difference from the reference value; zone B is the clinically acceptable zone, located above or below zone A, representing blood glucose values above 20% of the range relative to the reference value; zones C, D and E are the clinically incorrect zones. The data is not desirable. The more blood glucose values falling in zones A and B, the closer the model prediction is to the measured value, and the higher the prediction accuracy is. Figure 11(a)−(e) is the results of CEGA for predicting the change of blood glucose in the next 60 min for a patient using SVR, LSTM, RNN, IWT-GRU and GRU models respectively. The prediction results of the five algorithms accounted for 84.38, 92.64, 89.33, 98.69 and 95.26% in region A, respectively, which shows that the IWT-GRU model proposed in this paper also has the best prediction accuracy compared to other models in actual clinical outcomes.

6.   Summary and outlook

In this paper, an improved wavelet transform threshold denoising algorithm was proposed to smooth CGM data for its non-linearity and non-smoothness, and a novel blood glucose trend prediction model was constructed by combining GRU. The performance of the algorithm was validated on CGM data from 80 diabetic patients, and by comparing the RMSE, MAPE and ${R}^{2}$of SVR, RNN, LSTM, GRU and IWT-GRU models, the IWT-GRU model proposed in this paper was proved to have the best prediction performance under the same parameter conditions. Meanwhile, the clinical performance of the model was verified by Clarke Error Grid Analysis (CEGA), which improved the prediction accuracy of the model with reduced running time and can provide a reference for the research of artificial pancreas closed-loop control algorithm.

However, there are some limitations in this study, first, the prediction effect of data collected by different CGM devices was not compared in this paper, and second, the diabetic patients selected in this paper were all type 2 diabetic patients, and the model needs to be optimized by CGM data from other types of diabetic patients in the future. For the improved wavelet transform threshold denoising algorithm, the values of moderators α and β were selected based on mathematical experience in this paper. In the future, we need to further explore in depth what is the relationship between the values of different moderators α and β and different prediction horizon, how their combination affects the prediction performance of the model, and the IWT-GRU model can be added with features such as exercise, diet and medication status for multi-factor prediction. The model's predictive accuracy can be further improved.

In conclusion, all experiments are for practical clinical application, and the future glucose trend prediction model based on CGM data will still be optimized in the direction of high performance and high efficiency. Meanwhile, with the gradual development of non-contact blood glucose monitoring and non-invasive blood glucose monitoring technologies, the use of a wider range of physiological parameters and data assimilation techniques to establish algorithmic models for multimodal sensor data fusion will be another new research direction for blood glucose trend prediction in the future.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The study was supported by the Key Research and Development Support Plan of Chengdu Science and Technology Bureau (2019-YF09-00185-SN): Demonstration and promotion of diabetes graded linkage management technology and Application based on TCM cloud health platform, and Joint Innovation Fundation of JIICM (2021IR020): Study on remote MDT diagnosis, treatment and management mode of Type 2 diabetes mellitus with Integrated Traditional Chinese and Western Medicine.

Conflict of interest

The authors declare there is no conflict of interest.