1.
Introduction
1.1. Background and motivation
In order to ensure the communication quality, corresponding anti-jamming measures should be adopted according to different jamming [1]. The anti-jamming effect depends on the accurate identification of communication interference types, so the research of communication interference identification has important application value, which has attracted many researchers' attention. The current interference recognition methods include traditional and deep learning-based interference recognition algorithms.
The traditional interference recognition algorithm consists of feature extraction and pattern recognition. The algorithm process is generally as follows: first extract the signal features, such as signal high-order cumulant [2,3], signal space [4,5] and time-frequency domain analysis [6], and then use the pattern recognition algorithm to classify, including decision tree, support vector machine, back propagation neural network and other methods. The rationality of feature selection determines the recognition effect, and the feature selection is related to the cognition of professionals to interference, so human factors have great influence.
The key of interference recognition algorithm based on deep learning lies in data set, which avoids manual feature selection. The data set can be amplitude spectrum [7], IQ dual channel signal [7] and signal time-frequency diagram [8,9,10,11]. Literature [12] proved that convolution neural network (CNN) can extract features with good separability. This algorithm is better than the traditional interference recognition algorithm.
However, the electromagnetic environment is more and more complex, and new types of jamming are emerging. However, the existing algorithms can only recognize the known jamming types, that is, Closed Set Recognition (CSR). When a new type appears, the existing methods identify it as one of the known mistakenly, but cannot identify it as an unknown jamming accurately. Therefore, the Open Set Recognition (OSR) problem of communication jamming signal needs to be solved urgently.
In reference [13], OSR is defined as: the knowledge in training is incomplete, but the algorithm can detect and reject unknown classes samples in the process of testing. OSR methods include traditional machine learning-based methods and deep learning-based methods. The models of the former methods [14,15,16,17] cannot be applied to large-scale raw data without feature extraction, and the latter methods can not only overcome this problem, but also get better results. Open set recognition methods based on deep learning can be divided into two branches: discriminative model and generative model. At present, the proposed discriminative models are almost all for computer vision, text classification and other classification tasks, but cannot be directly applied to noisy signal recognition. The proposed generative models cannot get ideal effect when applied to OSR of noisy signals, because the generative models are reconstructed based on the training samples, when the training samples are noisy signals, the noise greatly affects the reconstruction effect. In order to cope with the OSR of noisy 1-dimensional jamming signals, an OSR network structure with Conditional Gaussian Encoder (CG-Encoder) is proposed, in this paper. CG-Encoder adopts the ResNet network structure [18] as a whole. After the convolution layer, it connects two parallel fully connected layers, which are used to learn the mean and variance of input to get their corresponding latent vectors. At the end, it is a SoftMax classifier. During training, the conditional posterior distributions approximate multiple multivariate Gaussian models, to enhance the discrimination of latent features between the classes and achieve better classification. Then, we obtain the Gaussian probability density thresholds by ensuring 98% training data to be recognized as known and the rest as unknown. When testing, the probability density function thresholds are used to judge whether test samples, which include known and unknown, are unknown. The results show that CG-Encoder algorithm achieves better effect in OSR and CSR recognition.
1.2. Related work
1.2.1. Discriminative model
Bendale et al. [19] proposed the OpenMax model and replaced the SoftMax activation layer in the neural network with the OpenMax layer, which is used to estimate the probability that input images come from unknown classes. This is the first solution for an open set deep network. Prakhya et al. [20] explored open set text categorization along the OpenMax model. Shu et al. [21] replaced SoftMax layer with 1-vs-rest layer, and proposed deep open classifier (DOC) model for text classification. Kardan et al. [22] proposed a COOL (Competitive Overcomplete Output Layer) neural network, and demonstrated the effectiveness of COOL by applying it to high-dimensional images. Dhamija et al. [23] solves the OSR problem by combining SoftMax with novel entropy open set and target ball loss. Shu et al. [24] proposed a joint open classification model to determine whether a pair of samples belong to the same class, where the sub-model can be used as a distance function of clustering to discover hidden classes in rejected samples. But these models cannot be directly applied to noisy signal recognition, which are suitable for computer vision, text classification and etc.
1.2.2. Generative model
Different from the discriminative model, the generative method uses GAN [25], auto-encoder [26] and flow-based model [27] to generate unknown or known samples to help the classifier learn the decision boundary between known and unknown samples. Ge et al. [28] proposed the G-OpenMax algorithm, which is a direct extension of OpenMax, using conditional generative to synthesize unknown classes. This algorithm provides explicit probability estimates of the generative unknown classes, enabling the classifier to locate decision margins based on the knowledge of known classes and generative unknown classes. Unlike G-OpenMax, Neal et al. [29] introduced a new data set enhancement technique called OSRCI, which uses the VAEGAN architecture to generate synthetic open set examples that are close to but not part of any known class. Similar to [29], Jo et al. [30] used GAN technology to generate pseudo data as unknown class data to further enhance the robustness of unknown class classifier. Yoshihashi et al. [31] proposed a Classification-Reconstruction Open Set Recognition (CROSR), which uses latent representations to reconstruct, enabling unknown class detection robustly without compromising the classification accuracy of known classes. Oza and Patel [32] proposed a C2AE model using a class conditional auto-encoder with novel training and testing methods, which uses class conditional auto-encoder to derive the decision boundary from EVT reconstruction errors. Variational Auto-Encoder (VAE) [33] is combined with clustering [34], one class [35] or Gaussian mixed model (GMM) [36] algorithm for OSR. The posterior distribution qϕ(z|x) in latent space is trained to approximate a prior distribution pθ(z), which enables VAE to correctly describe the known data, and the deviated samples will be identified as unknown. Xin et al. [26] provided VAE with a kind of conditional Gaussian distribution learning, which can detect unknown and classify known samples by forcing different latent features to approach different Gaussian models. Zhang et al. [27] proposed a joint embedded space consisting of a classifier and a flow-based density estimator. But these generative models cannot get ideal effect of OSR of noisy signals.
However, the CG-Encoder we propose in this paper not only classifies known jamming types, but also detects an unknown jamming accurately.
1.3. Contributions and structure of the paper
The contributions of this paper are mainly as follows:
● To our knowledge, we are the first to study open set recognition of communication interference signals.
● We propose a new classification model called CG-Encoder. Compared with previous methods based on convolution neural network, the proposed method not only achieves better classification results, but also can be used for unknown detection.
● We found a novel unknown detection method based on probability density function. The proposed algorithm is superior to other detection methods for unknown signals.
● We conduct experiments on nine common classes of communication jamming, and the results show that our method outperform existing methods and achieve new state-of-the-art performance.
The rest of the paper is organized as follows. Section 2 introduces briefly Variational Auto-Encoder (VAE) and Deep Residual Structure. Section 3 discusses Open Set Recognition Algorithm Based on CG-Encoder in detail. Finally, Section 4 gives the algorithm simulations and performance analysis in detail. Finally, Section 5 concludes the paper.
2.
Basic principles
2.1. Variational auto-encoder (VAE)
VAE [33] is generally composed of two neural networks: encoder and decoder. The parameters, input and output of the encoder are ϕ, sample x and latent representation z, respectively. The parameters, input and output of the decoder are θ, z and the probability distribution of samples. The loss function of VAE is as follows:
where DKL(qϕ(z∣x)‖pθ(z)) is the KL-divergence between the approximate posterior distribution qϕ(z|x) and the prior distribution pθ(z) and Eqϕ(z∣x)[logpθ(x∣z)] represents the reconstruction error.
In general, pθ(z) is multivariate standard normal Gaussian, so qϕ(z|x) is a multivariate Gaussian distribution with diagonal covariance matrix:
where the mean µ and the standard deviation σ are the encoding multilayered perceptrons' (MLPs) outputs. z is defined as:
where ξ∼N(0,I), ∙ is the element-wise product. The KL-divergence [18] can be calculated:
where J is the dimensionality of z. By minimizing L(θ,ϕ,x), the VAE is trained not only to reconstruct the input accurately, but also to force qϕ(z|x) in latent space to approximate pθ(z).
2.2. Deep residual structure
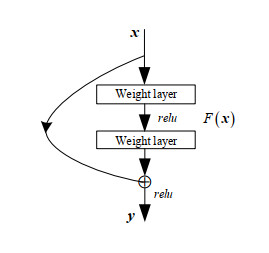
ResNet [18] is a deep residual structure, which is constructed from the basic block shown in Figure 1, it is defined as:
where x and y are the input and output vectors, the function F(W, x) represents the residual map to be learned, and relu is one of the nonlinear operations. The structure in Figure 1 has two layers, then F(W,x)=W2∗relu(W1∗x), where the bias term is ignored to simplify the representation.
The dimensions of x and F(W, x) must be equal in Eq. (5), which can be matched by linear projection Ws.
The form of residual function F is variable, and the trunk of basic block can stack more layers. For the sake of simplicity, the above symbol is about the fully connected layer. In fact, the function F(W, x) can represent multiple convolution layers, and the elements are added channel by channel on two feature maps.
3.
Open set recognition algorithm based on CG-Encoder
In the communication jamming recognition identification, the input sample is 1-dimensional jamming signal x=x0+noise, x0 is the jamming signal with a sampling length of l, and noise is Gaussian white noise with the same length. If the inputs are reconstructed by the usual VAE model, this will be affected by the noise, and the reconstruction loss cannot be used as the condition of unknown detection. Therefore, this paper only uses the encoder network to learn the latent feature distribution of the classes, and judges whether the test samples are known or unknown by their probability density value, so as to realize the unknown detection.
3.1. Design of the CG-Encoder structure
As shown in Figure 2, the structural block diagram of the jamming signal OSR method (CG-Encoder) consists of three modules. Encoder, Classifier, and Detector.
Encoder is a 1-dimensional residual network, which consists of 33 1-dimensional convolution layers (including 16 basic residual blocks), two 1-dimensional pooling layers and two fully connected layers. Its input is x; The outputs are the mean μ and variance σ2 obtained by the two parallel fully connected layers respectively. The nonlinear function softplus is used to ensure that all components of variance are greater than 0.
The input and output dimensions of the residual blocks of the solid shortcut in the Figure 2 are the same, and Eq. (5) is used to calculate output. And the dimensions are not same in the dotted shortcut, and the input and output should map linearly using Eq. (6).
The convolution layer parameters meanings are convolution kernel size, type of convolution layer, number of convolution kernel, and change of the sequence length through that layer. For example, the first layer parameters are {7 × 1 conv1d, 64, /2}, which mean that the layer uses 1-dimensional convolution (conv1d) with convolution kernel size of 7 × 1, the number of convolution kernel is 64, and the jamming sequence length after the layer is shortened by half. The pooling layers are max pool and adapt pool respectively. The former reduces the signal sequence length by half after, and the latter can accept inputs of any length sequence and make the output length fixed, here set a fixed value as 1.
Classifier is a fully connected layer with SoftMax as the activation function. Its input is z obtained by Eq. (3) and its output is a known class label.
Detector is modeled by information hidden in the latent representation z. During testing, the detector is viewed as a binary classifier. When output is 1, x is recognized as unknown jamming, and when output is 0, x is recognized as class y.
3.2. Closed set training phase
In the training phase, qϕ(z|x,k) are forced to approximate multiple multivariate Gaussian distributions pθ,k(z)=N(z;μk,I) for the above proposed model, where k is the index of a known class. μk is output of a fully connected layer and represents the mean vector of the k-th class Gaussian distribution. The KL-divergence (Eq. (4)) is modified as follows:
CG-Encoder has no decoder compared with VAE, so the loss function discards the reconstruction error in Eq. (1) and adds the classification loss
where num is the batch size, K is the number of known classes, zi is the feature of the i-th sample, yi is the class label corresponding to xi, and Wj and bj are the weight and bias of class j.
The loss function of CG-Encoder is
where λ is a constant. The parameters of CG-Encoder are optimized by minimizing the loss function L, and the training method is consistent with the common closed set training method. During training, the latent vector z of correctly classified training set samples is saved for later open set testing to use.
3.3. Open set testing phase
3.3.1. Establishment of multivariate gaussian model
According to the class labels of training samples, the latent vector z is divided into K sets, namely {z1}, {z2}, …, {zK}, each set contains only one class latent representation. The mean vector and covariance matrix of K kinds of multivariate Gaussian distribution models can be obtained from
where mk is the number of samples in {zk}. Furthermore, the probability density function of each kind of jamming signal multivariate Gaussian distribution model can be obtained as follows
where n is the dimension of latent space.
3.3.2. Threshold setting
Because the signal distribution can provide effective information for unknown detection, according to Eq. (12), the probability density values of all latent vectors in K sets {z1}, {z2}, …, {zK}, namely {p1}, {p2}, …, {pK} are calculated and arranged in descent in each set. In a manner similar to Reference [26], the threshold εk is set to less than the probability density of the first 98% and greater the probability density of the last 2%.
3.3.3. Open set test algorithm
The specific steps of the algorithm are as follows:
a) Calculate the latent space distribution model fk(zk) of each known class according to Eqs. (10) - (12).
b) According to section 3.3.2, set the threshold εk of each known class.
c) Input the test jamming sample xt to the trained encoder for obtaining its latent vector zt.
d) The probability density values of the latent vector zt in various Gaussian models fk(zt)=N(zt;μk,Σk),k=1,...,K calculated by Eq. (12).
e) If fk(zt)<εk, the Detector detects xt as unknown, otherwise, it gets its class y through Classifer.
4.
Algorithm simulation and performance analysis
The Adam optimizer with initial learning rate of 0.001 is used, and the batch size is fixed to 256; the dimension n of latent representation z is 32, parameter λ is set to 100.
4.1. Datasets
In order to test the performance of the proposed OSR method, simulation experiments are carried out on 9 kinds of jamming signals, including single-tone jamming, multi-tone jamming, periodic Gaussian pulse jamming, frequency hopping jamming, linear sweeping frequency jamming, second sweeping frequency jamming, BPSK modulation jamming, noise frequency modulation jamming and QPSK modulation jamming. The range of jamming-to-noise rate (JNR) is -10~18dB, with a value taken every 2dB. The additive noise is Gaussian white noise in the signal band. The sampling frequency is 10MHz, the number of sampling points is l, the size of jamming sample is expressed as 1 × l, and the parameters of each jamming type are shown in Table 1.
Figure 3 shows the time domain waveforms of the above 9 jamming signals randomly generated when JNR = 10dB and l = 1024.
4.2. Performance analysis of CSR and OSR
The performance of CSR and OSR of CG-Encoder algorithm and the following three algorithms with JNR of - 10 ~ 18dB is simulated and analyzed.
(1) CNN [12]. The network structure of this algorithm is similar to CG-Encoder, the difference is that there is no shortcut, and only one fully connected layer is connected after convolution layers to get the latent vector z. The threshold of unknown detection is the confidence that makes 98% of the correctly classified training samples known. If the confidence of test sample is greater than the threshold, it is known. If the confidence of test sample is less than the threshold, it is unknown. The model can be regarded as a traditional CNN.
(2) ResNet [18]. The network structure of this algorithm is similar to CG-Encoder, but only one fully connected layer is connected after convolution layers to get the latent vector z. Unknown detection algorithm is the same as CNN. This model can be regarded as a common ResNet structure.
(3) ResNet+G [26]. The network structure of this algorithm is similar to CG-Encoder, the difference is that the posterior distribution of all classes approximates a single multivariate Gaussian distribution. The open set testing phase is the same as section 3.3.3. This model can be regarded as that ResNet learning a multivariate Gaussian model, named ResNet+G.
4.2.1. CSR performance analysis
CSR is usually recognition for known classes, without using unknown detector. Set the number of sampling points to 1024. The training set classes include jam1 ~ jam8, each class has 2000 samples under each JNR, a total of 240000. The testing set classes are also jam1 ~ jam8, with 2000 samples for each category under each JNR. In this paper, the accuracy is used to measure the performance of the algorithm. The experimental results of the four algorithms are shown in Figure 4.
It can be seen from Figure 4 that the closed set recognition accuracy of the four algorithms increases with the increase of JNR. When JNR > -10dB, the accuracy is higher than 88%, and the accuracy is close to 1 when JNR > 0dB, so the recognition performance of four networks for known classes is better. Under the low JNR, CNN performance is slightly inferior to the other three networks. Under the high JNR, ResNet+G performance is slightly inferior to the other three networks. ResNet performance is better than CNN, which shows that shortcut in residual structure can improve recognition performance of known classes. ResNet performance is better than ResNet+G, which indicates that the difference between classes will be reduced by the approximation of posterior distribution to a single Gaussian model. CG-Encoder performance is equivalent to ResNet, which illustrates that the latent distribution of different classes approximates different Gaussian models, which can improve the performance of CSR.
4.2.2. OSR performance analysis
The training set of OSR is consistent with CSR, and jam9 is added to the testing set as the unknown class to verify the unknown detection performance of the four algorithms. The experimental results of OSR are shown in Figure 5.
In the case of OSR, the accuracy of open set recognition increases with the increase of JNR. The CG-Encoder algorithm has the best performance, which proves the OSR effectiveness of the algorithm for noisy jamming signals. When JNR = -10 ~ 0dB, the accuracy is low, which indicates that noise has a great influence on OSR performance. When JNR > 5dB, the change of accuracy is small, and the performance of each algorithm is stable.
When JNR > 0dB, the performance of OSR of network structure is CG-Encoder > ResNet > CNN > ResNet+G, and CG-Encoder is about 2%, 4% and 10% higher than the average accuracy of other three algorithms respectively. CG-Encoder > ResNet+G shows that the latent distribution of different classes approximates different Gaussian models, which not only makes the known classes more separable, but also improves the division between known and unknown classes. ResNet > CNN shows that the shortcut method improves the accuracy of known classes, and also indirectly benefits the performance of OSR. CNN > ResNet+G indicates that when all the latent distributions of all classes belong to one distribution, the unknown class will approach the distribution. Even if residual structure is adopted, the performance of ResNet+G will not be better than that of ordinary CNN network.
4.3. Visual analysis of latent space features
In order to better observe the latent space features of the samples, the dimension of latent representation z is set to 2, and four kinds of algorithm network models are retrained to visualize the latent space that each network learned on the 2-dimensional plane, as shown in Figure 6.
Figure 6 (a), (b), (c) and (d) is the 2-dimensional distribution of latent feature space learned by CNN, ResNet, ResNet+G and CG-Encoder algorithms respectively. Each point represents a sample, in which clusters of known classes are labeled at their corresponding positions, and the unknown class jam9 is represented by black cluster. In fact, the blank area is other unknown classes. It can be seen from Figure (a) and (b) that CNN and ResNet map the features of unknown class to the overlapping place of all known class, which are relatively far away from the center of each known class. As can be seen from Figure (c), ResNet+G network makes the unknown class almost coincide with jam4 and jam8, which is difficult to distinguish. As can be seen from Figure (d), CG-Encoder algorithm completely separates the known classes, whose effect the former three algorithms cannot achieve. Although the unknown class are close to jam4, they only overlap a little, and the Detector can effectively detect the unknown jamming.
4.4. Openness of OSR
Openness is related to the number of training classes Ntrain and the number of test class Ntest. The formula is given in Reference [13]. O=1−√2×NtrainNtrain + Ntest. In the experiment of this section, Ntrain = 2 ~ 8, Ntest = 9. And it means that the unknown class contains 1 ~ 7 different classes. According to the formula of openness, the larger Ntrain, the smaller O, the less unknown information.
Figure 5 shows that the OSR performance of the four algorithms is relatively stable when JNR > 0dB, so the average accuracy between JNR = 0 ~ 18dB is used to analyze the openness of the four algorithms. As shown in Figure 7, the horizontal axis represents the degree of openness. In order to be more intuitive, Ntrain v Ntest is used instead of its corresponding O value. On the whole, the OSR performance of the four algorithms increases with the increase of the number of known class, indicating that the less unknown information, the better the OSR performance. The CG-Encoder algorithm proposed in this paper has the best recognition effect under different openness. When Ntrain=2、Ntest=9, the OSR average accuracy of CG-Encoder algorithm is more than 70%, which is about 30% and 20% higher than CNN and ResNet+G, respectively. When the openness is the minimum, the OSR average accuracy of CG-Encoder algorithm can reach more than 95%.
It can also be concluded from Figure 7, when Ntrain⩽, the recognition performance of ResNet+G is better than that of CNN and ResNet algorithm, while when {N_{train}} \geqslant 5 , the recognition performance of ResNet+G is worse than that of ordinary CNN algorithm, which indicates that the more the number of known classes is, the more confusion between classes caused by using posterior distribution to approximate a single distribution will be, and the more features of each class need to be learned.
5.
Conclusion
In order to solve the problem that the existing jamming signal recognition algorithms mistakenly recognize the unknown class as a known class with a certain probability, a CG-Encoder network structure suitable for 1-dimensional signal OSR is constructed based on ResNet and multivariate Gaussian model. This paper not only defines a reasonable loss function for the training of the network, but also designs a specific OSR process. For nine types of jamming, simulation experiments are carried out under JNR = -10 ~ 18dB. The CSR and OSR performance of CNN, ResNet, ResNet+G and CG-Encoder network algorithms are compared. The feature learning ability of each algorithm is further compared by visualizing the latent space, and the algorithm openness on OSR is analyzed. The results show that CG-Encoder can achieve more than 98% CSR effect when JNR is -6dB, its OSR performance is better than the other three networks, and the OSR accuracy can reach more than 95% when the openness is the smallest.
Acknowledgment
This work was supported by the National Natural Science Foundations of China under grant nos. U19B2016, and Zhejiang Provincial Key Lab of Data Storage and Transmission Technology, Hangzhou Dianzi University.
Conflict of Interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad:









