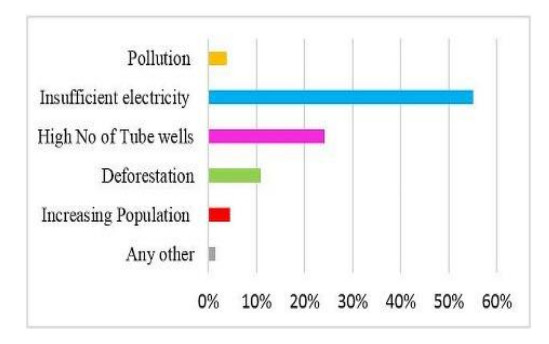
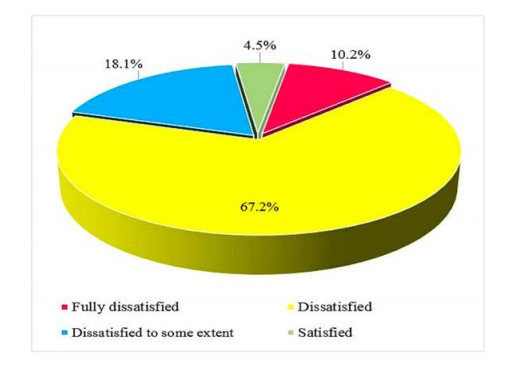
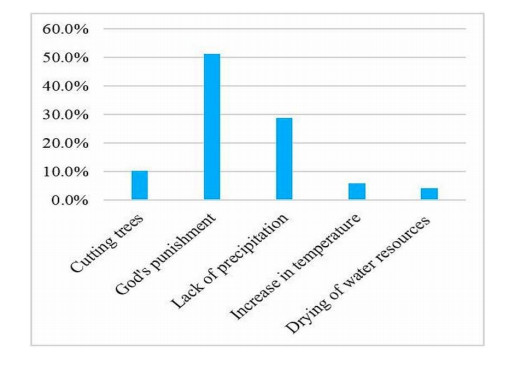
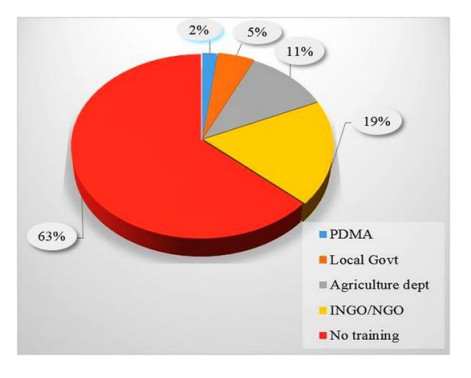
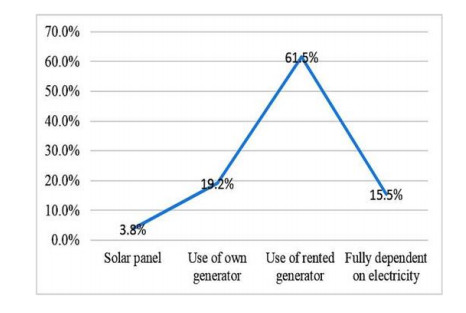
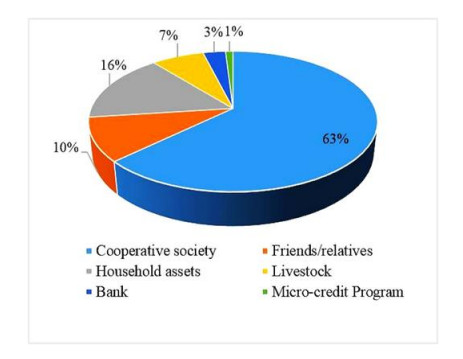
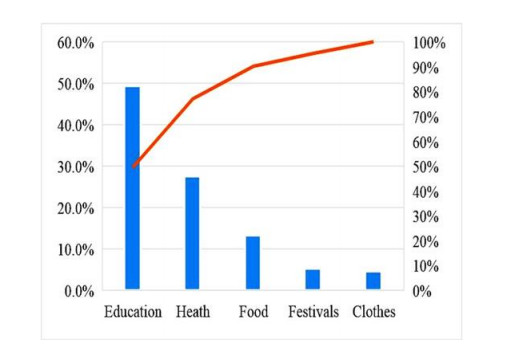
Frequent occurrence of drought is a major challenge to the farmers in the drought prone district of Balochistan province, Pakistan. The agricultural communities are facing threat to agricultural production and livestock due to socio-economic drought in the study area. The Socio-economic drought refers to the conditions in which water supply flops sustaining water demand, resulting in adverse effects on society, economy and environment. The intensity of drought impacts is normally analyzed through meteorological, agricultural and hydrological indices. However, this paper presents a study based on interviews to analyze farmer's risk perceptions, attitude and awareness towards socio-economic drought and risks associated with it. The study relies on a survey of 265 farm households, following a structured questionnaire, focus group discussions and key informant interviews. Results of the study revealed that farmers perceived a continuous variability in climate for the last two decades and identified drought as the most prevalent disaster in the region. Economic reliance on agriculture and livestock, abolishment of surface water resources, depletion of groundwater and insufficient supply of electricity has further increased their vulnerability to drought. Reduction in agriculture and livestock production as well as loss of employment were the immediate economic impacts of the socio-economic drought in the study area. Social impacts such as migration to other places, increase in social crimes, drop out of schoolchildren and impacts on health and festivals were also reported. The environmental impacts included constant increase in temperature, decrease in rainfall intensity and non-climatic factors. Understanding of farmer's risk perception to drought vulnerability may contribute in assisting policy makers for the most appropriate intervention strategies.
1.
Introduction
Kamps [22] introduced the model of GOSs as a unified approach to a variety of ordered random variables (RVs), including ordinary order statistics (OOSs), sequential order statistics (SOSs), progressive type Ⅱ censored order statistics (POSs), order statistics with a non-integer sample size, record values, and Pfeifer's record model. Since the GOSs model unifies the models of ordered RVs, the practical importance of GOSs is evident. For example, in reliability theory, the rth extreme OOS indicates the life-length of an (n−r+1)-out-of-n system, whereas the model of SOSs is an extension of the OOSs model that describes specific dependencies or interactions among system components induced by component failures. Furthermore, the POSs model is a valuable tool for collecting information in lifetime tests.
The uniform GOSs are defined via their joint probability density function (PDF) on a unit cone of Rn. More specifically, let n∈N, k≥1 and m1,m2,...,mn−1∈R be parameters such that γr=k+n−r+∑n−1j=rmj>0, r∈{1,2,...,n−1}.
If the RVs U(r,n,˜m,k)=U⋆r:n,r=1,2,...,n, possess a PDF of the form
on the cone {(u1,u2,...,un):0≤u1≤u2≤...≤un<1}⊂Rn, then they are called uniform GOSs. Furthermore, GOSs based on some distribution function (DF) F can be defined via the quantile transformation X(r,n,˜m,k)=X⋆r:n=F−1(U⋆r:n),r=1,2,...,n, where F−1 denotes the quantile function of F. On the other hand, by choosing the parameters appropriately, we can obtain different models of ordered RVs, such as m-GOSs (m1=m2=...=mn−1=m,γr=k+(n−r)(m+1),r=1,2,...,n); OOSs, a sub-model of m-GOSs (m=0 and k=1); order statistics with non-integral sample size, a sub-model of m-GOSs (m=0,k=α−n+1 and n−1<α∈R); SOSs (mi=(n−i+1)αi−(n−i)αi+1−1,i=1,2,...,n−1,0<αi∈R,k=αn); kth record values (m1=m2=...=mn−1=−1,k∈N); POSs with censoring scheme (R1,R2,...,RM)(mi=Ri,i=1,2,...,M−1, and mi=0,i=M,M+1,...,n−1 and k=RM+1); and Pfeifer's record model (mi=βi−βi+1−1,i=1,2,...,n−1,0<βi∈R and k=βn).
The marginal DF, Ψ(m,k)r:n(x)=P(X⋆r:n≤x), of the rth m-GOS is given in Kamps [22] by
where Cr−1=∏ri=1γi, r=1,2,...,n, γn=k, and ¯F(x)=1−F(x). Moreover, if m≠−1, (m+1)gm(x)=Gm(x)=1−¯Fm+1(x) is a DF, whereas g−1(x)=−log¯F(x). Under the condition m≠−1, the possible limit DFs of the maximum m-GOS and their domains of attraction under linear normalization were derived by Nasri-Roudsari [27]. Moreover, the limit DFs of Ψ(m,k)n:n(x) under power normalization were derived by Nasri-Roudsari [28]. The possible non-degenerate limit DFs and the rate of convergence of the upper extreme m-GOSs were discussed by Nasri-Roudsari and Cramer [29]. The necessary and sufficient conditions for weak convergence as well as the form of the possible limit DFs of extreme, central and intermediate m-GOSs, were derived by Barakat [4].
The bootstrap method, which was first introduced by Efron [20] for independent RVs, is an efficient procedure for solving many statistical problems based on re-sampling from the available data. It enables statisticians to perform statistical inference on a wide range of problems without imposing many structural assumptions on the data-generating random process (cf. [14,21,26]). For example, the bootstrap method is used to find standard errors for estimators, confidence intervals for unknown parameters, and p-values for test statistics under a null hypothesis.
There are several forms of the bootstrap method and additionally several other re-sampling methods that are related to it, such as jackknifing, cross-validation, randomization tests, and permutation tests. Let Xn=(X1,X2,...,Xn) be a random sample of size n from an unknown DF F. The idea of the bootstrap technique is to re-sample with replacement from the original sample Xn and form a bootstrapped version of the original statistic. For B=B(n)→∞, as n→∞, assume that Y1,Y2,...,YB are conditionally independent and identically distributed (i.i.d) RVs with distribution
Hence, (Y1,Y2,...,YB) is a re-sample of size B from the empirical distribution Fn of F based on Xn. Let Pj,j=1,2,...,n, be an independent RV with respective beta distribution Ix(γj,1),j=1,2,...,n. Thus, Pj follows a power function distribution with exponent γj=k+(B−j)(m+1),j=1,2,...,B. Now, in view of the results of Cramer [17], we can write the rth m-GOS based on the empirical DF Fn in the form
Moreover, let
be the bootstrap distribution of a−1n(X⋆n−r+1:n−bn), for suitable normalizing constants an>0 and bn, where n and B are the sample size and re-sample size, respectively.
It has been shown, for many statistics, that the bootstrap method is asymptotically consistent (cf. Efron [20]). That is, the asymptotic distribution of the bootstrap for a given statistic is the same as the asymptotic distribution of the original statistic. Many results for the bootstrap method and its applications can be found in the literature. For instance, the inconsistency, weak consistency and strong consistency for bootstrapping the maximum OOSs under linear normalization were investigated by Athreya and Fukuchi [2] and Fukuchi [21]. They showed that, in a full-sample bootstrap situation, the maximum OOSs fails to be consistent. Later, Barakat et al. [10] extended the results of Fukuchi and Athreya to the GOSs. Barakat et al. [12] obtained similar results for the OOSs with variable ranks as well. Furthermore, bootstrapping OOSs with variable rank under power normalization was investigated by Barakat et al. [13].
The main goal of this paper is to build on the findings of [10] by discussing the consistency of bootstrap central and intermediate GOSs for determining an appropriate re-sample size for known and unknown normalizing constants. Moreover, a simulation study is carried out to explain how the bootstrap sample size can be chosen numerically. This paper is structured as follows. In Section 2, we briefly review the main results concerning the asymptotic behaviour of the m-GOSs with variable rank. Sections 3 and 4 are devoted, respectively, to bootstrapping the intermediate and central m-GOSs. Finally, a simulation study is conducted in Section 5.
We end this section with some motivations that highlight the importance of our work.
Work motivation
The purpose of the bootstrap method is to construct an approximate sampling distribution for the statistic of interest. So, if the statistic of interest Sn follows a certain distribution, we would like our bootstrap distribution SB to converge to the same distribution. If we do not have this, then we can not trust the inferences made. For i.i.d. samples of size n, the ordinary bootstrap method is known to be consistent in many situations, but it may fail in important examples (cf. [10,12,13,21]). Using bootstrap samples of size B, where B→∞ and Bn→0, typically resolves the problem (cf. [10,12,13,21]). However, the choice of B is a key issue for the quality of the convergence (e.g., weak consistency and strong consistency). In this paper, we investigate the strong consistency of bootstrapping central and intermediate m-GOSs for an appropriate choice of re-sample size B for known and unknown normalizing constants. The critical choice problem of B is theoretically addressed in this paper. Furthermore, a simulation study is used to discuss it realistically.
The model of m-GOSs contains two practically important sub-models, OOSs and SOSs, on which this study focuses. For central OOSs and SOSs, one can use the bootstrap method to obtain a confidence interval for the pth population quantile. On the other hand, in many important applications such as flood hazard assessment [18], seismic hazard assessment [1] and analysis of bank operational risk [16], we need an estimator (confidence interval estimate) of an intermediate OOSs (SOSs) quantile. Moreover, it is well known that the asymptotic behavior of intermediate quantiles is one of the main factors in choosing a suitable value of threshold in the peak over threshold (POT) approach and constructing related estimators (the Hill estimators) of the tail index (cf. [9,19]). Therefore, the study of bootstrapping intermediate OOSs will pave the way to use and improve the modeling of extreme values via the POT approach. This potential application of bootstrapping intermediate OOSs will be the subject of future studies.
2.
Auxiliary and preliminary results
In this section, we briefly review the main results concerning the asymptotic behaviour of the intermediate and central m-GOSs, which are related to the present work.
2.1. Intermediate OOSs
The intermediate OOSs have a wide range of important applications. For instance, they can be used to estimate the probabilities of future extreme observations and to estimate tail quantiles of the underlying distribution that are extremes relative to the available sample size (cf. [30]). Furthermore, Pickands [30] has revealed that intermediate OOSs can be applied to construct consistent estimators for the shape parameter of the limiting extremal distribution in the parametric form. Teugels [32] and Mason [25] have also found estimators that are in part based on intermediate OOSs. A sequence {Xrn:n} is called a sequence of intermediate OOSs if rn→n∞ and rnn→n0 (lower intermediate) or rnn→n1 (upper intermediate), where the symbol (→n) stands for convergence as n→∞. Wu [33] (see also, Leadbetter et al. [23]) revealed that, if {rn} is any nondecreasing intermediate rank sequence, and there exist normalizing constants an>0 and bn such that
where w→n stands for weak convergence, as n→∞, Ψ(0,1)n−rn+1:n(x) is the DF of the upper rnth OOS (upper intermediate), and Ψ(0,1)(x) is a nondegenerate DF, then Ψ(0,1)(x) must be one and only one of the types N(Ui;α(x)),i=1,2,3, where N(.) denotes the standard normal DF, and α is a positive constant. Moreover,
and U3;α(x)=U3(x)=x,∀x. Furthermore, (2.1) is satisfied with Ψ(0,1)(x)=N(Ui;α(x)),i=1,2,3, if and only if
In this work we confine ourselves to a very wide intermediate rank sequence which is known as Chibisov's rank, where rnnω→nl2, 0<ω<1; for more details about Chibisov's rank, see ([6,7,15]). When (2.1) is satisfied for this rank, we say that F belongs to the intermediate domain of attraction of Ψ(0,1)(x)=N(Ui;α(x)) and write F∈D(l,ω)(N(Ui;α(x))). The following lemma is needed for studying the asymptotic distributions of the suitably normalized intermediate m-GOSs.
Lemma 2.1. (cf. Barakat [4])Let m>−1. Then, for any nondecreasing intermediate variable rank rn, there exist normalizing constants an>0 and bn such that
if and only if
where Ψ(m,k)(x) is a nondegenerate DF with Ψ(m,k)(x)=N(U(x)), and n⋆=n+km+1−1.
Theorem 2.1. (cf. Barakat [4])Suppose that m>−1, and rn is a nondecreasing intermediate variable rank. Moreover, let r⋆n be a variable rank defined by
where S(n)=rn⋆/(rn⋆/n⋆)1m+1. Then, there exist normalizing constants an>0 and bn for which (2.3) is satisfied for some nondegenerate DF Ψ(m,k)(x) if and only if there are normalizing constants αn>0 and βn for which
where Ψ(0,1)(x) is some nondegenerate DF. Equivalently,
with Ψ(0,1)(x)=N(Ui;α(x)),i=1,2,3. In this case, the normalizing constants an and bn can be chosen as an=αS(n) and bn=βS(n). Furthermore, U(x) in (2.4) takes the form (m+1)Ui;α(x).
2.2. Central OOSs
When the rank sequence rn→n∞ satisfies the regular condition rn=λn+o(√n), where 0<λ<1, rn is referred to as a central rank sequence, and Xrn:n is called central OOSs. There are numerous distinct results for central OOSs and their applications in the literature. Smirnov [31] showed that, if there exist normalizing constants cn>0 and dn such that
where Ψ(0,1)λ(x) is some nondegenerate DF, then Ψ(0,1)λ(x) must be one and only one of the types N(Vi;α(x)),i=1,2,3,4. Moreover,
where c=1√λ(1−λ) and c1=c/A,A>0. In that case, we say that the DF F belongs to the domain of normal λ-attraction of the limit type Vi,α(x),i=1,2,3,4, written F∈D(λ)(Vi;α(x)). Moreover, Smirnov [31] showed that (2.7) is satisfied if and only if
where Cλ=1/c=√λ(1−λ). The following lemma, which is due to Barakat [4], is a cornerstone of the asymptotic theory of central m-GOSs.
Lemma 2.2. (cf. Barakat [4]) Let m>−1. Moreover, let rn be a nondecreasing variable rank such that rn=λn+o(√n). Then, there exist normalizing constants cn>0 and dn such that
if and only if
where Ψ(m,k)λ(x) is a nondegenerate DF with Ψ(m,k)λ(x)=N(V(x)).
Theorem 2.2. (cf. Barakat [4])Let m>−1, and let rn be a nondecreasing variable rank such that rn=λn+o(√n). Then, there exist normalizing constants cn>0 and dn for which (2.9) holds, for some nondegenerate DF Ψ(m,k)λ(x), if and only if, for the same normalizing constants cn and dn, we have F∈Dλ(m)(Vi;α(x)),i=1,2,3,4, where λ(m)=λ1m+1.That is, in view of (2.10), we have
Moreover, Ψ(m,k)λ(x)=N((C⋆λ(m)/C⋆λ)(m+1)Vi(x)), where C⋆t=Ct/t.
3.
Bootstrapping intermediate m-GOSs
In this section, we study the asymptotic behaviour of bootstrapping intermediate m-GOSs with rank sequence rB. In other words, we are interested in the limiting distribution of H(m,k)rB,n,B(x)=  for different choices of the re-sample size B=B(n), when the normalizing constants an and bn are either known or unknown.
for different choices of the re-sample size B=B(n), when the normalizing constants an and bn are either known or unknown.
3.1. Consistency of bootstrapping intermediate m-GOSs when the normalizing constants are known
This subsection investigates the inconsistency, weak consistency and strong consistency of the bootstrap distribution H(m,k)rB,n,B(x) when the normalizing constants are known. More specifically, it is proved in the next theorem that the full-sample bootstrap (i.e., B=n) of H(0,k)rn,n,n(x) fails to be consistent with Ψ(0,k)(x). Moreover, in the same theorem it is shown that if m>0 and B=n, then H(m,k)rn,n,n(x) is a consistent estimator of Ψ(m,k)(x).
Theorem 3.1. Let the relation (2.3) be satisfied with Ψ(m,k)(x)=N((m+1)Ui;α(x)),i=1,2,3. Then,
where d→n stands for convergence in distribution as n→∞, and Z(x) has a normal distribution with mean Ui;β(x) and a variance of one. Moreover, if m>0, then
where p→n stands for convergence in probability as n→∞.
Proof. Since all of the limit types in (2.2) are continuous, the convergence in (2.3) is uniform in x. Therefore, we can write
where ξn(x)→n0 uniformly with respect to x, and B⋆=B+km+1−1→n∞. Suppose now that the condition B=n holds true; then, (3.3) can be expressed as
When m=0, after some routine algebraic calculations we can obtain (3.1), which is the same result of Theorem 4.2 in Barakat et al. [12]. Now, we have to prove (3.2) for m>0 when B=n. Since S(n)→n∞, (2.6) implies
Furthermore, from the central limit theorem we have
On the other hand, from Chibisov [15] and Barakat [4], S(n) can be written in the form S(n)=l2mm+1n1+ωmm+1(1+o(1)), where 0<ω<1 and l>0. Consequently, we get
Moreover, from Barakat [4], it is clear that r⋆S(n)∼S(n)¯F(αS(n)x+βS(n)). Thus, by (3.6) and (3.7), we obtain
Therefore, from (3.5) and (3.8) we get
From (3.9), we can write ¯Fn(αS(n)x+βS(n))=(r⋆S(n)S(n))(1−Ui;α(x)√r⋆S(n)(1+o(1))), which implies
Furthermore, from Barakat [4], it can be noted that r⋆S(n)∼rn⋆ and r⋆S(n)S(n)=(rn⋆n)1m+1. Thus, by using (3.10), we have
where
and
Substituting from (3.12) and (3.13) into (3.11), we get
which proves (3.2), and the proof is completed.
Theorem 3.2. Assume that there exist normalizing constants an>0 and bn from which the relation (2.3) holds, with Ψ(m,k)(x)=N((m+1)Ui;α(x)),i=1,2,3. Let S(B)=o(n). Then
Moreover, if B is chosen such that ∑∞n=1λ√nS(B)<∞, ∀ λ∈(0,1), then
where w.p.1→n stands for convergence with probability one as n→∞ (almost sure convergence).
Proof. By noting that S(B)→n∞, (2.6) implies
Define the statistic Kr⋆S(n),n,B(x) by the relation
Therefore, we get
and
where ˜r⋆S(B)=r⋆S(B)S(B)∼¯F(αS(B)x+βS(B))(1−¯F(αS(B)x+βS(B))). By combining (3.17) and (3.18), we obtain
which proves (3.15). In order to prove (3.16), it is sufficient to show that the convergence in (3.19) is w.p.1. First note that
and
Hence, the convergence in (3.19) becomes w.p.1 if we can show that
By the Borel-Cantelli lemma, it is sufficient to prove that
for every ϵ>0. For every θ>0, we have
where
From Markov's inequality, we get
where MB(θ) denotes the moment generating function of the standard normal distribution. Consequently, for sufficiently large n, we get
By a similar argument, for every ϵ>0, it can be shown that
Since the condition ∑∞n=1λ√nS(B)<∞, ∀ λ∈(0,1), ensures the convergence of the series ∑∞n=1exp{−θϵ√nS(B)} for every ϵ>0, we obtain
From (3.20), we can write
which implies
Therefore, we get
where
and
Consequently,
Thus, (3.16) is proved. This completes the proof.
3.2. Bootstrap consistency of the intermediate m-GOSs with unknown normalizing constants
One of the most important problems in statistical modeling is to reduce the required knowledge about the DF of the population from which the available data is obtained. In the bootstrap method, this situation leads to the case of unknown normalizing constants. In the rest of this section, we investigate the consistency property of the bootstrap intermediate m-GOSs when the normalizing constants are unknown.
Suppose now that the normalizing constants an and bn are unknown, and they are estimated from the sample data, Xn=(X1,X2,...,Xn). Let ˆaB and ˆbB be the estimators of an and bn, based on Xn, respectively, and
be the bootstrap distribution of Ψ(m,k)n−rn+1:n(anx+bn) with the estimated normalizing constants, ˆaB and ˆbB. The sufficient conditions for ˆH(m,k)rB,n,B(x) to be consistent are explored in the next theorem. The idea of this theorem was originally given in Theorem 2.6 for maximum OOSs in [21].
Theorem 3.3. Assume that ˆaB,ˆbB and B=B(n) are such that the following three conditions are satisfied:
Then,
Moreover, if we replace "w.p.1→n" with "p→n" in the conditions (C1)–(C3), the convergence (3.22) remains true.
Proof. First, we note that the condition (C1) is equivalent to
Furthermore, ∀ ϵ>0, the conditions (C2) and (C3) imply
and
respectively. By fixing x>0, the relations (3.23) and (3.24) yield
Therefore,
Since U(x) is continuous, we get
For x<0, the same limit relation can be accomplished using a similar argument. Consequently, (3.22) is proved. If the conditions (C1)–(C3) hold in probability, then for any subsequence {ni}∞i=1, there exists a subsequence {ni∗}∞i∗=1, such that the conditions (C1)–(C3) hold w.p.1. An application of the first part of the theorem, based on the new subsequence, yields
This completes the proof of the theorem.
In the next theorem, an appropriate choice of estimators of the normalizing constants which satisfy conditions (C2) and (C3) of Theorem 3.3 is accomplished for each domain of attraction. More specifically, we get a specific choice of ˆaB and ˆbB from which (3.22) holds true.
Theorem 3.4. Assume that r⋆′n=nS(B)r⋆S(B), r⋆″n=nS(B)(r⋆S(B)+√r⋆S(B)), xo is the right endpoint of F, and ˆxo=Xr⋆n:n. The estimators ˆaB and ˆbB can be chosen, respectively, as
(i) ˆaB=ˆxo−F−1n(r⋆S(B)S(B))=Xr⋆n:n−Xr⋆′n:n and ˆbB=Xr⋆n:n, if F∈D(l,ω)(N((m+1)U1;α(x))),
(ii) ˆaB=F−1n(r⋆S(B)S(B))=Xr⋆′n:n and ˆbB=0, if F∈D(l,ω)(N((m+1)U2;α(x))),
(iii) ˆaB=F−1n(r⋆S(B)+√r⋆S(B)S(B)−r⋆S(B)S(B))=Xr⋆′n:n−Xr⋆″n:n and ˆbB=F−1n(r⋆S(B)S(B))=Xr⋆′n:n, if F∈D(l,ω)(N((m+1)U3(x))).
Moreover, If S(B)=o(n), then
Furthermore, if ∑∞n=1λ√nS(B)<∞ for each λ∈(0,1), then (3.25) holds w.p.1.
Proof. Let F∈D(l,ω)(N((m+1)U1;α(x))). In order to prove conditions (C2) and (C3), we have to show that
and
both in probability or w.p.1. Firstly, let us consider the case of convergence in probability. Clearly,
Hence, (3.26) and (3.27) are proved if we can show that
and
On the other hand, for any γ>0, Lemma 3.1 in Barakat et al. [11] reveals that
where μ(n)=exp(√n). Thus, (3.28) is proved. Turning now to prove (3.29), it can be noted that
For every ϵ>0, (3.30) implies P(Xr⋆′n:n−xoaB<ϵ−1)→nN(∞)=1, or equivalently,
Similarly,
By combining (3.31) and (3.32), we get
which proves (3.29). Now, let F∈D(l,ω)(N((m+1)U2;α(x))). Condition (C3) of Theorem 2.4 is clearly proved (since ˆbB=0). Consequently, it is sufficient to prove only condition (C2). Thus, we have to show that
in probability or w.p.1. We start by proving the convergence in probability. It is clear that,
For every ϵ>0, (3.35) implies P(Xr⋆′n:naB<ϵ+1)→nN(∞)=1, which is equivalent to
Arguing similarly, we get
Based on the relations (3.36) and (3.37), we get
which proves (3.34). Finally, assume that F∈D(l,ω)(N((m+1)U3(x))). By Theorem 2.4, in order to prove conditions (C2) and (C3), it suffices to show that
and
both in probability or w.p.1. We start with the convergence in probability. Write
Consequently, to prove (3.39) and (3.40), we need to show that
and
First, we are going to prove (3.42). Since we have
from the assumption of the theorem, we have
Consequently,
Thus, for every ϵ>0, we get P(Xr⋆″n:n−bBaB<ϵ−1)→nN(∞)=1, and this implies
Further, we have
Hence, (3.45) and (3.46) lead to
which proves (3.42). Secondly, we are going to prove (3.43). Clearly,
For every ϵ>0, Eq (3.47) leads to P(Xr⋆′n:n−bBaB<ϵ)→nN(∞)=1, which yields
In the same way, we get
Thus, relations (3.48) and (3.49) imply
which proves (3.43). Finally, in the proof of Parts (ⅰ)–(ⅲ), in order to switch to the convergence w.p.1, we argue in the same way that we did at the end of Theorem 3.3's proof. This completes the proof of the theorem.
4.
Bootstrapping central m-GOSs
In this section, the asymptotic behaviour of the bootstrap distribution for central m-GOSs, H∗(m,k)rB,n,B(x)=P(Y⋆B−rB+1:B−dBcB≤x|Xn), is considered for different choices of the re-sample size B=B(n) when the normalizing constants cn and dn are assumed to be known or unknown.
4.1. Bootstrap consistency of the central m-GOSs with known normalizing constants
The next theorem discusses the consistency of the bootstrap distribution H∗(m,k)rB,n,B(x) in the case of full-sample bootstrap. It is revealed that the full-sample bootstrap distribution fails to be a consistent estimator of the DF Ψ(m,k)λ(x).
Theorem 4.1. Assume that the relation (2.9) is satisfied, where the weak limits are of the form
Then,
where Λ(x) has a normal distribution with mean C⋆λ(m)C⋆λ(m+1)Vi;α(x) and variance C⋆λ(m)C⋆λ(m+1).
Proof. Although the convergence in (2.9) does not yield continuous types in general, under the condition rn=λn+o(√n), Barakat and El-Shandidy [5] showed that the convergence is uniform. Consequently,
where ξn(x)→n0 uniformly with respect to x. Now, consider that the condition B=n holds. Since (2.8) is satisfied, we have
An application of the central limit theorem yields
where Z(x) is the standard normal RV. On the other hand, it is clear from relation (4.3) that ¯F(cnx+dn)→nλ(m), which implies
The two limit relations (4.3) and (4.5) enable us to apply Khinchin's type theorem on the relation (4.4) to get
As a result of (4.6), we get
Consequently,
Hence, the theorem is proved.
Theorem 4.2. Under the same conditions of Theorem 4.1, if B=o(n), then
Furthermore, if B is such that ∑∞n=1P√nB<∞, ∀ P∈(0,1), then
Proof. Write H∗(m,k)rB,n,B(x)=N(Sn,B(x))+ξn(x), where, Sn,B(x)=√B(λ(m)−¯Fn(cBx+dB)Cλ(m)), and ξn(x)→n0 uniformly with respect to x. It can be noted that
and
Accordingly,
We'll now show that the convergence in (4.12) is w.p.1. For this purpose, write
On the other hand, the assumptions of the theorem ensure that ¯F(cBx+dB)→nλ(m), and √B(λ(m)−¯F(cBx+dB)Cλ(m))→nVi;α(x). To prove the limit relation √B(λ(m)−¯Fn(cBx+dB)Cλ(m))w.p.1→nVi;α(x), it is sufficient to show that
According to the Borel-Cantelli lemma, we need to show that, for every ϵ>0,
For every θ>0, we have
where Tn,B is defined by
From Markov's inequality, we get
Consequently, for sufficiently large n, we get
By using the same method, we can show that, for every ϵ>0,
Since the condition, ∑∞n=1P√nB<∞, ∀ P∈(0,1), assures the convergence of the series ∑∞n=1exp{−θϵ√nB} for every ϵ>0, we have
Therefore,
Accordingly,
which was to be proved, and this completes the proof of the theorem.
4.2. Bootstrap consistency of the central m-GOSs for unknown normalizing constants
Assume that the normalizing constants cn and dn are unknown and that they must be estimated using the sample data Xn=(X1,X2,...,Xn). Let ˆcB and ˆdB be the estimators of cn and dn based on Xn and ˆH∗(m,k)rB,n,B(x)=P(Y⋆B−rB+1:B−ˆdBˆcB≤x|Xn) be the bootstrap distribution for appropriately normalized central m-GOSs. The next theorem gives sufficient conditions for ˆH∗(m,k)rB,n,B(x) to be consistent, where we restrict ourselves to the first three non-degenerate types, corresponding to Vi;α(x),i=1,2,3. Clearly, each of these three limit laws has at most one discontinuity point of the first type.
Theorem 4.3. Suppose that the conditions of Theorem 4.2 are satisfied. Moreover, suppose that ˆcB, ˆdB, and B=B(n) satisfy the following three conditions:
Then, supx∈Rc|^H∗(m,k)rB,n,B(x)−Ψ(m,k)λ(x)|w.p.1→n0, where Rc∈R is the set of all continuity points of Ψ(m,k)λ(x). Moreover, this theorem holds if "w.p.1→n" is replaced by "p→n".
Proof. The proof of the theorem is similar to the proof of Theorem 3.3.
Now, for the consistency of the bootstrap distribution ˆH∗(m,k)rB,n,B(x), the next theorem gives a proper choice for the normalizing constants ˆcB and ˆdB satisfying conditions (K2) and (K3) in Theorem 4.3 for each domain of attraction of N(C⋆λ(m)C⋆λ(m+1)Vi;α(x)),i=1,2,3.
Theorem 4.4. Let r′n=[λ(m)n]+1, r″n=[n√B+n]+1, and r‴n=[λ(m)n−n√B]+1. Then,
i. ˆcB=F−1n(λ(m)+1√B)−F−1n(λ(m))=Xr″n:n−Xr′n:n, and ˆdB=F−1n(λ(m))=Xr′n:n, if F∈Dλ(m)(N(V1;α(x)));
ii. ˆcB=F−1n(λ(m))−F−1n(λ(m)−1√B)=Xr′n:n−Xr‴n:n, and ˆdB=F−1n(λ(m))=Xr′n:n, if F∈Dλ(m)(N(V2;α(x)));
iii. ˆcB=F−1n(λ(m)+1√B)−F−1n(λ(m))=Xr″n:n−Xr′n:n, and ˆdB=F−1n(λ(m))=Xr′n:n, if F∈Dλ(m)(N(V3;α(x))).
Moreover, if B = o(n), then
Finally, if \sum_{n = 1}^{\infty}P^{\sqrt{\frac{n}{B}}} < \infty for each P \in (0, 1), then the convergence in (4.15) holds w.p.1.
Proof. Let F\in D^{\lambda_{(m)}}(\mathcal{N}(V_{1;\alpha}(x))). In view of Theorem 4.3, we need to show that
and
both in probability or w.p.1. We start with the convergence in probability. Clearly,
To prove (4.16) and (4.17), it is sufficient to show that
and
We will start by proving (4.18). In view of the relations \left[\frac{n}{\sqrt{B}}+\lambda_{(m)} n\right] = \frac{n}{\sqrt{B}}+\lambda_{(m)} n-\delta and \frac{1}{\sqrt{B}}+\lambda_{(m)} +\frac{1-\delta}{n}\sim \lambda_{(m)} for 0\leq \delta < 1, we get
Relation (4.20) is a direct consequence of the obvious relations,
The relation (4.20) yields P\left(\frac{X_{r^{''}_{n}:n}-d_{B}}{c_{B}} < \epsilon+1\right)\xrightarrow[\; \; n\; \; ]{}\mathcal{N}(\infty) = 1, which is equivalent to
Similarly, we get
From (4.21) and (4.22), we get P\left(\left|\frac{X_{r^{''}_{n}:n}-d_{B}}{{c}_{B}}-1\right| > \epsilon\right)\xrightarrow[\; \; n\; \; ]{}0, which proves (4.18). Now, we are going to prove (4.19). It is simple to derive that
Thus, from (4.23), we have P\left(\frac{X_{r^{'}_{n}:n}-d_{B}}{c_{B}} < \epsilon\right)\xrightarrow[\; \; n\; \; ]{}\mathcal{N}(\infty) = 1, which is equivalent to
Similarly, we get
Therefore, by combining the relations (4.24) and (4.25), we get P\left(\left|\frac{X_{r^{'}_{n}:n}-d_{B}}{{c}_{B}}\right| > \epsilon\right)\xrightarrow[\; \; n\; \; ]{}0, which proves (4.19). This completes the proof of Part ⅰ. Now, let F(c_nx+d_n)\in D^{\lambda_{(m)}}(\mathcal{N}(V_{2;\alpha}(x))). It is sufficient to establish from Theorem 4.3 that
and
both in probability or w.p.1. We begin with the situation of probability convergence, and we begin with
Hence, to prove (4.26) and (4.27), it is sufficient to show that
and
We are going to prove (4.28). By applying the relations [\lambda_{(m)}n-\frac{n}{\sqrt{B}}] = \lambda_{(m)}n-\frac{n}{\sqrt{B}}-\delta, \; 0 \leq\delta < 1, and \lambda_{(m)}-\frac{1}{\sqrt{B}} +\frac{1-\delta}{n}\sim \lambda_{(m)}, as n\to\infty, we can deduce that
Thus, on account of (4.30), we get P\left(\frac{X_{r^{'''}_{n}:n}-d_{B}}{c_{B}} < \epsilon-1\right)\xrightarrow[\; \; n\; \; ]{}{}\mathcal{N}(\infty) = 1, which implies
In a similar vein, we have
From (4.31) and (4.32), we get P\left(\left|\frac{X_{r^{'''}_{n}:n}-d_{B}}{{c}_{B}}+1\right| > \epsilon\right)\xrightarrow[\; \; n\; \; ]{}0. Hence, (4.28) is proved. We turn now to prove (4.29). We start with the obvious limit relation
which in turn implies that P\left(\frac{X_{r^{'}_{n}:n}-d_{B}}{c_{B}} < \epsilon\right)\xrightarrow[\; \; n\; \; ]{}\mathcal{N}(\infty) = 1, and hence
Moreover, the limit relation (4.33) yields
By combining (4.34) and (4.35), we get P\left(\left|\frac{X_{r^{'}_{n}:n}-d_{B}}{{c}_{B}}\right| > \epsilon\right)\xrightarrow[\; \; n\; \; ]{}0, which proves (4.29).
Finally, consider the case F\in D^{\lambda_{(m)}}(\mathcal{N}(V_{3;\alpha}(x))). From Theorem 4.3, it suffices to show that
and
both in probability or w.p.1. We first focus on the case of the convergence in probability, and we start with
Therefore, to prove (4.36) and (4.37), it is sufficient to show that
and
By proceeding in the same manner that we did in Parts ⅰ and ⅱ, we can easily show that
Relation (4.40) yields P\left(\frac{X_{r^{''}_{n}:n}-d_{B}}{c_{B}} < \epsilon+1\right)\xrightarrow[\; \; n\; \; ]{}\mathcal{N}(\infty) = 1, which is equivalent to
Similarly, we get
The two limit relations (4.41) and (4.42) yield
which in turn proves (4.38). On the other hand, the proof of the relation (4.37) follows also by proceeding as we did in Parts i and ii. Finally, in order to transfer to the convergence w.p.1 in Parts ⅰ–ⅱ, we argue in the same way we did at the end of the proof of Theorem 3.3. The proof of the theorem is now completed.
5.
Simulation study
In this section, a simulation study is conducted to explain how we can choose the bootstrap re-sample size B numerically, relying on the best fit of the bootstrapping DF of central and intermediate quantiles for different ranks. More specifically, we apply the Kolmogorov-Smirnov (K-S) goodness of fit test to test the null hypothesis H_0: The central (intermediate) quantiles follow a normal distribution at a 5% significance level. Moreover, we repeat the K-S test many times for different values of B and then select the value of B that corresponds to the largest average p -value for the fit. See Tables 1–3.
In this simulation, three m -GOSs sub-models based on the standard normal distribution are considered. Namely, these are OOSs ( \gamma_i = n-i+1 ), SOSs with m = 1 (i.e. \gamma_i = 2(n-i)+1 ) and SOSs with m = 2 (i.e., \gamma_i = 3(n-i)+1 ). Moreover, the full sample size is n = 20,000 (if we enlarge the sample size, the running time becomes very long, especially for the SOSs model), the number of replicates is M = 1000 , the central ranks are \lambda = 0.25 and \lambda = 0.5, for the re-sample bootstrap, B = 100 - 400(50) , and we choose the intermediate rank to be r_{n} = \sqrt{n}. The results are presented in Tables 1 and 2.
This study relies on the fact that the sample central and intermediate quantiles based on the standard normal distribution weakly converge to the normal distribution. Moreover, according, to the results of Sections 3 and 4, we expect that the bootstrapping DFs of central and intermediate quantiles converge to the normal distribution provided that B \ll n (i.e., B = o(n) ) for central ranks and S(B) \ll n (i.e., S(B) = o(n) ) for intermediate ranks. Moreover, based on the K-S test for normality and the corresponding p -values, the best value of B for central ranks (that corresponds to the largest p -value) should be chosen such that \sum_{n = 1}^{\infty}\lambda^{\sqrt{\frac{n}{B}}} < \infty, \forall \lambda\in(0, 1), while the best value of B for intermediate ranks should chosen such that \sum_{n = 1}^{\infty}\lambda^{\sqrt{\frac{n}{S(B)}}} < \infty, \forall \lambda\in(0, 1) (see Remark 5.3).
The simulation study is implemented by Mathematica 12.3 via the following algorithm:
Step 1. Select the m -GOSs model. That is, choose the values of \gamma_i .
Step 2. Generate an ordered sample of size n = 20000 , say {\bf{X}}_n , based on the standard normal distribution by the algorithm of Barakat et al. [8].
Step 3. Choose the central or intermediate rank.
Step 4. Select the bootstrap re-sample size B.
Step 5. Select M random samples, each of which is size B, from {\bf{X}}_n with replacement.
Step 6. Compute the quantile of each sample, and store them in Q_B .
Step 7. By using the K-S test, check the normality of the data sets Q_B to the normal distribution and then compute the p -value.
Step 8. Repeat Steps 5–7 many times (100 times) for each chosen value of B and then compute the average p -value.
Step 9. Repeat Steps 4–8 for different values of B , and then pick the largest average p -value and the corresponding value of B .
Remark 5.1. In the earlier version of this paper, in order to implement Step 7 of the previous algorithm, we fitted the data sets Q_B to the normal DF by using the K-S test after calculating the sample mean and standard deviation. However, we noted an important issue that the K-S test can be used to fit the normal distribution only when parameters are not estimated from the data (cf. [24]). Since our focus here is only on checking the normality of the bootstrap samples, we apply the K-S test to check the normality of the given sample bootstrapping statistics without estimating any parameters.
Remark 5.2. According to the results presented in Tables 1 and 2, it is noted that for n = 20000, the largest average p -values for selected central ranks are always achieved at B , which falls in the interval [100–200]. Moreover, the best average p -values for selected intermediate ranks are achieved at B falling in the interval [200–300]. However, it is shown that the accuracy of the goodness of fit depends on both the selected GOSs model and the selected ranks. Moreover, in view of the results given in Table 3, the average p -value for intermediate OSs increases as the sample size increases with the same bootstrap re-sample size.
Remark 5.3. Based on the results of Sections 3 and 4, the best performance of the bootstrapping DFs of the central m-GOSs occurs at the values of B for which \sum_{n = 1}^{\infty}\lambda^{\sqrt{\frac{n}{B}}} < \infty, \forall \lambda\in(0, 1) . On the other hand, according to [2], the condition \sqrt{B} = o(\frac{2\sqrt{n}}{\log n}) is a sufficient condition for \sum_{n = 1}^{\infty}\lambda^{\sqrt{\frac{n}{B}}} < \infty, \forall \lambda\in(0, 1), which implies that the best performance of the bootstrapping DFs of the central OSs occurs when B\ll800. Moreover, in the case of intermediate m-GOSs, the condition \sqrt{S(B)} = o(\frac{2\sqrt{n}}{\log n}) is a sufficient condition for \sum_{n = 1}^{\infty}\lambda^{\sqrt{\frac{n}{S(B)}}} < \infty, \forall \lambda\in(0, 1), which implies that the best performance of the bootstrapping DFs of intermediate m-GOSs occurs when S(B)\ll800. Since in our study we choose the intermediate rank r_{n} = \sqrt{n}, this implies B\ll7500. Therefore, the simulation output endorses this anticipated result.
6.
Conclusions
The bootstrap method is an efficient procedure for solving many statistical problems based on re-sampling from the available data. For example, the bootstrap method is used to find standard errors for estimators, confidence intervals for unknown parameters, and p-values for test statistics under a null hypothesis. One of the desired properties of the bootstrapping method is consistency, which guarantees that the limit of the bootstrap distribution is the same as the distribution of the given statistic. In this paper, we investigated the strong consistency of bootstrapping central and intermediate m -GOSs for an appropriate choice of re-sample size for known and unknown normalizing constants. Finally, a simulation study was conducted to to explain how we can choose the bootstrap re-sample size B numerically, relying on the best fit of the bootstrapping DF of central and intermediate quantiles for different ranks.
Acknowledgments
The authors are grateful to the editor and anonymous referees for their insightful comments and suggestions, which helped to improve the paper's presentation.
Conflict of interest
All authors declare no conflict of interest in this paper.









 for different choices of the re-sample size
for different choices of the re-sample size  DownLoad:
DownLoad: