1. Introduction
The extensive use of fossil fuels has led to the aggravation of environmental problems and the rapid depletion of natural reserves. To sustain the future development of human society, green and renewable processes to produce fuels and chemicals have to be explored. The U.S. Department of Energy has set goals to provide 30% of transportation fuels with biofuels, and to produce 25% of industrial chemicals from biomass by 2025 [1]. Though there are some successes in these aspects [2,3,4,5,6,7,8,9,10], most of chemicals are still not accessible from carbohydrates directly. To expand the scope of renewable chemicals, it is necessary to develop and optimize novel biosynthetic pathways to enlarge the metabolite repertoire of living systems.
Although there is no isobutyrate overproducer found in nature, it is possible to introduce an artificialsynthetic metabolic pathway in E. coli to enable the production in light of our previous works [11]. Isobutyrate is an importantplatform chemical that is currentlyused to high volume industrial chemicals (more than 100 million pounds annually) such as emulsifier sucrose acetate isobutyrate, plasticizer 2,2,4-trimethyl-1,3-pentanediol monoisobutyrate (Texanol) or diisobutyrate (TXIB) [12,13]. Moreover, isobutyrate can be converted to 3-hydroxyisobutyrate by some microorganisms [14]. Since methacrylic acid is chemically obtained by either catalytic oxidative dehydrogenation of isobutyrate [15] or dehydration of 3-hydroxyisobutyric acid [16], biosynthesis of isobutyrate or 3-hydroxyisobutyrate will enable the sustainable production of the blockbuster molecule methyl methacrylate (MMA), an ester of methacrylic acid. MMA is produced in the quantity of 6 billion pounds annually for the synthesis of plastic materials such as polymethyl methacrylate (PMMA) [17].
The firstgeneration E. coli strain we developed produced 11 g/isobutyrate from 40 g/L glucose in shake flask. The yield is 0.29 g/g glucose, only 59% of the theoretical maximum. Thus two concerns have to be immediately addressed for this process to be industrially relevant. Firstly, it is necessary to increase the carbon conversion from glucose to reduce the cost of raw material. Secondly, whether or not this process can be scaled up by a bioreactor determines its viability for the industrialproduction. In the present study, these challenges were solved by improving the engineered strains and optimizing the fermentation conditions.
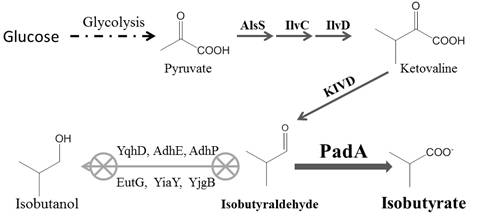
A major byproduct of fermentation is isobutanol, with a level of 0.8 g/L representing a loss of 8.1% of the target isobutyrate product. As shown in Figure 1, the synthetic pathway starts from biosynthesis of ketovaline, which is converted to isobutyraldehyde by KIVD decarboxylase. Isobutyraldehyde is then oxidized into the target product isobutyrate by a promiscuous phenylacetaldehyde dehydrogenase (PadA). However, endogenous alcohol dehydrogenases can compete with PadA and hence reduce the oxidation of isobutyraldehyde to isobutanol. There are six predicted alcohol dehydrogenases (AdhE, AdhP, EutG, YiaY, YqhD, and YjgB) in E. coli [18]. Except for YqhD, the other five dehydrogenases have not been characterized regarding their capabilities to produce isobutyrate. Our previous work demonstrated that yqhD knockout significantly reduced isobutanol accumulation and increased isobutyrate production [11]. Herein, two strategies were employed to further improve the yield of isobutyrate: inactivating one or more of the remaining five dehydrogenases and enhancing the cellular activity of aldehyde dehydrogenase PadA.
2. Materials and Methods
2.1. Bacterial strains and plasmids
All primers were from Eurofins MWG Operon and were listed in Table 1. The E. coli strains used in this study were listed in Table 1, and derived from the wild-type E. coli K-12 strain BW25113 with yqhD deletion. All cloning procedures were carried out in the E. coli strain XL10-gold (Stratagene). Plasmids pIBA1 and pIBA7 used to produce isobutyrate were from previous works [11]. To construct the pIBA11 plasmid carrying two copies of padA, the padA gene was amplified by PCR with oligos padA_SacIfwd and padA_SacIrev, digested with SacI and then ligated into pIBA7. In pIBA11, another copy of padA was in the same operon with ampicillin resistance gene bla, under the regulation of a constitutive promoter. IBA1 strain with yqhD deletion was used as the start strain. Strains with their respective adhE, adhP, eutG, yiaY or yjgB deletion were obtained from the Keio collection [19]. The P1 phages were used to transfect the above each deletion into the IBA1 strain to construct double knockout strains according to the method provided by manufacturer. All knockout strains were then transformed with pCP20 plasmid to remove the kanamycin marker. The correct knockouts were verified by PCRs using detection primers listed in Table 1. To produce isobutyrate, each of knockout strains was transformed with plasmids pIBA1 plus pIBA7, or pIBA1 plus pIBA11.
Table 1. Strains, plasmids and primers used in this study
|
Name
|
Relevant genotype
|
Reference
|
|
Strains
|
|
|
|
BW25113
|
rrnBT14 ΔlacZWJ16 hsdR514 ΔaraBADAH33 ΔrhaBADLD78
|
[20]
|
|
IBA1
|
BW25113 ΔyqhD
|
[11]
|
|
IBA11
|
BW25113 ΔyqhD ΔadhE
|
This work
|
|
IBA12
|
BW25113 ΔyqhD ΔadhP
|
This work
|
|
IBA13
|
BW25113 ΔyqhD ΔeutG
|
This work
|
|
IBA14
|
BW25113 ΔyqhD ΔyiaY
|
This work
|
|
IBA15
|
BW25113 ΔyqhD ΔygjB
|
This work
|
|
IBA1-1C
|
BW25113 ΔyqhD + pIBA1 and pIBA7
|
This work
|
|
IBA11-1C
|
BW25113 ΔyqhD ΔadhE + pIBA1 and pIBA7
|
This work
|
|
IBA12-1C
|
BW25113 ΔyqhD ΔadhP + pIBA1 and pIBA7
|
This work
|
|
IBA13-1C
|
BW25113 ΔyqhD ΔeutG + pIBA1 and pIBA7
|
This work
|
|
IBA14-1C
|
BW25113 ΔyqhD ΔyiaY + pIBA1 and pIBA7
|
This work
|
|
IBA15-1C
|
BW25113 ΔyqhD ΔygjB + pIBA1 and pIBA7
|
This work
|
|
IBA1-2C
|
BW25113 ΔyqhD + pIBA1 and pIBA11
|
This work
|
|
IBA13-2C
|
BW25113 ΔyqhD ΔeutG + pIBA1 and pIBA11
|
This work
|
|
IBA14-2C
|
BW25113 ΔyqhD ΔyiaY + pIBA1 and pIBA11
|
This work
|
|
IBA15-2C
|
BW25113 ΔyqhD ΔygjB + pIBA1 and pIBA11
|
This work
|
|
plasmids
|
|
|
|
pIBA1
|
p15A ori, KanR, PLlacO1::alsS ilvD
|
[11]
|
|
pIBA7
|
ColE1 ori, AmpR, PLlacO1::kivD padA
|
[11]
|
|
pIBA11
|
ColE1 ori, AmpR, PLlacO1::kivD padA padA
|
This work
|
|
Primers
|
|
|
|
adhEKOC-F
|
TTGCTTACGCCACCTGGAAGT
|
|
adhEKOC-R
|
GAACGGTCGCATGAGCAGAAAG
|
|
adhPKOC-F
|
TGACGATAATTTCTGGCAAGC
|
|
adhPKOC-R
|
GCAGGCTGACATTAAGTTCGT
|
|
eutGKOC-F
|
AGATTTGGCCTGCGGTGAAA
|
|
eutGKOC-R
|
CTGTTAGTTGTTATTTATTGGCGG
|
|
yiaYKOC-F
|
CATTTATTGCGCGACGCATTAT
|
|
yiaYKOC-R
|
ATAGCGGGCTTTTAACTTGAGG
|
|
yjgBKOC-F
|
CACTGAAGAGGTATGCGGAAAA
|
|
yjgBKOC-R
|
CTGGGCATTTTATGCCGGTAG
|
|
padA_SacIfwd
|
ctagtagagctcaAGGAGATATACCatgacagagccgcatgtagc
|
|
padA_SacIrev
|
GACTATGAGCTCTTAATACCGTACACACACCGACTTAGTT
|
2.2. Cell cultivation and shake flask fermentation
Unless otherwise stated, cells were grown in test tubes at 37 °C in 2×YT rich medium (16 g/L Bacto-tryptone, 10 g/L yeast extract and 5 g/L NaCl) supplemented with 100 mg/L ampicillin and 50 mg/L kanamycin. 200 μL of overnight cultures were transferred into 5 ml M9 minimal mediasupplemented with 5 g/L yeast extract, 40 g/L glucose, 100 mg/L ampicillin and 50 mg/L kanamycin in 125 ml conical flasks. Isopropyl-β-D-thiogalactoside (IPTG) was added at a final concentration of 0.1 mM to induce the overexpression of introduced genes for the production of isobutyrate. The fermentation broth was buffered by the presence of 0.5 g CaCO3. Fermentation was carried out in a shake incubator with a vigorous agitation at250rpm, 30 °C.
2.3. Culture media in the fermentor
The seeding medium for E. coli culture, in grams per liter, is as follows: glucose, 10; (NH4)2SO4, 1.8; K2HPO4, 8.76; KH2PO4, 2.4; sodium citrate, 1.32; yeast extract, 15; ampicillin, 0.1; kanamycin, 0.05. Fermentation medium for fermentor contains the following composition, in grams per liter: glucose, 30; (NH4)2SO4, 3; K2HPO4, 14.6; KH2PO4, 4; sodium citrate, 2.2; yeast extract, 25; MgSO4. 7H2O, 1.25; CaCl2. 2H2O, 0.015, calcium pantothenate, 0.001; Thiamine, 0.01; ampicillin, 0.1; kanamycin, 0.05; and 1ml/L of trace metal solutions. Trace metal solutions are (in grams per liter): NaCl, 5; ZnSO4. 7H2O, 1; MnCl2. 4H2O, 4; CuSO4. 5H2O, 0.4; H3BO3, 0.575; NaMoO4. 2H2O, 0.5; FeCl3. 6H2O, 4.75; 6N H2SO4, 12.5 ml. The feeding solution contains, (in grams per liter): glucose, 600; (NH4)2SO4, 5; MgSO4. 7H2O, 1.25; yeast extract, 5; CaCl2. 2H2O, 0.015; calcium pantothenate, 0.001; Thiamine, 0.01; ampicillin, 0.1; kanamycin, 0.05, 0.2mM of IPTG; and 1ml/L of trace elements.
2.4. Fermentor culture conditions
Culture of E. coli was performed in a 1.3 liter Bioflo 115 fermentor (NBS, Edison, NJ USA) using a working volume of 0.6 liter. The fermentor was inoculated with 10% of overnight seeding cultures and then cells were grown at 37 °C, 10% dissolved oxygen (DO) level, and pH 7.0. After OD600 reached 8.0, 0.2 mM IPTG was added and the temperature was shifted to 30 °C to initiate isobutyrate production. The pH was controlled at 7.0 by automatic addition of 10 M sodium hydroxidesolution, 50% v/v ammonia hydroxide, or 200 g/L calcium hydroxide suspension, respectively. Air flow rate was maintained at 1 vvm in each fermentation. DO was maintained at 10% with the saturated air by adjusting agitation speed from 300 to 800 rpm. The glucose level in the fermentor was maintained around 10 g/L by adding feeding medium automatically. When DO was over 40% and the isobutyrate yield did not increase, the fermentation was stopped. Samples at different time points were taken to determine the optical density and the concentrations of metabolites.
2.5. Metabolite analysis and dry cell weight determination
Fermentation products were analyzed using an Agilent 1260 Infinity HPLC equipped with an Aminex HPX 87H column (Bio-Rad, USA) and a refractive-index detector. The mobile phase is 5 mM H2SO4 with a flow rate 0.6 ml/min. The column temperature and detection temperature are 35 °C and 50 °C, respectively. Dry cell weight was determined by filtering 5ml samples through a 0.45 μm glass fiber filter (Michigan, USA). After removal of the culture medium, the filter was washed with 15 ml of MilliQ water, dried in an oven and then weighed. Dry cell weight was determined in triplicate.
2.6. Preparation of cell extracts and measurement of enzyme activity
The recombinant E. coli strains were cultivated in 2×YT medium to mid-logarithm phase at 37 °C, and then 0.1 mM IPTG was added to induce the protein expression. After induction for 4 h, the cells were harvested by centrifugation at 13,000×g for 5 min at 4 °C and washed with the sterilized water twice. The cells were then resuspended in a lysis buffer (50 µM Tris. HCl buffer, pH 7.0, 1 mM MgSO4, 1mM DTT), and then the protein was extracted using a vortex with 200 μL glass beads. The resultant lysates were centrifuged at 14,000×g for 10 min at 4 °C, and the supernatants obtained were then analyzed for enzymatic activities towards isobutyraldehyde in a reaction buffer described in [21]. Enzymeconcentrations in the supernatants were determined with a Bio-Rad protein analyzer. One unit of enzyme activity was defined as the amount of enzyme that reduced or oxidized 1 μmol NAD(P)+ or NAD(P)H per minute. These enzyme activities were determined with a Cary 50 MPR microplate reader coupled with a Cary 50 Bio UV-visible spectrophotometer (Varian, Inc.).
3. Results
3.1. Effect of alcoholdehydrogenases knockouts on isobutyrate production in shake flasks
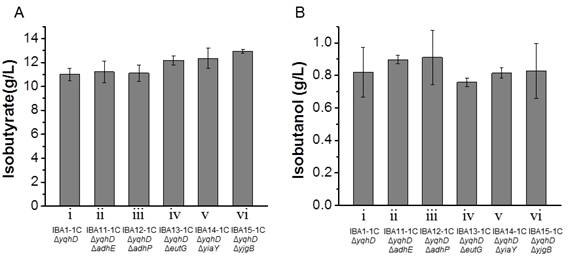
Isobutyraldehyde is the immediate precursor ofisobutyrate. It can be reduced to isobutanol by-product by endogenous alcohol dehydrogenases such as AdhE, AdhP, EutG, YiaY, YjgB and YqhD in E. coli [22,23]. YqhD has already been confirmed to play an important role inisobutanol formation since its deletion improved 50% of isobutyrate production [11]. However, even yqhD wasknockout, isobutanol was still present as a major fermentation byproduct with a concentration of 0.8 g/L. Therefore, it is important to investigate if knockouts of the other five genes in addition to yqhD can decrease isobutanol formation and then increase isobutyrate production. According to the fermentation results, the isobutanol production in all the knockout strains was in the range of 0.7-0.9 g/L (Figure 2B), suggesting that the double knockout strains did not decrease the isobutanol production significantly. The enzymatic assay of alcohol dehydrogenase was not significantly different among all the studied strains, which indicated that none of the other alcohol dehydrogenases played a key role to reduce isobutanol formation like YqhD in the recombinant E. coli (Table 2). Deletion of adhE or adhP did not affected the isobutyrate production (Figure 2A, ii and iii). The knockout strains of eutG, yiaY and ygjB produced 12.2, 12.4 and 12.9 g/L isobutyrate, which was 10.7%, 12.3% and 17.5% more than the control strain (Figure 2A, iv-vi). The ratio between isobutyrate and isobutanol was significantly increased in eutG, yiaY and ygjB knockout strains, which was 16.1, 15.2 and 15.6 vs 13.4 in control strain.
Table 2. Enzymatic assay results in different cell extracts
|
Strain
|
Isobutanol dehydrogenase
|
|
IBA1(ΔyqhD)
|
0.12 ± 0.023
|
|
IBA11(ΔyqhD ΔadhE)
|
0.11 ± 0.023
|
|
IBA12(ΔyqhD ΔadhP)
|
0.11 ± 0.010
|
|
IBA13(ΔyqhD ΔeutG)
|
0.13 ± 0.013
|
|
IBA14(ΔyqhD ΔyiaY)
|
0.13 ± 0.026
|
|
IBA15(ΔyqhD ΔygjB)
|
0.11 ± 0.024
|
|
Strain
|
Isobutyraldehyde dehydrogenase
|
|
IBA1-1C (single padA)
|
0.32 ± 0.03
|
|
IBA1-2C (double padA)
|
1.13 ± 0.14
|
Recently, one report used the same knockout strategy to investigate their effect on isobutylaldehyde production, and it was found that the knockouts of eutG, yiaY and ygjB significantly increased the isobutylaldehyde but not decrease the isobutanol significantly [24]. Because isobutylaldehyde is the direct precursor of isobutyrate, suggesting that the deletion of eutG, yiaY and ygjB did increase the carbon flux towards isobutyrate via isobutyraldehyde even with unknown details.
3.2. Effect of PadAexpression on the isobutyrate production
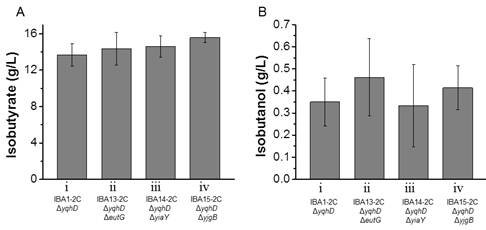
Since endogenous dehydrogenasesAdhE, AdhP, EutG, YiaY, and YjgB cannot significantly decrease isobutanol formation, it may be a good selection to screen potential enzymesfrom other microorganisms to complete this process. However, it is time-consuming. In this study, an alternative approach was employed by increasing the expression level of PadA to be more competitive towards the substrate than other alcohol dehydrogenases. Therefore, another copy of padA was introduced into the plasmid pIBA7 under the control of the constitutive promoter, yielding the plasmid pIBA11. Strains IBA1-2C, IBA13-2C, IBA14-2C and IBA15-2C bearing the plasmid pIBA11were chosen to investigate their fermentation performance.
Results from shake flasks showed that all the strains carrying additional padA produced isobutanol in the range of 0.3-0.5 g/L, which decreased about 50% comparing to that in the strains with single copy padA (Figure 3B). However, the isobutyrate titer of IBA1-2C, IBA13-2C, IBA14-2C and IBA15-2C produced 13.7, 14.3, 14.6, and 15.6 g/L isobutyrate (Figure 3A), which was 24.4%, 17.7%, 18.3% and 20.6% higher than IBA1-1C, IBA13-1C, IBA14-1C and IBA15-1C, respectively. These results demonstrated that boosting the expression level of PadA did greatly decrease isobutanol accumulation and increase isobutyrate production. Compared to control strain IBA1-2C, strains IBA13-2C, IBA14-2C and IBA15-2C with eutG, yiaY, ygjB knockout produced 4.8%, 6.8% and 13.9% more isobutyrate. The production profiles of isobutanol and isobutyrate among these four strains were consistent with above results. Activities of PadA enzymes from recombinant strains are shown in Table 2. Obviously, the activity of PadA from the IBA1-1C strain was much lower than those from the other strains. There was in good agreement with PadA activities and isobutyrate yields in these strains. Intriguingly, the decreased amount of isobutanol was less than the increased amount of isobutyrate. The possible reason may be that the production of isobutyrate is less stressful than that of isobutanol, so that cells produced some other byproducts and wasted less energy. For example, acetate was reduced from 0.6 g/L in IBA1-1C to 0.1 g/L in the IBA1-2C strain. The yield of isobutyrate from the best strain IBA15-2C was 0.39 g/g glucose, 80% of the theoretical maximum. However, there was still some isobutanol left in the fermentation medium. The future work can therefore be directed to further increase the expression level of PadA or identify unknown alcohol dehydrogenases in E. coli.
3.3. Optimization offermentation conditions in a fed-batch bioreactor
To explore the possibility of the scale-up productionof isobutyrate, fermentation experimentsat the fermentor level with the strain IBA15-2C were performed. To avoid the over-accumulation of acetate in the fermentor, glucose feeding rate was adjusted to keep glucose at a level below 10 g/L [25]. Since two molecules of NADH were generated for each molecule of isobutyrate produced, dissolved oxygen (DO) level was maintained at 10% to burn excess NADH. Higher DO level was not used in order to prevent excessive oxidation of substrate into CO2 through the TCA cycle.
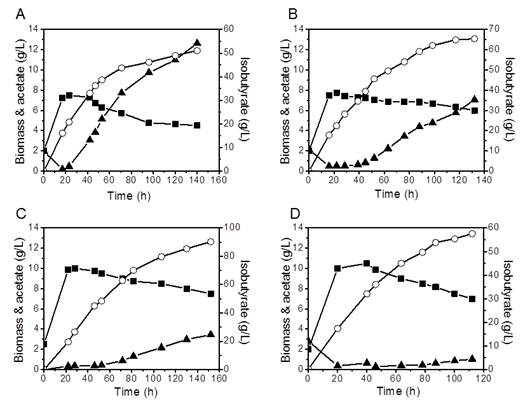
During biosynthesis of isobutyrate, pH decreased sharply if the base was not added. The effect of three bases, NH4OH, NaOH and Ca(OH)2 which were used to maintain the pH at 7.0 on the production of isobutyrate was investigated. As shown in Figure 4A-C (closed square), for all bases used, the biomass increased exponentially at the first 20 h, and then decreased gradually. The maximum biomass obtained using both NH4OH and NaOH was about 7.5 g/L, whereas it was about 10 g/L when Ca(OH)2 was used. Theseresultssuggest that excessive ammonium or sodium ion may have a negative impact on the cell growth. Ammonia hydroxide was previously used to control pH as well as supply nitrogen source [26,27], but it is not apparently optimal for isobutyrate production. With NH4OH, thefinaltiter of isobutyrate was only 51.1 g/L after 140 h (Figure 4A, open circle). While the maximal titer was 65.4 g/L with NaOH (Figure 4B, open circle), and 90.3 g/L with Ca(OH)2 (Figure 4C, open circle). The production of isobutyrate was inversely proportional to the acetate formation. Cultures adjusted by NH4OH accumulated 12.6 g/L acetate, while only 7.1 g/L and 3.4 g/L of acetate accumulated in the cultures adjusted by NaOH and Ca(OH)2, respectively (Figure 4A-C, closed up triangle). This was consistent with previous reports that acetate was a major inhibitor of E. coli fermentation [28,29]. In summary, using Ca(OH)2 to adjust pH had manybenefits: increasing cell density, improvingisobutyrate titer and decreasing acetate byproduct.
As a control, the fermentation of a single gene yqhD knockout strain IBA1-2C in the fermentor was also investigated. This strain produced 57.6 g/L isobutyrate and 1.0 g/L acetate after 122 h (Figure 4D), confirming that calcium hydroxide helps decrease acetate formation and increase isobutyrate production. However, IBA15-2C strain produced 57% more isobutyrate than IBA1-2Cstrain under the same condition, which suggested that ygjB knockout did significantly improve isobutyrate production in both shake flasks and the fermentor.
4. Discussion
Previously, our laboratory first reported the design of a synthetic metabolic pathway in E. coli to produce isobutyrate [11]. The purpose of this study was to investigate if this pathway could be further optimized to increase carbon conversion from glucose, and possible scale-upproduction in the fermentor. Among six knockout E. coli strains, one double knockout (DyqhD, DyjgB) produced 17% more isobutyrate than the single knockout strain (DyqhD). Furthermore, an additional copy of aldehyde dehydrogenase was introduced in a plasmid pIBA11 under the control of a constitutive promoter, which significantly reduced isobutanol formation (50% less) and increased isobutyrate production (21% more). Thus, an engineered strain was successfully constructed with an isobutyrate yield of 0.39 g/g glucose, 80% of the theoretical maximum.
In addition, the fermentation process was also scaled-up from shake flask to 1 L fermentor. Ca(OH)2 was found to be much better than NH4OH and NaOH for pH adjustment during fermentation. Ca(OH)2 increased cell density, decreased acetate formation and improved the final titer of isobutyrate to 90 g/L. Coincidently, a previous report showed that Ca(OH)2 was superior to NaOH for lactate fermentation [30]. Since the specific mechanism for this phenomenon remains unknown, it is worth in the future to investigate the relevant biological details. The study will improve our fundamental understanding on how cells respond to specific cations as well as provide a guiding principle for fermentation processes which require a significant quantity of base addition.
The isobutyrate productivity decreased substantially during the fermentation process, with an initial volumetric productivity of 1 g·L−1·h−1, finally decreasing to about 0.22 g·L−1·h−1. There may be two reasons for this phenomenon. Firstly, increasing concentration of isobutyrate may inhibit enzymatic activities, glycolysis rate, cellular metabolism or membrane integrity. Secondly, aging cells may be less productive in the later fermentation stage. To make our process more economical, in the future we will need to boost the productivity by maximizing metabolic flux [31], improving E. coli tolerance to isobutyrate [32], increasing glycolysis rate [3] or enzymatic turnover rate.
5. Conclusion
This work demonstrated isobutyrate can be produced from engineered bacteria with a high titer of 90 g/liter. This is the highest titer among new biobased products reported for the past several years [2,5,33,34,35,36,37,38]. The production of isobutyrate is comparable to fermentation of lactate [39] or succinate [40], two of the most promising renewable chemicals currently in commercial production. In 2004, from a list of 300 candidates that can be produced from biomass, “top 12” chemical building blocks such as 3-hydroxypropionate and succinate were identified. So far, only a few of the “top 12” blocks that have achieved high-yield and high-titer biosynthesis are gaining momentum in commercial production. It is obvious that the “top 12” list should be a dynamic guide, and there are opportunities for new compounds to diversify the portfolio. Since isobutyrate described in this work is so amenable to microbial fermentation, it can serve as a new platform chemical. For example, besides existing applications, it can be reduced to isobutanol for biogasoline [2], or esterified to be green solvent [39].
Acknowledgements
This work was supported by start-up funds from the University of Minnesota.
Conflict of Interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: