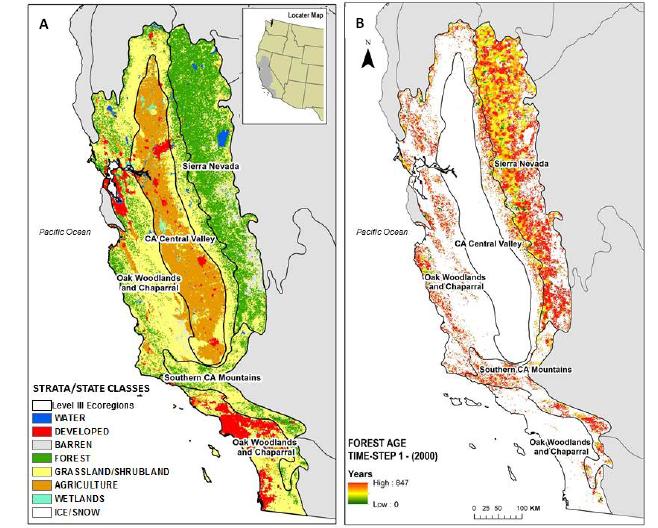
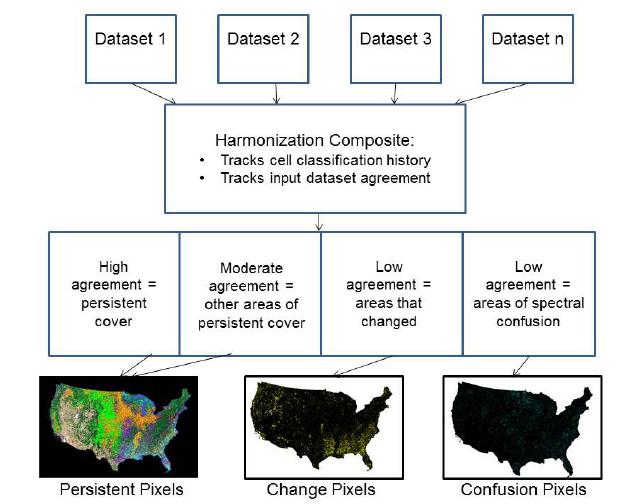
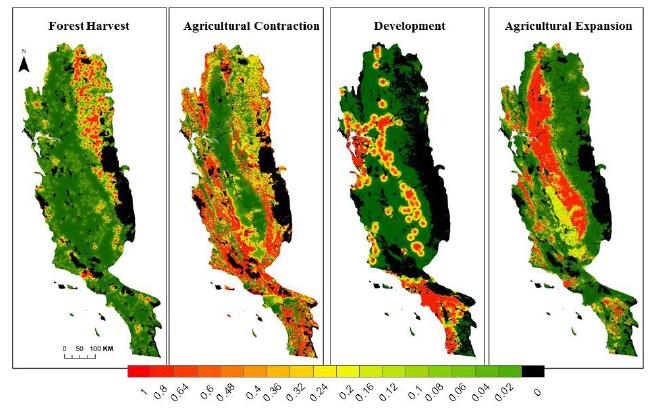
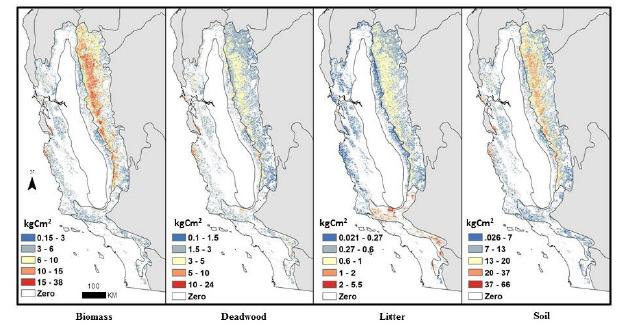
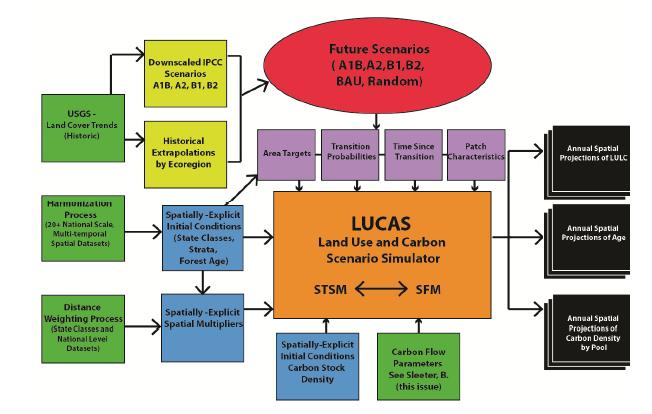
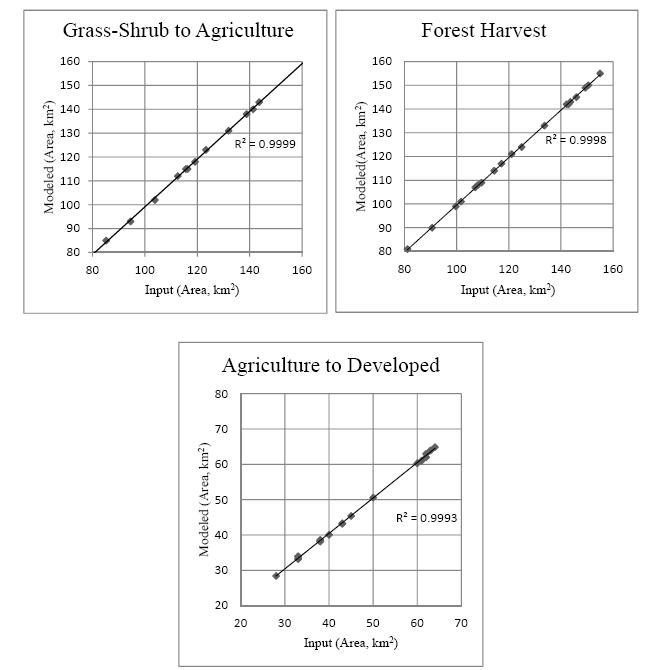
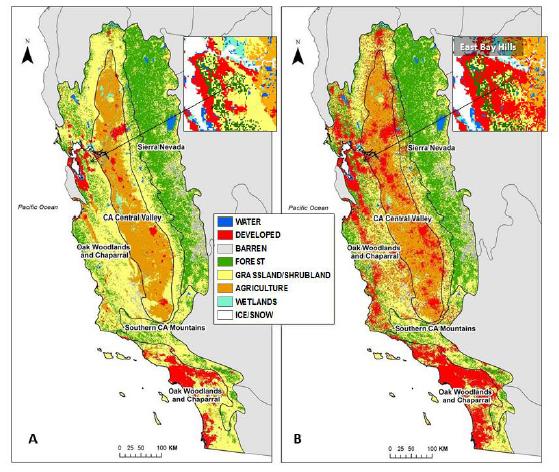
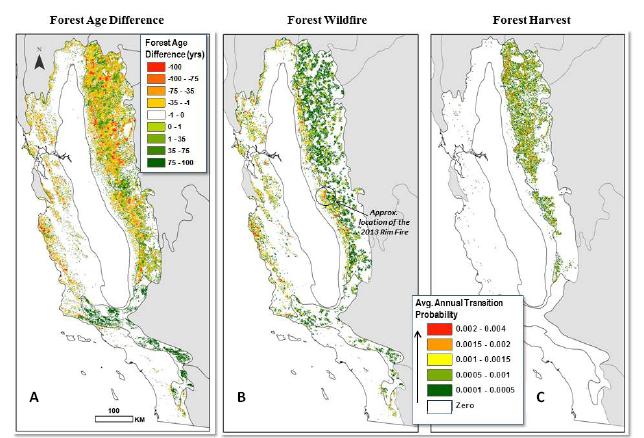
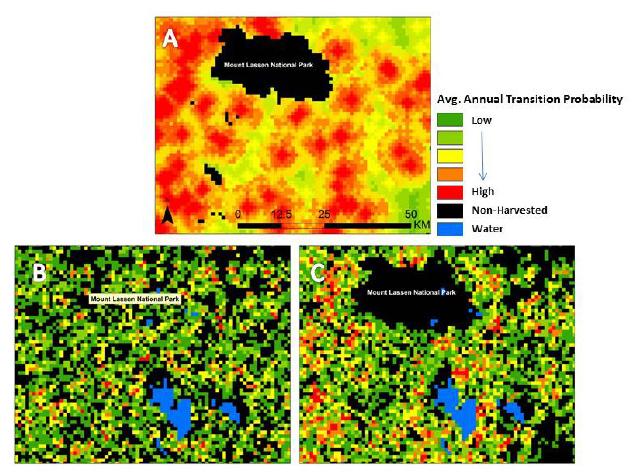
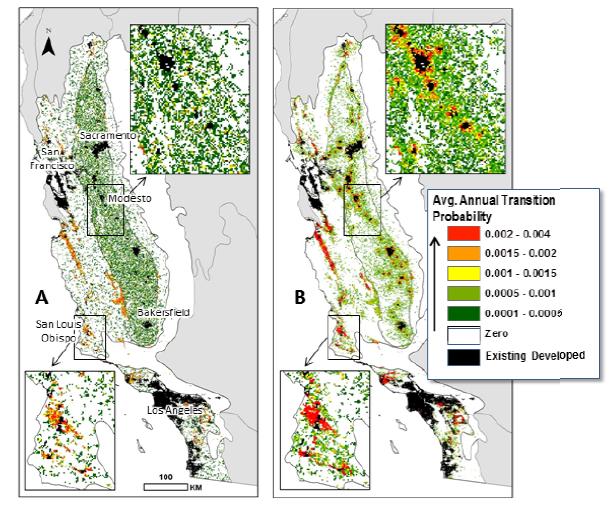
Spatially-explicit state-and-transition simulation models of land use and land cover (LULC) increase our ability to assess regional landscape characteristics and associated carbon dynamics across multiple scenarios. By characterizing appropriate spatial attributes such as forest age and land-use distribution, a state-and-transition model can more effectively simulate the pattern and spread of LULC changes. This manuscript describes the methods and input parameters of the Land Use and Carbon Scenario Simulator (LUCAS), a customized state-and-transition simulation model utilized to assess the relative impacts of LULC on carbon stocks for the conterminous U.S. The methods and input parameters are spatially explicit and describe initial conditions (strata, state classes and forest age), spatial multipliers, and carbon stock density. Initial conditions were derived from harmonization of multi-temporal data characterizing changes in land use as well as land cover. Harmonization combines numerous national-level datasets through a cell-based data fusion process to generate maps of primary LULC categories. Forest age was parameterized using data from the North American Carbon Program and spatially-explicit maps showing the locations of past disturbances (i.e. wildfire and harvest). Spatial multipliers were developed to spatially constrain the location of future LULC transitions. Based on distance-decay theory, maps were generated to guide the placement of changes related to forest harvest, agricultural intensification/extensification, and urbanization. We analyze the spatially-explicit input parameters with a sensitivity analysis, by showing how LUCAS responds to variations in the model input. This manuscript uses Mediterranean California as a regional subset to highlight local to regional aspects of land change, which demonstrates the utility of LUCAS at many scales and applications.
1.
Introduction
1.1. Motivation
Distribution systems usually consist of feeders with a radial configuration in which approximately 13% of the generated power is wasted as power losses [1]. The increasing demand and load led to the development of distribution systems which causes a further voltage drop, increases losses, as a result reduction of the bus voltage stability and load imbalance. Therefore, an appropriate installation of DGs and SCBs can reduce network losses, improve network performance, and postpone investment.
1.2. Literature review
Many meta-heuristics swarm techniques, which mimic the social behavior of swarms, herds, flocks, or schools of creatures in nature, have been proposed to resolve the issue of placement and sizing of DGs and SCBs. A Chaotic Artificial Bee Colony (CABC) algorithm was offered to find the best candidate locations and optimum sizes for DG units [2]. A Cuckoo Search Algorithm (CSA) was proposed to find optimal DG allocation and sizing in a radial distribution system [3]. A Whale Optimization Algorithm (WOA) was adopted for optimal allocation and sizing of DGs in RDSs [4]. In [5], the researchers used Particle Swarm Optimization (PSO), the Firefly algorithm (FA), and the Novel Bat Algorithm (NBA) methods to solve a multiobjective problem for various DG cases. A hybrid method of an improved PSO and Bat-Inspired Algorithm (BIA) for the optimal placement and sizing of DGs in RDSs was proposed in [6].
An Artificial Bee Colony (ABC) method was proposed for solving the SCBs problem [7,8,9]. A hybrid technique of the fuzzy and ABC approaches was introduced to obtain the optimal locations and sizing of SCBs [10]. Two stage approach of the fuzzy and Bat Algorithm (BA) methods was proposed to optimize the locations and sizes of SCBs in a radial distribution network [11]. The loss sensitivity and Cuckoo Search Algorithm (CSA) methods were suggested for solving the SCBs problem [12]. A Firefly Algorithm (FFA) method was offered [13,14]. The loss sensitivity and Fruit Fly optimization algorithm (FOA) methods were proposed in [15]. An Oppositional Krill Herd (OKH) approach was suggested to solve the SCBs problem in [16]. A PSO was proposed by other researchers in [17,18].
A fuzzy-dragonfly and fuzzy multi-verse optimizer methods were proposed to solve the SCBs problem in RDSs, and also a hybrid of the fuzzy and genetic algorithms was proposed to study the impact of temperature on SCBs placement in distorted RDSs [19,20,21,22]. A Multiobjective Particle Swarm Optimization (MOPSO) was suggested to determine optimal candidate locations and size of DGs and SCBs simultaneously in RDSs [23]. FFA and PSO methods were proposed to solve the DGs and SCBs placements problem in distribution systems [24,25].
Besides these swarm techniques, many remarkable researches have been carried out to solve either DGs/ SCBs placement problem or both stimulatingly. For example, A harmony search algorithm [26] was introduced to optimize the placement and sizing of DGs problem, in distribution network, aiming to improve the voltage profile, to reduce the power loss and to minimize the Total harmonic Distortion (THD). A hybrid of fuzzy decision-making tool and Multi-Objective Non-Sorting Genetic Algorithm (MONSGA) [27] was proposed to find the optimal placement and sizing of DGs in distribution networks through considering three objective functions i.e. power loss reduction, minimization of the comprehensive costs, and minimization of stability and security indices. In [28], two scenarios for DG placement in a distributions system were presented. In the first scenario, only real power loss reduction was considered. Both the optimal size and location of DGs were obtained as outputs from the system loss formula. In the next scenario, the voltage stability index was considered.
A water cycle algorithm [29] was presented to find the optimal placement and sizing of DGs and SCBs in RDSs aiming to minimize power losses, voltage deviation, total electrical energy cost, total emissions produced by generation sources and to improve the voltage stability. An elephant herding optimization algorithm [30] was introduced to find the optimal placement and sizing of DGs in distribution systems to improve the voltage profile and stability of system buses, to reduce the system loses, and to maximize the cost-savings.
PSO [31] was proposed to solve a multi-objective DGs sizing and placement problem for optimizing benefit-cost analysis of their installation and the total power losses during failures in distribution systems. Also, adaptive PSO [32] was introduced to efficiently tackle the problem of simultaneous placement of DG and CB to revamp voltage magnitude and reduce power loses in RDS. A Salp Swarm Algorithm (SSA) [33] was presented to find the optimal allocation of DGs to reduce active power loss and SCBs to improve bus voltages in RDS. Also, SSA [34] was proposed for locating and optimal sizing of DGs and SCBs on RDS for assuring the power quality (PQ) through enhancing the voltage level, minimizing the power losses, and the whole operating cost of the grid.
A hybrid of weight improved PSO and GSA algorithm [35] was proposed for optimizing the DGs and SCBs problem to achieve the reduction of power loss and enhancement of load ability in RDSs. A hybrid of fuzzy logic controller and ant-lion optimization algorithm with PSO based combination [36] was proposed to allocate the optimal placement of DGs in radial distribution systems. An enhanced genetic algorithm [37] was introduced to identify the optimal location and capacity of the simultaneous DGs/SCBs placement in the radial systems. A spring search algorithm [38] was proposed to find the optimal sizing and placement of SCBs and DGs in RDS with aiming to attain economic, technical, and environmental advantages.
1.3. Contribution and paper organization
In this study, a Multiobjective Grey Wolf Optimizer (MOGWO) is proposed to find the optimal DGs and SCBs placement locations and sizing simultaneously in distorted RDSs. The contributions proposed by this study are as follows:
1. To solve the DGs and SCBs placement problem by considering a a multi-objective method with Pareto fronts solutions.
2. To investigate the impact of ambient temperature on solving the DGs and SCBs placement problem.
3. To apply fuzzy set theory to select the optimal solution of non-dominated solutions.
4. To perform a MOGWO method on standard and real case studies.
5. To compare the obtained results with the MONSGA and MOPSO methods to show the effectiveness and capability of the proposed method in solving multi-objective problems when considering the temperature.
The rest of the paper is organized as follows. Section 2 describes a problem formulation which consist of objective functions, constrains, cost and temperature modelling, and a fuzzy decision-making mechanism. Section 3 introduces the proposed solution technique used in this paper. Section 4 describe results and discussion of standard and real case studies. Finally, Section 5 presents the conclusion, acknowledgments, and references.
2.
Problem formulation
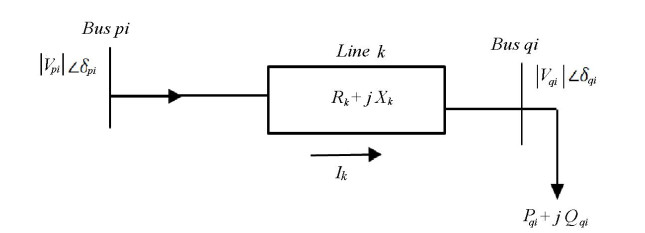
The optimizing of DGs and SCBs placement problem involves identifying the number and locations of DGs and SCBs to be placed simultaneously on distorted RDSs. The goals and objectives of this study are to reduce the total power loss ($ P_{loss} $), enhance the Voltage Stability Index (VSI), balance the loading of the Section Currents Index (SCI), reduce the Total Harmonic Distortion (THD) and maximize the cost-savings. A simplified system model that used for obtaining the objective functions i.e., the total $ P_{loss} $, VSI, and SCI values is
The optimization problem ($ f(X) $) that need to minimized is
Here, $ f_1(X) = Total P_{loss} $, $ f_2(X) = SCI $, $ f_3(X) = VSI $, and $ X $ is a solution vector subjected to $ g_i(X) $ and $ h_i(X) $ which are inequality and equality constraints, and $ R^n $ is the decision variable space.
2.1. Objective functions
The objective functions i.e., the total $ P_{loss} $, VSI, and SCI were calculated using the load follow studies. A load flow tool called a backward-forward sweep algorithm, was used to compute the fundamental system power loss [39].
Here, $ P_{loss}^f $ is the total fundamental active system loss, $ Pg_{qi} $ is the active power output of the DG at bus qi, $ Pd_{qi} $ is the active power demand at bus qi, $ V_{pi} $ and $ V_{qi} $ are the voltages at buses pi and qi, respectively. $ N_{b} $ is the number of system buses, $ Y_{qi} $ is the admittance between bus pi and bus qi, $ \delta_{pi} $ is the phase angle of voltage at bus pi, $ \delta_{qi} $ is the phase angle of voltage at bus qi and $ \theta_{qi} $ is the phase angle of $ Y_i $ ($ Y_{qi}e^{j\theta_{qi}} $)
The harmonic power flow method [40] was utilized to determine the harmonic power loss for the distorted RDSs:
The system loading is calculated as follows:
The stability index (SI)can be evaluated as follows [41]:
$ SI(qi) $ should be maximized. Therefore, the voltage stability index (VSI) will be:
2.2. Constraints
Equations (4–7), which are used as the objective functions for solving the DGs and SCBs placement problem are subject to the following constraints:
● Bus voltage:$ V_{i}^{min}\leq V_{i}\leq V_{i}^{max} $
● Power flow:$ |PF_i| \leq PF_{i}^{max} $
● System power factor: $ |p_{f_{system}} \ \ \ | \geq p_{f_{all}}^{min} $
● Installed reactive power: $ (Q_{C}^{Total}) \leq Q_{L}^{Total} $
● The DG source utilized must be permissible in the range of the size and power factor: $ pf_{min}^{DG}\leq (pf_{qi}^{DG}\leq pf_{max}^{DG} $
● The THD must be within the allowable limit [42].
2.3. Temperature modeling
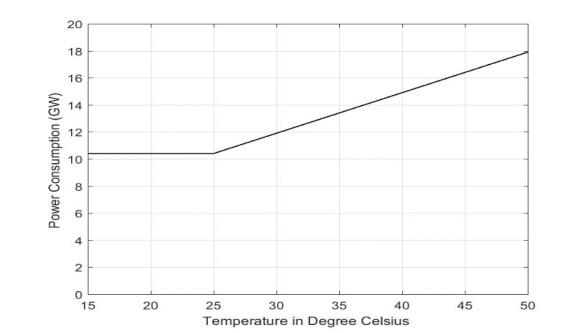
The IEEE 69-bus and 38-bus SEC RDSs (real data) were considered for this study. This was evaluated based on weather information using a least square method in which the power consumption increased by 300 MW per $ C^\circ $ based on the following equation derived from Figure 2 [43]:
For an IEEE 69-bus RDS with $ P_d $ = 3.80 MW, the slope of increasing power consumption can be found by ($ 300\times $ 3.80 $ MW $)/(10.4 $ GW $) = 110 $ kW/C^\circ $. Then, the relationship between power consumed by this system and the ambient temperature is
For a 38-bus SEC RDS with $ P_d $ = 8.34 MW,
$ P_d $ and y are in MW, and $ x $ is in the interval [$ 25^\circ $ – $ 50^\circ $].
2.4. Cost modeling
The cost of installation of SCBs and DG can be calculated as follows [44]:
The cost of power from substation before $ C_{bef.plac} $ and after $ C_{aft.plac} $ installation of SCBs and DG can be calculated as follows:
The presenting worth (PW) factor is formulated as follows:
The following equations for calculating the cost saving (S) and Benefit-to-Cost Ratio (BCR) are used:
$ C_{SCBs} $ is the installation cost of SCBs, $ K_C $ is the cost of commercial SCBs [45], and $ Q_C $ is the injected reactive power in $ kVAr $. $ C_{DG} $ is the cost of DG installation, $ {C_{DG}}_i $ is the installed capacity of a DG and $ K_{IDG} $ is the cost of DG investment ($318,000/MW). $ K_{EMP} $ is the energy cost ($49/MWh), $ V_s $ is the slack bus voltage, and $ I_s $ is the current fed from the slack bus to the entire system. $ PW $ is the worth factor, $ Inf_R $ is the inflation rate (2.2%), $ Int_R $ is interest rate (3%), T is 2190 h per year, and $ N_{yr} $ is 10 years.
2.5. Fuzzy decision making
A fuzzy decision-maker is utilized to select the optimal solution from the non-dominated solutions of MOGWO output. In the membership function $ M_{i}^{k} $, its largest value is the best optimal non-dominated solution, which computed as follows:
$ \mu_{i}^{k} $ is a membership function for each Pareto front solution $ k $, $ N_{nd} $ is the number of non-dominated solutions, and $ m $ is the number of targeted objective functions.
3.
Proposed solution technique
The MOGWO method is suggested to identify the optimal location placement and sizing of DGs and SCBs simultaneously in a distorted RDS. This method mimics the leadership hierarchy and hunting tactic of grey wolves in nature and is guided by paired leaders ($ \alpha $), subordinate wolves ($ \beta $), subordinate wolves ($ \delta $), and scapegoat wolves ($ \omega $)[46]. The mathematical model of the suggested approach is as follow:
$ t $ is the current iteration, $ \vec{A} $ and $ \vec{D} $ are coefficient vectors that help the GWO algorithm to explore and exploit the search space, $ \vec{X_p}(t) $ is the position vector of the prey, and $ \vec{X}(t) $ is the position vector of the grey wolf. The vectors $ \vec{A} $ and $ \vec{C} $ are calculated as follows:
The $ \alpha $ value linearly decreases from 2 to 0 during the course of the iterations and $ r_1 $ and $ r_2 $ are random vectors in [0, 1]. The range of $ \vec{C} $ is $ 2 \geq \vec{C} \geq 0 $ which improves the exploration when $ \vec{C} > 1 $ and the exploitation when $ \vec{C} < 1 $. The $ \vec{C} $ vector is generated randomly whose aim is to ensure that the exploration/exploitation at any stage can obtain the global optima while avoiding local optima.
The grey wolf optimizer begins by generating a set of random solutions as the first population. During the optimization, the three best-obtained solutions are saved and treated as $ \alpha $, $ \beta $, and $ \delta $ solutions. The next equations (21–23) update $ \alpha $, $ \beta $, and $ \delta $ wolf positions from the prey in order to simulate the hunting and discovery of promising areas of the search space:
The positions of wolves in the promising areas of the search space are modelled as follows:
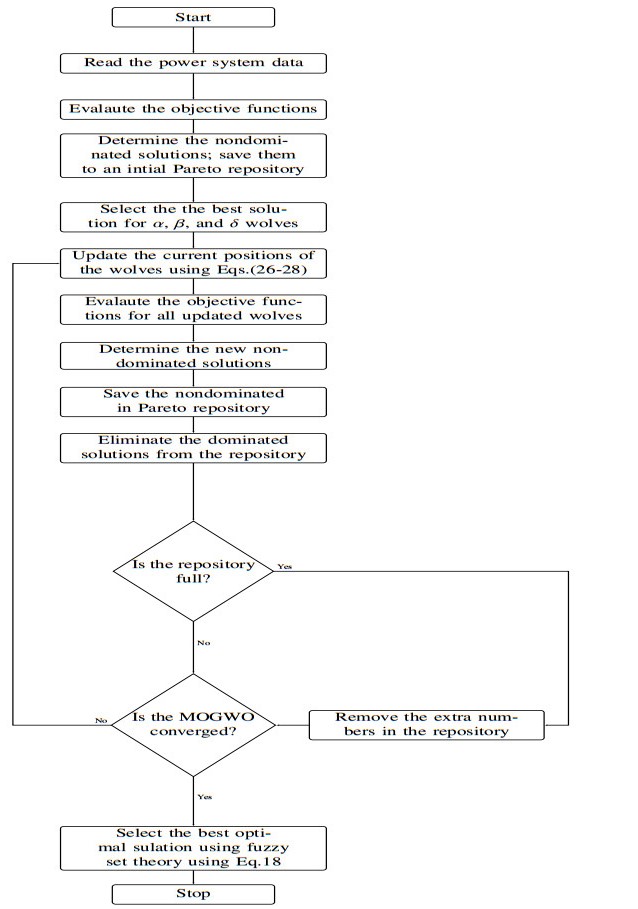
$ \vec{X_{\alpha}} $, $ \vec{X_{\beta}} $, and $ \vec{X_{\delta}} $ indicate wolf positions in the search space. $ \vec{X}(t+1) $ represents the random position of a wolf. The MOGWO is integrated with a repository and leader selection in order to perform the proposed multi-objective optimization. The repository is used to store the best solution (non-dominated solutions) obtained from the optimization algorithm. The leader strategy selects the better $ \alpha $, $ \beta $, and $ \delta $ wolves from the repository. Figure 3 shows a flowchart of the MOGWO technique for optimum multi-objective placement and sizing of DGs and SCBs with a fuzzy decision-maker.
4.
Results and discussion
The injection of harmonic currents is in the order of odd numbers (3–49) at a nominal frequency of 60 Hz, where 15% of each load at each load bus is assumed to be non-linear. The proposed method applied to two cases study with two scenarios as explained in Table 1.
4.1. Case study Ⅰ
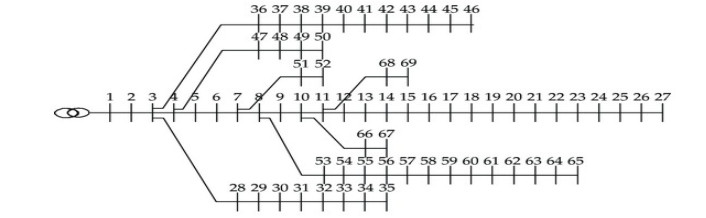
A typical 69-bus and 68-branch RDS is an IEEE standard RDS as shown in Figure 4. The system voltage and total load are 12.66 kV and 4.66 MVA, respectively [47].
4.1.1. Scenario 1
In this scenario, the impact of ambient temperature was not considered. The MONSGA, MOPSO and MOGWO algorithms discussed above were implemented for this system while considering all the objective functions and constraints. Various optimal results such as the optimal location, size, VSI, SCI and THD values, real power losses, reduction cost of power and energy losses and benefit-cost ratio (BCR) before and after installing of DGs and SCBs in the distorted 69-bus RDS were calculated. It can be observed that for the base case (before the installation of DGs and SCBs), the real power loss was 232.92 kW. By applying the MOGWO method, this loss was reduced to 30.13 kW, which was less than that in other methods as shown in Table 3. The VSI, SCI, and THD had permissible values which were 1.058 p.u., 0.331 p.u., and 2.20, respectively. The total annual reduction cost of the power losses was $ 1,265,500 for a cost-saving of $ 1,000,000. It can be seen that the calculated BCR was 1.22.
4.1.2. Scenario 2
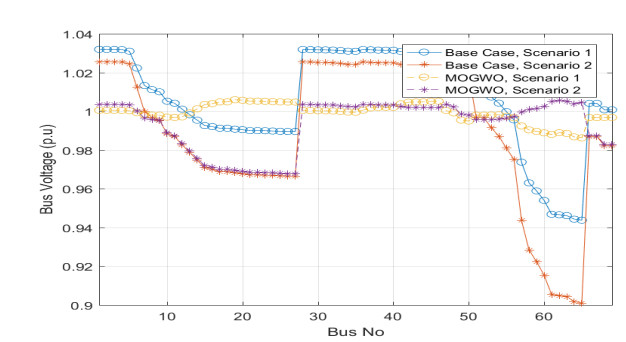
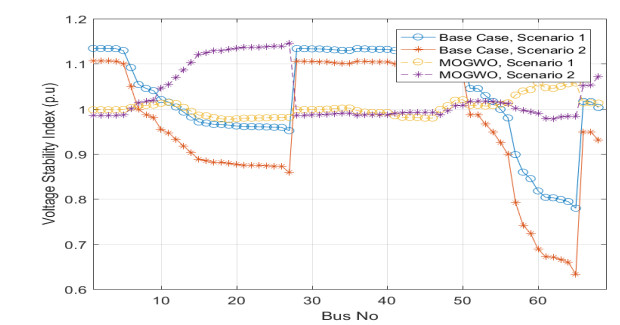
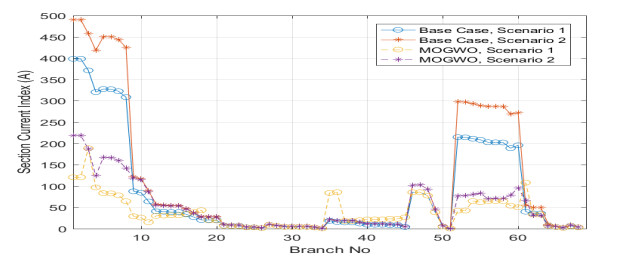
The impact of ambient temperature on this system was studied using Eq 9. One observes that in the base case, the real power loss was 438.48 kW and reduced to 105 kW after applying the MOGWO method which was less than in the other methods as shown in Table 3. The performance of the MOGWO method was compared to other methods through its elapsed time needed to converge as explained in Table 2 for both scenarios. The indices of VSI, SCI, and THD had permissible values comparing to other methods; these values were 1.15 p.u., 0.449 p.u., and 2.95, respectively. Figure 5 shows the voltage profile of this system. The figure compares the magnitudes of the voltage profile before and after installing DGs and SCBs for both scenarios. In the base case, the voltage profile was poor, which violates the lower limit of the voltage constraint. However, this voltage profile was improved after the installation of DGs and SCBs. Figure 6 shows VSI values on buses of the system, and Figure 7 shows the section current for also both scenarios. Almost all currents in all sections were decreased after installing of DGs and SCBs. The total annual reduction cost of the power losses was $ 2,195,500 for a cost-saving of $ 1,026,800. The calculated BCR was 1.36.
4.2. Case study Ⅱ
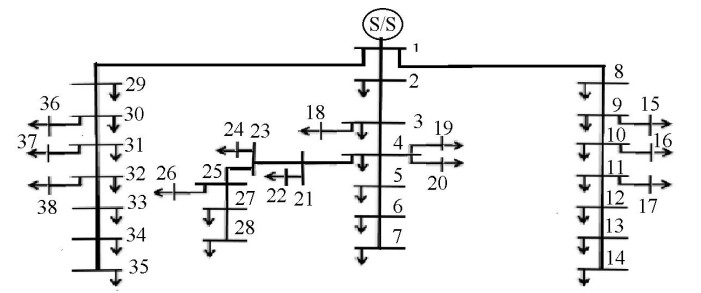
A typical 38-bus and 37-branch RDS as shown in Figure 8, is a SEC distribution system. The system voltage and total load are 13.8 kV and 8.77 MVA, respectively.
4.2.1. Scenario 1
The MONSGA, MOPSO and MOGWO algorithms were also implemented for this system while considering all the objective functions and constraints. Various optimal results such as the optimal location, size, VSI, SCI and THD values, real power losses, reduction cost of power and energy losses and BCR before and after installing of DGs and SCBs in the distorted 38-bus RDS were calculated. It can be observed that for the base case (before the installation of DGs and SCBs), the real power loss was 194.11 kW as shown in Table 5. By applying the MOGWO method, this loss was reduced to 128.12 kW, which was less than that in other methods. The VSI, SCI, and THD had permissible values which were 1.10 p.u., 0.220 p.u., and 2.29, respectively. The total annual reduction cost of the power losses was $ 2,298,500 for a cost-saving of $ 473,030. It can be seen that the calculated BCR was 1.46
4.2.2. Scenario 2
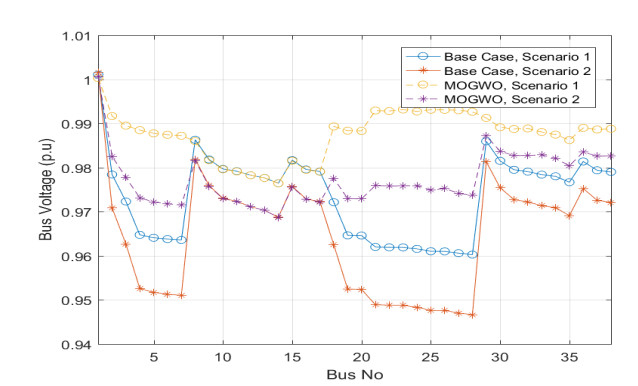
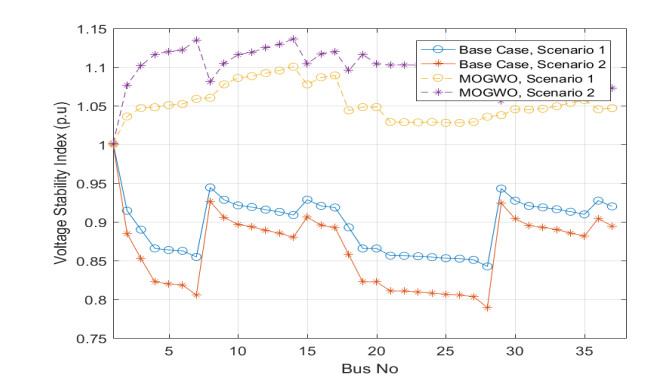
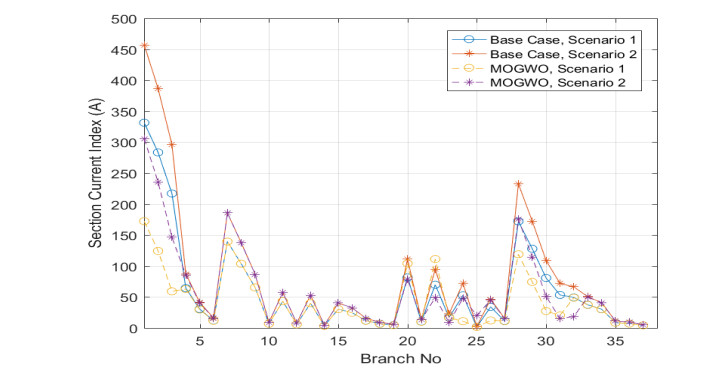
In the same way, the temperature effects on this system were studied using Eq 10. In the base case, the real power loss was 403.83 kW and reduced to 300 kW after applying the MOGWO method which was less than in the other methods as shown in Table 5. The performance of the MOGWO method was compared to other methods through its elapsed time needed to converge as explained in Table 4 for both scenarios. The indices of VSI, SCI, and THD had permissible values comparing to other methods; these values were 1.11 p.u., 0.310 p.u., and 3.05, respectively. Figure 9 shows the voltage profile of this system. The figure compares the magnitudes of the voltage profile before and after installing DGs and SCBs for both scenarios. In the base case, the voltage profile was poor, which violates the lower limit of the voltage constraint. However, this voltage profile was improved after the installation of DGs and SCBs. Figure 10 shows VSI values on buses of the system, and Figure 11 shows the section current for also both scenarios. Almost all currents in all sections were decreased after installing of DGs and SCBs. The total annual reduction cost of the power losses was $ 3.942,600 for a cost-saving of $ 1,204,100. The calculated BCR was 3.70.
5.
Conclusions
The MOGWO technique was proposed to identify the best candidate locations and optimum sizing of DGs and SCBs simultaneously under the impact of ambient temperature. The power loss reduction, voltage stability improvement of the system nodes, and load balancing in the sections were simulated as a multi-objective function. The best optimal solution was chosen via a fuzzy-based mechanism. The proposed method was applied to an IEEE 69-bus and 38-bus RDSs (real data from SEC). The obtained results were compared with the MONSGA and MOPSO methods, and showed better results in terms of system power loss reduction, voltage stability and voltage profile improvement, THD level, and load balancing. Additionally, economic benefits such as cost savings and BCR were evaluated. It is recommended that the power utilities adopt this technique to improve their technical capability and financial figures.
Acknowledgements
The authors extend their appreciation to the Deanship of Scientific Research, King Saud University for funding this work through research group no. (RG-1439-028).
Conflict of interest
The authors declare no conflict of interest in this paper.









 DownLoad:
DownLoad: