Optimal voltage controls of distribution systems with OLTC and shunt capacitors by modified particle swarm optimization: A case study

Abbreviations: OLTC: On-load tap changer; SC: Shunt capacitor; SVR: Step voltage regulator; DER: Distributed energy resource; DG: Distributed generation; PV: Photovoltaic; WT: Wind turbine; DFIG: Doubly-fed induction generator; DES: Distributed energy storage; BESS: Battery energy storage system; EV: Electric vehicle; PHEV: Plug-in hybrid electric vehicle; DSO: Distribution system operator; LV: Low-voltage; MV: Medium-voltage; DoD: Depth of discharge; AMI: Advanced metering infrastructure; ADS: Active distribution system; CT: Current transformer; PT: Potential transformer; OPF: Optimal power flow; AGA: Adaptive genetic algorithm; MSO: Moth search optimization;

Parameters and Variables: i, j: Bus index; N: Number of buses; t: Time index; T: Number of hours; S, P, Q: Complex, active and reactive power; V, δ: Voltage amplitude and angle; I, β: Current amplitude and angle; Z, R, X: Impedance, resistance and reactance; Y: Admittance; n: Normalized ratio; θ: Power angle, (θ = δ – β); R_set, X_set: Set resistance and reactance of OLTC; N_CT, N_PT: Turn ratio of CT and PT; α: Weighted factor; N_{Tap, max}: Tap switching limits; V_max, V_min: Voltage limits; I_max: Current limits; S_max: Power limits; P_Loss: Power loss; V_Dev: Voltage deviation; N_Tap: Tap index; x: Vector of variables, x = [V_LB, V_UB, Q_UB, Q_LB, cosθ_min]; V_LB, V_UB: Lower and upper bound voltage; Q_UB, Q_LB: Upper and lower bound reactive power; cosθ_min: Power factor limits; t_OLTC, t_SSC, t_SVR and t_FSC: Time delay of OLTC, SSC, SVR and FSC

1.   Introduction

Voltage stability and controls are crucial in power distributions to ensure a reliable and economic operation of the electric equipment. Currently, the standard voltage control relies on OLTC of distribution transformers, SC and SVR to maintain the system voltage within an acceptable level (from –10% to +5%) ^[1,2]. Because of large line impedances, load variations and particularly with the presence of DG, e.g., PV, WT, etc. and DES, e.g., BESS, PHEV, etc. the voltage control become challenges to the DSO. In addition, the voltage control also needs to consider the power losses, voltage fluctuation and the stress of regulating devices which can result in extra maintenance and replacement cost. In ^[1], the degradation of OLTC due to the arcing and carbonization of the contacts and insulation oils is studied. The dielectric withstand, voltage level and current through the taps of OLTC during commutations and short-circuits are further analyzed in which an electronic OLTC is proposed for the secondary side of the customer transformer in LV networks ^[2]. In ^[3], a linearized model of OLTC based on binary expansion scheme and Big-M method to address the nonlinearity and non-convexity of the tap operations is proposed for the OPF problem of radial distribution systems. A similar problem is extended in ^[4] by holomorphic-embedding methods for unbalanced distribution system with DFIG, PV and OLTC in which OLTC is modeled in the admittance matrix while DFIG and PV are considered by modifications of the current injection vector.

In ^[5], a decoupled three-phase OLTC which can adjust the voltage of each phase independently is proposed; in coordination with the reactive power from inverter-based PV, it can improve the hosting capacity of DG into the grid while mitigating the power losses, voltage rises under unbalanced loading conditions. The coordinated control of OLTC, SVR and DES to solve the voltage rise caused by high penetration of PV is further studied in ^[6]; the objective is not only maintaining the voltage of the network but also relieving the operation stress of OLTC, reducing peak load, power losses and guaranteeing the high durability of DES by limiting the DoD. In ^[7,8], the interaction of OLTC and inverter-based PV is analyzed; it shows that both reactive power control strategies such as fixed power factor (PF), watt/power factor, PF(P), volt/var, Q(V), etc. and the penetration of DG can result in an unintended switching operation of OLTC. The similar problem is extended in ^[9] considering the voltage stability of distribution networks; in which Q(V) control is commonly suggested but also can lead to instability problems if not designed properly. In ^[10], it is proposed to use the voltage measured by AMI for OLTC controls to improve the hosting capacity of PV for distribution networks; the correlation of OLTC design (5 or 9 steps) and the hosting capacity is also analyzed. The assessment of OLTC benefits versus the reinforcement of LV networks to adopt high penetration of domestic-scale PV is studied in ^[11]; using stochastic methods to cope with the location and capacity of PV, load variations and solar resource intermittences, it concludes that the network reinforcement is cheaper if the PV penetration is lower than 70%, otherwise the investment of OLTC and remote monitoring facilities are more economical.

In another approach, the OPF problem under multi-load levels of distribution systems by MSO is studied in ^[12]. It is scheduling the dispatchable DER, OLTC and SC to minimize the cost of power losses and voltage deviation, by this means, improving the value of the regulation devices and hosting capacity of the system. In ^[13], the voltage problem (rise and drop) caused by residential PV and EV in LV networks is resolved by managing the regulation devices. Two methods are proposed: rule-based control and OPF-based control in which the first method can effectively improve the system voltage while the second method can alleviate the tapping stress of OLTC. Furthermore, to improve the quality of distribution systems with a high penetration of PV, a coordinated control strategy for OLTC and PV smart inverters is proposed in ^[14]. A SCADA system is used to collect the data of voltage, PV and load power based on which the hourly tap position and injected reactive power from inverter-based PV are computed. In ^[15,16], the optimal allocation of DG (location and capacity) along with OLTC (location and ratio) to minimize the weighted power losses and voltage deviation is proposed using AGA. The optimal planning of ESS and OLTC in MV distribution systems is also studied in ^[17] with the objective is minimizing the investment and operation costs. The non-convexity and non-linearity of the formulated problem are resolved by second-order cone programming with binary expansion scheme and Big-M method. In ^[18], the optimal integration of different DER in coordination with the existing voltage scheme is proposed considering both with and without the effect of DER on annual energy losses and then solved by an improved GA method. The optimal allocation of DES for ADS with the multiple objectives is further studied in ^[19]. The objective function includes voltage deviations, line congestions, power losses, cost of investments, operation and load curtailments, the uncertainty of load and renewable generation.

Although a lot of researches have been done regarding to the voltage control of distribution systems, the applications in real-world are still limited. The IEEE Standard 1547–2018 working on the integration of DG expresses its concerns that the control of DG can conflict with other existing regulation devices; it recommends DG should not perform any active controls in distribution networks and simply works as negative loads ^[20]. Thus, the control strategies of inverter-based PV, e.g., PF(P), Q(V), etc. are not allowed ^[5,6,7]. Other studies only focus on the interaction of OLTC and DG penetration ^[8], charging/discharging scheme of DES ^[4] and hosting capability of DG ^[9,10,11]. In addition, the optimal operation and planning of DER, DES in coordination with the existing control scheme in monitoring the voltage profile ^{[12,13,14,15,16,17,18,19]}, but DER and DES are not allowed to perform active controls in reality ^[20]. Therefore, the voltage control of distribution networks still relies on the regulation devices such as OLTC, SC and SVR, etc.

In this paper, a comprehended formulation for the optimal voltage control of practical distribution systems with the standard regulation devices is proposed. The problem is to determine the set-points of the regulation devices which optimizes the performance of distribution networks with multiple objective function including power losses, switching operations, voltage deviation and voltage fluctuations, etc. It is subject to the constraint of allowable voltage ranges, stress of switching operation, capacity of distribution lines and transformers, etc. Due to the large-scale and high nonlinearity property of the formulated problem, PSO method is modified for solutions. Then, an actual 48-bus, 15-MVA, 22-kV, 50-Hz distribution system is investigated for testing the proposed control. The result of simulations demonstrates that the proposed method is effectively in determining the optimal setting of the voltage regulation devices with high convergences. The performance in the tested system shows that even the power loss is not reduced much, the index of voltage deviation, voltage fluctuation and the stress of switching operation of OLTC, SC and SVR can be improved remarkably. Therefore, compared to the previous works, this study makes contributions as follows.

-Modeling in details general distribution networks and voltage regulation devices: OLTC, SC and SVR, etc.

-Formulating a comprehended voltage control problem for general distribution systems with multiple objective functions.

-Deriving a modified PSO algorithm to solve the formulated problem with large-scale and high nonlinearity properties.

-The proposed method is effectively applied in an actual distribution system to improve the voltage deviation, fluctuation and reduce the stress of switching operation of regulation devices.

The remainder of the paper is organized as follows. Section II presents the modeling of conventional distribution networks and typical voltage regulation devices. Section III expresses the mathematical formulation of the voltage control problem with multiple objective functions and constraints. Section IV shows the solution method based on modified PSO algorithms. Section V shows the application of the proposed voltage control in a practical 15-MVA, 22-kV, 48-bus distribution network. The significant findings and conclusive points are summarized in Section VI.

2.   Distribution systems and voltage regulations

2.1.   Conventional distribution systems

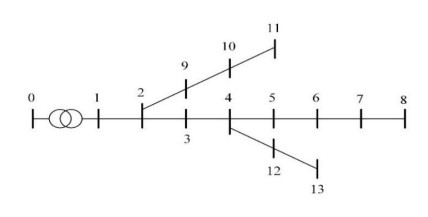
Generally, distribution systems are designed with radial forms and operated with unidirectional power flows, i.e., power is extracted from transmission systems to supply loads through distribution transformers and power lines. A typical 13-bus radial distribution network is shown in Figure 1.

Figure 1.  The conventional radial DS.

DownLoad: Full-Size Img PowerPoint

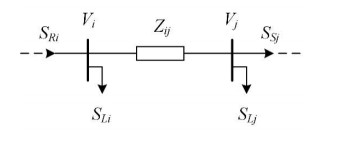
The active and reactive power sending or receiving of a distribution line between Bus i and j can be modelled in Figure 2.

Figure 2.  The modeling of distribution lines.

DownLoad: Full-Size Img PowerPoint

where S_R, S_S and S_L are the receiving, sending and loading power. For a bus, the receiving, the sending and load power are balanced, (S_R = S_S + S_L). The voltage drops in the line between Bus i and j can be estimated as follows:

It is noted that the receiving power of Bus j is the power transferred to Bus j through the power line between Bus i and j. The power losses in the line ij is given as:

With unidirectional power flows, the voltage is decreasing gradually from the feeder to the load. This results in a hierarchical voltage control scheme with OLTC, SC (in the station and/or feeder) and SVR.

2.2.   On-Load tap changer

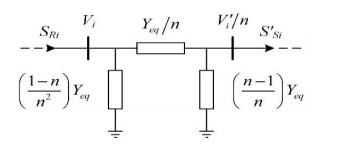
To control the voltage, tap changers are employed to adjust the turn ratio by adding or subtracting the effective turn of the transformer. OLTC means the tap commutation can be performed under loading conditions. Because the turn ratio varies in operations, OLTC transformer is modelled by normalized equivalent circuits.

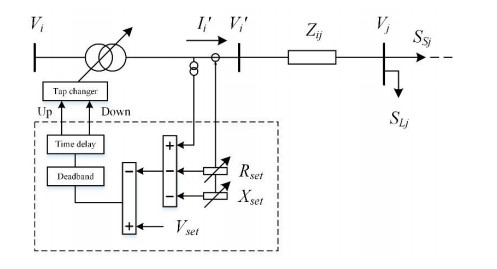
where V and V' are the primary and secondary voltage, Y_eq is the equivalent admittance of the transformers and n is the normalized coefficient of the turn ratio. To control the tap, measurement units such as PT and CT are employed. The arrangement of OLTC transformers is expressed in Figure 4.

Figure 3.  The model of OLTC transformers.

DownLoad: Full-Size Img PowerPoint

Figure 4.  The diagram of OLTC transformers.

DownLoad: Full-Size Img PowerPoint

The aim of OLTC is to adjust the voltage at load centers, e.g., Bus j, (V_j) within an acceptable range.

To avoid the need of communications, the voltage at load centers is normally estimated according to local measurements of the voltage and current at the station and compensated by the set resistance (R_set) and reactance (X_set).

where V_PT, I_CT are the physical value of voltage and current measurements, respectively. It is noted that the voltage is also limited at the station, the adjustable range of the voltage at load points (V_j) is given as follows.

where V_{i, max} and V_{i, min} are the maximum and minimum voltage at the station, I_{ij, max} and I_{ij, min} are the maximum and minimum of load currents, and θ is the power angle.

2.3.   Shunt capacitors

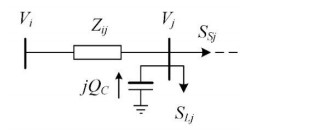
Capacitor banks provide a source of reactive power within distribution network. SC installed at Bus j as expressed in Figure 5.

Figure 5.  The shunt capacitor in DS.

DownLoad: Full-Size Img PowerPoint

The quantity of reactive power provided by SC at Bus j is given as:

where Q_{C, rated} is the rated capacity, V_rated is the rated voltage of SC. The voltage drops in the power line is modified by SC as:

It can be seen that parts of reactive power are supplied by SC, the current and power flow in the power line are reduced. As results, not only the voltage drop is decreasing but the power loss in the line is mitigated and the power factor is improved as well. In practices, a bunch of capacitors is employed in a bank, this can be located either in the substation at LV side of the transformer (SSC) or in the lateral of the feeder (FSC). In substations, SSC aims to reduce the quantity of reactive powers through transformers while in feeders, FSC is to improve the voltage profile at load points. Therefore, the SSC is normally controlled by the measurements of reactive power while the feeder capacitor is by the local voltage.

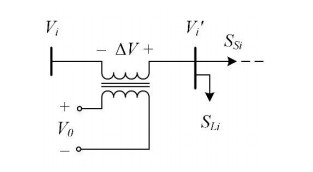
2.4.   Step voltage regulators

SVR enables active controls of the voltage in both magnitudes and phase angles. Employing a small transformer connected in series with the distribution lines, an additional voltage will be added at the output terminal as follows:

The output voltage (V'_i) is given as:

where α is the turn ratio; V₀ is the input voltage of the series transformer. The turn ratio can be adjusted similar to OLTC mechanisms, to change the added/subtracted voltage at the output. Also, the input voltage V₀ can be taken as the phase or line voltage, resulting in the magnitude or phase-shift SVR, respectively.

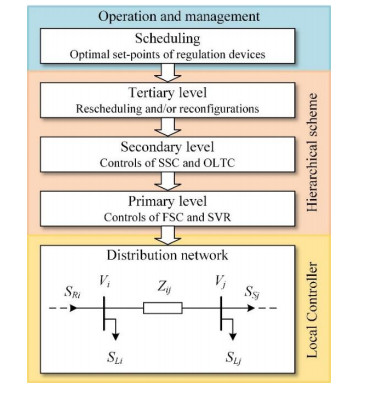
2.5.   Hierarchical voltage control

It can be seen in Figure 7 that the voltage regulation devices are arranged in hierarchical control schemes in which FCS and SVR serve in the primary level with Q-V droop feature while the secondary level includes OLTC and SSC to adjust the voltage of the entire feeder and restore the state of FCS and SVR in different time frames. The tertiary level deal with unexpected change of loads and/or voltage variation of the up-stream grid which may require re-dispatch or reconfiguration of the distribution network. In distribution systems, each regulation device is setup with a proper time delay to avoid conflictions:

Figure 6.  The diagram of voltage regulation.

DownLoad: Full-Size Img PowerPoint

Figure 7.  Hierarchical voltage control of distribution networks.

DownLoad: Full-Size Img PowerPoint

3.   Mathematical formulation

In this paper, the problem is to determine the set-point of OLTC (V_UB, V_LB), SSC (Q_UB, Q_LB, cosθ_min) and FSC (V_UB, V_LB) to optimize the performance of distribution systems. The objective function comprised of multiple technical indices such as power losses, voltage deviations, tap switching operations, etc. The solution is subject to the constraint of voltage limits, capacity limits, switching limits, etc. The problem is formulated as follows:

Subject to

4.   Particle swarm optimization

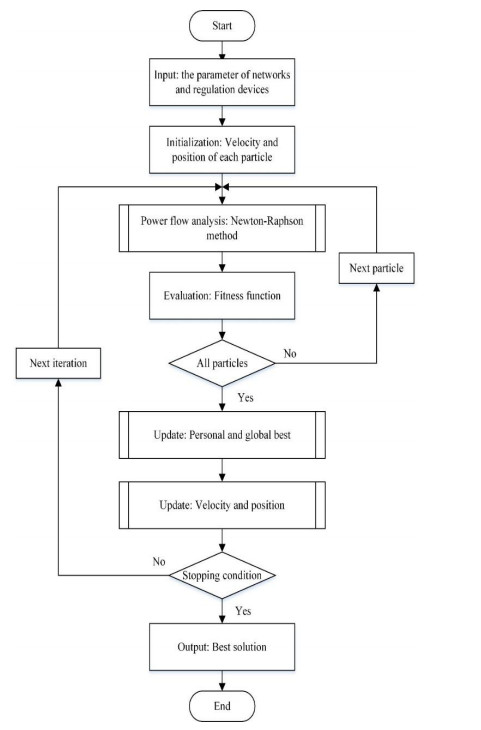
PSO was first introduced by Kennedy and Eberhard in 1995 with curiosities and doubts, but nowadays has been found as a powerful method of optimizations and successful in a variety of applications, particularly with nonlinear problems in electrical engineering and power systems. PSO is combined of heuristic, evolutionary algorithm and artificial intelligence in which a number of individuals (particles) are assigned in the search space with initial positions and velocities. Each particle can evaluate itself the fitness function at its location, compare with others and make the movement including three elements: (1) its inertia of velocity, (2) the history of its own and (3) the best location of the entire swarm or neighborhood, weighted by random perturbations. In this section, PSO is modified to solve the optimal voltage control problem of distribution systems with OLTC, SSC and FCS. The algorithm is expressed as follows:

Figure 8.  Schematic flowchart of the proposed algorithm.

DownLoad: Full-Size Img PowerPoint

Step 1: Initialize the position (p_i) and velocity (v_i) of each particle (i) of the swarm, as defined in Eq 10, each value is set uniformly random in the search space defined by the constraints.

Step 2: For each particle (i), an analysis simulation of the distribution system by Newton-Raphson method is run to evaluate the fitness function in Eq 11 including the power loss, RMS of voltage deviation and the switching operation of regulation devices, (Fitness_i).

Step 3: Update the new personal best (Pbest_i) for each particle and global best (Gbest) for the swarm with the current value of fitness functions and the previous best values.

Step 4: Determine the velocity and new position of each particle based on the updated personal and global best, and also the inertia velocity.

where w, c₁ and c₂ are the coefficients representing the influence of inertia, personal and global recognitions in the decision (0 ≤ w ≤ 1; 0 ≤ c₁, c₂ ≤ 2), rand is the uniform random variables which represent the perturbation of movements.

Step 5: Check the stopping condition which is the number of iterations or the solution convergence. If the condition is satisfied, the algorithm will terminate. Otherwise, repeat Step 2.

5.   Case study

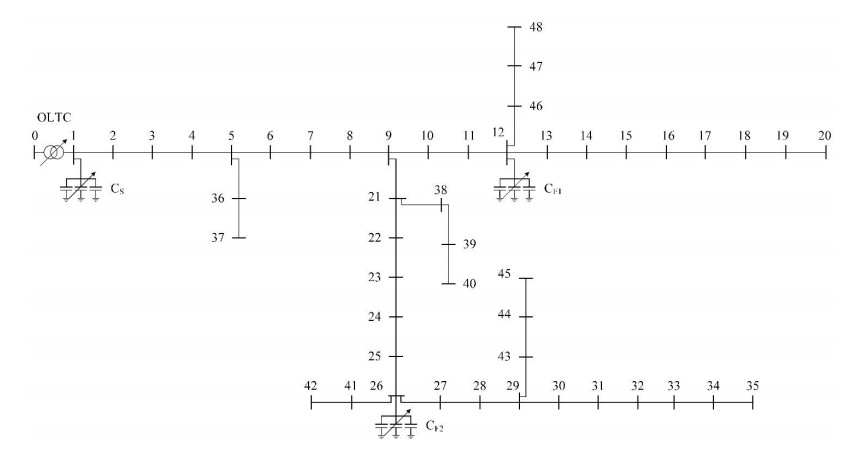
In this section, the proposed framework is applied to determine the optimal voltage control of a typical 15-MVA, 22-kV, 48-bus distribution system Figure 9.

Figure 9.  A practical 15-MVA, 22-kV, 48-bus distribution network.

DownLoad: Full-Size Img PowerPoint

5.1.   System specification

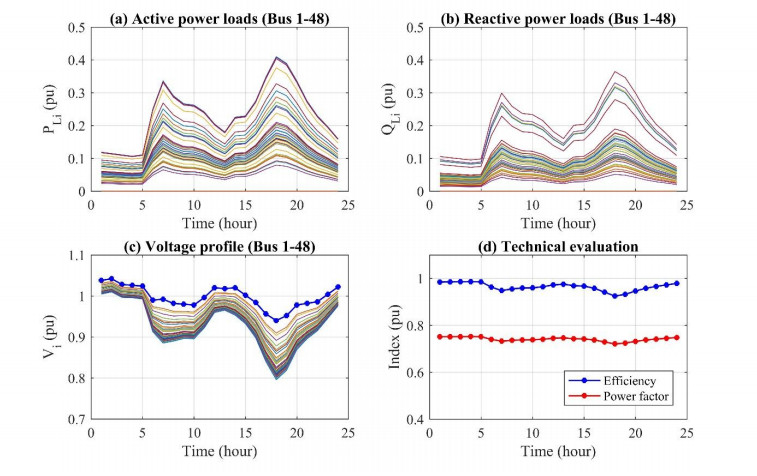
The distribution system is connected to the transmission system in a substation with a transformer characterized as 3-phase, 15-MVA, 110/22-kV, 60-Hz, z = 8%, x/r = 10. The system is supplying residential loads at 48 buses of an urban area in Thai Nguyen, Vietnam. The detail parameter of the distribution line and the rated active and reactive power of loads are shown in the Appendix, Table 1 and 2, respectively. The daily active and reactive power load of each bus are displayed in Figure 10, Part (a) and (b). Assumed there is no voltage regulation units, the natural voltages dropt through the distribution system are displayed in Figure 10, Part (c).

Figure 10.  The performance of distribution system without voltage controls.

DownLoad: Full-Size Img PowerPoint

In Figure 10, Part (c), the blue, circle-marked line represents the voltage input of the distribution transformer at Bus 0. This voltage is varying within [0.9-1.05 pu] which is assumed to be independent from the state of the distribution system. Without regulation units, the voltage drops naturally throughout the transformer and power lines, making the voltage of the drown-stream buses falls out of the acceptable range (0.9–1.05 pu) particularly when the load is high (07:00–10:00 AM and 16:00–22:00 PM). In this case, the total power loss is 4.9736 pu while the overall efficiency is 96.94%; the power factor is 0.7947 as displayed in Figure 10, Part (d). The RMS of voltage deviations is 5.8413%. The value of fitness function is 4.9969 pu.

5.2.   Voltage regulation devices

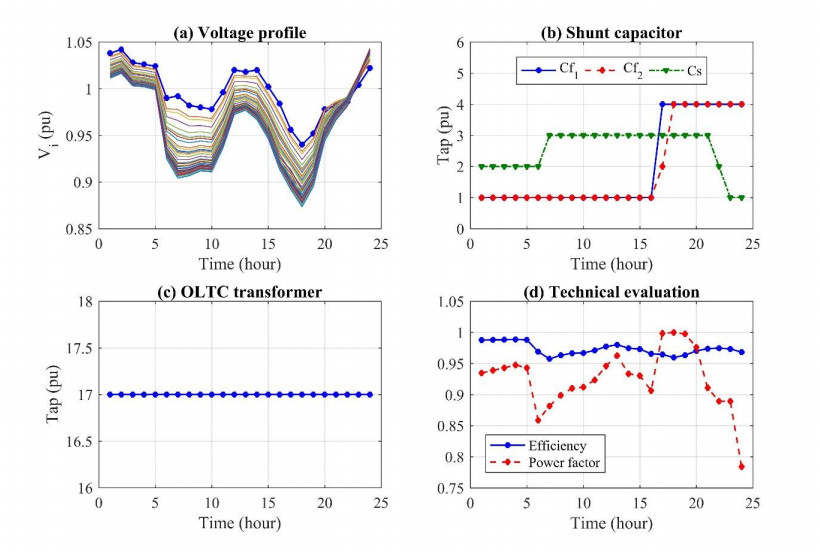
To control voltages, OLTC is incorporated in the distribution transformer which has 32 tap-changing steps, ±10% of voltage regulations. In addition, SC are deployed both in the station (SSC, 4-MVar, 22-kV, 3-switching bank) and in Feeder 1 and 2 (FSC, 3-MVar, 22-kV, 3-switching bank) as presented in Figure 8. In this case, it is assumed the voltage regulation units are set up with nominal values. OLTC is to maintain the voltage at the output terminal within the acceptable range, thus V_{UB, OLTC} = 1.05 pu, V_{LB, OLTC} = 0.9 pu. SSC is to keep the reactive power through the transformer within ±3 MVar (Q_{UB, SSC} = +3 pu, Q_{UB, SSC} = –3 pu) and the power factor greater than 0.85. FSC₁ and FSC₂ are to keep the voltage at Bus 12 and 26 within acceptable range, V_{UB, FSC1} = V_{UB, FSC2} = 1.05, V_{LB, FSC1} = V_{LB, FSC2} = 0.9 pu. The voltage profile and performance of the distribution system is displayed in Figure 11.

Figure 11.  The performance of distribution system with the nominal set-points.

DownLoad: Full-Size Img PowerPoint

In this case, the voltage is adjusted closer to the nominal value compared to Case 1, the voltage deviation is 4.4633%. However, the voltages at some buses are still under the limits (17:00–19:00 PM) as in Figure 11, Part (a). The station capacitor is utilized at the beginning because of lower power factors as displayed in the green, triangle-marked line in Figure 11, Part (b), at 21:00 PM, the station capacitor is tapped down because the reactive power exceeds the load, the distribution system supplies reactive power to the upstream grid, making the power factor is leading but under the threshold (0.85). The feeder capacitors start to use only when the load is critical high (16:00 PM) which leads the voltage at Bus 12 and 26 to decrease below the threshold (0.9 pu). However, it is not capable to lift the voltage to the acceptable range as presented in Figure 11, Part (c). OLTC is not activated over the day because the output voltage (at Bus 1) is always within the range (0.9–1.05 pu). In this case, the total power loss is 4.1937 pu, the overall efficiency is 97.30%, the power factor is 0.9256 and the fitness function is 4.0119 pu.

5.3.   Optimal voltage control

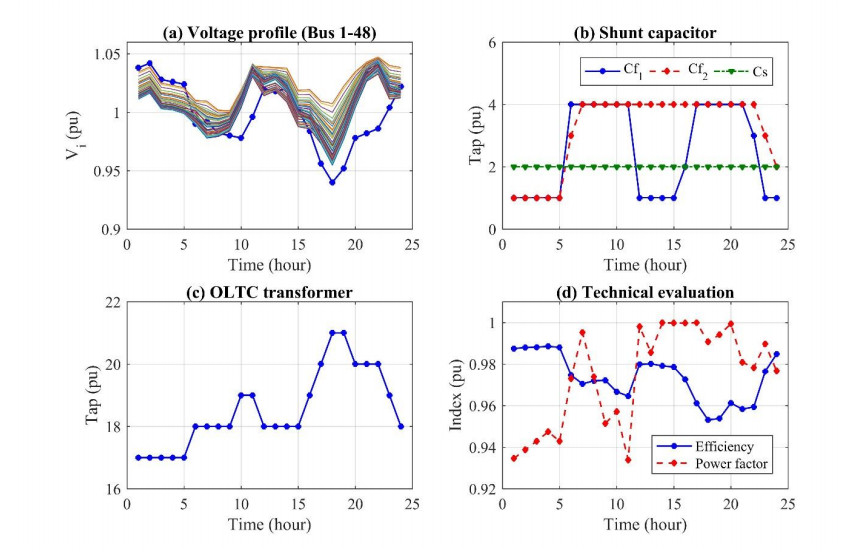
In this case, the proposed PSO algorithm is deployed to determine the optimum set-points of the voltage regulation units: V_UB and V_LB of the OLTC, Q_UB, Q_LB and cosϕ_min of the SSC and V_UB and V_UB of the FSC. Through trials, observation and analysis, the parameter of PSO is selected as w = 0.5, c₁ = 0.2, c₂ = 0.2. Also, the variables (set-points) are discretized with the interval of 0.05 pu. The algorithm is run with 20 particles and 50 iterations. The optimum set-point is obtained as V_{UB, OLTC} = 1.05, V_{LB, OLTC} = 1.0, cosϕ_min = 0.85, V_{UB, FSC1} = 1.05, V_{LB, FSC1} = 0.95, V_{UB, FSC2} = 1.05 and V_{LB, FSC2} = 0.95. The value of Q_{UB, SSC} and Q_{LB, SSC} are not relevant because the reactive power does not reach to the threshold in the entire day. The fitness function in this case is 2.6818 pu. The performance of the distribution system is displayed in Figure 12.

Figure 12.  The performance of the distribution system with voltage controls.

DownLoad: Full-Size Img PowerPoint

In this case, the voltage profile of the distribution system is adjusted by the coordination of OLTC, SSC and FSC, resulting the voltage remained closely to the nominal value (0.95–1.05 pu). The voltage deviation is reduced to as small as 1.9391%. From 00:00–05:00 AM, because the load is low, only the SSC is used (Level 2) to keep the power factor greater than cosϕ_min = 0.85. When the load increases, the voltage drops greater, both the OLTC and FSC are activated to lift the voltage at the station (Bus 1) and the feeder (Bus 12 and 26) above the lower bounds (V_{LB, OLTC} = 1.0 pu and V_{LB, FSC1} = V_{LB, FSC2} = 0.95 pu). As the variation of loads, the OLTC and FSC are responding accordingly, particularly from 18:00–22:00 PM, the load is extremely high, the feeder capacitors are used thoroughly (Level 4) and the tap of OLTC is at Level 21. As results, the efficiency and power factor of the distribution system are relatively high. In details, the total power loss is 4.1426 pu, the overall efficiency is 97.33%, and the power factor is 0.9743.

6.   Conclusions

This paper presents a new framework to optimize the voltage control of distribution systems by coordination of the regulation equipment such as OLTC and SC. The problem is to determine the set-points of OLTC, SSC and FSC which minimizes the multi-objective function including power losses, voltage deviations, tap movements, etc. The problem is formulated and solved by modified PSO method with discrete variables and trial-based techniques. The proposed framework is tested in a practical case study of 15-MVA, 22-kV, 48-bus distribution systems in Vietnam. The result of simulations shows that the voltage profile can be improved significantly: no bus voltage is out of the boundaries while the RMS of voltage deviations is as small as 1.9391%, the overall power loss is reduced (4.1426 pu) compared to those with the nominal setting are 4.4633% and 4.1937 pu, respectively. In this case of study, the power losses are similar between the conventional setup and the proposed voltage control (1.21%). However, the quality of the bus voltage is improved significantly not only in terms of the acceptable range but also the voltage profile though the distribution system (56.5%). In addition, the overall efficiency and power factor are improved as well. As DG becomes popular nowadays, in the future work the proposed method will be expanded considering the presence of DG in distribution systems. It will also analyze the ability of the existing voltage control units in adoptions of this new element.

Acknowledgments

This work is supported by Thai Nguyen University of Technology as its project on Smart grid and Distributed generation.

Conflict of interest

The author declares no conflict of interest.