Stochastic homogenization on perforated domains Ⅰ – Extension Operators

Martin Heida; Martin Heida

doi:10.3934/nhm.2023079

Networks and Heterogeneous Media

2023, Volume 18, Issue 4: 1820-1897. doi: 10.3934/nhm.2023079

Previous Article Next Article

Research article

Stochastic homogenization on perforated domains Ⅰ – Extension Operators

Martin Heida ^,

WIAS Berlin, Mohrenstr. 39, 10117 Berlin, Germany

Received: 09 December 2021 Revised: 12 July 2023 Accepted: 22 July 2023 Published: 20 November 2023

In this first part of a series of 3 papers, we set up a framework to study the existence of uniformly bounded extension and trace operators for $W^{1, p}$ -functions on randomly perforated domains, where the geometry is assumed to be stationary ergodic. We drop the classical assumption of minimally smoothness and study stationary geometries which have no global John regularity. For such geometries, uniform extension operators can be defined only from $W^{1, p}$ to $W^{1, r}$ with the strict inequality $r < p$ . In particular, we estimate the $L^{r}$ -norm of the extended gradient in terms of the $L^{p}$ -norm of the original gradient. Similar relations hold for the symmetric gradients (for ${\mathbb{R}^{d}}$ -valued functions) and for traces on the boundary. As a byproduct we obtain some Poincaré and Korn inequalities of the same spirit.

Such extension and trace operators are important for compactness in stochastic homogenization. In contrast to former approaches and results, we use very weak assumptions: local $(\delta, M)$ -regularity to quantify statistically the local Lipschitz regularity and isotropic cone mixing to quantify the density of the geometry and the mesoscopic properties. These two properties are sufficient to reduce the problem of extension operators to the connectivity of the geometry. In contrast to former approaches we do not require a minimal distance between the inclusions and we allow for globally unbounded Lipschitz constants and percolating holes. We will illustrate our method by applying it to the Boolean model based on a Poisson point process and to a Delaunay pipe process, for which we can explicitly estimate the connectivity terms.

Keywords:

Citation: Martin Heida. Stochastic homogenization on perforated domains Ⅰ – Extension Operators[J]. Networks and Heterogeneous Media, 2023, 18(4): 1820-1897. doi: 10.3934/nhm.2023079

Related Papers:

[1]	Naher Mohammed A. Alsafri . Solitonic behaviors in the coupled Drinfeld-Sokolov-Wilson system with fractional dynamics. AIMS Mathematics, 2025, 10(3): 4747-4774. doi: 10.3934/math.2025218
[2]	Chun Huang, Zhao Li . Soliton solutions of conformable time-fractional perturbed Radhakrishnan-Kundu-Lakshmanan equation. AIMS Mathematics, 2022, 7(8): 14460-14473. doi: 10.3934/math.2022797
[3]	Ghazala Akram, Saima Arshed, Maasoomah Sadaf, Hajra Mariyam, Muhammad Nauman Aslam, Riaz Ahmad, Ilyas Khan, Jawaher Alzahrani . Abundant solitary wave solutions of Gardner's equation using three effective integration techniques. AIMS Mathematics, 2023, 8(4): 8171-8184. doi: 10.3934/math.2023413
[4]	Imran Siddique, Khush Bukht Mehdi, Sayed M Eldin, Asim Zafar . Diverse optical solitons solutions of the fractional complex Ginzburg-Landau equation via two altered methods. AIMS Mathematics, 2023, 8(5): 11480-11497. doi: 10.3934/math.2023581
[5]	Naeem Ullah, Muhammad Imran Asjad, Jan Awrejcewicz, Taseer Muhammad, Dumitru Baleanu . On soliton solutions of fractional-order nonlinear model appears in physical sciences. AIMS Mathematics, 2022, 7(5): 7421-7440. doi: 10.3934/math.2022415
[6]	Musarat Bibi, Salah Mahmoud Boulaaras, Patricia J.Y. Wong, Muhammad Shoaib Saleem . Exploring families of soliton solutions for the fractional Akbota equation in optical fiber telecommunication systems. AIMS Mathematics, 2025, 10(5): 12254-12285. doi: 10.3934/math.2025555
[7]	Haitham Qawaqneh, Ali Altalbe, Ahmet Bekir, Kalim U. Tariq . Investigation of soliton solutions to the truncated M-fractional (3+1)-dimensional Gross-Pitaevskii equation with periodic potential. AIMS Mathematics, 2024, 9(9): 23410-23433. doi: 10.3934/math.20241138
[8]	Emad H. M. Zahran, Omar Abu Arqub, Ahmet Bekir, Marwan Abukhaled . New diverse types of soliton solutions to the Radhakrishnan-Kundu-Lakshmanan equation. AIMS Mathematics, 2023, 8(4): 8985-9008. doi: 10.3934/math.2023450
[9]	Mahmoud Soliman, Hamdy M. Ahmed, Niveen Badra, M. Elsaid Ramadan, Islam Samir, Soliman Alkhatib . Influence of the $\beta$ -fractional derivative on optical soliton solutions of the pure-quartic nonlinear Schrödinger equation with weak nonlocality. AIMS Mathematics, 2025, 10(3): 7489-7508. doi: 10.3934/math.2025344
[10]	Noor Alam, Mohammad Safi Ullah, Jalil Manafian, Khaled H. Mahmoud, A. SA. Alsubaie, Hamdy M. Ahmed, Karim K. Ahmed, Soliman Al Khatib . Bifurcation analysis, chaotic behaviors, and explicit solutions for a fractional two-mode Nizhnik-Novikov-Veselov equation in mathematical physics. AIMS Mathematics, 2025, 10(3): 4558-4578. doi: 10.3934/math.2025211

Abstract

1. Introduction

In numerous engineering and scientific domains, nonlinear fractional partial differential equations (NFDEs) have gained significant importance in the description and modelling of intricate processes. The memory and inherited characteristics of the system being modelled can be precisely captured via NFPDEs. These equations are particularly helpful for explaining anomalous diffusion phenomena and have a wide range of applications in disciplines like chemistry, physics, engineering, finance, biology, and economics ^{[1,2,3,4,5,6]}. As a result, in many application domains, the exploration of NFPDEs is crucial to comprehending and forecasting the behavior of complex systems. Nonetheless, there are special difficulties in resolving and interpreting fractional derivatives due to their non-locality and non-linearity. The solution and analysis of these equations may require the development of new methods and tools, as traditional analytical and numerical approaches might not be directly relevant. Notwithstanding these difficulties, research on NFPDEs has produced significant advances in a number of scientific and engineering domains ^[7,8,9]. Research opportunities have increased and our understanding of complicated processes has improved as a result of the development of new analytical and numerical techniques for solving and analyzing NFPDEs ^[10,11,12]. Exact solutions to nonlinear fractional problems can currently be obtained by a variety of effective methods, such as the generalized projective Riccati equation approach ^[13], sine-Gordon expansion method ^[14], generalized Riccati method and the auxiliary ordinary differential equation method ^[15], Lie symmetry approach ^[16], first integral method ^[17], modified Kudryashov method ^[18], extended exp ${(-\phi(\xi))}$ -expansion method ^[19], modified auxiliary equation method ^[20], unified method ^[21], $(\frac{G'}{G})$ -expansion methods ^[22,23,24], Khater methods ^[25,26], Poincaré-Lighthill-Kuo method ^[27], Riccati-Bernoulli Sub-ODE ^[28], exp-function method ^[29], fractional Sin-Gordon method ^[30], sub-equation method ^[31], tanh-method ^[32], extended direct algebraic method ^{[33,34,35,36]}, Sardar sub-equation method ^[37], exponential rational function method ^[38], and so on ^{[39,40,41,42,43,44]}.

Kundu et al. ^[45] introduced the Kundu-Mukherjee-Naskar equation (KMNE) for the first time in $2014$ and found optical soliton solutions for it. The KMNE has been the subject of extensive research recently. Its wave events are crucial for accurately modelling propagation pulses in high-speed data transfer in communication systems, optical fibers and the ocean currents of rogue waves ^[46,47,48]. One common application for optical fibers is the transmission of light between their two ends. Their long-distance and faster data transmission rate compared to wires makes them commonly employed in optical fiber communications. The goal of the current study is to construct and analyze optical soliton solutions for the gFKMNE, a fractional generalization of KMNE, which exhibits the following dimensionless display ^[49]:

$\begin{equation} i D^{\delta}_{t}z+a D^{\beta}_{y}(D^{\alpha}_{x} z)+i b z(z D^{\alpha}_{x} z^{*}-z^{*} D^{\alpha}_{x}) = 0, \end{equation}$

(1.1)

wherein $0 < \alpha, \beta, \delta \leq1$ , $z = z(t, x, y)$ is the quantity that represents a complex wave envelope, $z^{*}$ is the complex conjugate of $z$ . Furthermore, the dispersion term and the nonlinearity term are indicated by the two parameters $a$ , $b$ respectively. The wave's temporal history is represented by the first term in Eq (1), which is succeeded by the dispersion term $a D^{\beta}_{y}(D^{\alpha}_{x} z)$ . Ultimately, the coefficient of $b$ that is changed from the standard Kerr law nonlinearity represents the nonlinear portion. In optical fibers and communication systems, the pulse propagation is described by this equation. The fractional derivatives $D^{\alpha}_{x}(\circ)$ , $D^{\beta}_{y}(\circ)$ , and $D^{\delta}_{t}(\circ)$ are the generalized conformable fractional derivatives (gCFDs) of order $\alpha$ , $\beta$ , and $\delta$ respectively.

In many applications, such as irrigation and river flows, tidal waves, weather research and tsunami prediction, Eq (1.1) is used. Due to such significance, many researchers have developed an interest in examining Eq (1.1). For instance, Eq (1.1) was solved with new exact solutions by Günerhan et al. ^[50] through the use of an enhanced direct algebraic approach. Using the csch-approach, extended tanh-coth method, and extended rational sinh-cosh method, Rizvi et al. ^[51] were able to get the singular soliton, dark soliton, combination dark-singular soliton, and other hyperbolic solutions for Eq (1.1). Talarposhti et al. ^[52] derived optical soliton solutions for the KMNE using the exp-function approach. Onder et al. ^[53] used the novel Kudryashov techniques along with the Sardar sub-equation to introduce optical soliton solutions for the KMNE. Zafar et al. ^[54] found new soliton solutions for the KMNE by employing the exp-function approach and the extended Jacobi's elliptic expansion function. Kumar et al. ^[55] used the new auxiliary equation approach with the generalized Kudryashov method to find dark, bright, periodic U-shaped, and singular soliton solutions for Eq (1.1). Furthermore, this equation was investigated by other authors through the use of new precise solution techniques such the semi-inverse approach ^[56], the extended trial function method ^[57], the sine-Gordon and sinh-Gordon expansion methods ^[58], the Hamiltonian-based algorithm ^[59], Laplace-Adomian decomposition method ^[60], and other methods ^{[61,62,63,64,65]}.

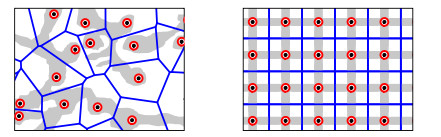
Inspired by current research, we seek to address gFKMNE expressed in (1.1) through two enhanced implementations of the $(\frac{G'}{G})$ -expansion technique: the extended $(\frac{G'}{G})$ -expansion method and the generalized $(r+\frac{G'}{G})$ -expansion method, which are based on the reduction of NFPDEs to integer-order NODEs produced by the model's wave transformation. The strategic techniques further transform the resultant NODEs into an algebraic system of nonlinear equations by assuming a series-form solution. These equations may then be solved using the Maple tool to produce dark soliton lattices for gFKMNE. The important solitons in these dark soliton lattices are organized regularly in an optical medium. Dark soliton formations are collections of dark solitaires arranged regularly inside a medium. They are frequently shaped like wave channels or optical fibers. Similar to the lattice of a crystal, these solitons are restricted to areas of decreased optical intensity within a larger field that retain their structure and amplitude while moving. Not only can dark soliton lattices be used to precisely control and manipulate optical waves, but they can also be used to process information and communications networks, provide insight into nonlinear optics phenomena, provide platforms for basic research on the behavior of wave propagation, and have potential applications in signal processing, optical communication, and sensing. Thus, dark soliton lattices offer a stimulating new topic for nonlinear optics research that will enable both basic and applied investigations ^[66,67,68].

The format of the present article is as follows: Section 1 provides an introduction. The operational mechanism for the $(\frac{G'}{G})$ -expansion methods and the description of gCFD are detailed in Section 2. We build many additional sets of optical soliton solutions for Eq (1.1) in Section 3. A few illustrations and a graphical representations of dark soliton lattices are presented and discussed in Section 4. Our study excursion comes to an end with the provided conclusion in Section 5.

2. Materials and methodology

In this section, the basic definition of used fractional derivative gCFD and the operational procedure of the proposed methods are presented.

2.1. The definition of gCFD

Explicit soliton solutions to nonlinear FPDEs can be obtained by taking use of the advantages that gCFDs have over conventional fractional derivative operators. Notably, alternate formulations of fractional derivatives do not provide the optical soliton solutions of Eq (1.1) because they violate the chain rule ^[69,70]. Consequently, gCFDs were added to Eq (1.1). ^[71] defined this derivative operator of order $\wp$ as follows:

$\begin{equation} ^{gCFD} D^\wp_\varphi z(\varphi) = \lim\limits_{\varpi \to 0} \frac{z( (\frac{\Gamma(n)}{\Gamma(n-\wp+1)})\varpi \varphi^{1-\wp}+\varphi)-z(\varphi)}{\varpi}, \quad \wp \in (0,1] \quad n \geq -1, \quad n \in R. \end{equation}$

(2.1)

We utilize the following characteristics of this derivative in this study:

$\begin{equation} ^{gCFD} D^\wp_\varphi \varphi^\gamma = \frac{\gamma \Gamma(n)}{\Gamma(n-\wp+1)} \varphi^{\gamma-\wp}, \quad \forall \gamma \in R, \end{equation}$

(2.2)

$\begin{equation} ^{gCFD} D^\wp_\varphi(\gamma_1\rho(\varphi)\pm \gamma_2\eta(\varphi)) = \gamma_1 {^{gCFD} D^\wp_\varphi(\rho(\varphi))}\pm \gamma_2 {^{gCFD} D^\wp_\varphi(\eta(\varphi))}, \end{equation}$

(2.3)

$\begin{equation} ^{gCFD} D^\wp_\varphi \omega[\zeta(\varphi)] = \omega'_\zeta(\zeta(\varphi)) {^{gCFD} D^\wp_\varphi \zeta(\varphi)} , \end{equation}$

(2.4)

where $\rho(\varphi)$ , $\eta(\varphi)$ , $\omega(\varphi)$ , and $\zeta(\varphi)$ are arbitrary differentiable functions, whereas $\gamma$ , $\gamma_1$ and $\gamma_2$ signify constants.

2.2. The working methodology of $(\frac{G'}{G})$ -expansion method

In this phase of our study, we discuss the processes of the $(\frac{G'}{G})$ -expansion approach, with a focus on solving the given general NFPDE:

$\begin{equation} R(z, D^{ \delta}_{t} z, D^{ \alpha}_{x_1}z, D^{ \beta}_{x_1} z,z D^{ \alpha}_{x_1} z, \ldots) = 0, \quad 0 < \alpha, \beta , \delta \leq1, \end{equation}$

(2.5)

where $z = z(t, x_1, x_2, x_3, \ldots, x_j)$ .

Equation (2.5) is solved using the following strategy:

(ⅰ). Starting with a variable transformation of the framework $z(t, x_1, x_2, x_3, \dots, x_j) = Z(\varphi)$ , where $\varphi$ can be stated in a number of ways. Equation (2.5) progresses via this transformation, resulting in the NODE that follows:

$\begin{equation} Q(Z,Z'Z,Z',\dots) = 0, \end{equation}$

(2.6)

where $Z' = \frac{d Z}{d\varphi}$ . On rare occasions, the NODE may become vulnerable to the homogeneous balancing principle due to the integration of Eq (2.6).

(ⅱ). Next, based on the method's version, we assume the following series-form solution for (2.6):

Version 1. For the extended $(\frac{G'}{G})$ -expansion method, we assume the following $(\frac{G'}{G})$ solution:

$\begin{equation} Z(\varphi) = \sum\limits_{l = -\rho}^{\rho}\tau_l(\frac{G'(\varphi)}{G(\varphi)})^l, \end{equation}$

(2.7)

Version 2. For the generalized $(r+\frac{G'}{G})$ -expansion method, we assume the following $(\frac{G'}{G})$ solution:

$\begin{equation} Z(\varphi) = \sum\limits_{l = -\rho}^{\rho}\tau_l(r+\frac{G'(\varphi)}{G(\varphi)})^l, \quad r \in R, \end{equation}$

(2.8)

where it is subsequently necessary to compute the values of $\tau_l's (l = -\rho... \rho)$ . The balance number $\rho$ , a positive integer in Eqs (2.7) and (2.8), can be found by homogeneously balancing the nonlinear terms and the derivative with the highest order terms in Eq (2.6). Greater accuracy can be achieved in determining the balance number $\rho$ by applying the following mathematical formulas:

$\begin{equation} D(\frac{d^p Z}{d\varphi^p}) = \rho+p, \ \ \text{and} \ \ D(Z^q (\frac{d^p Z}{d\varphi^p})^s) = \rho q+p(s+\rho), \end{equation}$

(2.9)

where $D$ expresses the degree of $Z(\varphi)$ , whereas $p, q$ , and $s$ are positive integers.

Moreover, the function $G(\varphi)$ in Eq (2.8) satisfies the subsequent second-order linear ODE:

$\begin{equation} G''(\varphi)+\lambda G'(\varphi)+\mu G(\varphi) = 0, \end{equation}$

(2.10)

where $\lambda, \mu$ are constants.

Moreover, with Eq (2.10)'s general solution, we have:

$\begin{equation} \bigg(\frac{G'(\varphi)}{G(\varphi)}\bigg) = \left\{ \begin{array}{ll} \frac{1}{2}\,{\frac {\sqrt {\kappa} \left( \nu_{{1}}\sinh \left( \frac{1}{2}\,\sqrt { \kappa}\varphi \right) +\nu_{{2}}\cosh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) \right) }{\nu_{{1}}\cosh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) +\nu_{{2}}\sinh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) }}-\frac{1}{2} \,\lambda, & \kappa < 0, \\ \frac{1}{2}\,{\frac {\sqrt {-\kappa} \left( -\nu_{{1}}\sin \left( \frac{1}{2}\,\sqrt {- \kappa}\varphi \right) +\nu_{{2}}\cos \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) \right) }{\nu_{{1}}\cos \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) +\nu_{{2}}\sin \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) }}-\frac{1}{2} \,\lambda, & \kappa > 0, \\ {\frac {\nu_{{2}}}{\nu_{{1}}+\nu_{{2}}\varphi}}, & \kappa = 0,\\ \end{array} \right. \end{equation}$

(2.11)

where $\kappa = \lambda^2-4\mu$ , while $\nu_1$ and $\nu_2$ in (2.11) are arbitrary constants.

(ⅲ). Next, we insert Eqs (2.8) or (2.7) into Eq (2.6) or into the Equation that we acquired from the integration of Eq (2.6), and we gather all the terms that have an analogous power of $(\frac{G'(\varphi)}{G(\varphi)})$ .

(ⅳ). The derived polynomial $(\frac{G'(\varphi)}{G(\varphi)})^i$ has all of its coefficients equal to zero, resulting in a collection of nonlinear algebraic equations in $\tau_l (l = -\rho..., \rho)$ , $\lambda$ , $\mu$ , and other necessary parameters.

(ⅴ). The unresolved parameters are discovered by using the Maple tool to solve the resulting system.

(ⅵ). To generate sets of soliton solutions for Eq (2.5), the values predicted from step 5 are subsequently substituted in Eqs (2.7) or (2.8), depending on the version.

3. Establishing optical soliton solutions for gFKMNE

We use the suggested methods in this section to build families of optical soliton solutions for (1.1). Using the subsequent wave modification as a component of the procedure, we can (1.1):

$\begin{equation} \begin{split} &z(x,y,t) = e^{i \xi} Z(\varphi),\quad \xi = \xi(t,x,y), \quad \varphi = \varphi(t,x,y), \\ & \varphi = {\frac {p_{{1}}\Gamma \left( n-\alpha+1 \right) {x}^{\alpha}}{\alpha \,\Gamma \left( n \right) }}+{\frac {p_{{2}}\Gamma \left( n-\beta+1 \right) {y}^{\beta}}{\beta\,\Gamma \left( n \right) }}-{\frac {\varrho\, \Gamma \left( n-\delta+1 \right) {t}^{\delta}}{\delta\,\Gamma \left( n \right) }}, \\ & \xi = -{\frac {q_{{1}}\Gamma \left( n-\alpha+1 \right) {x}^{\alpha}}{\alpha \,\Gamma \left( n \right) }}-{\frac {q_{{2}}\Gamma \left( n-\beta+1 \right) {y}^{\beta}}{\beta\,\Gamma \left( n \right) }}+{\frac { \omega\,\Gamma \left( n-\delta+1 \right) {t}^{\delta}}{\delta\, \Gamma \left( n \right) }}+\theta_{{0}}, \\ \end{split} \end{equation}$

(3.1)

where $Z(\varphi)$ symbolizes the amplitude part, $q_1$ and $q_2$ indicate wave numbers in the $x-$ and $y-$ directions, respectively, $\omega$ represents the frequency of the wave and $\theta_0$ is a constant, the parameters $p_1$ and $p_2$ indicate inverse width along the $x$ and $y$ directions, respectively, and $\varrho$ is used for the velocity, delivering the afterwards NODE from the real part of (1.1):

$\begin{equation} \begin{split} - a p_1 p_2 Z''-(\omega+a q_1 q_2) Z -2 b q_1 Z^3 = 0, \end{split} \end{equation}$

(3.2)

with the constraint from the imaginary part:

$\begin{equation} \varrho = -a \left( q_{{1}}p_{{2}}+q_{{2}}p_{{1}} \right). \end{equation}$

(3.3)

It is established that $\rho = 1$ when a homogeneous balancing condition between $Z''$ and $Z^3$ (given in (3.2)) has been created.

3.1. Implementation of the extended $(\frac{G'}{G})$ -expansion method

First, we wish to address (3.2) with the help of the extended $(\frac{G'}{G})$ -expansion method. Equation (2.7) yields the following closed form solution for (3.2) when $\rho = 1$ is substituted in it:

$\begin{equation} U(\varphi) = \sum\limits_{l = -1}^{1}\tau_l \bigg(\frac{G'(\varphi)}{G(\varphi)}\bigg)^l. \end{equation}$

(3.4)

By including (3.4) in (3.2) and bringing together terms with a comparable power of $\bigg(\frac{G'(\varphi)}{G(\varphi)}\bigg)$ , we get an expression based on the terms $\bigg(\frac{G'(\varphi)}{G(\varphi)}\bigg)$ . By setting the coefficients to zero, this formula can be converted into a set of algebraic nonlinear equations. The system can be solved using Maple in the following three cases of solutions:

Case 1.1.

$\begin{equation} \begin{split} &\tau_{{0}} = \frac{1}{2}\,{\frac {\tau_{{-1}}\lambda}{\mu}},\tau_{{1}} = 0,\tau_{ {-1}} = \tau_{{-1}},p_{{1}} = p_{{1}},p_{{2}} = p_{{2}},q_{{1}} = {\frac {ap_{ {1}}p_{{2}}{\mu}^{2}}{b{\tau_{{-1}}}^{2}}},\\ &q_{{2}} = q_{{2}},\omega = -\frac{1}{2} \,{\frac {ap_{{1}}p_{{2}} \left( -4\,\mu\,b{\tau_{{-1}}}^{2}+2\,a{\mu} ^{2}q_{{2}}+{\lambda}^{2}b{\tau_{{-1}}}^{2} \right) }{b{\tau_{{-1}}}^{ 2}}}. \end{split} \end{equation}$

(3.5)

Case 1.2.

$\begin{equation} \begin{split} &\tau_{{0}} = \frac{1}{2}\,\tau_{{1}}\lambda,\tau_{{1}} = \tau_{{1}},\tau_{{-1}} = 0 ,p_{{1}} = p_{{1}},p_{{2}} = p_{{2}},q_{{1}} = {\frac {ap_{{1}}p_{{2}}}{b{ \tau_{{1}}}^{2}}},\\ &q_{{2}} = q_{{2}},\omega = -\frac{1}{2}\,{\frac {ap_{{1}}p_{{2}} \left( -4\,\mu\,b{\tau_{{1}}}^{2}+2\,aq_{{2}}+{\lambda}^{2}b{\tau_{{1 }}}^{2} \right) }{b{\tau_{{1}}}^{2}}}. \end{split} \end{equation}$

(3.6)

Case 1.3.

$\begin{equation} \begin{split} \tau_{{0}} = \tau_{{0}},\tau_{{1}} = \tau_{{1}},\tau_{{-1}} = \tau_{{-1}},p _{{1}} = 0,p_{{2}} = p_{{2}},q_{{1}} = 0,q_{{2}} = q_{{2}},\omega = 0. \end{split} \end{equation}$

(3.7)

Considering case 1.1 and utilizing Eq (3.1), (3.4) and the corresponding general solution of (2.10), we construct the subsequent plethora of optical soliton solutions for (1.1):

Family 1.1.1. When $\tau > 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{1,1,1}(t,x,y) = & e^{i \xi}\bigg( \tau_{{-1}} \left( \frac{1}{2}\,{\frac {\sqrt {\kappa} \left( \nu_{{1}}\sinh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) +\nu_{{2}}\cosh \left( \frac{1}{2} \,\sqrt {\kappa}\varphi \right) \right) }{\nu_{{1}}\cosh \left( \frac{1}{2} \,\sqrt {\kappa}\varphi \right) +\nu_{{2}}\sinh \left( \frac{1}{2}\,\sqrt { \kappa}\varphi \right) }}-\frac{1}{2}\,\lambda \right) ^{-1}+\frac{1}{2}\,{\frac { \tau_{{-1}}\lambda}{\mu}} \bigg). \end{split} \end{equation}$

(3.8)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{1,1,2}(t,x,y) = & e^{i \xi}\bigg( {\frac {\tau_{{-1}}}{\frac{1}{2}\,\sqrt {\kappa}\coth \left( \frac{1}{2}\,\sqrt { \kappa}\varphi \right) -\frac{1}{2}\,\lambda}}+\frac{1}{2}\,{\frac {\tau_{{-1}} \lambda}{\mu}} \bigg). \end{split} \end{equation}$

(3.9)

(ⅲ) When $\nu_1\neq0$ , $\nu_2 = 0$

$\begin{equation} \begin{split} u_{1,1,3}(t,x,y) = & e^{i \xi}\bigg( {\frac {\tau_{{-1}}}{\frac{1}{2}\,\sqrt {\kappa}\tanh \left( \frac{1}{2}\,\sqrt { \kappa}\varphi \right) -\frac{1}{2}\,\lambda}}+\frac{1}{2}\,{\frac {\tau_{{-1}} \lambda}{\mu}} \bigg). \end{split} \end{equation}$

(3.10)

Family 1.1.2. When $\tau < 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{1,1,4}(t,x,y) = & e^{i \xi}\bigg( \tau_{{-1}} \left( \frac{1}{2}\,{\frac {\sqrt {-\kappa} \left( -\nu_{{1}}\sin \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) +\nu_{{2}}\cos \left( \frac{1}{2} \,\sqrt {-\kappa}\varphi \right) \right) }{\nu_{{1}}\cos \left( \frac{1}{2} \,\sqrt {-\kappa}\varphi \right) +\nu_{{2}}\sin \left( \frac{1}{2}\,\sqrt {- \kappa}\varphi \right) }}-\frac{1}{2}\,\lambda \right) ^{-1}+\frac{1}{2}\,{\frac { \tau_{{-1}}\lambda}{\mu}} \bigg). \end{split} \end{equation}$

(3.11)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{1,1,5}(t,x,y) = & e^{i \xi}\bigg( {\frac {\tau_{{-1}}}{\frac{1}{2}\,\sqrt {-\kappa}\cot \left( \frac{1}{2}\,\sqrt {- \kappa}\varphi \right) -\frac{1}{2}\,\lambda}}+\frac{1}{2}\,{\frac {\tau_{{-1}} \lambda}{\mu}} \bigg). \end{split} \end{equation}$

(3.12)

(ⅲ) When $\nu_1\neq0$ , $\nu_2 = 0$

$\begin{equation} \begin{split} u_{1,1,6}(t,x,y) = & e^{i \xi}\bigg( {\frac {\tau_{{-1}}}{-\frac{1}{2}\,\sqrt {-\kappa}\tan \left( \frac{1}{2}\,\sqrt {- \kappa}\varphi \right) -\frac{1}{2}\,\lambda}}+\frac{1}{2}\,{\frac {\tau_{{-1}} \lambda}{\mu}} \bigg). \end{split} \end{equation}$

(3.13)

Family 1.1.3. When $\tau = 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{1,1,7}(t,x,y) = & e^{i \xi}\bigg({\frac {\tau_{{-1}} \left( \nu_{{1}}+\nu_{{2}}\varphi \right) }{\nu_{ {2}}}}+\frac{1}{2}\,{\frac {\tau_{{-1}}\lambda}{\mu}} \bigg). \end{split} \end{equation}$

(3.14)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{1,1,8}(t,x,y) = & e^{i \xi}\bigg( {\frac {\tau_{{-1}}}{{\varphi }^{-1}-\frac{1}{2}\,\lambda}}+\frac{1}{2}\,{\frac {\tau_ {{-1}}\lambda}{\mu}} \bigg). \end{split} \end{equation}$

(3.15)

(ⅲ) When $\nu_1\neq0$ , $\nu_2 = 0$

$\begin{equation} \begin{split} u_{1,1,9}(t,x,y) = & e^{i \xi}\bigg( -2\,{\frac {\tau_{{-1}}}{\lambda}}+\frac{1}{2}\,{\frac {\tau_{{-1}}\lambda}{ \mu}} \bigg), \end{split} \end{equation}$

(3.16)

where $\varphi = {\frac {p_{{1}}\Gamma \left(n-\alpha+1 \right) {x}^{\alpha}}{\alpha \, \Gamma \left(n \right) }}+{\frac {p_{{2}}\Gamma \left(n-\beta+1 \right) {y}^{\beta}}{\beta\, \Gamma \left(n \right) }}-{\frac {\varrho\, \Gamma \left(n-\delta+1 \right) {t}^{\delta}}{\delta\, \Gamma \left(n \right) }}$ $\xi = -{\frac {q_{{1}}\Gamma \left(n-\alpha+1 \right) {x}^{\alpha}}{\alpha \, \Gamma \left(n \right) }}-{\frac {q_{{2}}\Gamma \left(n-\beta+1 \right) {y}^{\beta}}{\beta\, \Gamma \left(n \right) }}+{\frac { \omega\, \Gamma \left(n-\delta+1 \right) {t}^{\delta}}{\delta\, \Gamma \left(n \right) }}+\theta_{{0}}$ for $q_1$ and $\omega$ defined in Eq (3.5).

Considering case 1.2 and utilizing Eq (3.1), (3.4) and the corresponding general solution of (2.10), we construct the subsequent plethora of optical soliton solutions for (1.1):

Family 1.2.1. When $\tau > 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{1,2,1}(t,x,y) = & e^{i \xi}\bigg( \frac{1}{2}\,\tau_{{1}}\lambda+\tau_{{1}} \left( \frac{1}{2}\,{\frac {\sqrt {\kappa} \left( \nu_{{1}}\sinh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) +\nu _{{2}}\cosh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) \right) }{\nu_ {{1}}\cosh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) +\nu_{{2}}\sinh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) }}-\frac{1}{2}\,\lambda \right) \bigg). \end{split} \end{equation}$

(3.17)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{1,2,2}(t,x,y) = & e^{i \xi}\bigg( \frac{1}{2}\,\tau_{{1}}\lambda+\tau_{{1}} \left( \frac{1}{2}\,\sqrt {\kappa}\coth \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) -\frac{1}{2}\,\lambda \right) \bigg). \end{split} \end{equation}$

(3.18)

(ⅲ) When $\nu_1\neq0$ , $\nu_2 = 0$

$\begin{equation} \begin{split} u_{1,2,3}(t,x,y) = & e^{i \xi}\bigg( \frac{1}{2}\,\tau_{{1}}\lambda+\tau_{{1}} \left( \frac{1}{2}\,\sqrt {\kappa}\tanh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) -\frac{1}{2}\,\lambda \right) \bigg). \end{split} \end{equation}$

(3.19)

Family 1.2.2. When $\tau < 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{1,2,4}(t,x,y) = & e^{i \xi}\bigg( \frac{1}{2}\,\tau_{{1}}\lambda+\tau_{{1}} \left( \frac{1}{2}\,{\frac {\sqrt {-\kappa} \left( -\nu_{{1}}\sin \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) + \nu_{{2}}\cos \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) \right) }{ \nu_{{1}}\cos \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) +\nu_{{2}} \sin \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) }}-\frac{1}{2}\,\lambda \right) \bigg). \end{split} \end{equation}$

(3.20)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{1,2,5}(t,x,y) = & e^{i \xi}\bigg( \frac{1}{2}\,\tau_{{1}}\lambda+\tau_{{1}} \left( \frac{1}{2}\,\sqrt {-\kappa}\cot \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) -\frac{1}{2}\,\lambda \right) \bigg). \end{split} \end{equation}$

(3.21)

(ⅲ) When $\nu_1\neq0$ , $\nu_2 = 0$

$\begin{equation} \begin{split} u_{1,2,6}(t,x,y) = & e^{i \xi}\bigg( \frac{1}{2}\,\tau_{{1}}\lambda+\tau_{{1}} \left( -\frac{1}{2}\,\sqrt {-\kappa}\tan \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) -\frac{1}{2}\,\lambda \right) \bigg). \end{split} \end{equation}$

(3.22)

Family 1.2.3. When $\tau = 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{1,2,7}(t,x,y) = & e^{i \xi}\bigg( \frac{1}{2}\,\tau_{{1}}\lambda+{\frac {\tau_{{1}}\nu_{{2}}}{\nu_{{1}}+\nu_{{2} }\varphi }} \bigg). \end{split} \end{equation}$

(3.23)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{1,2,8}(t,x,y) = & e^{i \xi}\bigg( \frac{1}{2}\,\tau_{{1}}\lambda+\tau_{{1}} \left( {\varphi }^{-1}-\frac{1}{2}\,\lambda \right) \bigg), \end{split} \end{equation}$

(3.24)

Considering case 1.3 and utilizing Eq (3.1), (3.4) and the corresponding general solution of (2.10), we construct the subsequent plethora of optical soliton solutions for (1.1)

Family 1.3.1. When $\tau > 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{1,3,1}(t,x,y) = & e^{i \xi}\bigg( \tau_{{-1}} \left( \frac{1}{2}\,{\frac {\sqrt {\kappa} \left( \nu_{{1}}\sinh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) +\nu_{{2}}\cosh \left( \frac{1}{2} \,\sqrt {\kappa}\varphi \right) \right) }{\nu_{{1}}\cosh \left( \frac{1}{2} \,\sqrt {\kappa}\varphi \right) +\nu_{{2}}\sinh \left( \frac{1}{2}\,\sqrt { \kappa}\varphi \right) }}-\frac{1}{2}\,\lambda \right) ^{-1}\\ &+\tau_{{0}}+\tau_ {{1}} \left( \frac{1}{2}\,{\frac {\sqrt {\kappa} \left( \nu_{{1}}\sinh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) +\nu_{{2}}\cosh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) \right) }{\nu_{{1}}\cosh \left( \frac{1}{2}\,\sqrt { \kappa}\varphi \right) +\nu_{{2}}\sinh \left( \frac{1}{2}\,\sqrt {\kappa} \varphi \right) }}-\frac{1}{2}\,\lambda \right) \bigg). \end{split} \end{equation}$

(3.25)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{1,3,2}(t,x,y) = & e^{i \xi}\bigg( {\frac {\tau_{{-1}}}{\frac{1}{2}\,\sqrt {\kappa}\coth \left( \frac{1}{2}\,\sqrt { \kappa}\varphi \right) -\frac{1}{2}\,\lambda}}+\tau_{{0}}+\tau_{{1}} \left( \frac{1}{2} \sqrt {\kappa}\coth \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) -\frac{1}{2}\lambda \right) \bigg). \end{split} \end{equation}$

(3.26)

(ⅲ) When $\nu_1\neq0$ , $\nu_2 = 0$

$\begin{equation} \begin{split} u_{1,3,3}(t,x,y) = & e^{i \xi}\bigg( {\frac {\tau_{{-1}}}{\frac{1}{2}\,\sqrt {\kappa}\tanh \left( \frac{1}{2}\,\sqrt { \kappa}\varphi \right) -\frac{1}{2}\,\lambda}}+\tau_{{0}}+\tau_{{1}} \left( \frac{1}{2} \sqrt {\kappa}\tanh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) -\frac{1}{2} \lambda \right) \bigg). \end{split} \end{equation}$

(3.27)

Family 1.3.2. When $\tau < 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{1,3,4}(t,x,y) = & e^{i \xi}\bigg( \tau_{{-1}} \left( \frac{1}{2}\,{\frac {\sqrt {-\kappa} \left( -\nu_{{1}}\sin \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) +\nu_{{2}}\cos \left( \frac{1}{2} \,\sqrt {-\kappa}\varphi \right) \right) }{\nu_{{1}}\cos \left( \frac{1}{2} \,\sqrt {-\kappa}\varphi \right) +\nu_{{2}}\sin \left( \frac{1}{2}\,\sqrt {- \kappa}\varphi \right) }}-\frac{1}{2}\,\lambda \right) ^{-1}\\ &+\tau_{{0}}+\tau_ {{1}} \left( \frac{1}{2}\,{\frac {\sqrt {-\kappa} \left( -\nu_{{1}}\sin \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) +\nu_{{2}}\cos \left( \frac{1}{2} \,\sqrt {-\kappa}\varphi \right) \right) }{\nu_{{1}}\cos \left( \frac{1}{2} \,\sqrt {-\kappa}\varphi \right) +\nu_{{2}}\sin \left( \frac{1}{2}\,\sqrt {- \kappa}\varphi \right) }}-\frac{1}{2}\,\lambda \right) \bigg). \end{split} \end{equation}$

(3.28)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{1,3,5}(t,x,y) = & e^{i \xi}\bigg( {\frac {\tau_{{-1}}}{\frac{1}{2}\,\sqrt {-\kappa}\cot \left( \frac{1}{2}\,\sqrt {- \kappa}\varphi \right) -\frac{1}{2}\,\lambda}}+\tau_{{0}}+\tau_{{1}} \left( \frac{1}{2} \sqrt {-\kappa}\cot \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) -\frac{1}{2}\lambda \right) \bigg). \end{split} \end{equation}$

(3.29)

(ⅲ) When $\nu_1\neq0$ , $\nu_2 = 0$

$\begin{equation} \begin{split} u_{1,3,6}(t,x,y) = & e^{i \xi}\bigg( {\frac {\tau_{{-1}}}{-\frac{1}{2}\,\sqrt {-\kappa}\tan \left( \frac{1}{2}\,\sqrt {- \kappa}\varphi \right) -\frac{1}{2}\,\lambda}}+\tau_{{0}}+\tau_{{1}} \left( - \frac{1}{2}\,\sqrt {-\kappa}\tan \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) - \frac{1}{2}\,\lambda \right) \bigg). \end{split} \end{equation}$

(3.30)

Family 1.3.3. When $\tau = 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{1,3,7}(t,x,y) = & e^{i \xi}\bigg( {\frac {\tau_{{-1}} \left( \nu_{{1}}+\nu_{{2}}\varphi \right) }{\nu_{ {2}}}}+\tau_{{0}}+{\frac {\tau_{{1}}\nu_{{2}}}{\nu_{{1}}+\nu_{{2}} \varphi }} \bigg). \end{split} \end{equation}$

(3.31)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{1,3,8}(t,x,y) = & e^{i \xi}\bigg( {\frac {\tau_{{-1}}}{{\varphi }^{-1}-\frac{1}{2}\,\lambda}}+\tau_{{0}}+\tau_{{ 1}} \left( {\varphi }^{-1}-\frac{1}{2}\,\lambda \right) \bigg). \end{split} \end{equation}$

(3.32)

(ⅲ) When $\nu_1\neq0$ , $\nu_2 = 0$

$\begin{equation} \begin{split} u_{1,3,9}(t,x,y) = & e^{i \xi}\bigg( -2\,{\frac {\tau_{{-1}}}{\lambda}}+\tau_{{0}}-\frac{1}{2}\,\tau_{{1}}\lambda \bigg), \end{split} \end{equation}$

(3.33)

where $\varphi = {\frac {p_{{2}}\Gamma \left(n-\beta+1 \right) {y}^{\beta}}{\beta\, \Gamma \left(n \right) }}-{\frac {\varrho\, \Gamma \left(n-\delta+1 \right) {t}^{\delta}}{\delta\, \Gamma \left(n \right) }} \xi = -{\frac {q_{{2}}\Gamma \left(n-\beta+1 \right) {y}^{\beta}}{\beta\, \Gamma \left(n \right) }}+\theta_{{0}}$ .

3.2. Implementation of the generalized $(r+\frac{G'}{G})$ -expansion method

Now, we wish to address (3.2) with the help of the generalized $(r+\frac{G'}{G})$ -expansion method. Equation (2.8) yields the following closed-form solution for (3.2) when $\rho = 1$ is substituted in it:

$\begin{equation} U(\varphi) = \sum\limits_{l = -1}^{1}\tau_l \bigg(r+\frac{G'(\varphi)}{G(\varphi)}\bigg)^l. \end{equation}$

(3.34)

We obtain an expression based on the terms $\bigg(r+\frac{G'(\varphi)}{G(\varphi)}\bigg)$ by including (3.34) in (3.2) and combining terms with similar powers of $\bigg(r+\frac{G'(\varphi)}{G(\varphi)}\bigg)$ . By setting the coefficients to zero, this formula can be converted into a set of algebraic nonlinear equations. Following Maple's solution to this system, the following six cases of solutions are generated:

Case 2.1.

$\begin{equation} \begin{split} \tau_{{0}} = \tau_{{0}},\tau_{{1}} = 0,\tau_{{-1}} = -\tau_{{0}}\sqrt { \kappa},p_{{1}} = p_{{1}},p_{{2}} = p_{{2}},q_{{1}} = 0,q_{{2}} = q_{{2}}, \omega = \kappa\,ap_{{1}}p_{{2}},r = \frac{1}{2}\,\lambda+\frac{1}{2}\,\sqrt {\kappa}. \end{split} \end{equation}$

(3.35)

Case 2.2.

$\begin{equation} \begin{split} &\tau_{{0}} = \tau_{{0}},\tau_{{1}} = 0,\tau_{{-1}} = -2\,{\frac {\tau_{{0}} \left( {r}^{2}-\lambda\,r+\mu \right) }{2\,r-\lambda}},p_{{1}} = p_{{1} },q_{{1}} = \frac{1}{4}\,{\frac { \left( 4\,{r}^{2}-4\,\lambda\, r+{\lambda}^{2} \right) ap_{{1}}p_{{2}}}{{\tau_{{0}}}^{2}b}},\\ &q_{{2}} = q _{{2}},\omega = -\frac{1}{4}\,{\frac { \left( 4\,aq_{{2}}{r}^{2}-4\,aq_{{2}} \lambda\,r-8\,{\tau_{{0}}}^{2}b\mu+2\,{\tau_{{0}}}^{2}b{\lambda}^{2}+a q_{{2}}{\lambda}^{2} \right) ap_{{1}}p_{{2}}}{{\tau_{{0}}}^{2}b}},p_{{2}} = p_{{2}},r = r. \end{split} \end{equation}$

(3.36)

Case 2.3.

$\begin{equation} \begin{split} &\tau_{{0}} = \frac{1}{2}\,\tau_{{1}}\lambda-\tau_{{1}}r,\tau_{{1}} = \tau_{{1}}, \tau_{{-1}} = 0,p_{{1}} = p_{{1}},p_{{2}} = p_{{2}},q_{{1}} = {\frac {ap_{{1}} p_{{2}}}{b{\tau_{{1}}}^{2}}},\\ &q_{{2}} = q_{{2}},\omega = -\frac{1}{2}\,{\frac {ap_{ {1}}p_{{2}} \left( {\lambda}^{2}b{\tau_{{1}}}^{2}+2\,aq_{{2}}-4\,\mu\, b{\tau_{{1}}}^{2} \right) }{b{\tau_{{1}}}^{2}}},r = r. \end{split} \end{equation}$

(3.37)

Case 2.4.

$\begin{equation} \begin{split} &\tau_{{0}} = 0,\tau_{{1}} = \tau_{{1}},\tau_{{-1}} = -\mu\,\tau_{{1}}+\frac{1}{4}\, \tau_{{1}}{\lambda}^{2},p_{{1}} = p_{{1}},p_{{2}} = p_{{2}},q_{{1}} = { \frac {ap_{{1}}p_{{2}}}{b{\tau_{{1}}}^{2}}},\\ &q_{{2}} = q_{{2}},\omega = -{ \frac {ap_{{1}}p_{{2}} \left( -8\,\mu\,b{\tau_{{1}}}^{2}+2\,{\lambda}^ {2}b{\tau_{{1}}}^{2}+aq_{{2}} \right) }{b{\tau_{{1}}}^{2}}},r = \frac{1}{2}\, \lambda. \end{split} \end{equation}$

(3.38)

Case 2.5.

$\begin{equation} \begin{split} &\tau_{{0}} = \tau_{{0}},\tau_{{1}} = 0,\tau_{{-1}} = -2\,\tau_{{0}} \left( \frac{1}{2}\,\lambda+\frac{1}{2}\,\sqrt {-\kappa} \right) +\lambda\,\tau_{{0}},p_{{1}} = p_{{1}},p_{{2}} = p_{{2}},q_{{1}} = -\frac{1}{4}\,{\frac {\kappa\,ap_{{1}}p_{{2}} }{{\tau_{{0}}}^{2}b}},\\ &q_{{2}} = q_{{2}},\omega = -\frac{1}{4}\,{\frac { \left( -8 \,{\tau_{{0}}}^{2}b\mu+2\,{\tau_{{0}}}^{2}b{\lambda}^{2}+4\,aq_{{2}} \mu-aq_{{2}}{\lambda}^{2} \right) ap_{{1}}p_{{2}}}{{\tau_{{0}}}^{2}b}} ,r = \frac{1}{2}\,\lambda+\frac{1}{2}\,\sqrt {-\kappa}. \end{split} \end{equation}$

(3.39)

Case 2.6.

$\begin{equation} \begin{split} &\tau_{{0}} = 0,\tau_{{1}} = \tau_{{1}},\tau_{{-1}} = \mu\,\tau_{{1}}-\frac{1}{4}\, \tau_{{1}}{\lambda}^{2},p_{{1}} = p_{{1}},p_{{2}} = p_{{2}},q_{{1}} = { \frac {ap_{{1}}p_{{2}}}{b{\tau_{{1}}}^{2}}},\\ &q_{{2}} = q_{{2}},\omega = -{ \frac {ap_{{1}}p_{{2}} \left( 4\,\mu\,b{\tau_{{1}}}^{2}-{\lambda}^{2}b {\tau_{{1}}}^{2}+aq_{{2}} \right) }{b{\tau_{{1}}}^{2}}},r = \frac{1}{2}\,\lambda. \end{split} \end{equation}$

(3.40)

Considering case 2.1 and utilizing Eq (3.1), (3.34) and the corresponding general solution of Eq (2.10), we construct the subsequent plethora of optical soliton solutions for (1.1):

Family 2.1.1. When $\tau > 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,1,1}(t,x,y) = & e^{i \xi}\bigg( -\tau_{{0}}\sqrt {\kappa} \left( \frac{1}{2}\,\sqrt {\kappa}+\frac{1}{2}\,{\frac { \sqrt {\kappa} \left( \nu_{{1}}\sinh \left( \frac{1}{2}\,\sqrt {\kappa} \varphi \right) +\nu_{{2}}\cosh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) \right) }{\nu_{{1}}\cosh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) +\nu_{{2}}\sinh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) }} \right) ^{-1}+\tau_{{0}} \bigg). \end{split} \end{equation}$

(3.41)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,1,2}(t,x,y) = & e^{i \xi}\bigg( -{\frac {\tau_{{0}}\sqrt {\kappa}}{\frac{1}{2}\,\sqrt {\kappa}+\frac{1}{2}\,\sqrt { \kappa}\coth \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) }}+\tau_{{0}} \bigg). \end{split} \end{equation}$

(3.42)

(ⅲ) When $\nu_1\neq0$ , $\nu_2 = 0$

$\begin{equation} \begin{split} u_{2,1,3}(t,x,y) = & e^{i \xi}\bigg( -{\frac {\tau_{{0}}\sqrt {\kappa}}{\frac{1}{2}\,\sqrt {\kappa}+\frac{1}{2}\,\sqrt { \kappa}\tanh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) }}+\tau_{{0}} \bigg). \end{split} \end{equation}$

(3.43)

Family 2.1.2. When $\tau < 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,1,4}(t,x,y) = & e^{i \xi}\bigg( -\tau_{{0}}\sqrt {\kappa} \left( \frac{1}{2}\,\sqrt {\kappa}+\frac{1}{2}\,{\frac { \sqrt {-\kappa} \left( -\nu_{{1}}\sin \left( \frac{1}{2}\,\sqrt {-\kappa} \varphi \right) +\nu_{{2}}\cos \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) \right) }{\nu_{{1}}\cos \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) +\nu_{{2}}\sin \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) }} \right) ^{-1}+\tau_{{0}} \bigg). \end{split} \end{equation}$

(3.44)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,1,5}(t,x,y) = & e^{i \xi}\bigg( -{\frac {\tau_{{0}}\sqrt {\kappa}}{\frac{1}{2}\,\sqrt {\kappa}+\frac{1}{2}\,\sqrt {- \kappa}\cot \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) }}+\tau_{{0}} \bigg). \end{split} \end{equation}$

(3.45)

(ⅲ) When $\nu_1\neq0$ , $\nu_2 = 0$

$\begin{equation} \begin{split} u_{2,1,6}(t,x,y) = & e^{i \xi}\bigg( -{\frac {\tau_{{0}}\sqrt {\kappa}}{\frac{1}{2}\,\sqrt {\kappa}-\frac{1}{2}\,\sqrt {- \kappa}\tan \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) }}+\tau_{{0}} \bigg). \end{split} \end{equation}$

(3.46)

Family 2.1.3. When $\tau = 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,1,7}(t,x,y) = & e^{i \xi}\bigg( -\tau_{{0}}\sqrt {\kappa} \left( \frac{1}{2}\,\lambda+\frac{1}{2}\,\sqrt {\kappa}+{ \frac {\nu_{{2}}}{\nu_{{1}}+\nu_{{2}}\varphi }} \right) ^{-1}+\tau_{{0 }} \bigg). \end{split} \end{equation}$

(3.47)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,1,8}(t,x,y) = & e^{i \xi}\bigg( -{\frac {\tau_{{0}}\sqrt {\kappa}}{\frac{1}{2}\,\sqrt {\kappa}+{\varphi }^{-1} }}+\tau_{{0}} \bigg). \end{split} \end{equation}$

(3.48)

(ⅲ) When $\nu_1\neq0$ , $\nu_2 = 0$

$\begin{equation} \begin{split} u_{2,1,9}(t,x,y) = & -\tau_{{0}} e^{i \xi}, \end{split} \end{equation}$

(3.49)

Considering case 2.2 and utilizing Eq (3.1), (3.34) and the corresponding general solution of Eq (2.10), we construct the subsequent plethora of optical soliton solutions for (1.1):

Family 2.2.1. When $\tau > 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,2,1}(t,x,y) = & e^{i \xi}\bigg( \frac{ -2\,\tau_{{0}} ( {r}^{2}-\lambda\,r+\mu ) }{( 2\,r- \lambda ) \left( r+\frac{1}{2}\,{\frac {\sqrt {\kappa} \left( \nu_ {{1}}\sinh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) +\nu_{{2}}\cosh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) \right) }{\nu_{{1}}\cosh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) +\nu_{{2}}\sinh \left( \frac{1}{2} \,\sqrt {\kappa}\varphi \right) }}-\frac{1}{2}\,\lambda \right) }+\tau_{{0 }} \bigg). \end{split} \end{equation}$

(3.50)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,2,2}(t,x,y) = & e^{i \xi}\bigg( -2\,{\frac {\tau_{{0}} \left( {r}^{2}-\lambda\,r+\mu \right) }{ \left( 2\,r-\lambda \right) \left( r+\frac{1}{2}\,\sqrt {\kappa}\coth \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) -\frac{1}{2}\,\lambda \right) }}+ \tau_{{0}} \bigg). \end{split} \end{equation}$

(3.51)

(ⅲ) When $\nu_1\neq0$ , $\nu_2 = 0$

$\begin{equation} \begin{split} u_{2,2,3}(t,x,y) = & e^{i \xi}\bigg( -2\,{\frac {\tau_{{0}} \left( {r}^{2}-\lambda\,r+\mu \right) }{ \left( 2\,r-\lambda \right) \left( r+\frac{1}{2}\,\sqrt {\kappa}\tanh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) -\frac{1}{2}\,\lambda \right) }}+ \tau_{{0}} \bigg). \end{split} \end{equation}$

(3.52)

Family 2.2.2. When $\tau < 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,2,4}(t,x,y) = & e^{i \xi}\bigg( \frac{ -2\,\tau_{{0}} ( {r}^{2}-\lambda\,r+\mu ) }{ ( 2\,r- \lambda ) \left( r+\frac{1}{2}\,{\frac {\sqrt {-\kappa} \left( - \nu_{{1}}\sin \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) +\nu_{{2}} \cos \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) \right) }{\nu_{{1}} \cos \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) +\nu_{{2}}\sin \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) }}-\frac{1}{2}\,\lambda \right) }+\tau_{{0}} \bigg). \end{split} \end{equation}$

(3.53)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,2,5}(t,x,y) = & e^{i \xi}\bigg( -2\,{\frac {\tau_{{0}} \left( {r}^{2}-\lambda\,r+\mu \right) }{ \left( 2\,r-\lambda \right) \left( r+\frac{1}{2}\,\sqrt {-\kappa}\cot \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) -\frac{1}{2}\,\lambda \right) }}+ \tau_{{0}} \bigg). \end{split} \end{equation}$

(3.54)

(ⅲ) When $\nu_1\neq0$ , $\nu_2 = 0$

$\begin{equation} \begin{split} u_{2,2,6}(t,x,y) = & e^{i \xi}\bigg( -2\,{\frac {\tau_{{0}} \left( {r}^{2}-\lambda\,r+\mu \right) }{ \left( 2\,r-\lambda \right) \left( r-\frac{1}{2}\,\sqrt {-\kappa}\tan \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) -\frac{1}{2}\,\lambda \right) }}+ \tau_{{0}} \bigg). \end{split} \end{equation}$

(3.55)

Family 2.2.3. When $\tau = 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,2,7}(t,x,y) = & e^{i \xi}\bigg( -2\,\tau_{{0}} \left( {r}^{2}-\lambda\,r+\mu \right) \left( 2\,r- \lambda \right) ^{-1} \left( r+{\frac {\nu_{{2}}}{\nu_{{1}}+\nu_{{2}} \varphi }} \right) ^{-1}+\tau_{{0}} \bigg). \end{split} \end{equation}$

(3.56)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,2,8}(t,x,y) = & e^{i \xi}\bigg( -2\,{\frac {\tau_{{0}} \left( {r}^{2}-\lambda\,r+\mu \right) }{ \left( 2\,r-\lambda \right) \left( r+{\varphi }^{-1}-\frac{1}{2}\,\lambda \right) }}+\tau_{{0}} \bigg). \end{split} \end{equation}$

(3.57)

(ⅲ) When $\nu_1\neq0$ , $\nu_2 = 0$

$\begin{equation} \begin{split} u_{2,2,9}(t,x,y) = & e^{i \xi}\bigg( -2\,{\frac {\tau_{{0}} \left( {r}^{2}-\lambda\,r+\mu \right) }{ \left( 2\,r-\lambda \right) \left( r-\frac{1}{2}\,\lambda \right) }}+\tau_{{0 }} \bigg), \end{split} \end{equation}$

(3.58)

Considering case 2.3 and utilizing Eq (3.1), (3.34) and the corresponding general solution of Eq (2.10), we construct the subsequent plethora of optical soliton solutions for (1.1):

Family 2.3.1. When $\tau > 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,3,1}(t,x,y) = & e^{i \xi}\bigg( \frac{1}{2}\,\tau_{{1}}\lambda-\tau_{{1}}r+\tau_{{1}} \left( r+\frac{1}{2}\,{\frac { \sqrt {\kappa} \left( \nu_{{1}}\sinh \left( \frac{1}{2}\,\sqrt {\kappa} \varphi \right) +\nu_{{2}}\cosh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) \right) }{\nu_{{1}}\cosh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) +\nu_{{2}}\sinh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) }} -\frac{1}{2}\,\lambda \right) \bigg). \end{split} \end{equation}$

(3.59)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,3,2}(t,x,y) = & e^{i \xi}\bigg( \frac{1}{2}\,\tau_{{1}}\lambda-\tau_{{1}}r+\tau_{{1}} \left( r+\frac{1}{2}\,\sqrt { \kappa}\coth \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) -\frac{1}{2}\,\lambda \right) \bigg). \end{split} \end{equation}$

(3.60)

(ⅲ) When $\nu_1\neq0$ , $\nu_2 = 0$

$\begin{equation} \begin{split} u_{2,3,3}(t,x,y) = & e^{i \xi}\bigg( \frac{1}{2}\,\tau_{{1}}\lambda-\tau_{{1}}r+\tau_{{1}} \left( r+\frac{1}{2}\,\sqrt { \kappa}\tanh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) -\frac{1}{2}\,\lambda \right) \bigg). \end{split} \end{equation}$

(3.61)

Family 2.3.2. When $\tau < 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,3,4}(t,x,y) = & e^{i \xi}\bigg( \frac{1}{2}\,\tau_{{1}}\lambda-\tau_{{1}}r+\tau_{{1}} \left( r+\frac{1}{2}\,{\frac { \sqrt {-\kappa} \left( -\nu_{{1}}\sin \left( \frac{1}{2}\,\sqrt {-\kappa} \varphi \right) +\nu_{{2}}\cos \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) \right) }{\nu_{{1}}\cos \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) +\nu_{{2}}\sin \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) }} -\frac{1}{2}\,\lambda \right) \bigg). \end{split} \end{equation}$

(3.62)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,3,5}(t,x,y) = & e^{i \xi}\bigg( \frac{1}{2}\,\tau_{{1}}\lambda-\tau_{{1}}r+\tau_{{1}} \left( r+\frac{1}{2}\,\sqrt {- \kappa}\cot \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) -\frac{1}{2}\,\lambda \right) \bigg). \end{split} \end{equation}$

(3.63)

(ⅲ) When $\nu_1\neq0$ , $\nu_2 = 0$

$\begin{equation} \begin{split} u_{2,3,6}(t,x,y) = & e^{i \xi}\bigg( \frac{1}{2}\,\tau_{{1}}\lambda-\tau_{{1}}r+\tau_{{1}} \left( r-\frac{1}{2}\,\sqrt {- \kappa}\tan \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) -\frac{1}{2}\,\lambda \right) \bigg). \end{split} \end{equation}$

(3.64)

Family 2.3.3. When $\tau = 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,3,7}(t,x,y) = & e^{i \xi}\bigg( \frac{1}{2}\,\tau_{{1}}\lambda-\tau_{{1}}r+\tau_{{1}} \left( r+{\frac {\nu_{{2 }}}{\nu_{{1}}+\nu_{{2}}\varphi }} \right) \bigg). \end{split} \end{equation}$

(3.65)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,3,8}(t,x,y) = & e^{i \xi}\bigg( \frac{1}{2}\,\tau_{{1}}\lambda-\tau_{{1}}r+\tau_{{1}} \left( r+{\varphi }^{-1} -\frac{1}{2}\,\lambda \right) \bigg). \end{split} \end{equation}$

(3.66)

(ⅲ) When $\nu_1\neq0$ , $\nu_2 = 0$

$\begin{equation} \begin{split} u_{2,3,9}(t,x,y) = & e^{i \xi}\bigg( \frac{1}{2}\,\tau_{{1}}\lambda-\tau_{{1}}r+\tau_{{1}} \left( r-\frac{1}{2}\,\lambda \right) \bigg), \end{split} \end{equation}$

(3.67)

Considering case 2.4 and utilizing Eq (3.1), (3.34) and the corresponding general solution of Eq (2.10), we construct the subsequent plethora of optical soliton solutions for (1.1):

Family 2.4.1. When $\tau > 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,4,1}(t,x,y) = & e^{i \xi}\bigg( 2\,{\frac { \left( -\mu\,\tau_{{1}}+\frac{1}{4}\,\tau_{{1}}{\lambda}^{2} \right) \left( \nu_{{1}}\cosh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) +\nu_{{2}}\sinh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) \right) }{\sqrt {\kappa} \left( \nu_{{1}}\sinh \left( \frac{1}{2}\,\sqrt { \kappa}\varphi \right) +\nu_{{2}}\cosh \left( \frac{1}{2}\,\sqrt {\kappa} \varphi \right) \right) }}\\ &+\frac{1}{2}\,{\frac {\tau_{{1}}\sqrt {\kappa} \left( \nu_{{1}}\sinh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) +\nu _{{2}}\cosh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) \right) }{\nu_ {{1}}\cosh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) +\nu_{{2}}\sinh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) }} \bigg). \end{split} \end{equation}$

(3.68)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,4,2}(t,x,y) = & e^{i \xi}\bigg( 2\,{\frac {-\mu\,\tau_{{1}}+\frac{1}{4}\,\tau_{{1}}{\lambda}^{2}}{\sqrt { \kappa}\coth \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) }}+\frac{1}{2}\,\tau_{ {1}}\sqrt {\kappa}\coth \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) \bigg). \end{split} \end{equation}$

(3.69)

(ⅲ) When $\nu_1\neq0$ , $\nu_2 = 0$

$\begin{equation} \begin{split} u_{2,4,3}(t,x,y) = & e^{i \xi}\bigg( 2\,{\frac {-\mu\,\tau_{{1}}+\frac{1}{4}\,\tau_{{1}}{\lambda}^{2}}{\sqrt { \kappa}\tanh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) }}+\frac{1}{2}\,\tau_{ {1}}\sqrt {\kappa}\tanh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) \bigg). \end{split} \end{equation}$

(3.70)

Family 2.4.2. When $\tau < 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,4,4}(t,x,y) = & e^{i \xi}\bigg( 2\,{\frac { \left( -\mu\,\tau_{{1}}+\frac{1}{4}\,\tau_{{1}}{\lambda}^{2} \right) \left( \nu_{{1}}\cos \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) +\nu_{{2}}\sin \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) \right) }{\sqrt {-\kappa} \left( -\nu_{{1}}\sin \left( \frac{1}{2}\,\sqrt {- \kappa}\varphi \right) +\nu_{{2}}\cos \left( \frac{1}{2}\,\sqrt {-\kappa} \varphi \right) \right) }}\\ &+\frac{1}{2}\,{\frac {\tau_{{1}}\sqrt {-\kappa} \left( -\nu_{{1}}\sin \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) + \nu_{{2}}\cos \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) \right) }{ \nu_{{1}}\cos \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) +\nu_{{2}} \sin \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) }} \bigg). \end{split} \end{equation}$

(3.71)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,4,5}(t,x,y) = & e^{i \xi}\bigg( 2\,{\frac {-\mu\,\tau_{{1}}+\frac{1}{4}\,\tau_{{1}}{\lambda}^{2}}{\sqrt {- \kappa}\cot \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) }}+\frac{1}{2}\,\tau_{ {1}}\sqrt {-\kappa}\cot \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) \bigg). \end{split} \end{equation}$

(3.72)

(ⅲ) When $\nu_1\neq0$ , $\nu_2 = 0$

$\begin{equation} \begin{split} u_{2,4,6}(t,x,y) = & e^{i \xi}\bigg( -2\,{\frac {-\mu\,\tau_{{1}}+\frac{1}{4}\,\tau_{{1}}{\lambda}^{2}}{\sqrt {- \kappa}\tan \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) }}-\frac{1}{2}\,\tau_{ {1}}\sqrt {-\kappa}\tan \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) \bigg). \end{split} \end{equation}$

(3.73)

Family 2.4.3. When $\tau = 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,4,7}(t,x,y) = & e^{i \xi}\bigg( \left( -\mu\,\tau_{{1}}+\frac{1}{4}\,\tau_{{1}}{\lambda}^{2} \right) \left( \frac{1}{2}\,\lambda+{\frac {\nu_{{2}}}{\nu_{{1}}+\nu_{{2}}\varphi }} \right) ^{-1}+\tau_{{1}} \left( \frac{1}{2}\,\lambda+{\frac {\nu_{{2}}}{\nu_{{1}}+\nu_ {{2}}\varphi }} \right) \bigg). \end{split} \end{equation}$

(3.74)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,4,8}(t,x,y) = & e^{i \xi}\bigg( \left( -\mu\,\tau_{{1}}+\frac{1}{4}\,\tau_{{1}}{\lambda}^{2} \right) \varphi +{\frac {\tau_{{1}}}{\varphi }} \bigg), \end{split} \end{equation}$

(3.75)

Considering case 2.5 and utilizing Eq (3.1), (3.34) and the corresponding general solution of Eq (2.10), we construct the subsequent plethora of optical soliton solutions for (1.1):

Family 2.5.1. When $\tau > 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,5,1}(t,x,y) = & e^{i \xi}\bigg( \frac{ \left( -2\,\tau_{{0}} \left( \frac{1}{2}\,\lambda+\frac{1}{2}\,\sqrt {-\kappa} \right) +\lambda\,\tau_{{0}} \right) }{ \left( \frac{1}{2}\,\sqrt {-\kappa}+\frac{1}{2} \,{\frac {\sqrt {\kappa} \left( \nu_{{1}}\sinh \left( \frac{1}{2}\,\sqrt { \kappa}\varphi \right) +\nu_{{2}}\cosh \left( \frac{1}{2}\,\sqrt {\kappa} \varphi \right) \right) }{\nu_{{1}}\cosh \left( \frac{1}{2}\,\sqrt {\kappa} \varphi \right) +\nu_{{2}}\sinh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) }} \right) }+\tau_{{0}} \bigg). \end{split} \end{equation}$

(3.76)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,5,2}(t,x,y) = & e^{i \xi}\bigg( {\frac {-2\,\tau_{{0}} \left( \frac{1}{2}\,\lambda+\frac{1}{2}\,\sqrt {-\kappa} \right) +\lambda\,\tau_{{0}}}{\frac{1}{2}\,\sqrt {-\kappa}+\frac{1}{2}\,\sqrt {\kappa }\coth \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) }}+\tau_{{0}} \bigg). \end{split} \end{equation}$

(3.77)

(ⅲ) When $\nu_1\neq0$ , $\nu_2 = 0$

$\begin{equation} \begin{split} u_{2,5,3}(t,x,y) = & e^{i \xi}\bigg( {\frac {-2\,\tau_{{0}} \left( \frac{1}{2}\,\lambda+\frac{1}{2}\,\sqrt {-\kappa} \right) +\lambda\,\tau_{{0}}}{\frac{1}{2}\,\sqrt {-\kappa}+\frac{1}{2}\,\sqrt {\kappa }\tanh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) }}+\tau_{{0}} \bigg). \end{split} \end{equation}$

(3.78)

Family 2.5.2. When $\tau < 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,5,4}(t,x,y) = & e^{i \xi}\bigg( \frac{ \left( -2\,\tau_{{0}} \left( \frac{1}{2}\,\lambda+\frac{1}{2}\,\sqrt {-\kappa} \right) +\lambda\,\tau_{{0}} \right) }{ \left( \frac{1}{2}\,\sqrt {-\kappa}+\frac{1}{2} \,{\frac {\sqrt {-\kappa} \left( -\nu_{{1}}\sin \left( \frac{1}{2}\,\sqrt {- \kappa}\varphi \right) +\nu_{{2}}\cos \left( \frac{1}{2}\,\sqrt {-\kappa} \varphi \right) \right) }{\nu_{{1}}\cos \left( \frac{1}{2}\,\sqrt {-\kappa} \varphi \right) +\nu_{{2}}\sin \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) }} \right) }+\tau_{{0}} \bigg). \end{split} \end{equation}$

(3.79)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,5,5}(t,x,y) = & e^{i \xi}\bigg( {\frac {-2\,\tau_{{0}} \left( \frac{1}{2}\,\lambda+\frac{1}{2}\,\sqrt {-\kappa} \right) +\lambda\,\tau_{{0}}}{\frac{1}{2}\,\sqrt {-\kappa}+\frac{1}{2}\,\sqrt {- \kappa}\cot \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) }}+\tau_{{0}} \bigg). \end{split} \end{equation}$

(3.80)

(ⅲ) When $\nu_1\neq0$ , $\nu_2 = 0$

$\begin{equation} \begin{split} u_{2,5,6}(t,x,y) = & e^{i \xi}\bigg( {\frac {-2\,\tau_{{0}} \left( \frac{1}{2}\,\lambda+\frac{1}{2}\,\sqrt {-\kappa} \right) +\lambda\,\tau_{{0}}}{\frac{1}{2}\,\sqrt {-\kappa}-\frac{1}{2}\,\sqrt {- \kappa}\tan \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) }}+\tau_{{0}} \bigg). \end{split} \end{equation}$

(3.81)

Family 2.5.3. When $\tau = 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,5,7}(t,x,y) = & e^{i \xi}\bigg( \left( -2\,\tau_{{0}} \left( \frac{1}{2}\,\lambda+\frac{1}{2}\,\sqrt {-\kappa} \right) +\lambda\,\tau_{{0}} \right) \left( \frac{1}{2}\,\lambda+\frac{1}{2}\,\sqrt {-\kappa}+{\frac {\nu_{{2}}}{\nu_{{1}}+\nu_{{2}}\varphi }} \right) ^{- 1}+\tau_{{0}} \bigg). \end{split} \end{equation}$

(3.82)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,5,8}(t,x,y) = & e^{i \xi}\bigg( {\frac {-2\,\tau_{{0}} \left( \frac{1}{2}\,\lambda+\frac{1}{2}\,\sqrt {-\kappa} \right) +\lambda\,\tau_{{0}}}{\frac{1}{2}\,\sqrt {-\kappa}+{\varphi }^{-1}}}+ \tau_{{0}} \bigg). \end{split} \end{equation}$

(3.83)

(ⅲ) When $\nu_1\neq0$ , $\nu_2 = 0$

$\begin{equation} \begin{split} u_{2,5,9}(t,x,y) = & e^{i \xi}\bigg( 2\,{\frac {-2\,\tau_{{0}} \left( \frac{1}{2}\,\lambda+\frac{1}{2}\,\sqrt {-\kappa} \right) +\lambda\,\tau_{{0}}}{\sqrt {-\kappa}}}+\tau_{{0}} \bigg), \end{split} \end{equation}$

(3.84)

Considering case 2.6 and utilizing Eq (3.1), (3.34) and the corresponding general solution of Eq (2.10), we construct the subsequent plethora of optical soliton solutions for (1.1):

Family 2.6.1. When $\tau > 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,6,1}(t,x,y) = & e^{i \xi}\bigg( 2\,{\frac { \left( \mu\,\tau_{{1}}-\frac{1}{4}\,\tau_{{1}}{\lambda}^{2} \right) \left( \nu_{{1}}\cosh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) +\nu_{{2}}\sinh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) \right) }{\sqrt {\kappa} \left( \nu_{{1}}\sinh \left( \frac{1}{2}\,\sqrt { \kappa}\varphi \right) +\nu_{{2}}\cosh \left( \frac{1}{2}\,\sqrt {\kappa} \varphi \right) \right) }}\\ &+\frac{1}{2}\,{\frac {\tau_{{1}}\sqrt {\kappa} \left( \nu_{{1}}\sinh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) +\nu _{{2}}\cosh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) \right) }{\nu_ {{1}}\cosh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) +\nu_{{2}}\sinh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) }} \bigg). \end{split} \end{equation}$

(3.85)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,6,2}(t,x,y) = & e^{i \xi}\bigg( 2\,{\frac {\mu\,\tau_{{1}}-\frac{1}{4}\,\tau_{{1}}{\lambda}^{2}}{\sqrt {\kappa }\coth \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) }}+\frac{1}{2}\,\tau_{{1}} \sqrt {\kappa}\coth \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) \bigg). \end{split} \end{equation}$

(3.86)

(ⅲ) When $\nu_1\neq0$ , $\nu_2 = 0$

$\begin{equation} \begin{split} u_{2,6,3}(t,x,y) = & e^{i \xi}\bigg( 2\,{\frac {\mu\,\tau_{{1}}-\frac{1}{4}\,\tau_{{1}}{\lambda}^{2}}{\sqrt {\kappa }\tanh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) }}+\frac{1}{2}\,\tau_{{1}} \sqrt {\kappa}\tanh \left( \frac{1}{2}\,\sqrt {\kappa}\varphi \right) \bigg). \end{split} \end{equation}$

(3.87)

Family 2.6.2. When $\tau < 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,6,4}(t,x,y) = & e^{i \xi}\bigg( 2\,{\frac { \left( \mu\,\tau_{{1}}-\frac{1}{4}\,\tau_{{1}}{\lambda}^{2} \right) \left( \nu_{{1}}\cos \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) +\nu_{{2}}\sin \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) \right) }{\sqrt {-\kappa} \left( -\nu_{{1}}\sin \left( \frac{1}{2}\,\sqrt {- \kappa}\varphi \right) +\nu_{{2}}\cos \left( \frac{1}{2}\,\sqrt {-\kappa} \varphi \right) \right) }}\\ &+\frac{1}{2}\,{\frac {\tau_{{1}}\sqrt {-\kappa} \left( -\nu_{{1}}\sin \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) + \nu_{{2}}\cos \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) \right) }{ \nu_{{1}}\cos \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) +\nu_{{2}} \sin \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) }} \bigg). \end{split} \end{equation}$

(3.88)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,6,5}(t,x,y) = & e^{i \xi}\bigg( 2\,{\frac {\mu\,\tau_{{1}}-\frac{1}{4}\,\tau_{{1}}{\lambda}^{2}}{\sqrt {- \kappa}\cot \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) }}+\frac{1}{2}\,\tau_{ {1}}\sqrt {-\kappa}\cot \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) \bigg). \end{split} \end{equation}$

(3.89)

(ⅲ) When $\nu_1\neq0$ , $\nu_2 = 0$

$\begin{equation} \begin{split} u_{2,6,6}(t,x,y) = & e^{i \xi}\bigg( -2\,{\frac {\mu\,\tau_{{1}}-\frac{1}{4}\,\tau_{{1}}{\lambda}^{2}}{\sqrt {- \kappa}\tan \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) }}-\frac{1}{2}\,\tau_{ {1}}\sqrt {-\kappa}\tan \left( \frac{1}{2}\,\sqrt {-\kappa}\varphi \right) \bigg). \end{split} \end{equation}$

(3.90)

Family 2.6.3. When $\tau = 0$ ,

(ⅰ) When $\nu_1\neq0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,6,7}(t,x,y) = & e^{i \xi}\bigg( \left( \mu\,\tau_{{1}}-\frac{1}{4}\,\tau_{{1}}{\lambda}^{2} \right) \left( \frac{1}{2}\lambda+{\frac {\nu_{{2}}}{\nu_{{1}}+\nu_{{2}}\varphi }} \right) ^ {-1}+\tau_{{1}} \left( \frac{1}{2}\,\lambda+{\frac {\nu_{{2}}}{\nu_{{1}}+\nu_{ {2}}\varphi }} \right) \bigg). \end{split} \end{equation}$

(3.91)

(ⅱ) When $\nu_1 = 0$ , $\nu_2\neq0$

$\begin{equation} \begin{split} u_{2,6,8}(t,x,y) = & e^{i \xi}\bigg( \left( \mu\,\tau_{{1}}-\frac{1}{4}\,\tau_{{1}}{\lambda}^{2} \right) \varphi + {\frac {\tau_{{1}}}{\varphi }} \bigg), \end{split} \end{equation}$

(3.92)

4. Discussion and graphs

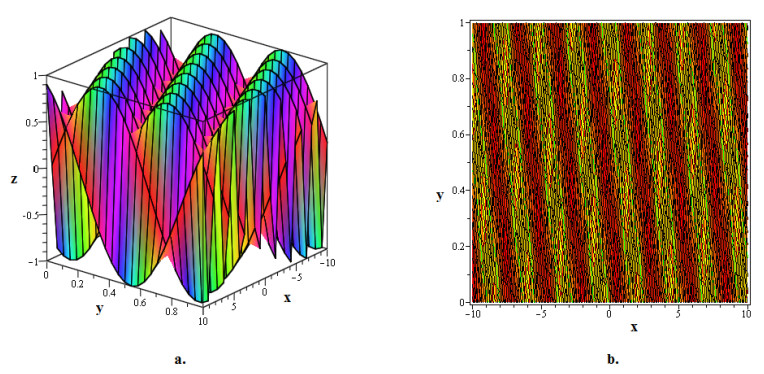
We present graphic representations of several wave patterns observed in the (2+1)-dimensional gFKMNE under study in this section. In contour and 3D visuals, we found and visualized wave patterns using the extended $(\frac{G'}{G})$ -expansion method and generalized $(r+\frac{G'}{G})$ -expansion method. The depictions show that the created soliton solutions, often referred to as dark soliton lattices, are cyclically structured in optical media. Dark soliton formations are collections of dark solitaires arranged regularly inside a medium. They are frequently shaped like wave channels or optical fibers. Similar to the lattice of a crystal, these solitons are restricted to areas of decreased optical intensity within a larger field that retain their structure and amplitude while moving. Not only can dark soliton lattices be used to precisely control and manipulate optical waves, but also to process information and communications networks, provide insight into nonlinear optics phenomena, provide platforms for basic research on the behavior of wave propagation, and have potential applications in signal processing, optical communication, and sensing. Thus, dark soliton lattices offer a stimulating new topic for nonlinear optics research that will enable both basic and applied investigations.

Figure 1. The 3D and contour visuals of the periodic soliton solution

$u_{1,1,2}$ articulated in (3.9) are graphed for

$\lambda = 4,\mu = 3,n = 2,\alpha = 1,\beta = 1$ ,

$\delta = 1,\tau_{{-1}} = 5,p_{{1}} = 2 ,p_{{2}} = 1$ ,

$q_{{2}} = 5,a = 10,b = 3,\theta_{{0}} = 0,t = 0$ .

DownLoad: Full-Size Img PowerPoint

Figure 2. The 3D and contour visuals of the periodic soliton solution

$u_{1,1,6}$ articulated in (3.13) are graphed for

$\lambda = 1,\mu = 2,n = 2,\alpha = 1$ ,

$\beta = 1,\delta = 0.9,\tau_{{-1}} = 10,p_{{1 }} = 3,p_{{2}} = 4$ ,

$q_{{2}} = 1,a = 2,b = 4,\theta_{{0}} = 1,t = 10$ .

DownLoad: Full-Size Img PowerPoint

Figure 3. The 3D and contour visuals of the periodic soliton solution

$u_{1,1,8}$ articulated in (3.15) are graphed for

$\lambda = 4,\mu = 4,n = 2,\alpha = 0.7,\beta = 0.8,\delta = 0.9$ ,

$\tau_{{-1}} = 5, p_{{1}} = 1,p_{{2}} = 2$ ,

$q_{{2}} = 3,a = 5,b = 1,\theta_{{0}} = 2,t = 20$ .

DownLoad: Full-Size Img PowerPoint

Figure 4. The 3D and contour visuals of the periodic soliton solution

$u_{1,2,3}$ articulated in (3.19) are graphed for

$\lambda = 4,\mu = 1,n = 3,\alpha = 0.3,\beta = 0.5$ ,

$\delta = 0.2,\tau_{{1}} = 6,p _{{1}} = 3,p_{{2}} = 1$ ,

$q_{{2}} = 7,a = 10,b = 10,\theta_{{0}} = 1,t = 50$ .

DownLoad: Full-Size Img PowerPoint

Figure 5. The 3D and contour visuals of the periodic soliton solution

$u_{2,2,3}$ articulated in (3.52) are graphed for

$\lambda = 3,\mu = 1,n = 1,\alpha = 1,\beta = 1$ ,

$\delta = 1,\tau_{{0}} = 6,p_{{1}} = 10 ,p_{{2}} = 5$ ,

$q_{{2}} = 6,a = 2,b = 2,\theta_{{0}} = 0,t = 100,r = 1$ .

DownLoad: Full-Size Img PowerPoint

Figure 6. The 3D and contour visuals of the periodic soliton solution

$u_{2,2,8}$ articulated in (3.57) are graphed for

$\lambda = 6,\mu = 9,n = 2,\alpha = 1,\beta = 1,\delta = 0.5$ ,

$\tau_{{0}} = 1,p_{{1}} = 20,p_{{2}} = 1,q_{{2}} = 8$ ,

$a = 1,b = 4,\theta_{{0}} = 100,t = 30,r = 10$ .

DownLoad: Full-Size Img PowerPoint

Figure 7. The 3D and contour visuals of the periodic soliton solution

$u_{2,4,2}$ articulated in (3.69) are graphed for

$\lambda = 5,\mu = 0,n = 1,\alpha = 1,\beta = 0.9$ ,

$\delta = 0.5,\tau_{{1}} = 1,p_{{ 1}} = 5,p_{{2}} = 3$ ,

$q_{{2}} = 1,a = 2,b = 5,\theta_{{0}} = 0,t = 50$ .

DownLoad: Full-Size Img PowerPoint

Figure 8. The 3D and contour visuals of the periodic soliton solution

$u_{2,4,6}$ articulated in (3.73) are graphed for

$\lambda = 0,\mu = 1,n = 2,\alpha = 1,\beta = 1$ ,

$\delta = 1,\tau_{{1}} = 15,p_{{1}} = 2 ,p_{{2}} = 7$ ,

$q_{{2}} = 3,a = 5,b = 10,\theta_{{0}} = 1,t = 100$ .

DownLoad: Full-Size Img PowerPoint

5. Conclusions

In summary, this study derived optical soliton solutions for the (2+1)-dimensional gFKMNE, a nonlinear model that explains pulse transmission in communication structures and optical fibers. The two improved versions of the $(\frac{G'}{G})$ -expansion method were the extended $(\frac{G'}{G})$ -expansion method and the generalized $(r+\frac{G'}{G})$ -expansion method. These techniques relied on the model's wave translation into integer-order NODEs. By assuming a series-form solution, the strategic techniques further turned the resulting NODEs into a system of nonlinear algebraic equations. Using the Maple program, these equations were solved to produce the gFKMNE's optical soliton solutions. In comparison with the extended $(\frac{G'}{G})$ -expansion method, it was observed that the generalized $(r+\frac{G'}{G})$ -expansion method produced more families of optical soliton solutions. Furthermore, all of the results obtained by the extended $(\frac{G'}{G})$ -expansion method could be obtained from the results of the generalized $(r+\frac{G'}{G})$ -expansion method with $r = 0$ . As a result, the generalized $(r+\frac{G'}{G})$ -expansion method was found to be more effective and superior. Furthermore, using 3D and contour visuals, it was demonstrated that the generated soliton solutions are periodically structured in optical media, which are called dark soliton lattices. Such dark soliton lattices have applications in optical communications, optical signal processing, and nonlinear optics, among other areas. Moreover, the effectiveness and dependability of the methods used in this study show how widely relevant they are to nonlinear issues in a range of scientific fields. The soliton dynamics and their implications for the models studied have been greatly improved by the $(\frac{G'}{G})$ -expansion approaches; however, it is important to recognize that this technique has limitations, especially when the highest derivative is not uniformly balanced with the nonlinear term. Notwithstanding this shortcoming, the paper highlights the amount of unaddressed concerns regarding nonlinear behavior and soliton dynamics and provides fresh avenues for future research in the area.

References

[1]	R. A Adams, J. J. F Fournier, Sobolev Spaces, Netherlands: Elsevier, 2003.
[2]	S. K. Berberian, Measure and Integration, New York: Chelsea Pub, 1970.
[3]	D. Cioranescu, J. S. J. Paulin, Homogenization in open sets with holes, J Math Anal Appl, 71 (1979), 590–607. https://doi.org/10.1016/0022-247X(79)90211-7 doi: 10.1016/0022-247X(79)90211-7
[4]	D. J. Daley, D. Vere-Jones, An Introduction to the Theory of Point Processes, New York: Springer-Verlag, 1988.
[5]	Ricardo G Durán and Maria Amelia Muschietti. The Korn inequality for Jones domains. Electron. J. Differ. Equ., 2004 (2004), 1–10. Available from: http://ejde.math.txstate.edu
[6]	L. C. Evans, Partial Differential Equations, Providence: American Mathematical Society, 2010.
[7]	M. Gahn, M. Neuss-Radu, P. Knabner, Homogenization of reaction–diffusion processes in a two-component porous medium with nonlinear flux conditions at the interface, SIAM Journal on Applied Mathematics, 76 (2016), 1819–1843. https://doi.org/10.1137/15M1018484 doi: 10.1137/15M1018484
[8]	A. Giunti, Derivation of Darcy's law in randomly punctured domains, arXiv: 2101.01046, [preprint], (2021) [cited 2023 November 20]. Available from: https://doi.org/10.48550/arXiv.2101.01046
[9]	N. Guillen, I. Kim, Quasistatic droplets in randomly perforated domains, Arch Ration Mech Anal, 215 (2015), 211–281. https://doi.org/10.1007/s00205-014-0777-2 doi: 10.1007/s00205-014-0777-2
[10]	M. Heida, An extension of the stochastic two-scale convergence method and application, Asymptot. Anal., 72 (2011), 1–30. https://doi.org/10.3233/ASY-2010-1022 doi: 10.3233/ASY-2010-1022
[11]	M. Höpker, Extension Operators for Sobolev Spaces on Periodic Domains, Their Applications, and Homogenization of a Phase Field Model for Phase Transitions in Porous Media, (German), Doctoral Thesis of University Bremen, Bremen, 2016.
[12]	M. Höpker, M. Böhm, A note on the existence of extension operators for Sobolev spaces on periodic domains, Comptes Rendus Math., 352 (2014), 807–810. https://doi.org/10.1016/j.crma.2014.09.002 doi: 10.1016/j.crma.2014.09.002
[13]	P. W Jones, Quasiconformal mappings and extendability of functions in Sobolev spaces, Acta Math., 147 (1981), 71–88.
[14]	J. L. Kelley, General Topology, New York: Van Nostrand, 1955.
[15]	S. M. Kozlov, Averaging of random operators, Matematicheskii Sbornik, 151 (1979), 188–202. https://doi.org/10.1070/SM1980v037n02ABEH001948 doi: 10.1070/SM1980v037n02ABEH001948
[16]	U. Krengel, A. Brunel, Ergodic theorems, Berlin: Walter de Gruyter, 1985.
[17]	P. Marcellini, C. Sbordone, Homogenization of non-uniformly elliptic operators, Appl Anal, 8 (1978), 101–113. https://doi.org/10.1080/00036817808839219 doi: 10.1080/00036817808839219
[18]	G. Matheron, Random sets and integral geometry, New York: Wiley, 1975.
[19]	J. Mecke, Stationäre zufällige Maße auf lokalkompakten abelschen Gruppen, Probab Theory Relat Fields, 9 (1967), 36–58. https://doi.org/10.1007/BF00535466 doi: 10.1007/BF00535466
[20]	J. A. Nitsche, On Korn's second inequality, RAIRO. Analyse numérique, 15 (1981), 237–248.
[21]	O. A. Oleïnik, A. S Shamaev, G. A Yosifian, Mathematical problems in elasticity and homogenization, Netherlands: Elsevier Science, 2009.
[22]	G. C. Papanicolaou, S. R. S. Varadhan, Boundary value problems with rapidly oscillating random coefficients, Colloq. Math. Soc. János Bolyai, 27 (1979), 835–873.
[23]	G Papanicolau, A Bensoussan, J. L Lions, Asymptotic analysis for periodic structures, Netherlands: Elsevier, 1978.
[24]	A. Piatnitski, M. Ptashnyk, Homogenization of biomechanical models of plant tissues with randomly distributed cells, Nonlinearity, 33 (2020), 5510. https://doi.org/10.1088/1361-6544/ab95ab doi: 10.1088/1361-6544/ab95ab
[25]	B. Schweizer, Partielle Differentialgleichungen: Eine Anwendungsorientierte Einfuhrung, Berlin: Springer, 2013.
[26]	Elias M Stein, Singular integrals and differentiability properties of functions (PMS-30), Princeton NJ: Princeton University Press, 2016.
[27]	A. A. Tempel'man, Ergodic theorems for general dynamical systems. Trudy Moskovskogo Matematicheskogo Obshchestva, 26 (1972), 95–132.
[28]	G. Xia, The stretch factor of the delaunay triangulation is less than 1.998, SIAM J Sci Comput, 42 (2013), 1620–1659. https://doi.org/10.1137/110832458 doi: 10.1137/110832458
[29]	C. L. Yao, G. Chen, T. D. Guo, Large deviations for the graph distance in supercritical continuum percolation, J Appl Prob, 48 (2011), 154–172. https://doi.org/10.1239/jap/1300198142 doi: 10.1239/jap/1300198142
[30]	G. Yosifian, Homogenization of some contact problems for the system of elasticity in perforated domains, Rendiconti del Seminario Matematico della Università di Padova, 105 (2001), 37–64.
[31]	G. A Yosifian, Some unilateral boundary-value problems for elastic bodies with rugged boundaries, J. Math. Sci., 108 (2002), 574–607. https://doi.org/10.1023/A:1013162423511 doi: 10.1023/A:1013162423511
[32]	M. Zaehle, Random processes of hausdorff rectifiable closed sets, Math. Nachr., 108 (1982), 49–72. https://doi.org/10.1002/mana.19821080105 doi: 10.1002/mana.19821080105

Reader Comments

Your name:*

Email:*
© 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)