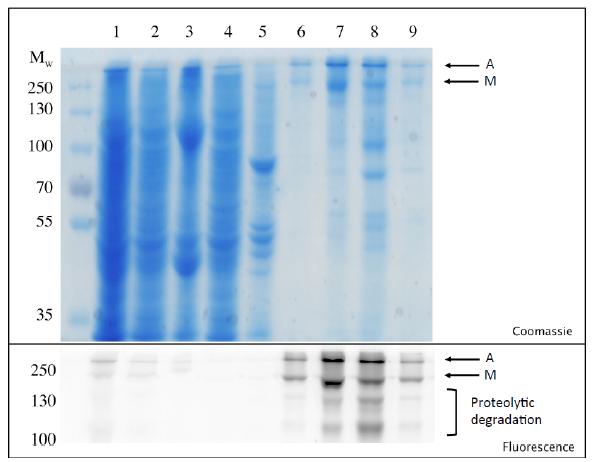
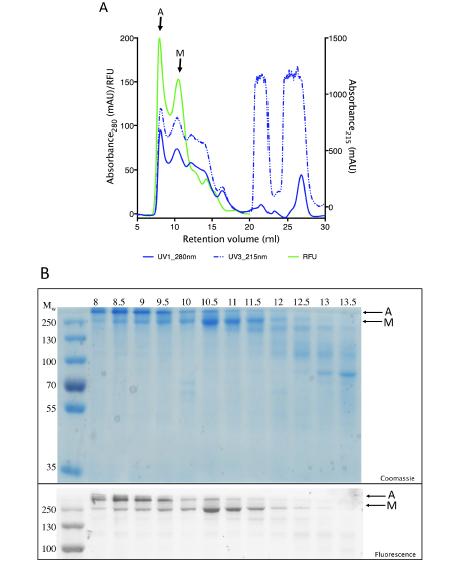
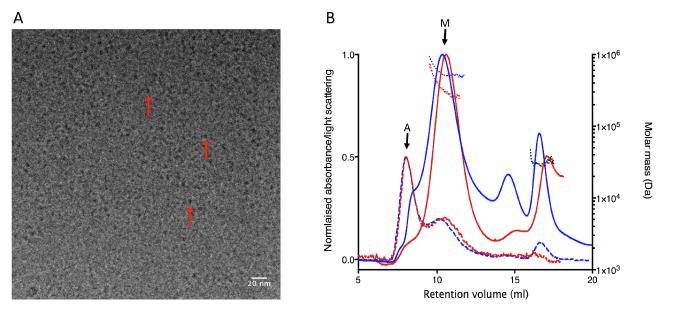
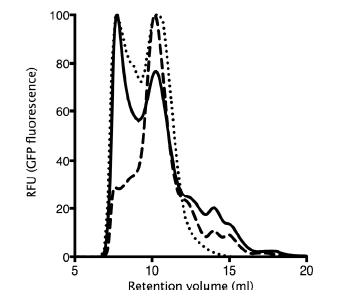
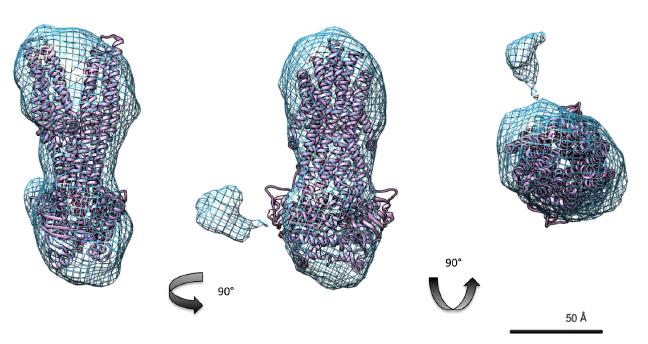
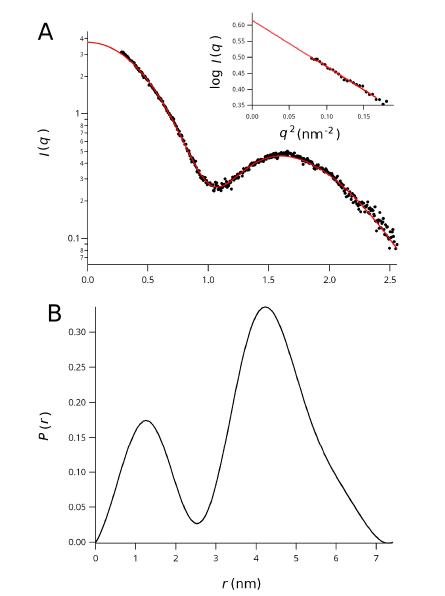
The cystic fibrosis transmembrane conductance regulator protein (CFTR) is a chloride channel highly expressed in the gills of Salmo salar, with a role in osmoregulation. It shares 60% identity with the human CFTR channel, mutations to which can cause the common genetic disorder cystic fibrosis CF. The expression and localisation of salmon CFTR have been investigated, but the isolated protein has not been extensively characterised. Here we present a protocol for the purification of recombinant salmon CFTR, along with biophysical and structural characterisation of the purified protein. Salmon CFTR was overexpressed in Saccharomyces cerevisiae, solubilised in the detergent LPG-14 and chromatographically purified by nickel-affinity and size-exclusion chromatography methods. Prior to size-exclusion chromatography samples of salmon CFTR had low purity, and contained large quantities of aggregated protein. Compared to size-exclusion chromatography profiles of other orthologues of CFTR, which had less evidence of aggregation, salmon CFTR appeared to have lower intrinsic stability than human and platypus CFTR. Nonetheless, repeated size-exclusion chromatography allowed monodisperse salmon CFTR to be isolated, and multi-angle light scattering was used to determine its oligomeric state. The monodispersity of the sample and its oligomeric state were confirmed using cryo-electron microscopy and small-angle X-ray scattering (SAXS). These data were also processed to calculate a low-resolution structure of the salmon CFTR, which showed similar architecture to other ATP-binding cassette proteins.
1.
Introduction
Rolling mill is a key equipment in the steel industry and an important equipment in the modern heavy machinery field. It is a complex working system, and its safe and stable operation is crucial to ensure efficient production of rolled products. With the development of society, higher requirements have been put forward for the surface quality of strip mills, so the requirements of high precision and high dynamic performance have been promoted for rolling mills [1]. However, the high rolling speed and strength of modern rolling mills often result in unstable rolls during the rolling process. For example, due to the presence of many nonlinear factors within the system, the rolling mill roll system exhibits complex nonlinear vibration characteristics. When rolling high strength and thin strip steel, the mill frequently appears "ghost" vibration, which mostly includes vertical vibration, horizontal vibration, axial oscillation, transverse and longitudinal vibration of the strip steel, torsional vibration, and axial vibration of the main drive system [2]. These vibrations seriously affect the working performance and reliability of the rolling mill system and restrict the stability of the rolling production process [3,4]. Therefore, it is necessary to strengthen the analysis and study of the vibration causes of rolling mill and deal with the problems in time to ensure the stable operation of the equipment.
The study of nonlinear dynamics of vibration in rolling systems has attracted widespread attention and has been ongoing for decades. Many experts and scholars have conducted many beneficial exploratory studies from various angles. These researchers mainly focus on why rolling mills vibrate, how they vibrate, and how to suppress vibration (see [5,6,7,8,9,10,11,12,13] and the reference therein). The authors in [5] assumed that the workpiece is an elastic part with linear stiffness and established a linear vertical vibration model for the rolling mill frame based on linear vibration theory. In order to study the vibration characteristics of the rolling mill, the authors in [6] studied the effect of tension on nonlinear vibration of rolling mills. By changing the external excitation frequency to analyze the stability of the rolling mill vibration system, it was concluded that rolling speed and strip thickness have a significant impact on system stability. A horizontal friction vibration model of the rolling mill rolls was established in [7], and simulation analysis was conducted under the conditions of eliminating the bearing clearance of the rolling mill frame and adding a floating support for the coupling. By analyzing the effects of changes in workpiece thickness and motor speed on the connection angle and roll gap friction, a nonlinear torsional vibration model of the rolling mill was established in [9], indicating that reducing damping coefficient and nonlinear stiffness helps to reduce vibration intensity. In terms of research on vibration control, the authors in [11] designed a global sliding mode controller for the rolling mill drive system to suppress the uncertainty of rolling parameters and achieved good tracking performance. In [12], a displacement time-delay feedback link was introduced to control the vibration of the roller system, and different time-delay parameters were selected to test the control effect. The research results indicated that appropriate time-delay feedback parameters can suppress the unstable vibration of the roller system. The authors in [13] studied the vibration characteristics of the corrugated roller system and designed a time-delay feedback controller to control the parameter excitation vibration of the system.
In recent years, fractional calculus and its application in different fields have attracted widespread attention, providing a very useful mathematical tool for describing the memory and genetics of various materials and processes, such as fractional modeling of robotic manipulator [14], bibliographic analysis on artificial neural networks based on fractional calculus [15], fractional model of cerebral aneurysm [16], fractional model of ENSO phenomenon [17], fractional mechanics [18], fractional memristor circuit [19], fractional infectious disease model [20], and so on. Even if all individuals in the system have integer order dynamic characteristics, the overall dynamic characteristics of the system may still be fractional order. It can better describe the viscoelasticity of materials, such as suspension [21], air spring [22], magneto rheological damper [23] and hydraulic bushing [24]. In the research of rolling systems, fractional calculus has also begun to be involved [25,26,27,28]. Among them, the authors in [26,27] introduced a fractional derivative term when establishing a horizontal nonlinear vibration model for rolling mills. In [28], the resonance characteristics of the fractional roller system under high-frequency and low-frequency excitation signals were studied.
With the continuous development of active control technology, there is an increasing amount of research on actively utilizing time-delay feedback to achieve various control objectives. Time-delayed feedback control, as an effective control method, has been widely applied in the field of vibration control [29,30,31]. Adding fractional order factors to the simulation of rolling mill systems is more reasonable, but there are many problems that need to be solved urgently in the current research on fractional order nonlinear systems. For example, complex dynamic characteristics such as the influence of system parameters on periodic solutions under time-delay feedback, as well as many problems such as bifurcation control, require further research. Therefore, based on the superiority of fractional calculus and time-delayed feedback control, it is necessary to study the dynamic characteristics of fractional order nonlinear rolling systems and the bifurcation control problem under time-delayed feedback, which has important theoretical significance and application value. Motivated by [13,26,27,28], we focus on the vibration characteristics of the system and time-delay feedback controllability of the horizontal nonlinear roller system, and corrects the expression errors in existing literature. The innovation lies in systematically studying the resonance of fractional roller systems and conducting corresponding vibration control, further validating the effectiveness of the theoretical research through numerical simulation, providing new ideas for the research of roller system vibration theory.
The paper is organized as follows: In the second section, the fractional derivative term is considered in the horizontal nonlinear roller system, and the nonlinear vibration model is established. In the third section, the amplitude-frequency response equations of the primary resonance and time-delay feedback control are obtained using the multiple scale method, and numerical analysis is conducted. In the fourth section, we mainly present the amplitude-frequency response equations of the secondary resonance and time-delay feedback control and analyze the numerical simulation results to verify the effectiveness of theoretical research. The comparison of approximate analytical solution and numerical solution is fulfilled in the fifth section. In the last section, we conclude this paper.
2.
Nonlinear vibration model
2.1. Problem formulation
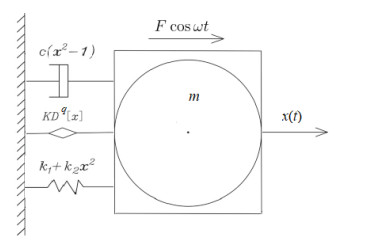
Referring to the model of the horizontal roller system in [26,27,28], in order to study the nonlinear vibration characteristics of the strip rolling mill in the horizontal direction, the Duffing and the Van der Pol oscillators were introduced, and the nonlinear damping and stiffness within interface of the rolling mill were considered to establish a fractional horizontal nonlinear parametric vibration model for the rolling mill work roll, as shown in Figure 1.
The vibration model can be given by a second-order non-autonomous differential equation as follows
where $ x $ is the horizontal displacement of the roller system and is a function of time $ t $, $ m $ is equivalent mass of the roll, $ c(x^2-1) $ represents nonlinear damping coefficient term between roller system and rolling piece, $ c $ is the nonlinear damping coefficient. $ k_1+k_2x^2 $ represents nonlinear stiffness coefficient term between roller system and frame, and $ k_1 $ is the linear stiffness coefficient, $ k_2 $ is the nonlinear stiffness coefficient. $ D_t^{q}x $ is the $ q $-order derivative of $ x $ with respect to time represents fractional derivative term, $ K $ is a positive coefficient. Due to the presence of friction, clearance, and additional bending moments, the roll system is subjected to a horizontal resultant force, which is defined as the horizontal excitation force $ F\cos \omega t $, with the amplitude and frequency parameters $ F $ and $ \omega $, respectively. There are many definitions available for the fractional-order derivative, in this study, $ D_t^{q}x $ with $ 0\leq q\leq1 $ is the Caputo's fractional derivative of $ x(t) $ described by
in which $ \Gamma(z) $ is Gamma function satisfying $ \Gamma(z+1) = z\Gamma(z) $.
The roll system of the rolling mill is a highly nonlinear hysteresis system. In the rolling process of composite plates, the elastic-plastic deformation process of the rolled piece is a nonlinear deformation process with time delay characteristics. The time-delay feedback control method is one of the effective methods for studying bifurcation control of nonlinear systems. We adopt time-delay feedback control to suppress the nonlinear vibration. The block diagram is shown in Figure 2.
2.2. Multiple scale method
The horizontal vibration of the roller system is a weak vibration, and the multiple scale method can be used to conduct an approximate resonant solution of Eq (2.1), for which a small time scale parameter $ \varepsilon $ is required. This method begins by introducing new time variables $ T_n = \varepsilon^n t, (n = 0, 1) $, then an approximate solution of Eq (2.1) with small amplitudes can be represented by
For such a small parameter $ \varepsilon $, the following variable substitution is introduced for the system,
where $ \omega_0 $ is the undamped natural frequency of the system, $ \alpha $, $ \beta $, $ \mu $ are equivalent nonlinear damping coefficient, equivalent fractional derivative coefficient and equivalent cubic stiffness coefficient, respectively.
Then, Eq (2.1) becomes
The derivatives with respect to $ t $ can be expressed in terms of the new scaled times $ T_n $ as a series of partial derivatives (see [16]),
in which $ D_0^q = \frac{\partial^q}{\partial T_0^q} $, $ D_n = \frac{\partial}{\partial T_n} $, $ D_n^2 = \frac{\partial^2}{\partial T_n^2}, (n = 0, 1) $.
3.
Primary resonance and time-delay feedback control
The nonlinear vibration characteristics of the horizontal roller system may lead to various resonance phenomena during the rolling process, such as internal resonance, primary resonance, and secondary resonance. First, we analyze the primary resonance when the excitation frequency is close to the natural frequency.
3.1. Primary resonance
3.1.1. Amplitude-frequency response equation
Regarding the primary resonance, soft excitation is applied implying that the amplitude of excitation is small, thus the external force is given by
and the resonance relation is considered to be $ \omega = \omega_0 $ or $ \omega\approx\omega_0 $, a detuning parameter $ \sigma $ describing the nearness of $ \omega $ to $ \omega_0 $ is introduced by
then $ \omega t = \omega_0T_0+\sigma T_1 $. Substituting (2.2), (2.5a)–(2.5c) into (2.4) leads to the following equation
Equating the coefficients of the same power of $ \varepsilon $, a set of linear differential equations are obtained:
from which $ x_0 $ and $ x_1 $ can be solved one-by-one respectively. In this way, the resonant solution $ x $ is dominated by $ x_0 $, collected by $ \varepsilon x_1 $.
The general solution of Eq (3.3) is of the form,
where $ A(T_1) $ and $ \overline{A}(T_1) $ are unknown functions, $ \overline{A}(T_1) $ denotes the complex conjugate of $ A(T_1) $.
To solve Eq (3.4), the $ q $th-order $ (0\leq q\leq1) $ derivative of $ {\rm e}^{{\rm i}\omega t} $ is approximated written as following (see [32]),
Substituting (3.5) and (3.6) into Eq (3.4) and using
the right-hand of Eq (3.4) becomes
where $ NST $ stands for the terms that do not produce secular terms, $ cc $ denotes the complex conjugate of the preceding terms.
In order that $ x_1 $ is periodic, the secular terms with $ {\rm e}^{{\rm i}\omega_0T_0} $ must be zero, namely
To solve Eq (3.8), we write $ A(T_1) $ in the polar form as following
in which $ a(T_1) $ and $ \theta(T_1) $ are real functions of $ T_1 $.
With the help of the Euler formula
let $ \label{eq15}\varphi\overset{\text{def}}{ = }\sigma T_1-\theta $, by separating the real and imaginary parts of Eq (3.8), the differential equations governing amplitude $ a(T_1) $ and $ \varphi(T_1) $ of $ A(T_1) $ are expressed as follows respectively
The steady state motions for the primary resonance response correspond to the fixed points of (3.11a) and (3.11b), that is, $ D_1a = 0 $ and $ D_1\varphi = 0 $, namely
By performing square operations and eliminating $ \varphi $ from Eqs (3.12a) and (3.12b), the following amplitude-frequency response equation is determined,
The amplitude of the response is a function of external detuning parameter and the amplitude of excitation. It should be pointed out that in [26], the multiple scale method was used to obtain the amplitude-frequency response equation of Eq (2.1) for the primary resonance, but the coefficients in the expression were incorrect. In addition, when $ \mu = 0 $, Eq (2.4) is transformed into an integer-order model, and the corresponding amplitude-frequency response equation for the primary resonance has been studied in [13], but the expression has certain problems.
3.1.2. Stability of the steady resonant solutions
To determine the stability of steady state motion through the nature of singular points in Eqs (3.11a) and (3.11b), the following method can be used. Assume that $ (a, \varphi) = (a^*, \varphi^*) $ is a steady solution of Eqs (3.11a) and (3.11b), let $ {\rm\Delta} a = a-a^* $ and $ {\rm\Delta}\varphi = \varphi-\varphi^* $. According to Eqs (3.12a) and (3.12b), the linearized differential equations governing $ {\rm\Delta}a $ and $ {\rm\Delta}\varphi $ are
Let $ P = \frac{\mu}{2}\omega_0^{q-1}\sin\frac{q\pi}{2}-\frac{\alpha}{2}+\frac{3\alpha(a^*)^2}{8}, Q = \frac{\mu}{2}\omega_0^{q-1}\sin\frac{q\pi}{2}-\frac{\alpha}{2}+\frac{\alpha (a^*)^2}{8}$, $M = \sigma-\frac{\mu}{2}\omega_0^{q-1}\cos\frac{q\pi}{2}-\frac{3\beta}{8\omega_0}(a^*)^2, N = \sigma-\frac{\mu}{2}\omega_0^{q-1}\cos\frac{q\pi}{2}-\frac{9\beta}{8\omega_0}(a^*)^2, $ then the characteristic equation can be rewritten as
By expanding the determinant, one has
Consider when $ P+Q > 0 $, then the steady solution $ (a, \varphi) = (a^*, \varphi^*) $ is asymptotically stable if and only if $ \Lambda > 0 $, where
3.1.3. Analysis of the resonant solutions
The influence of different parameters on the amplitude of resonance solution is investigated numerically, as shown in the Figures 3 and 4. With fixed parameter values, all the figures exhibit typical characteristics of hardening spring.
First, the influence of fractional order $ q $ on the resonant solutions is shown in Figure 3, where the parameters are selected to be, $ \alpha = 0.04 $, $ \beta = 0.1 $, $ \omega_0 = 1 $, $ \mu = 0.02 $ and $ f = 0.1 $. It can be seen that the smaller the order $ q $ is, the larger the maximum amplitude is. In addition, compared with the integer order case when $ q = 1 $, the bending degree, resonance peak, and resonance region of the amplitude-frequency curve of the fractional system change accordingly with the decrease of the fractional order $ q $. The reason for this is that the fractional differential term has both stiffness and damping characteristics, which have a significant impact on the amplitude frequency response curve of the system. When the fractional-order $ q $ approaches 0, the fractional differential term is almost equivalent to the effect of linear stiffness; When $ q $ tends towards 1, the fractional differential term is almost equivalent to the effect of linear damping, and the larger the damping, the smaller the peak value.
Figure 4 presents parameter effect on resonant amplitudes with respect to $ \mu $, $ f $, $ \alpha $ and $ \beta $. Here, the fractional-order $ q = 0.9 $ and the natural frequency $ \omega_0 = 1 $. In Figure 4(a), with the increase of $ \mu $, the nonlinear jump of the system weakens and the resonance amplitude of the system decreases. In other words, as $ \mu $ increases, the unstable portions decrease. In Figure 4(b), with the increase of pulse pressure $ f $, the nonlinear jump of the system is more obvious, and the resonance range and resonance amplitude of the system increase. In Figure 4(c), when the value of $ \alpha $ increases, the amplitude of the system decreases. Since $ \alpha $ is the nonlinear damping coefficient, increasing $ \alpha $ means that the damping term increases, and the amplitude of resonance correspondingly decreases. In Figure 4(d), when the nonlinear stiffness coefficient $ \beta $ increases, the curve shifts to the right and and the degree of curvature increases. It can also be observed that the jumping phenomenon occur in the system, leading to system oscillations. Another phenomenon is that the amplitude does not change with the stiffness coefficient and remains consistent. According to the above analysis results, a controller should be designed to reduce the influence of primary resonance.
3.2. Time-delay feedback control of primary resonance
3.2.1. Amplitude-frequency response equation
In order to eliminate the jumping and hysteresis phenomena of the primary resonance in the horizontal roller system, the time-delay displacement feedback strategy is adopted here, and the fractional equation with time-delay feedback control can be established as follows:
where $ g_1 $ is the linear control gain, $ g_2 $ is the nonlinear control gain, $ \tau_1 $ and $ \tau_2 $ are time-delay parameters.
Substituting (2.2), (2.5a)–(2.5c) into (3.18) leads to the following equation
Thus, a set of linear differential equations can be obtained:
Assume that the general solution of Eq (3.19) is (3.5), substituting (3.5) into Eq (3.20), the right-hand of Eq (3.20) becomes
where $ NST $ stands for the terms that do not produce secular terms, $ cc $ denotes the complex conjugate of the preceding terms.
Through setting the coefficient of $ {\rm e}^{{\rm i}\omega_0T_0} $ equal to zero to eliminate the secular terms, the following equation can be obtained as:
Similar to the previous discussion, the following differential equations about amplitude and phase can be obtained,
The steady state motions for the primary resonance response correspond to the fixed points of (3.23a) and (3.23b), that is, $ D_1a = 0 $ and $ D_1\varphi = 0 $, namely
The amplitude-frequency response equation of primary resonance with time-delay control can be obtained as:
in which
From Eq (3.25), it can be seen that the amplitude of the response is a function of external detuning parameter, feedback gain, time delay and the amplitude of excitation.
3.2.2. Numerical simulation
The impact of adding time-delay feedback control on the amplitude-frequency response curve of the primary resonance is presented through numerical simulation, as shown in Figure 5. In Figure 5, the primary resonance amplitude and resonance region can be controlled, the primary resonance bifurcations can be reduced by properly adjusting the delay parameters $ (\tau_1, \tau_2) $ and feedback gains $ (g_1, g_2) $. After adding time-delay feedback control, the resonance peak value decreases, the curvature of the curve also decreases and the jumping phenomenon has also weakened. It can also be seen from Figure 5(a) that the control effect of simultaneously adjusting delay parameters $ (\tau_1, \tau_2) $ and feedback gains $ (g_1, g_2) $ is better than that of separately adjusting linear feedback gain $ g_1 $ or nonlinear feedback gain $ g_2 $.
In Figure 5(b), as the linear gain $ g_1 $ and nonlinear gain $ g_2 $ gradually increase, the amplitude of the primary resonance of the system gradually decreases, and the jumping phenomenon of the curve is eliminated. Therefore, it can be seen that when using only feedback control gain as the control parameter, if both linear and nonlinear feedback control gains increase simultaneously, the primary resonance phenomenon of the system can be reasonably controlled. In Figure 5(c), as the delay parameters $ (\tau_1, \tau_2) $ gradually increase, the amplitude and the resonance domain of the system gradually decreases. However, the adjustment of delay parameters has little effect on the degree of curve curvature. On the contrary, by adjusting the feedback control gains $ g_1 $ and $ g_2 $, it is relatively easy to eliminate the jumping phenomenon of the primary resonance. This indicates that using feedback control gain as the control object has a better control effect than using delay parameters as the control object.
4.
Secondary resonance and time-delay feedback control
In this section, we will discuss secondary resonance, namely superharmonic and subharmonic resonance. Only superharmonic resonance is considered here, and the issue of subharmonic resonance will be studied in subsequent papers.
4.1. Third-order superharmonic resonance
4.1.1. Amplitude-frequency response equation
During the inspection process of third-order superharmonic resonance, when the excitation frequency is far away from the natural frequency, unless its amplitude is sufficiently large, the impact of excitation is minimal. Therefore, in superharmonic resonance, the excitation amplitude is of order $ \varepsilon^0 $. Third-order superharmonic resonance with limited amplitude occurs in the Eq (2.4) when $ 3\omega = \omega_0 $ or $ 3\omega\approx\omega_0 $, the resonance relation is represented as
in which $ \sigma $ is again the detuning parameter, then $ 3\omega T_0 = \omega_0T_0+\sigma T_1 $. The following derivations in this section are similar to those in the previous section, only the main steps will be retained for ease of reading.
Substituting (4.1), (2.5a)–(2.5c) into (2.4) leads to the following equation
Equating the coefficients of the same power of $ \varepsilon $, a set of linear differential equations are obtained:
The general solution of Eq (4.2) is of the following form,
where $ A(T_1) $ and $ \overline{A}(T_1) $ are complex functions in terms of slow time scale, $ \overline{A}(T_1) $ denotes the complex conjugate of $ A(T_1) $ and $ B = \frac{f}{2(\omega_0^2-\omega^2)} $.
Substituting (4.4) into Eq (4.3), the right-hand of Eq (4.3) becomes
where $ NST $ stands for the terms that do not produce secular terms, $ cc $ denotes the complex conjugate of the preceding terms.
Thus, the solvability condition takes the form
Separating the real and imaginary parts, and letting $ \varphi\overset{\text{def}}{ = }\sigma T_1-\theta $ to transform this into an autonomous system. Seeking the steady state, we let $ D_1a = 0 $ and $ D_1\varphi = 0 $. Eliminating $ \varphi $ leads to the nonlinear the amplitude-frequency equation
From Eq (4.7), it can be concluded that there is an interaction between the nonlinear term and the external force term to the third-order superharmonic resonance of the first-order perturbation analysis. According to Eq (4.7), different superharmonic resonance amplitude-frequency characteristic curves can be obtained by different $ \mu $, $ \alpha $, $ \beta $, and $ f $.
4.1.2. Numerical simulation
First, we present an image of the amplitude-frequency response curve of third-order superharmonic resonance, as shown in Figure 6. Here, the parameters are selected to be, $ q = 0.9 $, $ \alpha = 0.08 $, $ \beta = 0.2 $, $ \omega_0 = 1 $, $ \mu = 0.08 $, and $ f = 0.24 $. It can be clearly seen from Figure 6 that the fractional roller system generates superharmonic resonance under the above parameter conditions.
By changing the nonlinear damping coefficient $ \alpha $, nonlinear stiffness coefficient $ \beta $, rolling force amplitude $ f $, and fractional damping coefficient $ \mu $ of the roller system, the superharmonic resonance curves with different amplitude-frequency characteristics can be obtained, as shown in Figure 7. Here, the fractional order $ q = 0.9 $ and the natural frequency $ \omega_0 = 1 $. In Figure 7(a), when the nonlinear damping coefficient $ \alpha $ increases, the amplitude decreases and the resonance domain decreases. In Figure 7(b), with the nonlinear stiffness coefficient $ \beta $ increases, the curve shifts to the right and the bending degree increases. In Figure 7(c), with the increase of rolling force, the amplitude and resonance region of the system increase obviously. In Figure 7(d), when $ \mu $ increases, the amplitude and the resonance domain decrease, and the nonlinear jump of the system weakens.
4.2. Time-delay feedback control of superharmonic resonance
4.2.1. Amplitude-frequency response equation
In order to study the control problem of superharmonic resonance, the fractional equation with time-delay feedback control can be established as follows:
Substituting (4.1), (2.5a)–(2.5c) into (4.8), we can obtain
Equating the coefficients of the same power of $ \varepsilon $, a set of linear differential equations are obtained:
Assume that the solution of the zeroth approximation equation (4.9) is (4.4), substituting (4.4) into Eq (4.10), the right-hand of Eq (4.10) becomes
where $ NST $ stands for the terms that do not produce secular terms, $ cc $ denotes the complex conjugate of the preceding terms.
The solvability condition takes the form
Based on the condition of steady solution, the nonlinear amplitude-frequency equation of superharmonic vibration with time-delay control can be obtained as follows
in which
From Eq (4.13), it can be concluded that there is an interaction between the feedback gain, time delay, nonlinear term and the external force term to the third-order superharmonic resonance of the first-order perturbation analysis.
4.2.2. Numerical simulation
The impact of adding time-delay feedback control on the amplitude-frequency response curve of the third-order superharmonic resonance is presented through numerical simulation, as shown in Figure 8. Figure 8 shows that the amplitude and resonance region can be controlled and the superharmonic resonance bifurcations can be reduced by properly adjusting the delay parameters $ (\tau_1, \tau_2) $ and feedback gains $ (g_1, g_2) $. After adding time-delay feedback control, the resonance peak value decreases, the curvature of the curve decreases, and the jumping phenomenon has weakened.
In Figure 8(a), as the feedback gains $ (g_1, g_2) $ gradually increase, the amplitude of the system gradually decreases, the resonance domain gradually decreases, and the curve bifurcation is eliminated. The resonance domain also shows significant movement. It can be concluded that using feedback control gain as the control parameter and increasing both linear and nonlinear feedback control gains can effectively control the phenomenon of superharmonic vibration in the system. In Figure 8(b), when the delay parameters $ (\tau_1, \tau_2) $ gradually increases, the amplitude of the system gradually decreases and the resonance domain gradually decreases. Through comparison, it can be found that whether using feedback control gains or time-delay parameters as the control object, the control effect is significant during the control of superharmonic vibration.
At the end of this section, a time history diagram is used to briefly illustrate the impact of feedback control on the model. Figure 9 shows the time history of the superharmonic resonance under feedback control. The various parameters of the system in Figure 9 are $ q = 0.9 $, $ \omega_0 = 1 $, $ \alpha = 0.08 $, $ \beta = 0.2 $, $ \mu = 0.08 $, and $ f = 0.24 $. It can be observed that the amplitude of the resonance decreases obviously after the delay control is added, and the larger the delay is, the greater the amplitude reduction is.
5.
Comparison between approximate analytical solution and numerical solution
According to Eq (3.13), the primary resonance amplitude-frequency response curve of the system can be drawn. For comparison, we adopt the power series method introduced in reference [33,34], and its calculation formula is
where $ t_n = nh $ is the sample points, $ h $ is the sample step, and $ C_j^q $ is the fractional binomial coefficient with the iterative relationship as
According to Eqs (5.1) and (5.2), the numerical scheme for Eq (2.4) can be expressed as
The numerical amplitude-frequency curve marked with circle in Figure 10, where the stepsize of time is $ h = 0.005 $, and the total computation time is 100s with the first 25s neglected. It shows that the resonant amplitude calculated from Eq (3.13) is in good agreement with the numerical results, especially when the $ \omega\approx\omega_0 $.
6.
Conclusions
In the present research, we study the nonlinear vibration characteristics and time-delay feedback controllability of a fractional horizontal roll systems for rolling mill, described by a damped fractional Duffing-van der Pol oscillator under external harmonic excitation. In response to the inaccurate conclusions in existing literature, we conducted rigorous derivation. The accurate amplitude-frequency response equations were obtained by the multiple scale method. The influence of parameters on system characteristics was studied using amplitude frequency response equation. Furthermore, the time-delay feedback controller is designed to control the parameter excitation vibration. The numerical simulation results verified the effectiveness of the time-delay controller in eliminating the jumping and hysteresis phenomena of the rolling system. It can also be concluded that fractional order and the damping coefficient are very important in fractional horizontal roll systems. For example, a larger fractional order and larger damping coefficient can reduce the effective amplitude of resonance and change the resonance frequency.
Through the study of the roll model, it is inspired that in the design process of strip rolling mills, the influence of rolling force amplitude on primary resonance and superharmonic resonance should be avoided and reduced. Further research is needed to combine active vibration control techniques such as PID control, adaptive control, fuzzy control, and other control methods to analyze the vibration control effect of the rolling mill.
Author contributions
Zhoujin Cui performed the conceptualization, methodology, writing-original draft and writing-review & editing; Xiaorong Zhang performed the investigation and validation; Tao Lu performed the validation and supervision. All authors have read and approved the final version of the manuscript for publication.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The authors express gratitude to the reviewers and editors for their helpful comments and suggestions, as well as to the financial support from High Level Talent Research Launch Fund of Jiangsu Second Normal University (No. 928201/058).
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: