Exponential synchronization of fractional order fuzzy memristor neural networks with time-varying delays and impulses

1.   Introduction

Fractional calculus was developed more than 300 years ago, however, it has not been intensively studies until the last 20 years. For example, important results have been achieved in the fields of fluid mechanics ^[1], physics ^[2], pharmaceutics ^[3], and neural networks. Fractional calculus, with its arbitrary positive real-order derivatives and integrals, alongside its memory inheritance properties, has been applied by some researchers to neural networks to more accurately study their related properties, thus forming fractional neural networks ^[4,5].

In 1971, Zeili used the symmetry theory to derive the fourth circuit element in addition to inductors, capacitors, and resistors, and named it the memristor ^[6]. Then, in 2008, HP LABS demonstrated the memristor in real life for the first time ^[7]. After that, the memristor gradually came into the public eye, and research has shown that it has the benefits of having a small size, a low power consumption, and scalability; thus, it can replace traditional resistors ^[8,9]. After the switch is turned off, the memristor can also record the history of the charge, which is similar to the synaptic response of a biological neuron when stimulated, which makes the memristor highly sought after ^[10,11]. Satheesh and Sakthivel ^[12] studied the synchronization problem of multi-memristive neural networks with a fault-tolerant anti-interference control, delay, mismatched, and matched interference. Fu and Zhong ^[13] studied the projection synchronization of fuzzy memory neural networks with a fixed impulse control. Zhang and Bao ^[14] proposed a five-dimensional isomorphic memristive coupled adaptive synaptic neuron (mCASN) network using non-ideal memristive coupled two-dimensional adaptive synapses. Fu and Zhong ^[15] studied the exponential synchronization of memory neural networks (MNNs) with inertia and nonlinear coupling terms.

Due to sudden external interference, various systems will deviate in real life from their original trajectories at certain points. This interference is called a pulse. The short-term interference of pulses is inevitably going to have some impact on the system. Therefore, when analyzing the dynamic characteristics of a nonlinear power grid, it is necessary to consider the effects of pulses and delays. Yang et al. ^[16] obtained some new results on global synchronization using multiple recurrent neural networks with delay and pulse interactions. LaMar and Smith ^[17] studied the effect of the correlation between input and output degrees on the performance of the same pulse-coupled oscillator synchronization system in a random directed network. Zhang ^[18] studied the finite-time (FNT) synchronization and pulse synchronization of fractional-order quaternion neural networks (with fractional-order quaternion numerical neural networks and delays). Fu and Jiang ^[19] studied the (FNT) and fixed-time (FXT) synchronization problems of complex networks with semi-Markov switching and pulse effects. Ling and Shi ^[20] studied the exponential synchronization problem of a class of time-delayed coupled neural networks with a delay compensation and impulse control.

There are additional real-life factors to consider when discussing pulse systems, including approximation, uncertainty, and vagueness. In 1996, Yang ^[21] combined the cellular neural networks (CNNs) pioneered by Chua and Yang ^[22] with fuzzy logic to form fuzzy cellular neural networks (FCNNs). Compared to traditional neural networks, fuzzy neural networks can maintain local connections between units and output binary signals. Due to the uncertainty of its origin, FCNNs can achieve nonlinear filtering, which makes it better suited to handle real-world problems. It is inevitable to consider the performance, stability, and synchronization of the neural network, and consequently, related research has also been widely developed. Liu ^[23] studied the global stability of the delayed fuzzy cellular neural networks (FCNNS) with constant and time-varying delays by constructing suitable Lyapunov functions. Huang ^[24] studied the stability of the distributed delay fuzzy neural networks with the minimum feedback kernel. The finite-time synchronization problem of fuzzy neural networks with time-varying delays was studied using inequality techniques and analytical methods based on finite-time theory in ^[25].

Synchronization is an important behavior in dynamics, and it also has significant implications in the research of intelligent control, secure communication, medical treatment, and image processing. At the same time, the research methods for neural network synchronization are also very extensive, such as anti-synchronization, fixed-time synchronization, global asymptotic synchronization, exponential synchronization, etc.; for example, see ^{[26,27,28,29]}. Among the synchronization methods mentioned above, exponential synchronization is undoubtedly an important solution to deal with synchronization problems. Peng et al. ^[30] discussed the non-fragile fixed-time synchronization problem of discrete continuous neural networks (FONNs) with nonlinearly growing activation functions. Fan ^[31] studied the global Mittag-Leffler synchronization problem of fractional-order time-delay memory neural networks (FMNNs) by constructing appropriate Lyapunov functions under several synchronization conditions. Zhao ^[32] designed two discrete control schemes with leakage and a transmission delay, and proposed several new delay-independent algebraic conditions to ensure the FXT synchronization of the driven response (FOMFNN). Zhang ^[33] designed two control systems with fractional-order impulse effects based on the two-layer structure for the response-order (FMBAMNN).

The above scholars conducted in-depth research into various neural network models, but there is little literature on the exponential synchronization and impulsive effects of fractional-order fuzzy neural networks under time-varying delays. Therefore, there is great need for research in this area.

Inspired by the above discussion, the exponential synchronization of fractional order fuzzy memristor neural networks with time-varying delays and impulses is studied in this paper. The main contributions of this paper can be summarized as follows:

(a) This paper relaxes some of the limitations of the finite activation assumption in activation functions from the literature ^{[34,35,36,37]} to make activation functions more general and less conservative in the results.

(b) Compared to the literature ^[38], the system considered in this paper is more flexible, and two controllers have been designed to avoid the use of symbolic functions, thereby enabling the control system to avoid chattering and save costs.

(c) Compared to the literature ^[38], we propose a new dynamic impulse gain concept to replace the static impulse gain in the reference, and effectively combine synchronous and desynchronization pulses to provide a clear view of their impact on the system.

2.   Preliminaries

In this section, some assumptions, definitions, and lemmas will be introduced.

(Al) The activation function $f_l(\cdot)$ satisfies the Lipschitz condition; for any $\mu, \nu\in R$ and $\mu\neq\nu$, there exists a constant $L_l$ such that

where $l = 1, 2, 3, ..., n$.

Remark 2.1. In the systematic discussion, many literatures impose certain restrictions on the activation function, such as ^{[34,35,36,37]}; this paper weakens this condition, which makes the results less conservative.

Definition 2.1. ^[39] The Caputo fractional derivative of order $q \in (0, 1)$ for a function $h(t) \; \in \; R^{1}([0, +\infty), R)$ is defined as follows:

Definition 2.2. ^[40] A set-valued map F with nonempty values is said to be upper-semi continuous at $y_0\in\epsilon\subset R^{n}$, if there exists a neighborhood O of $y_0$ such that $F(O)\subset M$ for any open set M containing F(y0). $F(y)$ is said to have a closed (convex, compact) image if $F(y)$ is closed for each $y\in \epsilon$.

Definition 2.3. ^[41] Consider the system $\frac{dy}{dt} = f(y), y\in R^{n}$ with discontinuous right-hand sides; a set-valued map is defined as follows:

where $\overline{co}$ is the closure of the convex hull of set F, $B(y, \delta) = \{z||z-y||\leq \delta\}$, and $\mu(M)$ is the Lebesgue measure of the set M. A solution in Filippovs sense of the Cauchy problem for this system with the initial condition $y(0) = y_0$ is an absolutely continuous function $y(t), t\in[0, T]$, which satisfies $y(0) = y_0$ and the differential inclusion:

for $t\in[0, T]$.

Definition 2.4. Define the following M-L fuction:

where $\alpha > 0, \beta > 0$, and $E_\alpha(t) = E_{\alpha, 1}(t).$

Definition 2.5. ^[42] If $\alpha\in(0, 1)$, $V(t)\in[t_0, \infty)$ is a continuous function, and

for the constant $\rho$, then

Definition 2.6. ^[43] Consider the impulsive sequence $\{t_k\}$; $o(t_0, t)$ represents the number of impulsive times the impulsive sequence $\{t_ k\}$ appears in the time interval $(t_0, t)$. If T and $T_0$ satisfy

then $T$ is called the average impulsive interval of the impulsive sequence $\{t_ k\}$.

Lemma 2.1. ^[44] Let $g(t)$ be a continuously differentiable function on $t\in[0, +\infty)$; then, for $0 < q < 1$, one has the following:

Lemma 2.2. ^[38] Under Assumption 1,

Lemma 2.3. ^[45] Suppose $u_j$ and $v_j$ are two states of neural networks (1); then, we have the following:

Lemma 2.4. ^[46] If $0 < \alpha < 1$, $|arg(s)| < \frac{\pi}{2}$, and make $N > 1, s\neq0$, then the M-L function expansion is as follows:

In this paper, we consider the following fractional-order memristive neural network with time-varying delay and impulsive interference:

where $p = 1, 2, 3, ..., n, n$ is the number of neurons, $a_p > 0$ is the self-regulating parameter of the neurons, $0 < q < 1$ is the fractional order, $x_p(t)$ is the state variable connected with the ith neuron, $f_l(\cdot)$ is the activation function. $\tau_l(t)$ is a time-varying delay and a continuously differentiable function which satisfies $0 < \tau_l(t)\leq\tau$ and $\dot{\tau}_l(t)\leq \tau_1 < 1$. $\bigwedge\limits_{l = 1}^n$ and $\bigvee\limits_{l = 1}^n$ denote the fuzzy AND and the fuzzy OR operation, respectively, $d_{pl}$ signifies the fuzzy feed-forward template, $S_{pl}$ and $H_{pl}$ are the elements of the fuzzy feed-forward MIN template and the fuzzy feed-forward MAX template, respectively. The elements of the fuzzy feedback MIN and MAX template are $\alpha_{pl}$ and $\beta_{pl}$, respectively. $v_{l}$ signifies the bias of the pth and lth neuron. $\Delta x_p(t_i) = x_p(t_i^{+})- x_p(t_i^{-})$, and $x_p(t_i) = lim_{t\rightarrow t_i^{+}}x_p(t_i) = x_p(t_i^{+})$. $\mu_p(t_i)$ is time-varying impulsive gain which satisfies $\mu_p(t_i)\le \mu_p$, where $\mu_p$ is constant. $I_p$ is the constant external input, $b_{pl}(x_l(t))$ and $c_{pl}(x_l(t))$ are the memristive connection weights, which are defined as follows:

where the switching jump $T_p > 0$, $b_{pl}(\pm T_p) = \acute{b}_{pl}$ or $\grave{b}_{pl}$, $c_{pl}(\pm T_p) = \acute{c}_{pl}$ or $\grave{c}_{pl}$, $\acute{b}_{pl}$, $\grave{b}_{pl}$, $\acute{c}_{pl}$, and $\grave{c}_{pl}$ are all constants. The initial condition of system (1) is $x_{p}(s) = \varphi(s)$, $s\in[-\tau, 0]$.

Using the differential inclusion theory and the set-valued mapping theory, one can obtain a system solution in the sense of Filippov. System (2.1) can be represented as follows:

where

and $co\{\acute{b}_{pl}, \grave{b}_{pl}\} = [ \underline{b}_{pl}, \overline{b}_{pl} ]$, $\underline{b}_{pl} = \min\{\acute{b}_{pl}, \grave{b}_{pl}\}$, $\overline{b}_{pl} = \max\{\acute{b}_{pl}, \grave{b}_{pl}\}$, $co\{\acute{c}_{pl}, \grave{c}_{pl}\} = [\underline{c}_{pl}, \overline{c}_{pl}]$, $\underline{c}_{pl} = \min\{\acute{c}_{pl}, \grave{c}_{pl}\}$, $\overline{c}_{pl} = \max\{\acute{c}_{pl}, \grave{c}_{pl}\}$, $co\{\acute{d}_{pl}, \grave{d}_{pl}\} = [ \underline{d}_{pl}, \overline{d}_{pl}]$, $b_{pl} = \max\{|\acute{b}_{pl}|, |\grave{b}_{pl}|\}$, and $c_{pl} = \max\{|\acute{c}_{pl}|, |\grave{c}_{pl}|\}$. Alternatively, there exist ${b}_{pl}^\star\in co[b_{pl}(x_p(t))]$, and ${c}_{pl}^\star\in co[c_{pl}(x_p(t))]$ such that

We can regard system (2.1) as the driving system, in which case the corresponding response system would be as follows:

where $u_p(t)$ is the controller, the memristive connection weights $b_{pl}(y_l(t))$ and $c_{pl}(y_l(t))$ are defined as

and the initial condition of system (2.4) is given by $y_p(s) = \psi(s)$, $s\in(-\tau, 0]$.

Similarly, system (2.4) is rewritten as follows:

where $b_{pl}^{\star\star}\in co[b_{pl}(y_p(t))]$, $c_{pl}^{\star\star}\in co[c_{pl}(y_p(t))]$ and

The synchronization error is defined as $e_p(t) = y_p(t)-x_p(t)$; then, we have the following:

and the initial condition of system (2.6) is given by $e_p(s) = \psi(s)-\varphi(s)$.

3.   Main results

In this section, an appropriate state feedback controller is designed to ensure exponential synchronization between the driving system (2.1) and the response system (2.4). Furthermore, some sufficient conditions for exponential synchronization of the neural network with time-varying delay and a fractional memristive impulse are obtained through a rigorous mathematical proof.

In this part, we assume the state feedback controller as follows:

where $\sigma_p > 0$ and $\xi > 0$ are the parameters to be determined later.

Remark 3.1. Compared with the literature ^[32], the controller designed in this paper is able to effectively avoid the problem of a system jitter caused by the existing controllers, and the model considered takes the pulse control into account; thus, the conclusion is less conservative.

Remark 3.2. Compared with the literature ^[38], the boundaries of the activation function $f_l(\cdot)$ in this paper are relaxed, and there is no symbolic function that affects a system jitter in the designed controller; thus, the results are less conservative.

Remark 3.3. If $||e(t)||_1$ = 0, then the driven response system (2.1) and the response system (2.4) can achieve synchronization; thus, the controller (3.1) is no longer needed, that is, $u_p(t) = 0$. Compared with some previous controllers (such as ^[47,48]), the above controller does not use symbolic functions to reduce the system's sensitivity to jitter, which makes the system more practical and useful in real-world applications.

Remark 3.4. According to the literature, in the synchronization controller design of fractional-order time-varying delay memory neural networks, most authors design a symbolic controller to handle constant terms that arise in mathematical derivations, such as ^[47,48]. While this controller design solves the problem, it can easily cause a system signal jitter, which results in conservative results.

Theorem 3.1. Under assumption $\mathop{\rm (A1)}$, the drive-response systems (2.1) and (2.4) will achieve exponential synchronization under controller (3.1), if the following conditions are satisfied:

(C1) $N = \xi-\sum\limits_{p = 1}^n\sum\limits_{l = 1}^n\bigg[[|\acute{b}_{pl}-\grave{b}_{pl}|+|\acute{c}_{pl}-\grave{c}_{pl}|](L_lT_l+|f_l(0)|)+[c_{pl}+|\alpha_{pl}|+|\beta_{pl}|]L_l(\psi(s)-\varphi(s))\bigg] \ge0$;

(C2) $\epsilon = M^{\frac{1}{q}}+\frac{ln(\frac{\nu}{q})}{T} < 0$

with $M = \left\{\sum\limits_{l = 1}^n\left\{b_{lp}+c_{lp}+|\alpha_{lp}|+|\beta_{lp}|\right\}L_p-a_p-\sigma_p\right\}$.

Proof. Construct the following Lyapunov functional:

For $t \in (t_{i-1}, t_i]$, by Lemma 2.1, $V(t)$ can be calculated as follows:

According to assumption (A1) and Lemma 2.2, the following inequality can be yielded:

Similarly,

Substituting (3.4) and (3.3) into (3.2), we have the following:

Based on Lemma 2.3, we can obtain the following:

Substituting (3.7) and (3.6) into (3.5), we have the following:

On the other hand,

By putting (3.9) into (3.8), and combining conditions (C1) and (C2), we obtain the following:

From Definition 2.5, we have the following:

For any $i\in N$, we obtain the following:

where $max\{|1+\mu_p|\} = \nu.$ From (3.10) and (3.11), for $t\in(t_0, t_1]$, $V(t)\leq E_q(p(t-t_0)^{q})V(t_0^{+})$, then we get $V(t_1)\leq E_q(p(t_1-t_0)^{q})V(t_0^{+})$ and $V(t_1^{+})\leq \nu E_q(p(t_1-t_0)^{q})V(t_0^{+})$. When $t\in(t_1, t_2]$, $V(t_2^{+})\leq\nu^{2}E_q(p(t_2-t_1)^{q})V(t_1^{+})E_q(p(t_1-t_0)^{q})V(t_0^{+}).$ Similarly, when $t\in(t_i, t_{i+1}]$, $V(t)\leq\prod\limits_{k = 1}^{i}E_q(p(t_k-t_{k-1})^{q})\nu^{i}E_q(M(t-t_i)^{q})V(t_0^{+}).$ Based on Lemma 2.4, we obtain the following:

By Definition 2.6, we can obtain the following:

By putting (3.12) and (3.13) into (3.14), and combining conditions (C1) and (C2), for $t > t_0$, if $0 < \frac{\nu}{q} < 1$, then we can obtain the following:

If $\frac{\nu}{q}\ge1$, then we derive the following:

Make $\kappa = max\{(\frac{\nu}{q})^{T_0}\frac{1}{q}, (\frac{\nu}{q})^{-T_0}\frac{1}{q}\}$, $\epsilon = M^{\frac{1}{q}}+\frac{ln(\frac{\nu}{q})}{T} < 0$; then, $V(t)\leq\kappa e^{\epsilon}V(t_0^{+}).$ Therefore, when $t\rightarrow \infty$, $V(t)\rightarrow0$. This indicates that the error system (2.6) is exponentially synchronizable.□

We designed an anti-resonant adaptive controller for the response system to achieve synchronization between the response system and the driving system. The expression of the adaptive controller is as follows:

where $D^{q}{\sigma}_p(t) = \omega|e_p(t)|-\epsilon_1(\sigma_p(t)-\widetilde{\sigma})$, $D^{q}{\xi}(t) = \chi-\epsilon_2(\xi(t)-\widetilde{\xi})$, $\omega > 0$, $\chi > 0$, and a $\epsilon_1$ and $\epsilon_2$ are appropriate constants.

Theorem 3.2. Under the assumption $\mathop{\rm (A1)}$, the drive-response systems (2.1) and (2.4) will achieve exponential synchronization under the control of the controller (3.17) if the following conditions are satisfied:

(C3) $N = \widetilde{\xi}-\sum\limits_{p = 1}^n\sum\limits_{l = 1}^n\bigg[[|\acute{b}_{pl}-\grave{b}_{pl}|+|\acute{c}_{pl}-\grave{c}_{pl}|](L_lT_l+|f_l(0)|)+[c_{pl}+|\alpha_{pl}|+|\beta_{pl}|]L_l(\psi(s)-\varphi(s))\bigg] \ge0$;

(C4) $\zeta = R^{\frac{1}{q}}+\frac{ln(\frac{\nu}{q})}{T} < 0$, where $R = \max\{Q, -2\epsilon_1, -2\epsilon_2\}$ with $Q = \left\{\sum\limits_{l = 1}^n\left\{b_{lp}+c_{lp}+|\alpha_{lp}|+|\beta_{lp}|\right\}L_p-a_p-\widetilde{\sigma}\right\}$.

Proof. Construct the following Lyapunov functional:

where

and $\widetilde{\sigma}_p$ and $\widetilde{\xi}$ are the parameters to be determined later. By combining the calculations of Theorem 3.1, for $t \in (t_{i-1}, t_i]$, $U(t)$ can be calculated as follows:

For any $i\in N$, we obtain the following:

For $t > t_0$, and similar to the calculations in Theorem 3.1, if $0 < \frac{\nu}{q} < 1$, then we can obtain the following:

If $\frac{\nu}{q}\ge1$, then we derive the following:

Make $\ \gamma = max\{(\frac{\nu}{q})^{T_0}\frac{1}{q}, (\frac{\nu}{q})^{-T_0}\frac{1}{q}\}$, and $\zeta = R^{\frac{1}{q}}+\frac{ln(\frac{\nu}{q})}{T} < 0$; then, $U(t)\leq\gamma e^{\zeta}U(t_0^{+}).$ Therefore, when $t\rightarrow \infty$, $U(t)\rightarrow0$. This shows that the error system (2.6) is exponentially synchronous. □

Remark 3.5. Compared with Reference ^[49], this paper further discusses fractional-order models and relaxes the restriction on activation functions. The controller used in the discussion does not contain sign functions, which can prevent the system signal from jittering and make the results less conservative.

Remark 3.6. It is worth noting that the method discussed by the author is only applicable to continuous-type memristive neural network systems, and its effect in discrete-type memristive neural network systems needs to be further verified.

4.   Numerical examples

Here are two numerical examples to illustrate the applicability of our criterion.

Example 4.1. Next, we consider the exponential synchronization problem of fractional-order fuzzy resistive neural networks with time-varying delay and impulses, where the driving system is composed of the following parts:

where

$a_1 = 1.2$, $a_2 = 1.4$, $f_1(x) = f_2(x) = tanh(x-1)$, $\tau_l(t) = \frac{e^{t}}{1+e^{t}}$, $v_1 = v_2 = 1, \; \begin{pmatrix}\alpha_{pl}\end{pmatrix}_{2\times2} = \begin{pmatrix}1.6 & & -1.3\\-1.1 & & 1.2\end{pmatrix}$, $\begin{pmatrix}\beta_{pl}\end{pmatrix}_{2\times2} = \begin{pmatrix}1.1 & & -1.5\\-0.5 & & 1.2\end{pmatrix}$, $\left(d_{pl}\right)_{2\times2} = \left(S_{pl}\right)_{2\times2} = \left(H_{pl}\right)_{2\times2} = \left(\begin{matrix}0.2 & 0\\0 & 0.3\end{matrix}\right),$

and the initial values are $(\varphi_1(0), \varphi_2(0)) = (0.3, -0.5)^{T}$. The impulsive moment $t_i$ satisfies the following:

$t_{8q+1} = \frac{\pi}{4}+2\pi l$, $t_{8q+2} = \frac{\pi}{2}+2\pi l$, $t_{8q+3} = \frac{3\pi}{4}+2\pi l$, $t_{8q+4} = \pi+2\pi l$, $t_{8q+5} = \frac{5\pi}{4}+2\pi l$, $t_{8q+6} = \frac{3\pi}{2}+2\pi l$, $t_{8q+7} = \frac{7\pi}{4}+2\pi l$, $t_{8q+8} = 2\pi+2\pi l$, $t_{8q+9} = \frac{9\pi}{4}+2\pi l$, $q = 0, 1, 2, ..., \; \frac{\nu}{q} = 4.4 > 1$, $I_1 = 0.1$, $I_2 = 0.3$,

$\left.\mathrm{b}_{11}(x_1(t)) = \left\{\begin{array}{l}1.6, \; \; \; \; |x_1(t)| < 1, \\ 1.4, \; \; \; \; |x_1(t)| > 1, \end{array}\right.\right.$

$\left.\mathrm{b}_{12}(x_1(t)) = \left\{\begin{array}{l}1.5, \; \; \; \; \; \; |x_1(t)| < 1, \\ -1.3, \; \; \; \; |x_1(t)| > 1, \end{array}\right.\right.$

$\left.\mathrm{b}_{21}(x_2(t)) = \left\{\begin{array}{l}1.1, \; \; \; \; |x_2(t)| < 1, \\ 1.2, \; \; \; \; |x_2(t)| > 1, \end{array}\right.\right.$

$\left.\mathrm{b}_{22}(x_2(t)) = \left\{\begin{array}{l}-1.4, \; \; \; \; |x_2(t)| < 1, \\ 1.5, \; \; \; \; \; \; \; |x_2(t)| > 1, \end{array}\right.\right.$

$\left.\mathrm{c}_{11}(x_1(t)) = \left\{\begin{array}{l}-1.1, \; \; \; |x_1(t)| < 1, \\ 1.3, \; \; \; \; \; |x_1(t)| > 1, \end{array}\right.\right.$

$\left.\mathrm{c}_{12}(x_1(t)) = \left\{\begin{array}{l}1.3, \; \; \; \; \; \; |x_1(t)| < 1, \\ -1.4, \; \; \; \; |x_1(t)| > 1, \end{array}\right.\right.$

$\left.\mathrm{c}_{21}(x_2(t)) = \left\{\begin{array}{l}-1.6, \; \; \; |x_2(t)| < 1, \\ 1.1, \; \; \; \; \; |x_2(t)| > 1, \end{array}\right.\right.$

$\left.\mathrm{c}_{22}(x_2(t)) = \left\{\begin{array}{l}1.4, \; \; \; \; \; \; \; |x_2(t)| < 1, \\ -1.3, \; \; \; \; |x_2(t)| > 1, \end{array}\right.\right.$

and the corresponding response system of (4.1) is given in the following form:

where the initial values are $(\psi_1(0), \psi_2(0)) = (-0.7, 0.5)^{T}$. The rest of the parameters used are the same as for the drive. If $u_p(t) = 0$, then drive and respond to states $x_1(t)$ and $y_1(t)$ no longer achieve synchronization under control of the curve is shown in Figure 1, drive and respond to states $x_2(t)$ and $y_2(t)$ no longer achieve synchronization under control of the curve is shown in Figure 2, and the synchronization error evolution is shown in Figure 3, which leads to the conclusion that the systems (4.1) and (4.2) are not exponentially synchronized without a controller. Choose $L_l = K_l = 1$, $f(0) = g(0) = -1.56$. Additionally, the feedback gains are set as $\sigma_1 = 11$, $\sigma_2 = 8$, and $\xi = 43$. Then,

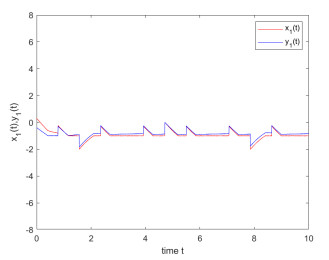
That is, conditions (C1) and (C2) are satisfied. According to Theorem 3.1, drive and response states $x_1(t)$ and $y_1(t)$ under controller (3.1) can achieve synchronization, as shown in Figure 4. Drive and response states $x_2(t)$ and $y_2(t)$ under controller (3.1) can achieve synchronization, as shown in Figure 5. Under the controller (3.1), system (4.1) synchronizes with system (4.2), as shown in Figure 6.

Example 4.2. Here, considering the exponential synchronization problem of fractional-order fuzzy resistive neural networks with time-varying delay and impulses, the driving system is composed of the following parts:

where

$a_1 = 1.6$, $a_2 = 1.8$, $f_1(x) = f_2(x) = sin(x+1)$, $\tau_l(t) = \frac{e^{t}}{1+e^{t}}$, $v_1 = v_2 = 1, \; \begin{pmatrix}\alpha_{pl}\end{pmatrix}_{2\times2} = \begin{pmatrix}1.7 & & -1.5\\-1.3 & & 1.2\end{pmatrix}$, $\begin{pmatrix}\beta_{pl}\end{pmatrix}_{2\times2} = \begin{pmatrix}-1.2 & & -0.4\\-1.1 & & -0.7\end{pmatrix}$, $\left(d_{pl}\right)_{2\times2} = \left(S_{pl}\right)_{2\times2} = \left(H_{pl}\right)_{2\times2} = \left(\begin{matrix}0.3 & 0\\0 & 0.5\end{matrix}\right),$

and the initial values are $(\varphi_1(0), \varphi_2(0)) = (-0.4, 0.7)^{T}$. The impulsive moment $t_i$ is the same as in Example 4.1.

$\frac{\nu}{q} = 0.69 < 1$, $I_1 = 0.6$, $I_2 = -0.3$,

$\left.\mathrm{b}_{11}(x_1(t)) = \left\{\begin{array}{l}1.5, \; \; \; \; \; \; |x_l(t)| < 1, \\ -1.3, \; \; \; |x_1(t)| > 1, \end{array}\right.\right.$

$\left.\mathrm{b}_{12}(x_1(t)) = \left\{\begin{array}{l}1.6, \; \; \; \; \; \; |x_1(t)| < 1, \\ -1.4, \; \; \; \; |x_1(t)| > 1, \end{array}\right.\right.$

$\left.\mathrm{b}_{21}(x_2(t)) = \left\{\begin{array}{l}1.7, \; \; \; \; \; |x_2(t)| < 1, \\ 1.2, \; \; \; \; |x_2(t)| > 1, \end{array}\right.\right.$

$\left.\mathrm{b}_{22}(x_2(t)) = \left\{\begin{array}{l}-1.4, \; \; |x_2(t)| < 1, \\ 1.1, \; \; \; \; |x_2(t)| > 1, \end{array}\right.\right.$

$\left.\mathrm{c}_{11}(x_1(t)) = \left\{\begin{array}{l}-1.3, \; \; \; |x_1(t)| < 1, \\ 1.6, \; \; \; \; \; |x_1(t)| > 1, \end{array}\right.\right.$

$\left.\mathrm{c}_{12}(x_1(t)) = \left\{\begin{array}{l}1.1, \; \; \; \; \; |x_1(t)| < 1, \\-1.6, \; \; \; |x_1(t)| > 1, \end{array}\right.\right.$

$\left.\mathrm{c}_{21}(x_2(t)) = \left\{\begin{array}{l}-1.6, \; \; \; |x_2(t)| < 1, \\ 1.5, \; \; \; \; |x_2(t)| > 1, \end{array}\right.\right.$

$\left.\mathrm{c}_{22}(x_2(t)) = \left\{\begin{array}{l}1.5, \; \; \; \; |x_2(t)| < 1, \\ -1.6, \; \; |x_2(t)| > 1, \end{array}\right.\right.$

and the corresponding response system of (4.3) is given in the following form:

where the initial values are $(\psi_1(0), \psi_2(0)) = (0.6, -0.3)^{T}$. The rest of the parameters used are the same as for the drive. If $u_p(t) = 0$, then time evolution diagram of drive response states $x_1(t)$ and $y_1(t)$ without controller no longer achieve synchronization in Figure 7, time evolution diagram of drive response states $x_2(t)$ and $y_2(t)$ without controller no longer achieve synchronization in Figure 8, and the synchronization error evolution diagram is expressed in Figure 9, which shows that the systems (4.3) and (4.4) are not exponentially synchronized without a controller. Choose $L_l = K_l = 1$, and $f(0) = g(0) = 0.84$. By calculation, we have $\sigma_1(t) = 10$, $\sigma_2(t) = 10$, and $\widetilde{\xi} = 38$. Choose the initial conditions of the adaptive laws as follows: $\sigma_1(t) = 12$, $\sigma_2(t) = 13$, $\xi(t) = 11.6$, $\epsilon_1 = 0.6$, and $\epsilon_2 = 0.5$. Then,

Therefore, conditions (C3) and (C4) are satisfied. According to Theorem 3.2, time evolution diagram of the drive response states $x_1(t)$ and $y_1(t)$ under controller (3.17) can achieve synchronization, as shown in Figure 10. Time evolution diagram of the drive response states $x_2(t)$ and $y_2(t)$ under controller (3.17) can achieve synchronization, as shown in Figure 11. The systems (4.3) and (4.4) achieve exponential synchronization under under the control of (3.17), as shown in Figure 12.

5.   Conclusions

This paper studied the exponential synchronization problem of fractional-order memristive neural networks with time-varying delay and impulses. By establishing a sign-function state feedback controller and an adaptive controller, the problem of a system jitter caused by the controller setting was solved. A Lyapunov function was established using the norm and calculus knowledge, and several new sufficient conditions for system exponential synchronization were discussed. Finally, two simulation experiments were used to verify the theoretical results. In future work on neural networks, we will continue to study the synchronization problem of non-autonomous neural networks with diffusion and impulses.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the National Natural Science Foundation of China under Grant 61573010, the Opening Project of Sichuan Province University Key Laboratory of Bridge Non-Destruction Detecting and Engineering Computing under Grant 2021QYJ06.

Conflict of interest

There are no conflicts of interest regarding this work.