Practical exponential stability with respect to $h-$manifolds of discontinuous delayed Cohen–Grossberg neural networks with variable impulsive perturbations

1.   Introduction

Let $Z$ be a random variable (RV) having probability density function (PDF) $g_Z(z)$. Shannon ^[33] defined entropy for a RV $Z$ as

The non-additive generalization of Shannon's entropy of order $\eta$, suggested by Tsallis ^[37], is known as Tsallis entropy. This measure plays an important role in the uncertainty measurements of an RV $Z$, which is defined as

where $0 < \eta\neq1.$ When $\eta\longrightarrow 1$, Tsallis entropy approaches Shannon entropy.

There are many applications of this new entropy, especially in physics ^[7], earthquakes ^[2], stock exchanges ^[20], plasma ^[23], and income distribution ^[35]. For more information about Tsallis entropy, we recommend reading Tsallis ^[38]. Several generalizations of Shannon entropy have been developed, which make these entropies sensitive to different kinds of probability distributions via the addition of a few additional parameters. A new measure of Shannon entropy, cumulative residual entropy (CRE), was introduced by Rao et al. ^[30] by taking into account the survival function instead of the probability density function. CRE is considered more stable and mathematically sound due to its more regular survival function (SF) than the PDF. Moreover, distribution functions exist even when probability density functions do not exist (e.g., Govindarajulu, power-Pareto, and generalized lambda distributions). CRE measure is based on SF $\overline G_Z(z)$. According to his definition, CRE is defined as

A cumulative residual Tsallis entropy (CRTE) of order $\eta$, which is represented by $\zeta_{\eta}(Z)$, was introduced by Sati and Gupta ^[32]. This CRTE is defined as

When $\eta\longrightarrow 1$, CRTE approaches CRE.

The CRTE may also be represented in terms of the mean residual life function of $Z$, which is another useful representation defined as

Rajesh and Sunoj ^[31] unveiled an alternative measure for CRTE denoted by the order $\eta$, which is defined as

The characteristics of the residual Tsallis entropy for order statistics (OSs) were studied by Shrahili and Kayid ^[34]. Mohamed ^[24] recently conducted a study on the CRTE and its dynamic form, which is based on the Farlie-Gumbel-Morgenstern (FGM) family. When prior information is presented in the form of marginal distributions, it is advantageous to model bivariate data using marginal distributions. The FGM family is one of these families that has been the subject of a significant amount of study. The FGM family is represented by the bivariate cumulative distribution function (CDF) $G_{Z, X}(z, x) = G_Z(z)G_X(x)[1+\theta(1-G_Z(z))(1-G_X(x))],$ $-1\leq\theta\leq 1,$ where $G_Z(z)$ and $G_X(x)$ are the marginal CDFs of two RVs $Z$ and $X$, respectively. Literature indicates that several modifications have been implemented in the FGM family to increase the correlation between its marginals. Extensive families have been the subject of a great number of studies, each of which has a unique point of view. Examples of these studies are Barakat et al. ^[6], Abd Elgawad and Alawady ^[1], Alawady et al. ^[4], Chacko and Mary ^[10], Husseiny et al. ^[17,18], and Nagy et al. ^[26]. It was demonstrated by Huang and Kotz ^[15] that a single iteration may result in a doubling of the correlation between marginals in FGM. This was established through the use of a single iteration. The joint CDF iterated FGM (IFGM) family with a single iteration is denoted by IFGM$(\gamma, \omega)$ and defined as

The corresponding joint PDF (JPDF) is given by

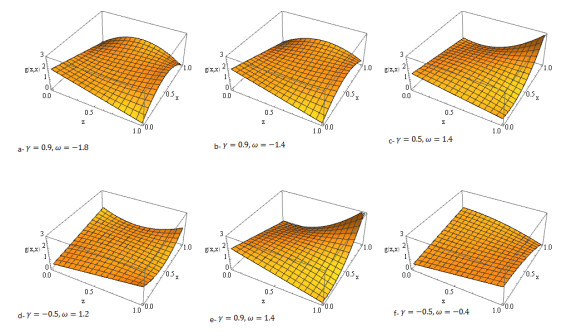
Classical FGM can clearly be regarded as a special case of the IFGM$(\gamma, \omega)$ family (1.5)–(1.6) by putting $\omega = 0$. If the two marginals $G_Z(z)$ and $G_X(x)$ are continuous, Huang and Kotz ^[15] showed that the natural parameter space $\Omega$ (which is the admissible set of the parameters $\gamma$ and $\omega$ that makes $G_{Z, X}(z, x)$ is a genuine CDF) is convex, where $\Omega = \{(\gamma, \omega):-1\leq \gamma\leq 1;$$-1\leq \gamma+\omega; \omega\leq\frac{3-\gamma+\sqrt{9-6\gamma-3\gamma^{2}}}{2}\}$. Additionally, if the marginals are uniform, the correlation coefficient is $\rho = \frac{\gamma}{3}+\frac{\omega}{12}.$ Finally, the maximal correlation coefficient attained for this family is $\max\rho = 0.434,$ versus $\max\rho = \frac{1}{3} = 0.333$ achieved for $\gamma = 1$ in the original FGM ^[16]. The JPDF of the IFGM copula is plotted in Figure 1. Figure 1 illustrates subfigures that exhibit unique parameter values. Each subfigure from (a) to (f) had the parameter values arranged in a vector form $(\gamma, \omega)$.

As a unifying model for ascendingly ordered RVs, generalized order statistics (GOSs) have drawn more and more attention. The GOSs model was first presented by Kamps ^[21]. It is made up of several pertinent models of ordered RVs, such as order statistics (OSs), record values, sequential OSs (SOSs), and progressive censored type-Ⅱ OSs (POS-II). The RVs $Z(r, n, \tilde{m}, \kappa), r = 1, 2, ..., n,$ are called GOSs based on a continuous CDF $G_Z(z)$ with the PDF $g_Z(z),$ if their JPDF has the form

where $G^{-1}_{}(0)\leq z_1\leq...\leq z_n\leq G^{-1}_{}(1),$ $\kappa > 0, \gamma_{i} = n+\kappa-i+\sum_{t = i}^{n-1} m_{t} > 0, i = 1, \ldots, n-1, \text { and } \tilde{m} = (m_{1}, m_{2}, \ldots, m_{n-1}) \in \mathbb{R}.$ In this paper, we assume that the parameters $\gamma_{1}, \dots, \gamma_{n-1},$ and $\gamma_{n} = \kappa,$ are pairwise different, i.e., $\gamma_{t} \neq \gamma_{s}, t\neq s, \; t, s = 1, 2, ..., n.$ We obtain a very wide subclass of GOSs that contains $m$-GOSs (where $m_1 = ... = m_{n-1} = m$), OSs, POS-II, and SOSs. The PDF of the $r$th GOS and the JPDF of the $r$th and $s$th GOSs, $1\leq r < s\leq n,$ respectively, are given by Kamps and Cramer ^[22].

where $\overline{G} = 1-G$ is (SF) of $G,$ $C_{r} = \prod\limits_{i = 1}^{r} \gamma_{i}, \; \alpha_{i; r} = \prod\limits_{j = 1 \atop j \neq i}^{r} \frac{1}{\gamma_{j}-\gamma_{i}}, \; 1 \leq i \leq r \leq n,$ and $\alpha_{i; r;s} = \prod\limits_{j = r+1 \atop j \neq i}^{s} \frac{1}{\gamma_{j}-\gamma_{i}}, \; r+1 \leq i \leq s \leq n.$

When dealing with selection and prediction difficulties, the meaning of concomitants is a vital tool. The idea of concomitants of OSs (COSs) was first proposed by David ^[11]. Refer to David and Nagaraja ^[12] for a comprehensive understanding of the COS. Many studies have been published on the concomitants of the GOSs (CGOSs) model. Researchers such as Alawady et al. ^[5], Beg and Ahsanullah ^[8], and Domma and Giordano ^[13] have studied this issue. The CGOSs models, however, have only been studied in a restricted number of studies when $\gamma_t\neq \gamma_s, t\neq s, \; t, s = 1, 2, ..., n.$ These include Abd Elgawad and Alawady ^[1], and Mohie El-Din et al. ^[25].

Let $(Z_i, X_i), i = 1, 2, ..., n,$ be a random sample from a continuous bivariate CDF $G_{Z, X}(z, x).$ If we denote $Z(r, n, \tilde{m}, \kappa)$ as the $r$th GOS of the $Z$ sample values, then the $X$ values associated with $Z(r, n, \tilde{m}, \kappa)$ is called the concomitant of the $r$th GOS and is denoted by $X_{[r, n, \tilde{m}, \kappa]}, r = 1, 2, ..., n.$ The PDF of the concomitant of $r$th GOS is given by

More generally, for $1\leq r < s\leq n,$ the JPDF of the concomitants of $r$th and $s$th GOSs is given by

Motivation and the purpose of the work

Mohamed ^[24] exhibited CRTE features in CGOSs that were based on FGM. Suter et al. ^[36] conducted another study that examined Tsallis entropy in CGOSs resulting from FGM. We generalize the previous articles by investigating Tsallis measures in CGOS from IFGM in more general scenarios. The objectives that inspired this study are as follows: Tsallis entropy measures based on CGOSs with interesting features are introduced in a broad framework. We considered sub models through a comprehensive numerical analysis, including OSs, record values, and k-record values. An in-depth analysis of reaching satisfactory results using the nonparametric estimate of these measures. More sophistication and flexibility are provided by the suggested distribution (IFGM) for modeling complicated data sets. This is why we used actual data in our analysis.

The arrangement of this paper is organized as follows: In Section 2, we obtain some characterization results on concomitants $X_{[r, n, \tilde{m}, k]}$ based on IFGM$(\gamma, \omega)$ as Tsallis entropy, CRTE, and alternate measure of CRTE. In Section 3, we extend and compute some examples of information measures for the concomitants $X_{[r, n, \tilde{m}, k]}$ from IFGM$(\gamma, \omega)$. We use the empirical method in combination with CGOS based on the IFGM family, to estimate the CRTE in Section 4. Finally, in Section 5, a bivariate real-world data set has been probed, and we examine the Tsallis entropy and CRTE. Finally, Section 6 concludes the work.

2.   Theoretical results

In this section, we derived Tsallis entropy, CRTE, and an alternative measure CRTE for CGOS based on the IFGM$(\gamma, \omega)$ family. First, we will point out some important results that we will use in deducing these measures. Husseiny et al. ^[17] derived the PDF, CDF, and SF for the concomitant $X_{[r, n, \tilde{m}, k]}$ of the $r$th GOS, respectively, as follows:

and

where $V_{i}\sim G^{i+1}_{X}, i = 1, 2, \; \;$ $\delta^{(\tilde{m}, k)}_{r, n:1} = \gamma C_{r-1}\sum \limits_{i = 1}^{r}a_{i}(r)\left(\frac{1-\gamma_{i}}{1+\gamma_{i}}\right)$ and $\; \delta^{(\tilde{m}, k)}_{r, n:2} = \omega C_{r-1}\sum \limits_{i = 1}^{r}a_{i}(r)\left(\frac{1-\gamma_{i}}{1+\gamma_{i}}\right)\left(\frac{3-\gamma_{i}}{2+\gamma_{i}}\right)$.

2.1.   Tsallis entropy for CGOS of ordered $\eta$

Theorem 2.1. Tsallis entropy of concomitants of the $r$th GOS based on the IFGM$(\gamma, \omega)$ is given by

where $\mathcal{N}(x) = \infty,$ if $x$ is non-integer, and $\mathcal{N}(x) = x,$ if $x$ is integer, and $U$ is a uniform RV on (0, 1).

Proof. Using (1.1) and (2.1), Tsallis entropy is provided by

□

Remark 2.1. If $\tilde{m} = 0$ and $k = 1.$ The Tsallis entropy of the concomitant of the rth OS based on the IFGM$(\gamma, \omega)$ is given by

where $\Omega_{1, r:n} = \frac{\gamma(n-2r+1)}{n+1}$ and $\Omega_{2, r:n} = \omega \left[\frac{r(2n-3r+1)}{(n+1)(n+2)}\right],$ (cf. Husseiny et al. ^[17]).

Remark 2.2. If $\tilde{m} = -1$ and $k = 1.$ Tsallis entropy of the concomitant of the $n$th upper record value based on IFGM$(\gamma, \omega)$ is given by

where $\Delta_{n:1} = \gamma(2^{-(n-1)}-1)$ and $\Delta_{n:2} = \omega(2^{-(n-2)}-3^{-(n-1)}-1).$

Remark 2.3. Tsallis entropy for the concomitant of the $n$th upper $k$-record value based on IFGM$(\gamma, \omega)$ is given by

where $\nabla_{n, k:1} = \gamma\left(2(\frac{k}{k+1})^{n}-1\right)$ and $\nabla_{n, k:2} = \omega\left(4(\frac{k}{k+1})^{n}-3(\frac{k}{k+2})^{n}-1\right).$ (cf. Nagy and Alrasheedi ^[27]).

2.2.   CRTE for CGOS of ordered $\eta$

Theorem 2.2. CRTE for CGOS based on the IFGM$(\gamma, \omega)$ is given by

where $U$ is a uniform RV on (0, 1).

Proof. Using (1.2) and (2.3), then CRTE is provided by

□

Remark 2.4. If $\tilde{m} = 0$ and $k = 1.$ The CRTE of the concomitant of the rth OS based on the IFGM$(\gamma, \omega)$ is given by

Remark 2.5. If $\tilde{m} = -1$ and $k = 1.$ CRTE of the concomitant of the $n$th upper record value based on the IFGM$(\gamma, \omega)$ is given by

Remark 2.6. CRTE of the concomitant of the $n$th upper $k$-record value based on the IFGM$(\gamma, \omega)$ is given by

2.3.   Alternate measure of CRTE for CGOS of ordered $\eta$

For the concomitant $X_{[r, n, \tilde{m}, k]}$ of the $r$th GOS, the moment of $X_{[r, n, \tilde{m}, k]}$ based on the IFGM$(\gamma, \omega)$ (cf. Husseiny et al. ^[17]) is given by

Theorem 2.3. The alternative measure of CRTE for CGOS based on IFGM$(\gamma, \omega)$ is given by

where $U$ is a uniform RV on (0, 1).

Proof. Using (1.4) and (2.6), the alternative measure of CRTE is provided by

□

Theorem 2.4. Let $X_{[r, n, \tilde{m}, k]}$ be a CGOS based on a continuous CDF $G_X(x)$ with the PDF $g_X(x)$. For all $\eta > 0,$ we have

where

Proof. Using (1.3) and $m_{[r, n, \tilde{m}, k]}(x)\lambda_{[r, n, \tilde{m}, k]}(x) = 1+m'_{[r, n, \tilde{m}, k]}(x),$ where

Then, we obtain

for all $\eta > 0.$ Upon using Fubini's theorem, we obtain

This gives the desired result. □

Remark 2.7. If $\tilde{m} = 0$ and $k = 1.$ The alternative measure of CRTE for concomitant of the rth OSs based on the IFGM$(\gamma, \omega)$ is given by

Remark 2.8. If $\tilde{m} = -1$ and $k = 1.$ The alternative measure of CRTE for concomitant of the $n$th upper record value based on the IFGM$(\gamma, \omega)$ is given by

Remark 2.9. The alternative measure of CRTE for concomitant of the $n$th upper $k$-record value based on the IFGM$(\gamma, \omega)$ is given by

3.   Illustrative examples with numerical study of Tsallis entropy and CRTE

In this section, we study the Tsallis entropy, CRTE, and alternate measure of CRTE for CGOS in IFGM$(\gamma, \omega)$ for some popular distributions. We consider the extended Weibull (EW) family of distributions, which was developed by Gurvich et al. ^[14], as a case study. The CDF of EW is given by

where $H(x; \varepsilon)$ is a differentiable, nonnegative, continuous, and monotonically increasing function when $x$ depends on the parameter vector $\varepsilon.$ Also, $H(x; \varepsilon)\longrightarrow 0^{+}$ as $x\longrightarrow 0^{+}$ and $H(x; \varepsilon)\longrightarrow +\infty$ as $x\longrightarrow +\infty.$ This CDF is denoted by EW $(\tau, \varepsilon)$ and has the following PDF:

where $h(x; \varepsilon)$ is the derivative of $H(x; \varepsilon)$ with respect to $x.$ Several important models are included in the EW, including the Rayleigh, Pareto, Weibull, uniform, and exponential distributions (ED). For further details about this family, see Jafari et al. ^[19].

Example 3.1. Consider two variables, Z and X, that possess ED from IFGM (represented by IFGM-ED) (i.e. $G_{X}(x) = 1-e^{-\theta x}, x, \theta > 0$). Based on (2.4), we get the Tsallis entropy in $X_{[r, n, \tilde{m}, k]}$ as follows:

Example 3.2. Consider $Z$ and $X$ to be power distributions derived from IFGM (i.e. $G_{X}(x) = x^{c}, 0\leq x\leq1, c > 0$). Then $\mathcal{H}_{\eta[r, n, \tilde{m}, k]}(x)$ is given by

Example 3.3. Suppose that $Z$ and $X$ have EW based on IFGM with (i.e. $G_{X}(x) = 1-e^{-\tau H(x; \varepsilon)}, \; x > 0, \tau > 0,$). Then, we have the Tsallis entropy in $X_{[r, n, \tilde{m}, k]}$ as follows:

Example 3.4. Assume that $Z$ and $X$ both possess IFGM-ED. Based on (2.5), we obtain the CRTE in $X_{[r, n, \tilde{m}, k]}$ as follows:

Example 3.5. Assume that the uniform distributions of $Z$ and $X$ come from an IFGM (i.e. $G_{X}(x) = x, \; 0\leq x\leq1$). Based on (2.5), we obtain the CRTE in $X_{[r, n, \tilde{m}, k]}$ as follows:

Example 3.6. Let us say that $Z$ and $X$ have EW according to IFGM. From (2.5), we get the CRTE in $X_{[r, n, \tilde{m}, k]}$ as follows:

Example 3.7. Assume that $Z$ and $X$ both possess IFGM-ED. Based on (2.7), we have the alternate measure of CRTE in $X_{[r, n, \tilde{m}, k]}$ as follows:

Example 3.8. Assume that the uniform distributions of $Z$ and $X$ come from IFGM. Based on (2.7), we obtain the alternate measure of CRTE in $X_{[r, n, \tilde{m}, k]}$ as follows:

Example 3.9. Let us say that $Z$ and $X$ have EW, according to IFGM. Based on (2.7), we obtain the alternate measure of CRTE in $X_{[r, n, \tilde{m}, k]}$ as follows:

As shown in Tables 1–4 of the IFGM-ED, the Tsallis entropy and the CRTE for $X_{[r:n]}$ and $X_{[n]}$ are presented. After running the numbers through MATHEMATICA version 12, we can deduce the following properties from Tables 1–4.

● When $\gamma = 0.9$, $\eta = 5$, and $\theta = 0.5$, the value of $\mathcal{H}_{\eta[r:n]}(x)$ goes up as $n$ goes up. When $\gamma = -0.5$, $\eta = 10$, and $\theta = 1$, the value of $\mathcal{H}_{\eta[r:n]}(x)$ goes down as $n$ goes up. But $\mathcal{H}_{\eta[r:n]}(x)$ stays the same for all $\omega$ values when $n = 7$ and $r = 5$ (look at Table 1).

● We see that when $\gamma$ is 0.9, $\eta$ is 5, and $\theta$ is 0.5, and when $\gamma$ is -0.5, $\eta$ is 10, and $\theta$ is 1, the value of $\mathcal{H}_{\eta[n]}(x)$ goes down as $n$ goes up, and it almost stays the same when $n = 10$ (look at Table 2).

● When $\gamma = 0.9$, $\eta = 5$, and $\theta = 0.5$, the value of $\zeta_{\eta[r:n]}(x)$ goes down as $n$ goes up. On the other hand, when $\gamma = -0.5$, $\eta = 10$, and $\theta = 1$, the value of $\zeta_{\eta[r:n]}(x)$ goes up as $n$ goes up. It gets bigger as $n$ gets bigger, but $\zeta_{\eta[r:n]}(x)$ stays the same for all $\omega$ values when $n = 7$ and $r = 5$ (look at Table 3).

● When $\gamma = 0.9$, $\eta = 5$, and $\theta = 0.5$, the value of $\zeta_{\eta[n]}(x)$ goes down as $n$ goes up. When $\gamma = -0.5$, $\eta = 10$, and $\theta = 1$, the value of $\zeta_{\eta[n]}(x)$ goes up as $n$ goes up, and the value of $\zeta_{\eta[n]}(x)$ stays the same at $n = 22$ (look at Table 4).

4.   Estimating of CRTE

For the purpose of calculating the CRTE for concomitant $X _{[r, n, \tilde{m}, k]}$, we employ empirical estimators in this section. Next, we'll examine the issue of estimating the CRTE for CGOS using the empirical CRTE. Consider the IFGM sequence $(Z_i, X_i)$ for each $i = 1, 2, ..., n$. In accordance with (2.7), the emperical CRTE of the set $X_{[r, n, \tilde{m}, k]}$ can be computed as follows:

where for any CDF $G(.),$ the symbol $\hat G(.)$ stands for the empirical CDF of $G(.),$ and $\Delta_{j} = x_{(j+1)}-x_{(j)},$ $j = 1, 2..., n-1,$ are the sample spacings based on ordered random samples of $X_{j}.$

Example 4.1. Define a random sample from the IFGM-ED as $(Z_i, X_i),$ where $i$ ranges from $1$ to $n$. The sample spacings, denoted by $\Delta_j$, are considered to be independent RVs. Furthermore, $\Delta_j$ exhibits the ED with a mean of $\frac{1}{\theta(n-j)}$, where $j$ ranges from 1 to $n-1$. For additional information, refer to Chandler ^[9] and Pyke ^[29]. Then the expected value and variance of the empirical CRTE in $X_{[r]}^\star$ are given by

Example 4.2. Again, for completeness, we study here the empirical CRTE of the concomitant $X_{[r]}^\star$ of the $r$th upper record value $Z_r^\star$ based on the IFGM copula. In this case, the sample spacings $\Delta_j,$ $j = 1, 2, ..., n-1,$ are independent, and each of them has the beta distribution with parameters $1$ and $n.$ According to Pyke ^[29], the expectation and variance of the empirical CRTE of the concomitant $X_{[r]}^\star$ are as follows:

Figures 2 and 3 illustrate the relationship between CRTE and empirical CRTE in $X_{{[r:n]}}$ from IFGM-ED $(\gamma, \omega)$, at $n = 50.$ Figures 2 and 3 can be used to obtain the following properties:

(1) When the $\theta$ values are increased, the CRTE and the empirical CRTE have values that are practically identical to one another.

(2) At most $\omega$ and $\gamma$ values, CRTE and empirical CRTE have identical results, particularly when $\omega = 0$ for all $r$ values.

5.   Real data application

This section includes analyses of a real-world data set. The data set relates to $n = 50$ simulated simple computer series systems consisting of a processor and a memory. The data was gathered and analyzed based on Oliveira et al. ^[28]. The data set contains $n = 50$ simulated rudimentary computer systems with processors and memory. An operating computer will be able to operate when both parts are working properly (the processors and memory). Assume the system is nearing the end of its lifecycle. The degeneration advances rapidly in a short period of time ^[3]. In a short time (in hours), the degeneration advances rapidly. In the case of the first component, a deadly shock can destroy either it or the second component at random, due to the system's greater vulnerability to shocks. We fit the ED to the processor lifetime and memory lifetime separately. As an illustration of the data, Figures 4 and 5 provide a basic statistical analysis. The maximum likelihood estimates of the scale parameters $(\theta_i), \; i = 1, 2,$ are $1.24079$ and $1.08616,$ $\gamma = 0.175473,$ and $\omega = 2.16024$. Table 5 examines the Tsallis entropy and CRTE for IFGM-ED$(0.17543$, $2.16024).$ For the concomitants $X_{[r:50]}$, $r = 1, 2, 24, 25, 49, 50,$ i.e., the lower and upper extremes' concomitants, and the central values' concomitants. We observe that the $\mathcal{H}_{\eta[r:50]}(x)$ and $\zeta_{\eta[r:50]}(x)$ have maximum values at extremes.

6.   Conclusion and future work

Given its simplicity and adaptability, IFGM surpasses most FGM generalizations, even though its efficiency is similar to some of those generalizations (such as the Huang\textendash Kotz FGM) in that it has a similar range of correlation coefficients. The CDFs used in this work were consistently formed by linearly combining simpler distributions, due to the advantages they offer. Tsallis entropy and its associated measures for concomitant were derived from IFGM, and a numerical analysis was conducted to uncover certain characteristics of these measures based on GOSs. Special cases were also extracted from this study, for example, OSs, record values, and k-record values. Furthermore, non-parametric estimators of CRTE were derived. The outcomes of an empirical examination of the CRTE are distinct. Finally, an illustrative analysis of a bivariate real-world data set was performed, and the proposed method performs exceptionally well. In the future work, some bivariate distribution families will be considered, including the Huang-kotz, Cambanis, and Sarmanov families, as well as various applications of the CRTE in CGOS. Additionally, we will investigate the quantile function based on Tsallis measures from concomitants. Also, for the estimation problem, we will discuss at least two estimation methods for this model: maximum likelihood and Besyain. Further, a Monte Carlo simulation will be conducted to test the estimator's performance against the empirical measure as well as the exact formula presented in this paper.

Author contributions

I. A. Husseiny: Conceptualization, Writing original draft, Formal analysis, Software, Investigation, Methodology, Supervision; M. Nagy: Validation, Resources, Writing-review & editing, Data curation, Methodology; A. H. Mansi: Writing-review & editing, Investigation; M. A. Alawady: Conceptualization, Formal analysis, Writing original draft, Software, Investigation, Methodology, Supervision. All authors have read and agreed to the published version of the manuscript.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was conducted under a project titled "Researchers Supporting Project", funded by King Saud University, Riyadh, Saudi Arabia under grant number (RSPD2024R969).

The authors are grateful to the editor and anonymous referees for their insightful comments and suggestions, which helped to improve the paper's presentation.

Funding

This research was conducted under a project titled "Researchers Supporting Project", funded by King Saud University, Riyadh, Saudi Arabia under grant number (RSPD2024R969).

Conflict of interest

The authors declare no conflict of interest.