1.
Introduction
Manchester has a rich industrial heritage, a very diverse economy and a center for cultural industries, retail, transport, logistics, finance and manufacturing. Manufacturing companies rely on efficient and optimized production methods to create their products. But even the most efficient method of manufacturing plants inevitably generates some form of waste. The selection of the best place to dispose of the waste from manufacturing plants requires the need to first understand the type of waste. There are three main types of waste in manufacturing: solid waste, chemical waste and toxic waste. Solid waste includes paper, metal or carbon-based materials that are leftover after basic manufacturing processes have been completed. Some types of waste can be recycled and some cannot be recycled; the latter must be undergo proper disposal; otherwise, it will endanger the health of the workers. The second category is chemical waste, which includes the waste of residual chemicals. Some manufacturing processes may generate large amounts of chemical waste. Solid waste can be placed in the bin, but chemical waste should be handled in a specific way to prevent the dangerous effects of these chemicals. The third is toxic waste, which is a by-product of many manufacturing processes. We cannot reduce the toxicity of certain types of waste, but we should ensure that these toxic substances do not contaminate the surrounding environment. Some other types of waste are manufacturing waste, green waste, organic waste, metal and plastic waste, etc. Manufacturing waste includes dust, sand, broken glass, etc. Green garbage includes trees, leaves, grass, fruit, wood, etc. Organic waste includes food, leftover manure, straw, etc. Metal and plastic waste include bottle caps, batteries, etc. The form of waste that cannot be reused or recycled is often thrown into landfills. Landfills can be found all over the UK, in particular, Manchester has a lot of landfills. Some use the "landfill" method, and some use the "land-raising" method. Landfills are designed in such a way that the risk of contaminating the environment is minimized. They should be built away from industrial and residential areas. Although, landfills are a good source of waste disposal, but there are also some drawbacks. The main issues with landfills as follows:
1. toxins,
2. leachates,
3. greenhouse gases.
Electronic material when it becomes waste, contains toxic substances. These toxins leach into the soil and become hazardous. This leachate pollutes the groundwater and waterways. Landfills contain a lot of waste that can create leachates and become harmful to the environment. Some secondary side effects of landfills include the following:
1. nauseous odors,
2. unpleasant view,
3. rat and seagull infestations.
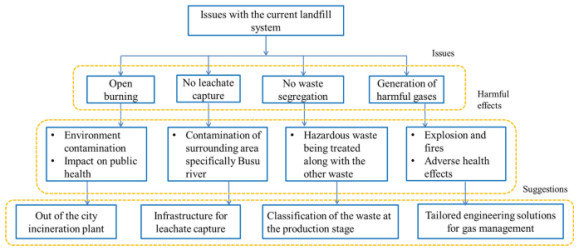
Even though it has a lot of disadvantages, it is still necessary because with increasing population waste is increasing day by day. Even with increasing recycling rates, it is still general waste which is to be disposed of in landfills. But there are a lot of problems with the current landfill system. Some of the issues with the current landfill system according to Doaemo et al. [1] are shown in Figure 1. Choosing the appropriate location for a landfill is very important because a wrong site selection causes a lot of health issues. The main objective of this research article is to propose the best method for the solid waste disposal location selection (SWDLS) problem of manufacturing plants in Manchester. The proposed methodology is based on the use of the weighted aggregated sum product assessment (WASPAS) method with 2-tuple linguistic Fermatean fuzzy sets (2TLFFSs). According to the ratings given by decision-makers (DMs), the simple multi-attribute rating technique (SMART) [2] is used to get the criteria weights. This method is also developed in many other fuzzy environments.
Zadeh [3] introduced the concept of fuzzy sets in 1965. The concept of an intuitionistic fuzzy set (IFS) was proposed by Atanassov [4] in 1986. Szmidt and Kacprzyk [5] introduced the medical applications of IFSs. Further, Yager [6] proposed the concept of a Pythagorean fuzzy set (PFS). PFS models are more powerful than IFS models in addressing real-world applications, but these collections have some limitations. Some applications may contain the decision maker's opinion as (0.8,0.9). In such cases, PFSs and IFSs failed to apply. To overcome the limitations of IFSs and PFSs, Senapati and Yager [7] introduced Fermatean fuzzy sets (FFSs). The FFSs are those sets in which the cube sum of the membership degree (MD) and non-MD is less than or equal to 1. Senapati and Yager introduced the solution of some multi-criteria decision-making (MCDM) problems based on FFSs [8,9]. The utilization of FFSs in MAGDM (multi-attribute group decision-making) approaches have been proposed in [10,11]. Liu et al. [12] proposed an MAGDM method with probabilistic linguistic information based on an adaptive consensus reaching model and evidential reasoning. Liu et al. [13] presented an opinion dynamics and minimum adjustment-driven consensus model for multi-criteria large-scale group decision making under a novel social trust propagation mechanism. Liu et al. [14] proposed MCDM with incomplete weights based on 2-D uncertain linguistic Choquet integral operators.
The 2-tuple linguistic representation model was first proposed by Herrera and Martinez [15,16]. Several decision methods based on 2-tuple linguistic data have been presented. Fazi et al. [17] introduced worst-case methods and Hamacher aggregation operations for an intuitive 2-tuple linguistic set. Herrera and Herrera-Viedma [18] introduced the linguistic decision analysis procedure for solving decision problems with linguistic information. Recently, many applications for MAGDM issues have been developed [19,20] Zavadskas et al. [21] introduced the WASPAS method to solve the MAGDM problem. It is a combination of two models i.e., the weighted aggregated sum model (WeSM) and weighted aggregated product model (WePM). WASPAS is more precise than the WePM and WeSM. Zavadskas et al. [22] considered the single-valued neurotrophic WASPAS and discussed its applications in alternative site construction. Mishra et al. [23] presented a hesitant fuzzy HF WASPAS and illustrated its application in green supplier selection. Schitea et al. [24] discussed intuitionistic fuzzy (IF) WASPAS-COPRAS (COmplex PRoportional ASsessment)-EDAS (Evaluation based on Distance from Average Solution) and its application in site selection. Mardani et al. [25] described HF-strengths, Weaknesses, Opportunities, and Threats (SWOT)-stepwise weight assessment ratio analysis (SWARA)-WASPAS and its application in the assessment of digital technologies intervention. Akram and Niaz [26] recently proposed a 2-tuple linguistic Fermatean fuzzy (2TLFF) decision-making method based on combined compromise solution with criteria importance through inter-criteria correlation for drip irrigation system analysis. Rani et al. [27] studied the IF type-2 WASPAS and its application in physician selection. The existing studies based on the WASPAS method are shown in Table 1.
The selection of a suitable place for disposal of the solid waste of different industries is one of the important concerns for municipalities and manufacturers. Many researchers have solved the MAGDM problems related to waste disposal systems. Yazdani et al. [48] evaluated the best location for HCW (health care waste) disposal. Mishra et al. [49] proposed an entropy-based EDAS model to find out a health care waste disposal method using IFSs. Yahya et al. [50] evaluated the waste water treatment technologies using the technique for order of preference by similarity to an ideal solution (TOPSIS) method. Suntrayuth et al. [51] in 2020, based on an improved entropy-TOPSIS method, presented an evaluation method for industrial sewage treatment projects. Liu et al. [52] proposed a novel PFS combined compromise solution framework for the assessment of medical waste treatment technology in 2021. Mussa and Suryabhagavan [53] presented a solid waste dumping site selection using geographic information system based multi-criteria spatial modeling in 2021. Aslam et al. [54] provided the identification and ranking of landfill sites for municipal solid waste management in 2022. Bui et al. [55] presented opportunities and challenges for solid waste reuse and recycling in emerging economies in 2022.
In this study, we expand the WASPAS method with a 2-tuple linguistic Fermatean fuzzy set (2TLFFS) and apply an extended method to evaluate the best place to dispose of manufacturing solid waste. The MAGDM problem using the 2TLFF-WASPAS method has not been previously defined in any studies. The following are the motivations for this study:
1. As an improvement of 2-tuple linguistic PFS, the concept of 2TLFFSs has been proved to be a superior tool for modeling the imprecise and uncertain information that arises in practical applications. Combined with its unique benefits, this research focuses on the 2TLFFS environment.
2. In the conventional FFS, the MD and non-MD are determined by numerical values that fall within the range of [0, 1], whereas in the 2TLFFS, the degrees are determined by the 2-tuple linguistic model which is more useful for addressing those real-world MAGDM issues where experts communicate their opinions using linguistic labels.
3. The Hamacher t-conorm and t-norm are more comprehensive, complete and dynamic extensions of the algebraic and Einstein t-norm and t-conorm.
4. The decision-making potential, ease of use and attractiveness theories of the WASPAS approach are the main incentives to explore this approach in order to expand the literature on 2-tuple linguistic FFSs (2TFFSs).
5. The proposed operators are very general. They overcome the shortcomings and limitations of the current operators and provide outstanding service for 2TLFF information as well as 2-tuple linguistic IF (2TLIF) and 2-tuple linguistic Pythagorean fuzzy (2TLPF).
6. The proposed operators are more accurate when used to solve real-world MAGDM problems based on 2-tuple linguistic Pythagorean fuzzy (2TLFF) data because they can take correlated arguments into account.
The main contributions of this study are as follows:
1. An MAGDM method is proposed using the WASPAS method and 2-tuple linguistic Pythagorean fuzzy numbers (2TLFFN).
2. The ability of the proposed method to select the best site for disposing of manufacturing solid waste is proved.
3. An explanatory numerical example is presented to unfold the application of the proposed approach in real-life decision-making situations. The dominance and authenticity of the proposed approach is verified via comparative analysis.
4. The advantages of the proposed technique are thoroughly elaborated.
Remainder of the paper is subsequently arranged to achieve the goals of this study. Some basic concepts of 2-tuple language terminology and several Hamacher operators of 2TLFFSs and their important properties are defined in the Section 2. Section 3 details the complete procedure for extending the WASPAS method with 2TLFFNs. A numerical example of SWDLS is solved using 2TLFF Hamacher weighted average (2TLFFHWA) operator, 2TLFF Hamacher weighted geometric (2TLFFHWG) operator, WePM and WeSM in Section 4. Parametric analysis of the numerical examples is given in Section 5. In Section 6, comparative analysis with the combinative distance based assessment (CODAS) method for the 2TLPFHWA operator, generalized 2-tuple linguistic Pythagorean fuzzy weighted Heronian mean operator (G2TLPFWHMO) [56], 2-tuple linguistic Pythagorean fuzzy weighted geometric Heronian mean operator (2TLPFWGHMO) [56], dual generalized 2-tuple linguistic Pythagorean fuzzy weighted Bonferroni mean operator (DG2TLPFWBMO) [57], dual generalized 2-tuple linguistic Pythagorean fuzzy weighted geometric Bonferroni mean operator (DG2TLPFWGBMO) [57] is provided. In Section 8, we conclude the discussion and illustrate some future directions.
2.
Preliminaries
Some basic definitions are reviewed in this section.
Definition 2.1. [16] Let there exist a linguistic term (LT) set ˙S={ˉsi|i=0,1,…,t}, where ˉsi indicates a possible LT for a linguistic variable (LV). For instance, an LT set ˙S having three terms can be described as follows:
If ˉsi,ˉsk∈˙S, then the LT set has the following characteristics:
(i) ˉsi>ˉsk, iff i>k.
(ii) max(ˉsi,ˉsk)=ˉsi, iff i≥k.
(iii) min(ˉsi,ˉsk)=ˉsi, iff i≤k.
(iv) Neg(ˉsi)=ˉsk such that k=t−i.
Definition 2.2. [16] Let ˊβ be the outcome of an aggregation of the indices of a set of labels assessed in a LT set ˙S, i.e., the outcome of a symbolic aggregation operation, i∈[0,t], where t is the cardinality of ˙S. Let i=round(ˊβ) and α=ˊβ−i be two values such that i∈[0,t] and α∈[−12,12), then, α is called a symbolic translation.
Definition 2.3. [16] Let ˙S={ˉsi|i=0,…,t} be a LT set and i∈[0,t] be a number value representing the aggregation outcome of the linguistic symbol. Then the function Δ used to obtain the 2-tuple linguistic information equivalent to ˊβ is defined as
Definition 2.4. [16] Let ˙S={ˉsi|i=0,…,t} be a LT set and (ˉsi,αi) be a 2-tuple, there exists a function Δ−1 that can restore the 2-tuple to its equivalent numerical value ˊβ∈[0,t]⊂R, where
Definition 2.5. [9] Let X be a fixed set. A FFS is an object having the form
where the function μF is from X to [0, 1] specifying the MD, and νF is from X to [0, 1] specifying the non-MD of an element x∈X to F. For every x∈X, it satisfies (μF(x))3+(νF(x))3≤1.
Definition 2.6. [58] Let δ={¯s0,¯s1,¯s2,…,¯st} be a LT set, having odd cardinality. If δ={(ˉsϕ,ϕ),(ˉsθ,θ)} is defined for ˉsϕ,ˉsθ∈δ and θ,ϕ∈[−0.5,0.5), where (ˉsϕ,ϕ) and (ˉsθ,θ) express the MD and non-MD by 2-tuple linguistic term sets. Then the 2TLFFS can be defined as follows:
where (ˉsϕj,ϕj),(ˉsθj,θj) are 2-tuple linguistic terms such that 0≤Δ−1(ˉsϕj,ϕj)≤t, 0≤Δ−1(ˉsθj,θj)≤t and 0≤(Δ−1(ˉsϕj,ϕj))3+(Δ−1(ˉsθj,θj))3≤t3. In order to simplify computation, δj={(ˉsϕj,ϕj),(ˉsθj,θj)}, denote 2TLFFN.
Definition 2.7. [58] Let δ1={(ˉsϕ1,ϕ1),(ˉsθ1,θ1)} be a 2TLFFN in P. Then the score and accuracy functions for a 2TLFFN are defined as
Definition 2.8. [58] Let δ1={(ˉsϕ1,ϕ1),(ˉsθ1,θ1)} and δ2={(ˉsϕ2,ϕ2),(ˉsθ2,θ2)} be two 2TLFFNs and λ>0 be real numbers, where ˉsϕ1,ˉsθ1,ˉsϕ2,ˉsθ2∈˙S={ˉsα|ˉs0≤ˉsα≤ˉst,α∈[0,t]}. Then some basic operations on 2TLFFNs are defined as follows:
1. δ1⊕δ2={Δ(t3√(Δ−1(ˉsϕ1,ϕ1)/t)3+(Δ−1(ˉsϕ2,ϕ2)/t)3−(Δ−1(ˉsϕ1,ϕ1)/t)3(Δ−1(ˉsϕ2,ϕ2)t)3),Δ(t(Δ−1(ˉsθ1,θ1)/t)3(Δ−1(ˉsθ2,θ2)/t)3)},
2. δ1⊗δ2={Δ(t(Δ−1(ˉsϕ1,ϕ1)/t)3(Δ−1(ˉsϕ2,ϕ2)/t)3),Δ(t3√(Δ−1(ˉsθ1,θ1)/t)3+(Δ−1(ˉsθ2,θ2)/t)3−(Δ−1(ˉsθ1,θ1)/t)3(Δ−1(ˉsθ2,θ2)/t)3)},
3. λδ1={Δ(t3√(1−(1−(Δ−1(ˉsϕ1,ϕ1)/t)3)λ)),Δ(t(Δ−1(ˉsθ1,θ1)/t)3λ)},
4. δ1λ={Δ(t(Δ−1(ˉsϕ1,ϕ1/t))3λ),Δ(t3√(1−(1−(Δ−1(ˉsθ1,θ1)/t)3)λ))}.
Definition 2.9. [59] Let δ1={(ˉsϕ1,ϕ1),(ˉsθ1,θ1)} and δ2={(ˉsϕ2,ϕ2),(ˉsθ2,θ2)} be two 2TLFFNs and γ,λ>0 be real numbers, where ˉsϕ1,ˉsθ1,ˉsϕ2,ˉsθ2∈˙S={ˉsα|ˉs0≤ˉsα≤ˉst,α∈[0,t]}. Then some basic Hamacher operations on 2TLFFNs are defined as follows:
Definition 2.10. [59] Let δj={(ˉsϕj,ϕj),(ˉsθj,θj)},(1≤j≤n) be a group of 2TLFFNs. Its weight vector (WV) is u=(u1,u2,…,un)T, satisfying uj∈[0,1] and ∑nj=1u=1. Then the 2TLFFHWA operator is given by
Proposition 2.1. [59] Let δj={(ˉsϕj,ϕj),(ˉsθj,θj)},(1≤j≤n) be a group of 2TLFFNs. The result by the 2TLFFHWA operator is a 2TLFFN, where
Definition 2.11. [59] Let δj={(ˉsϕj,ϕj),(ˉsθj,θj)},(1≤j≤n) be a group of 2TLFFNs with the WV u=(u1,u2,…,un)T, which satisfies uj∈[0,1] and ∑nj=1u=1. Then we can define the 2TLFFHWG operator as
Proposition 2.2. [59] Let δj={(ˉsϕj,ϕj),(ˉsθj,θj)},(1≤j≤n) be a group of 2TLFFNs. The outcome by the 2TLFFHWG operator is also a 2TLFFN, where
3.
Extended WASPAS method with 2-tuple linguistic Fermatean fuzzy numbers
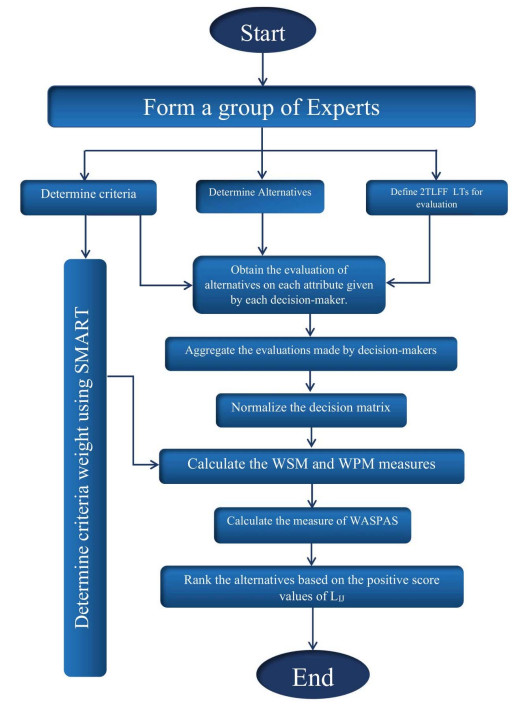
The WASPAS method is an MAGDM method which is used in a lot of MAGDM problems. WASPAS method is a combination of the WeSM and WePM [21]. We are going to propose an effective method based on the 2TLFFHWA operator and WASPAS to select the best disposal location for solid waste of manufacturing plants. The 2TLFFHWA and 2TLFFHWG operators mentioned in Propositions 2.1 and 2.2, respectively have been used to enhance the WASPAS method. A flowchart of the proposed WASPAS method using 2TLFFNs is shown in Figure 2. The following substitutions are used for alternatives, criteria and DMs, i.e., p stands for alternative, q stands for criteria and r for DM. Following are the steps used in our proposed method.
1. We choose a number of DMs who have a complete mastery over the topic.
2. In this step, the DMs define a set of alternatives. The selected DMs list the alternatives that are essential for the evaluation process after fully understanding the problem.
3. Define a set of attributes. The selected DMs list the alternatives that are essential for evaluation process. These attributes are defined with the help of previous studies on the particular subject.
4. In this step, the DM uses the SMART method [60] to determine the weight of each attribute. In this method, the DM is asked to assign 10 points to the least important criterion/criteria. The sum of the points for each criterion is calculated. The final criteria weights are determined by normalization of the sum of points.
5. Define the LTs and corresponding 2TLFFNs. These linguistic terms and corresponding 2TLFFNs are defined by the DMs.
6. Obtain the judgment of the DMs on each attribute in the form of linguistic terms.
7. Convert the linguistic matrices into assessing matrices (AsMs).
8. In this step, the DM can evaluate alternatives using the 2TLFFHWAO and 2TLFFHWGO, i.e., the ith alternative is evaluated by the kth DM on the basis of the jth criteria.
9. In this step, if the criterion is a beneficial criterion (BeC), then it does not change, but if it is a non-beneficial criterion (NoC), we take the complement as defined in this Equation 3.3.
The normalized decision matrix can be calculated as
10. We calculate the WeSM and WePM measures by using Propositions 2.1 and 2.2 (using γ=1).
Lsij=2TLFFHWA(δ1ij,δ2ij,…,δmij)=⨁mk=1(ωj⊗Lkij)=(Δ(t3√1−∏mk=1(1−(Δ−1(ˉsϕkij,ϕkij)/t)3)ωk)),Δ(t∏mk=1(Δ−1(ˉsθkij,θkij)/t)ωj)),
Lpij=2TLFFHWG(δ1ij,δ2ij,…,δmij)=⨂mk=1(ωj⊗Lkij)=(Δ(t∏mk=1(Δ−1(ˉsθkij,θkij)/t)ωj),Δ(t3√1−∏mk=1(1−(Δ−1(ˉsϕkij,ϕkij)/t)3)ωj)).
Now calculate the measure of WASPAS by using Equation 3.5.
Calculate the ranking of the alternatives using the formula given below, where ˙Sp(δ1) represents the positive score function and ˙S(δ1) represents the score function.
4.
Application
In this section, we extend the WASPAS method with the 2TLFFHWA operator, 2TLFFHWG operator, WeSM and WePM under the 2TLFF environment.
Example 4.1 (SWDLS problem). In many cities of the United Kingdom, manufacturing companies are trendy and a key concern. Manchester is a city of the UK with a lot of cultures. There are many public and private manufacturing companies in Manchester. These manufacturing plants produce a lot of solid waste and pollution. Solid waste can cause various diseases in humansuch as bacillary dysentery, amoebic dysentery, cholera, jaundice, gastero, enteric diseases, endemic typhus, salmonellosis, trichinosis, diarrhea, plague, etc. Nowadays, disposal of this type of waste is a big issue. Consequently, finding the best place to dispose of such waste is an essential job of manufacturing organizations. We have used three main manufacturing companies of Manchester namely, Manchester manufacturing group, Automation technology and Iceland manufacturing limited to choose the best location for disposal of their solid waste. The waste management procedures of the above-mentioned manufacturing plants were monitored and we collected the information about collection, storage and disposal of their solid waste. The total waste bags produced were recorded. The weights of each waste bag were also recorded from each company. Although these companies have proper disposal system, due to continued enlargement and increasing product demand of these companies, the administration is supposed to build a proper waste disposal location. The aim of this research article is to introduce MAGDM methodology to select the best location for the disposal of waste.
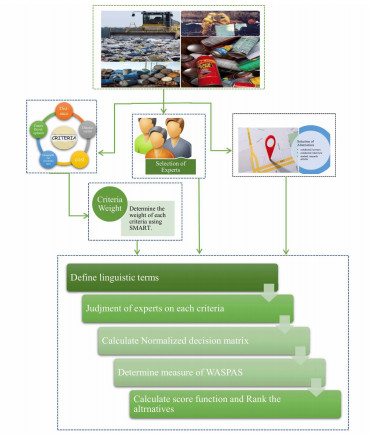
We have selected the attributes and alternatives on the basis of the DM's opinion, research articles, case studies, etc. A flowchart of the application using the WASPAS method is shown in Figure 3.
A. Solution of SWDLS problem using the extended WASPAS method with the 2TLFFHWAO
We solve the SWDLS problem by using the extended WASPAS measure with the 2TLFFHWGO which is defined in 2.1.
1. We have selected three DMs (E1, E2 and E3). The first DM is the plant manager, second is the factory engineer and third is the production manager. The collective opinions of all these DMs were used in decision-making. The WV of DMs the (0.2, 0.5, 0.3).
2. The DMs thoroughly studied and checked out the history of methods to dispose waste. On the basis of their study and after screening the list of possible landfill locations, they obtained a set of 4 alternatives (W1 to W4). The following four alternatives have been selected as listed in Table 2.
3. For defining the criteria and the DMs studied research articles, literature and conducted surveys. Following five attributes have been selected as listed in Table 3.
4. To calculate criteria weights, we used the SMART method [60]. The results are recorded in Table 4.
5. Now we define LT for the 2TLFFNs which are given in Table 5.
6. Each DM judges the alternatives on each criteria. The results are given in Table 6.
7. We convert the LAM given in Table 6 into AsMs. The outcomes are given in Table 7.
8. The AsMs were aggregated based on Equation 3.1. Then we obtained Qij. The results are recorded in Table 8.
9. The calculated results of the normalized decision matrix using Equation 3.4 are given in Table 9.
10. The calculated result of the WeSM, WePM and WASPAS measures by using the following equations and results are recorded in Table 10. Lsij=2TLFFHWA(δ1ij,δ2ij,…,δmij)
=⨁mk=1(ωj⊗Lkij)=(Δ(t3√1−∏mk=1(1−(Δ−1(ˉsϕkij,ϕkij)/t)3)ωk)),Δ(t∏mk=1(Δ−1(ˉsθkij,θkij)/t)ωj)),Lpij=2TLFFHWG(δ1ij,δ2ij,…,δmij)=⨂mk=1(ωj⊗Lkij)=(Δ(t∏mk=1(Δ−1(ˉsθkij,θkij)/t)ωj),Δ(t3√1−∏mk=1(1−(Δ−1(ˉsϕkij,ϕkij)/t)3)ωj)).
11. The calculated results of the score function of Lij based on Definition 2.7 and the ranking of locations are given in Table 11.
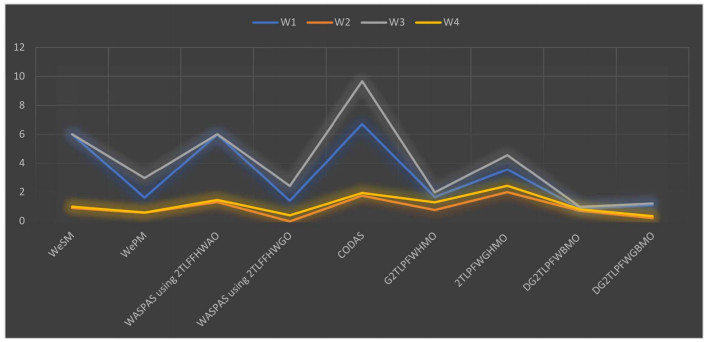
From Table 11, we can deduce that W3>W1>W4>W2. Thus, W3 is the best location to dispose of the solid waste.
B. Solution of SWDLS problem using the extended WASPAS method with the 2TLFFHWGO
We solved the SWDLS problem by the extended WASPAS measure with the 2TLFFHWGO which is defined in 2.2.
1. The AsMs were aggregated based on Equation 3.2. The results are recorded in Table 12.
2. The calculated results of the normalized decision matrix are given in Table 13.
3. We calculated the WeSM, WePM and WASPAS measures by the Definition 2.9 with γ=1. The results are recorded in Table 14.
4. The calculated results of the score function of Lij using Definition 2.7 and the ranking of locations are given in Table 15. From Table 15, we conclude that W3>W1>W4>W2. Thus, W3 is the best location to dispose of the solid waste of manufacturing plants.
C. Solution of SWDLS problem using the extended WeSM with the 2TLFFNs
We solved the SWDLS problem by the extended WeSM measure with 2TLFFNs. In the WeSM, we put τ=1 in Equation 3.5. The results obtained are shown in Tables 16 and 17.
From Table 17, we conclude that W3=W1>W4>W2. Thus, W3 and W1 are the best locations to dispose of the solid waste of manufacturing plants.
D. Solution of SWDLS problem using the extended WePM with the 2TLFFNs
Now we solve the SWDLS problem by the extended WePM with 2TLFFNs. In the WePM, we put τ=0 in Equation 3.5. The results obtained are shown in Tables 18 and 19.
From Table 19, we can infer that W3>W1>W4>W2. Thus, W3 is the best location to dispose of the solid waste of manufacturing plants.
5.
Parametric analysis
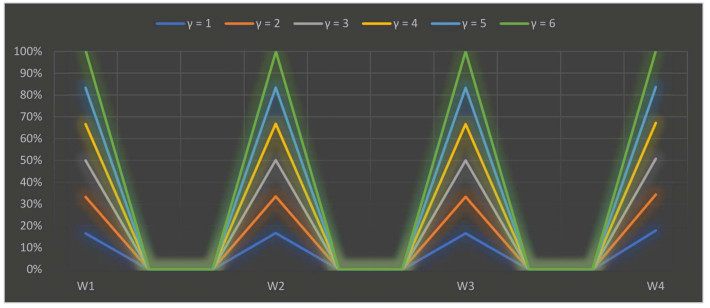
The parameter γ is used in our research study to explain the interdependency between distinct quantifiable attributes. Various numerical values of the parameter γ illustrate the various decision-making possibilities and circumstances. We assigned numerical values from 1 to 6 to γ the results are shown in Tables 20 and 21. The scoring values of each selected alternative varied depending on the crisp value of the parameter, but the derived results are roughly the same. When we allocated distinguishable numerical values to the parameter γ, the best alternative is O3 for the SWDLS problem solved with the extended 2TLFF-WASPAS method using two different operators, i.e., the 2TLFFHWA operator and 2TLFFHWG operator. We can also summarize from the appraisal scoring results as shown in Tables 20 and 21 that the 2TLFFHWA and 2TLFFHWG operators proposed in this research study are the best approaches to summarize aggregated 2TLFF information. A graph of the ranking results of SWDLS by the 2TLFFHWAO using different values of γ is shown in Figure 4.
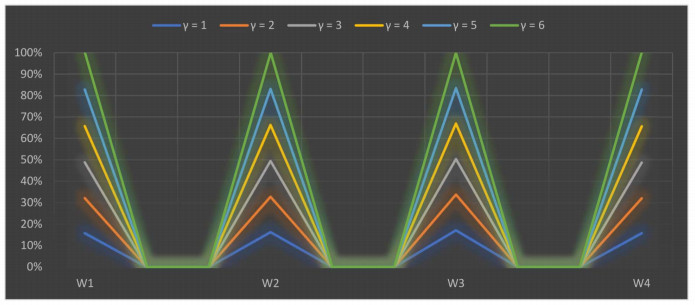
A graph of the ranking results of SWDLS by the 2TLFFHWGO using different values of γ is shown in Figure 5.
6.
Comparative analysis
We solved the problem of SWDLS using the CODAS method for 2TLPFNs [61].
1. We converted the linguistic assessing matrices which are given in Table 6, into assessing matrices. The outcomes are given in Tables 22, 23 and 24.
2. The calculated results of the collective 2TLPF matrices are given in Table 25.
3. The results for 2TLPF weighted matrices are given in Table 26.
4. The calculated results for the negative ideal solution are given in Table 27.
5. Calculations of Euclidean distance (UDi) and Hamming distance (ADi) are given below:
6. The results for the Relative assessment matrix are shown in Table 28.
7. The average results are given below:
8. The ranking order is
and W3 is the best among four alternatives.
We have solved a problem of SWDLS for manufacturing plants in Manchester. For this purpose, we have used the extended 2TLFF-WASPAS method with Hamacher aggregation operators. We have solved the SWDLS problem by using the WASPAS method with the 2TLFFHWA operator and 2TLFFHWG operator. Also, we have solved the SWDLS problem using the extended-WeSM measure and extended-WePM measure. To check the feasibility of our proposed method, we have compared the SWDLS problem with the operators including G2TLPFWHMO [56], 2TLPFWGHMO, DG2TLPFWBMO [57] and DG2TLPFWGBMO. We have also compared it with the CODAS method [61] for 2TLPFNs. From the above analysis, we have the same best landfill location, i.e., W3. The comparative analysis shows that the proposed WASPAS method yields valid results. Neither 2TLISs nor 2TLPFSs can handle the situation when the sum of squares of the 2-tuple linguistic MD and non-MD exceeds 1. Hence, it is necessary to develop a new model in this case. Also the proposed 2TLFF-WASPAS method is superior to the existing CODAS method [61], because the existing CODAS method [61] can only be used for 2TLPF data whereas the proposed method can be used for both 2TLPF data and 2TLFF data. The combined ranking of all above-mentioned applications is shown in Table 29. A graph of the ranking of all above-mentioned methods is shown in Figure 6.
7.
Discussion
MAGDM methods have been widely used in the field of SWDLS problems. This study is the first to take into account the MAGDM of SWDLS in the context of 2TLFFSs. Many MAGDM techniques, though, which are used for evaluation with many criteria, have not yet been modified for this setting. One of the effective MAGDM techniques is the WASPAS approach, which has been used to solve numerous MAGDM issues in the real world. In this paper, a novel integrated strategy based on the WASPAS method is put forth to address MAGDM issues with 2TLFFNs. The principles and arithmetic operations of 2TFFSs have been applied in this technique to adapt the WASPAS method to 2TLFF information, and various modifications have been made in the process. In this work, we modified the WePM and WeSM processes, and we suggested an expanded WASPAS that can tackle MAGDM issues in such a scenario. Additionally, the SMART technique has been applied to get more accurate criteria weights using data with 2TLFFSs as a defining characteristic. One of the main issues with the decision-making process is the calculation of criteria weights. The proposed approach has been validated using a SWDLS example. To do this, the findings of the suggested strategy were compared to those of several other methods, and a sensitivity analysis was carried out by altering a method parameter. The analysis' findings indicate that the integrated strategy that has been suggested is valid for evaluating SWDLS and may work well for many other MAGDM issues.
1. The WASPAS method selects the option with the greatest utility, whereas previous methods prefer alternatives that are close to the ideal solution.
2. WASPAS is a combination of the WeSM and WePM and its accuracy is more consistent than the WePM and WeSM.
3. In the proposed 2TLFF-WASPAS, the standard weights are computed based on the SMART method [60], while in the CODAS method [61], Deng et al. [57] and Wei et al. [56], assuming standard weights, this leaves no room for dealing with ambiguity.
4. The advantages of the proposed WASPAS method include its efficiency of use in MCDM problems, the flexibility of using a FFS and 2-tuple LTs to define the information expressed by the DM and its applicability to various decision-making problems.
8.
Conclusions
The WASPAS method is important among the available methods because of its ability to improve ranking accuracy. The 2TLFFS is a new generalization of the 2TLPFS and 2TLIFS, as it can handle more general cases than the 2TLPFS and 2TLIFS. In this research study, we have selected the best sites for manufacturing industrial solid waste in Manchester to dispose of. We have solved the SWDLS problem using the WASPAS method of the 2TLFFHWA operator. Furthermore, we have solved it using the WASPAS method for the 2TLFFHWG operator, WePM measurement and WeSM measurements. We also conducted a comparative study with existing methods [61] and operators, namely the G2TLPFWHMO [56], 2TLPFWGHMO [56] and DG2TLPFWBMO [57] DG2TLPFWGBMO [57] to show the applicability of its integrity.
Various MAGDM applications in other industries, i.e., agriculture, healthcare, etc., can be handled using the proposed technique. Certain new methods, such as double normalization-based multiple aggregation, gained and lost dominance score, ORESE, and measurement of alternatives and ranking according to the compromise solution in the fuzzy context of FFS and the 2TLFF can be used for future development. These methods can be used to solve SWDLS problems in different regions. Furthermore, the proposed 2TLFF-WASPAS method could be coupled with some other subjective criteria weighting methods such as analytic hierarchy process, Best Worst Method and analytic network process. Finally, the proposed method can be used to solve other emerging MAGDM problems.
The proposed method is based on FFS theory, which is a generalization of the PFS and IFS theories. Therefore, there are currently no significant limitations in the application of the proposed approach. The only real limitation that is observed is the selection of attributes. Only five attributes were selected, although many other factors, such as groundwater depth, proximity to surface water, elevation, land slope, soil permeability, soil stability, flooding susceptibility, lithology and stratification, faults, land use type, nearby settlements and urbanization, proximity to cultural and protected sites, wind direction, roads, railroads, proximity to building materials, pipelines, powerlines and proximity to airports are considered while selecting a disposal site. These factors can be considered in future studies.
Acknowledgments
The research of Santos-García was funded by the Spanish project ProCode-UCM (PID2019-108528RB-C22) from the Ministerio de Ciencia e Innovación.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: