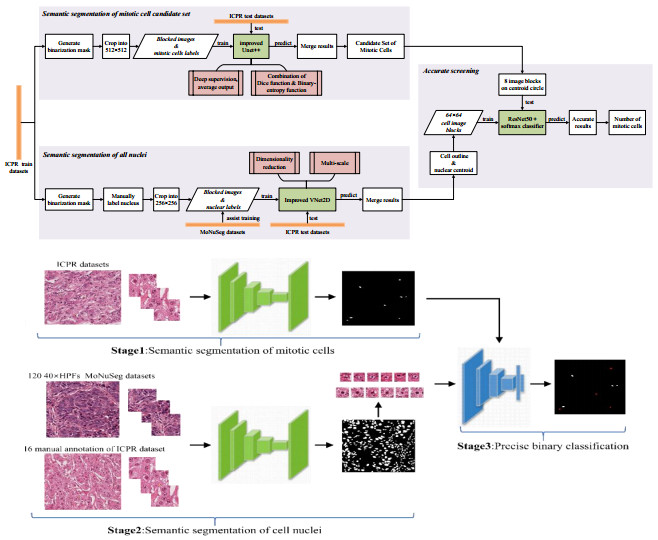
The number of mitotic tumor cells detected in each slide is one of the key indicators of breast cancer prognosis. However, accurate mitotic cell counts are still a difficult problem for pathologists and related experts. Traditional methods use manual design algorithms to extract features of mitotic cells, and most methods rely on sliding windows to achieve pixel-level classification through deep learning. However, the complex background and high resolution of pathological images make the above methods time-consuming and ineffective. In order to solve the above problems, we propose a new cascaded convolutional neural network UBCNN (cascaded CNN based on UNet), which consists of three parts: semantic segmentation and classification to detect mitosis. First, we use an improved UNet ++ segmentation network to locate the candidate set of mitotic targets. Secondly, an adequately labeled cell nucleus data set is sent to an improved two-dimensional VNet network, and the cell nucleus is located by means of semantic segmentation to obtain accurate image blocks of mitotic and non-mitotic cells. Finally, the obtained cell image block is used to train a convolutional neural network to achieve binary classification, and the candidate set area is screened to retain the final result of mitosis cells. This paper verifies the detection effect of the above-mentioned cascade detection algorithm on the ICPR 2012 and 2014 mitosis automatic detection competition data sets. The evaluation indicators include accuracy, recall and F-score. Our cascade detection algorithm based on segmentation and classification reached 0.831 on the ICPR 2012 data set and 0.576 on the ICPR 2014 data set. Compared with other existing algorithms, the detection effect was improved, which was very competitive.
1.
Introduction
The most recommended breast cancer grading system by the World Health Organization (WHO) is the Nottingham grading system [1]. Clinical pathologists mainly determine the patient's breast cancer pathological grade by three indicators in the field of vision: (a) the composition of the adenoid tube. (b) the heterogeneous nucleus. (c) cell fissure number. Among them, mitotic activity is one of the most powerful prognostic factors for invasive breast cancer, and the number of mitotic cells is the most important indicator for evaluating the malignancy of breast cancer. Currently, in clinical diagnosis, breast biopsy specimens are fixed with paraffin and stained with hematoxylin and eosin (H & E) dyes. After acquiring images of these stained blocks, histological slide images (WSI) are obtained. The method commonly adopted is to use a microscope to observe the pathological tissue slice image region by region to find the region of interest (ROI), and on the basis of ROI, rate them according to these three criteria. However, the biological differences of mitotic cells bring great challenges to manual labeling and identification, which is time-consuming and often misdiagnosed. Under different collection instruments and conditions, the differences of pathological sections already exist, while the shape and configuration of mitotic cells in different growth stages (prophase, metaphase, anaphase and telophase) are constantly changing. In addition, many cells (such as lymphocytes, apoptotic cells, dense nuclei) are very similar to mitosis in appearance, which makes it difficult to effectively reduce the false-positive rate in the test results [2]. Under the circumstances, Computer-aided diagnosis has become a hot topic in medical research, which can be roughly divided into two categories: traditional feature extraction algorithm and deep learning application. The former requires researchers to comprehensively understand the shape, texture and color characteristics of cells, and make a lot of experiments to verify the rationality and accuracy of the algorithm. The latter can automatically identify any feature of the image, train a model with strong generalization ability to complete the diagnosis task in pathological sections.
2.
Related work
Since 2012, various international competitions have been held in the field of mitotic cell detection of breast pathological images, including ICPR2012 [3] and ICPR2014 [4]. Many researchers are dedicated to the detection of mitosis cells from H & E staining images. The first type of algorithm is the method of manually extracting the features of mitotic cells for subsequent classification [5,6,7,8,9], such as in reference [5], the author proposed to use a pixel-based classifier to generate a probabilistic heat-map for the candidate set. In this step the Ilastik [6] (an open source tool dedicated to biological image analysis) was been used to segment mitosis cells by threshold, and then trained a classifier based on the texture strength and shape of the existing sample, which can quickly divide the candidate set and detects mitotic cells. Reference [7] used Gaussian function to smooth out the nuclear area, selected some local maximum values in these areas to join the candidate set, and used a new method called exclusive independent component analysis (XICA) on the candidate set to extract the different components between the two categories in the training set for classification. As another example, in reference [8], according to the different edge distribution of mitotic cells and non-mitotic cells, Gamma-Gaussian mixed model was used to detect and classify different cells [8]. Similarly, the 143-dimensional collection of statistical and morphological feature structures in multi-color channels proposed in reference [9], CLBP and GLCM texture features and LBP texture information in [10] and [11] are all semi-automatic detection algorithms designed by manual feature extraction methods to assist subsequent classification [10,11]. However, due to the different shape and texture, the definition of such characteristics is difficult to fully cover the characteristics of mitotic cells.
With the rapid development and wide application of deep learning, many representative mitotic automatic detection algorithms based on deep learning have emerged [12,13,14,15]. Reference [12] proposed the strategy of integrating CNN extracted features with artificially labeled features, which not only takes advantage of the neural network's self-training features, but also reduces the sensitivity of manual sample selection. MFF-CNN [13] designed a multiscale fusion CNN to extract mitotic and non-mitotic block images from blue ratio images and train them to detect directly in 40 × pathological images with a Fully Convolutional Network (FCN) model. Given the complexity of the pathological picture background, the improvement of the one-step detection model cannot meet the accuracy requirements of mitotic cell detection. In this case, the application of the cascade method has become widespread. Ciresan [14] built a 13-layer DNN to train classifier on the ICPR2012 datasets which used sliding windows to sample on the original image, and then sent samples to classifier to achieve pixel classification, which won the first prize in the ICPR2012 mitotic detection competition. Hao Chen et al. proposed a two-stage technique [15], in which the cells are segmented using a FCN in the first stage, and in the second stage, all detected targets are further refined by an additional CNN. MSSN [16] also adopted a two-step deep learning framework for mitosis detection. Firstly, four different sub-networks were used to collect the candidate set of mitosis, and then the same model was used to search for false positive cells for screening.
Recently, numerous excellent algorithms have emerged [17,18,19]. Maroof [17] et al. proposed a method of mixing feature spaces. First, they used the hybrid feature space to combine color features with morphological and texture features, and then changed the color channel to calculate normalized and cumulative histograms in the wavelet domain to better distinguish between mitotic and non-mitotic nuclei. The direct identification of mitotic cell nuclear characteristics also provides a new way for future mitotic cell identification. The widely used region-based CNN has performed well in many computer vision applications [20,21,22,23,24,25,26,27,28,29,30,31]. This kind of algorithm is also widely used in the detection of mitotic cells. Li et al. presented a method [20] based on Faster region convolutional neural network (Faster R-CNN) [21] and residual network ResNet-50 [22], in which Faster R-CNN is responsible for locating and frame selection of mitotic cells, and ResNet-50 constitutes a classifier to judge the result again. On this basis, Reference [23] proposed an improved RCNN mitosis detection model. It used a CNN to extract deep and shallow features of different layers, which are combined and input into the Regional Proposal Network (RPN) to generate mitotic candidates. These candidate signals were then classified by an improved RCNN to produce the final detection results. In addition to the object bounding box regression, the improved RCNN also uses two classification sub-networks and uses different feature selection methods to predict object categories. This method achieved the most advanced performance on the 2012 ICPR mitosis dataset, with an F-score of 0.851. They further proposed improved solutions to the problems of small data sets and large parameters, such as the use of lightweight backbone [24] and concentric circle algorithm [25] to solve the problem of weak labeling of data sets. Similarly, the Mask R-CNN [26] algorithm also has good performance in mitosis detection. For example, Dodballapur [27] proposed a detection scheme based on Mask RCNN, in which ResNet-50 is used as the feature extraction network. On the ICPR2014 data set, this method obtained a very high recall rate result, making its F-score reach 0.68, which is also the method to get the best score at this stage. Talking about the problem of data set labeling, the latest mitosis detection algorithm has begun to consider the strong and weak labeling problems of the ICPR2012 and ICPR2014 data sets. PartMitosis [32] proposed by Meriem used a semantic segmentation framework of a two-way fully convolutional network to segment breast cancer stained slides. The first branch of the model was trained with weak tags, while the second branch was trained with strong tags and two FCN prediction score charts were fused to obtain more accurate detection results. This method obtained 0.788 and 0.575 f-scores on ICPR12 and ICPR14 data sets respectively. In addition, their team also proposed Mask Mitosis [33], an algorithm based on the Mask RCNN instance segmentation network. On the one hand, mitotic cells were located and classified according to the strong label data set; on the other hand, the model trained with the strong label provides training samples and labels for the weak label data set. It finally achieved scores of 0.863 and 0.475.
However, the above methods have two common problems. One is that the more accurate methods are too time-consuming, and the other is that the positioning results of candidate sets are too rough in cascade method. Therefore, we propose an improved cascade detection method UBCNN.
3.
Methods
3.1. Overall algorithm process
3.2. Description of datasets
(a) ICPR 2012 mitosis dataset
The ICPR 2012 Dataset [3] comprises 5 slides of breast cancer biopsies slides, stained with hematoxylin and eosin (H & E). In each slide, the pathologist selected 10 high power views (HPF) at 40 power magnification, which of size is 2084 × 2084 pixels. Each image represents a 512 × 512 µm2 HPF generated by an AperioXT scanner with a resolution of 0.2456 µm per pixel. These 50 HPFs contain more than 300 mitoses in total, of which 35 HPFs and 226 mitotic cells are used for training and 15 HPFs and 101 mitotic cells are used for evaluation. It is labeled as the coordinates of each mitotic pixel and belongs to the data set of strong annotation type.
(b) ICPR 2014 mitosis dataset
The ICPR 2014 dataset [4] includes 1200 HPF for training and 496 HPF for testing. Each HPF image had 1539 × 1376 pixels, 0.2455 µm per pixel, and there were 749 mitotic cells in the training data. For this data set, the pathologist provided only the centroid pixel annotation of mitosis. The area centered on mitosis and with a radius of 15 pixels was mitosis point, which was a weakly labeled data set.
(c) MoNuSeg dataset
The MoNuSeg dataset [34] contains 40 × magnification captured H & E staining pathological images across multiple organs and patients, including 120 512 × 512 resolution images and about 22,000 nuclear boundary annotation training data. It is suitable for the training of general nuclear segmentation model, with great generalization.
3.3. Model building
3.3.1. Locating candidate set–based on UNet ++
The first step of the cascade detection of mitosis is to obtain all the candidate sets of mitotic cells directly based on the label. The resolution of the 40 × HPF image in the data set is as high as one million pixels. It is too time-consuming to classify images pixel by pixel using a sliding window with a set step size. The semantic segmentation network was selected for pixel classification to realize the positioning of mitotic cells. Among the numerous semantic segmentation networks, UNet [35] has gained excellent performances on medical imaging. Its low-resolution information after multiple down-sampling provides the contextual semantic information of the segmentation target in the entire image. At the same time, through concatenate operation, the high resolution information is directly transferred from encoder to decoder on the same height, providing finer features for segmentation.
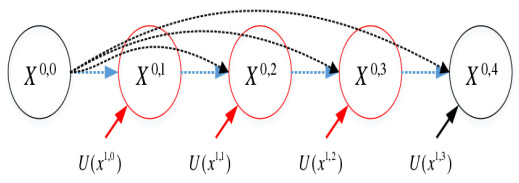
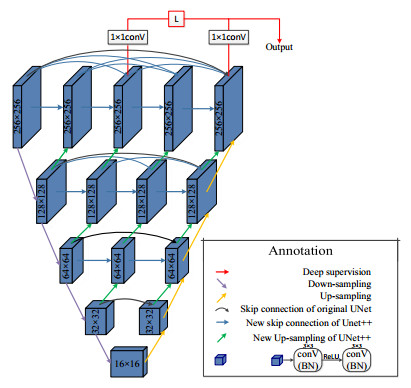
On this basis, Z. W. Zhou [36] proposed the UNet ++ network architecture in 2018. Compared with UNet, it overlays more features at different levels, obtains the receptive field of different sizes, and is highly sensitive to targets of different sizes. The addition of deep supervision allows the middle layer to feel the gradient of transmission and participate in the output together. UNet ++ performs up-sampling after each down-sampling, and bridges the semantic gap between feature maps using skip links and dense convolution blocks on the skip path, combining shallow and deep features in depth [36]. The improved structure calculation method is shown in Figure 2.
As can be seen from Figure 2, let xi, j represent the output of Xi, j, and the stack calculation formula of the represented feature mapping is shown as Eq 2.1:
The function H (·) is a convolution operation, followed by an activation function, U (·) represents an up-sampling layer, and (·) represents a connection layer [36]. When it is used to provide candidate sets for mitotic cell segmentation, the rich intermediate information allows extremely similar features of mitotic cells and complex backgrounds to be collected and considered, which is more accurate than the results of UNet segmentation.
However, the following problems still exist: (a) The positive and negative samples are unbalanced. (b) The size of the mitotic target is extremely small, and the network model is not sensitive enough to small targets. (c) The candidate sets require a higher recall rate, and the higher depth of this model may lose some mitotic targets. The above points make it difficult to combine the accuracy and integrity of the mitotic cell candidate sets. In this regard, two changes have been made to UNet ++ in this paper. One thing to note here, since UNet ++ can be pruned, for the convenience of definition, we named each of the remaining subnetworks according to their depth as UNet ++ L1, L2, L3, L4, or L1–L4 for short. So one of our changes is to add deep supervision to the output results L2 and L4, and the final result takes the average value of L2 and L4 as the output. In this change, the concrete implementation operation of deep supervision is to add a convolution kernel of 1x1 after X0, 1, X0, 2, X0, 3, X0, 4 in the Figure 2, which is equivalent to supervising the output of each level or each branch. The other change is to improve the model's loss function based on dice function and cross entropy function. The frame structure is shown in Figure 3.
Different from the original UNet ++, we conduct deep supervision [37] on L2 and L4. L2 is obtained through 2 down-sampling, 3 up-sampling, and the inter-layer connection in the middle. It combines the information returned from the deep network, which makes it focus on the sensitivity of the segmentation target with a certain degree of accuracy guaranteed. Although the real target and the false positive target cannot be accurately discriminated by L2, the information such as the location and shape of the lower layer gives it sufficient ability to include the entire candidate set to prevent the omission of the target.
L4 is obtained through 4 down-sampling, 10 up-sampling and intermediate cross-layer connections. With extremely deep high-level information, it can fully extract the unique and deep characteristics of mitotic cells in the pathological image with complex background, and can accurately locate and identify the target. We choose the model that performs best on the validation set, and averages the output results of L2 and L4. The output results are as in Eq 2.2.
In this way, there are low-level information to ensure the sensitivity of the model, and high-level information to correctly identify mitotic cells, which provides accurate and complete information about the position and diameter of the candidate set for subsequent screening.
The positive and negative samples (1 or 0) in the normal natural image (binary classification) labels are relatively balanced, while the mitotic and non-mitotic pixels in the mitotic data sets of ICPR2012 and ICPR2014 are very unbalanced. Unbalanced datasets have a certain probability causing the network to converge in the wrong direction when using the binary cross-entropy loss function to train UNet ++. Therefore, Dice loss [38] is introduced and summed with Binary cross-entropy loss to make the model converge towards the improvement of accuracy. The original UNet ++ used the balanced binary cross-entropy loss function shown in Eq 2.3.
Where Yb and ˆYb represent the pixel level prediction of label and the real value, N represents batch size, and b represents the bth picture. In order to avoid ignoring tiny mitotic pixels in pursuit of high Dice loss and make detection more sensitive, the Loss function is improved as shown in Eq 2.4:
As many candidate sets of mitotic pixels as possible can be found as the basis of subsequent cascade classification.
3.3.2. Nuclear segmentation–based on VNet2D
In the process of semantic segmentation, the non-mitotic region of the image block contains calcium salt mucus, cytoplasm and other background impurities. The complex features extracted make the distinction between non-mitotic cells and mitotic cells not emphasized by the neural network, which probably cause part of normal cells with similar morphology to be misdiagnosed as mitotic cells.
Precise binary classification has a significant effect on screening out false positive cells and improving accuracy. While Training an accurate binary classifier requires sufficient mitotic cell image blocks and non-mitotic cell image blocks to collect cell-level features, and nuclear localization is the key to collecting cell block data sets.
In the pre-slicing process, the H & E staining method changes the chromatin in the nucleus and the nucleic acid in the cytoplasm to purple-blue and mainly makes the components in the cytoplasm and extracellular matrix red [39]. Traditionally, the blue ratio threshold method can assign higher weight to the blue channel with higher strength, so that the RGB image can be transformed into the BR image and the nucleus can be prominent [40]. Then a reasonable threshold can be set to locate the nucleus. Although this method is simple and fast, it is difficult to determine the threshold value in HPF images with extremely complex background, and there are situations of adhesion and blurring with the background, so the segmentation effect is extremely poor. Therefore, the semantic segmentation method was selected to locate the nucleus. Since there was no nucleus annotation in the ICPR2012 and ICPR2014 data sets, we selected one from each group (A00–A04 in ICPR2012, A03–A18 in ICPR2014) for manual annotation. In addition, the MoNuSeg data set with good robustness is used to assist training. Same as ICPR data, HPF pictures are all at 40 × magnification. After dyeing and normalization, all of them are cut into 512 × 512 size slices and input to the segmentation network.
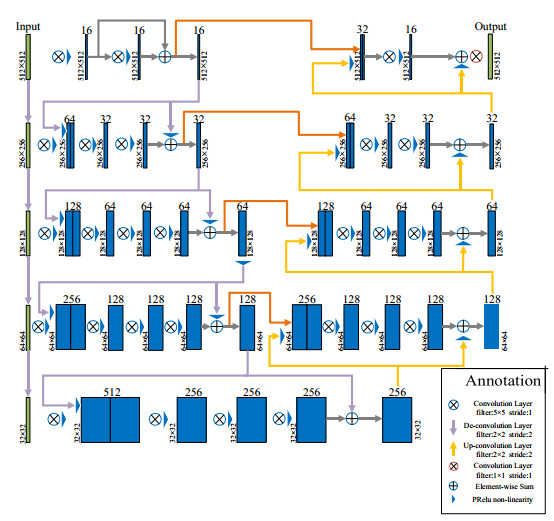
UNet performs well in medical segmentation, however, the semantic segmentation of cell contours requires high accuracy and a good sense of position. Cell-level image processing requires more complex spatial feature information, and higher requirements for lower-level position information. Traditional UNet cannot meet the needs of the two with only one jump connection. VNet [41] was proposed by the Fausto Milletari team in 2016, it was mainly proposed for three-dimensional medical imaging, and has more special designs to fuse more information than UNet. The main force naturally has a better ability to extract information, and the improvement of low-level information fusion makes it meet the needs of this stage. Here, the magic modification UNet is selected to achieve segmentation. Given that the research object in our paper two-dimensional pathological image, the structure is maintained on the basis of VNet, and several changes have been made, which have the following advantages.
(a) Use 2D convolution kernel to build VNet2D according to VNet network.
(b) From the perspective of structure, it inherits the residual block of VNet to include the underlying information and improve the convergence speed; Elementwise sum replaces the concatenation in skip layers to reduce parameters; convolution replaces pooling to realize the lower sampling step and integrates more information to prevent the perception field from being too small.
(c) From the perspective of loss function, the target function of Dice coefficient enables iteration to be proceeded in the correct direction and has a good segmentation effect on small targets.
(d) An additional branch input is concatenated before the output of each down-sampling. The original image is down-sampled to the same size as the output image of each down-sampling, integrated into the encoder for training to better combine the features of the high and low layers.
The topological structure of the improved multi-scale VNet model is shown in Figure 4.
After the semantic segmentation, the post-processing of erosion and dilation is performed, and the edges are outlined using the Canny operator to show the cells in the original image. The segmentation results provide accurate cell locations for the subsequent collection of cell data sets.
3.3.3. Cell classifier-based on ResNet50
After nuclear localization, the normal cell image block is extracted according to the nucleus segmentation result, and the mitotic cell image block is extracted according to the center coordinates of the mitotic pixel provided by the label of the dataset. These two kinds of image blocks are used as data sets to train the classifier to avoid the interference of invalid information from the background features to the classification network. The size of the cells in a 40 × HPF image of a breast cancer slice is about 30 × 30 pixel–34 × 34 pixel. Then, positive and negative examples should be used to train the precision classifier to screen false positive targets in the candidate set.
In this paper, the method of fine screening is to select 8 points on the circle centered on the center of the connected region of the candidate set, and send them into the classifier for judgment as the center-cut image blocks. Considering that the maximum radius of the circumference of 8 points is the cell radius, that is, 30–34 pixel. When these 8 points are used as the center of the image block, in order to include the whole cell, the length of the image block should be 60–68 pixel. So it is appropriate to set the size of the image block sent into the classification network to 64 × 64pixel.
The classification network selection is based on ResNet50 [42]. When the input is 64 × 64, direct training will cause the dimension of feature map to drop to 1 before reaching the full connection layer, and the following convolution cannot be carried out, resulting in training failure. Zero padding operation to enlarge the size will make the image information lose too much in training, so we modified the stride of the conv4_x (Named according to the original ResNet-50) residual block so that the dimension of the feature map remained unchanged after passing through the conv4_x residual block. Softmax classifier is a commonly used regression classifier, which can transform classification problems into probability problems [43]. The model parameters were shown in Table 1.
4.
Experiment and results
4.1. Experimental design details
The entire cascade detection experiment is completed under the Tensorflow framework built under Windows. The experimental platform configuration is as follows: the processor is Inter Ⓡ Xeon E5-2620 v4 CPU 2.4GHz, and the whole experiment is run over a NVIDIA RTX2080 GPU with 8G GPU memory.
4.1.1. Segmentation of mitotic cell candidate set
In the stage of candidate set segmentation, the 40 × HPF images provided by ICPR2012 and ICPR2014 data sets are firstly preprocessed, then cropped into patches and sent to improve UNet ++. The specific steps are as follows: (a) Color normalization [44]. (b) Generating binary mask. (c) Cropping images and masks into 256 × 256 patches, considering video memory and down-sampling to the level of cells. After processing, ICPR2012 mitosis datasets obtained 2240 image blocks, of which 75 contained mitotic pixels, and ICPR 2014 mitosis datasets obtained approximately 35120 image blocks, of which about 714 contained mitotic pixels.
In order to prevent model overfitting, positive image block data were augmented by rotation angle of -10°–10°, 10 pixels of shift on width and height, horizontal and vertical flip, scale of shear and zoom from 0.9 to 1.1, while negative image block was randomly selected.
Training UNet ++ uses the Adam optimizer, the learning rate is 1e-4, the pooling layer is followed by Dropout (coefficient 0.5), and the batch size is set to 4. All convolutional layers of UNet ++ along the layer jump path Xi, j use k convolution kernels of size 3 × 3, where k = 32 × 2i. Deep supervision attaches a 1 × 1 convolutional layer on L2 and L4 target nodes, and the average segmentation output is the candidate set for subsequent processing.
4.1.2. Nuclear segmentation
In this step, 5 images from ICPR2012 and 10 images from ICPR2014 are manually labeled and cropped into 180 pieces of 512 × 512 blocks and 120 images are provided by MoNuSeg datasets. Images are first processed through color normalization, and then are augmented by rotation angle of -10°–10°, the shift scale of 0.05, scale of shear and zoom from 0.95–1.05, horizontal and vertical flip and the random fluctuation
Training UNet ++ uses the Adam optimizer, the learning rate is 2e-5, decay is 1e-6 to prevent outfitting and batch size is set to 2. The model is a fully convolutional structure. Ordinary convolution uses a 5 × 5 convolution kernel, the number of which is 16 × 2(s-1), where s represents the number of layers (the default is 3 when s < 3). Down-sampling uses a 2 × 2 convolution kernel and uses convolution instead of pooling. And add a 1 × 1 convolution kernel to the output result and use the sigmoid function to output the score to achieve the semantic segmentation result. In the cell nucleus segmentation result, locate the nuclear centroid through the centroid function, and cut out a 64 × 64 image block centered on it, and hand it over to the subsequent classification network training and screening.
4.1.3. Precise binary classification
In the image block data set obtained in the previous step, the mitotic cell image block is taken as a positive example according to the ground truth, and the non-mitotic cell image block is taken as a negative example to train the classifier. ResNet50 is used to train an accurate classifier, and the con4_x residual block's convolution step is adjusted. To speed up the convergence, the weights of ResNet50 trained on ImageNet [45] for transfer learning are fine-tuned.
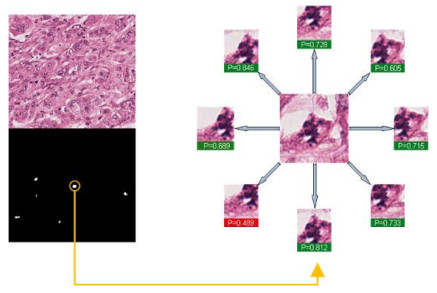
On the result of candidate set, centroid coordinates of connected region are obtained by OpenCV centroid function. Then take the centroid as the center of the circle and take a point every 45° on the circumference with a radius of 15 pixels, a total of 8 points. And then 8 image blocks whose size are 64 × 64 are cut off from the center of 8 pixels and sent into the trained classifier. If the proportion of the 8 image blocks belonging to the mitotic category exceeds 75% of the set threshold, the connected area is retained, otherwise it is determined as a false positive area for screening.
4.2. Results analysis
4.2.1. Analysis of segmentation results of mitotic candidate set
In the detection stage of candidate sets, the evaluation criteria for the candidate set semantic segmentation effect are mean dice coefficient, True positive rate, which are defined as follows.
Where TP (True Positive) represents correctly detected mitotic pixels; FP (False Positive) represents falsely detected mitotic pixels; FN (False Negative) represents undetected mitotic pixels, and N is the number of test pictures. The average Dice coefficient can accurately determine the similarity between the segmentation result and the label mask and TPR (sensitivity) is also an important indicator of the proportion of true mitotic cells that would ideally be detected by the model.
The comparison between the average dice coefficient, precision rate and recall rate of the improved classical UNet, UNet ++ and the improved deep supervision and loss function was conducted. The comparison of segmentation results is shown in Figure 5, and the evaluation index is shown in Table 2.
4.2.2. Nuclei segmentation
Nucleus segmentation was performed in Ostu [46], UNet, and Improved VNet2D with the same HPF image, as shown in Figure 6.
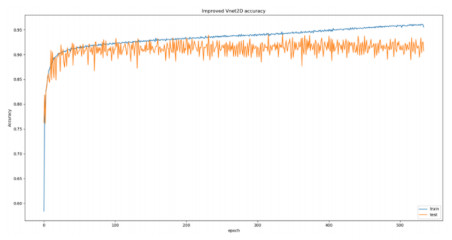
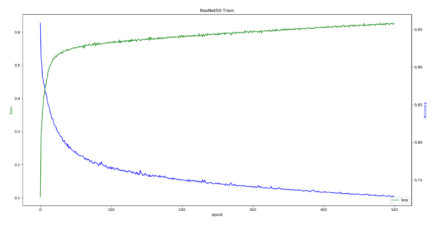
This step is to cut out enough cell data sets for the next classification, so the accuracy of nuclear segmentation needs to be evaluated. We set epoch as 600, each epoch 300 steps, if accuracy and loss no longer change in the right direction, early stopping will occur. The model training results are shown in Figure 7.
And the comparison with the traditional blue ratio threshold segmentation method and the UNet model segmentation results is shown in Table 3.
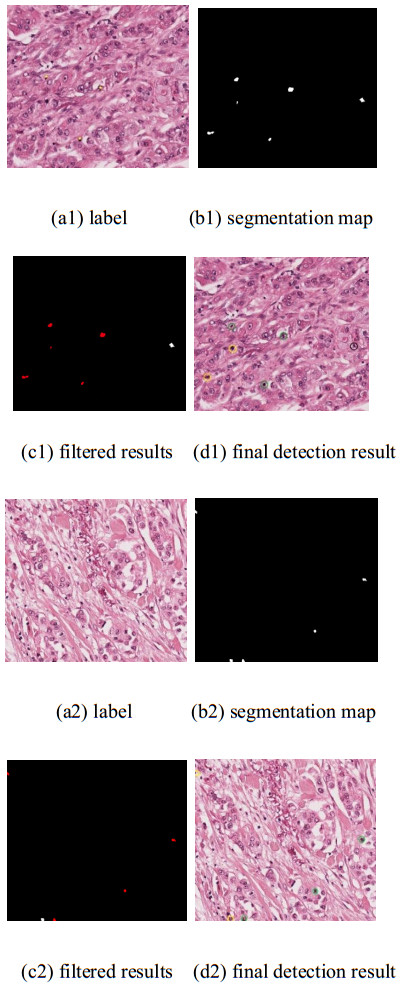
After the segmentation result is obtained and after the erosion and expansion operations, the edge of the cell nucleus is extracted with the Canny operator and displayed in the original image result of cascade method, as shown in Figure 8.
4.2.3. Precise classification and screening
After obtaining the nuclear center coordinates, the 64 × 64 image block was sent to ResNet50. Mitotic cell image patches as positive patches are extremely rare, so they were augmented by rotation, horizontal and vertical flipping, scaling and translation in all directions. Negative patches were not processed, and the training curve is shown in Figure 9.
Then start to take the image block from the circle centered on the center of the mitotic candidate set and send it to the classifier for scoring, and the candidate regions whose number exceeds the set threshold are retained. An example of the ICPR2014 test set is shown in Figure 10.
4.3. Evaluation on ICPR datasets
4.3.1. Evaluation criterion
Various international competitions on mitosis detection have adopted the same set of evaluation indicators, so the same evaluation criteria are used in the experiments in this paper. The distance between the center point of the correctly detected mitotic cells and the center point of the ground truth should be less than 5μm (about 20 pixels) on the 2012 data set, and less than 8μm (about 32 pixels) on the 2014 data set, and the detection fell on the ground truth coordinate point cells outside the range are all false positive cells.
The evaluation criteria are Precise rate, recall rate and F-sore, as shown in Eq 3.3–3.5.
Where TP (true positive) is the number of mitotic cells correctly detected; FP (false positive) represents the number of mitotic cells wrongly detected (actually normal cells); FN (false negative) represents the number of undetected mitotic cells. F-score shows the final detection effect.
4.3.2. Evaluation on 2012 ICPR MITOSIS dataset
Figure 11 shows a cascade detection result in the ICPR 2012 test set for representation.
The circles in the figure are the final test results. The green circle represents TP, the yellow circle represents FP, the blue circle represents FN and the black circle represents the FP correctly filtered out. Calculate the TP, FP and FN of 15 images in the statistical test set, and obtain three detection indexes.
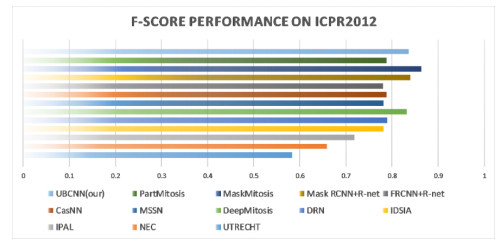
Table 4 and Figure 12 shows the performance of the proposed UBCNN and some other classic methods and the latest research methods in the detection of mitotic cells on ICPR2012 data set. As can be seen, compared with several classic methods, our cascade method improves the prediction rate and significantly improves the recall rate. Compared with the latest algorithms such as regional network, the accuracy rate is slightly poor, but the most significant feature of regional network is that it is extremely time-consuming and has a large number of parameters. Therefore, our method is more competitive when the F-score is in normal time consumption. Finally, the F-score reaches 0.836.
4.3.3. Evaluation on 2014 ICPR MITOSIS dataset
We use random 20% of each set of A3–A18 as the validation sets, and the remaining 80% for training. Therefore, the training set contains 489 mitotic cells and 145 validation sets. Figure 13 shows two HPF detection results in A14 on the validation set, which show the division of mitotic cells in different locations. As can be seen, because the cells on the image boundary are incomplete, there are certain FP samples, but there is no missing check. The effect of boundary contour segmentation is acceptable.
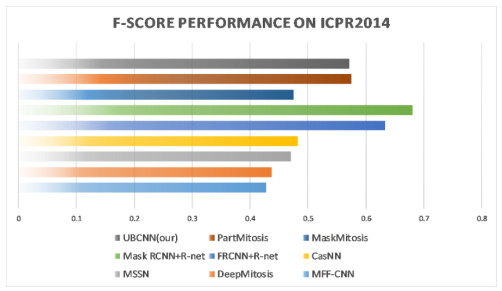
We applied the trained model to the 2014 MITOSIS test set and submitted the mitotic detection results to the challenge organizer. The experimental results of our method and some other previously proposed methods in the ICPR2014 test set are compared. The F-score of our cascading method is 0.571, which is competitive. Table 5 shows the comparison between UBCNN and MFF-CNN, DeepMitosis, MSSN, CasNN, RCNN series, PartMitosis and MaskMitosis on the three detection indicators. Similarly, except that the F-score is slightly less than that of the extremely time-consuming RCNN method, the recall rate and F-score is greatly improved compared with other methods.
Figure 14 shows more visually the performance comparison between UBCNN model and other latest methods on the ICPR2014 MITOSIS test set.
5.
Conclusions
Automatic detection of mitotic cells is of great significance for the diagnosis of breast cancer, which provides information of breast cancer grade and prognosis. In this paper, a cascade detection algorithm based on deep convolutional neural network has been proposed to solve the problems of low detection sensitivity and large number of false positives in traditional mitotic cell detection algorithms and innovatively proposed: (Ⅰ) In the rough semantics of mitotic cells: (a) introduce the deep supervision of the most significant segmentation output layer for breast cell detection, taking into account the high and low level information; (b) improved the loss function based on Dice coefficient, which is more suitable for small targets, improves model sensitivity, and prevents missed detection; (Ⅱ) used a segmentation network to segment cell nuclei to extract normal cell blocks, which solves the dilemma of locating the nucleus of normal cells under complex cell background, and the significance of this step is to provide a pure cell image block data set for the subsequent training of the accurate classifier, free from the interference of background (Ⅲ) In this step of semantic segmentation of the nucleus, we proposed a VNet2D segmentation model after dimensionality reduction from the three-dimensional convolutional neural network VNet and each layer concatenates the subsampled information of the original image to achieve a multi-scale effect. After a number of comparative experiments, the performance of the proposed improved algorithm exceeds that of the traditional algorithm, achieving an 0.836 F-score on the ICPR2012Mitosis dataset, a good performance on both precision and recall, and a 0.571 score on the ICPR2014 Mitosis datasets. It also has good competitiveness among many latest methods. The algorithm framework proposed in this paper has strong transferability. In theory, the algorithm in this paper can also be applied to other image data sets and more medical images. The idea of cascade is the core and can be used in more complicated medical tasks. In the future, we aim to integrate other mitotic cell data sets to remove better generalized network models. In addition to the detection of mitosis, we are committed to the related medical tasks of nuclear anisotropy and glandular duct, considering all three in a comprehensive rating method.
Acknowledgement
This work was partly supported by the National Natural Science Foundation of China (81773109), Joint key project funded by Southeast University and Nanjing Medical University (2242019K3DN09, 2019DN0011).
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: