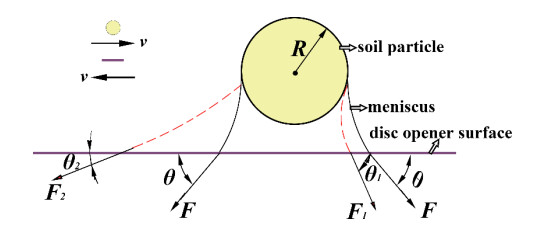
|
[1]
|
D. P. Darmora, K. P. Pandey, Evaluation of performance of furrow openers of combined seed and fertiliser drills, Soil Till. Res., 34 (1995), 127-139.
|
|
[2]
|
C. Sawant, A. Kumar, I. Mani, J. K. Singh, Soil bin studies on the selection of furrow opener for conservation agriculture, J. Soil Water Conserv., 15 (2016), 107-112.
|
|
[3]
|
P. Y. Guo, M. A. Choudhary, Preliminary studies of a modified slot opener for direct drilling seeds, New Zeal. J. Exp. Agric., 1 (1985), 85-95.
|
|
[4]
|
A. Bahri, R. K. Bansal, Evaluation of different combination of furrow openers and press wheels for no till seeding, Homme. Terre. Eaux., 22 (1992), 55-66.
|
|
[5]
|
A. Ozmerzi, Seed distribution performance of furrow openers used on drill machines, AMA-Agr. Mech. Asia AF., 17 (1986), 32-34.
|
|
[6]
|
F. Ahmad, D. Weimin, D. Qishuo, M. Hussain, K. Jabran, Forces and straw cutting performance of double disc furrow opener in no-till paddy soil, PLoS One, 10 (2015), e0119648.
|
|
[7]
|
T. Vamerali, M. Bertocco, L. Sartori, Effects of a new wide-sweep opener for no-till planter on seed zone properties and root establishment in maize (Zea mays, L.): A comparison with double-disk opener, Soil Till. Res., 89 (2006), 196-209.
|
|
[8]
|
A. A. Tagar, C. Ji, J. Adamowski, J. Malard, C. S. Qi, Q. S. Ding, N. A. Abbasi, Finite element simulation of soil failure patterns under soil bin and fieldtesting conditions, Soil Till. Res., 145 (2015), 157-170.
|
|
[9]
|
H. A. Nidal, C. R. Randall, A nonlinear 3D finite element analysis of the soil forces acting on a disk plow, Soil Till. Res., 74 (2003), 115-124.
|
|
[10]
|
H. Bentaher, A. Ibrahmi, E. Hamza, M. Hbaieb, G. Kantchev, A. Maalej, W. Arnold, Finite element simulation of moldboard-soil interaction, Soil Till. Res., 134 (2013), 11-16.
|
|
[11]
|
B. A. Collins, D. B. Fowler, Effect of soil characteristics, seeding depth, operating speed, and opener design on draft force during direct seeding, Soil Till. Res., 39 (1996), 199-211.
|
|
[12]
|
S. Q. Zhang, X. Ma, C. C. Zuo, C. L. Ma, H. W. Wang, Y. J. Sun, Forces acting on disk colter and computer simulation, Trans. CSAE., 11 (1995), 52-56.
|
|
[13]
|
S. Q. Zhang, C. C. Zuo, C. L. Ma, The study on the model of disc coulter force, Trans. CSAM, 29 (1998), 71-75.
|
|
[14]
|
J. L. Jiang, L. N. Gong, M. F. Wang, Study on the working performance of the no-tillage planter unit, Trans. CSAE, 16 (2000), 64-66.
|
|
[15]
|
E. M. Tice, J. G. Hendricks, Disc coulter forces: evaluation of mathematical models, Trans. ASAE, 34 (1991), 2291-2298.
|
|
[16]
|
J. Tong, B. Z. Moayad, Y. H. Ma, J. Y. Sun, D. H. Chen, H. L. Jia, L. Q. Ren, Effects of biomimetic surface designs on furrow opener performance, J. Bionic. Eng., 6 (2009), 280-289.
|
|
[17]
|
L.Q. Ren, Progress in the bionic study on anti-adhesion and resistance-reducing of terrain machines, Sci. China Ser. E., 52 (2009), 273-284.
|
|
[18]
|
L. Q. Ren, D. X. Chen, J. G. Hu, Preliminary analysis on the rules of decreasing viscosity and removing rabbits of soil animals, J. Agr. Eng., 6 (1993), 15-20.
|
|
[19]
|
B. C. Cheng, L. Q. Ren, X. B. Xu, Bionic study on soil adhesion (two) A preliminary study on the anti-viscosity and desorption of the body surface of typical soil animals, J. Agr. Eng., 6 (1990), 2-6.
|
|
[20]
|
L. Q. Ren, Experimental Design and Optimization, Science Press, (2009).
|
|
[21]
|
D. W. Bechert, M. Bruse, W. Hage, J. G. T. van der Hoeven, G. Hoppe, Experimentson drag reducing surfaces and their optimization with an adjustable geometry, J. Fluid Mech., 338 (1997), 59-87.
|
|
[22]
|
J. B. Zhang, J. Tong, Y. H. Ma, Abrasive wear characteristics of subsoiler tines with bionic rib structure surface, Jilin Daxue Xuebao (Gongxueban),45 (2015), 174-180.
|
|
[23]
|
Z. J. Zhang, H. L. Jia, J. Y. Sun, Abrasive wear characteristics of subsoiler tines with bionic rib structure surface, Adv. Mech. Eng., 7 (2015), 1-11.
|
|
[24]
|
V. Zorba, E. Stratakis, M. Barberoglou, E. Spanakis, C. Fotakis, Biomimetic artificial surfaces quantitatively reproduce the water repellency of a lotus leaf, Adv. Mater., 20 (2008), 4049-4054.
|
|
[25]
|
H. Lee, B. P. Lee, P. B. Messersmith, A reversible wet/dry adhesive inspired by mussels and geckos, Nature, 448(2007), 338-341.
|
|
[26]
|
X. Li, T. Chen, Enhancement and suppression effects of a nanopatterned surface on bacterial adhesion, Phys. Rev. E, 93(2016), 52419.
|
|
[27]
|
D. C. Zeng, Mechanical Soil Dynamics, Beijing Science and Technology Press, (1995).
|
|
[28]
|
L. D. Bevel, W. H. Gardner, W. R. Gardner, Soil Physics, John Wiley & Sons., (1956).
|
|
[29]
|
P. G. Huray, Maxwell's Equations, Wiley-IEEE Press, (2009).
|
|
[30]
|
D. H. Qian, J. X. Zhang, A summary of study of adhesion and friction between soil and metals, Trans. CSAM, 1 (1984), 71-80.
|
|
[31]
|
D. H. Qian, A summary of study of adhesion and friction between soil and metals, Trans. CSAM, 2 (1965), 47-52.
|
|
[32]
|
L. Q. Ren, Soil Adhesion Mechanics, China Machine Press, (2011).
|
|
[33]
|
R. E. Baier, E. G. Shafrin, W. A. Zisman, Adhesion: mechanisms that assist or impede it, Science, 162 (1968), 1360-1368.
|
|
[34]
|
R. A. Fisher, Further note on the capillary forces in an ideal soil, J. Agr. Sci., 18 (1928), 406-410.
|
|
[35]
|
M. L. Nichols, The sliding of metal over soil, Agric. Eng., 6 (1925), 80-84.
|
|
[36]
|
W. B. Haines, Studies in the physical properties of soils: I. Mechanical properties concerned in cultivation, J. Agr. Sci., 15 (1925), 178-200.
|
|
[37]
|
S. Q. Deng, L. Q. Ren, Y. Liu, Z. W. Han, Tangent resistance of soil on moldboard and the mechanism of resistance reduction of bionic moldboard, J. Bionic Eng., 2 (2005), 33-46.
|
|
[38]
|
L. Q. Ren, J. Tong, J. Q. Li, B. C. Chen, Soil adhesion and biomimetics of soil-engaging components: a review, J. Agr. Eng. Res., 79 (2001), 239-263.
|
|
[39]
|
W. R. Gill, C. E. Vandenberg, Soil Dynamics in Tillage and Traction, Chinese Agricultural Machinery Press, (1983).
|
|
[40]
|
B. A. Lewis, Manual for LS-DYNA Soil Material Model 147, Federal Highway Administration, (2004).
|
|
[41]
|
I. Ahmadi, Development and assessment of a draft force calculator for disk plow using the laws of classical mechanics, Soil Till. Res.,163 (2016), 32-40.
|
|
[42]
|
A. Armin, R. Fotouhin, W. Szyszkowski, On the FE modeling of soil-blade interaction in tillage operations, Finite Elem. Anal. Des., 92 (2014), 1-11.
|
|
[43]
|
N. Eu-Gene, D. K. Aspinwall, Modeling of hard part machining, J. Mater. Process. Tech., 127 (2002), 222-229.
|
|
[44]
|
J. M. Huang, J. T. Black, An evaluation of chip separation criteria for the fem simulation of machining, J. Manuf. Sci. Eng., 118 (1996), 461-469.
|
|
[45]
|
A. P. Markopoulos, Finite Element Method in Machining Process, Springer, (2013).
|
|
[46]
|
A. Z. Shmulevich, D. Rubinstein, Interaction between soil and a wide cutting blade using the discrete element method, Soil Till. Res., 97 (2007), 37-50.
|
|
[47]
|
D. L. Jing, S. K. Yi, Electroosmotic flow in tree-like branching microchannel network, Fractals, 27 (2019), 1950095.
|
|
[48]
|
D. L. Jing, J. Song, Y. Sui, Hydraulic and thermal performances of laminar flow in fractal treelike branching microchannel network with wall velocity slip, Fractals, 28 (2020), 2050022.
|
|
[49]
|
X. Jia, Unsmooth cuticles of soil animals and theoretical analysis of their hydrophobicity and anti-soil-adhesion mechanism, J. Colloid Inter. Sci., 295 (2006), 490-494.
|
|
[50]
|
E. R. Fountaine, Investigations into the mechanism of soil adhesion, J. Soil Sci., 5 (1954), 251-263.
|
|
[51]
|
F. M. Fowkes, Additivity of intermolecular forces at interfaces. I determination of the contribution to surface and interfacial tensions of dispersion forces in various liquids, J. Phys. C, 67 (1963), 2538-2541.
|
|
[52]
|
I. Lifshitz, The kinetics of precipitation from supersaturated solid solutions, J. Phys. Chem. Solid, 19 (1961), 35-50
|
|
[53]
|
J. Bachmann, A. Ellies, K.H. Hartgea, Development and application of a new sessile drop contact angle method to assess soil water repellency, J. Hydrol., 231-232 (2000), 66-75.
|









 DownLoad:
DownLoad: