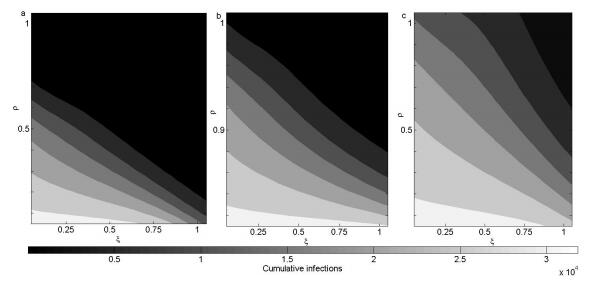
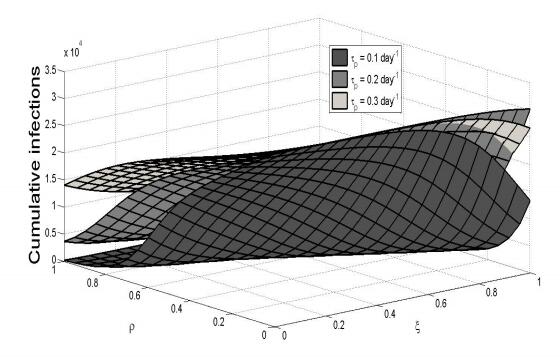
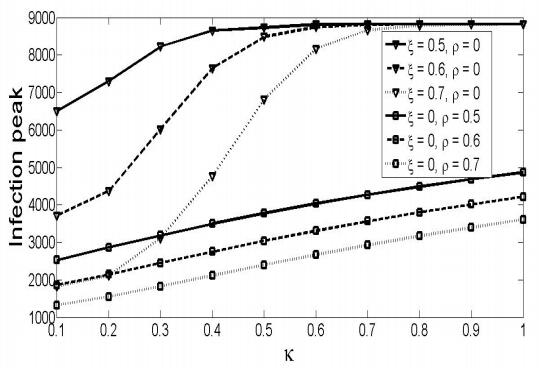
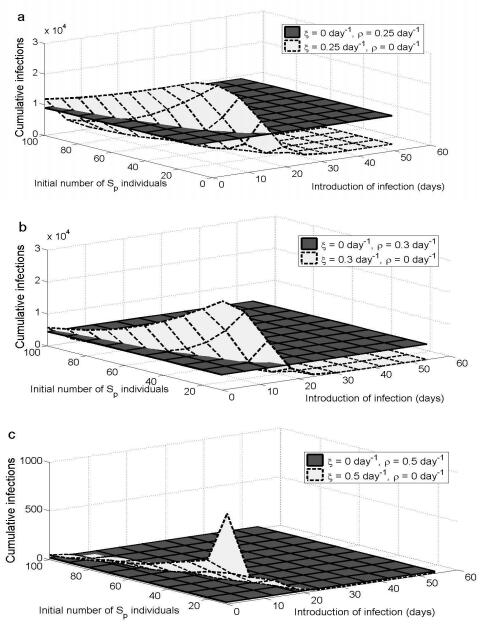
Pair approximation models have been used to study the spread of infectious diseases in spatially distributed host populations, and to explore disease control strategies such as vaccination and case isolation. Here we introduce a pair approximation model of individual uptake of non-pharmaceutical interventions (NPIs) for an acute self-limiting infection, where susceptible individuals can learn the NPIs either from other susceptible individuals who are already practicing NPIs ("social learning"), or their uptake of NPIs can be stimulated by being neighbours of an infectious person ("exposure learning"). NPIs include individual measures such as hand-washing and respiratory etiquette. Individuals can also drop the habit of using NPIs at a certain rate. We derive a spatially defined expression of the basic reproduction number R0 and we also numerically simulate the model equations. We find that exposure learning is generally more efficient than social learning, since exposure learning generates NPI uptake in the individuals at immediate risk of infection. However, if social learning is pre-emptive, beginning a sufficient amount of time before the epidemic, then it can be more effective than exposure learning. Interestingly, varying the initial number of individuals practicing NPIs does not significantly impact the epidemic final size. Also, if initial source infections are surrounded by protective individuals, there are parameter regimes where increasing the initial number of source infections actually decreases the infection peak (instead of increasing it) and makes it occur sooner. The peak prevalence increases with the rate at which individuals drop the habit of using NPIs, but the response of peak prevalence to changes in the forgetting rate are qualitatively different for the two forms of learning. The pair approximation methodology developed here illustrates how analytical approaches for studying interactions between social processes and disease dynamics in a spatially structured population should be further pursued.
1.
Introduction
In recent years, fractional partial differential equations (FPDEs) have been widely used in natural science and engineering technology [1,2,3,4]. The advantage of FPDEs lies in their ability to better describe materials and processes that exhibit memory and genetic properties [5,6]. However, the solutions of FPDEs are much more complex. Many researchers have exploited diverse techniques for the investigation of FPDEs such as the finite difference method (FDM) [7], finite element method [8], spectral method [9], virtual element method [10], etc. The development of effective numerical methods to approximate FPDEs has been the goal of some researchers.
In recent years, neural networks (NNs) have been successfully applied to solve problems in various fields [11,12,13]. Due to the high expressiveness of NNs in functional approximation [14,15,16], using NNs to solve differential and integral equations has become an active and important research field. Physics-informed neural networks (PINNs) [17,18,19,20] are machine learning models that combine deep learning with physical knowledge. PINNs embed PDEs into the loss function of the NNs, enabling the NNs to learn solutions to PDEs. The PINNs algorithm is meshless and simple, and can be applied to various types of PDEs, including integral differential equations, FPDEs, and random partial differential equations. Moreover, PINNs solved the inverse problem of PDEs just as easily as they solved the forward problem [17]. PINNs have been successfully applied to solve various problems in scientific computing [21,22,23]. Pang et al. [24] used the FDM to approximate the fractional derivatives that cannot be automatically differentiated, thus extending the PINNs to fPINNs for solving FPDEs.
Despite the success of deep learning in the past, solving a wide range of PDEs is theoretically and practically challenging as complexity increases. Therefore, many aspects of PINNs need to be further improved to achieve more accurate predictions, higher computational efficiency, and robustness of training. Lu et al. [25] proposed DeepXDE, a deep learning library for solving PDEs, introduced a new residual-based adaptive refinement method to improve the training efficiency of PINNs, and new residual points were added at the position where the residuals of the PDEs were large, so that the discontinuities of PDEs could be captured well. Zhang et al. [26] combined fPINNs with the spectral method to solve the time-fractional phase field models. It had the characteristics of reducing the approximate number of discrete fractional operators, thus improving the training efficiency and obtaining higher error accuracy. Wu et al. [27] conducted a comprehensive study on two types of sampling of PINNs, including non-adaptive uniform sampling and adaptive non-uniform sampling, and the research results could also be used as a practical guide for selecting sampling methods. Zhang et al. [28] removed the soft constraints of PDEs in the loss function, and used the Lie symmetry group to generate the labeled data of PDEs to build a supervised learning model, thus effectively predicting the large amplitude and high frequency solutions of the Klein-Gordon equation. Zhang et al. [29] introduced the symmetry-enhanced physics-informed neural network (SPINN), which incorporated the invariant surface conditions derived from Lie symmetries or non-classical symmetries of PDEs into the loss function of PINNs, aiming to improve accuracy of PINNs. Lu et al. [30] and Xie et al. [31] introduced gradient-enhanced physics-informed neural networks (gPINNs) to solve PDEs and the idea of embedding the gradient information from the residuals of PDEs into the loss functions has also proven to be effective in other methods such as Gaussian process regression [32].
In this paper, inspired by the above works, gfPINNs are applied to solve the forward and inverse problems of the multiterm time-fractional Burger-type equation. The integer order derivatives are handled using the automatic differentiation capability of the NNs, while the fractional derivatives of the equation are approximated using finite difference discretization [33,34]. Subsequently, the residual information of the equation is then incorporated into the loss function of NNs and optimized to yield optimal parameters. For the inverse problems of the multiterm time-fractional Burger-type equation, their overall form are known but the coefficient and the orders of time-fractional derivatives are unknown. The gfPINNs explicitly incorporate information from the equation by including the differential operators of the equation directly into the optimization loss function. The parameters to be identified appear in the differential operators, which are then optimized by minimizing the loss function associated with those parameters. A numerical comparison between fPINNs and gfPINNs is conducted using numerical examples. The numerical results demonstrate the effectiveness of gfPINNs in solving the multiterm time-fractional Burger-type equation.
The structure of this paper is as follows. In Section 2, we define forward and inverse problems for the multiterm time-fractional Burger-type equation. In Section 3, we introduce fPINNs and gfPINNs and give the finite difference discretization to approximate the time-fractional derivatives. In Section 4, we demonstrate the effectiveness of gfPINNs in solving the forward and inverse problems of the multiterm time-fractional Burger-type equation by numerical examples, and compare the experimental results of fPINNs and gfPINNs. Finally, we give the conclusions of this paper in Section 5.
2.
Multiterm time-fractional Burger-type equation
We consider the following multiterm time-fractional Burger-type equation defined on the bounded domain Ω:
where (x,t)∈Ω×[0,T] and the initial and boundary conditions are given as
where u(x,t) is the solution of the equation, f(x,t) is the forcing term whose values are only known at scattered spatio-temporal coordinates, v is the kinematic viscosity of fluid, g(x) is a sufficiently smooth function, the fractional orders α and γ have been restricted to (0, 1) and (1, 2), respectively, C0Dθtu(x,t) is the Caputo time-fractional derivative of order θ (θ>0,n−1≤θ<n) of u(x,t) with respect to t [35,36]:
where Γ(⋅) is the gamma function.
The forward and inverse problems of solving the multiterm time-fractional Burger-type equation are described as follows. For the forward problem, under the given preconditions of the fractional orders α and γ, the forcing term f, and the initial and boundary conditions, the solution u(x,t) is solved. For the inverse problem, under the given preconditions of the initial and boundary conditions, the forcing term f, and additional concentration measurements at the final time u(x,t)=h(x,t), the fractional orders α and γ, the flow velocity v, and the solution u(x,t) are solved.
3.
Methodology
3.1. fPINNs
This subsection introduces the idea of fPINNs and we consider both the forward and inverse problems, along with their corresponding NNs. We first consider the forward problem of the multiterm time-fractional Burger-type equation in the following form:
where L{⋅} is a nonlinear operator and L{u(x,t)}=c1C0Dαtu(x,t)+c2C0Dγtu(x,t)+u(x,t)∂u(x,t)∂x−v∂2u(x,t)∂x2. We divide the nonlinear operator L{⋅} into two parts, L=LAD+LnonAD. The first part is an integer derivative operator, which can be automatically differentiated (AD) using the chain rule. We have
and the second category consists of operators that lack automatic differentiation capabilities:
For LnonAD, we can discretize it using FDM and denote by LFDM the discretization version of LnonAD.
During the NNs training process, our goal is to optimize its parameters in order to ensure that the approximate solution of the equation closely satisfies the initial and boundary conditions. The approximate solution is chosen as
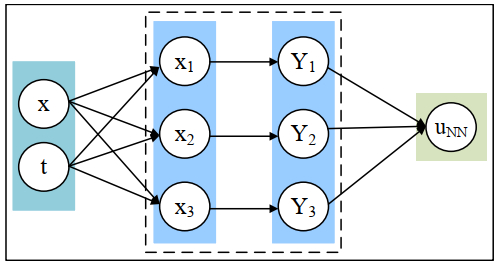
where uNN represents the output of the NNs. The NNs acts as a surrogate model, approximating the relationship between spatio-temporal coordinates and the solution of the equation. It is defined by its weights and biases, forming the parameter vector μ; see Figure 1 for a simple NN. This is fully connected with a single hidden layer consisting of three neurons. In this network, x and t are two inputs, which go through a linear transformation to obtain x1=w1x+w4t+b1, x2=w2x+w5t+b2, and x3=w3x+w6t+b3 in the hidden layer, and then, they go through a nonlinear transformation to get Yi=f(xi) for i=1,2,3. We choose the hyperbolic tangent function tanh(⋅). Yi to go through a linear transformation to obtain the output of the NNs, uNN(x,t;μ)=w7Y1+w8Y2+w9Y3+b4. The vector of parameters μ is comprised of the weights wi and biases bi. ρ(0)=ρ(1)=0 and the auxiliary function ρ(x) is preselected. g(x) is the initial condition function such that it satisfies the initial and boundary conditions automatically.
The loss function of fPINNs for the forward problem with the approximate solution is defined as the mean-squared error of the equation residual
where SF⊂Ω×[0,T] and |SF| represents the number of training points. Then, we train the NNs to optimize the loss function of the forward problem with respect to the NNs parameters μ, thus obtaining the optimal parameters μbest. Finally, we specify a set of arbitrary test points to test the trained NNs and observe the training performance.
The codes for solving the forward and inverse problems of the equation using NNs is similar. We only need to incorporate the parameters to be identified in the inverse problem into the loss function to be optimized in the forward problem, and no other changes are necessary. Next, we consider the following form of the inverse problem:
where ξ is the parameter of the equation, so the loss function LIV for the inverse problem under consideration is
where α∈(0,1) and γ∈(1,2), SI1⊂Ω×[0,T] and SI2⊂Ω×[0,T] are two sets of different training points, and WI1 and WI2 are preselected weight coefficients. We train the NNs to minimize the loss function, thereby obtaining αbest and γbest, the flow velocity vbest, and the optimal parameters μbest of the NNs.
3.2. gfPINNs
We incorporate the residual information of the equation into the loss function of NNs and train the NNs to minimize this loss function, thus obtaining the optimal parameters of NNs. If the residuals in the PDEs are zero, then the gradient of the residuals in the PDEs should also be zero. Therefore, adding gradient information to the loss function is a necessary condition for training NNs. One motivation behind gfPINNs is that the residual in the loss function often fluctuates near zero. Penalizing the slope of the residual can reduce these fluctuations, making the residual closer to zero. In this section, we continue to consider the formulation of the forward and inverse problems of the equation discussed in the previous section.
We first consider the forward problem in the form of (3.1) and provide the loss function of gfPINNs for this form:
where
and the approximate solution of the equation is the same as Eq (3.4): ˜u(x,t)=ρ(x)uNN(x,t)+g(x). The expression LFW as shown in Eq (3.5), where WF, Wg1F, and Wg2F are preselected weighting coefficients, Sg1F⊂Ω×[0,T] and Sg2F⊂Ω×[0,T] are two sets of different training points.
Next, we consider the inverse problem in the form of (3.6) and provide the loss function of gfPINNs for this form. The approach for the inverse problem of gfPINNs is similar to that of fPINNs. We provide the loss function for the inverse problem of gfPINNs.
where
and the expression LIV{μ,ξ={α,γ,v}} as shown in Eq (3.7), where WI, Wg1I, Wg2I, Wg1I1, Wg1I2, Wg2I1, and Wg2I2 are preselected weighting coefficients, Sg1I1,Sg2I1⊂Ω×[0,T], Sg1I2,andSg2I2⊂Ω×[0,T] are four sets of different training points.
This defines the loss function of gfPINNs, which is exactly the same as discussed above for fPINNs. We train the NNs to obtain the optimal parameters of the NNs.
3.3. Finite difference discretization for time-fractional derivatives
In the x direction [0,M], we take the mesh points xp=ihx,i=0,1,2,...,M1, and in the t direction [0,T], we take the mesh points tn=nτ,n=0,1,...,N, where hx=MM1 and τ=TN are the uniform spatial step size and temporal step size, respectively. Denote Ωh≡{0≤i≤M1}, Ωτ≡{0≤n≤N}. Suppose uni = u(xi,tn) is a grid function on Ωh×Ωτ.
We approximate the fractional derivatives of the equation using the finite difference discretization [33,34].
For α∈(0,1), we have C0Dαtu(x,t)∣(xi,tn)=Dατ˜uni+R1(˜uni),
where ˜uni=˜u(xi,tn), R1≤C(τ2−α), and aαk=(k+1)1−α−k1−α.
Lemma 3.1. [33] α∈(0,1), aαl=(l+1)1−α−l1−α, l=0,1,2,…,
(1) 1=aα0>aα1>aα2>⋯>aαl>0,liml→∞aαl→0,
(2) (1−α)l−α<a(α)l−1<(1−α)(l−1)−α,l≥1.
For γ∈(1,2), C0Dγtu(x,t)∣(xi,tn)=Dγτ˜uni+R2(˜uni),
where δtu(x,t)=∂u(x,t)∂t, R2≤C(τ3−γ), and bγk=(k+1)2−γ−k2−γ.
Given the spatial position x, it can be seen from the finite difference discretization that the time-fractional derivative of ˜u(x,t) evaluated at time t depends on the value of ˜u(x,t) calculated at all previous times 0, τ, 2τ, ⋯, t. We call the current time and the previous time the training points and the auxiliary points, respectively.
4.
Numerical examples
In this section, we demonstrate the effectiveness of gfPINNs in solving forward and inverse problems of the multiterm time-fractional Burger-type equation and we compared fPINNs with gfPINNs. We solve the forward problems of the equation and present the experimental results in Section 4.1. We solve the inverse problems and present the experimental results in Section 4.2.
We give a fabricated solution to the problem u(x,t)=tpsin(πx). In the given approximate solution (3.4), the auxiliary function ρ(⋅) is defined as ρ(⋅)=1−‖x‖22. We use the following form of L2 relative error:
to measure the performance of the NNs, where ˜u denotes the approximated solution, u is the exact solution, and (xk,tk) denotes the k-th test point.
We wrote the code in Python and took advantage of the automatic differentiation capability of TensorFlow [37]. The stochastic gradient descent Adam algorithm [38] was used to optimize the loss function. We initialized the NNs parameters using normalized Glorot initialization [39]. Otherwise, when training a neural network, we set the learning rate, the number of neurons, the number of hidden layers, and the activation function as 1×10−3, 20, 4, and tanh(x), respectively.
4.1. Forward problems
In this section, we consider the the multiterm time-fractional Burger-type equation of the form (2.1) with initial and boundary conditions (2.2). We let v=1, (x,t)∈[0,1]×[0,1], and g(x)=0, considering the smooth fabricated solution u(x,t)=tpsin(πx) and the forcing term
Case 1: We choose c1=1, c2=0, and α=0.5, considering the smooth fabricated solution u(x,t)=t4sin(πx) and the forcing term f(x,t)=3.5Γ(5)Γ(4.5)t3.5sin(πx)+t8sin(πx)cos(πx)+π2t4sin(πx). We consider M1−1 training points of the spatial domain: xi=ihx for i=1,2,⋯,M1−1 and N training points of the time domain: tn=nτ for n=1,2,⋯,N. We do not need to place training points on the initial and boundary since the approximate solution ˜u(x,t)=tx(1−x)uNN(x,t;μ) satisfies the initial and boundary conditions automatically. For fPINNs, the loss function can be written as
The loss function of gfPINNs can be given as
By substituting Eqs (4.3)–(4.5) into Eq (3.8), we get the gfPINNs loss function LgFW with WF=1, Wg1F=1, and Wg2F=1. Next, we selected 2000 training points to train fPINNs and gfPINNs and other parameters of the NNs are set to those described at the beginning of this section. Figures 2–4 present a comparison between the predicted solutions from the fPINNs and gfPINNs models and the exact solution of the equation, demonstrating that gfPINNs can effectively solve the equation. Figure 5 shows the absolute errors between the exact solution and the solutions predicted by fPINNs and gfPINNs, and it can be seen that the prediction performance of gfPINNs is better than that of fPINNs. Figure 6 illustrates the L2 relative errors of both fPINNs and gfPINNs models for a single experiment as the iteration count varies, showing that while both can achieve errors as low as 10−4, gfPINNs exhibits comparatively lower error and reduced oscillation.
Case 2: We choose c1=0, c2=1, and γ=1.5, considering the smooth fabricated solution u(x,t)=t4sin(πx) and the forcing term f(x,t)=2.5Γ(5)Γ(3.5)t2.5sin(πx)+t8sin(πx)cos(πx)+π2t4sin(πx). Similarly, we give the loss function of fPINNs as
For gfPINNs, the loss function can be written as
By substituting Eqs (4.6)–(4.8) into Eq (3.8), we get the gfPINNs loss function LgFW with WF=1, Wg1F=0.16, and Wg2F=0.16. Next, we selected 2000 training points to train fPINNs and gfPINNs and other parameters of the NNs are set to those described at the beginning of this section. Figures 7–9 present a comparison between the predicted solutions from the fPINNs and gfPINNs models and the exact solution of the equation, demonstrating that gfPINNs can effectively solve the equation. Figure 10 illustrates the absolute errors between the exact solution and the solutions predicted by both fPINNs and gfPINNs, revealing that the gfPINNs exhibit a relatively smaller absolute error. Figure 11 presents the iteration convergence curves for both the fPINNs and gfPINNs models for a single experiment, revealing that while both can achieve L2 relative errors of 10−4 with increasing iterations, the prediction errors of gfPINNs are relatively low and more stable, resulting in superior prediction performance compared to fPINNs.
4.2. Inverse problems
We use the code that solves the forward problem to solve the inverse problem. We simply add the parameters to be identified in the inverse problem to the list of parameters to be optimized in the forward problem, without changing anything else. In this section, gfPINNs are applied to solve the inverse problems of the multiterm time-fractional Burger-type equation of the form (3.6). We let v=1, (x,t)∈[0,1]×[0,1], g(x)=0, and considering additional concentration measurements at the final time u(x,1)=h(x,1). Here, we still consider the smooth fabricated solution u(x,t)=tpsin(πx) and the forcing term of formula (4.2).
Case 1: We choose c1=1 and c2=0. Similarly, we get the gfPINNs loss function LgFW with WI=1, Wg1I=0.25, and Wg2I=0.25. We set the fractional derivative to be 0.6. We selected 470 training points to train fPINNs and gfPINNs and other parameters of the NNs are set to those described at the beginning of this section. Figures 12–14 display a comparison between the predicted solutions from the fPINNs and gfPINNs models and the exact solution of the equation, demonstrating that gfPINNs can effectively solve the problem. Figure 15 illustrates the absolute errors between the exact solution and the solutions predicted by both fPINNs and gfPINNs, revealing that the gfPINNs exhibit a relatively smaller and more stable absolute error. Figure 16 illustrates the iteration convergence curves for the fPINNs and gfPINNs for a single experiment, indicating that although gfPINNs incur a higher computational cost for solving the inverse problem due to an additional loss term, both models can achieve L2 relative errors of 10−4 as iterations progress, with gfPINNs showing a lower and more stable error curve compared to fPINNs.
Case 2: We choose c1=0 and c2=1. Similarly, we get the gfPINNs loss function LgFW with WI=1, Wg1I=0.16, and Wg2I=0.0001. We set the fractional derivative to be 1.6. We selected 400 training points to train fPINNs and gfPINNs and other parameters of the NNs are set to those described at the beginning of this section. For fPINNs and gfPINNs, we get the similar conclusion as Case 1 by training the NNs and observing the experimental results. Figures 17–19 display a comparison between the predicted solutions from the fPINNs and gfPINNs models and the exact solution of the equation, demonstrating that gfPINNs can effectively solve the problem. Figure 20 illustrates the absolute errors between the exact solution and the solutions predicted by both fPINNs and gfPINNs, revealing that the gfPINNs exhibit a relatively smaller absolute error. Figure 21 compares the L2 relative errors of fPINNs and gfPINNs for a single experiment as iterations progress, revealing that while gfPINNs incurs a higher computational cost due to an additional loss term, both models can achieve an L2 relative error of 10−3, with gfPINNs demonstrating a lower and more stable error curve than fPINNs.
5.
Conclusions
In this paper, the effectiveness of gfPINNs in solving the forward and inverse problems of the multiterm time-fractional Burger-type equation is verified through numerical examples. The L2 relative errors for solutions predicted by both fPINNs and gfPINNs can achieve 10−4 for forward problems and 10−3 or even 10−4 for inverse problems. The experimental results indicate that gfPINNs demonstrate relatively lower and more stable errors with the increase of training iterations, thereby enhancing prediction performance. Nonetheless, the inclusion of an additional loss term in gfPINNs may result in a higher computational cost, such as when solving inverse problems, fPINNs exhibit faster convergence compared to gfPINNs.
Author contributions
Shanhao Yuan, Yanqin Liu, Qiuping Li and Chao Guo: Conceptualization, Methodology; Yibin Xu, Shanhao Yuan and Yanfeng Shen: Software, Visualization, Validation; Shanhao Yuan: Writing–Original draft preparation; Yanqin Liu: Writing–Reviewing & editing. All authors have read and approved the final version of the manuscript for publication.
Acknowledgments
We appreciated the support by the Natural Science Foundation of Shandong Province (ZR2023MA062), the National Science Foundation of China (62103079), the Belt and Road Special Foundation of The National Key Laboratory of Water Disaster Prevention (2023491911), and the Open Research Fund Program of the Data Recovery Key Laboratory of Sichuan Province (DRN19020).
Conflict of interest
The authors declare that they have no conflicts of interest.









 DownLoad:
DownLoad: