Modeling of the kinetics of vitamin D$_3$ in osteoblastic cells

1.   Introduction

The largest contributing factor to species extinction and declining biodiversity is habitat loss and fragmentation e.g., ^[1,2,3,4,5]. Across terrestrial ecosystems worldwide, landscapes are becoming highly spatially heterogeneous with varying degrees of human modification ^[6]. Many studies show that fragmentation is often associated with significant changes in density and that individual species can be differentially affected by fragmentation ^{[7,8,9,10,11]}. In fact, understanding effects of fragmentation has become a central focus of how to guide conservation efforts ^[12].

Much habitat fragmentation research has historically been based upon the theories of island biogeography and metapopulation dynamics. Both theories assume a simple binary representation of landscapes consisting either of habitat patches or inhospitable, homogeneous matrix, which is viewed as unimportant ^[13]. This dichotomous view of a landscape has been the guide for most fragmentation research in the past decades ^[13]. Researchers have placed much emphasis on patch-level attributes such as patch-size and largely ignored heterogeneity of the landscape context (i.e., matrix) ^{[12,13,14,15]}. As such, their ability to make accurate predictions of real-world patterns of patch occurrence, population persistence, and dispersal has been diminished ^[6]. The relative importance of landscape heterogeneity and matrix composition compared to focal habitat configuration and composition remains an unanswered question ^[16].

Notwithstanding, terrestrial habitat patches are often surrounded by complex mosaics of many different land cover types, which are rarely ecologically neutral or completely inhospitable environments ^[16]. Edge effects are also predicted to play a major role in shaping population dynamics ^[17]. Even with an early mention in the literature, incorporation of effects of a heterogeneous matrix into habitat fragmentation study has only recently been made ^[12]. Even though this has been discussed by landscape ecologists, only a few authors have attempted to develop models which simulate effects of a heterogeneous matrix on population persistence and movement patterns in hypothetical landscapes ^[12]. These models often employ arbitrarily chosen values for matrix characteristics and lack a mechanistic underpinning.

Connecting the wealth of empirical information available about individual movement and mortality in response to matrix composition to predictions about patch-level persistence is a formidable task ^[18]. The sheer complexity of realistic landscapes has hampered efforts to develop modeling frameworks capable of capturing all important spatial features ^[12]. However, adaptation of the reaction diffusion framework has seen some recent success in incorporating certain aspects of matrix heterogeneity into the model in order to study population persistence at the patch-level. Recently, the authors have developed a modeling framework built upon reaction diffusion models to study effects of variable matrix hostility and habitat loss on population persistence at the patch-level. The framework extends pioneering work done by authors who first attempted to incorporate matrix hostility and edge effects into reaction diffusion models for organisms dwelling in a one-dimensional patch-matrix system ^[18,19,20] to two- and three-dimensional landscapes ^[21]. The framework provides a mechanistic connection of individual-level assumptions regarding dispersal in the patch and matrix, growth processes in the patch, hostility in the matrix, and habitat preference at the patch/matrix interface to patch-level predictions of population persistence ^[21]. Subsequent studies employing this framework have uncovered important consequences of matrix hostility, edge effects, and habitat preference on population persistence ^{[22,23,24,25,26]}.

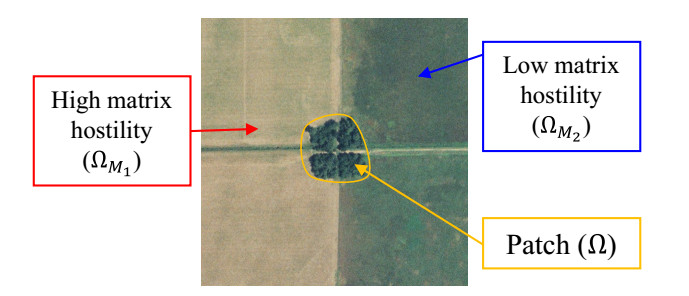
This framework has allowed a more realistic study of landscapes in which each patch can be modeled with different assumptions regarding movement, hostility, and habitat preference in the local matrix surrounding the patch. Even though landscape heterogeneity is incorporated into the framework, there is an implicit assumption that the matrix immediately surrounding a patch is spatially homogeneous. We define this type of spatial homogeneity within a heterogeneous landscape as locally homogeneous matrix. The present work is an attempt to extend the framework to the case where spatial heterogeneity is present even within the matrix immediately surrounding a patch, which we define as locally heterogeneous matrix. In particular, we envision a patch surrounded by a locally heterogeneous matrix with two functionally different matrix types (as in ^[27], functionally different refers to differences noticeable to the organism of interest which may or may not be noticeable to humans). Figure 1 illustrates this scenario with a forested patch ($ \Omega $) surrounded by active farmland on the left ($ \Omega_{M_1} $) and inactive farmland on the right ($ \Omega_{M_2} $).

We initiate this study by focusing on investigation of population persistence in the presence of spatial heterogeneity in the matrix for a one-dimensional analog of the landscape illustrated in Figure 1 (see Figure 2).

1.1.   Modeling Framework

Here, we describe the modeling framework for our one-dimensional patch-matrix system. The model is built upon the reaction diffusion framework which has seen tremendous success in studying spatially structured systems (see ^{[28,29,30,31,32,33,34]} and references therein for a detailed history of the framework). We make the assumption that a single species is dwelling in a focal patch $ \tilde{\Omega} = (0, \ell) $ with patch size $ \ell > 0 $ that is surrounded by a locally heterogeneous matrix ($ \tilde{\Omega}_M $) with two functionally different components denoted by $ \tilde{\Omega}_{M_1} = (-\infty, 0) $ and $ \tilde{\Omega}_{M_2} = (\ell, \infty) $. We further assume that organisms disperse with an unbiased random walk with diffusion rate $ D^0_i > 0 $ and experience exponential decay at fixed rate $ S^0_i > 0 $ for each matrix component $ \tilde{\Omega}_{M_i} $, respectively, $ i = 1, 2 $. Denote the boundary of $ \tilde{\Omega} $ by $ \partial \tilde{\Omega} = \{0, \ell\} $. The variables $ t $ and $ x $ represent time and spatial location within the patch. Inside the patch, organisms are assumed to follow logistic growth and an unbiased random walk, while at the patch/matrix interface a discontinuity between the density in the patch and matrix is allowed (via a biased random walk). However, continuity in the flux is assumed, as has been shown to arise naturally from a landscape-level random walk derivation ^[18,20,35]. In this case, organisms recognize the patch/matrix interface and potentially modify their random walk movement probability (i.e., probability of an organism moving at a given time step in the random walk process), random walk step length (i.e., distance that an organism moves during a given time step), and/or probability of remaining in the patch (say $ \alpha_i $). Here, we equate dispersal from the patch to organisms reaching the patch/matrix interface, leaving the patch with probability $ 1 - \alpha_i $ (taken to be constant), and entering the matrix, where they still have the opportunity to re-enter the patch at the interface. A straightforward modification of the derivation given in ^[21], gives the following reaction diffusion model:

which will exactly model the described study system in the sense that steady states of (1.1) and their stability properties will be exactly the same as those of the study system (see ^[21] and references therein). Here, $ D > 0 $ represents patch diffusion rate, $ r > 0 $ patch intrinsic growth rate, $ K > 0 $ patch carrying capacity, $ u_0(x) $ initial population density distribution in the patch, and $ \alpha_i $ the probability of an individual staying in the patch upon reaching the boundary interfacing with $ \tilde{\Omega}_{M_i} $. Note that the parameter $ S_i^* = \frac{\sqrt{S^0_i D^0_i}}{\kappa_i} \geq 0 $ represents the effective matrix hostility towards an organism in $ \tilde{\Omega}_{M_i} $, has units of length by time, and can assume different forms depending upon the patch/matrix interface assumptions as encoded in $ \kappa_i $. Table 1 shows different cases for $ \kappa_i $ corresponding to different patch/matrix interface assumptions as derived in ^[21]. Notice that when $ \alpha_i \equiv 0 $, the boundary interfacing with $ \tilde{\Omega}_{M_i} $ is absorbing, i.e., all individuals that reach the boundary will emigrate into $ \tilde{\Omega}_{M_i} $, while, $ \alpha_i \equiv 1 $, implies the boundary interfacing with $ \tilde{\Omega}_{M_i} $ is reflecting, i.e., emigration rate into matrix $ \tilde{\Omega}_{M_i} $ is zero. See Table 2 for a summary of model parameters.

Introducing a standard scaling ^[21],

and dropping the tilde, the patch becomes $ \Omega = (0, 1) $, left matrix becomes $ \Omega_{M_1} $, right matrix becomes $ \Omega_{M_2} $, and (1.1) becomes

with steady state equation

where $ \lambda > 0 $ is a composite parameter which is proportional to patch size squared and $ \gamma_i $ is a composite parameter proportional to effective matrix hostility in matrix component $ \Omega_{M_i} $. Table 3 gives a summary of these composite parameters and their definitions in the different scenarios outlined in Table 1, i.e., Continuous Density (CTS) and Type Ⅰ - Ⅲ Discontinuous Density (DD).

In the present work, we consider the following two cases:

● Case 1: Effective matrix hostility in $ \Omega_{M_2} $ is fixed and finite, while allowed to vary in $ \Omega_{M_1} $.

● Case 2: Matrix component $ \Omega_{M_1} $ is immediately lethal to organisms, while effective matrix hostility is allowed to vary in $ \Omega_{M_2} $.

Notice that in Case 2, when $ \gamma_1 \rightarrow \infty $ we have that (1.4) becomes:

It is easy to see that similar results to Cases 1 & 2 hold when changing the matrix component with fixed hostility. We analyze the structure and stability properties of positive solutions for (1.4) in Case 1 and (1.5) in Case 2, providing a complete description of the dynamics of the system.

1.2.   Population dynamics with a locally homogeneous matrix

Here, we recall population dynamics of a single species (with density denoted as $ u $) dwelling in a patch ($ \Omega $) located in heterogeneous landscape but with a locally homogeneous matrix ($ \Omega_M $) as previously studied in ^[21,39]. Namely, the authors studied the structure and stability properties of positive steady state solutions of (1.1) in the case when the combined matrix hostility is the same, i.e., $ \gamma_1 = \gamma_2 = \gamma $ via:

The authors gave a complete description of the dynamics of (1.1) in this case as summarized in Theorem 1.1.

Theorem 1.1 (see ^[22,39]). Let $ \gamma > 0 $ be fixed. Then the following hold:

(1) if $ \lambda \leq E_1(\gamma) $ then (1.6) has no positive solution and the trivial solution is globally asymptotically stable;

(2) if $ \lambda > E_1(\gamma) $ then (1.6) has a unique globally asymptotically stable positive solution $ u_\lambda $ such that $ \|u_{\lambda}\|_{\infty} \rightarrow 1^- $ as $ \lambda \rightarrow \infty $, $ \|u_{\lambda}\|_{\infty} \rightarrow 0 $ as $ \lambda \rightarrow E_1(\gamma)^+ $, and $ u_\lambda $ is symmetric about the center of the patch ($ x = \frac{1}{2} $).

These results also established an exact bifurcation diagram of positive solutions for (1.6) as illustrated in Figure 3.

Here, given a $ \gamma > 0 $, we denote $ E_1(\gamma) > 0 $ as the principal eigenvalue of the problem:

with corresponding eigenfunction $ \phi $ chosen such that $ \phi(x) > 0;\ \overline{\Omega} $. Note that existence of this eigenvalue was discussed in ^[39]. The bifurcation diagram of positive solutions of (1.6) illustrated in Figure 3 shows existence of a minimum patch size given by:

In Section 2, we present some mathematical preliminaries, followed by our main results and biological conclusions in Section 3. We provide proofs of our main results in Section 4. Finally, we give closing remarks in Section 5 and provide proofs of some technical details of our arguments in the Appendix.

2.   Preliminaries

In this section, we introduce definitions of a sub- and supersolution of (1.4) and then an existence result. We also state several important lemmas that we will use to establish our results.

By a subsolution of (1.4) we mean $ \psi\in C^{2}((0, 1))\cap C^1([0, 1]) $ that satisfies

By a supersolution of (1.4) we mean $ Z\in C^{2}((0, 1))\cap C^1([0, 1]) $ that satisfies

By a strict subsolution of (1.4) we mean a subsolution which is not a solution. By a strict supersolution of (1.4) we mean a supersolution which is not a solution. The definitions of sub- and supersolution of (1.5) are analogous.

We now state the following well-known result ^[40]:

Lemma 2.1. Let $ \psi $ and $ Z $ be a sub- and supersolution of (1.4), respectively, such that $ \psi \le Z; \ \overline{\Omega} $. Then (1.4) has a solution $ u\in C^{2}((0, 1))\cap C^1([0, 1]) $ such that $ u\in [\psi, Z];\ \overline{\Omega} $.

Remark 2.1. An analogous result holds for (1.5).

Next, we state several lemmas that we will use to construct sub-super solutions. First, denote $ E_1(\gamma_1, \gamma_2) $ as the principal eigenvalue of:

Lemma 2.2. For $ \gamma_1, \gamma_2, $ and $ \lambda > 0 $, let $ \sigma_\lambda(\gamma_1, \gamma_2) $ be the principal eigenvalue of the problem:

Then $ \sigma_\lambda(\gamma_1, \gamma_2) < 0 $ for $ \lambda > E_1(\gamma_1, \gamma_2) $ and $ \lambda \approx E_1(\gamma_1, \gamma_2) $, and $ \sigma_\lambda(\gamma_1, \gamma_2) > 0 $ for $ \lambda < E_1(\gamma_1, \gamma_2) $ and $ \lambda \approx E_1(\gamma_1, \gamma_2) $. Furthermore, $ \sigma_\lambda(\gamma_1, \gamma_2) \rightarrow 0 $ as $ \lambda\rightarrow E_1(\gamma_1, \gamma_2) $. (See appendix for details).

Lemma 2.3. The principal eigencurve, $ \beta = \beta(\mu) $, of the eigenvalue problem:

with $ \mu > 0 $, is increasing, concave, and $ \lim\limits_{\mu\rightarrow \infty}\beta(\mu) = E_1^D $. Here, $ E_1^D $ is the principal eigenvalue of

(See appendix for details)

Lemma 2.4. For $ \lambda > 0 $, let $ \tilde{\sigma}_\lambda(\gamma_2) $ be the principal eigenvalue of the problem:

then $ \tilde{\sigma}_\lambda(\gamma_2) < 0 $ for $ \lambda > \tilde{E_1}(\gamma_2) $ and $ \tilde{\sigma}_\lambda(\gamma_2) > 0 $ for $ \lambda < \tilde{E_1}(\gamma_2) $. Further, $ \tilde{\sigma}_\lambda(\gamma_2) \rightarrow 0 $ as $ \lambda\rightarrow \tilde{E_1}(\gamma_2) $. Here, $ \tilde{E_1}(\gamma_2) \big( = \lim\limits_{\gamma_1 \rightarrow \infty} E_1(\gamma_1, \gamma_2)\big) $ is the principal eigenvalue of:

(See appendix for details).

3.   Results

In this section, we present analytical and numerical results for both of the aforementioned cases.

3.1.   Case 1: Effective matrix hostility in $ \Omega_{M_2} $ is fixed and finite, while allowed to vary in $ \Omega_{M_1} $

We begin with some analytical results for (1.4). The first result provides a means of computing a bifurcation diagram of positive solutions for (1.4). This is an extension of the quadrature method introduced for Dirichlet problems in ^[41], and for the case of linear boundary conditions with $ \gamma_1 = \gamma_2 $ in ^[39].

Theorem 3.1. Let $ \lambda > 0 $ and $ \rho \in (0, 1) $. Then (1.4) has a positive solution $ u $ with $ \|u\|_\infty = \rho $ if and only if there exist $ q_1, q_2 \in (0, \rho) $ such that $ u(0) = q_1 $, $ u(1) = q_2 $, and $ \lambda, \rho, q_1, q_2 $ satisfy:

and

where $ F(z) = \int_{0}^{z} s(1-s)ds $. Furthermore, (3.2) uniquely determines $ q_1( = q_1(\rho)) $, $ q_2( = q_2(\rho)) $ and $ \lambda ( = \lambda(\rho)) $ defines a continuous function of $ \rho $ on $ (0, 1) $.

Remark 3.1. We note that for $ \lambda > 0 $ if $ u $ is a positive solution of (1.4) with $ ||u||_{\infty} = \rho \in (0, 1) $, then there exists a unique $ x^{*}\in(0, 1) $ such that $ u $ is symmetric about the point $ x^{*} $, increasing on $ (0, x^{*}) $, decreasing on $ (x^{*}, 1) $, $ u'(x^{*}) = 0 $, and $ ||u||_{\infty} = u(x^{*}) $ where

and $ q_1 = u(0) $, $ q_2 = u(1) $ are uniquely determined by (3.2) (see Figure 4).

The next analytical result gives a complete description of the dynamics of (1.3) in this case.

Theorem 3.2. Let $ \gamma_2 > 0 $ be fixed. Then for all $ \gamma_1 > 0 $ the following hold:

1) if $ \lambda \leq E_1(\gamma_1, \gamma_2) $ then (1.4) has no positive solution and the trivial solution is globally asymptotically stable;

2) if $ \lambda > E_1(\gamma_1, \gamma_2) $ then (1.4) has a unique globally asymptotically stable positive solution $ u_\lambda $ such that $ \|u_{\lambda}\|_{\infty} \rightarrow 1^- $ as $ \lambda \rightarrow \infty $ and $ \|u_{\lambda}\|_{\infty} \rightarrow 0 $ as $ \lambda \rightarrow E_1(\gamma_1, \gamma_2)^+ $. In fact, $ u_{\lambda} \rightarrow 1^- $ uniformly on compact subsets of $ (0, 1) $ as $ \lambda \rightarrow \infty. $

Recall, $ E_1(\gamma_1, \gamma_2) $ is the principal eigenvalue of:

Figure 5 illustrates Theorem 3.2.

Remark 3.2. We show in the appendix that

Note that for a fixed $ \gamma_2 > 0 $,

1) $ E_1(\gamma_1, \gamma_2) \in \Big([\tan^{-1}(\gamma_2)]^2, [\pi+\tan^{-1}(-\frac{1}{\gamma_2})]^2 \Big) $ for $ \gamma_1 > 0 $;

2) $ E_1(\gamma_1, \gamma_2) \rightarrow [\tan^{-1}(\gamma_2)]^2 $ as $ \gamma_1 \rightarrow 0 $ and $ E_1(\gamma_1, \gamma_2) \rightarrow \Big[\pi+\tan^{-1}(-\frac{1}{\gamma_2}) \Big]^2 $ as $ \gamma_1 \rightarrow \infty $;

3) $ E_1(\gamma_1, \gamma_2) \rightarrow \frac{\pi^2}{4} $ as $ \gamma_1 \rightarrow \frac{1}{\gamma_2} $ and $ E_1 \Big(\frac{1}{\gamma_2}, \gamma_2 \Big) = \frac{\pi^2}{4} $;

4) $ E_1(\gamma_1, \gamma_2) $ is continuous and increasing in $ \gamma_1 $.

The next result establishes that positive solutions of (1.4) have an ordering with respect to $ \gamma_1 $ for a fixed $ \gamma_2 $ (see Figure 6).

Theorem 3.3. Let $ \gamma_2 > 0 $ be fixed. Then for $ \gamma_1 > \gamma_1^{*} > 0 $, if $ w_{\lambda} : = u_{\lambda}(\gamma_1, \gamma_2) $ and $ v_{\lambda} : = u_{\lambda}(\gamma_1^{*}, \gamma_2) $ are positive solutions of (1.4), then $ w_{\lambda} < v_{\lambda}; \ [0, 1] $.

The final analytical result for this case shows that if $ \gamma_1 \neq \gamma_2 $ then $ u(0) = q_1 \neq q_2 = u(1) $. In other words, local matrix heterogeneity can cause density profiles to become asymmetric. Theorem 3.4 is illustrated in Figure 7.

Theorem 3.4. Let $ \gamma_2 > 0 $ be fixed. If $ \gamma_1 > \gamma_2 $ ($ \gamma_1 < \gamma_2 $) and $ u_{\lambda} $ is a positive solution of (1.4) with $ \|u_{\lambda}\|_\infty = \rho $, $ u_{\lambda}(0) = q_1 $, and $ u_{\lambda}(1) = q_2 $, then $ q_1 < q_2 $ ($ q_1 > q_2 $). Further, if $ \gamma_1 = \gamma_2 $, then $ q_1 = q_2 $.

Remark 3.3. We note that $ q_1 < q_2 $ implies that $ x^*\in(\frac{1}{2}, 1) $, $ q_1 > q_2 $ implies that $ x^*\in(0, \frac{1}{2}) $, and $ q_1 = q_2 $ implies that $ x^* = \frac{1}{2} $.

Next, we present numerically generated bifurcation diagrams of positive solutions for (1.4) using the following procedure:

$ 1) $ Fix $ \gamma_1, \gamma_2 > 0 $ and define $ \rho_i = \frac{i}{n+1}; \; i = 1, ..., n $, where $ n \geq 1 $ is the desired number of interpolation points.

$ 2) $ Using $\texttt{fzero}$ in MATLAB (The Mathworks, Inc. version: R2022a), numerically find the roots of (3.2), i.e., $ q_{i_1} = q_1(\rho_i) $ and $ q_{i_2} = q_2(\rho_i) $, for a given $ \rho_i $.

$ 3) $ The values of $ \rho_i, q_{i_1}, q_{i_2} $ are then substituted into (3.1) and the corresponding $ \lambda_i $-value is numerically computed using $\texttt{integral}$.

$ 4) $ Repeating (2)–(3) for $ i = 1, 2, ..., n $, we obtain $ (\lambda_i, \rho_i) $ points, generating a bifurcation curve of $ \lambda $ vs. $ \rho = \|u\|_\infty $ for positive solutions of (1.4).

In terms of computational complexity, a single bifurcation diagram was able to be computed in about one second using a standard laptop.

Employing Theorem 3.2, the model predicts a minimum patch size (MPS) below which organisms cannot colonize the patch. Using the definition of $ \lambda $ from Table 3, we can give an explicit form for the predicted MPS,

Remark 3.2 now gives limiting behavior of MPS with respect to $ \gamma_1 $ for fixed $ \gamma_2 > 0 $ as presented in Remark 3.4.

Remark 3.4. Let $ \gamma_2 > 0 $ be fixed. Then we have:

1) $ \lim\limits_{\gamma_1 \rightarrow 0^{+}} \ell^{*}(\gamma_1, \gamma_2) = \tan^{-1}\Big(\gamma_2\Big) \sqrt{\frac{D}{r}} ( = \ell^{*}(0, \gamma_2) \; {\rm{ say}}) $;

2) $ \lim\limits_{\gamma_1 \rightarrow \infty} \ell^{*}(\gamma_1, \gamma_2) = \left(\pi + \tan^{-1} \Big(-\frac{1}{\gamma_2}\Big)\right) \sqrt{\frac{D}{r}} ( = \ell^{*}(\infty, \gamma_2) \; {\rm{ say}}) $;

3) $ \ell^*(\infty, \gamma_2) - \ell^*(0, \gamma_2) = \frac{\pi}{2} \sqrt{\frac{D}{r}} $.

From Remark 3.2, it immediately follows that $ \ell^*(\gamma_1, \gamma_2) \in \left[ \ell^*(0, \gamma_2), \ell^*(\infty, \gamma_2)\right] $ and the length of this interval is a constant independent of the value of $ \gamma_2 > 0 $.

Figure 8 shows an evolution of bifurcation curves as $ \gamma_1 $ varies with $ \gamma_2 = 1 $ and $ r = D $ chosen for convenience of presentation. In Figure 8a, we consider $ \gamma_1 $ going to zero from the right and observe that MPS approaches $ \ell^*(0, 1) = \frac{\pi}{4} $ from the right, shifting the bifurcation curves to the left. In Figure 8b, we consider $ \gamma_1 $ approaching $ \infty $ and observe MPS approaching $ \ell^*(\infty, 1) = \frac{3 \pi}{4} $ from the left as $ \gamma_1 \rightarrow \infty $, this time shifting the bifurcation curves to the right. Further, we observe that MPS ranges over $ (\frac{\pi}{4}, \frac{3 \pi}{4}) $, increases in $ \gamma_1 $, and causes bifurcation curves to move to the right as $ \gamma_1 $ increases.

In Figure 9, we provide the evolution of MPS ($ \ell^*(\gamma_1, \gamma_2) $) as $ \gamma_1 $, $ \gamma_2 $ both vary with $ r = D $ chosen for convenience of presentation. Here, we observe that for any fixed $ \gamma_2 > 0 $ ($ \gamma_1 > 0 $), $ \ell^*(\gamma_1, \gamma_2) $ is an increasing function of $ \gamma_1 $ ($ \gamma_2 $). Furthermore, we observe that MPS approaches $ 0^+ $ as $ \gamma_1, \gamma_2 \rightarrow 0 $ and approaches $ \sqrt{E_1^D} = \pi $ as $ \gamma_1, \gamma_2 \rightarrow \infty $, where $ E_1^D $ is the principal eigenvalue of (2.4). Recall that these facts were proved analytically and stated in Remark 3.2.

3.2.   Case 2: Matrix component $ \Omega_{M_1} $ is immediately lethal to organisms, while effective matrix hostility is allowed to vary in $ \Omega_{M_2} $

We begin by presenting some analytical results for (1.4) in the case when $ \gamma_1 \rightarrow \infty $, namely (1.5).

The first result is a modification of the time map analysis presented in Theorem 3.1 for this case.

Theorem 3.5. Let $ \lambda > 0 $ and $ \rho \in (0, 1) $. Then (1.5) has a positive solution $ u $ such that $ \|u\|_\infty = \rho $ if and only if there exists $ q \in (0, \rho) $ such that $ u(1) = q $ and $ \lambda, \rho, q $ satisfy:

and

where $ F(z) = \int_{0}^{z} s(1-s)ds $. Furthermore, (3.7) uniquely determines $ q( = q(\rho)) $ and $ \lambda( = \lambda(\rho)) $ defines a continuous function of $ \rho $ on $ (0, 1) $.

Remark 3.5. We note that for $ \lambda > 0 $ if $ u $ is a positive solution of (1.5) with $ ||u||_{\infty} = \rho \in (0, 1) $, then there exists a unique $ x^{*} \in (0, 1) $ such that $ u $ is symmetric about the point $ x^{*} $, increasing on $ (0, x^{*}) $, decreasing on $ (x^{*}, 1) $, $ u'(x^{*}) = 0 $, and $ ||u||_{\infty} = u(x^{*}) $ where

and $ q = u(1) $ is uniquely determined by (3.7) (see Figure 10).

The next analytical result gives a complete description of the dynamics of (1.3) in the case when $ \gamma_1 \rightarrow \infty $.

Theorem 3.6. Let $ \gamma_2 > 0 $ be fixed. Then the following hold:

(1) if $ \lambda \leq \tilde{E_1}(\gamma_2) $ then (1.5) has no positive solution and the trivial solution is globally asymptotically stable;

(2) if $ \lambda > \tilde{E_1}(\gamma_2) $ then (1.5) has a unique globally asymptotically stable positive solution $ u_\lambda $ such that $ \|u_{\lambda}\|_{\infty} \rightarrow 1^- $ as $ \lambda \rightarrow \infty $ and $ \|u_{\lambda}\|_{\infty} \rightarrow 0 $ as $ \lambda \rightarrow \tilde{E_1}(\gamma_2)^+ $. In fact, $ u_{\lambda} \rightarrow 1^- $ uniformly on compact subsets of $ (0, 1) $ as $ \lambda \rightarrow \infty. $

Recall, $ \tilde{E_1}(\gamma_2) = E_1(\infty, \gamma_2) \Big( = \lim\limits_{\gamma_1 \rightarrow \infty} E_1(\gamma_1, \gamma_2) \Big) $ is the principal eigenvalue of (2.6).

Figure 11 illustrates Theorem 3.6.

Remark 3.6. We show in the appendix that

Note that for a fixed $ \gamma_2 > 0 $,

1) $ \tilde{E_1}(\gamma_2)\in (\frac{\pi^2}{4}, \pi^2) $ for $ \gamma_2 > 0 $;

2) $ \tilde{E_1}(\gamma_2) \rightarrow \frac{\pi^2}{4} $ as $ \gamma_2 \rightarrow 0 $, and $ \tilde{E_1}(\gamma_2) \rightarrow E_1^D = \pi^2 $ as $ \gamma_2 \rightarrow \infty $;

3) $ \tilde{E_1}(\gamma_2) $ is continuous and increasing in $ \gamma_2 $.

The next result establishes that positive solutions of (1.5) have an ordering with respect to $ \gamma_2 $ (see Figure 12).

Theorem 3.7. Let $ \gamma_2 > \gamma_2^{*} > 0 $ be fixed. If $ w_{\lambda}: = u_{\lambda}(\gamma_2) $ and $ v_{\lambda}: = u_{\lambda}(\gamma_2^{*}) $ are positive solutions of $ (1.5) $, then $ w_{\lambda} < v_{\lambda}; \ (0, 1] $.

Finally, combining Theorems 3.3, 3.7 and Remarks 3.2, 3.6, we observe the limiting behavior of bifurcation curves of positive solutions for (1.4) as $ \gamma_1 \rightarrow \infty $ in Figure 13a for a fixed $ \gamma_2 > 0 $ and in Figure 13b for $ \gamma_2 \rightarrow \infty $.

Following the methodology outlined in Section 3.1, we numerically obtain the evolution of bifurcation curves of positive solutions for (1.5) with respect to $ \gamma_2 $ using MATLAB. Remark 3.6 now allows a characterization of MPS in this case:

Remark 3.7. We have the following:

1) $ \lim\limits_{\gamma_2 \rightarrow 0^{+}}\ell^{*}(\infty, \gamma_2) = \frac{\pi}{2} \sqrt{\frac{D}{r}} = \sqrt{\frac{E_1^D}{4} \frac{D}{r}} ( = \ell^{*}(\infty, 0) \; {{ say}}) $;

2) $ \lim\limits_{\gamma_2 \rightarrow \infty} \ell^{*}(\infty, \gamma_2) = \pi \sqrt{\frac{D}{r}} = \sqrt{E_1^D \frac{D}{r}} ( = \ell^{*}(\infty, \infty) \; {{ say}}) $.

Figure 14 shows an evolution of bifurcation curves as $ \gamma_2 $ varies and $ r = D $ is chosen for convenience of presentation. Remark 3.7 is reflected in both Figure 14a where we observe shifting bifurcation curves to the left and Figure 14b where we observe shifting bifurcation curves to the right. Further, we observe that MPS ($ \ell^*(\infty, \gamma_2) $) ranges over $ \left(\frac{\pi}{2}, \pi \right) $, increases in $ \gamma_2 $, and causes bifurcation curves to move to the right as $ \gamma_2 $ increases.

In Figure 15, we provide the evolution of MPS ($ \ell^*(\infty, \gamma_2) $) as $ \gamma_2 $ varies with $ r = D $ chosen for convenience of presentation. Here, we observe that $ \ell^*(\infty, \gamma_2) $ is an increasing function of $ \gamma_2 $, approaches $ \sqrt{\frac{E_1^D}{4}} = \frac{\pi}{2} $ as $ \gamma_2 \rightarrow 0^+ $, and approaches $ \sqrt{E_1^D} = \pi $ as $ \gamma_2 \rightarrow \infty $, where $ E_1^D $ is the principal eigenvalue of (2.4).

3.3.   Biological conclusions

The model predicts that patches with size ($ \ell $) less than or equal to the minimum patch size, i.e., $ \ell^*(\gamma_1, \gamma_2) $, cannot support a population as losses due to mortality caused by interaction with the hostile matrix fail to be overcome by growth inside the patch. However, for patches with $ \ell > \ell^*(\gamma_1, \gamma_2) $, the model predicts that organisms with a positive initial density profile will be able to successfully colonize the patch and persist. Our results also show that as patch size approaches $ \ell^*(\gamma_1, \gamma_2) $ from the right, maximum density of the unique steady state density profile will tend towards zero in a continuous fashion. On the other hand, as patch size becomes large, a core habitat will form in the center of the patch for which organisms dwelling in the core are not likely to exhibit mortality at the patch/matrix interface. As patch size grows, this core habitat will approach 100% of the overall patch. Our results further show that the steady state density profile will approach 100% of patch carrying capacity ($ K $) in this habitat core.

The composite parameter $ \gamma_i $ measures the overall effect of matrix hostility from interaction with $ \Omega_{M_i} $ on population persistence as the MPS is an increasing function of $ \gamma_i $. As Table 3 reveals, this effect is determined by the ratio of matrix death rate to patch intrinsic growth rate, habitat preference as measured by emigration probability (i.e., $ 1 - \alpha_i $, where $ \alpha_i $ is the probability that an organism will remain in the patch upon reaching the boundary), and in the Type Ⅱ DD scenario the ratio of patch diffusion rate to matrix diffusion rate. In all patch/matrix interface scenarios, increasing matrix death rate, increasing patch diffusion rate, decreasing patch intrinsic growth rate, or increasing emigration probability will cause an increase in MPS (holding all other factors fixed). In the Type Ⅱ DD scenario, increasing matrix diffusion rate will actually lower MPS. This suggests that for species with no difference between random walk step length in the matrix versus patch, decreasing movement resistance in the matrix can actually lower their MPS requirement. However, for organisms falling under the remaining scenarios, movement resistance in the matrix is not predicted to have any impact on MPS.

One matrix component's combined hostility measure remaining fixed as the other component's is varied (as was studied in Case 1 of our analysis) can arise naturally in a couple of different ways. Local matrix heterogeneity may occur in an obvious way as one matrix component is affected by consistent anthropogenic activities such as farming (e.g., increasing the matrix death rate in that component by excessive pesticide use), while the other component remains untouched. However, our results reveal that a second more stealthy situation may arise in which both matrix components are identical to the organism (e.g., matrix death rate and emigration probability are equal and fixed, while movement resistance in both matrix components is increasing in a similar fashion causing a reduction in matrix diffusion rate), but one matrix component is functionally different enough from the other to cause movement step lengths on one side to be the same in the matrix versus patch and different in the other. In this case, as matrix diffusion rate increases in both matrix components, combined hostility in the matrix component with similar movement step lengths between patch and matrix increases on that side, but no change in hostility occurs on the other side. These results indicate that even simple assumptions regarding movement at the individual-level could have lasting impacts at the patch-level via increasing of MPS requirement.

Also, MPS estimates in Case 1 of our analysis were shown to be confined to an envelope of possible values dictated by the fixed component's $ \gamma_i $-value. For example, we considered the case when $ \gamma_2 = 1 $ and combined matrix hostility was allowed to vary in $ \Omega_{M_1} $. Our results show that MPS $ \ell^*(\gamma_1, \gamma_2) \in \left[ \ell^*(0, \gamma_2), \ell^*(\infty, \gamma_2)\right] $). Although both lower and upper bounds on MPS are dependent on $ \gamma_2 $, the length of this interval was always $ L_0 = \frac{\pi}{2} \sqrt{\frac{D}{r}} $–independent of $ \gamma_2 $. This result sheds some light on the consequences of making an assumption of a homogeneous (or even locally homogeneous) matrix when modeling a population residing in a patch with locally heterogeneous matrix. In fact, we are able to employ this result to provide some bounds on the potential error incurred by assuming a locally homogeneous matrix. In our one-dimensional landscape, using the same $ \gamma_i $-value for both matrix components yields a MPS prediction at worse $ L_0 $ from the correct estimate.

When neither matrix component is immediately hostile to organisms, the model predicts that all positive steady state density profiles will be symmetric about the center of the patch if and only if the combined matrix hostility in each component is the same (i.e., composite parameters $ \gamma_1 $ and $ \gamma_2 $ are equal). Such a prediction arises from the fact that equal mortality at both patch/matrix interfaces create a symmetric spatial structure as shown in Figure 7b. This result captures what was found in ^[22,39] for the locally homogeneous matrix case. However, our results show that local heterogeneity in the matrix can create steady state density profiles with asymmetric spatial structure (see Figure 7a, c). In fact, peak density in a steady state profile is predicted to occur closer to the patch/matrix interface with lower combined hostility (e.g., $ \gamma_1 < \gamma_2 $ implies that peak density of the steady state profile will occur closer to $ \Omega_{M_1} $). When one matrix component is close to being immediately hostile to organisms and the other not, the steady state density profile will always be skewed with the peak occurring closer to the other latter component. This fact can be used as a tool to give a quick evaluation of the presence of local matrix heterogeneity. For example, population densities empirically estimated from a patch that show such a skewed spatial structure where the peak density is closer to one part of the patch/matrix interface could indicate presence of local matrix heterogeneity and suggest the need for further investigation of matrix hostility, dispersal, and organismal habitat preference.

4.   Proofs of main results

In this section, we present proofs of our main results. First, we provide proofs of Theorems 3.1–3.4 from Case 1.

Proof of Theorem 3.1: Here, we extend the study in ^[41], where a quadrature method was first introduced for the Dirichlet boundary conditions, and in ^[39] where it was extended for the case of linear boundary conditions with $ \gamma_1 = \gamma_2 $.

Suppose $ u $ is a positive solution to (1.4) with $ ||u||_{\infty} = \rho $. Clearly $ u'' < 0; (0, 1) $. Further, the boundary conditions imply that $ u'(0) > 0 $ and $ u'(1) < 0 $. Hence, there exists a unique $ x^{*} \in (0, 1) $ such that $ u'(x^{*}) = 0 $ and $ ||u||_{\infty} = u(x^{*}) = \rho $. Also, since the differential equation is autonomous, the solution must be symmetric about this $ x^{*} $. Multiplying both sides of the differential equation in (1.4) by $ u' $ and integrating we obtain

Next, integrating (4.1) yields

where $ q_1 = u(0) $ and $ q_2 = u(1) $.

Now, taking $ x \rightarrow x^{*} $, $ \lambda $, $ \rho $, $ q_1 $, $ q_2 $, and $ x^{*} $ must satisfy:

From (4.4) and (4.5), we obtain

and

By the boundary conditions in (1.4) and by (4.1), we see that

Note here that since $ 2F(s)+ \gamma_i s^2; i = 1, 2 $ are strictly increasing on $ (0, 1) $, $ q_1 ( = q_1(\rho)) $ and $ q_2 ( = q_2(\rho)) $ are uniquely determined for a given $ \rho \in (0, 1) $.

Next, let $ \lambda, q_1, q_2 $, and $ \rho $ satisfy (3.1) and (3.2). Define $ u:[0, 1]\xrightarrow{}[0, \rho] $ such that $ u $ satisfies (4.2) for $ x \in (0, x^{*}) $ and (4.3) for $ x \in (x^{*}, 1) $. Note that $ u $ is well-defined for $ x \in (0, x^{*}) $ since both $ \int_{q_1}^{u} \frac{dz}{\sqrt{F(\rho)-F(z)}} $ and $ \sqrt{2\lambda} x $ increase from 0 to $ \int_{q_1}^{\rho} \frac{dz}{\sqrt[]{F(\rho)-F(z)}} $ as $ u $ increases from $ q_1 $ to $ \rho $ and $ x $ increases from $ 0 $ to $ x^{*} $. Similarly we can see that $ u $ is well defined for $ x \in (x^{*}, 1) $. Define $ H:(0, x^{*}) \times (q_1, \rho) \rightarrow \mathbb{R} $ by

Clearly, $ H $ is $ C^1 $, $ H(x, u(x)) = 0 $ for $ x \in (0, x^{*}) $, and

By the Implicit Function Theorem, $ u $ is $ C^1 $ on $ (0, x^{*}) $. Similarly we can show that $ u $ is $ C^1 $ on $ (x^{*}, 1) $. Differentiating (4.2) and (4.3), we obtain

Now, from (4.9), it is easy to show that $ u\in C^2(0, 1) $ and is a solution of $ -u''(x) = \lambda f(u(x)); \; (0, 1) $. Further, $ u \in C^1[0, 1] $ and from (3.2) and (4.9), we obtain $ -u'(0) + \sqrt{\lambda} \gamma_1 u(0) = 0 $. Similarly, we see that $ u'(1)+\sqrt{\lambda} \gamma_2 u(1) = 0 $.

Finally, we recall the study in ^[41] where the corresponding $ \lambda $ (for the Dirichlet case $ q_1 = 0 = q_2 $) was proved to be a well-defined and continuous function of $ \rho $ (using the fact that $ f(\rho) > 0 $). Here $ q_1 $ and $ q_2 $, though not zero, are still continuous functions of $ \rho $ by (3.2). Hence, the arguments in ^[41] can be extended to show that $ \lambda $ in (3.1) is also well-defined and continuous for $ \rho $ on $ (0, 1) $.

Proof of Theorem 3.2: First, when $ \lambda > E_1(\gamma_1, \gamma_2) $ and $ \lambda \approx E_1(\gamma_1, \gamma_2) $, we establish existence of a positive solution $ u_{\lambda} $ such that $ ||u_{\lambda}||_{\infty} \rightarrow 0 $ as $ \lambda \rightarrow E_1(\gamma_1, \gamma_2)^{+} $. Let $ \lambda > E_1(\gamma_1, \gamma_2) $, $ \lambda \approx E_1(\gamma_1, \gamma_2) $, and let $ \sigma_\lambda(\gamma_1, \gamma_2) $ be the principal eigenvalue of (2.2) and $ \phi_{\lambda} $ be the corresponding normalized eigenfunction such that $ \phi_\lambda > 0;\ \overline{\Omega} $ (see proof of Lemma 2.2 and Remark.1). Let $ \psi_\lambda = \tau \phi_{\lambda} $, with $ \tau > 0 $. Then we have

for $ \tau \approx 0 $ since by Lemma 2.2 we have $ \sigma_\lambda(\gamma_1, \gamma_2) < 0 $. It is also clear that $ \psi_\lambda $ satisfies the boundary conditions of (1.4). Thus, $ \psi_\lambda $ is a subsolution of (1.4) for $ \tau \approx 0 $. Now, let $ Z_\lambda = \delta_{\lambda} \phi_{\lambda} $, where $ \delta_{\lambda} = \frac{-\sigma_\lambda(\gamma_1, \gamma_2)}{\lambda \min_{[0, 1]} \phi_{\lambda}} $. We note that $ \delta_{\lambda} > 0 $ and $ \delta_{\lambda}\rightarrow 0 $ as $ \lambda\rightarrow E_1(\gamma_1, \gamma_2)^+ $ since $ \sigma_\lambda(\gamma_1, \gamma_2) < 0 $, $ \sigma_\lambda(\gamma_1, \gamma_2) \rightarrow 0 $ as $ \lambda \rightarrow E_1(\gamma_1, \gamma_2)^+ $, and $ \min\limits_{x\in [0, 1]} \phi_{\lambda} \not\rightarrow 0 $ as $ \lambda \rightarrow E_1(\gamma_1, \gamma_2)^+ $. Then we have

It is also easy to see that $ Z_\lambda $ satisfies the boundary conditions of (1.4). Thus, $ Z_\lambda $ is a supersolution of (1.4) such that $ ||Z_\lambda||_{\infty} \rightarrow 0^{+} $ as $ \lambda \rightarrow E_1(\gamma_1, \gamma_2)^{+} $.

Further, we have $ \psi_\lambda \leq Z_\lambda $ for $ \tau \approx 0 $. By Lemma 2.1, (1.4) has a positive solution $ u_\lambda \in [\psi_\lambda, Z_\lambda] $ such that $ ||u_{\lambda}||_{\infty} \rightarrow 0 $ as $ \lambda \rightarrow E_1(\gamma_1, \gamma_2)^{+} $. We emphasize that this shows existence of a positive solution for $ \lambda > E_1(\gamma_1, \gamma_2) $ and $ \lambda \approx E_1(\gamma_1, \gamma_2) $.

It is well known that

has a unique positive solution $ v_{\lambda} $ for $ \lambda > E_1^D $ such that $ ||v_{\lambda}||_{\infty} \rightarrow 1^{-} $ as $ \lambda \rightarrow \infty $. In fact, $ v_{\lambda} \rightarrow 1^- $ uniformly on compact subsets of $ \Omega $ as $ \lambda \rightarrow \infty. $ Since $ v_{\lambda}'(1) < 0 $ and $ v_{\lambda}'(0) > 0 $, is it easy to see that $ v_{\lambda} $ is a subsolution of (1.4) for $ \lambda \gg 1 $. Recall that $ Z \equiv 1 $ is a supersolution of (1.4). By Lemma 2.1, (1.4) has a positive solution $ u_{\lambda} \in [v_{\lambda}, 1] $ for $ \lambda > E_1^D. $ Furthermore, $ u_{\lambda} \rightarrow 1^- $ uniformly on compact subsets of $ \Omega $ as $ \lambda \rightarrow \infty $ since $ v_{\lambda} $ does the same. This immediately implies that $ ||u_{\lambda}||_{\infty} \rightarrow 1^{-} $ as $ \lambda \rightarrow \infty $. Our previous results together with Theorem 3.1 imply that (1.4) has a positive solution $ u_\lambda $ for $ \lambda > E_1(\gamma_1, \gamma_2) $ such that $ ||u_\lambda ||_{\infty} \rightarrow 0 $ as $ \lambda \rightarrow E_1(\gamma_1, \gamma_2)^+ $ and $ ||u_\lambda ||_{\infty} \rightarrow 1 $ as $ \lambda \rightarrow \infty $.

Next, we show that (1.4) has at most one positive solution for any $ \lambda > 0 $. Suppose that (1.4) has two distinct positive solutions $ u_1 $ and $ u_2 $. (Note: Nontrivial, non-negative solutions are positive in the interior). Since $ Z \equiv m $ is a global supersolution for all $ m \geq 1 $, without loss of generality we can assume that $ u_2 $ is the maximal positive solution of (1.4). Therefore, $ u_1 \leq u_2 $ in $ [0, 1] $. Integration by parts yields

However, by (1.4), we have

Combining these results, it follows that

This is a contradiction since $ u_1 $ and $ u_2 $ are distinct positive solutions with $ u_1 \leq u_2 $. Therefore, we must have $ u_1 \equiv u_2 $. Hence, (1.4) has at most one positive solution $ u_\lambda $ for $ \lambda > 0 $.

Combining the above results that at most one positive solution exists for $ \lambda > 0 $, existence of a positive solution $ u_{\lambda} $ for $ \lambda > E_1(\gamma_1, \gamma_2) $ and $ \lambda \approx E_1(\gamma_1, \gamma_2) $ such that $ ||u_{\lambda}||_{\infty} \rightarrow 0 $ as $ \lambda \rightarrow E_1(\gamma_1, \gamma_2)^{+} $ and $ ||u_{\lambda}||_{\infty} \rightarrow 1 $ as $ \lambda \rightarrow \infty $, and the continuity of $ \lambda $ for $ \rho $ on $ (0, 1) $ from Theorem 3.1, it follows that there is no positive solution for $ \lambda \leq E_1(\gamma_1, \gamma_2). $ Therefore, the exact bifurcation diagram illustrated in Figure 5 is established. Stability results immediately follow from uniqueness of positive steady states and the sub-supersolution construction ^[42].

Proof of Theorem 3.3: Let $ \gamma_1 > \gamma_1^* > 0 $ and $ \lambda > E_1(\gamma_1, \gamma_2) $. Further, let $ w_{\lambda} = u_{\lambda}(\gamma_1, \gamma_2) $ be the positive solution of:

and $ v_{\lambda} = u_{\lambda}(\gamma_1^*, \gamma_2) $ be the positive solution of:

We claim that $ w_{\lambda} $ is a subsolution of (4.12). To see this, observe that

since $ \gamma_1 > \gamma_1^{*} $. Thus, $ w_{\lambda} $ is a strict subsolution of (4.12). Note that $ Z \equiv 1 $ is a supersolution of (4.12). By Lemma 2.1, (4.12) has a positive solution $ y_{\lambda} $ satisfying $ w_{\lambda} \leq y_{\lambda} \leq 1 $. Since $ w_{\lambda} $ is a strict subsolution of (4.12), it is easy to see that $ w_{\lambda} < y_{\lambda} $. However, since $ v_{\lambda} $ is the unique solution of (4.12), we have $ y_{\lambda} = v_{\lambda} $ and hence $ w_{\lambda} < v_{\lambda} $.

Proof of Theorem 3.4: First we show that if $ \gamma_1 > \gamma_2 $, then $ q_1 < q_2 $. Let $ u_{\lambda} $ be a positive solution of (1.4) with $ \|u_{\lambda}\|_\infty = \rho $, $ u_{\lambda}(0) = q_1 $, and $ u_{\lambda}(1) = q_2 $. Suppose that $ q_1 \geq q_2 $. Combining the equations in (3.2), we obtain $ 2[F(q_1)-F(q_2)] = \gamma_2^2 q_2^2 - \gamma_1^2 q_1^2 $. Since $ F(u) = \int_0^u s(1-s)ds = \frac{1}{2}u^2 - \frac{1}{3}u^3 $ is a strictly increasing function for $ u\in (0, 1) $, we have $ F(q_1) \geq F(q_2) $. This implies that $ \gamma_2^2 q_2^2 - \gamma_1^2 q_1^2 = (\gamma_2q_2 + \gamma_1 q_1)(\gamma_2 q_2 - \gamma_1 q_1) \geq 0 $. Hence, we have $ \gamma_2 q_2 - \gamma_1 q_1 \geq 0 $, or equivalently, $ \frac{\gamma_2}{\gamma_1} \geq \frac{q_1}{q_2} $. This is a contradiction since $ q_1 \geq q_2 $ and $ \gamma_1 > \gamma_2 $. Thus, we have $ q_1 < q_2 $. Similarly we can show that if $ \gamma_1 < \gamma_2 $, then $ q_1 > q_2 $, and if $ \gamma_1 = \gamma_2 $, then $ q_1 = q_2 $.

Second, we provide proofs for Theorems 3.5–3.7 from Case 2.

Proof of Theorem 3.5: This is a special case of Theorem 3.1 where $ q_1 = 0 $.

Proof of Theorem 3.6: First, we establish nonexistence of a positive solution when $ \lambda \leq \tilde{E_1}(\gamma_2) $. Suppose that $ u_{\lambda} $ is a positive solution of (1.5) for $ \lambda \leq \tilde{E_1}(\gamma_2) $. Let $ \tilde{\sigma}_{\lambda}(\gamma_2) $ be the principal eigenvalue and $ \phi_{\lambda} $ be the normalized positive eigenfunction of the eigenvalue problem (2.5) (see proofs of Lemma 2.3, 2.4 and Remark.2). Using integration by parts, we have

By (2.5), we also have

since $ \tilde{\sigma}_{\lambda}(\gamma_2) \geq 0 $ for $ \lambda \leq \tilde{E_1}(\gamma_2) $ by Lemma 2.3. This is a contradiction. Thus, (1.5) has no positive solution when $ \lambda \leq \tilde{E_1}(\gamma_2) $.

Next, we establish existence of a positive solution for $ \lambda > \tilde{E_1}(\gamma_2) $. Let $ \psi_{\lambda} : = \omega \phi_{\lambda} $, where $ \omega > 0 $ is a constant to be chosen later. Then for $ x \in (0, 1) $, we have $ \phi_{\lambda} \Big\{ \tilde{\sigma}_{\lambda}(\gamma_2) + \lambda \omega \phi_{\lambda} \Big\} \leq 0 $ for $ \omega \approx0 $ since $ \tilde{\sigma}_{\lambda}(\gamma_2) < 0 $ for $ \lambda > \tilde{E_1}(\gamma_2) $. This implies that

Also, on the boundary we have $ \psi_{\lambda}(0) = \omega \phi_{\lambda}(0) = 0 $ and $ \psi'(1) + \sqrt{\lambda} \gamma_2 \psi_{\lambda}(1) = \omega \phi'_{\lambda}(1) + \sqrt{\lambda} \gamma_2 \omega \phi_{\lambda}(1) = 0 $. Thus, $ \psi_{\lambda} $ is a subsolution of (1.5) for $ \omega \approx0 $. Further, it is clear that $ Z \equiv 1 $ is a supersolution for (1.5). Hence by Lemma 2.1, (1.5) has a positive solution $ u_\lambda \in [\psi_{\lambda}, Z] $ for $ \lambda > \tilde{E_1}(\gamma_2) $.

We note that the proof of uniqueness of positive solutions for $ \lambda > \tilde{E_1}(\gamma_2) $ is very similar to the proof of the uniqueness in Theorem 3.2. Hence we omit the proof here. Further, following the same argument as in Theorem 3.2, it follows that $ ||u_{\lambda}||_{\infty} \rightarrow 1^{-} $ as $ \lambda \rightarrow \infty $. Finally, we show that $ ||u_{\lambda}||_{\infty} \rightarrow 0 $ as $ \lambda \rightarrow \tilde{E_1}(\gamma_2)^{+} $. We note that Theorem 3.5 together with the facts that (1.5) has no positive solution for $ \lambda \leq \tilde{E_1}(\gamma_2) $ and has a unique positive solution $ u_{\lambda} $ for $ \lambda > \tilde{E_1}(\gamma_2) $ such that $ u_{\lambda} \rightarrow 1^- $ uniformly on compact subsets of $ \Omega $ as $ \lambda \rightarrow \infty $, immediately implying that $ ||u_{\lambda}||_{\infty} \rightarrow 1^{-} $ as $ \lambda \rightarrow \infty $. These facts also establish that $ ||u_{\lambda}||_{\infty} \rightarrow 0 $ as $ \lambda \rightarrow \tilde{E_1}(\gamma_2)^{+} $ since by Theorem 3.5, $ \lambda $ is a continuous function of $ \rho $ on $ (0, 1) $. Hence, the exact bifurcation diagram illustrated in Figure 9 is established.

Proof of Theorem 3.7: This argument is similar to the proof of Theorem 3.3. Hence, we omit the proof.

5.   Conclusions

Fragmentation and loss of natural habitats have driven a widespread decline in terrestrial biodiversity ^[16]. As demands for natural resources and land increase, landscapes will be increasingly altered and fragmented creating spatial heterogeneity ^[2]. Overall, effects of heterogeneity in landscapes and, particularly, matrix have been largely understudied compared with assessments based upon habitat amount or configuration ^[27]. Crucial to the area of conservation research is to what extent does loss of habitat area versus habitat fragmentation per se versus matrix heterogeneity contribute to population viability ^[43]. One of the most important conservation questions to be answered is: how much must be conserved for persistence of a population to be ensured ^[2]? This question is often addressed at the patch-level by determining the minimum patch size necessary to promote a viable population. Modeling studies suggest dependence of minimum patch size on several factors including reproduction rate, emigration rate, population genetics of the organism, and various stochastic factors ^[2]. However, it has become apparent that the "matrix matters" in prediction of population persistence ^[12,13]. A key guide for conservation is a better understanding of the role played by matrix quality in fragmented landscapes ^[13].

In this paper, we have extended an established reaction diffusion modeling framework to model effects of matrix heterogeneity in population persistence at the patch level. This new framework allows for predicting persistence of populations residing in a patch surrounded by a locally heterogenous matrix. Our results give the exact dynamics of a population exhibiting logistic growth, an unbiased random walk in the patch and matrix, habitat preference at the patch/matrix interface, and two functionally different matrix types for a one-dimensional landscape. We show existence of a minimum patch size, below which population persistence is not possible. This MPS can be estimated via empirically derived estimates of patch intrinsic growth rate and diffusion rate, habitat preference, and matrix death and diffusion rates. Mechanistic derivation of MPS allows us to analyze qualitative dependence of MPS on these parameters.

Recently, ecologists have begun focusing more and more attention to matrix habitat quality ^[44,45]. Our theoretical results provide additional support to the notion that local matrix heterogeneity can greatly change model predictions. Asymmetries not found in a locally homogeneous matrix can occur, giving rise to a steady state density profile with peak density closer to the matrix component with less severe combined matrix hostility. This result suggests a test of local matrix heterogeneity. Empirical estimates of density throughout a patch that show peak density near the center of the patch would suggest local matrix homogeneity for that patch. However, asymmetric spatial patterns in the density with a peak closer to one part of the patch/matrix interface would suggest presence of local matrix heterogeneity and suggest further investigation into the cause of the functional differences in matrix components. Our results also suggest that MPS estimates can be much less accurate when local heterogeneity is ignored in the modeling framework. For our one-dimensional landscape system, we have derived an upper bound on the MPS error in making such an assumption. Finally, our results agree with and strengthen previous authors' claims ^[2] that conservation strategies should not only consider patch size, configuration, and quality, but also quality and spatial structure of the surrounding matrix.

Acknowledgments

This work is supported by NSF grants Goddard (DMS-1853372) and Shivaji (DMS-1853352).

Conflict of interest

All authors declare no conflicts of interest in this paper.

Appendix

Proof of Remark 3.2: First, we note that the eigenvalues need to be positive. Now the general solution of the differential equation in (2.1) for $ E > 0 $ is $ \phi(x) = c_1 \cos(\sqrt{E}x) + c_2 \sin(\sqrt{E}x) $, with $ c_1, c_2 $ constants to be determined. Using the boundary conditions, we obtain the following eigenvalue equation:

Assuming $ \gamma_1\gamma_2 \neq 1 $, this becomes

For $ \gamma_1 \gamma_2 > 1 $, we know $ \frac{\gamma_1+\gamma_2}{1-\gamma_1\gamma_2} < 0 $. Hence there exists a unique $ E \in (\frac{\pi^2}{4}, \pi^2) $ such that (A.2) is satisfied. Now, if $ \gamma_1 \gamma_2 < 1 $, we know $ \frac{\gamma_1 \gamma_2}{1-\gamma_1\gamma_2} > 0 $. Hence there exists a unique $ E \in (0, \frac{\pi^2}{4}) $ such that (A.2) is satisfied. In both cases, this shows the existence of the principal eigenvalue. From (A.2), we obtain the following explicit form of the principal eigenvalue:

It follows from (A.1) and (A.3) that $ E_1(\gamma_1, \gamma_2) \rightarrow \frac{\pi^2}{4} $ as $ \gamma_1 \rightarrow \frac{1}{\gamma_2} $, $ E_1 \Big(\frac{1}{\gamma_2} \Big) = \frac{\pi^2}{4} $, and $ E_1(\cdot, \gamma_2) $ is continuous and increasing in $ \gamma_1 $.

Proof of Remark 3.6: Again, we first note that the eigenvalues need to be positive. Now for fixed $ \gamma_2 > 0 $, the general solution of the differential equation in (2.6) for $ E > 0 $ is $ \phi(x) = c_1 \cos(\sqrt{E} x) + c_2 \sin(\sqrt{E} x) $, with $ c_1, c_2 $ constants to be determined. Using the boundary conditions, we obtain the following eigenvalue equation:

Since $ \tan(\sqrt{E}) \in (-\infty, \infty) $ and $ -\frac{1}{\gamma_2} < 0 $, there exists a unique $ E \in (\frac{\pi^2}{4}, \pi^2) $ such that (A.4) is satisfied. This shows the existence of the principal eigenvalue. From (A.4), we obtain its explicit form:

From (A.5), it is easy to see that as $ \gamma_2 \rightarrow 0 $, $ \tilde{E_1}(\gamma_2) \rightarrow \frac{\pi^2}{4} $ and as $ \gamma_2 \rightarrow \infty $, $ \tilde{E_1}(\gamma_2) \rightarrow \pi^2 $. It is also easy to see that $ \tilde{E_1}(\gamma_2) $ is continuous and increasing in $ \gamma_2 $.

Proof of Lemma 2.2: First, we consider the case $ \gamma_1 \gamma_2 \neq 1 $ and establish the existence and uniqueness of the principal eigenvalue $ \sigma_{\lambda}(\gamma_1) $ by an application of the Implicit Function Theorem. Let $ \lambda > 0 $ be fixed with $ \lambda + \sigma > 0 $ in (2.2). Then the general solution of (2.2) has the form $ \phi_\lambda(x) = c_1 \cos(\sqrt{\lambda+\sigma} x) + c_2 \sin(\sqrt{\lambda+\sigma} x) $, where $ c_1 $ and $ c_2 $ are constants. Using the boundary conditions and the fact that $ \lambda+\sigma > 0 $, we obtain the following eigenvalue equation:

Since $ \gamma_1 \gamma_2 \neq 1 $, we obtain an equivalent form of (A.6):

Using (A.7), we define

Note that $ F(E_1(\gamma_1, \gamma_2), 0) = 0 $.

Next, we show that $ F_{\sigma}(E_1(\gamma_1, \gamma_2), 0) > 0 $. A simple calculation will show that

By (A.9), it is easy to see that $ F_{\sigma}(E_1(\gamma_1, \gamma_2), 0) > 0 (\neq 0) $. By the Implicit Function Theorem, there exists $ \varepsilon > 0 $ and a unique $ C^1 $ function $ \sigma(\lambda) = \sigma_{\lambda}(\gamma_1) $ defined on $ I : = (E_1(\gamma_1, \gamma_2)-\varepsilon, E_1(\gamma_1, \gamma_2)+\varepsilon) $ satisfying $ F(\lambda, \sigma(\lambda)) = 0 $ on $ I $ with $ F(E_1(\gamma_1, \gamma_2), 0) = 0 $. This establishes the existence and uniqueness of the principal eigenvalue, $ \sigma_{\lambda} $, of (2.2) as a root of (A.8).

Next, we show that $ F_{\lambda}(E_1(\gamma_1, \gamma_2), 0) > 0 $. Observe that

For $ \lambda = E_1(\gamma_1, \gamma_2) $ and $ \sigma = 0 $, we have

Using the fact that $ F(\lambda, \sigma(\lambda)) = 0 $ on $ \Big(E_1(\gamma_1, \gamma_2)-\varepsilon, E_1(\gamma_1, \gamma_2) +\varepsilon \Big) $ and differentiating (A.8) with respect to $ \lambda $, we have $ F_\lambda +F_\sigma \sigma'(\lambda) = 0 $, which implies $ \sigma'(\lambda) = - \frac{F_\lambda}{F_\sigma} $. Since $ F_\lambda(E_1(\gamma_1, \gamma_2), 0) > 0 $ and $ F_\sigma(E_1(\gamma_1, \gamma_2), 0) > 0 $, it follows that $ \sigma'(E_1(\gamma_1, \gamma_2)) < 0 $. This means $ \sigma(\lambda) $ is decreasing on $ (E_1(\gamma_1, \gamma_2)-\varepsilon, E_1(\gamma_1, \gamma_2)+\varepsilon) $. Therefore, we have $ \sigma(\lambda) < 0 $ for $ \lambda > E_1(\gamma_1, \gamma_2) $ and $ \lambda \approx E_1(\gamma_1, \gamma_2) $, and $ \sigma(\lambda) > 0 $ for $ \lambda < E_1(\gamma_1, \gamma_2) $ and $ \lambda \approx E_1(\gamma_1, \gamma_2) $. Further, it is easy to see that $ \sigma(\lambda) \rightarrow 0 $ as $ \lambda\rightarrow E_1(\gamma_1, \gamma_2) $.

Now we focus on the case when $ \gamma_1\gamma_2 = 1 $. We first show that $ \sigma_{\lambda}(\gamma_1) $ exists and then establish that $ \sigma_{\lambda}(\gamma_1) < 0 $ for $ \lambda > E_1(\gamma_1, \gamma_2) $ and $ \lambda \approx E_1(\gamma_1, \gamma_2) $ and $ \sigma_{\lambda}(\gamma_1) \rightarrow 0 $ as $ \lambda \rightarrow E_1(\gamma_1, \gamma_2)^{+} $. Fix $ \lambda > E_1(\gamma_1, \gamma_2) $ such that $ \lambda = \frac{\pi^2}{4} + \eta $ where $ \eta > 0 $ and $ \eta \approx 0 $. Setting $ \gamma_1 \gamma_2 = 1 $ in (A.6), we obtain a new eigenvalue equation:

Let $ g(\sigma) = \tan(\sqrt{\frac{\pi^2}{4}+\eta+\sigma}) $ and $ h(\sigma) = \Big[ (\gamma_1+\gamma_2)\sqrt{\frac{\pi^2}{4}+\eta} \Big] \frac{\sqrt{\frac{\pi^2}{4}+\eta+\sigma}}{\sigma} $, defined for $ \sigma \in [-\frac{\pi^2}{4}-\eta, \infty) $, with the exception of singularities. Note that $ g $ has its first singularity when $ \sqrt{\lambda+\sigma} = \frac{\pi}{2} $, or equivalently, when $ \sigma = -\eta $. Also, since $ g $ is increasing on $ [-\frac{\pi^2}{4}-\eta, -\eta) $ with $ g(\sigma) > 0 $ and $ h $ is decreasing on $ [-\frac{\pi^2}{4}-\eta, -\eta) $, with $ h(\sigma) < 0 $, we know $ g(s) \neq h(s) $ for $ \sigma \in [-\frac{\pi^2}{4}-\eta, -\eta) $. This means no eigenvalue exists on this interval (see Figure A1).

Next, observe that $ g $ is increasing on $ (-\eta, 0) $ and $ g(\sigma) \rightarrow -\infty $ as $ \sigma \rightarrow -\eta^+ $. We also have $ h(-\eta) < 0 $, $ h $ is decreasing on $ (-\eta, 0) $ and $ h(\sigma) \rightarrow -\infty $ as $ \sigma \rightarrow 0^- $. This implies that (A.10) has a unique minimum solution on $ (-\eta, 0) $. Thus, (2.2) has a unique principal eigenvalue $ \sigma_\lambda(\gamma_1, \gamma_2)(<0) $. It is easy to see that $ \sigma_\lambda(\gamma_1, \gamma_2) \rightarrow 0 $ as $ \lambda \rightarrow \frac{\pi^2}{4}^+ $. Thus, we have $ \sigma_\lambda(\gamma_1, \gamma_2) \rightarrow 0 $ as $ \lambda \rightarrow E_1(\gamma_1, \gamma_2)^{+} $. A similar argument will show that $ \sigma_{\lambda}(\gamma_1) > 0 $ for $ \lambda < E_1(\gamma_1, \gamma_2) $ and $ \lambda \approx E_1(\gamma_1, \gamma_2) $ and $ \sigma_{\lambda}(\gamma_1) \rightarrow 0 $ as $ \lambda \rightarrow E_1(\gamma_1, \gamma_2)^{-} $.

Remark.1. We note that the eigenfunction, $ \phi_\lambda(x) $, corresponding to (2.2) is given by

Setting $ \lambda = E_1(\gamma_1, \gamma_2) $ and $ \sigma_{\lambda}(\gamma_1) = 0 $, it follows that

Using the value of $ E_1(\gamma_1, \gamma_2) $ in the case $ \gamma_1\gamma_2 \neq 1 $, it is not hard to see that $ \phi_\lambda(x) > 0 $ when $ \lambda = E_1(\gamma_1, \gamma_2) $ and $ \sigma_{\lambda}(\gamma_1) = 0 $. By continuity, we have $ \phi_\lambda > 0 $ for $ \lambda \approx E_1(\gamma_1, \gamma_2) $.

Proof of Lemma 2.3: Denote $ \beta = \beta(\mu) $ as the principal eigenvalue of (2.3) with corresponding eigenfunction $ \phi $, chosen such that $ \phi (x) > 0;\ \Omega $. We denote $ \phi_\mu $ as the derivative of $ \phi $ with respect to $ \mu $ for fixed $ x $ and use $ ' $ to denote differentiation with respect to $ x $ for fixed $ \mu $. However, we denote $ \beta'(\mu) $ as differentiation of $ \beta $ with respect to $ \mu $. Now, differentiating (2.3) with respect to $ \mu $ yields

Next, we calculate $ \beta'(\mu) $ for any $ \mu > 0 $. By Green's Second Identity and the fact that $ \phi(\mu)(0) = \phi_\mu(0) = 0 $, we have that

From (2.3) and (A.11), we obtain

and

Combining (A.13) and (A.14) gives

Thus, $ \beta(\mu) $ is increasing in $ \mu $ for $ \mu > 0 $.

Green's First Identity and (2.3) yields

We also have

Combining (A.16) and (A.17), we have that

Now by (A.15) and (A.18) we obtain

which implies that

for $ \mu > 0 $. Thus, $ \beta $ is a concave function of $ \mu $ for $ \mu > 0 $.

Now let $ \beta(\mu) = [m(\mu)]^2 $ in (2.3), where $ m > 0 $. We note that the general solution of (2.3) has the form $ \phi(x) = c_1 \cos(mx) + c_2 \sin(mx) $, where $ c_1 $ and $ c_2 $ are constants. Using the boundary conditions and the fact that $ m > 0 $, we obtain the following eigenvalue equation:

or equivalently,

Since we are interested in the principal eigenvalue $ \beta(\mu) $ for $ \mu > 0 $, we have $ m \in (\frac{\pi}{2}, \pi) $. Define $ j(m) = m\cot(m) $ for $ m \in (\frac{\pi}{2}, \pi) $. It is easy to see that $ j $ is decreasing, continuous, $ j(\frac{\pi}{2}) = 0 $ and $ \lim\limits_{m \rightarrow \pi} j(m) = -\infty $. Thus, for each $ \mu > 0 $, there exists a unique $ m \in (\frac{\pi}{2}, \pi) $, or equivalently, $ \beta(\mu) \in (\frac{\pi^2}{4}, \pi^2) $ which satisfies (A.22). This implies that $ \lim\limits_{\mu\rightarrow \infty}\beta(\mu) = E^D_1 = \pi^2 $.

Proof of Lemma 2.4: Observe in Figure A2 that $ \tilde{E_1}(\gamma_2) $ is the $ y $-coordinate of the intersection of $ \beta(\mu) $ and $ \frac{\mu^2}{\gamma_2^2}. $ Recall that $ \frac{\pi^2}{4} < \tilde{E_1}(\gamma_2) < \pi^2 $ for $ \gamma_2 > 0 $. Let $ \lambda > E_1(\gamma_2) $ be fixed. Observe $ \frac{\mu^2}{\gamma_2^2} = \lambda $ when $ \mu = \sqrt{\lambda} \gamma_2 $. Note that $ \beta(\sqrt{\lambda}\gamma_2) = \lambda + \tilde{\sigma_{\lambda}}(\gamma_2) $. In Figure A2, we see that $ \gamma_2\sqrt{\lambda} > \gamma_2 \sqrt{\tilde{E_1}(\gamma_2)} $, therefore, $ \beta(\gamma_2\sqrt{\lambda}) < \lambda $. Then we have $ \lambda + \tilde{\sigma}_{\lambda}(\gamma_2) < \lambda $ which implies $ \tilde{\sigma}_{\lambda}(\gamma_2) < 0 $. Using a similar argument and the geometry of Figure A2 we can show that $ \tilde{\sigma}_{\lambda}(\gamma_2) > 0 $ when $ \lambda < \tilde{E_1}(\gamma_2) $ and $ \tilde{\sigma}_\lambda(\gamma_2) \rightarrow 0 $ as $ \lambda\rightarrow \tilde{E_1}(\gamma_2) $.

Remark.2. The eigenfunction corresponding to (2.5) is $ \phi_{\lambda}(x) = \sin(\sqrt{\lambda+\tilde{\sigma}_{\lambda}(\gamma_2)}x) $. By Figure A2 we have $ \frac{\pi}{2} < \sqrt{\tilde{E_1}(\gamma_2)} < \sqrt{\lambda+\tilde{\sigma}_{\lambda}(\gamma_2)} < \pi $. For $ x \in (0, 1) $, this implies $ 0 < \sqrt{\lambda+\tilde{\sigma}_{\lambda}(\gamma_2)}x < \pi $. On the interval $ (0, \pi) $, the sine function is positive, hence $ \phi_{\lambda} > 0 $.